Similar presentations:
Модуль числа. Решение уравнений и неравенств, содержащих модуль
1. Модуль числа. Решение уравнений и неравенств, содержащих модуль.
Составила учитель математикиПривалова М.В.
2. 1.Понятие модуля числа
a, если a ≥ 0|a|=
-a, если a<0
Примеры:
1) |3|=3
2) |1/5|=1/5
3) |-1|=-(-1)=1
4) |-10|=-(-10)=10
5) |0|=0
Модулем действительного
числа а называется само
это число, если оно
неотрицательное, и
противоположное ему
число, если данное число
отрицательно.
Из определения модуля следует:
1) |a| ≥0
2) |a|= |-a|
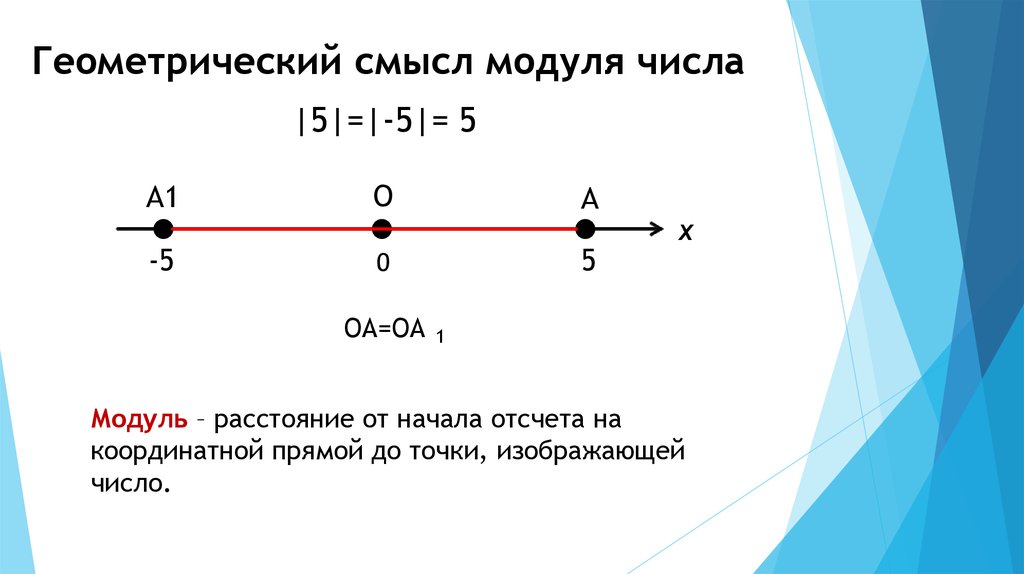
3. Геометрический смысл модуля числа
|5|=|-5|= 5A1
O
A
-5
0
5
OA=OA
x
1
Модуль – расстояние от начала отсчета на
координатной прямой до точки, изображающей
число.
4.
2.Уравнения, содержащие неизвестноепод знаком модуля
Примеры:
а)|х|=7 (в учебнике)
б)|х+1|=3
в)|3х+2|=1 (в учебнике)
5.
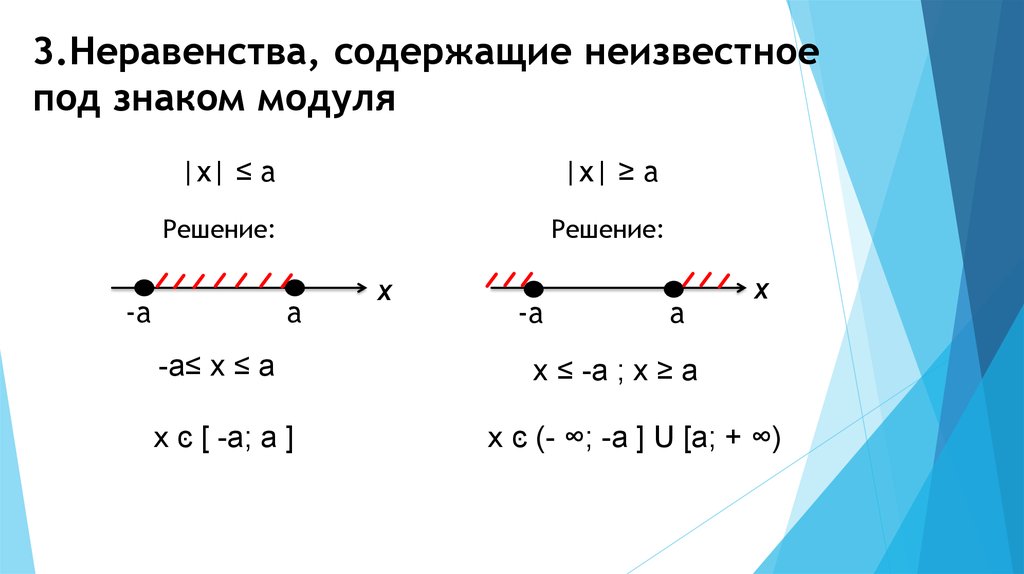
3.Неравенства, содержащие неизвестноепод знаком модуля
|х| ≤ a
|х| ≥ a
Решение:
Решение:
-a
a
-a≤ х ≤ a
x ͼ [ -a; a ]
x
-a
a
x
х ≤ -a ; x ≥ a
x ͼ (- ∞; -a ] U [a; + ∞)
6.
Решите неравенства1.|х|<7
-7< х < 7
2. |х|>6
х<-6; х>6
3.|х-6|<5
-5< х-6 <5
1< х <11
4.|х+5|≥ 2
х+5≤-2
х+5≥2
x ≤ -2 -5
х ≥ 2-5
х ≤ -7
х ≥ -3
5.|6х+1|<2
-2<6х+1<2
-3<6х<1
-1/2 <х< 1/6
7. Домашнее задание.
§10(учить определения),№ (на доске)





 mathematics
mathematics








