Similar presentations:
Выражения, уравнения и неравенства, содержащие модуль
1. Выражения, уравнения и неравенства, содержащие модуль.
ВЫРАЖЕНИЯ, УРАВНЕНИЯИ НЕРАВЕНСТВА,
СОДЕРЖАЩИЕ МОДУЛЬ.
2.
Модулем (абсолютной величиной) действительного числа аназывается само это число, если а
, и противоположное
число –а, если а 0. Модуль числа а обозначается . Итак,
=
Геометрически модулем числа а называют расстояние (в
единичных отрезках) от начала координат до точки А(а).
Свойства модулей:
1.
2.
3.
=
4.
5.
3. Модуль в выражениях
МОДУЛЬ В ВЫРАЖЕНИЯХЗадание №1
Раскроем модуль в выражении
Рассуждаем так:
Если 2х-4
, т.е. х
, то
Если 2х-4
, т.е. х
, то
.
.
Эти рассуждения записываем коротко с помощью
формулы:
4.
Задание №2Упростим выражение:
Решение.
Воспользуемся тождеством
=
=
+1
( т. к.
=
=2
,а1
.
).
5. Уравнения, содержащие переменную под знаком модуля.
УРАВНЕНИЯ, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮПОД ЗНАКОМ МОДУЛЯ.
Решим уравнение:
.
Аналитическое решение
I способ «Определение модуля»
Рассуждать будем, исходя из определения модуля.
Если х-2
, то уравнение примет вид: х-2=3
Если х-2
, то уравнение примет вид: х-2=-3
Таким образом, получаем, либо х-2=3, либо х-2=-3
Решение уравнения можно записать так:
х-2=3
х=5
х-2= 3,
Ответ: х1=5, х2=
х=
6. II способ «Метод интервалов»
II СПОСОБ «МЕТОД ИНТЕРВАЛОВ»1. Установим при каких значениях х модуль равен
нулю:
х-2=0, х=2
2. Получим два промежутка: (
и (2; + , на
каждом из которых решим уравнение. Получим две
смешанных системы:
1)
2)
Решив первую систему, получим х=
Решив вторую систему, получим х=5
Ответ: х1=5, х2=
(
(2; +
.
.
7. Графический способ
ГРАФИЧЕСКИЙ СПОСОБРешим графически уравнение
.
Строим графики функций:y=
и y=3.
а) для построения графика функции y=
, построим график
функции y=x 2- это прямая, пересекающая ось ОХ в точке (2; 0) а
ось OY в точке
(0; 2). Затем часть прямой, лежащую ниже оси ОХ зеркально
отобразим относительно оси ОХ.
б)
график функции y=3- прямая, параллельная оси ОХ и
проходящая через точку (0; 3) на оси OY.
Абсциссы точек пересечения графиков функций дадут решения
уравнения. Прямая y=3 пересеклась с графиков функции y=
в
точках с
координатами (-1; 3) и (5; 3), следовательно, решениями уравнения
будут абсциссы точек: х=
Ответ: х1=5, х2=
8.
9. Решим уравнение:
РЕШИМ УРАВНЕНИЕ:Поскольку в левой части модуль, а в правой части –
выражение, содержащее переменную, необходимо
потребовать
чтобы
это
выражение
было
неотрицательным. Получим две смешанных системы:
и
Решим каждую систему:
, х= .
1)
2)
,
х= 2
Ответ: х1=
, х2= .
10. Решим уравнение
РЕШИМ УРАВНЕНИЕСправа 1-const. Раскрываем последовательно внешний
модуль:
2-
3-2
х=
2-
3-2
=
х=
Ответ: -3,-2,-1,0,1,2,3.
3-2
х=0
3-2
х=
11. Итак,
ИТАК,мы рассмотрели уравнения трех типов:
I тип:
,
II тип:
,
III тип:
.
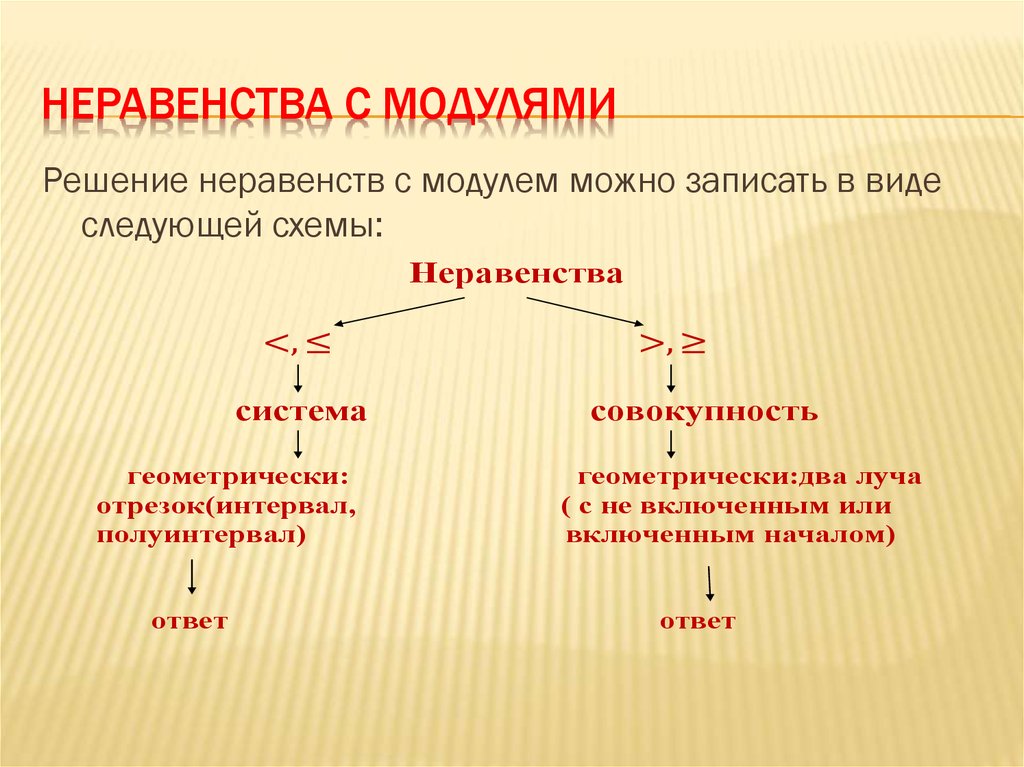
12. Неравенства с модулями
НЕРАВЕНСТВА С МОДУЛЯМИРешение неравенств с модулем можно записать в виде
следующей схемы:
Неравенства
система
геометрически:
отрезок(интервал,
полуинтервал)
ответ
совокупность
геометрически:два луча
( с не включенным или
включенным началом)
ответ
13. Решим неравенства:
РЕШИМ НЕРАВЕНСТВА:Пример №1
2х-1 3,
2х-1
х
,
х -1
Пример №2
2х-1
2х-1
,
х
Ответ: (-1;2)
Ответ: (
х
х
,
14. Решим неравенство:
РЕШИМ НЕРАВЕНСТВО:Возведем обе части неравенства в квадрат,
получим
неравенство
4х2-4х+1 9х2+6х+1,
5х2+10х
,
х(х+2) 0, откуда находим х
.
Ответ: х
.
,
15. Решим неравенство:
РЕШИМ НЕРАВЕНСТВО:.
1)Приравниваем к нулю выражения, стоящие под знаком модуля
х-3=0,
х+2=0,
х=3.
х=
.
2)Решим неравенство на следующих промежутках:
[3;+
.
а) Если х
, то неравенство примет вид –
х
.
(
[
,
, т. е.
Из соотношений х
следует, что х
является
решением данного неравенства.
б) Если -2
, то неравенство примет вид –х+3+х+2-х
, т.е. х
.
Из соотношений -2
, следует, что -2
является
решением данного неравенства.
в) Если х
, то неравенство примет вид х-3+х+2-х
, т.е. х
, что и
является решением данного неравенства.
Объединив найденные решения данного неравенства на различных
промежутках, получим решение неравенства: (
;0)
(6; +
.
Ответ: (
;0)
(6; +
.















 mathematics
mathematics








