Сложение векторов

1. Сложение векторов

2. Домашнее задание:

п.79- 81 – читать, записать в тетрадь
Правила и Законы из презентации
Вопросы 1-11 (стр.213-214) - письменно
№ 754, 755, 759
2

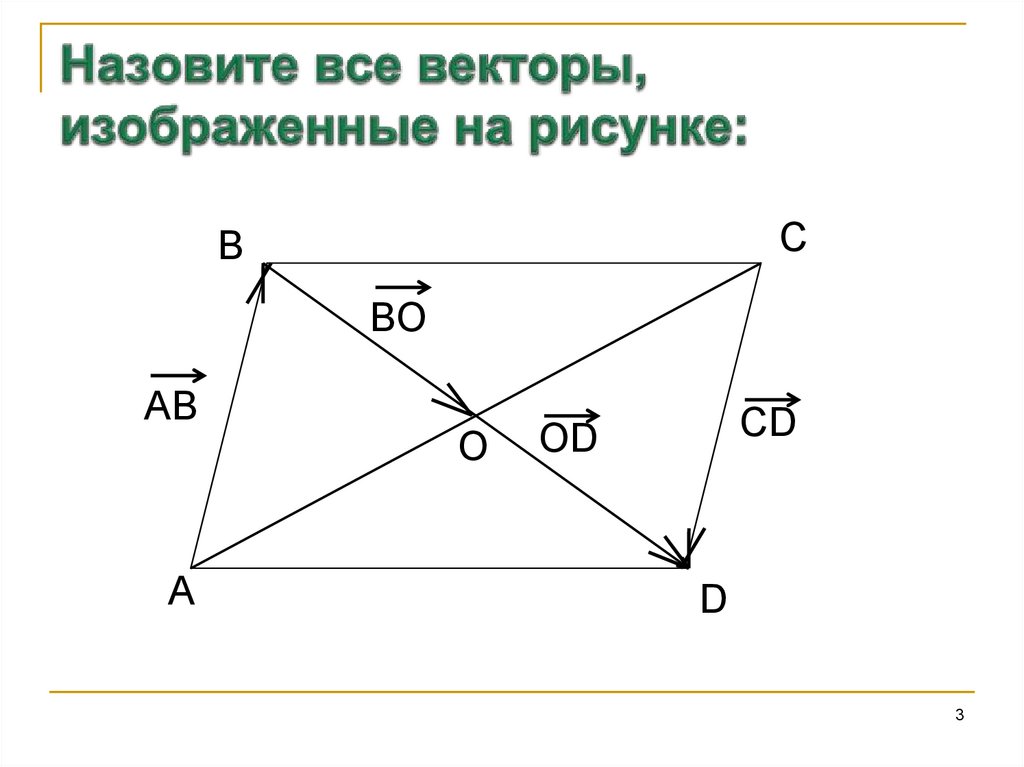
3. Назовите все векторы, изображенные на рисунке:

C
B
BO
AB
O
A
CD
OD
D
3

4. Среди изображенных на рисунке векторов укажите коллинеарные:

C
B
O
A
D
4

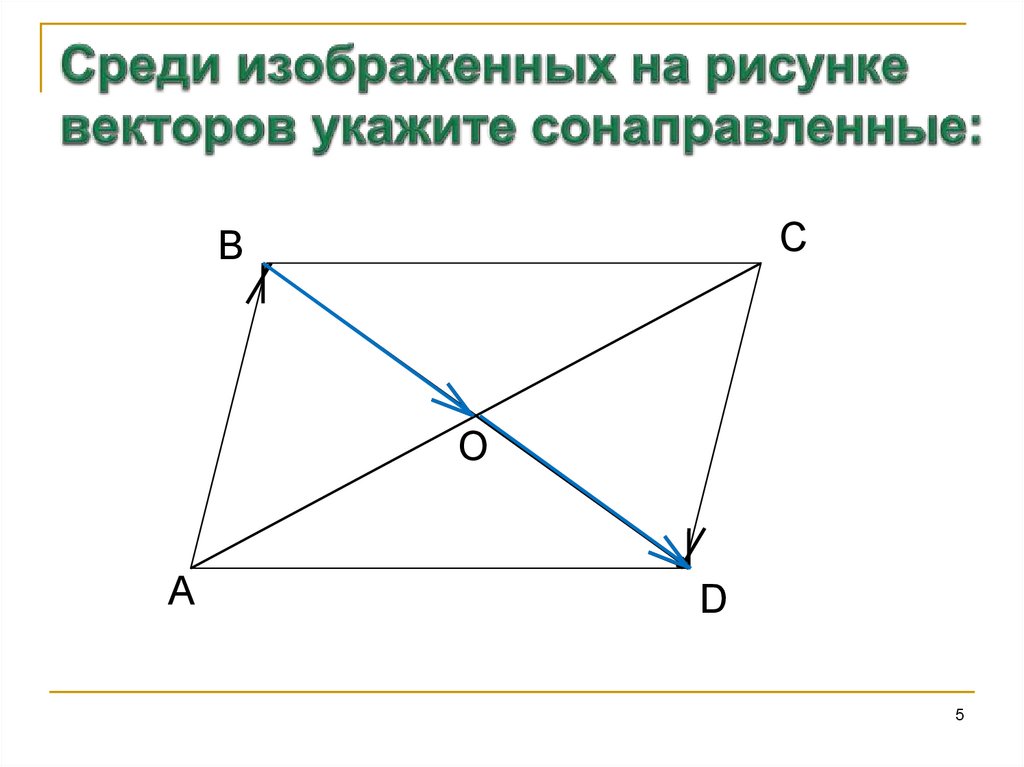
5. Среди изображенных на рисунке векторов укажите сонаправленные:

C
B
O
A
D
5

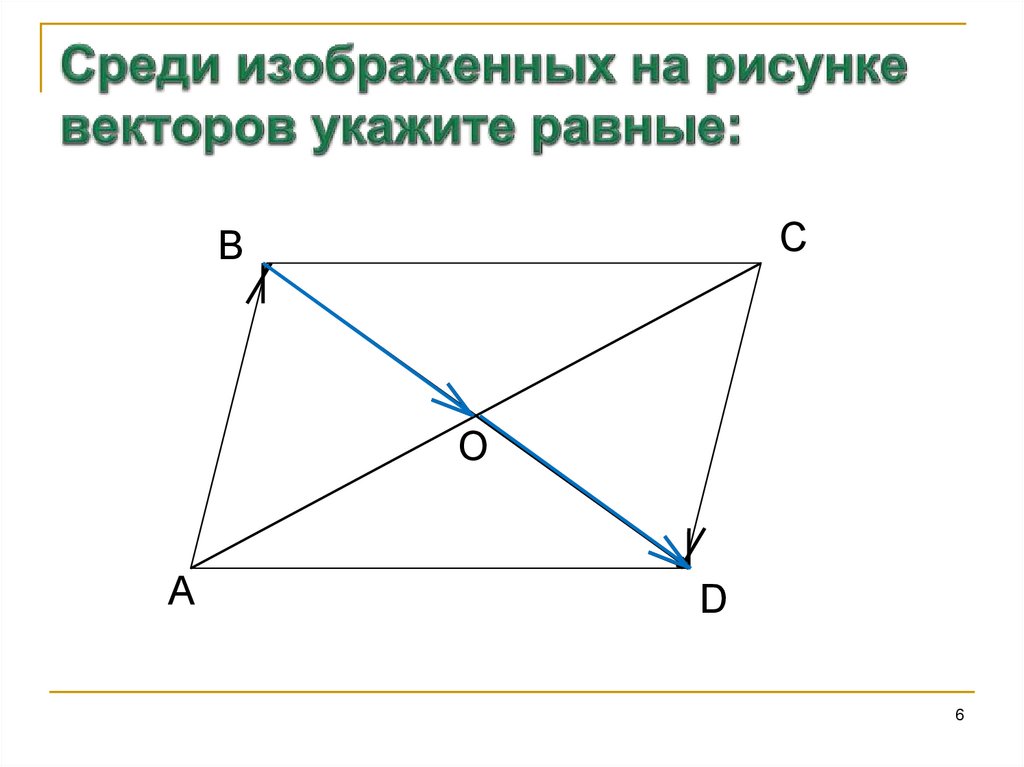
6. Среди изображенных на рисунке векторов укажите равные:

C
B
O
A
D
6

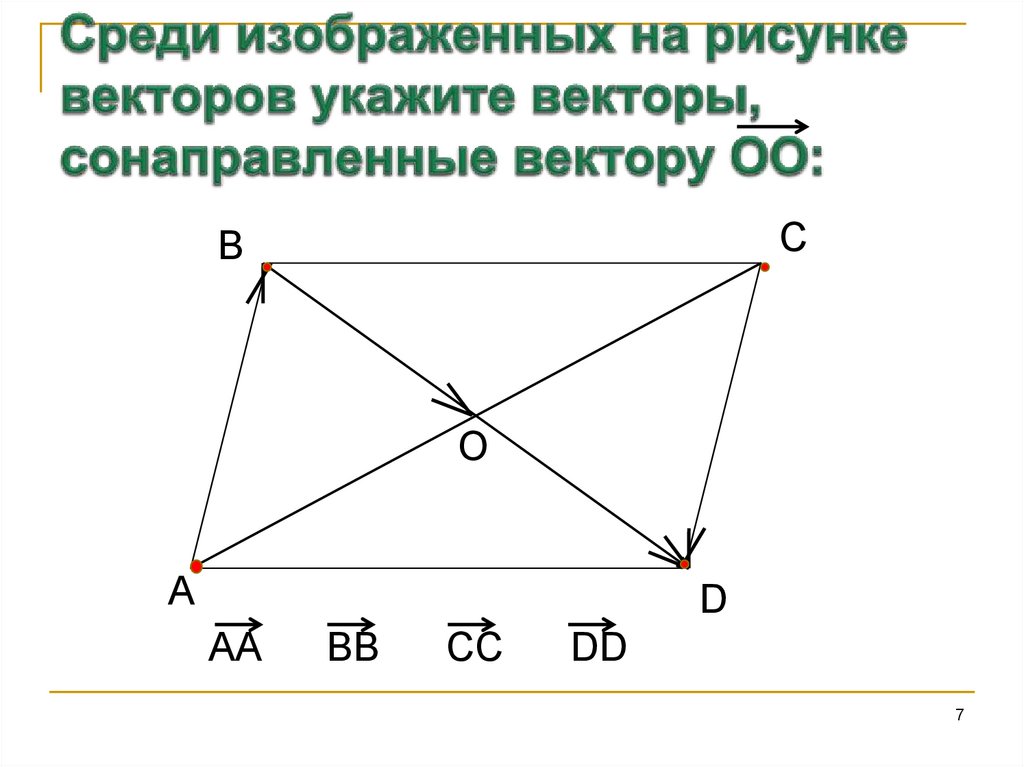
7. Среди изображенных на рисунке векторов укажите векторы, сонаправленные вектору ОО:

C
B
O
A
D
AA
BB
CC
DD
7

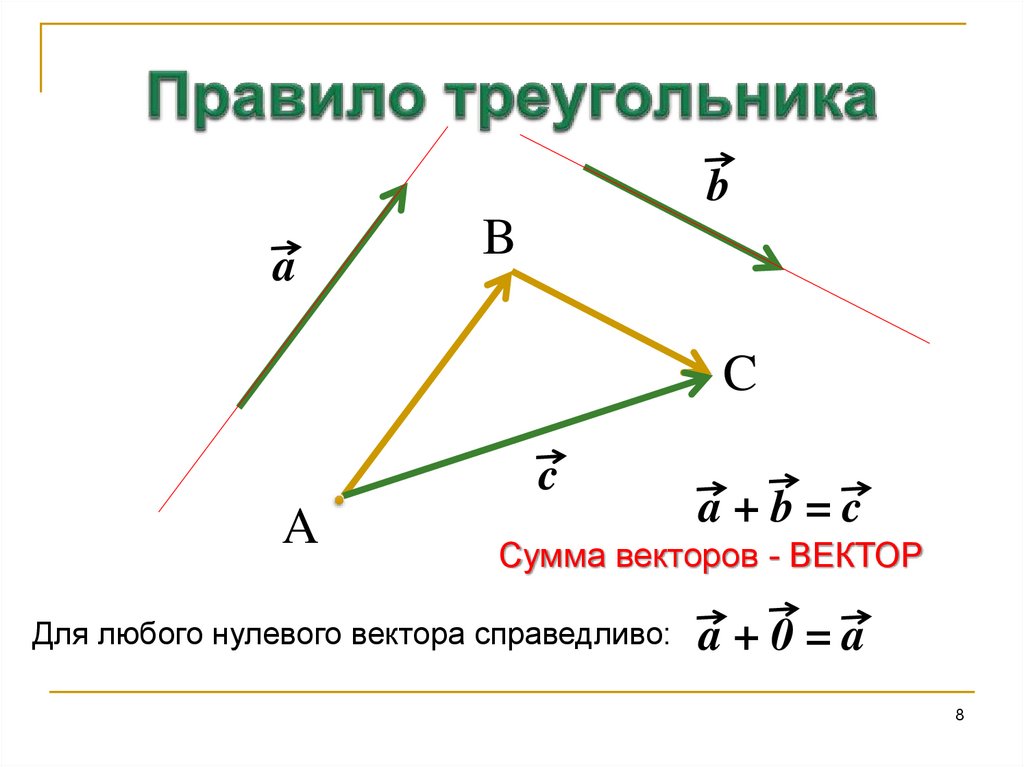
8. Правило треугольника

b
a
B
C
c
A
a+b=c
Сумма векторов - ВЕКТОР
Для любого нулевого вектора справедливо:
a+0=a
8

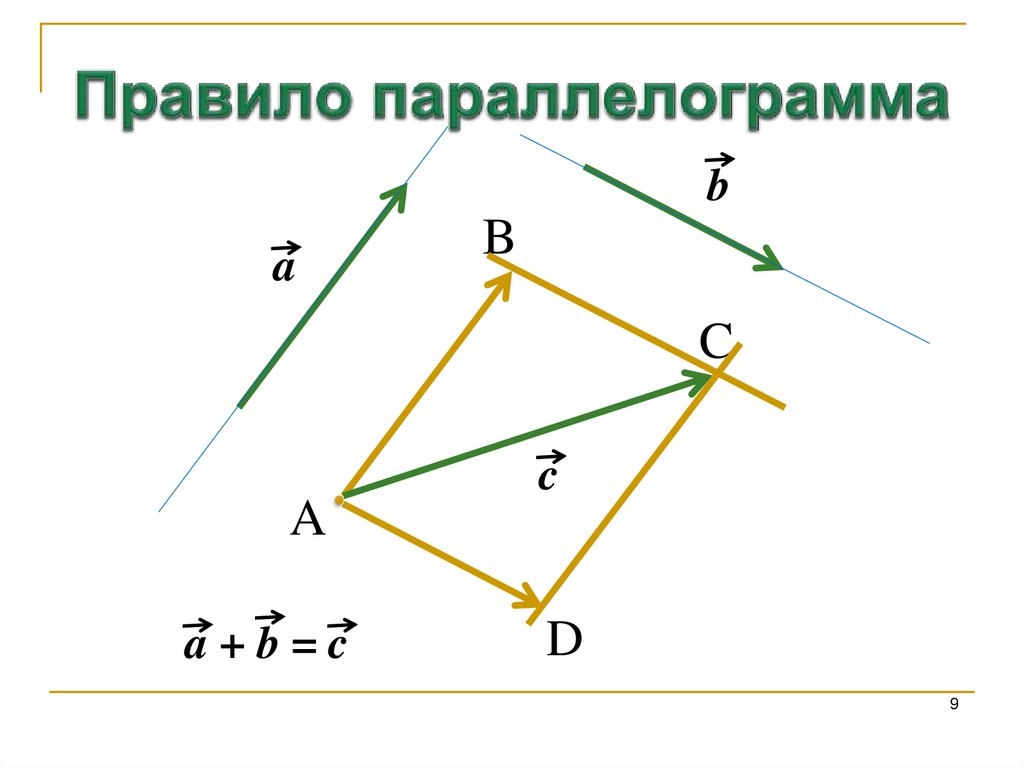
9. Правило параллелограмма

b
a
B
C
c
A
a+b=c
D
9

10.

B
C
C
c
A
c
A
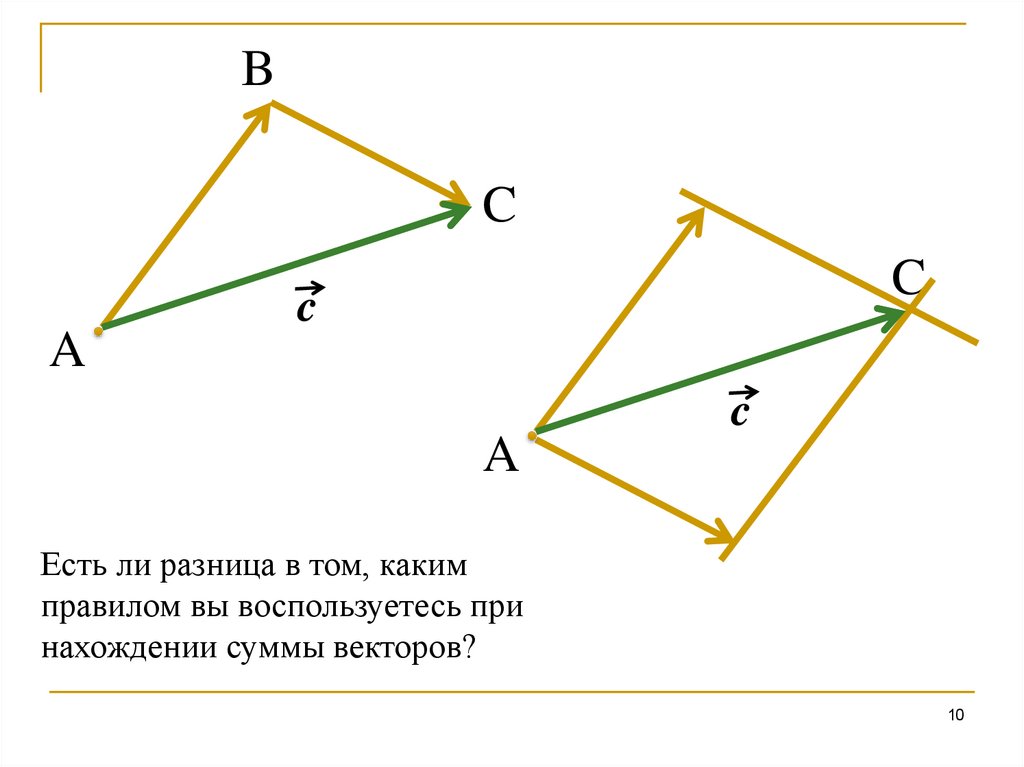
Есть ли разница в том, каким
правилом вы воспользуетесь при
нахождении суммы векторов?
10

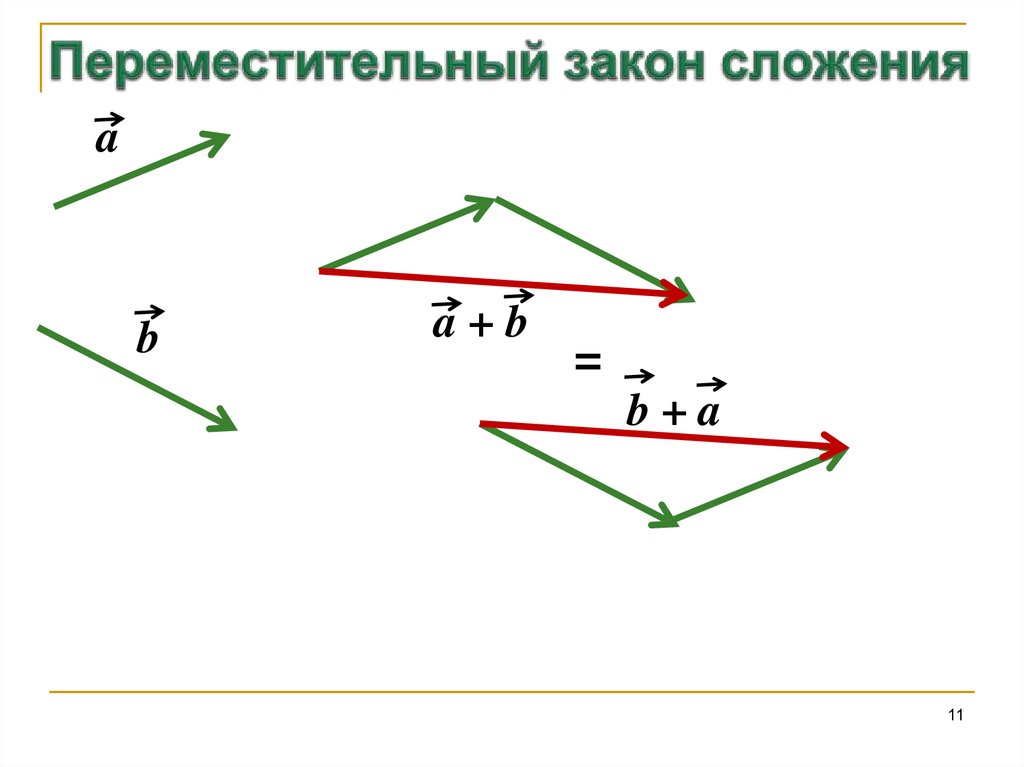
11. Переместительный закон сложения

a
b
a+b
=
b+a
11

12.

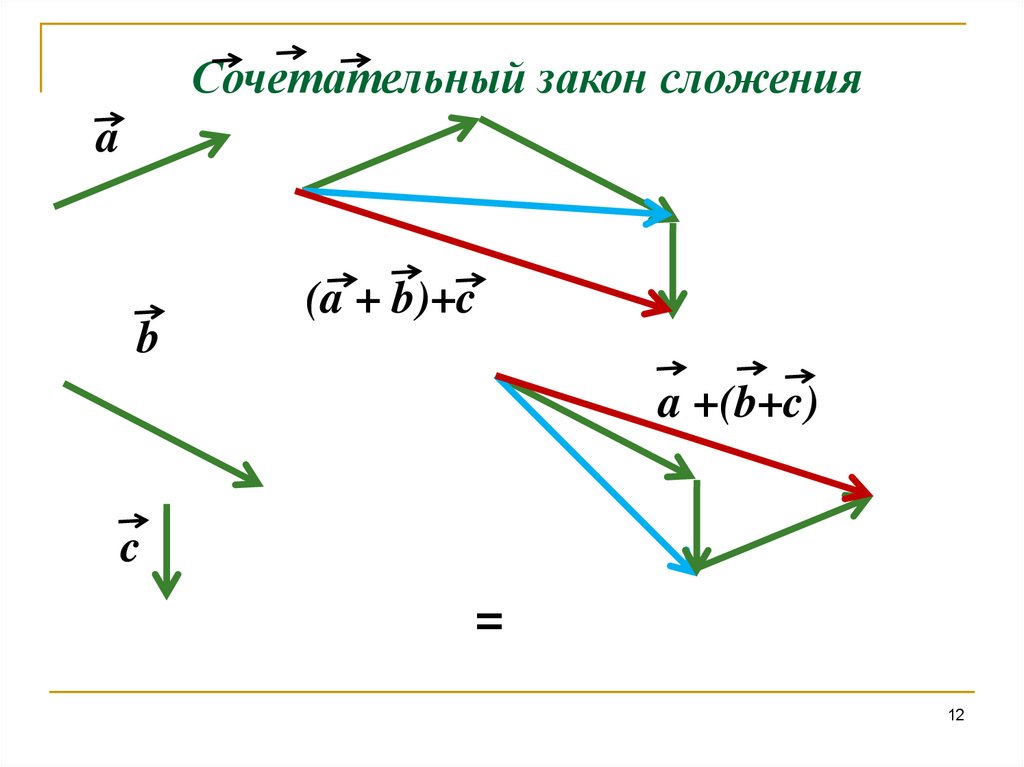
Сочетательный закон сложения
a
b
(a + b)+c
a +(b+c)
c
=
12

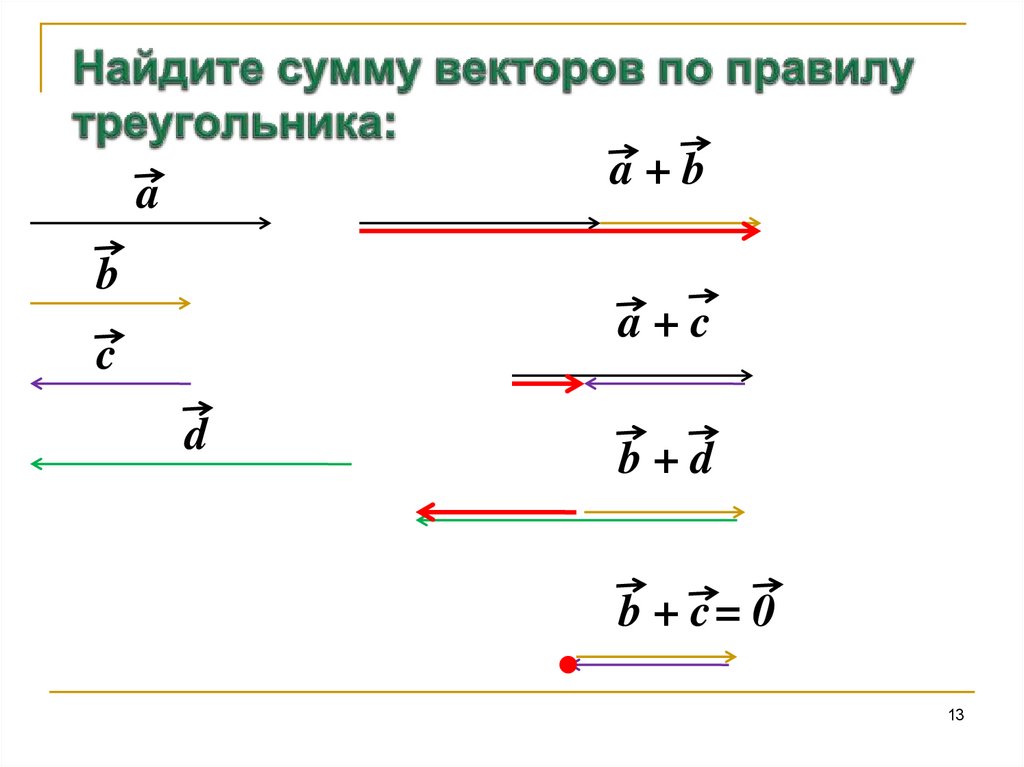
13. Найдите сумму векторов по правилу треугольника:

a+b
a
b
a+c
c
d
b+d
b + c= 0
13

14. Сумма нескольких векторов

Правило многоугольника
s= a+ b+ c+ d+ e+ f
m
d
c
n
r
b
e
a
f
s
k
O
p
k+n+m+r+p=0

15.

А) PM+MT=PT
Б) CH+HC=CC
В) AВ+ 0 =AB+BB=AB
Г) 0+ CE =CC+CE=CE
15

16. Итог урока

Какие правила можно использовать для
нахождения суммы векторов?
Какова последовательность выполнения при
использовании этих правил?
Есть ли разница в том, каким правилом вы
воспользуетесь при нахождении суммы векторов?
Что можно сказать при сложении ненулевого
вектора с нулевым?
16