Similar presentations:
Сложение векторов
1. Сложение векторов
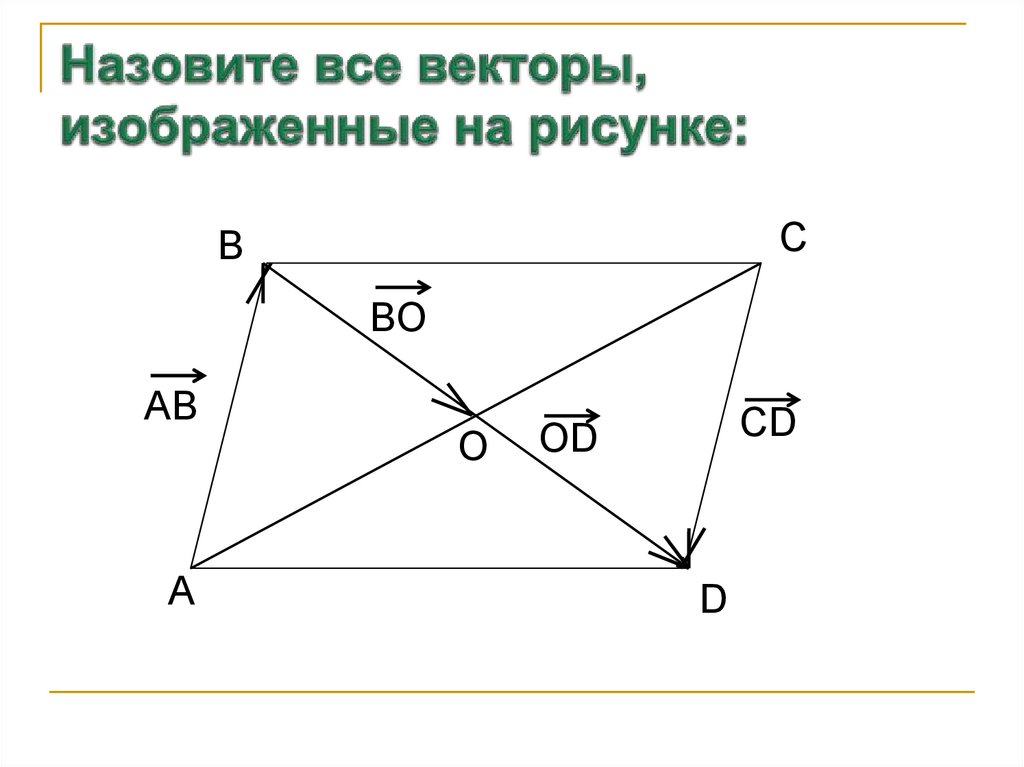
09.11.2021 г.2. Назовите все векторы, изображенные на рисунке:
CB
BO
AB
O
A
CD
OD
D
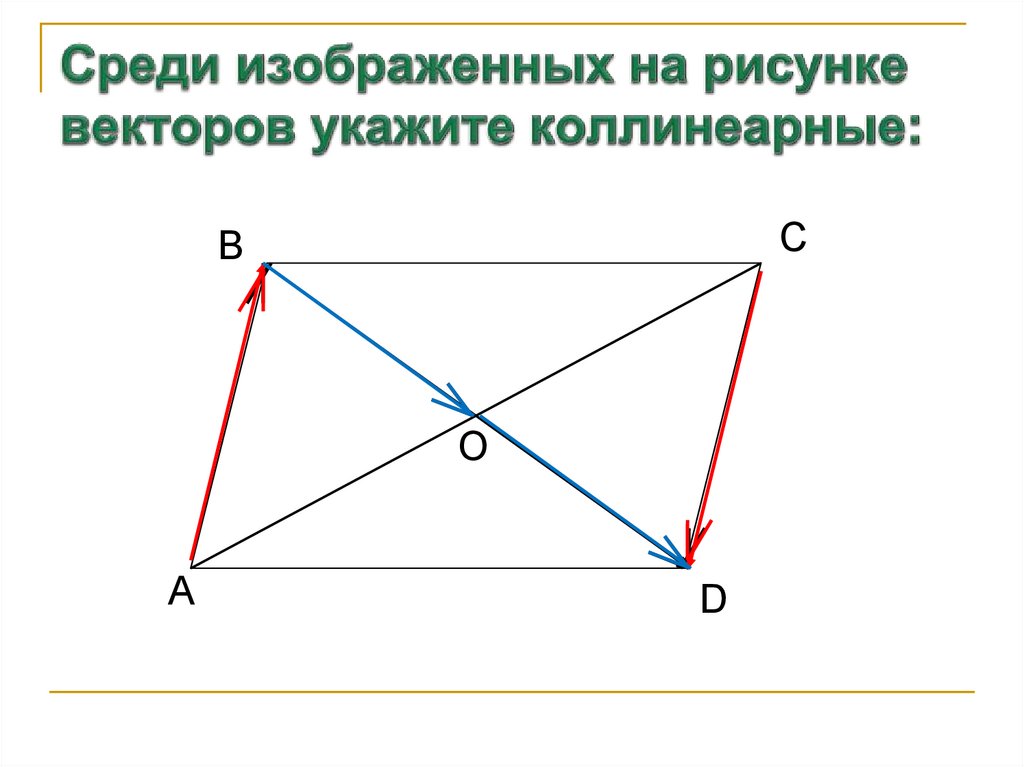
3. Среди изображенных на рисунке векторов укажите коллинеарные:
CB
O
A
D
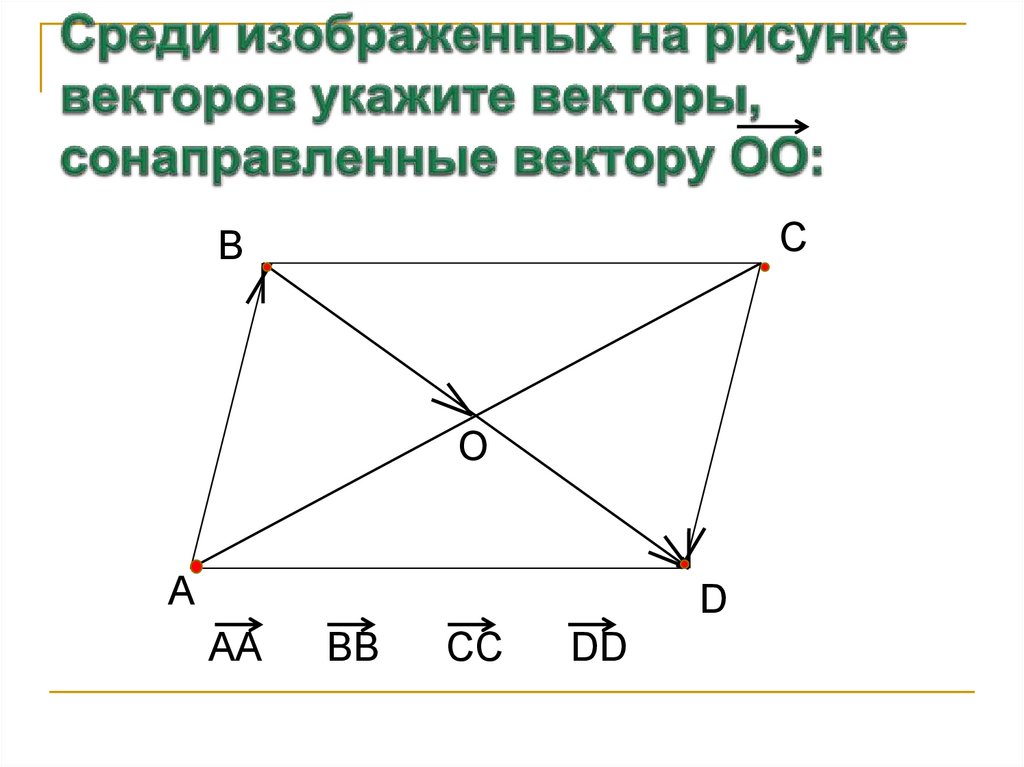
4. Среди изображенных на рисунке векторов укажите векторы, сонаправленные вектору ОО:
CB
O
A
D
AA
BB
CC
DD
5.
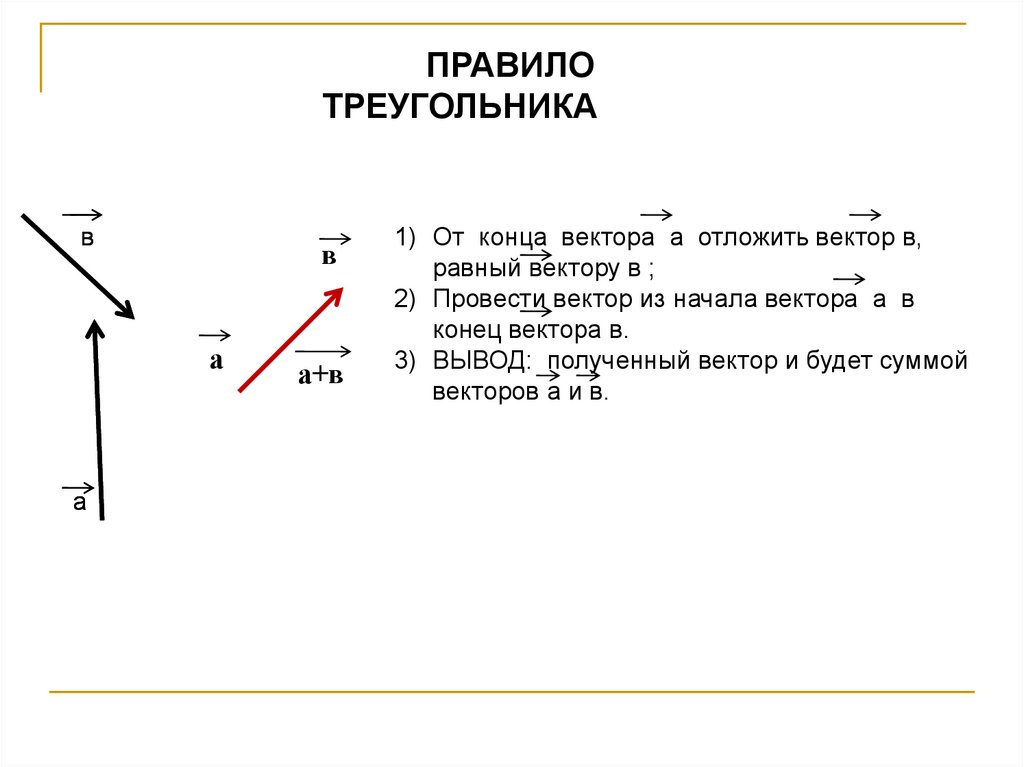
ПРАВИЛОТРЕУГОЛЬНИКА
в
в
а
а
а+в
1) От конца вектора а отложить вектор в,
равный вектору в ;
2) Провести вектор из начала вектора а в
конец вектора в.
3) ВЫВОД: полученный вектор и будет суммой
векторов а и в.
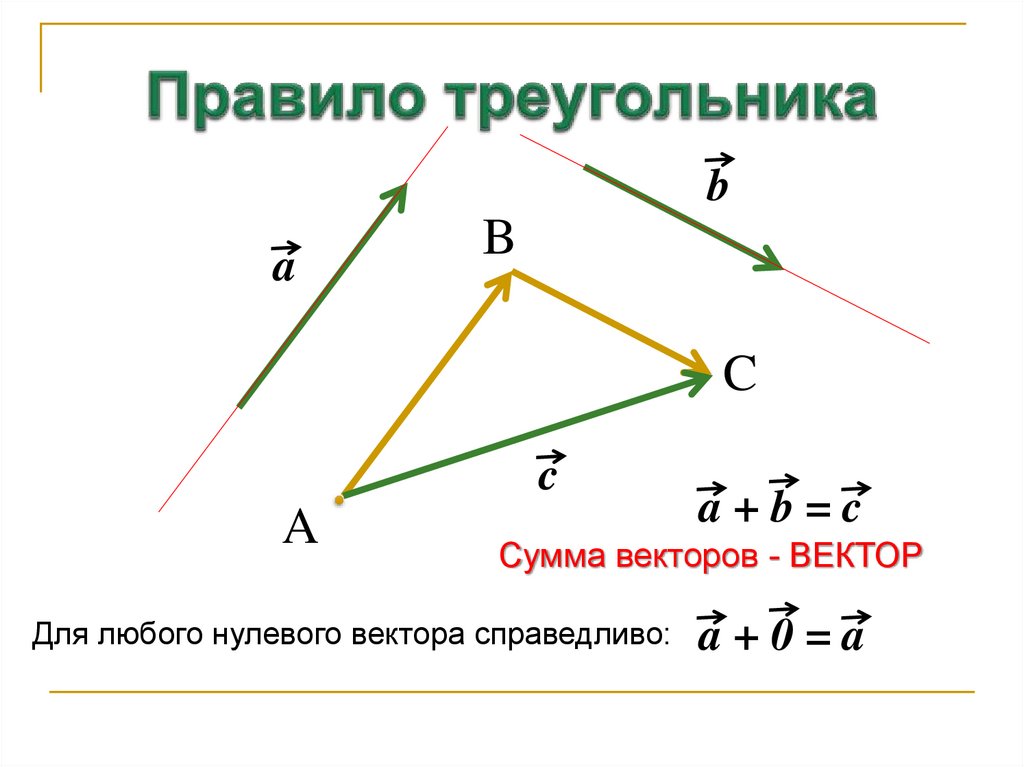
6. Правило треугольника
ba
B
C
c
A
a+b=c
Сумма векторов - ВЕКТОР
Для любого нулевого вектора справедливо:
a+0=a
7.
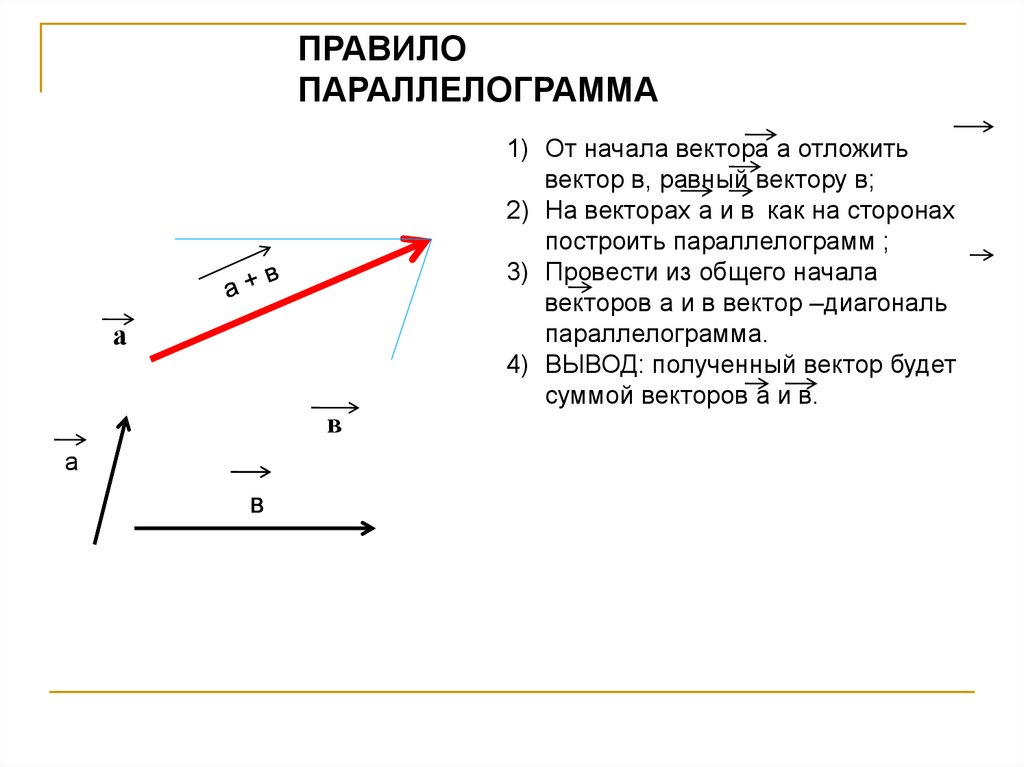
ПРАВИЛОПАРАЛЛЕЛОГРАММА
а
в
а
в
1) От начала вектора а отложить
вектор в, равный вектору в;
2) На векторах а и в как на сторонах
построить параллелограмм ;
3) Провести из общего начала
векторов а и в вектор –диагональ
параллелограмма.
4) ВЫВОД: полученный вектор будет
суммой векторов а и в.
8. Правило параллелограмма
ba
B
C
c
A
a+b=c
D
9.
BC
C
c
A
c
A
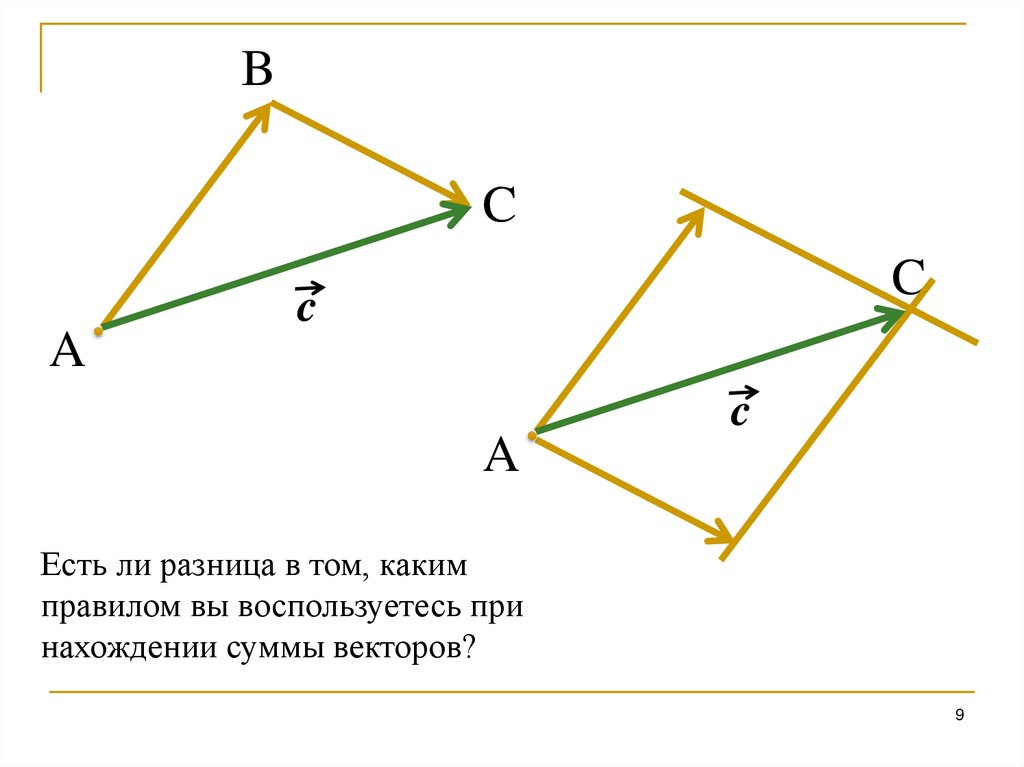
Есть ли разница в том, каким
правилом вы воспользуетесь при
нахождении суммы векторов?
9
10.
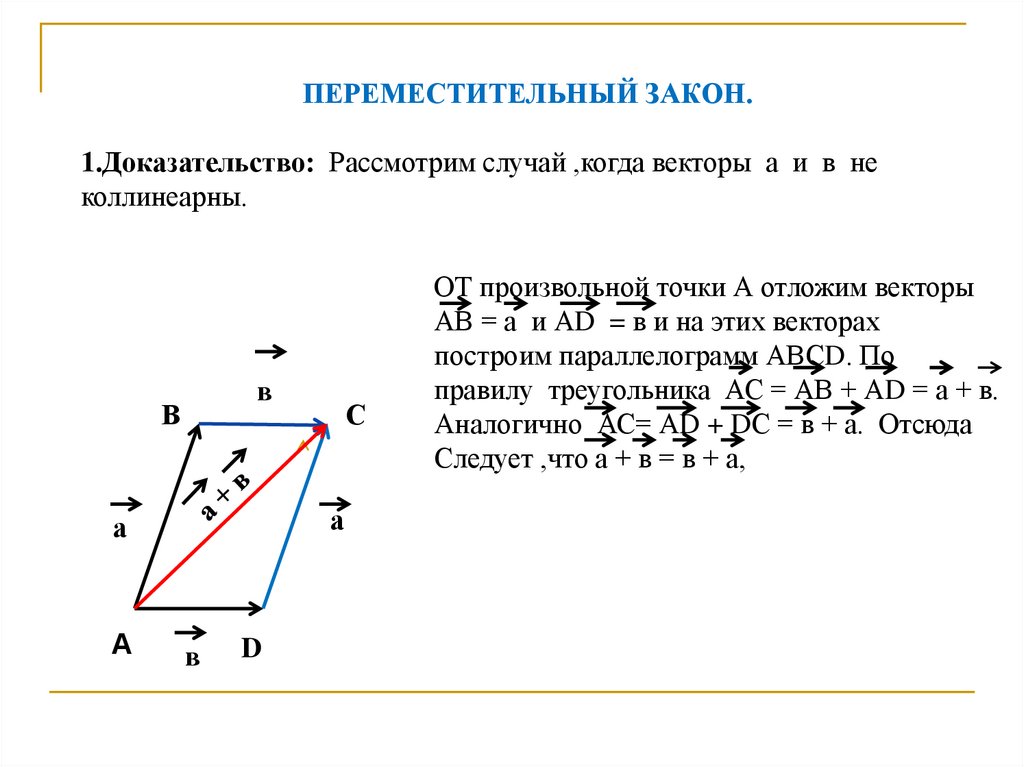
ПЕРЕМЕСТИТЕЛЬНЫЙ ЗАКОН.1.Доказательство: Рассмотрим случай ,когда векторы а и в не
коллинеарны.
в
В
а
а
А
С
в
D
ОТ произвольной точки А отложим векторы
АВ = а и АD = в и на этих векторах
построим параллелограмм АВСD. По
правилу треугольника АС = АВ + АD = а + в.
Аналогично АС= АD + DС = в + а. Отсюда
Следует ,что а + в = в + а,
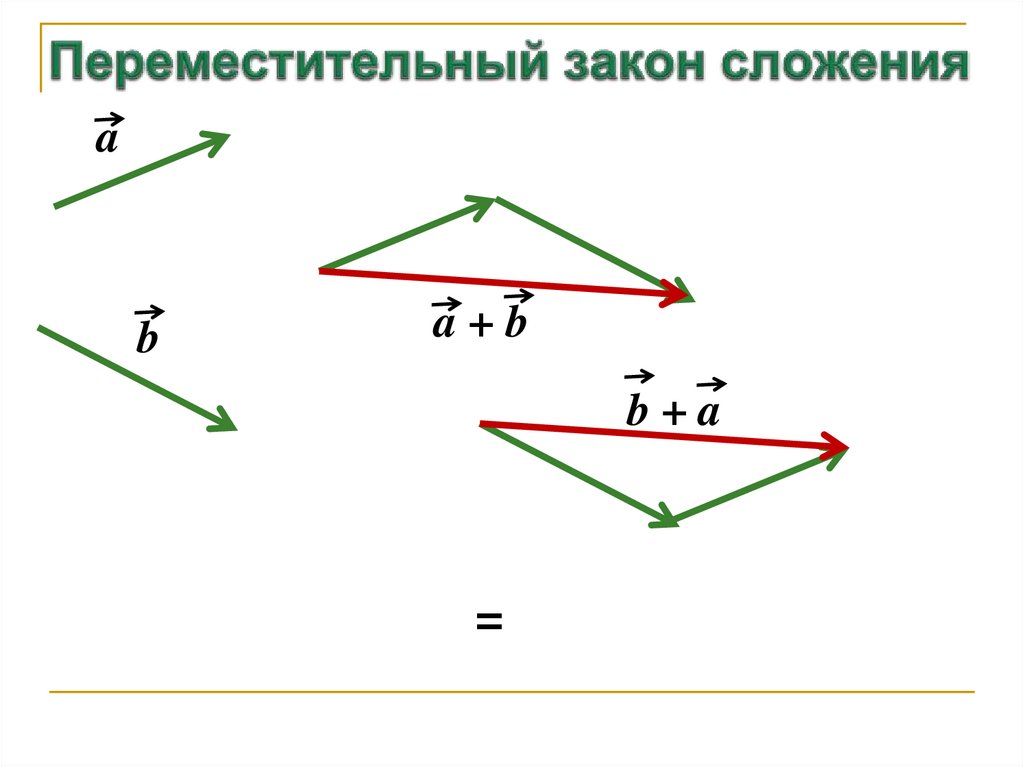
11. Переместительный закон сложения
ab
a+b
b+a
=
12.
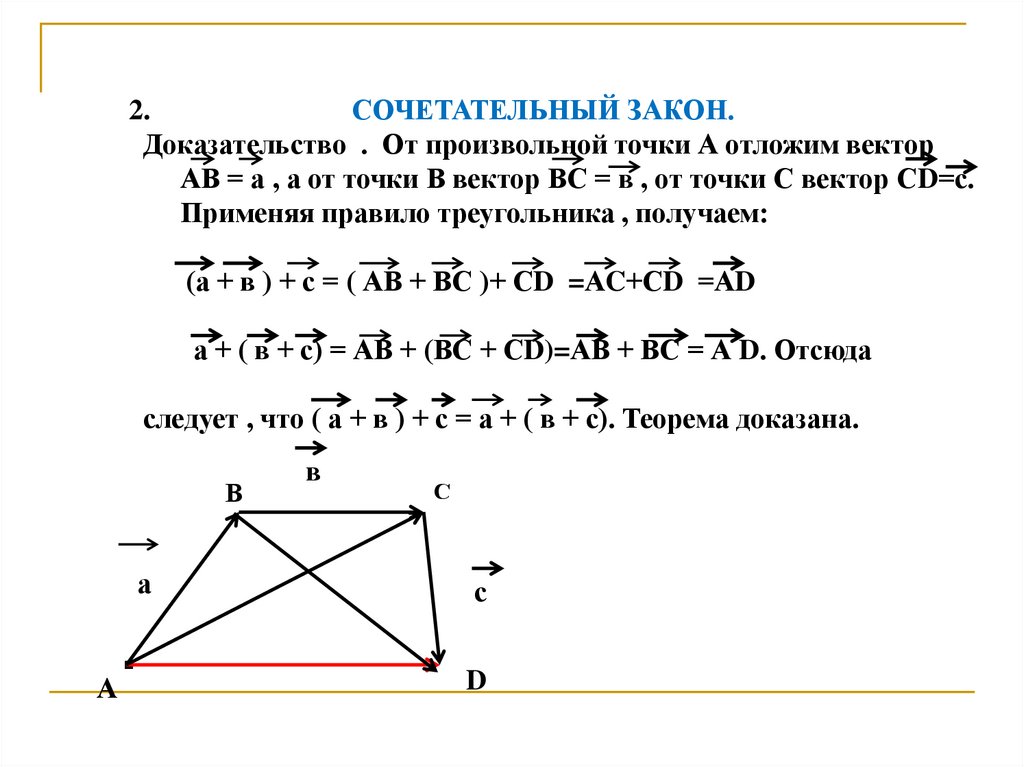
2.СОЧЕТАТЕЛЬНЫЙ ЗАКОН.
Доказательство . От произвольной точки А отложим вектор
АВ = а , а от точки В вектор ВС = в , от точки С вектор СD=с.
Применяя правило треугольника , получаем:
(а + в ) + с = ( АВ + ВС )+ СD =АC+СD =АD
а + ( в + с) = АВ + (ВС + СD)=АВ + ВС = А D. Отсюда
следует , что ( а + в ) + с = а + ( в + с). Теорема доказана.
В
а
.
А
в
С
с
D
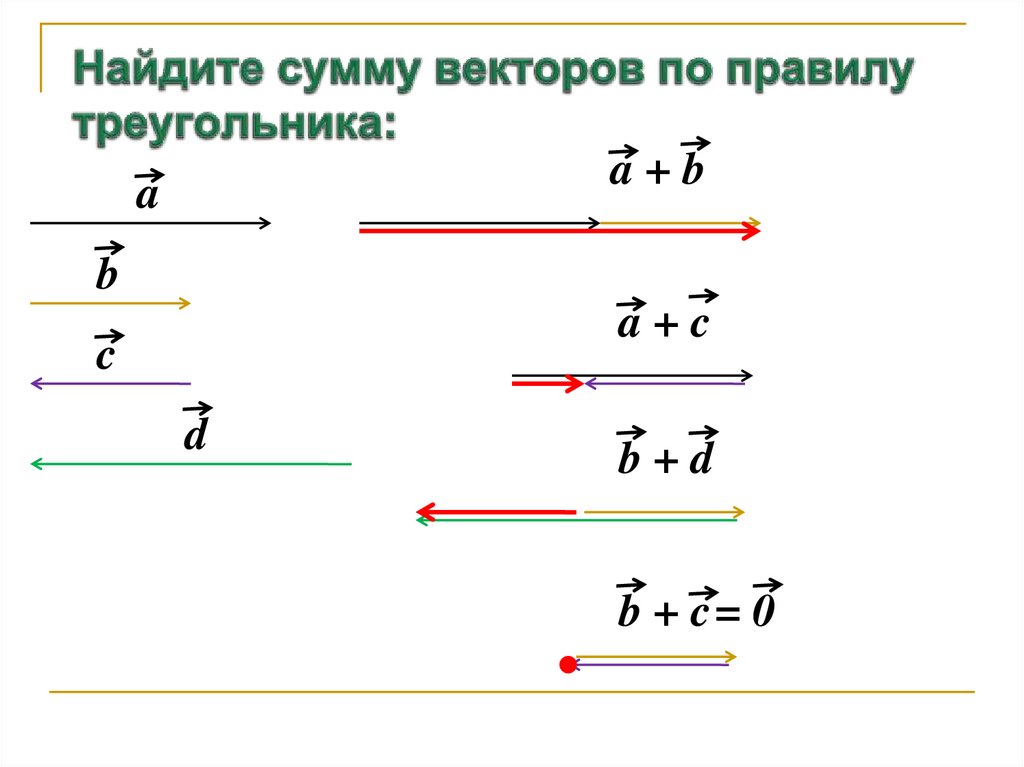
13. Найдите сумму векторов по правилу треугольника:
a+ba
b
a+c
c
d
b+d
b + c= 0
14.
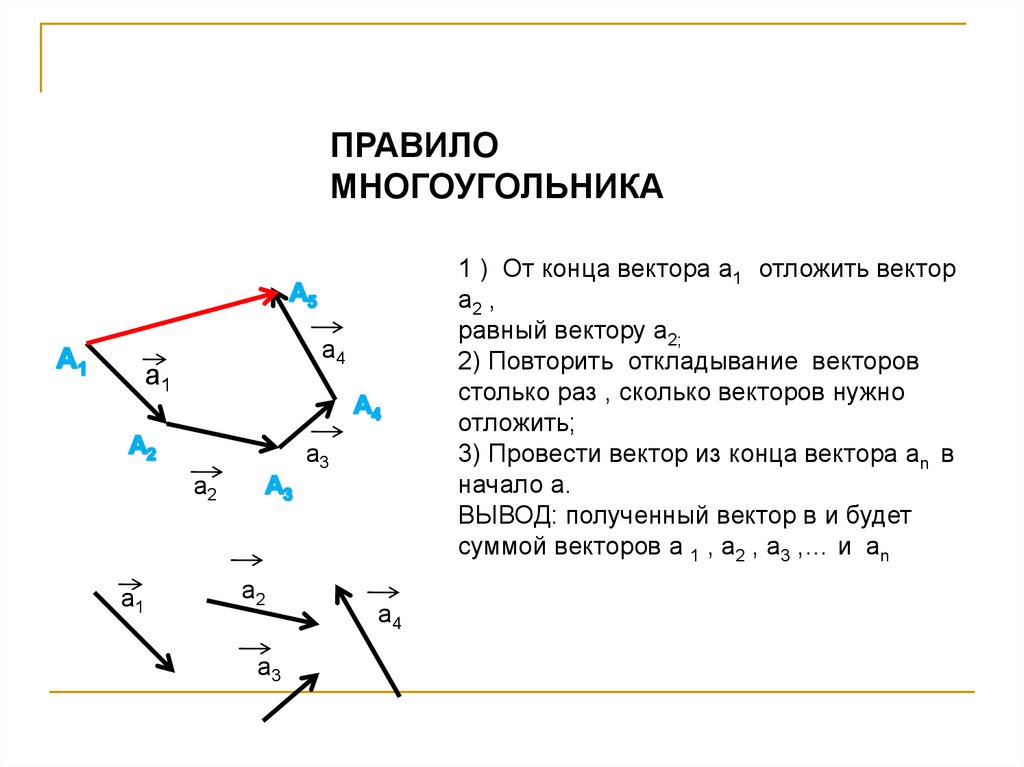
ПРАВИЛОМНОГОУГОЛЬНИКА
а4
а1
а3
а2
а1
1 ) От конца вектора а1 отложить вектор
а2 ,
равный вектору а2;
2) Повторить откладывание векторов
столько раз , сколько векторов нужно
отложить;
3) Провести вектор из конца вектора аn в
начало а.
ВЫВОД: полученный вектор в и будет
суммой векторов а 1 , а2 , а3 ,… и аn
а2
а3
а4
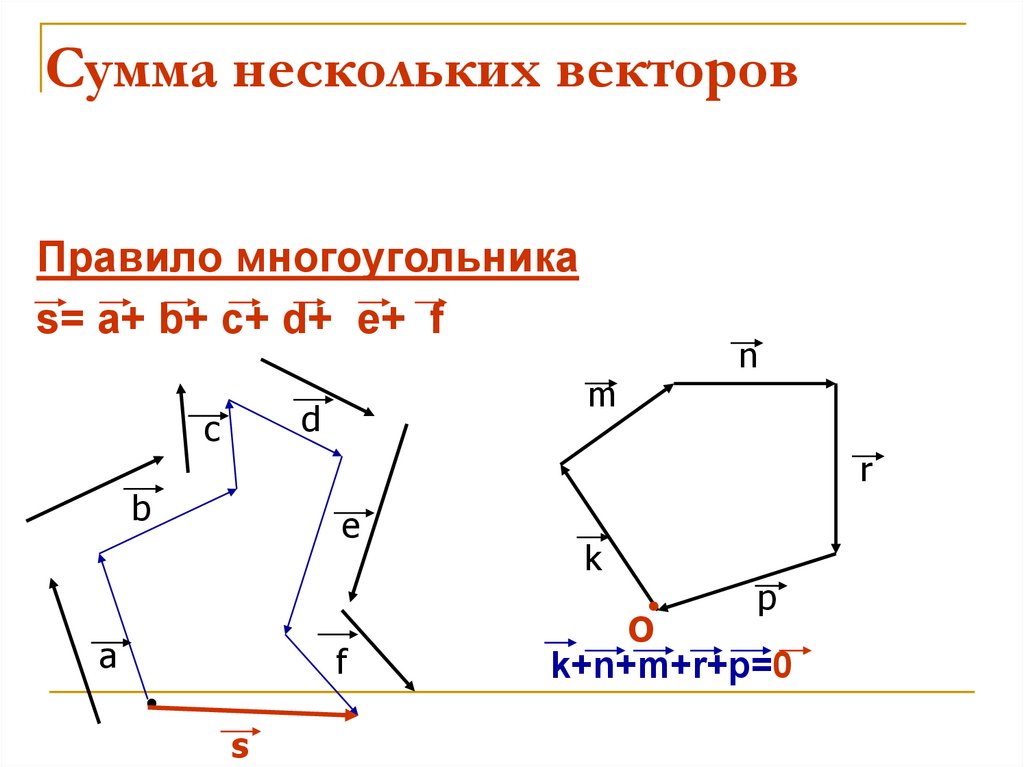
15. Сумма нескольких векторов
Правило многоугольникаs= a+ b+ c+ d+ e+ f
m
d
c
n
r
b
e
a
f
s
k
O
p
k+n+m+r+p=0
16.
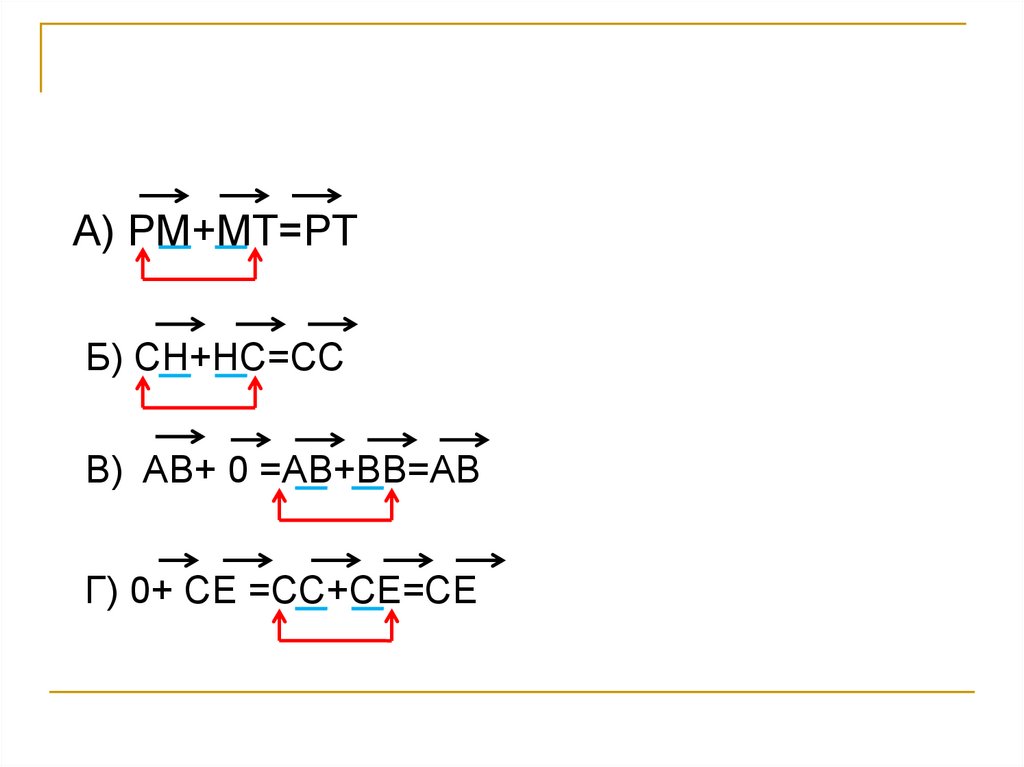
А) PM+MT=PTБ) CH+HC=CC
В) AВ+ 0 =AB+BB=AB
Г) 0+ CE =CC+CE=CE
17.
Задача:Используя правило
треугольника, найдите сумму векторов: а)
РМ и МТ, б) СН и НС,
в) АВ + 0,г) 0 +СЕ.
Решение: а)РМ + МТ = РТ
б) СН +НС= СС= 0
в) АВ + 0 = АВ
г) 0 + СЕ= СЕ
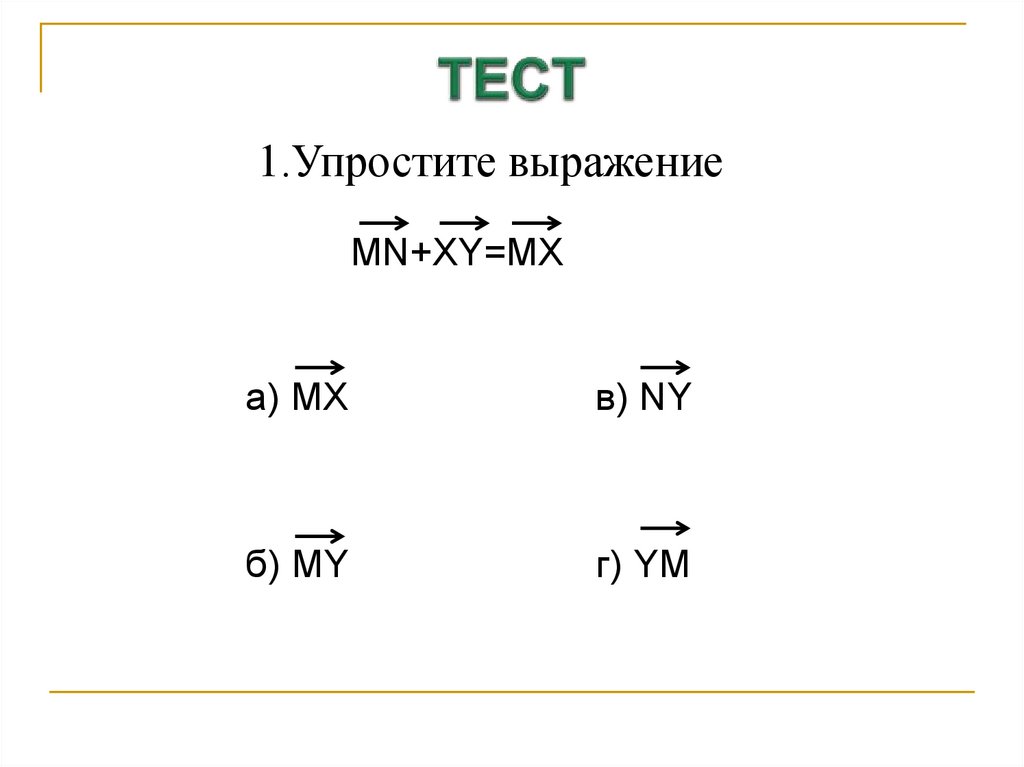
18. ТЕСТ
1.Упростите выражениеMN+XY=MX
а) MX
в) NY
б) MY
г) YM
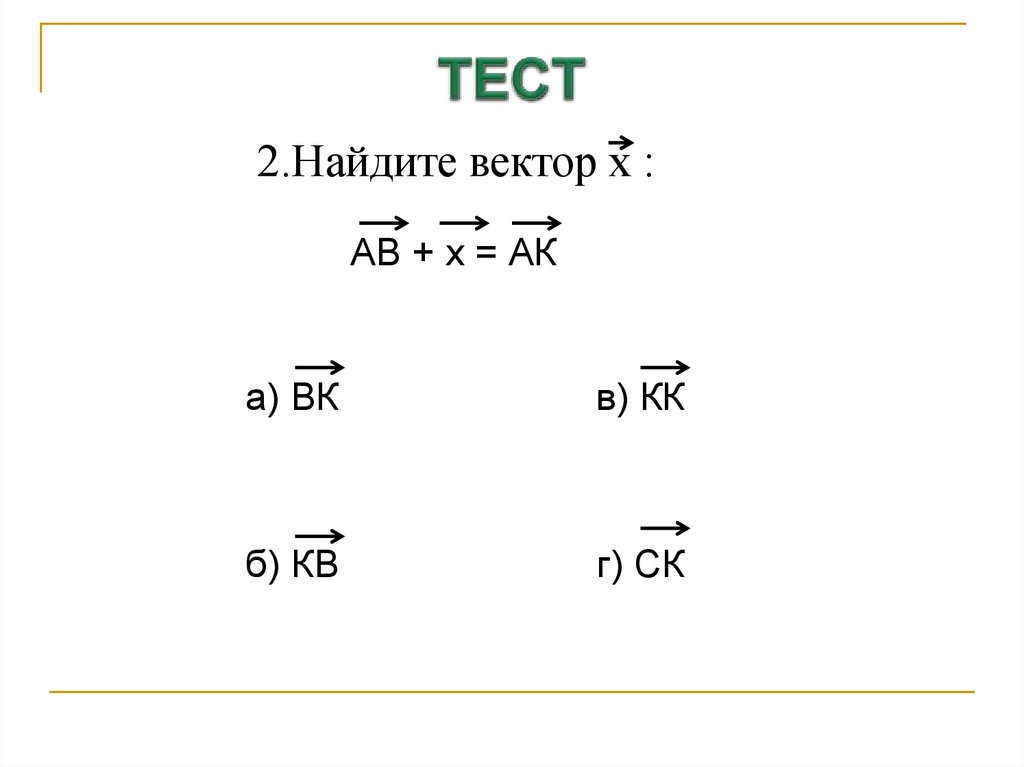
19. ТЕСТ
2.Найдите вектор х :АВ + х = АК
а) ВК
в) КК
б) КВ
г) СК
20. ТЕСТ
3.Найдите вектор a+b,используя правило треугольника :
b
а)
в)
a
a
a+b
a+b
b
б)
г)
a
a+b
b
b
a
a+b
21. ТЕСТ
4.Найдите вектор a+b,используя правило параллелограмма:
а)
в)
a
a
a+b
a+b
b
b
б)
г)
a
a+b
b
b
a
a+b
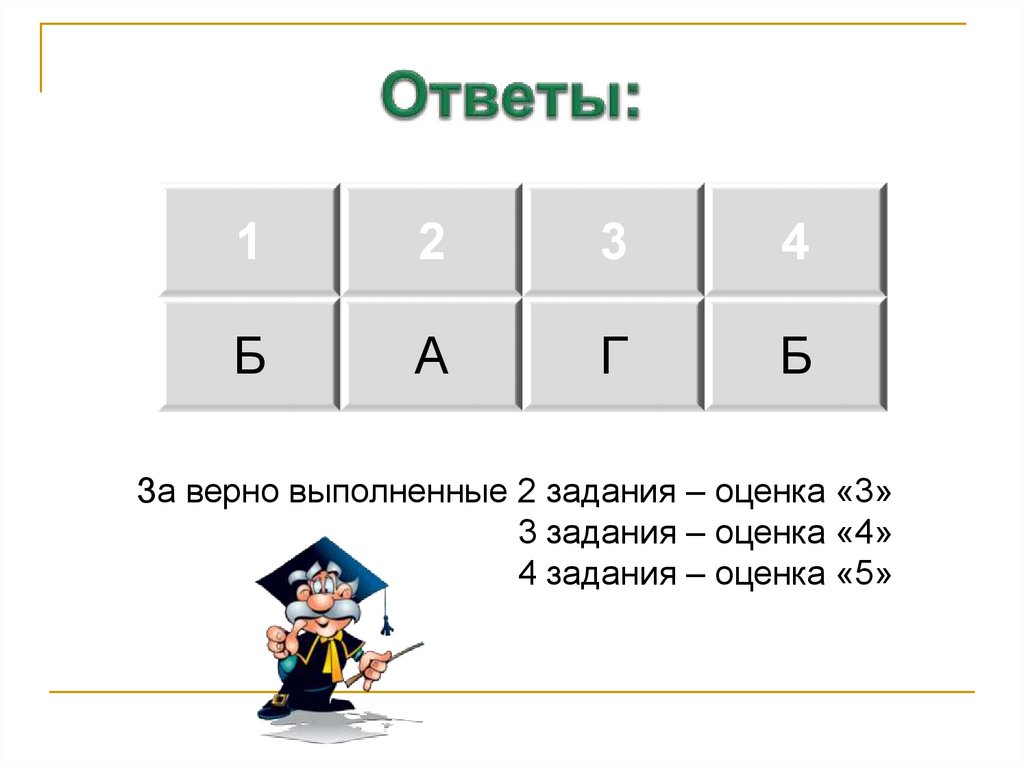
22. Ответы:
12
3
4
Б
А
Г
Б
За верно выполненные 2 задания – оценка «3»
3 задания – оценка «4»
4 задания – оценка «5»
23. Домашнее задание:
Посмотреть видеоурок https://clck.ru/N7kQcВыполнить необходимые записи в рабочей
тетради с указанием темы урока
Выполнить задание на платформе Skysmart
https://clck.ru/Yge8a (при регистрации
обязательно указать ФИ, класс)
Учебник стр.195-198, §2, пункт 82-84
23






 mathematics
mathematics








