Similar presentations:
Понятие вектора
1. Вектор
Вектор – отрезок, для которогоуказано,
какой из его концов считается
началом,
а какой – концом.
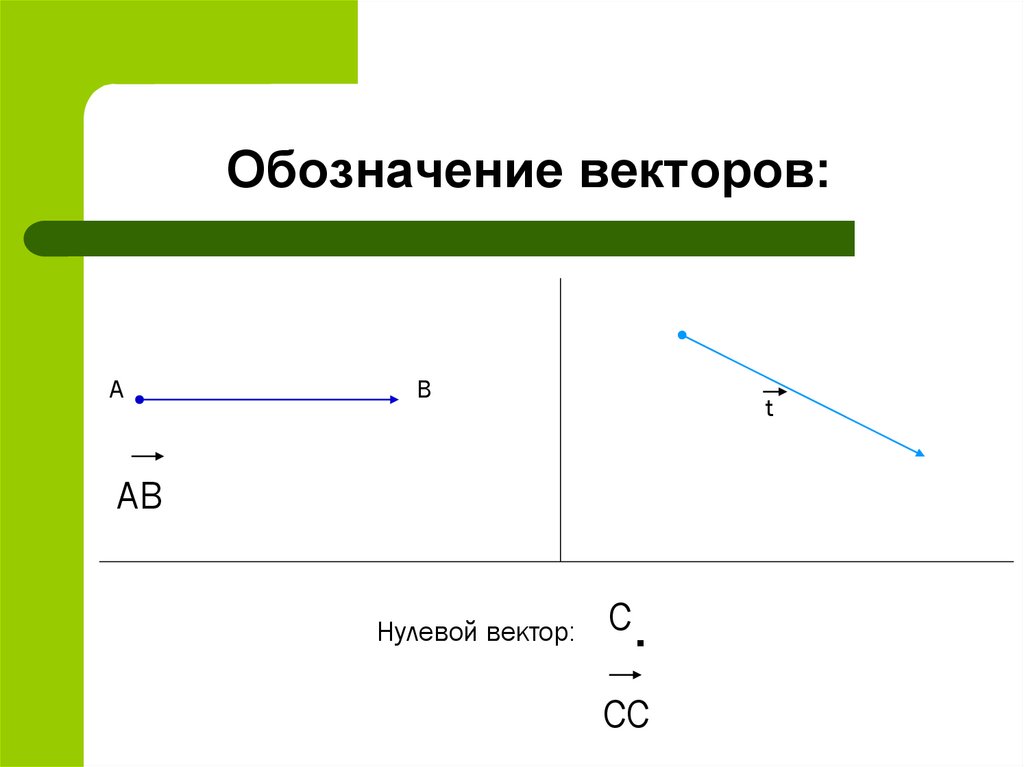
2. Обозначение векторов:
АВ
t
АВ
Нулевой вектор:
С.
СС
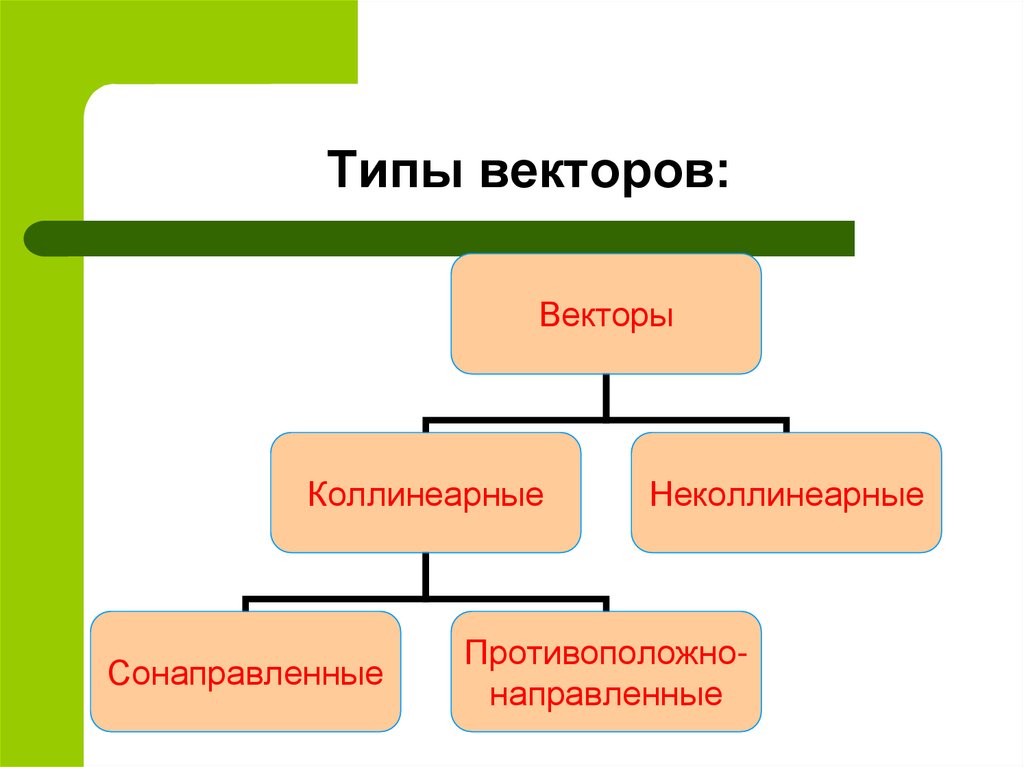
3. Типы векторов:
ВекторыКоллинеарные
Сонаправленные
Неколлинеарные
Противоположнонаправленные
4. Коллинеарные вектора:
AV
а
G
B
b
M
N
К
KF
и
NM
F
t
s
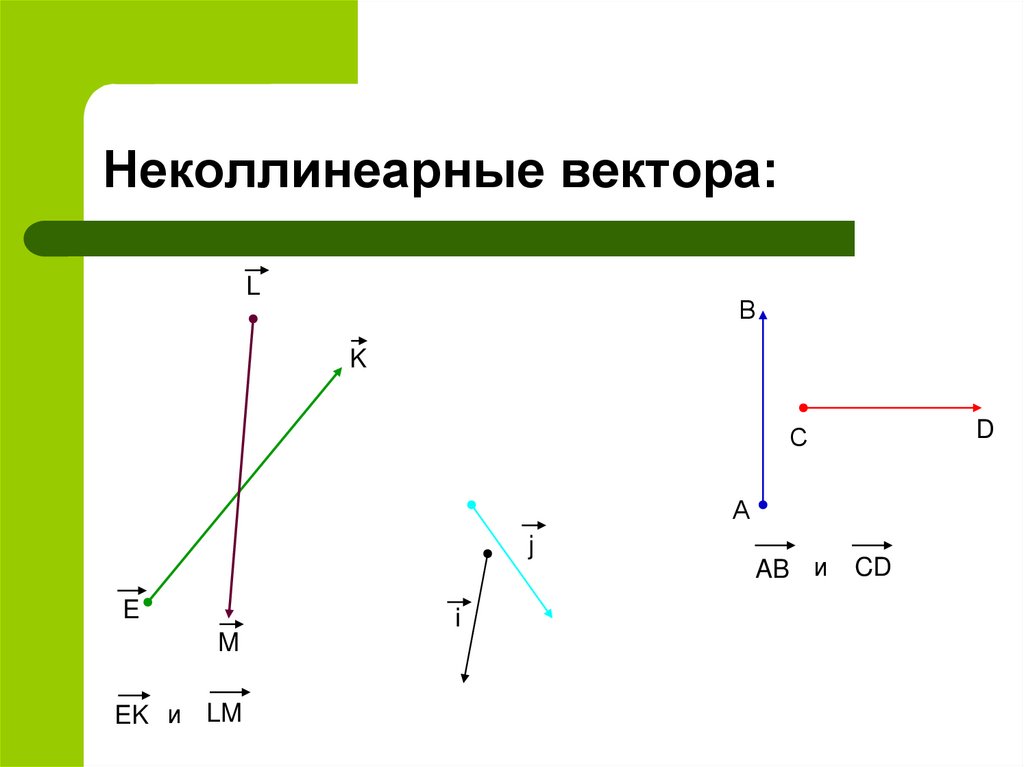
5. Неколлинеарные вектора:
LВ
K
D
С
А
j
E
i
M
EK и LM
AB и
CD
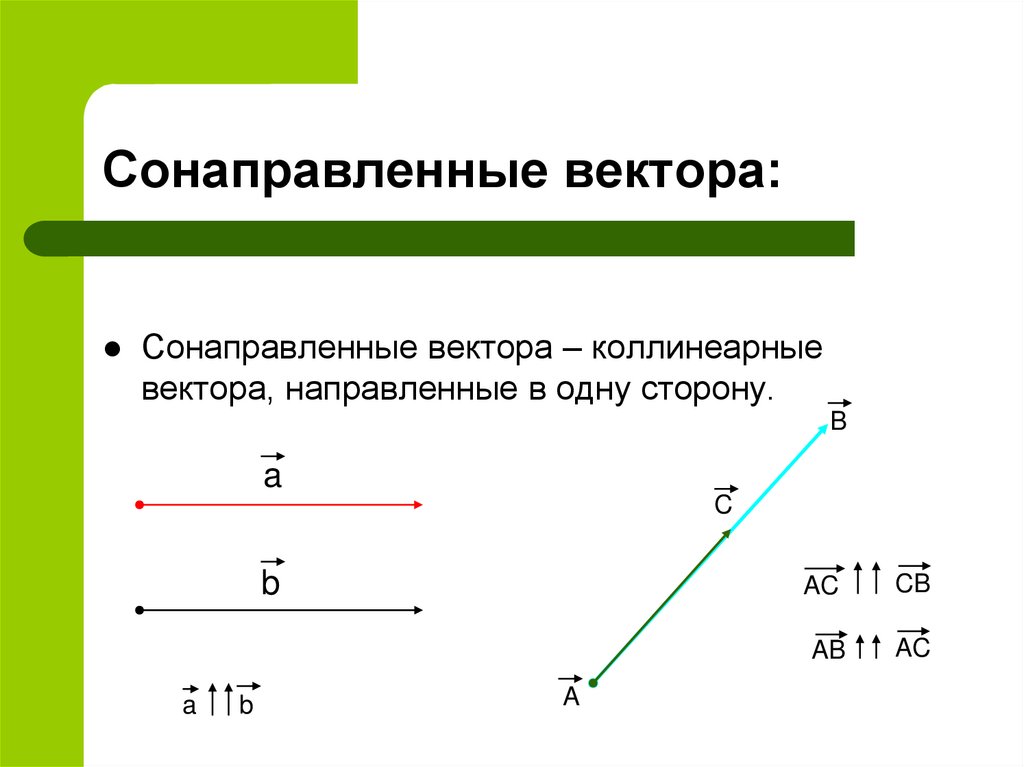
6. Сонаправленные вектора:
Сонаправленные вектора – коллинеарныевектора, направленные в одну сторону.
B
a
C
b
a
b
A
AC
CB
AB
AC
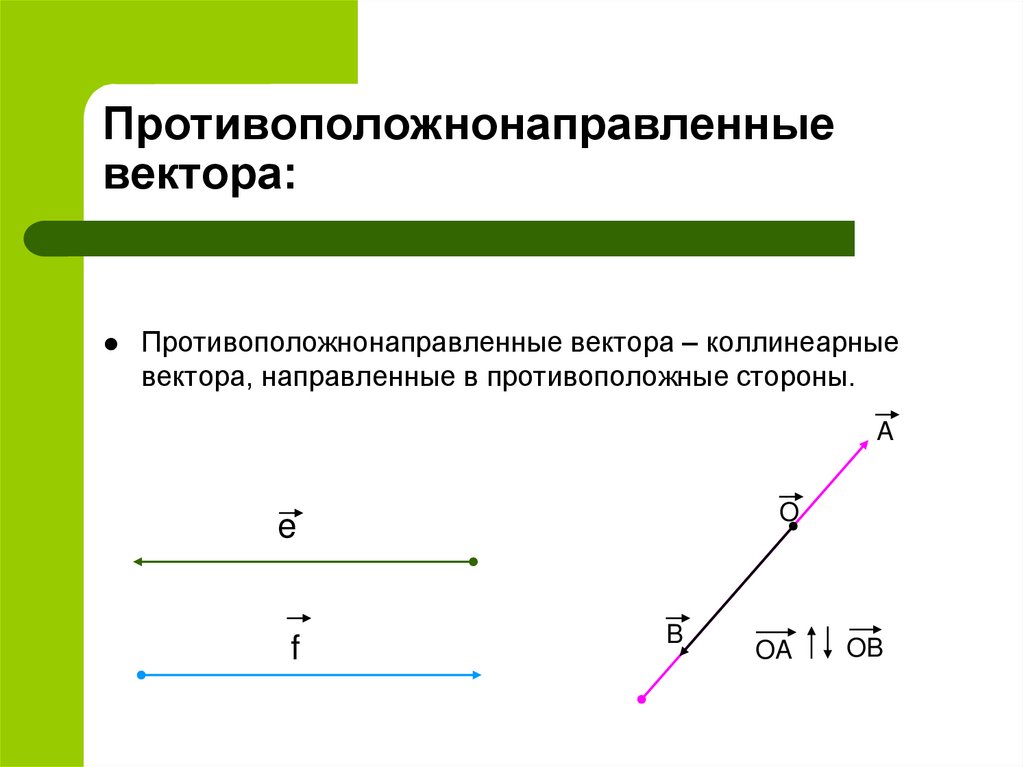
7. Противоположнонаправленные вектора:
Противоположнонаправленные вектора – коллинеарныевектора, направленные в противоположные стороны.
A
O
e
f
B
OA
OB
8. Сложение векторов
Сложение:Правило треугольника
Правило параллелограмма
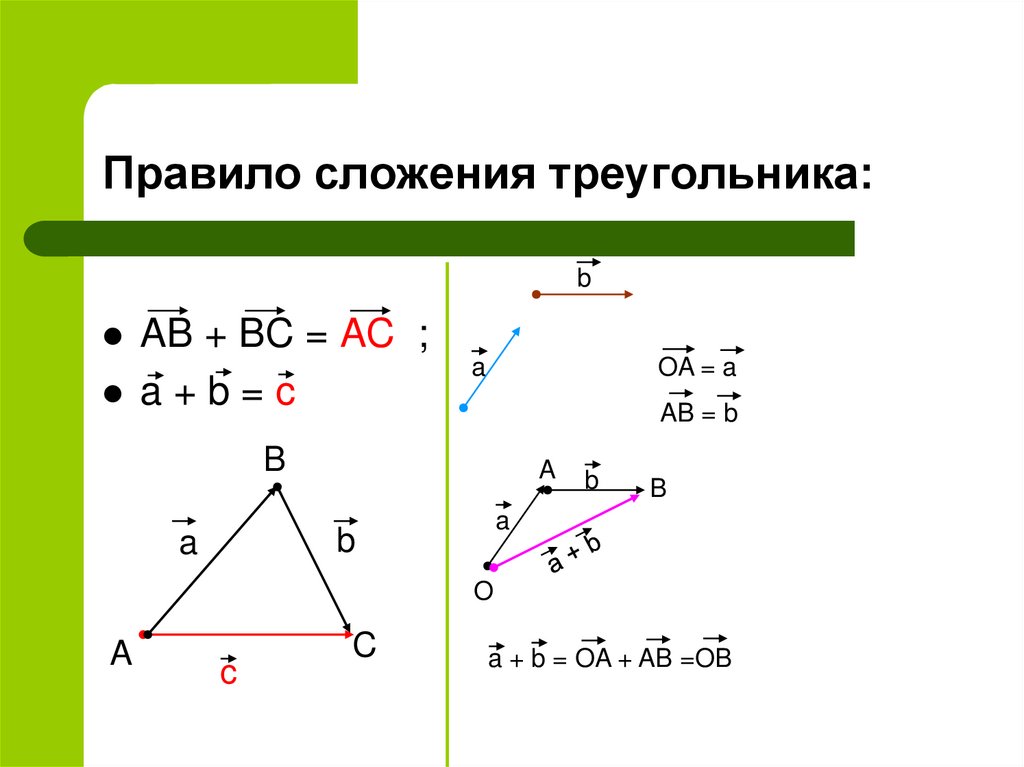
9. Правило сложения треугольника:
bAB + BC = AC ;
a+b=c
a
OA = a
AB = b
B
A
B
a
b
a
b
O
A
c
C
a + b = OA + AB =OB
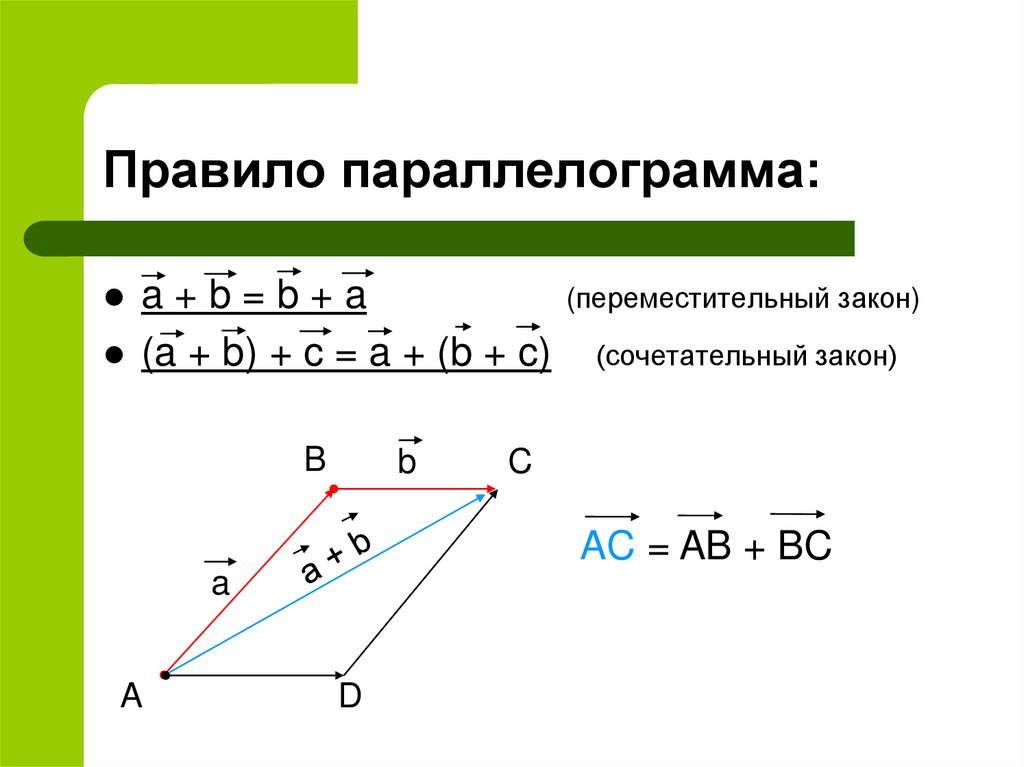
10. Правило параллелограмма:
a+b=b+a(a + b) + c = a + (b + c)
B
b
(переместительный закон)
(сочетательный закон)
C
AC = AB + BC
a
A
D
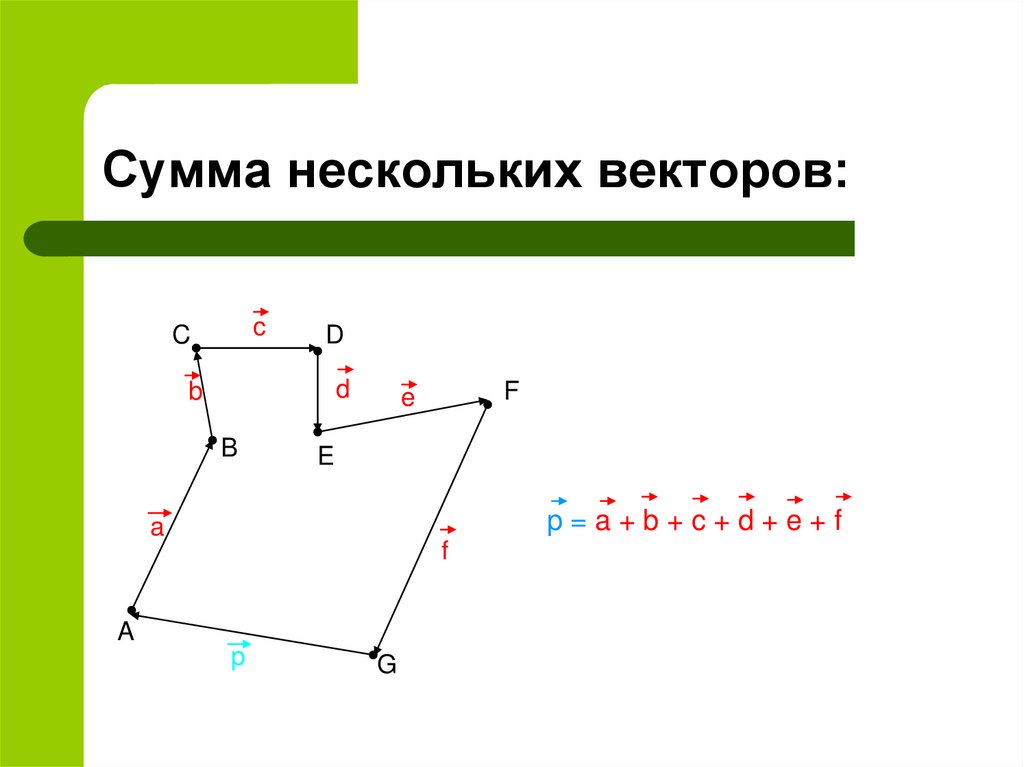
11. Сумма нескольких векторов:
cC
D
d
b
B
F
e
E
p=a+b+c+d+e+f
a
f
A
p
G
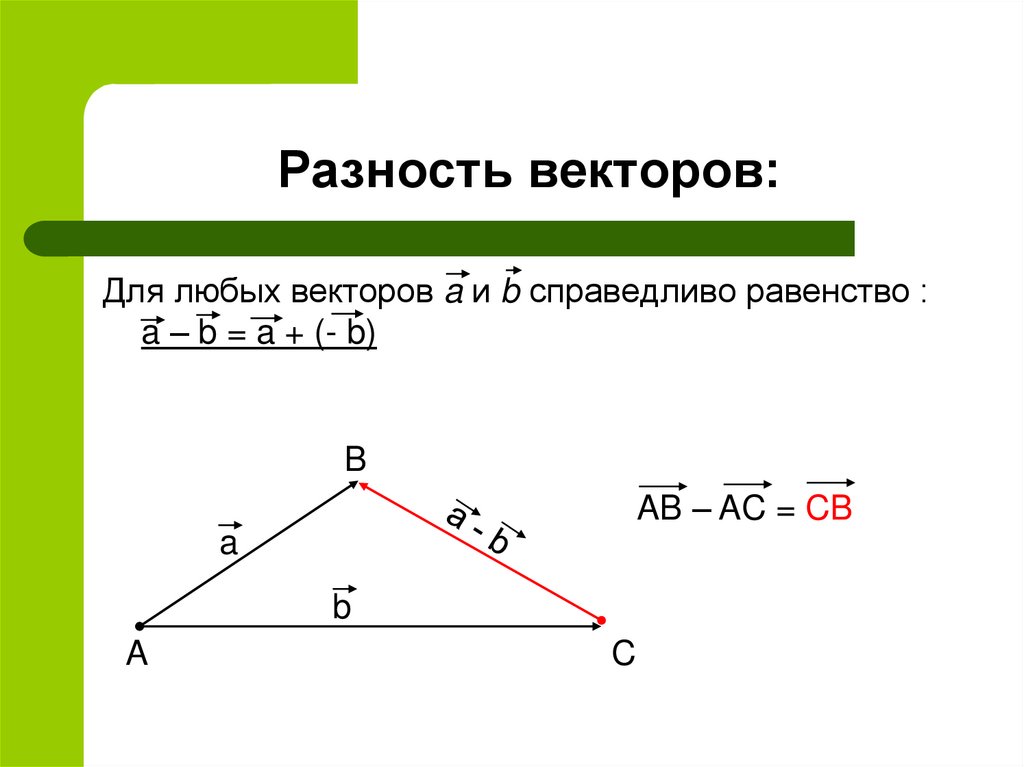
12. Разность векторов:
Для любых векторов a и b справедливо равенство :a – b = a + (- b)
B
AB – AC = CB
a
b
A
C
13. Умножение вектора на число:
1.2.
3.
4.
(kl) • a = k • (la) (сочетательный закон)
(k + l) • a = ka + la (первый распределительный закон)
k (a + b) = ka + kb (второй распределительный закон)
k, l – числа ; a, b - вектора
c
a
b
c = -4a
b = 3a
b = ka, где k – число, a = 0
|b| = |k| • |a|
b
b
a , если k > 0
a , если k < 0
14.
Автор:Шинарёв Роман
9 «В» класс
2007г.
Учитель геометрии
Володина Марина Викторовна





 mathematics
mathematics








