Простейшие задачи векторной алгебры

1.

§2. Простейшие задачи векторной алгебры
Пусть на плоскости (в пространстве) задана декартова
прямоугольная система координат. Выберем во множестве
V(3) (V(2)) декартов прямоугольный базис i, j, k (i, j).
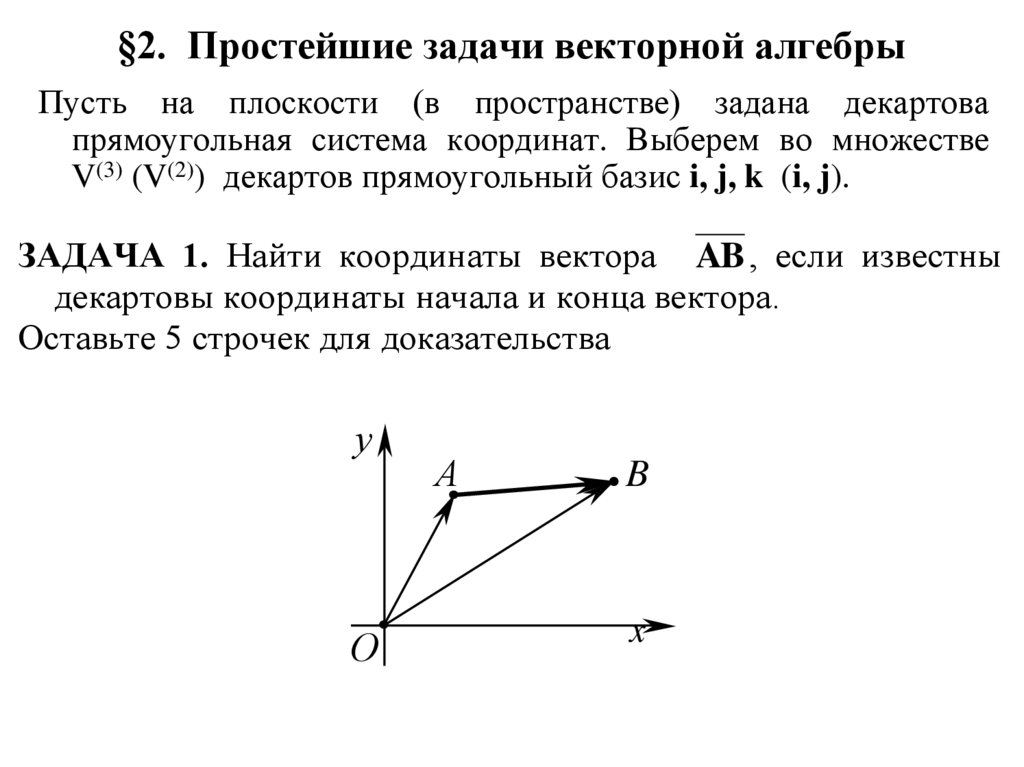
ЗАДАЧА 1. Найти координаты вектора AB , если известны
декартовы координаты начала и конца вектора.
Оставьте 5 строчек для доказательства
y
O
A
B
x

2.

• ЗАДАЧА 2. Найти длину вектора, если известны его
координаты в декартовом прямоугольном базисе.
• Оставьте 5 строчек для доказательства
y
B
ay
A
O
ax
C
x
ЗАДАЧА 3. Известны координаты вектора. Найти координаты
его орта.
ОПРЕДЕЛЕНИЕ. Ортом вектора a называется вектор a0 ,
сонаправленный с вектором a и имеющий единичную
длину.

3.

Геометрический смысл координат орта вектора
Будем обозначать через , и углы, которые вектор a
образует с координатными осями
Ox ,
Oz
Oy и
соответственно.
cos , cos , cos называются направляющими косинусами
a
вектора a .
a
1
x
x
A1
B1
Координаты орта вектора a являются его направляющими
косинусами.
Замечание. Так как a0 1 и a0 cos ; cos ; cos , то
cos 2 cos 2 cos 2 1 .
Это равенство называют основным
направляющих косинусов вектора.
тождеством
для

4.

ЗАДАЧА 4. Известны координаты концов отрезка. Найти
координаты точки, которая делит отрезок в заданном
отношении.
ОПРЕДЕЛЕНИЕ. Говорят, что точка
M0
делит отрезок
M1M 2 в отношении ( 1) если M1M 0 M 0M 2 .
Если λ > 0 , то точка M0 лежит между точками M1 и M2. В этом
случае говорят, что точка M0 делит отрезок M1M2 во
внутреннем отношении.
Если λ < 0 , то точка M0 лежит на продолжении отрезка M1 M2.
В этом случае говорят, что точка M0 делит отрезок M1M2 во
внешнем отношении.
Оставьте 5 строчек для доказательстваM
1
r1
r0
O
M0
r2
M2

5.

§3. Нелинейные операции на множестве векторов
1. Скалярное произведение векторов
2. Векторное произведение векторов
3. Смешанное произведение векторов
1. Скалярное произведение векторов
ОПРЕДЕЛЕНИЕ. Скалярным произведением двух
ненулевых векторов a и b называется число,
равное произведению их модулей на косинус угла
между ними, т.е. число a b cos .
Если a 0 или b 0 , то скалярное произведение векторов
a и b полагают равным нулю.
СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
После каждого свойства оставьте 3-5 строк для доказательства
1) Скалярное произведение векторов коммутативно, т.е.
(a, b ) (b, a )

6.

2) Скалярное произведение ненулевых векторов a и b равно
произведению длины вектора a на проекцию вектора b
на вектор a (длины вектора b на проекцию a на b ).
( a , b ) a Пр a b b Пр b a
ОПРЕДЕЛЕНИЕ. Проекцией вектора a на
вектор b называется проекция вектора
a на ось, определяемую вектором b .
a
b
3) Числовой множитель любого из двух векторов можно
вынести за знак скалярного произведения. Т.е.
( a , b ) ( a , b ) ( a , b )
4) Если один из векторов записан в виде суммы,
то их скалярное произведение тоже можно
записать в виде суммы. Т.е.
(a1 a2 , b ) (a1, b ) (a2 , b )
(a, b1 b2 ) (a, b1) (a, b2 )
a1 a2
a1
a2
b

7.

5) Скалярное произведение вектора на себя (скалярный квадрат
2
(
a
,
a
)
a
вектора) равно квадрату его длины. Т.е.
6) Ненулевые векторы a
иb
перпендикулярны тогда и
только тогда, когда их скалярное произведение равно нулю
(критерий перпендикулярности векторов).
7) Если в декартовом прямоугольном базисе векторы a и b
имеют координаты: a {ax ; ay ; az } , b {bx ; by ; bz },
то
(a, b ) axbx a yby az bz .
(1)
Формулу (1) называют выражением скалярного произведения
через декартовы координаты векторов.
8) Если под действием постоянной силы F точка перемещается по прямой из точки M1 в M 2 , то работа силы F
будет равна A F, M1M 2
го произведения).
(физический смысл скалярно-

8.

2. Векторное произведение векторов
ОПРЕДЕЛЕНИЕ. Тройка векторов a , b и c
называется правой, если поворот от
вектора a к вектору b на меньший угол
виден из конца вектора c против часовой
стрелки.
c
b
a

9.

ОПРЕДЕЛЕНИЕ. Векторным произведением двух ненулевых
векторов a
и b
называется вектор c ,
удовлетворяющий следующим условиям:
1) | c | | a | | b | sin , где – угол между векторами a
и b;
2) вектор c ортогонален векторам a и b ;
3) тройка векторов a , b и c – правая.
Если хотя бы один из векторов a или b нулевой, то их
векторное произведение полагают равным нулевому
вектору.
Обозначают [a, b] или a b .

10.

СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
1) При перестановке векторов a
иb
их векторное
произведение меняет знак, т.е.
[a, b] [b, a ] .
2) Числовой множитель любого из двух векторов можно
вынести за знак векторного произведения. Т.е.
[ a, b] [a , b] [a, b] .
[a, b] ( 0 )
[a, b]
a ( 0 )
b
a
[a, b]
b
a
a ( 0 )
[a, b] ( 0 )

11.

3) Если один из векторов записан в виде суммы, то
векторное произведение тоже можно записать в виде
[a1 a 2 , b] [a1, b] [a 2 , b] ,
суммы. А именно:
[a, b1 b2 ] [a, b1 ] [a, b2 ] .
4) Ненулевые векторы a и b коллинеарные тогда и только
тогда, когда их векторное произведение равно нулевому
вектору (Критерий коллинеарности векторов).
5) Модуль векторного произведения неколлинеарных векторов a и b равен площади параллелограмма, построенного на этих векторах (Геометрический смысл векторного произведения).

12.

6) Если в декартовом прямоугольном базисе векторы a и b
имеют координаты: a {ax ; ay ; az } , b {bx ; by ; bz }, то
i j k
a y az az ax ax a y
[a, b ]
;
;
a x a y az .
b
b
b
b
b
b
x
y
z
x
y z
bx by bz
7) (Механический смысл векторного произведения). Если
вектор F это сила, приложенная к точке M , то
векторное произведение OM, F представляет собой
момент силы F относительно точки O .
Оставьте место для доказательства свойств

13.

3. Смешанное произведение векторов
ОПРЕДЕЛЕНИЕ. Смешанным произведением трех векторов
a, b
и c
называется число, равное скалярному
произведению вектора a
на векторное произведение
векторов b и c , т.е. ( a, [b, c ]) .
Обозначают: ( a, b, c ) или a bc .
СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ
ВЕКТОРОВ
1) При циклической перестановке векторов a , b , c их
смешанное произведение не меняется, т.е.
( a, b, c ) ( b, c, a ) ( c, a, b) .

14.

2) При перестановке любых двух векторов их смешанное
произведение меняет знак.
3) Числовой множитель любого из трех векторов можно
вынести за знак смешанного произведения. Т.е.
( a, b, c ) ( a, b, c ) ( a, b, c ) ( a, b, c ) .
4) Если один из векторов записан в виде суммы, то смешанное произведение тоже можно записать в виде суммы. А
именно: ( a1 a 2 , b, c ) ( a1, b, c ) ( a 2 , b, c ) ,
( a, b1 b2 , c ) ( a, b1, c ) ( a, b2 , c ) ,
( a, b, c1 c2 ) ( a, b, c1 ) ( a, b, c2 ) .

15.

5) Ненулевые векторы a , b , c
компланарны тогда и
только тогда, когда их смешанное произведение равно
нулю (Критерий компланарности векторов).
[a , b ]
c
c
b
b
a
рис. 1
a
рис. 2

16.

( a , b, c ) 0 , то векторы a , b , c
образуют
правую тройку. Если ( a , b, c ) 0 , то тройка векторов
a , b , c – левая.
6) Если
[a , b ]
[a , b ]
c
b
a
рис. 3
b
a
c
рис.4

17.

7) Модуль смешанного произведения некомпланарных векторов a , b , c равен объему параллелепипеда, построенного на этих векторах (Геометрический смысл смешанного произведения).
[a , b ]
[a , b ]
b
c
a
b
c
a
рис. 5
рис. 6

18.

8) (Следствие свойства 7). Объем пирамиды, построенной на
1
a
c
векторах
, b ,
равен
модуля их смешанного
6
произведения.
9) Если в декартовом прямоугольном базисе векторы a , b ,
b {bx ; by ; bz },
c имеют координаты: a {ax ; ay ; az },
c {cx ;cy ;cz } , то
a x a y az
( a, b, c ) bx by bz .
cx c y cz