Similar presentations:
Преобразование графиков функций, содержащих модуль
1. Преобразование графиков функций, содержащих модуль
2.
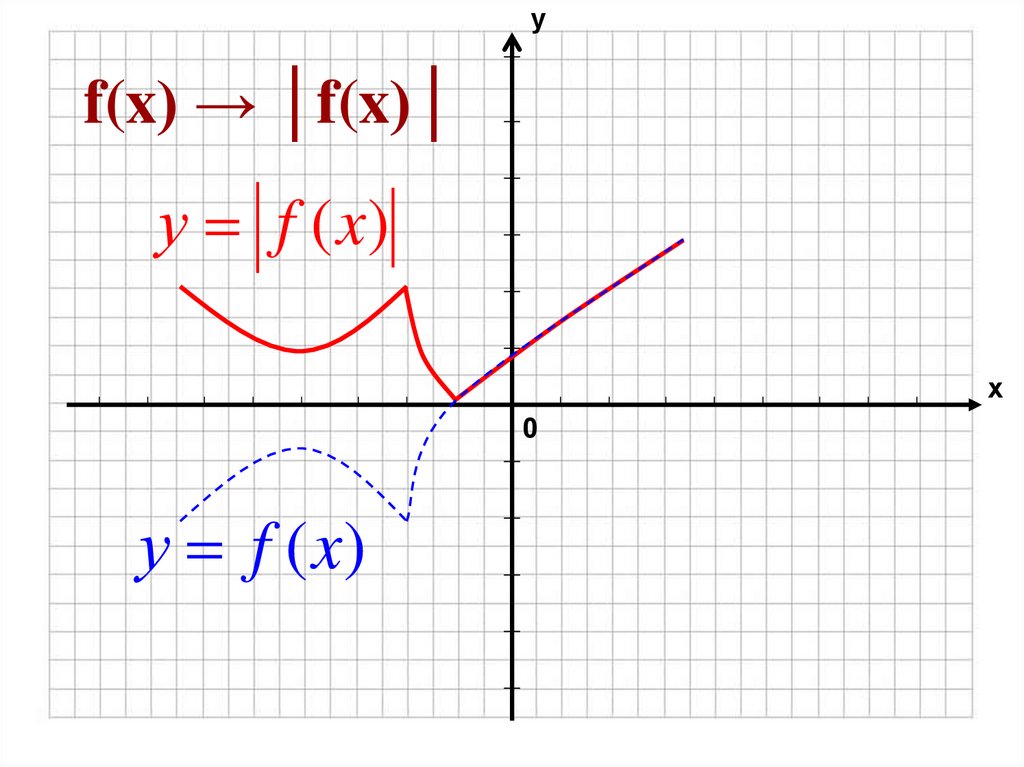
Чтобы построить график функцииy=|f(x)|,надо сначала построить график
функции y=f(x), а затем участки этого
графика, лежащие выше оси абсцисс,
оставить без изменения, а участки,
лежащие ниже оси абсцисс, зеркально
отразить относительно этой оси.
3. f(x) → │f(x)│
уf(x) → │f(x)│
у f (x)
х
0
у f (x)
4.
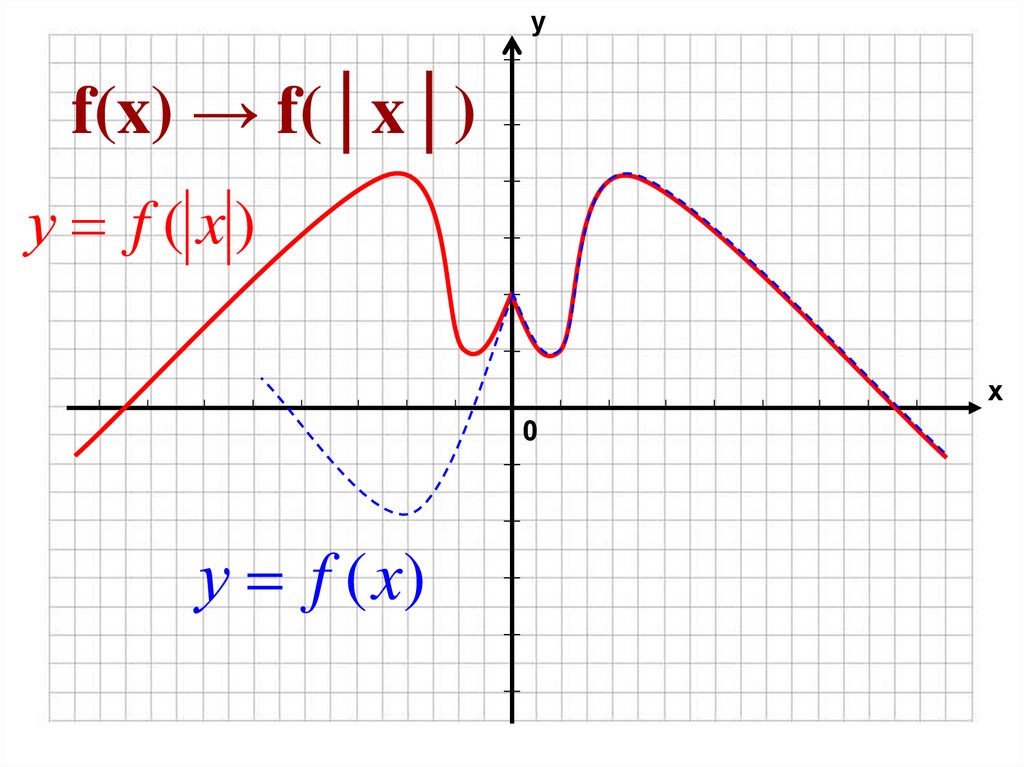
Так как f (|-x|) = f (|x|), то функция y = f (|x|)чётная и для построения её графика
следует удалить точки графика функции
f (x), находящиеся слева от оси Оу, а все
точки, лежащие на оси Оу и справа от
неё, отобразить симметрично
относительно оси Оу.
5. f(x) → f(│x│)
уf(x) → f(│x│)
у f ( x)
х
0
у f (x)
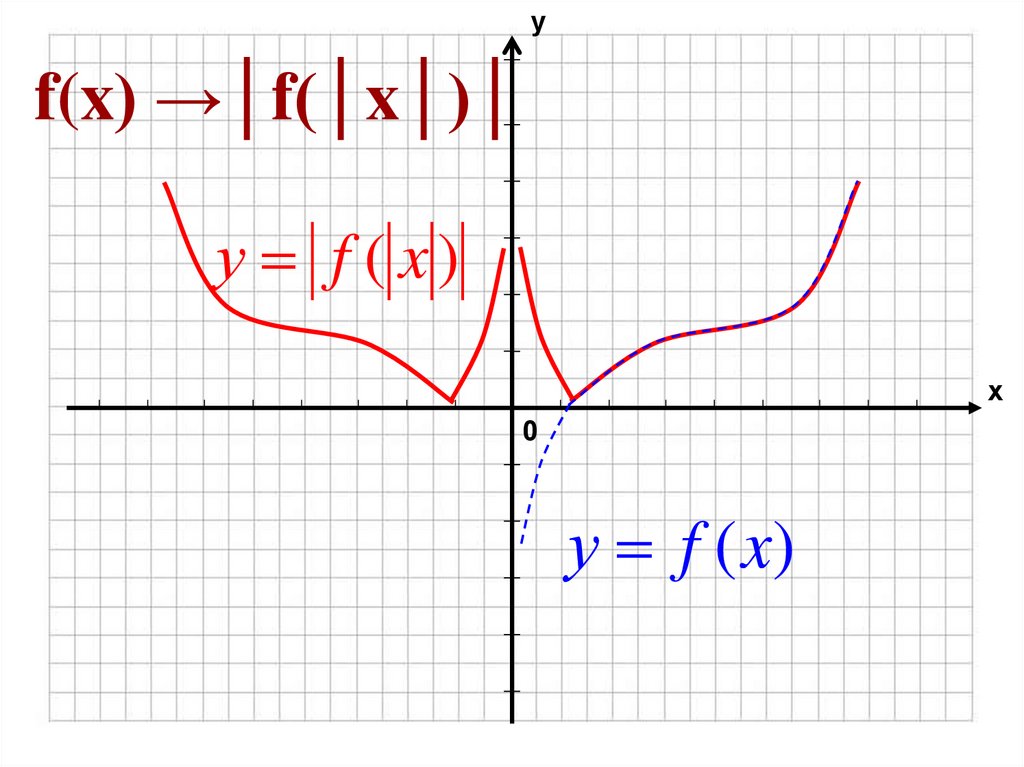
6. Построение графика функции у = |f(|x|)|
Последовательность действий в этом случаепредставим следующим образом:
1. построить график функции y = f(x) для x 0 ;
2. отобразить построенную часть графика
симметрично относительно оси ординат;
3. участки полученного графика, лежащие
ниже оси абсцисс, зеркально отразить
относительно этой оси.
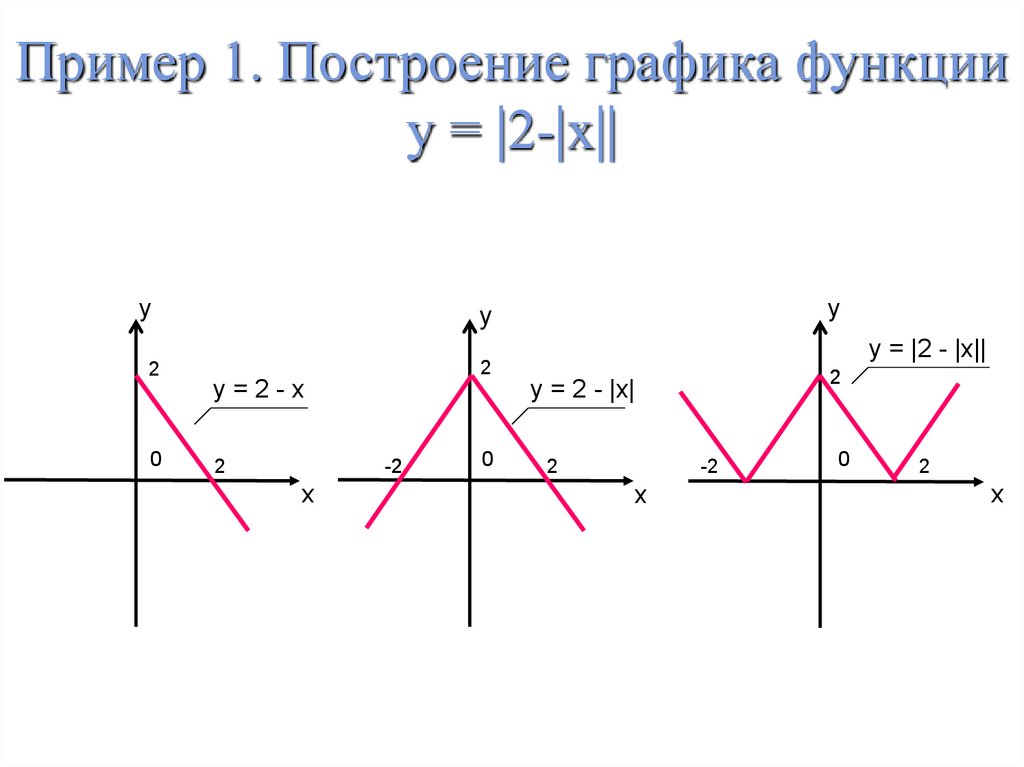
7. Пример 1. Построение графика функции у = |2-|x||
y2
0
y
y
y = |2 - |x||
2
y=2-x
2
-2
x
2
y = 2 - |x|
0
2
-2
x
0
2
x
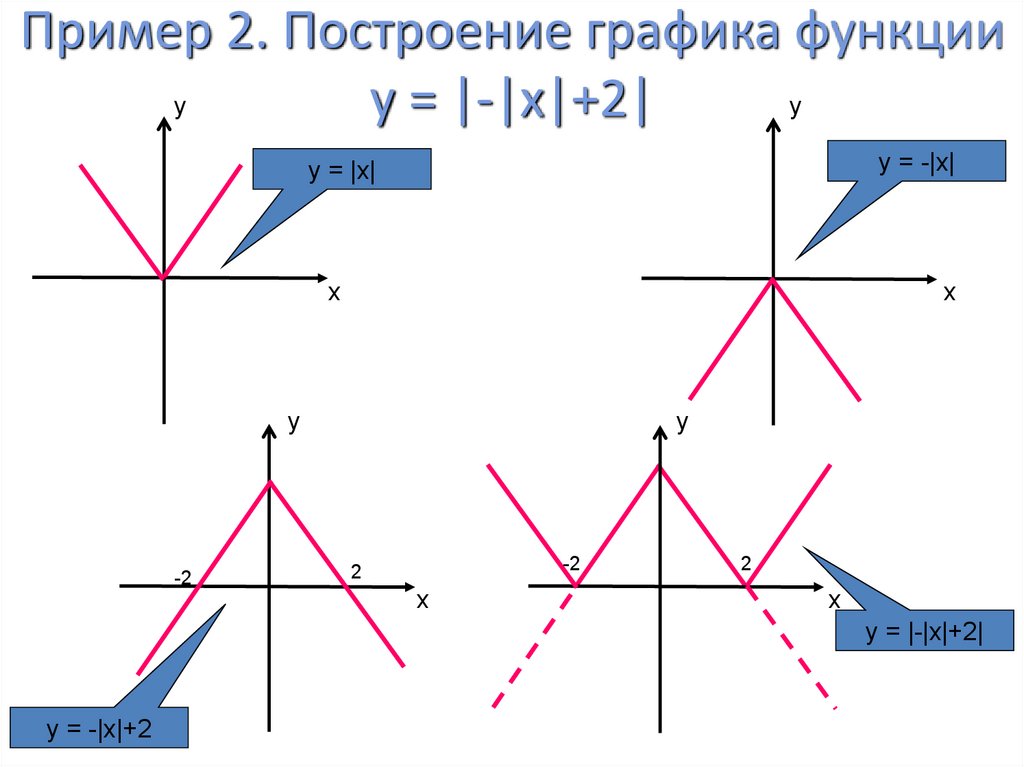
8. Пример 2. Построение графика функции у = |-|x|+2|
Пример 2. Построение графика функцииy
y
у = |-|x|+2|
y = -|x|
y = |x|
x
x
y
-2
y
-2
2
x
2
x
y = |-|x|+2|
y = -|x|+2
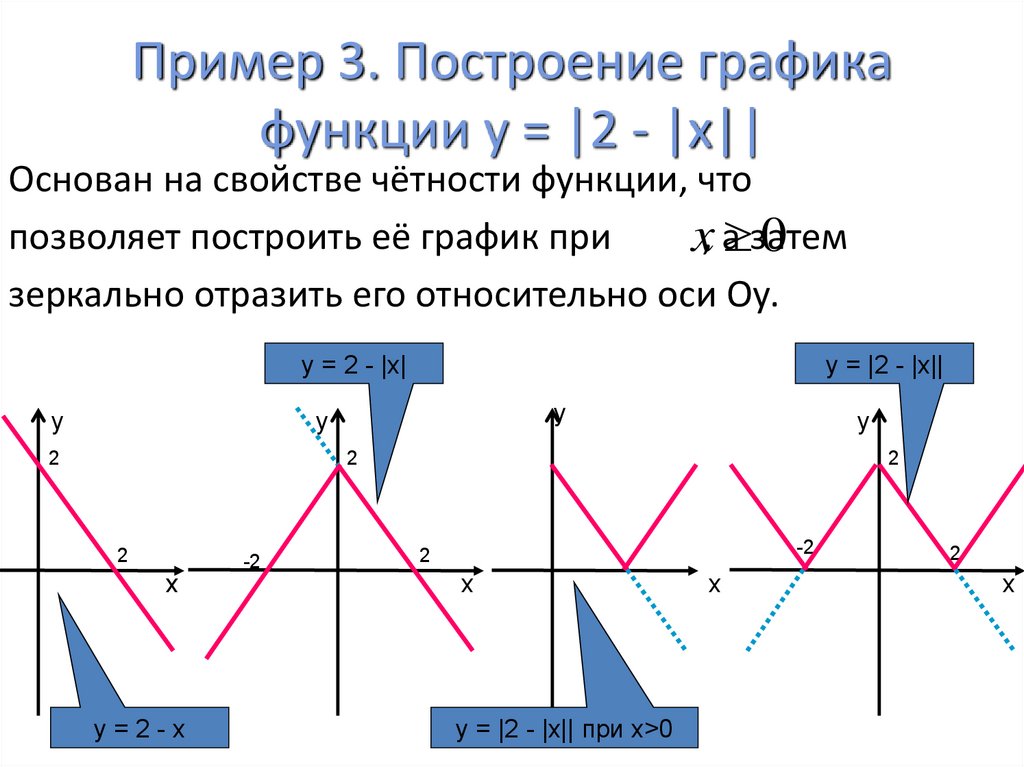
9. Пример 3. Построение графика функции у = |2 - |x||
Основан на свойстве чётности функции, чтопозволяет построить её график при
x, а затем
0
зеркально отразить его относительно оси Оу.
y = 2 - |x|
y
y = |2 - |x||
y
y
y
2
2
2
-2
x
y=2-x
2
-2
2
x
y = |2 - |x|| при x>0
x
2
x
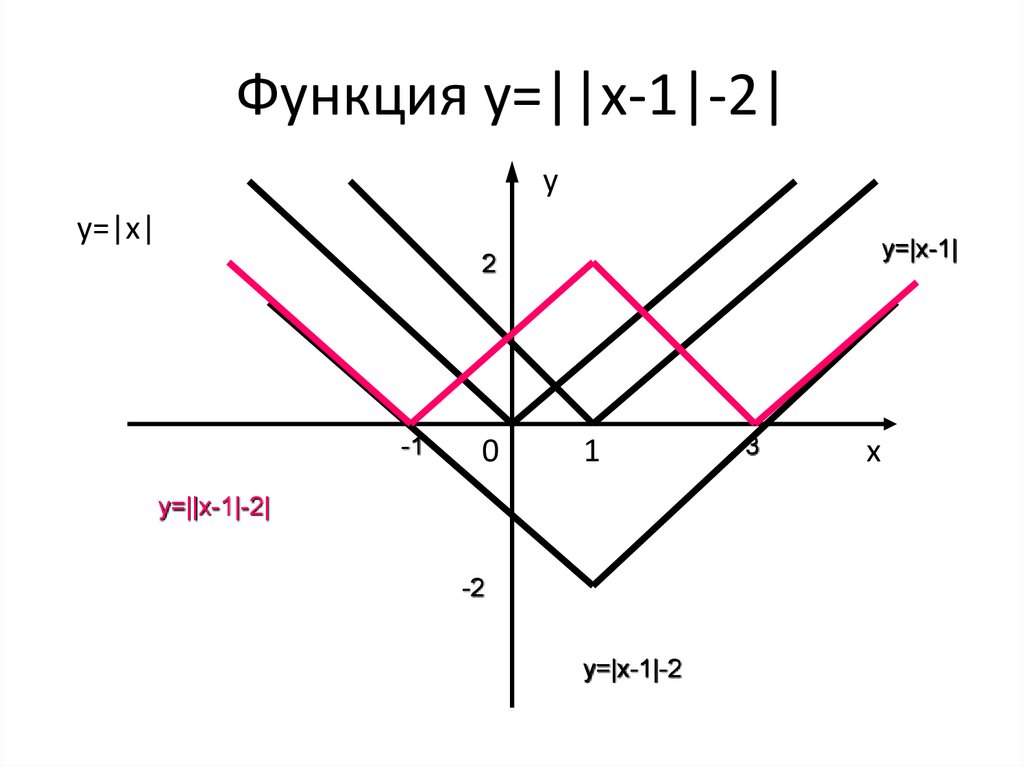
10. Функция y=||x-1|-2|
• Построение.1)Строим график функции y=|x|.
2)Строим график функции y=|x-1|.
3)Строим график функции y= |x-1|-2.
4)Применяем к графику y=|x-1|-2 операцию
“модуль”.
11. Функция y=||x-1|-2|
yy=|x|
y=|x-1|
2
-1
0
1
y=||x-1|-2|
-2
y=|x-1|-2
3
x
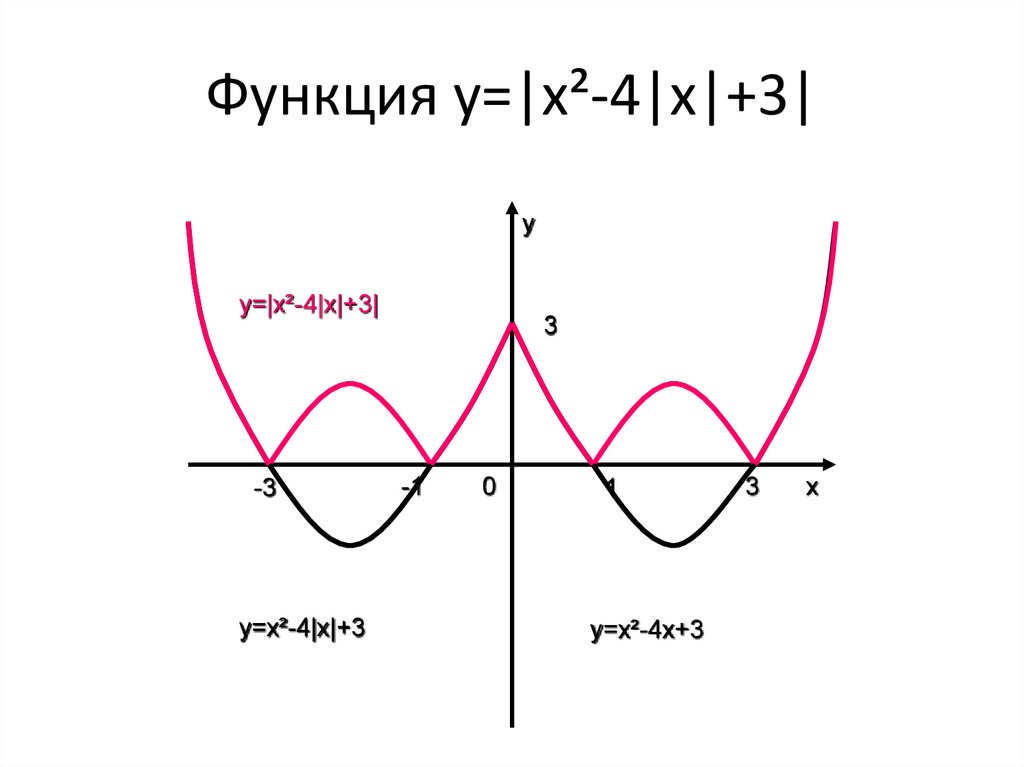
12. Функция y=|x²-4|x|-3|
• Построение.1)Строим график y=x²-4x+3для х≥0
2)y=x²-4|x|+3 — отражаем полученный график в п.1
относительно оси ординат. Функция чётная.
3)y=|x²-4|x|+3| — часть графика, расположенную в
нижней полу плоскости,
отражаем относительно оси абсцисс. Полученная в
верхней полуплоскости линия и будет графиком
заданной функции.
13. Функция y=|x²-4|x|+3|
yy=|x²-4|x|+3|
-3
y=x²-4|x|+3
3
-1
0
1
y=x²-4x+3
3
x
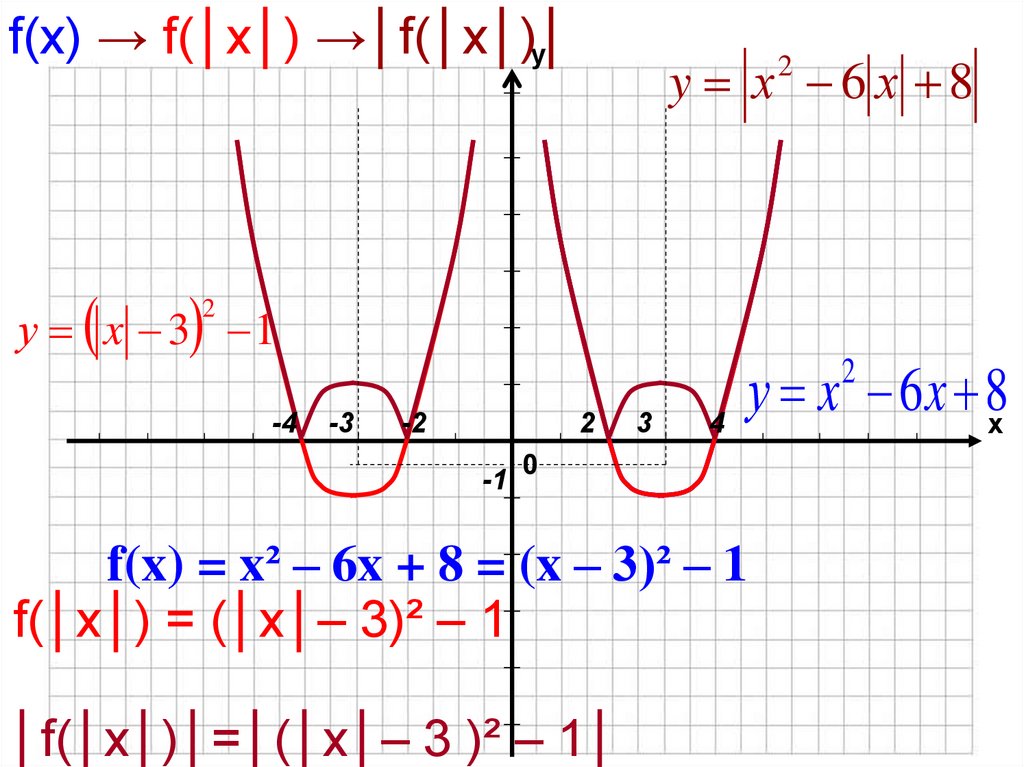
14. f(x) →│f(│x│)│
уf(x) →│f(│x│)│
у f ( x)
х
0
у f (x)
15. f(x) = x² – 6x + 8 = (x – 3)² – 1
f(x) → f(│x│) →│f(│x│)│у
y х 6 х 8
2
у x 3 1
2
-4
у x 6 x 8х
2
-3
-2
2
-1
3
4
0
f(x) = x² – 6x + 8 = (x – 3)² – 1
f(│x│) = (│x│– 3)² – 1
│f(│x│)│=│(│x│– 3 )² – 1│
16. Построение графика функции |y| = f(x) при f(x)
0По определению абсолютной величины у = f (x),
где f(x) 0. Строго говоря, у нельзя назвать
Функцией х, так как каждому значению аргумента
х будут соответствовать два значения
функции: + f(x) и –f(x). Рассмотрим теперь
последовательность действий:
1. установить, для каких х выполняется условие f(x) 0
2. на найденных промежутках значений х построить график
функции у = f(x);
3. осуществить зеркальное отражение графика относительно
оси Ох
17. Построение графиков функций |y| = |f(x)|
Очевидно, что у = f (x) , т.е. график функции будетсимметричен относительно абсцисс.
Соответствующая последовательность действий:
1. построить график функции у = |f(x)|;
2. осуществить его зеркальное отражение
относительно оси Ох.
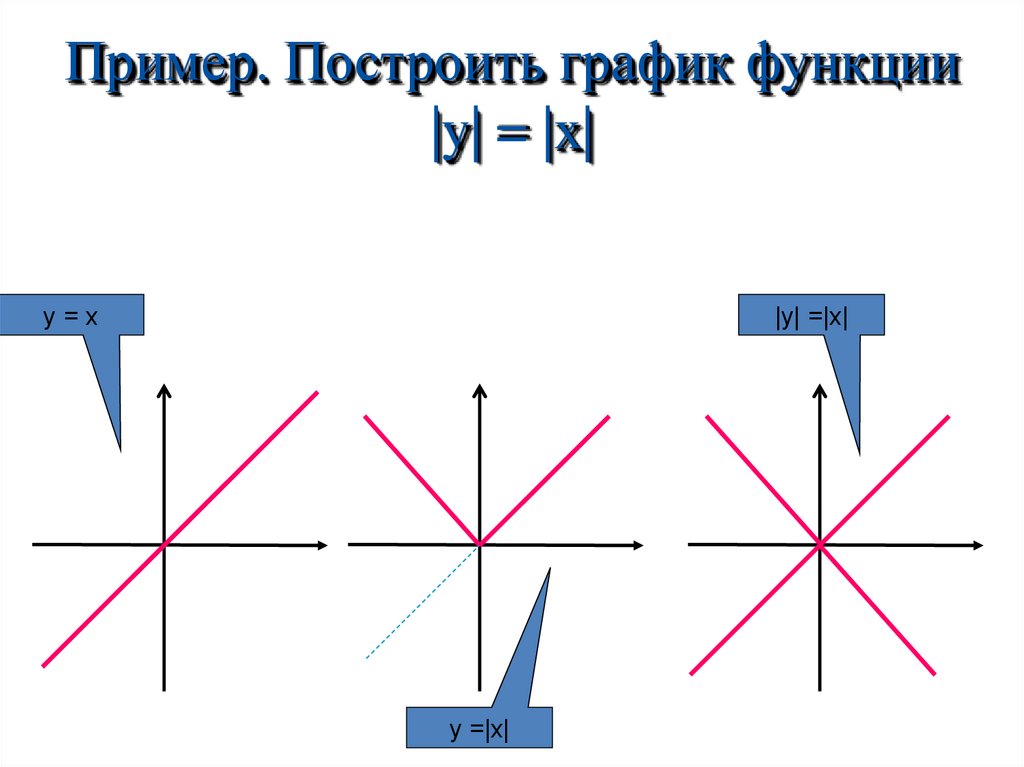
18. Пример. Построить график функции |y| = |x|
y=x|y| =|x|
y =|x|
19. Построение графиков функций вида y = |x – x1| + |x – x2| + ...+ |x – xn|
Укажем последовательность действий:1. Найдём абсциссы точек перелома графика функции. В данном
случае используем для этого условия: хn – 1=0; xn=1; xn – 2=0,
xn = 2
2. Рассмотрим далее функцию на каждом из полученных
промежутков. В рассматриваемом примере
их три ( ;1 1;2 2;
а) х 2; . Так как оба слагаемых неотрицательны, то на этом
промежутке графиком функции будет прямая, выражаемая
уравнением у = 2х-3.
б) х 1;2 . Первое слагаемое на данном промежутке
неотрицательно, второе отрицательно и потому графиком будет
прямая у = 1.
в) х 2; . Оба слагаемых отрицательны и потому графиком
будет прямая у = 3-2х
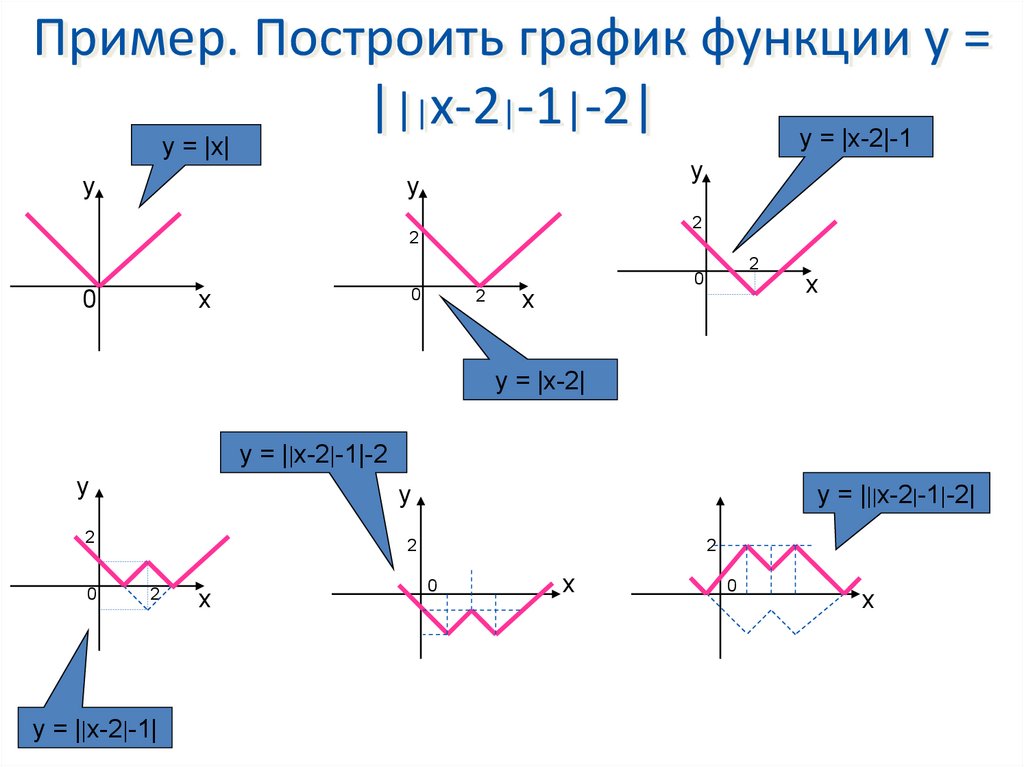
20. Пример. Построить график функции у = |||x-2|-1|-2|
y = |x-2|-1y = |x|
y
y
y
2
2
х
0
0
2
2
0
х
х
y = |x-2|
y = ||x-2|-1|-2
y
y
2
2
0
2
y = ||x-2|-1|
х
y = |||x-2|-1|-2|
2
0
х
0
х
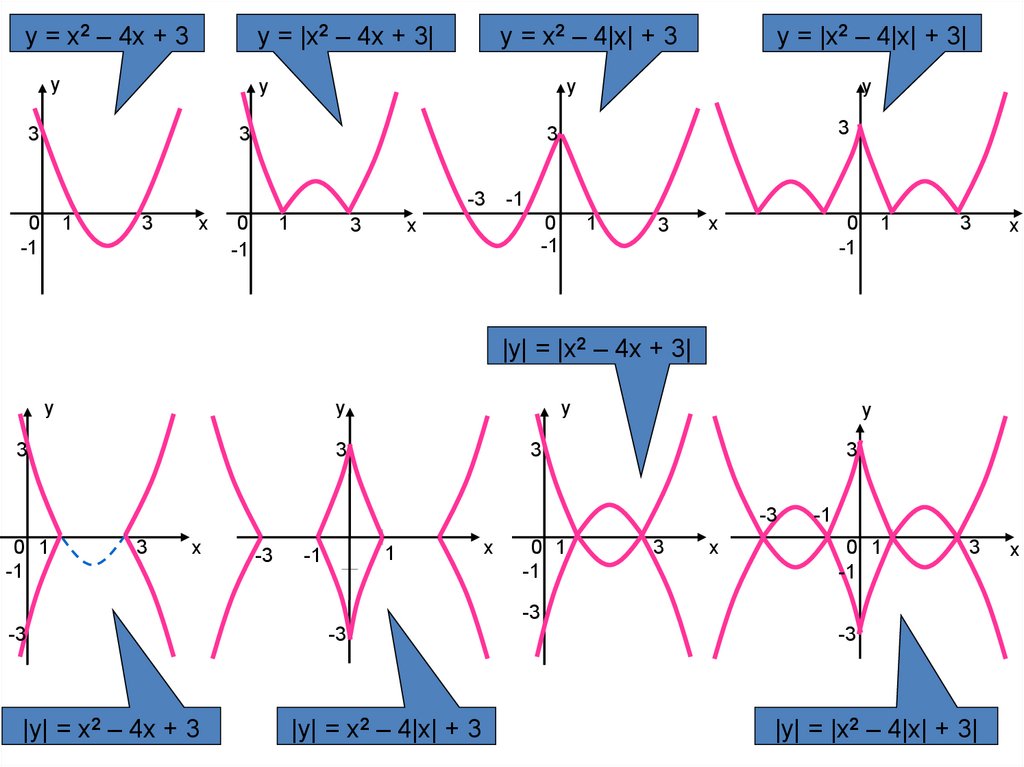
21. График функции y = x2 – 4x + 3
22.
y = x2 – 4x + 3y = |x2 – 4x + 3|
y
y = x2 – 4|x| + 3
y
3
y
3
1
3
х
y
3
3
-3
0
-1
y = |x2 – 4|x| + 3|
0
-1
1
-1
х
3
0
-1
1
3
х
0
-1
1
3
х
|y| = |x2 – 4x + 3|
y
y
3
y
3
y
3
3
-3
0 1
-1
3
х
-3
1
-1
х
0 1
-1
3
х
-1
0 1
-1
3
-3
-3
|y| = x2 – 4x + 3
-3
|y| = x2 – 4|x| + 3
-3
|y| = |x2 – 4|x| + 3|
х
23.
1График функции y =
x-1
24.
y1
x 1
y
y
1
x 1
y
y
y
х
1
x 1
1
x 1
y
х
у
1
x 1
y
y
х
у
1
x 1
х
х
у
y
y
y
х
х
y
1
x 1
1
x 1
х
25.
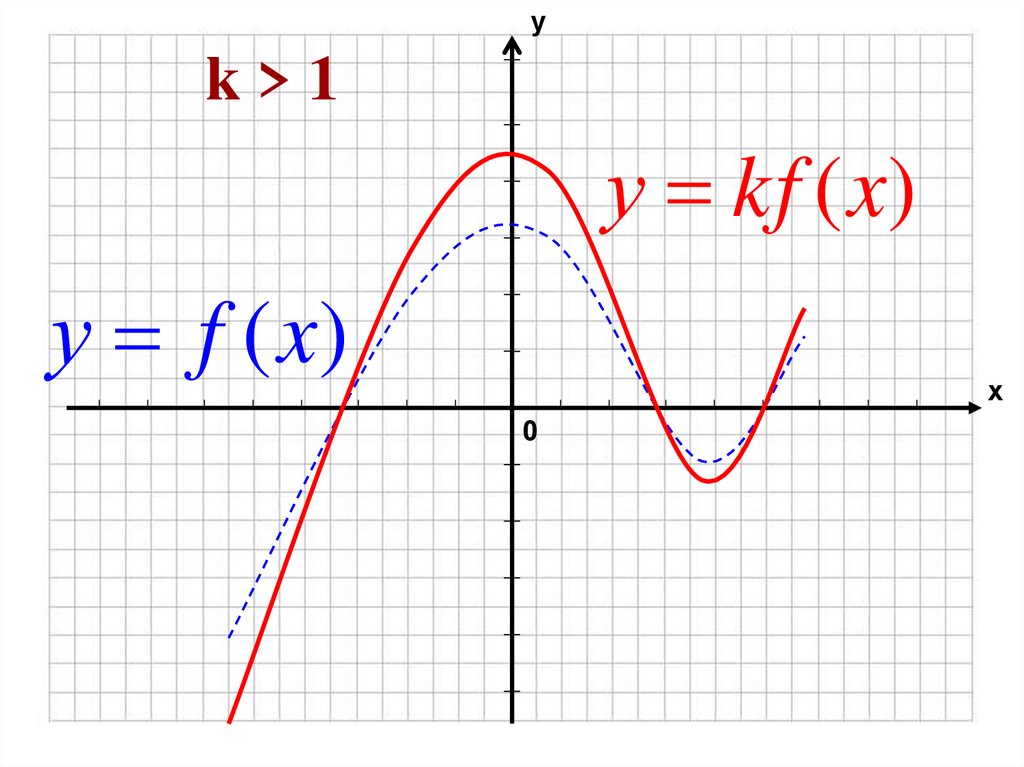
f (x) kf (x), где k 01. k > 1
2. 0 < k < 1
26.
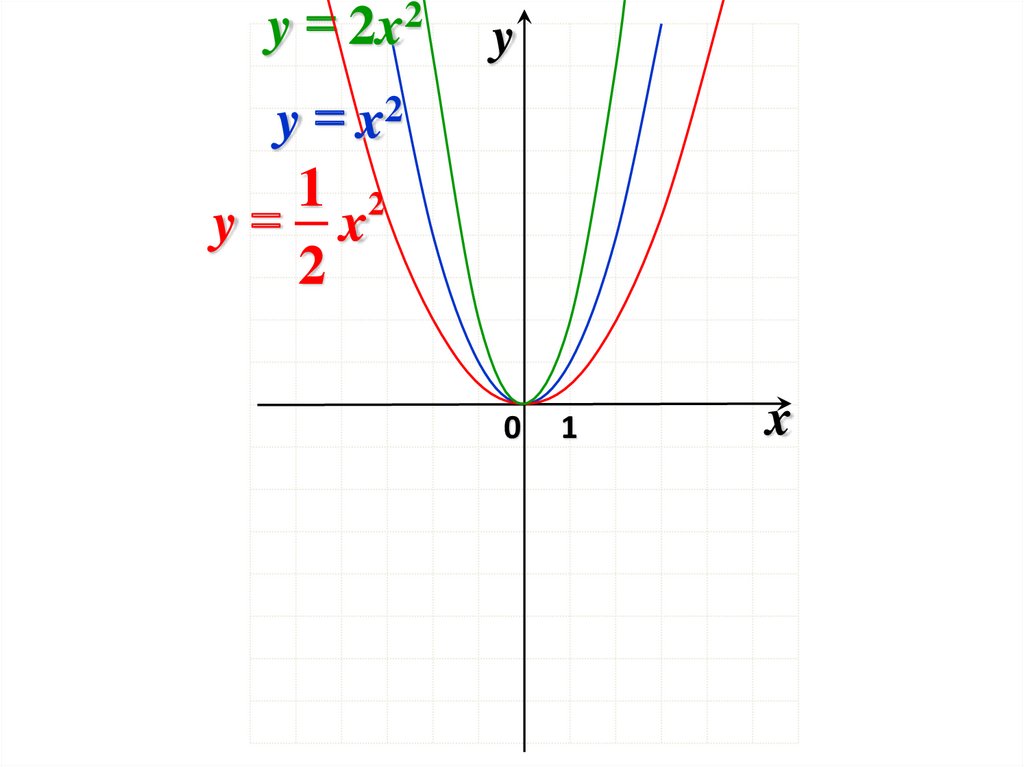
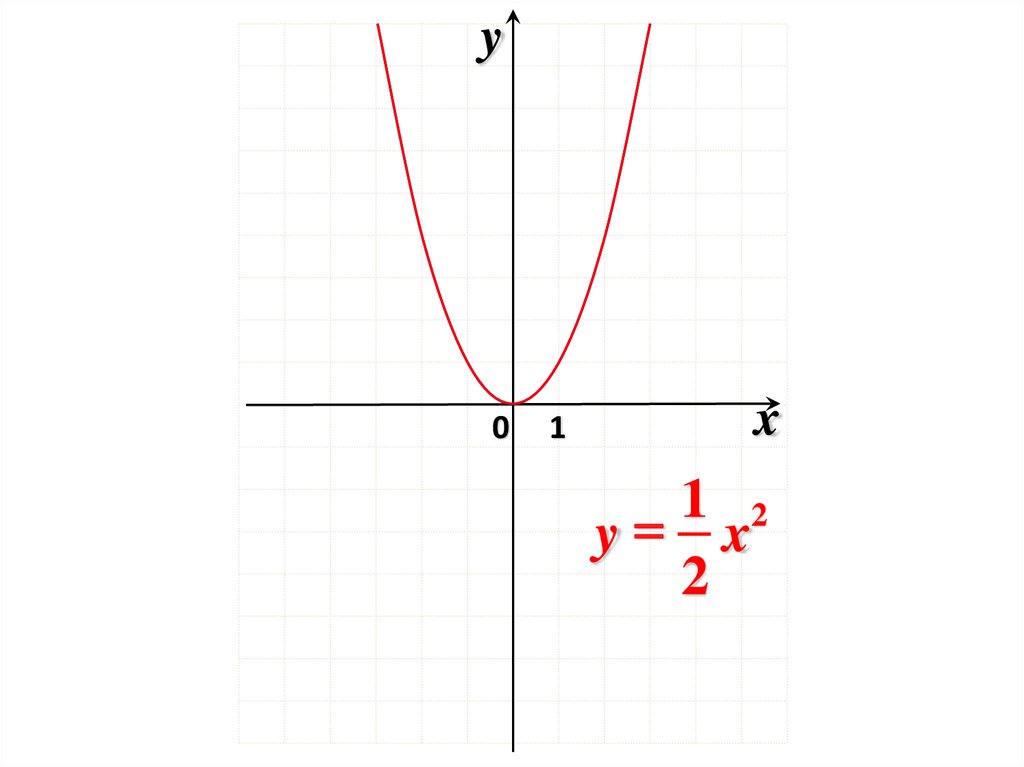
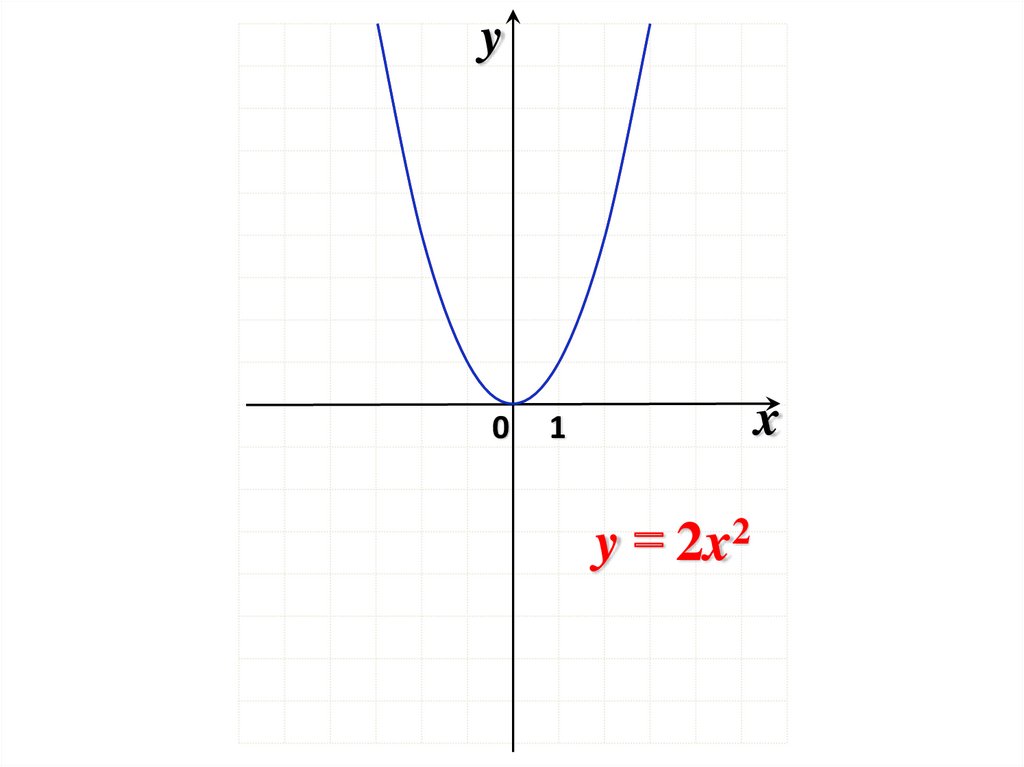
y 2x2y
y x2
1 2
y x
2
0
1
x
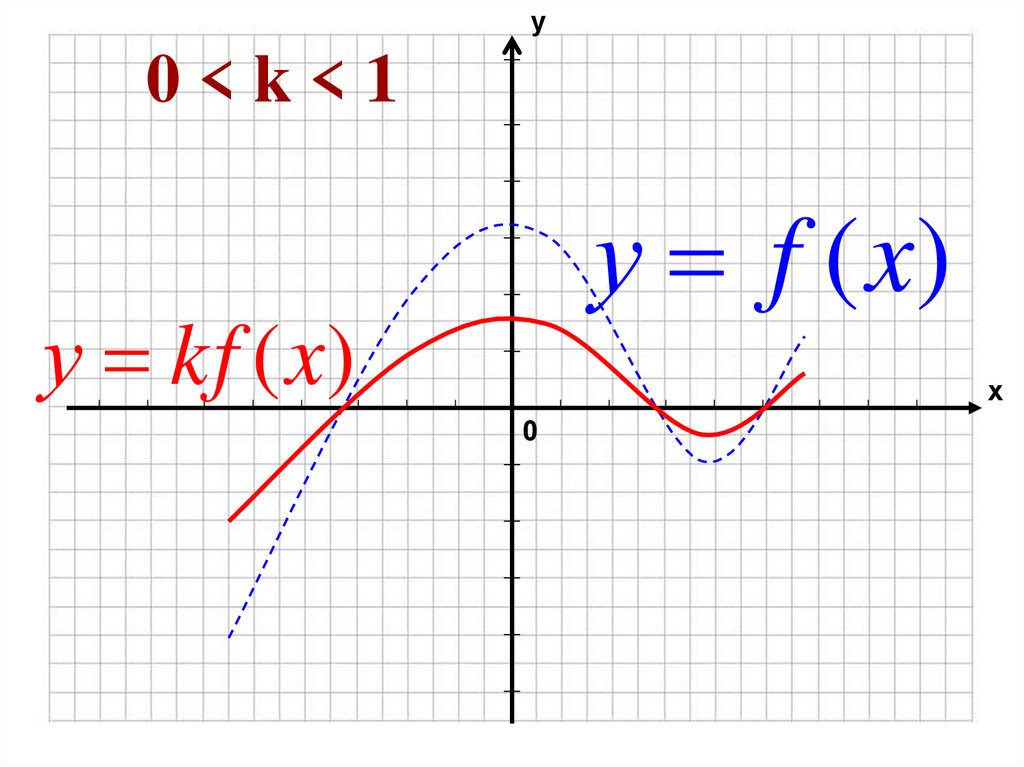
27. 0 < k < 1
у0<k<1
у f (x)
у kf (x)
х
0
28.
y0
1
x
1 2
y x
2
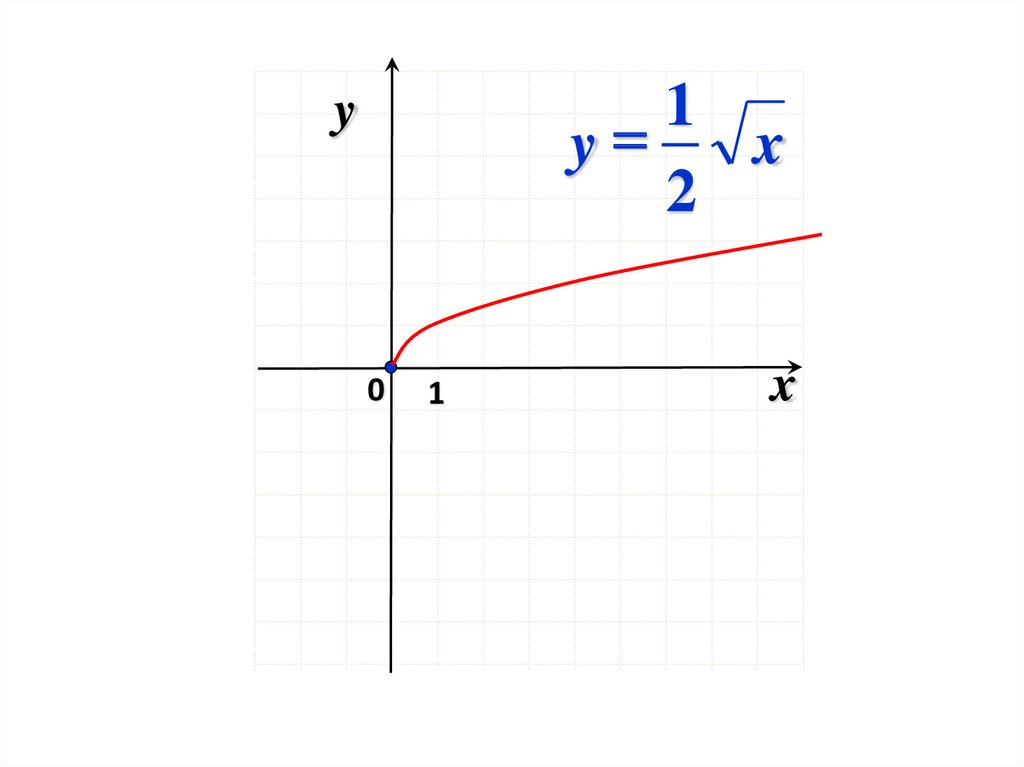
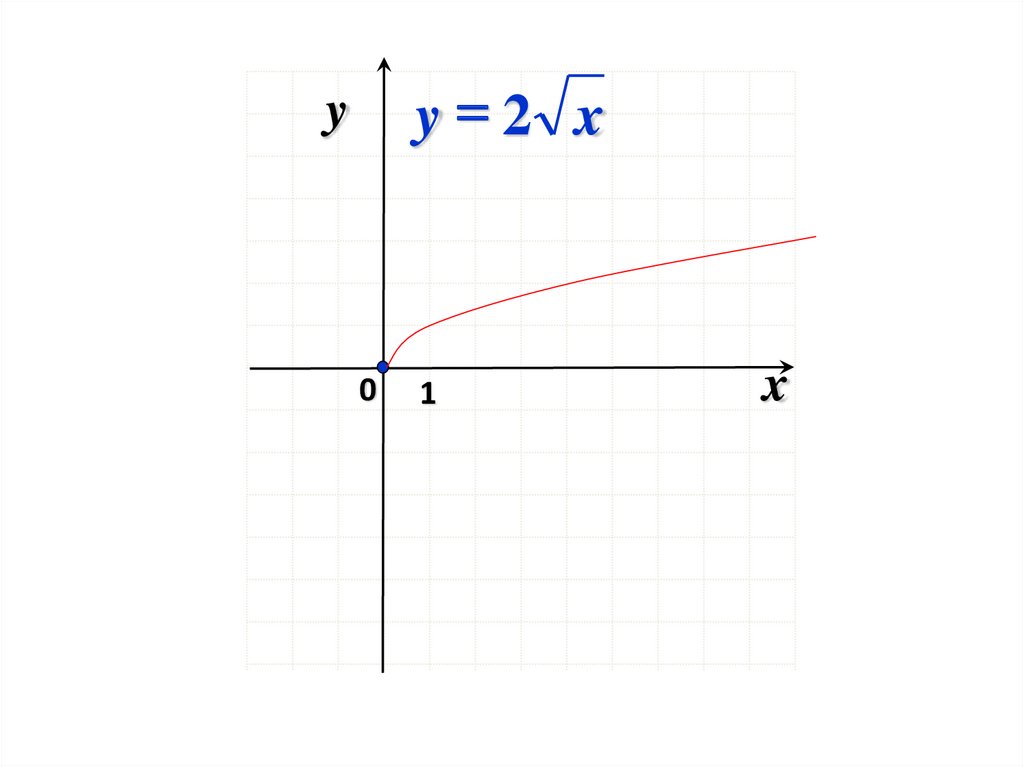
29.
1y
x
2
y
0
1
x
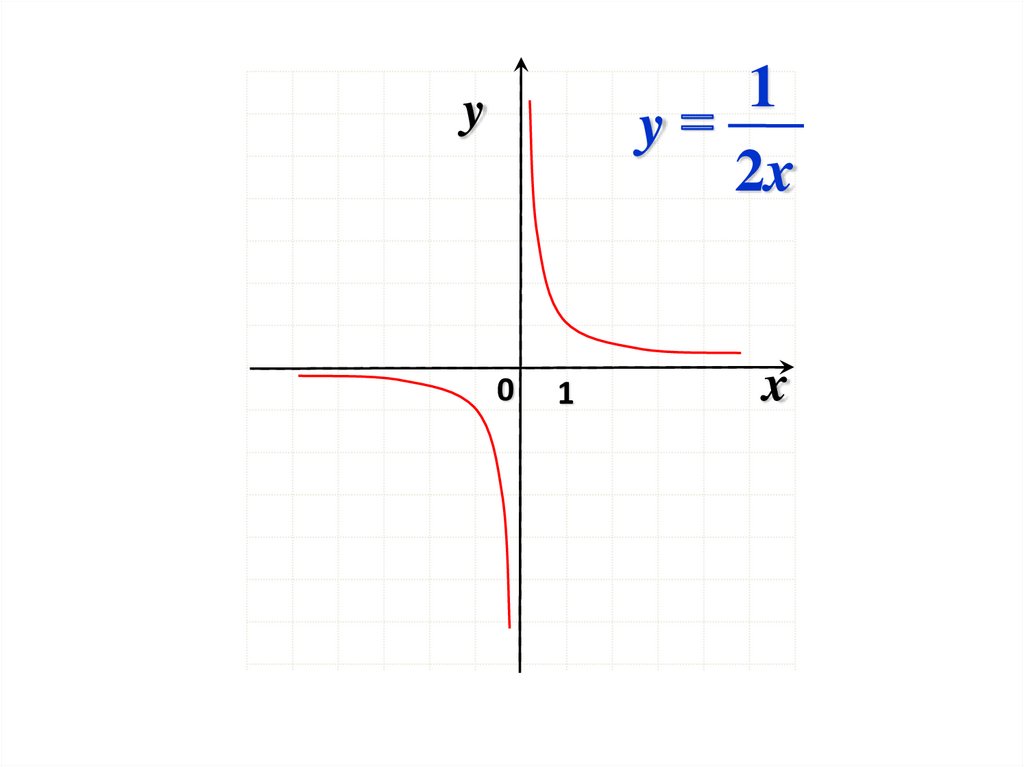
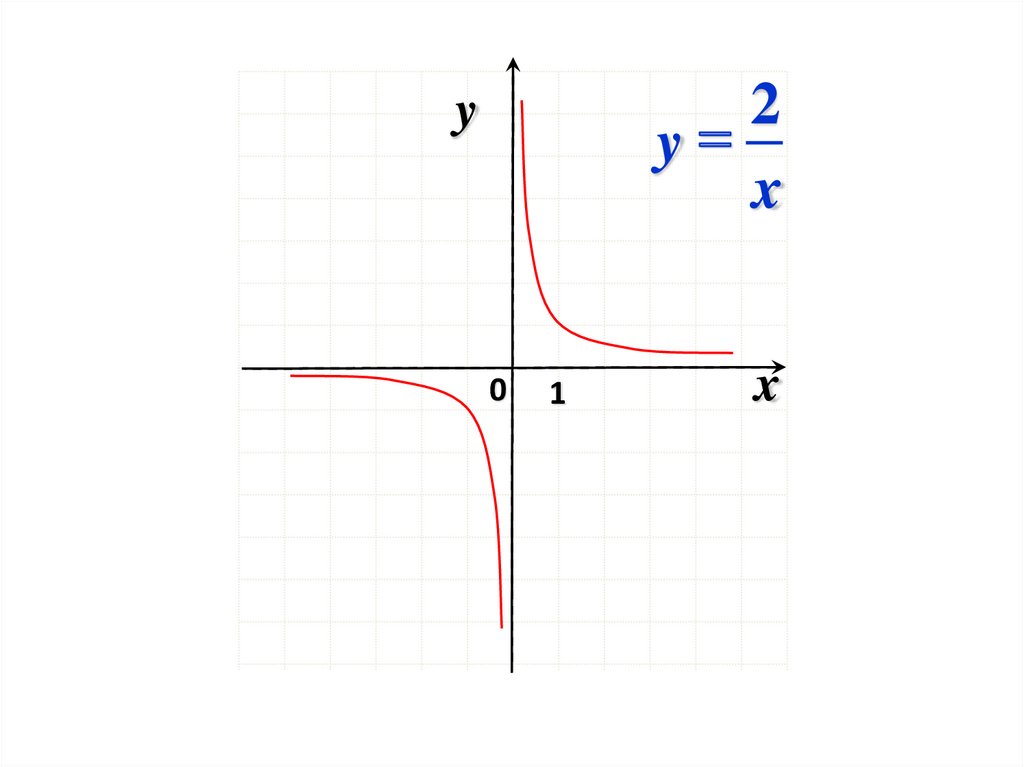
30.
1y
2x
y
0
1
x
31. k > 1
уk>1
у kf (x)
у f (x)
х
0
32.
y0
x
1
y 2x2
33.
y 2 xy
0
1
x
34.
2y
x
y
0
1
x
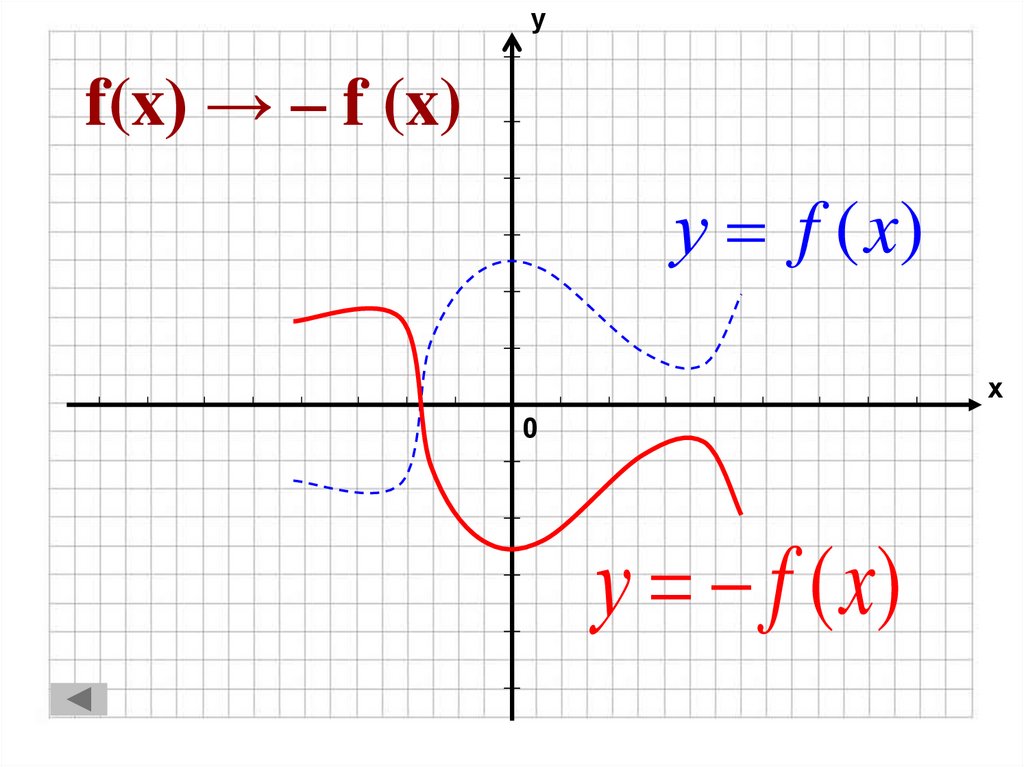
35. f(x) → – f (x)
уf(x) → – f (x)
у f (x)
х
0
у f (x)
36. f(x) → f(kx)
1.2.
0<k<1
k>1
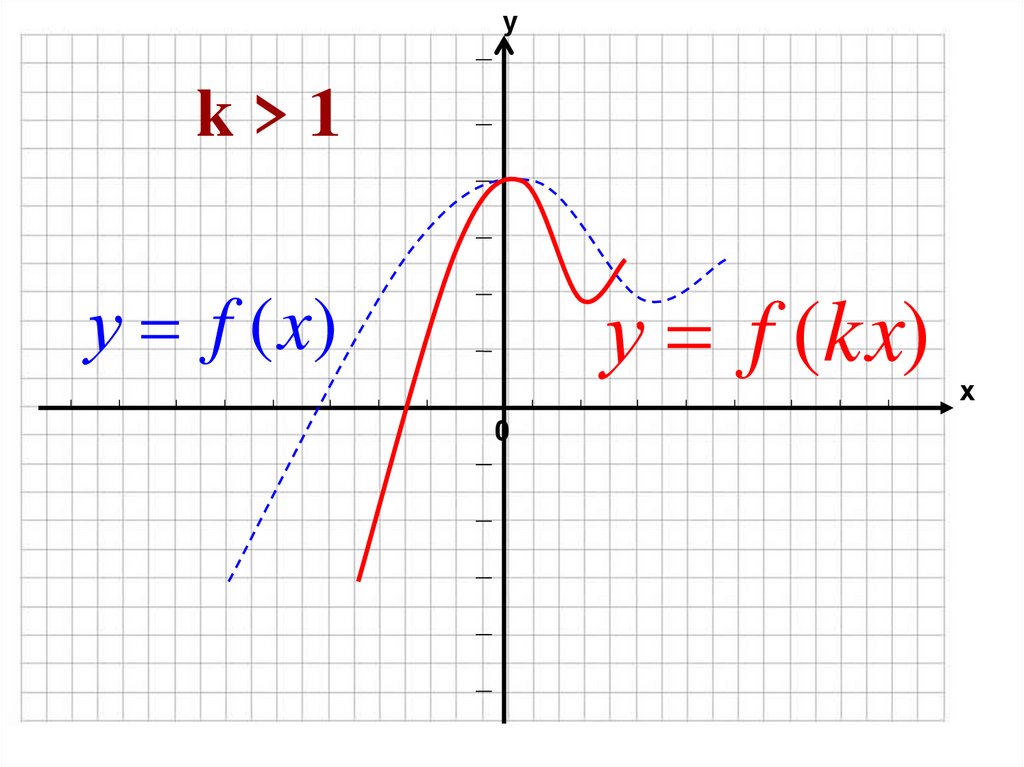
37. k > 1
уk>1
у f (kx)
у f (x)
0
х
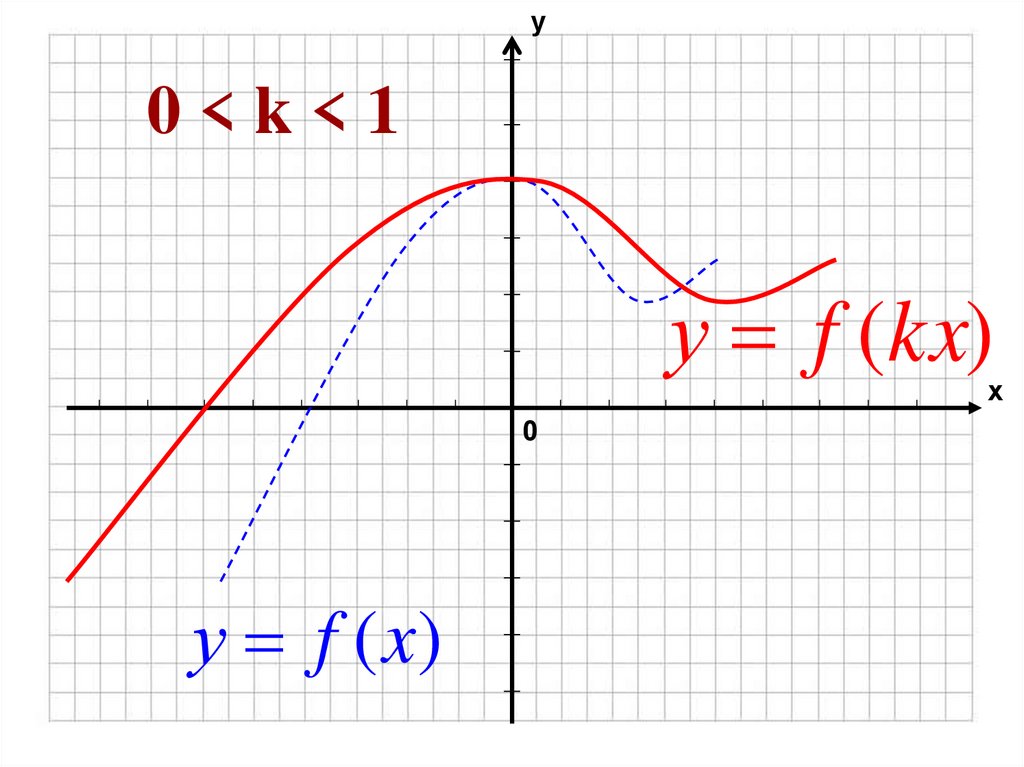
38. 0 < k < 1
у0<k<1
у f (kx)
х
0
у f (x)
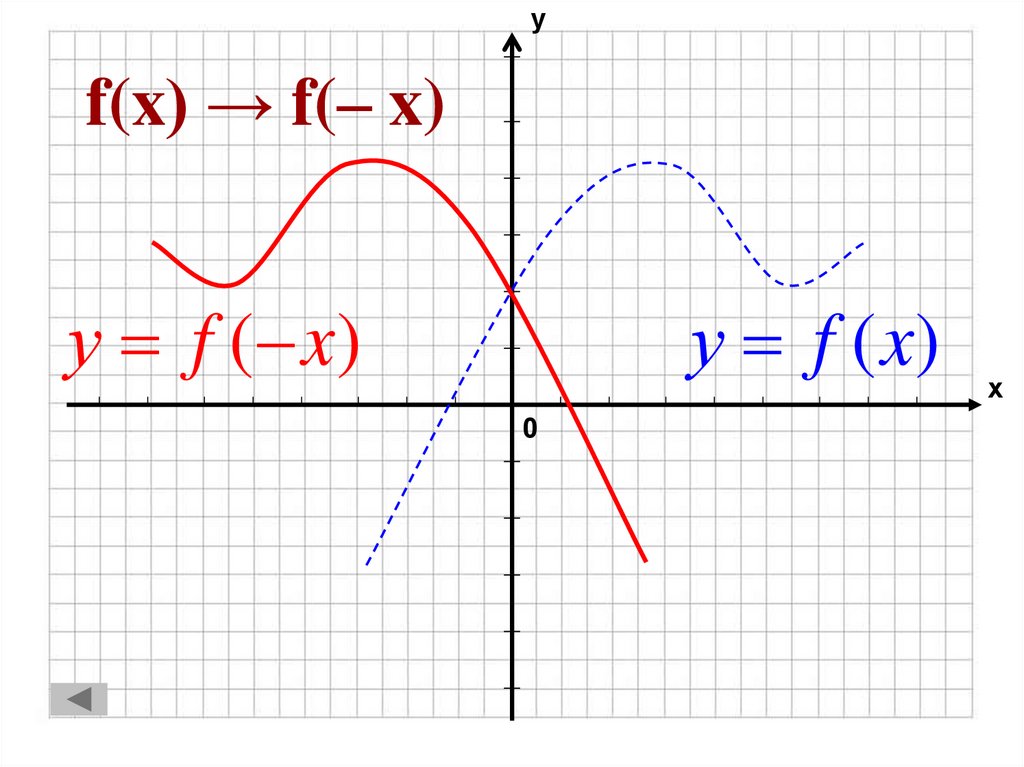
39. f(x) → f(– x)
уf(x) → f(– x)
у f ( x)
у f (x)
0
х
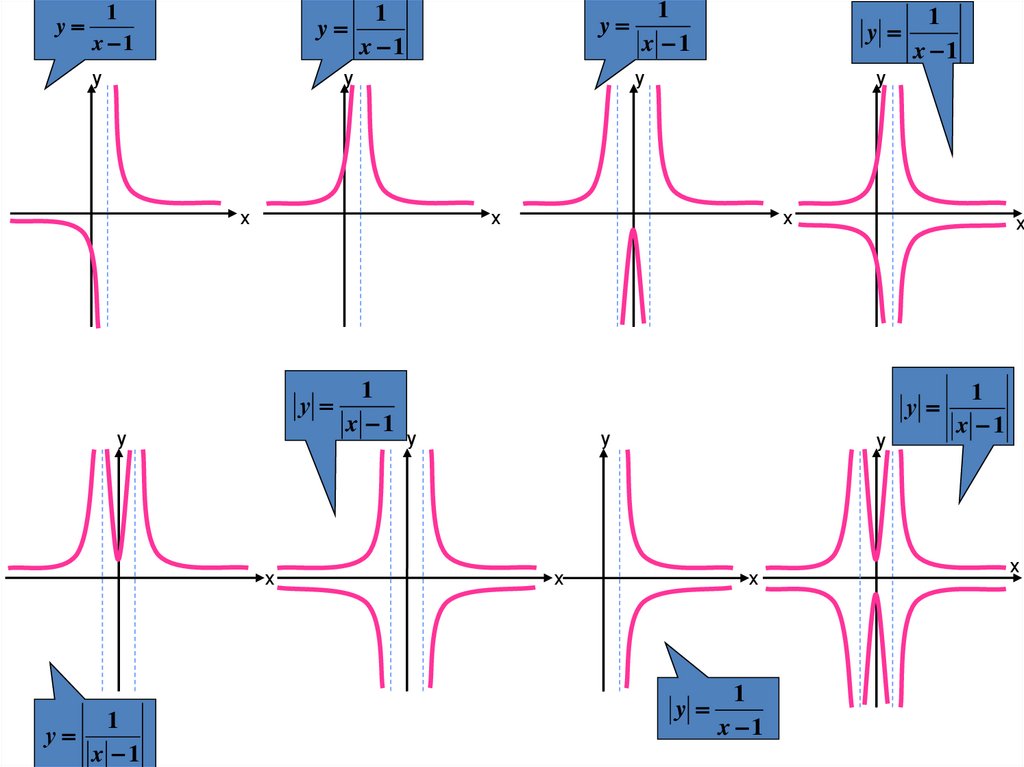
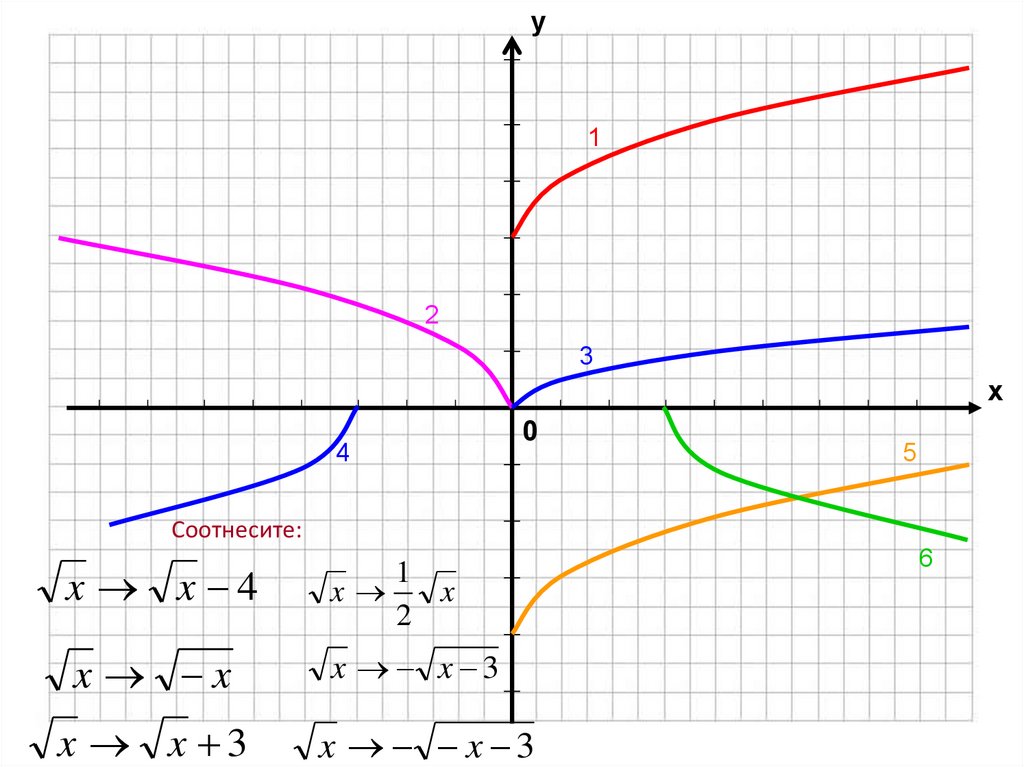
40. Соотнесите:
у1
2
3
х
4
0
5
Соотнесите:
x x 4
1
x
x
2
x x
x x 3
x x 3
x x 3
6











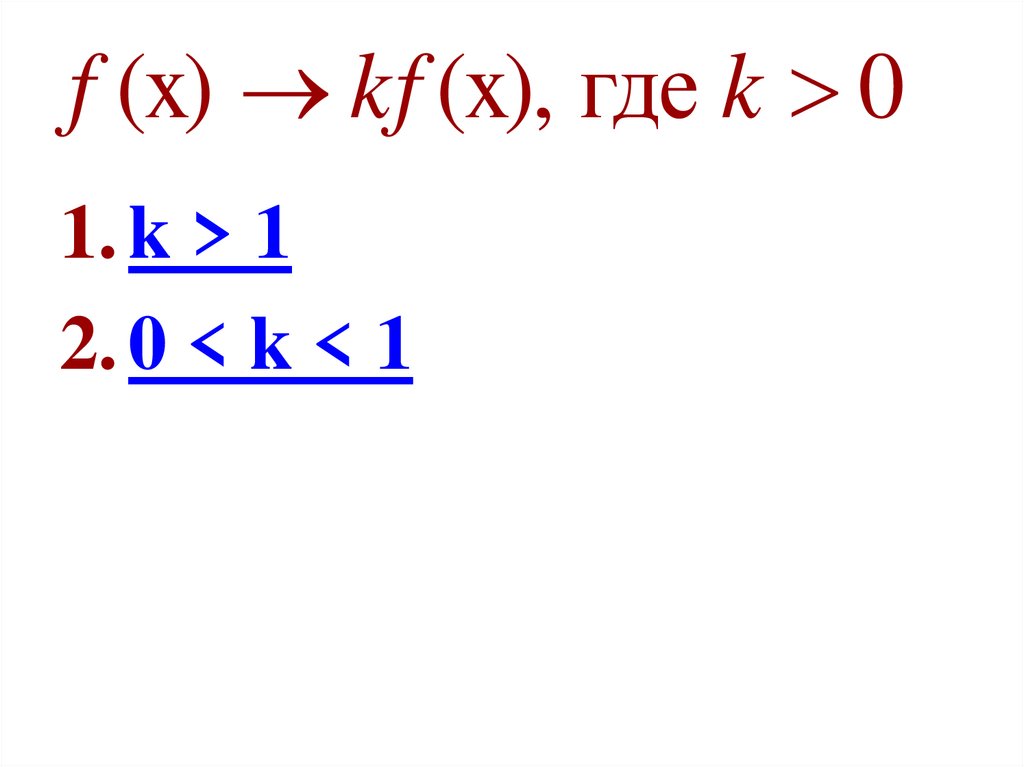
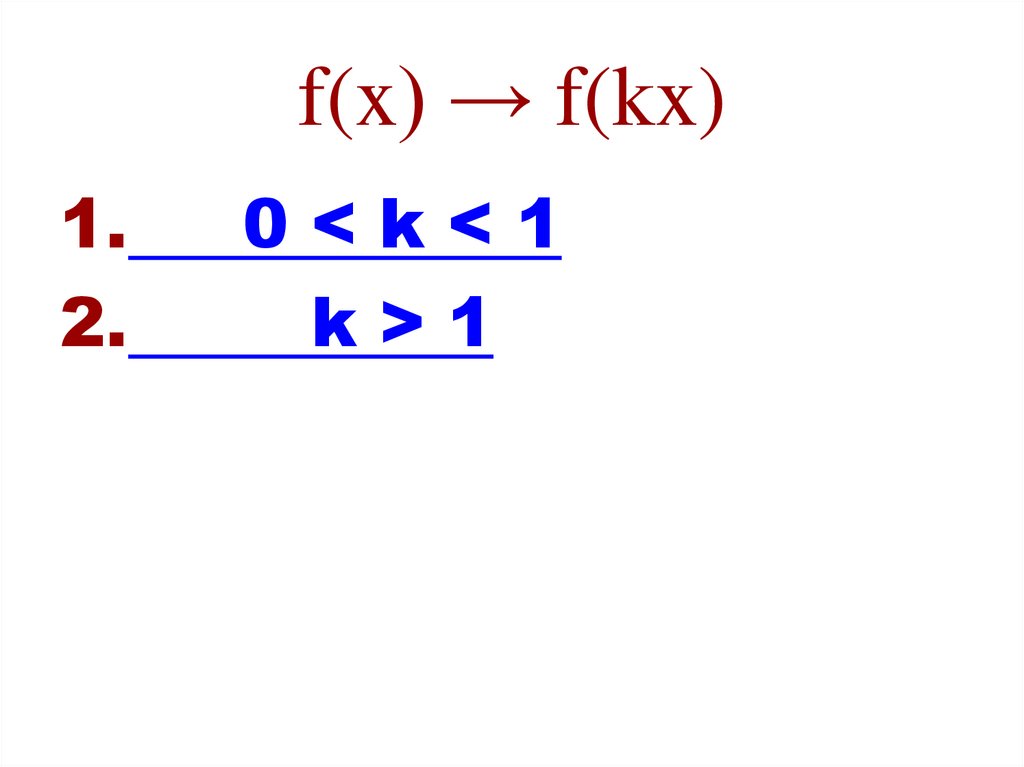
 mathematics
mathematics








