Similar presentations:
Построение графиков квадратичной функции, содержащей модуль
1. Построение графиков квадратичной функции, содержащей модуль
2. Актуализация опорных знаний
1.2.
3.
4.
5.
6.
7.
8.
Определение квадратичной функции
Алгоритм построения квадратичной функции
Как, зная график функции y=f(x) построить графики следующих
функций:
y=f(-x)
y=-f(x)
y=f(x+m)
y=f(x)+n
y=f(x+m)+n
y=kf(x)
y=|f(x)|
y=f(|x|)
3. Устно Дан график функции y = x2 – 4x + 3. Составьте формулу функции, график которой:
1) симметричен данному относительно оси:а) x;
б) y;
2) получается из данного параллельным переносом на
1а) y = –x2 + 4x – 3;
1б) y = x2 + 4x + 3
2
y = x2 – 6x + 6;
(1; 2)
3) получается из данного растяжением в 2 раза от оси
а) x;
б) y
4) получается из данного сжатием в 2 раза к оси
а) x;
б) y
3а) y = 0,25x2 – 2x + 3;
3б) y = 2x2 – 8x + 6;
4а) y = 4x2 – 8x + 3
4б) y = 0,5x2 – 2x + 1,5;
4.
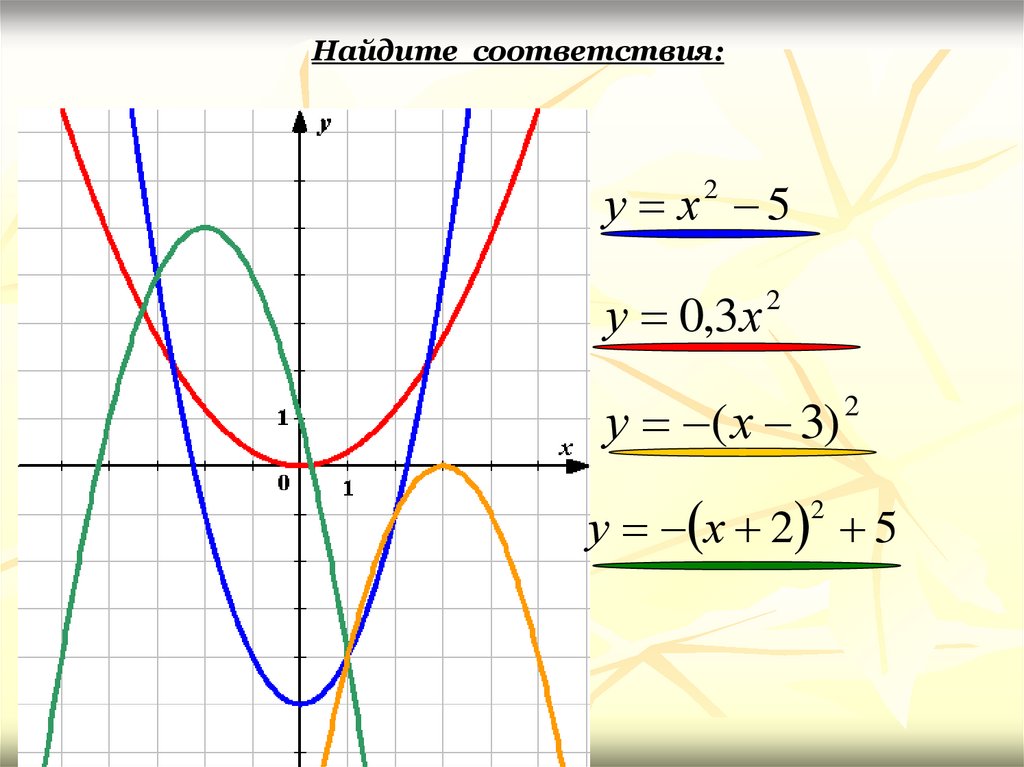
Найдите соответствия:у х2 5
у 0,3х
2
у ( х 3)
2
у х 2 5
2
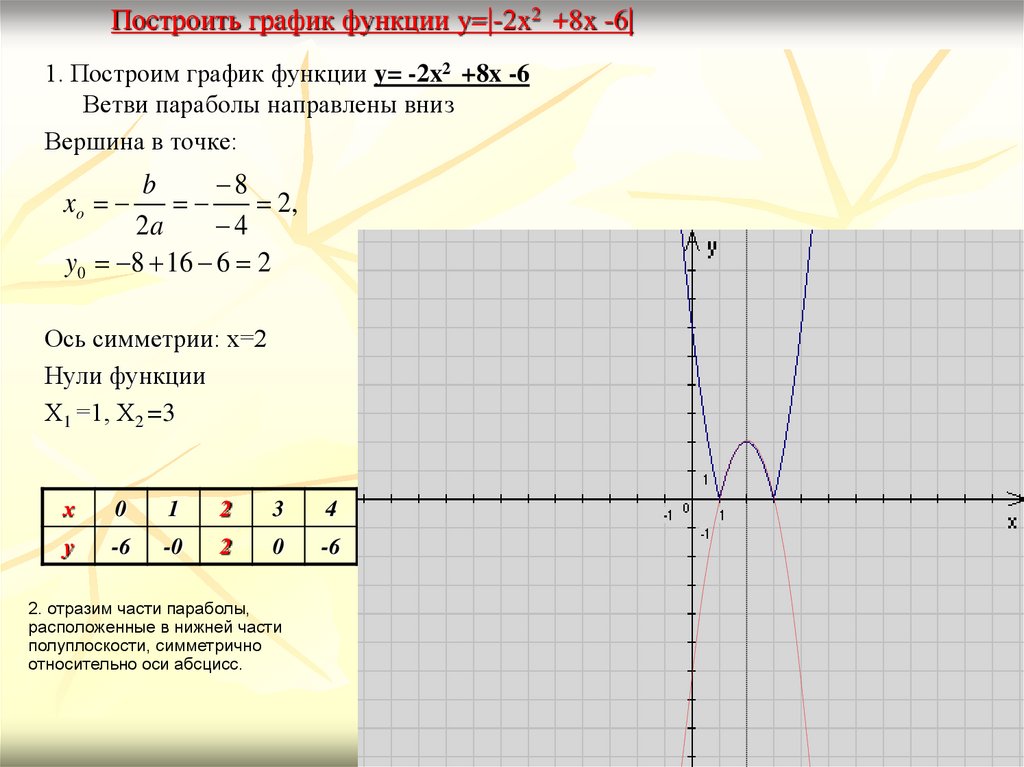
5. Построить график функции y=|-2x2 +8x -6|
1. Построим график функции y= -2x2 +8x -6Ветви параболы направлены вниз
Вершина в точке:
b
8
2,
2a
4
y0 8 16 6 2
xo
Ось симметрии: х=2
Нули функции
Х1 =1, Х2 =3
х
0
1
2
3
4
у
-6
-0
2
0
-6
2. отразим части параболы,
расположенные в нижней части
полуплоскости, симметрично
относительно оси абсцисс.
6.
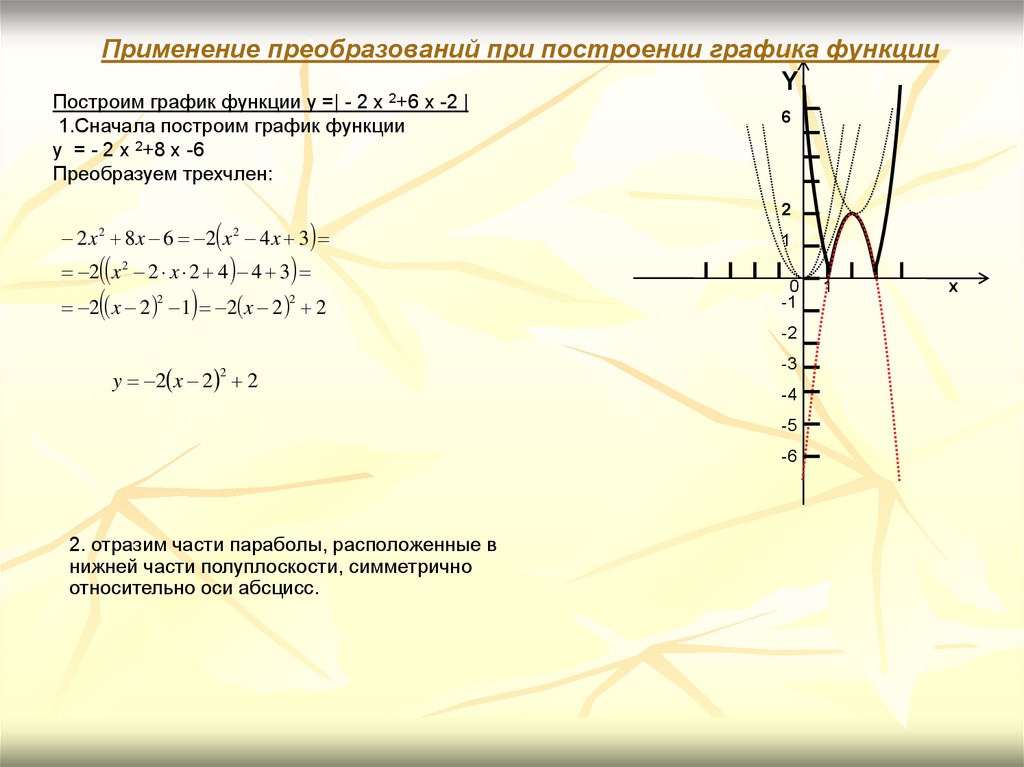
Применение преобразований при построении графика функцииY
2
Построим график функции y =| - 2 x +6 x -2 |
1.Сначала построим график функции
y = - 2 x 2+8 x -6
Преобразуем трехчлен:
2 x 8 x 6 2 x 4 x 3
2
2
2 x 2 2 x 2 4 4 3
2 x 2 1 2 x 2 2
2
2
6
2
1
0
-1
-2
y 2 x 2 2
2
-3
-4
-5
-6
2. отразим части параболы, расположенные в
нижней части полуплоскости, симметрично
относительно оси абсцисс.
1
x
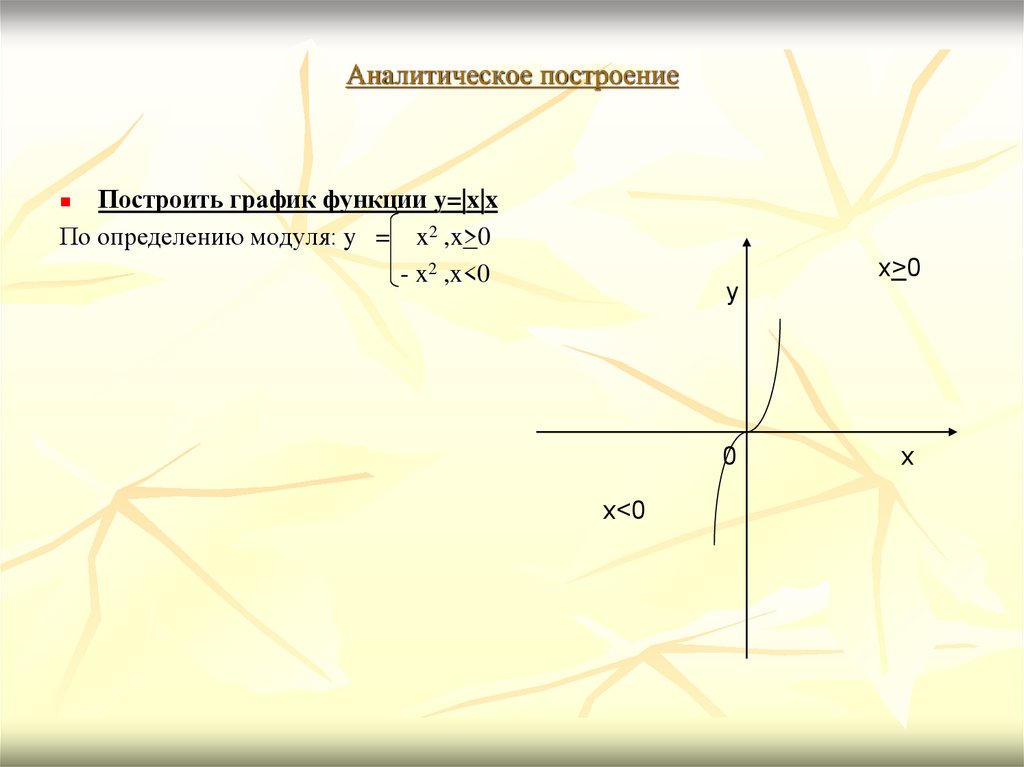
7. Аналитическое построение
Построить график функции y=|x|xПо определению модуля: y = x2 ,x>0
- x2 ,x<0
x>0
y
0
x<0
x
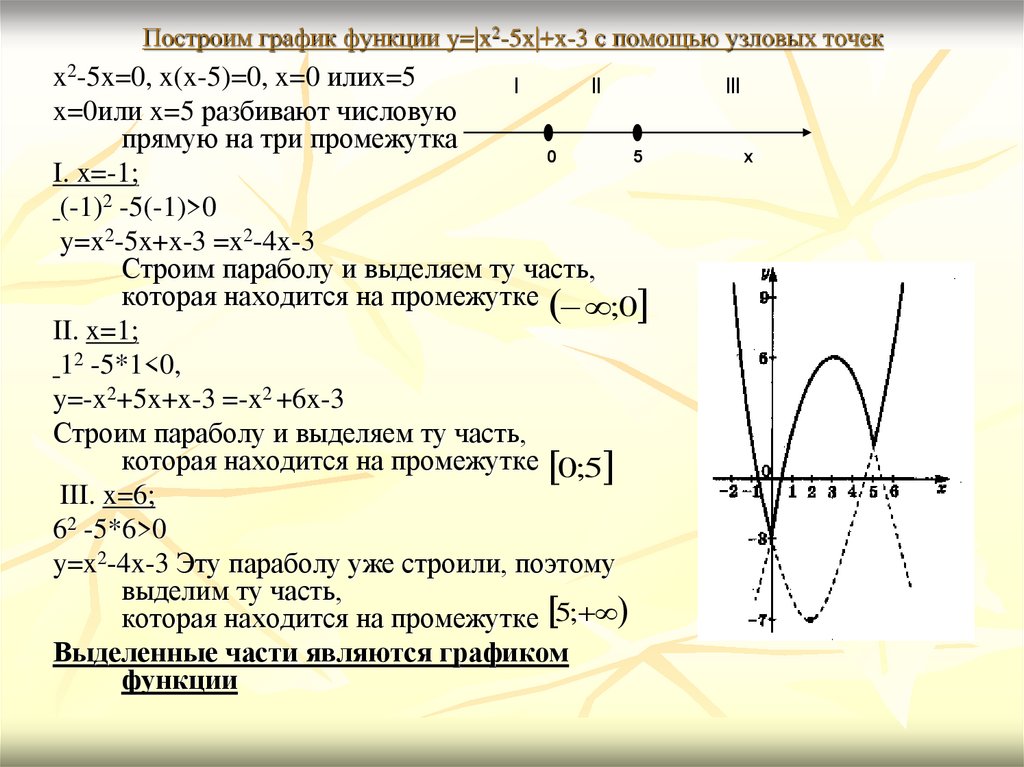
8. Построим график функции y=|x2-5x|+x-3 с помощью узловых точек
x2-5x=0, x(x-5)=0, x=0 илиx=5|
||
x=0или x=5 разбивают числовую
прямую на три промежутка
0
5
I. x=-1;
(-1)2 -5(-1)>0
y=x2-5x+x-3 =x2-4x-3
Строим параболу и выделяем ту часть,
которая находится на промежутке ;0
II. x=1;
12 -5*1<0,
y=-x2+5x+x-3 =-x2 +6x-3
Строим параболу и выделяем ту часть,
которая находится на промежутке 0;5
III. x=6;
62 -5*6>0
y=x2-4x-3 Эту параболу уже строили, поэтому
выделим ту часть,
которая находится на промежутке 5;
Выделенные части являются графиком
функции
|||
x
9. Постройте графики функций:
Вариант 1а) y=|x2 -4|
б) y=|2x-x2 |
Вариант 2
а)y=|x2 -1|
б) y=|x2 +2x-1|
Вариант 3
Вариант 4
а) y=|(x-3)2 -1| б) а) y=|-(x+2)2 +3|
y=x2 -|x-1|
б) y=|2+4|x|-x2|
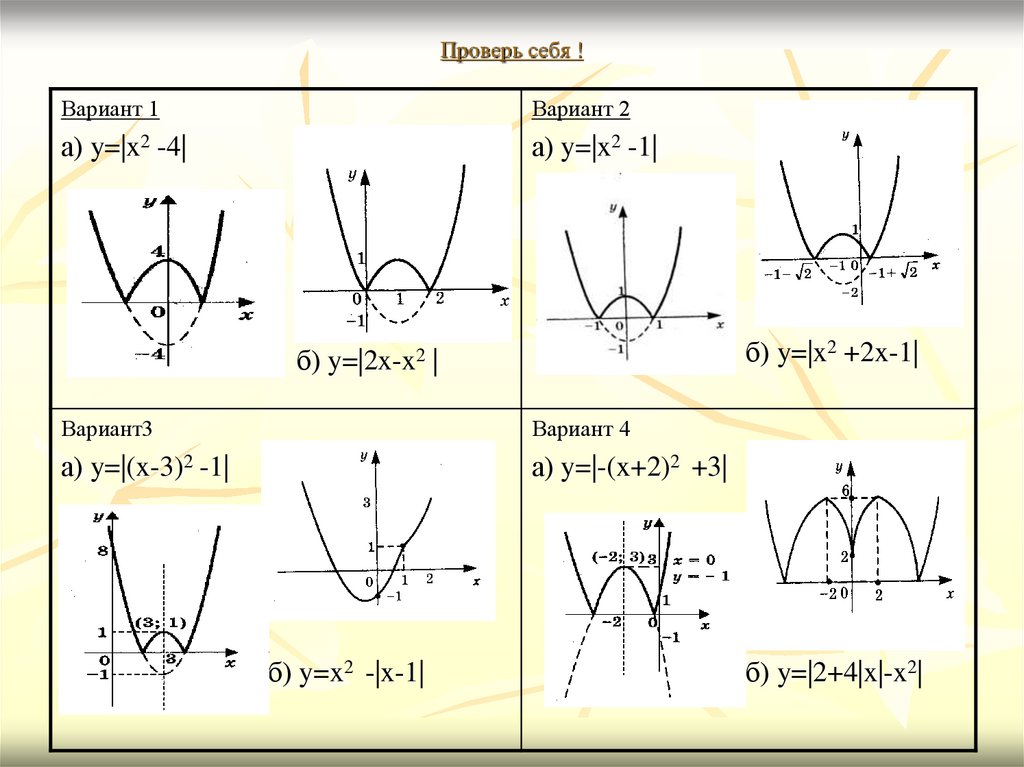
10. Проверь себя !
Вариант 1Вариант 2
а) y=|x2 -4|
а) y=|x2 -1|
б) y=|x2 +2x-1|
б) y=|2x-x2 |
Вариант3
Вариант 4
а) y=|(x-3)2 -1|
а) y=|-(x+2)2 +3|
б) y=x2 -|x-1|
б) y=|2+4|x|-x2|
11. Основные преобразования графиков:
параллельные переносы;симметрии относительно осей координат;
растяжения (сжатия) от (к) осей (осям) координат;
преобразования, связанные с модулями.
12. Алгоритм построения графика функции у = ах2 + bх +с.
1. Определить направление ветвей параболы.2. Найти координаты вершины параболы
(т; п).
3. Провести ось симметрии.
4. Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
5. Составить таблицу значений функции
с учетом оси симметрии параболы.
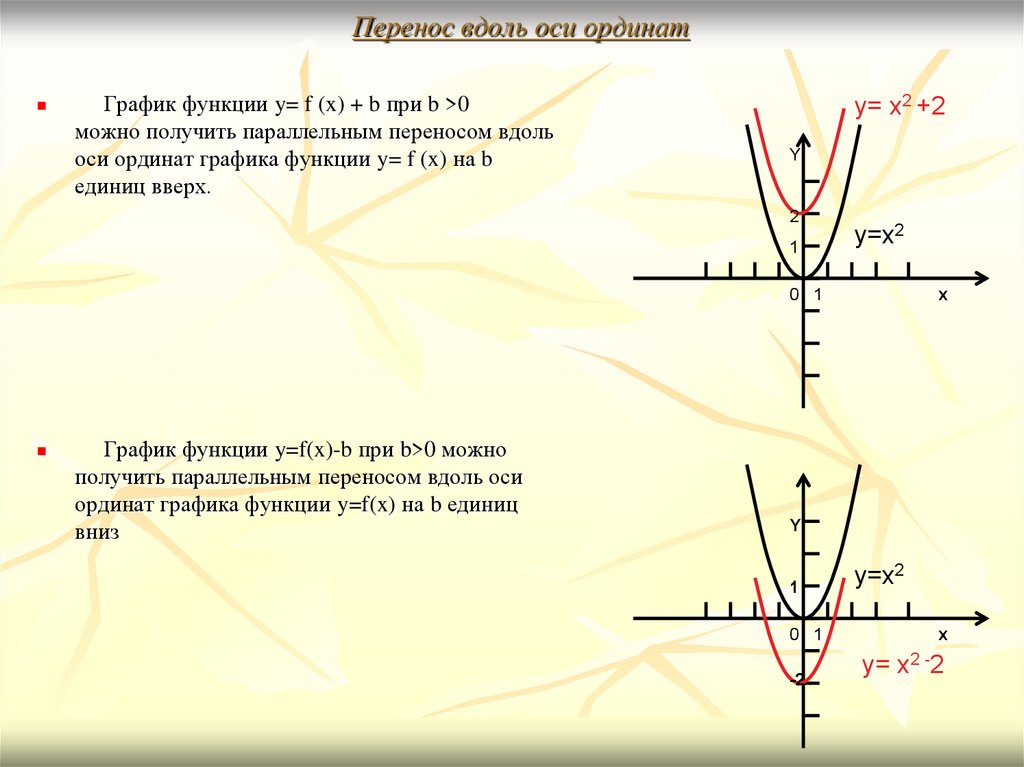
13. Перенос вдоль оси ординат
График функции y= f (x) + b при b >0можно получить параллельным переносом вдоль
оси ординат графика функции y= f (x) на b
единиц вверх.
y= x2 +2
Y
2
1
y=x2
0 1
График функции y=f(x)-b при b>0 можно
получить параллельным переносом вдоль оси
ординат графика функции y=f(x) на b единиц
вниз
x
Y
1
0 1
-2
y=x2
x
y= x2 -2
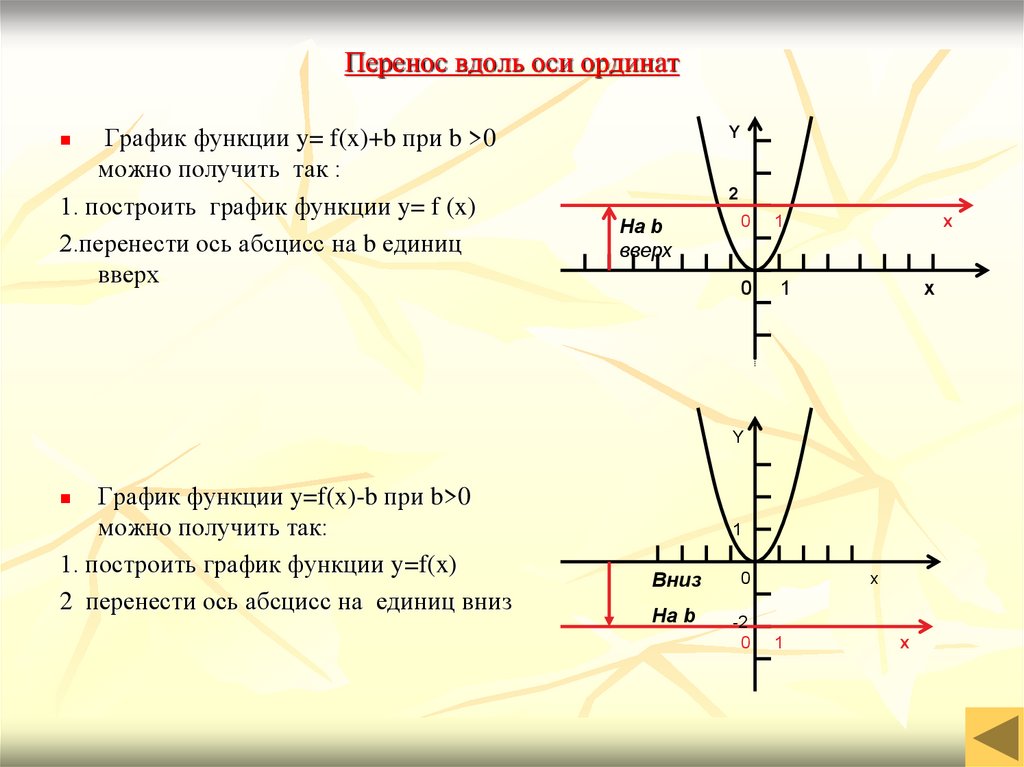
14. Перенос вдоль оси ординат
График функции y= f(x)+b при b >0можно получить так :
1. построить график функции y= f (x)
2.перенести ось абсцисс на b единиц
вверх
Y
2
На b
вверх
0
0
1
x
1
x
Y
График функции y=f(x)-b при b>0
можно получить так:
1. построить график функции y=f(x)
2 перенести ось абсцисс на единиц вниз
1
Вниз
На b
0
-2
0
x
1
x
15. Перенос вдоль оси абсцисс
График функции y= f (x + c) можно получитьпараллельным переносом вдоль оси абсцисс графика
функции y= f (x) на |c| единиц влево при c >0 .
Y
y=x2
1
-2
0
1
x
y=(x+2)2
График функции y=f(x+c) можно получить
параллельным переносом вдоль оси абсцисс графика
функции y=f(x) на |c| единиц вправо при c<0
y=x2
Y
y=(x-2)2
1
0
1
2
x
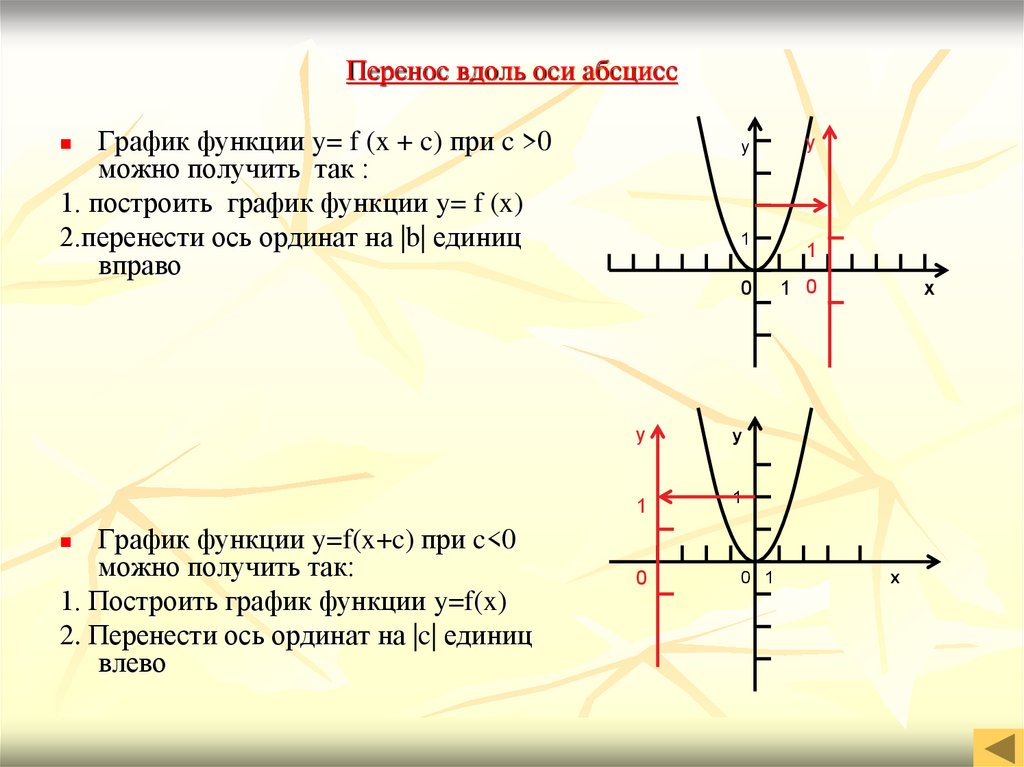
16. Перенос вдоль оси абсцисс
График функции y= f (x + c) при c >0можно получить так :
1. построить график функции y= f (x)
2.перенести ось ординат на |b| единиц
вправо
y
1
0
График функции y=f(x+c) при c<0
можно получить так:
1. Построить график функции y=f(x)
2. Перенести ось ординат на |c| единиц
влево
y
y
1
1
y
1
1 0
x
0
0 1
x
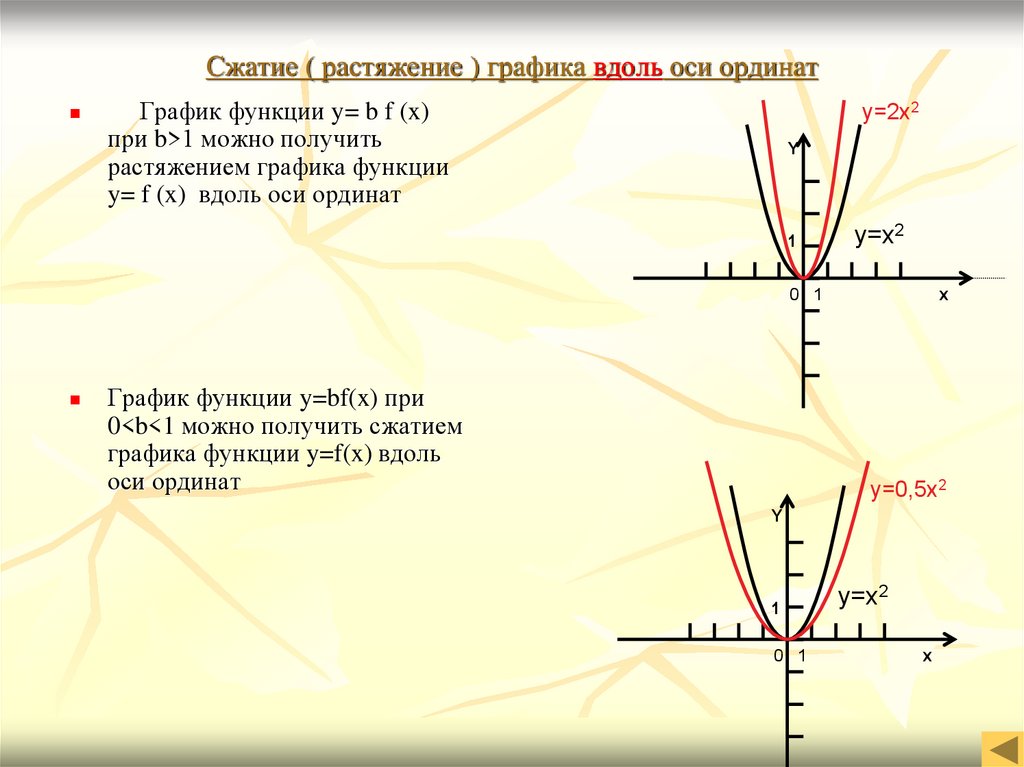
17. Сжатие ( растяжение ) графика вдоль оси ординат
График функции y= b f (x)при b>1 можно получить
растяжением графика функции
y= f (x) вдоль оси ординат
y=2x2
Y
1
y=x2
0 1
График функции y=bf(x) при
0<b<1 можно получить сжатием
графика функции y=f(x) вдоль
оси ординат
x
y=0,5x2
Y
1
0 1
y=x2
x
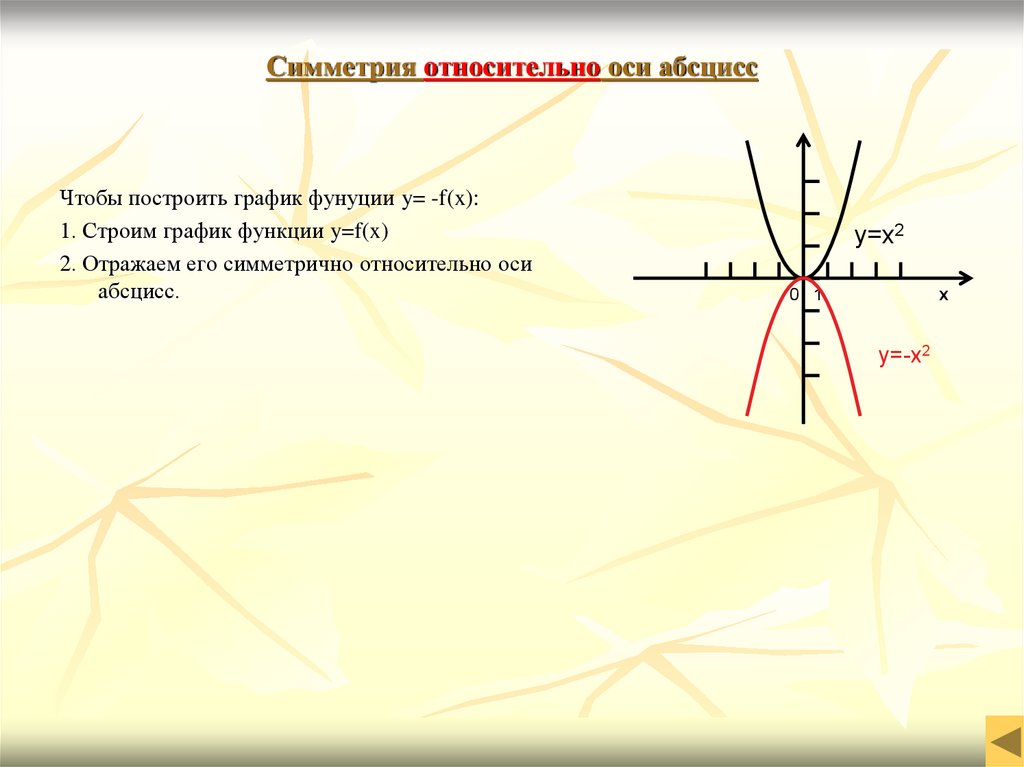
18. Симметрия относительно оси абсцисс
Чтобы построить график фунуции y= -f(x):1. Строим график функции y=f(x)
2. Отражаем его симметрично относительно оси
абсцисс.
y=x2
0 1
x
y=-x2
19. график функции y = f(|x|), y = |f(x)|
график функции y = f(|x|) получается из графика функции y = f(x)следующим преобразованием:
1)
точки графика, имеющие неотрицательные абсциссы – неподвижны;
2) точки графика, имеющие отрицательные абсциссы заменяются на
точки, полученные из неподвижных отражением относительно оси y.
график функции y = |f(x)| получается из графика функции y = f(x)
следующим преобразованием:
1)
точки графика, имеющие неотрицательные ординаты – неподвижны;
2) точки графика, имеющие отрицательные ординаты, отражаются
относительно оси x.
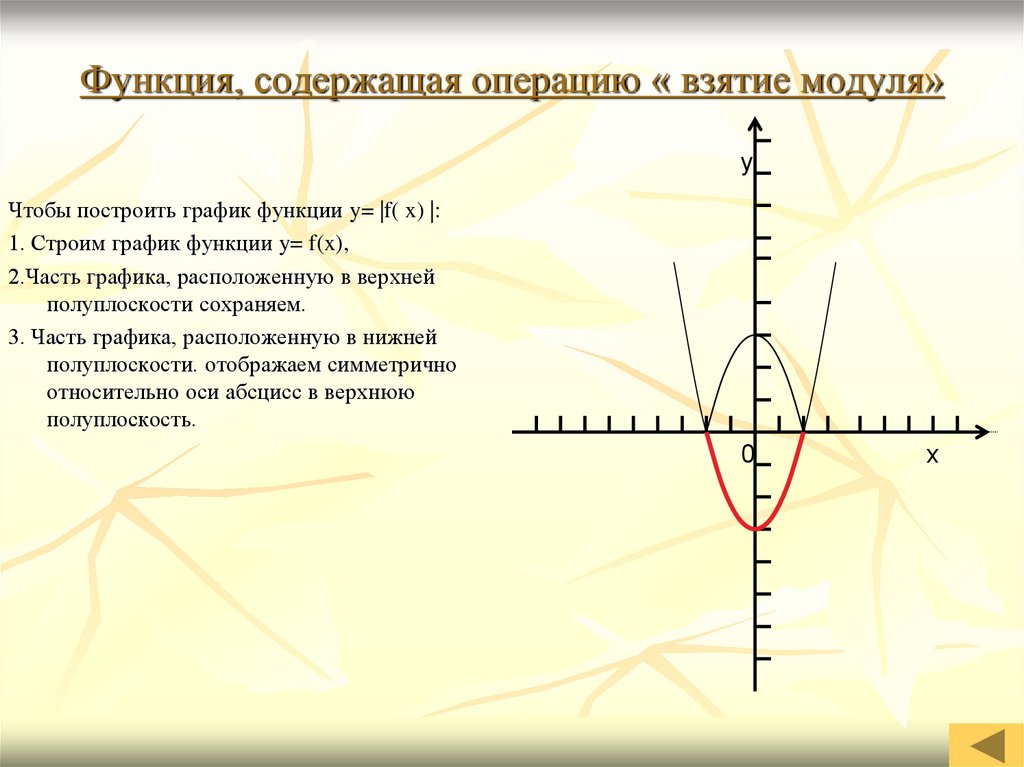
20. Функция, содержащая операцию « взятие модуля»
yЧтобы построить график функции y= |f( x) |:
1. Строим график функции y= f(x),
2.Часть графика, расположенную в верхней
полуплоскости сохраняем.
3. Часть графика, расположенную в нижней
полуплоскости. отображаем симметрично
относительно оси абсцисс в верхнюю
полуплоскость.
0
x








 mathematics
mathematics








