Построение графиков квадратичной функции

1.

Построение графиков
квадратичной функции.
Презентация выполнена учителем
математики МОУ “СОШ № 27”

2. Построение графика функции с помощью графика функции .

Построение графика функции g x x m 2 с
помощью графика функции f x x 2 .
Пусть построен график квадратичной функции f(x) . График функции g(x)
можно получить из графика функции f(x) путем его сдвига на |m| единиц
вдоль оси x вправо , если m>0 или влево , если m<0 . График функции
g(x) является параболой с вершиной в точке (m,0) .
2
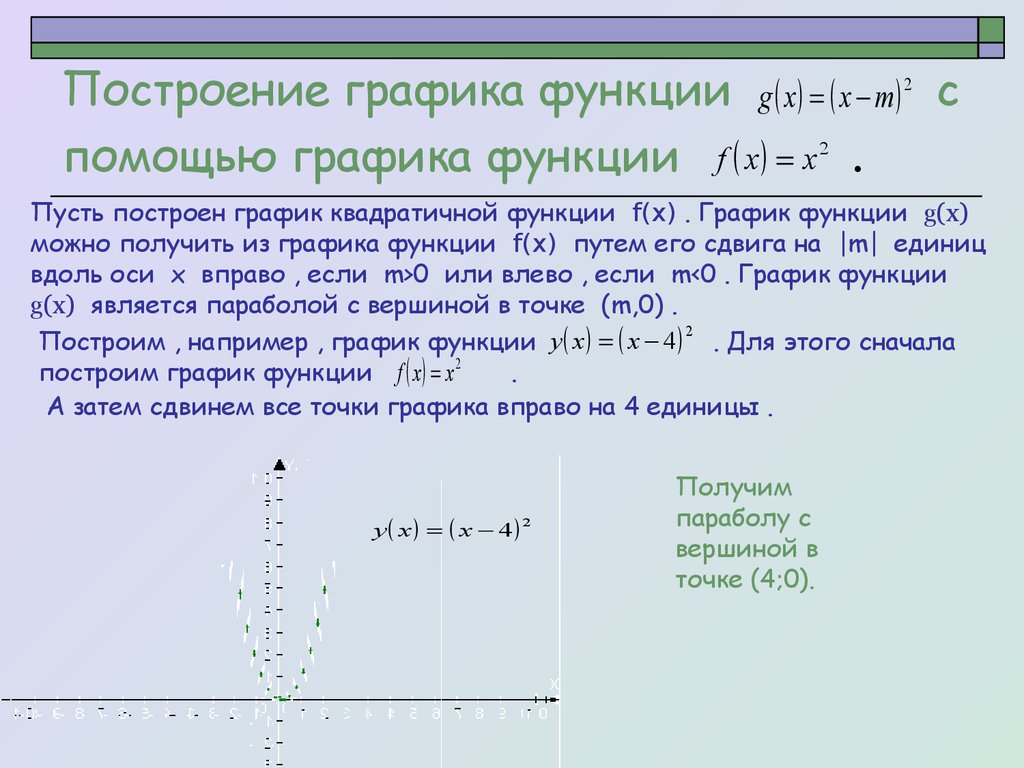
Построим , например , график функции y x x 4 . Для этого сначала
построим график функции f x x 2
.
А затем сдвинем все точки графика вправо на 4 единицы .
y x x 4
2
Получим
параболу с
вершиной в
точке (4;0).

3. Построим, например ,график функции .

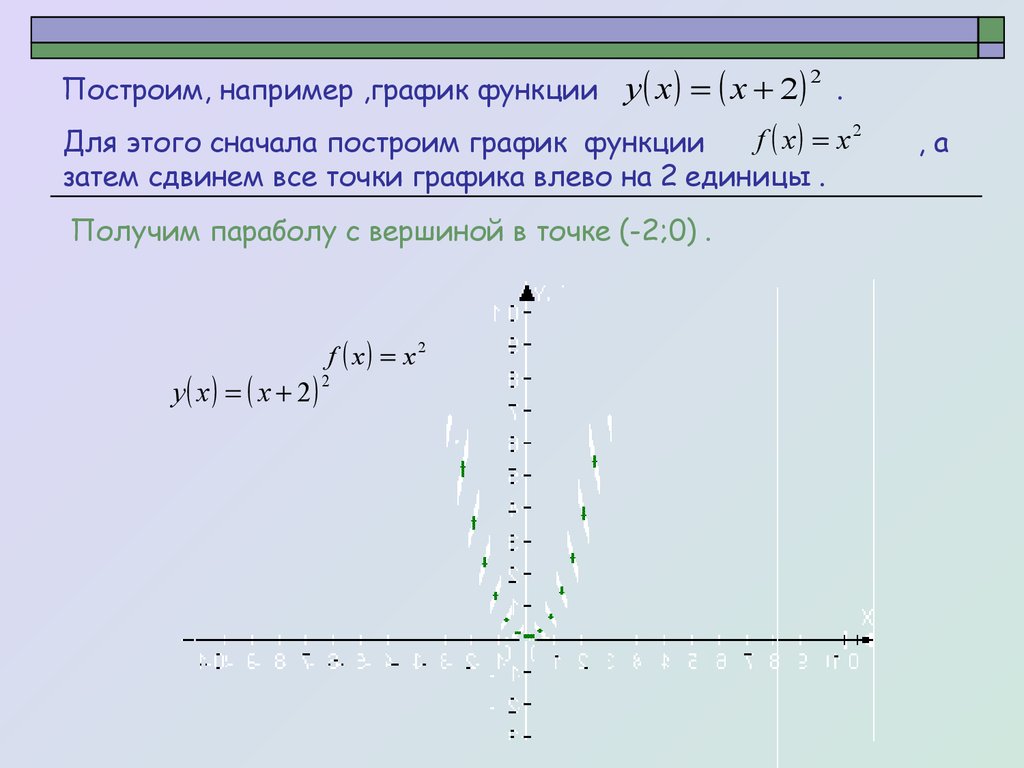
Построим, например ,график функции y x x 2
2
.
f x x2
Для этого сначала построим график функции
затем сдвинем все точки графика влево на 2 единицы .
Получим параболу с вершиной в точке (-2;0) .
y x x 2
f x x2
2
,а

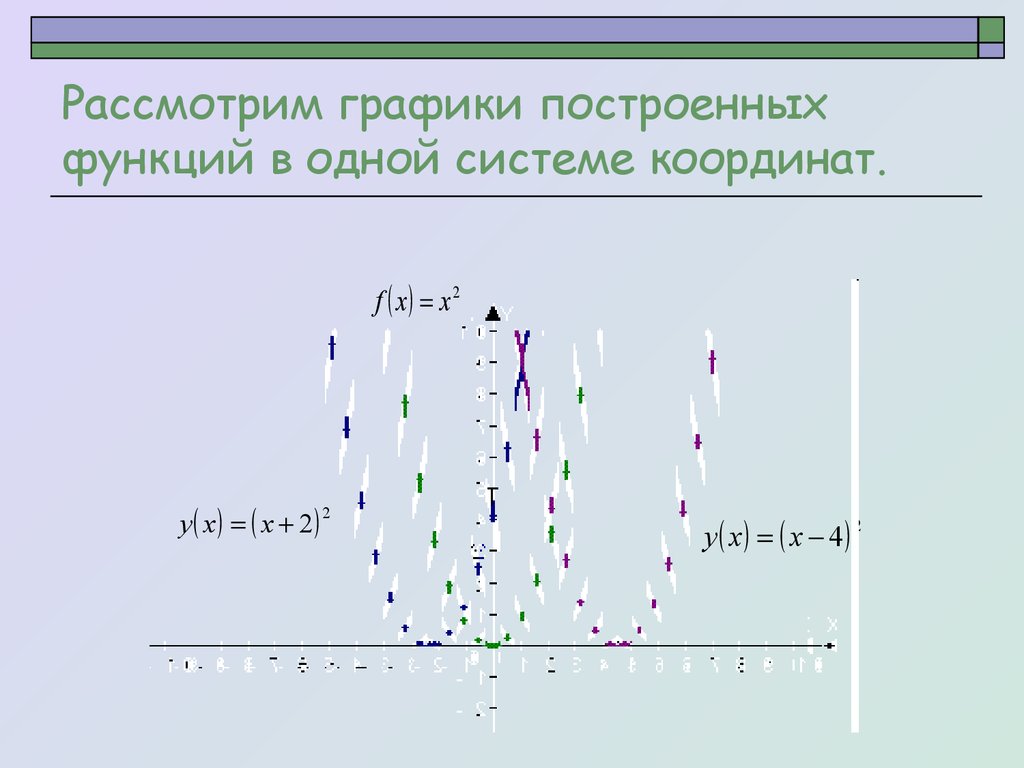
4. Рассмотрим графики построенных функций в одной системе координат.

f x x2
y x x 2
2
y x x 4
2

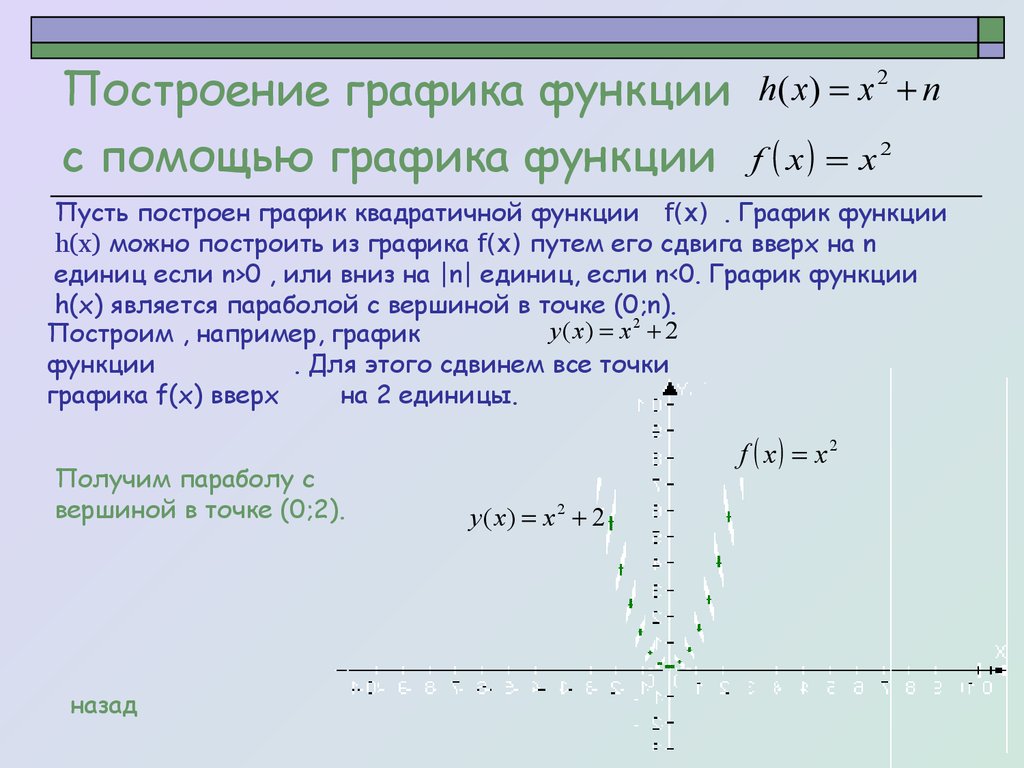
5. Построение графика функции с помощью графика функции

f x x 2
h( x ) x 2 n
Пусть построен график квадратичной функции f(x) . График функции
h(x) можно построить из графика f(x) путем его сдвига вверх на n
единиц если n>0 , или вниз на |n| единиц, если n<0. График функции
h(x) является параболой с вершиной в точке (0;n).
y ( x) x 2 2
Построим , например, график
функции
. Для этого сдвинем все точки
графика f(x) вверх
на 2 единицы.
Получим параболу с
вершиной в точке (0;2).
f x x2
y ( x) x 2 2

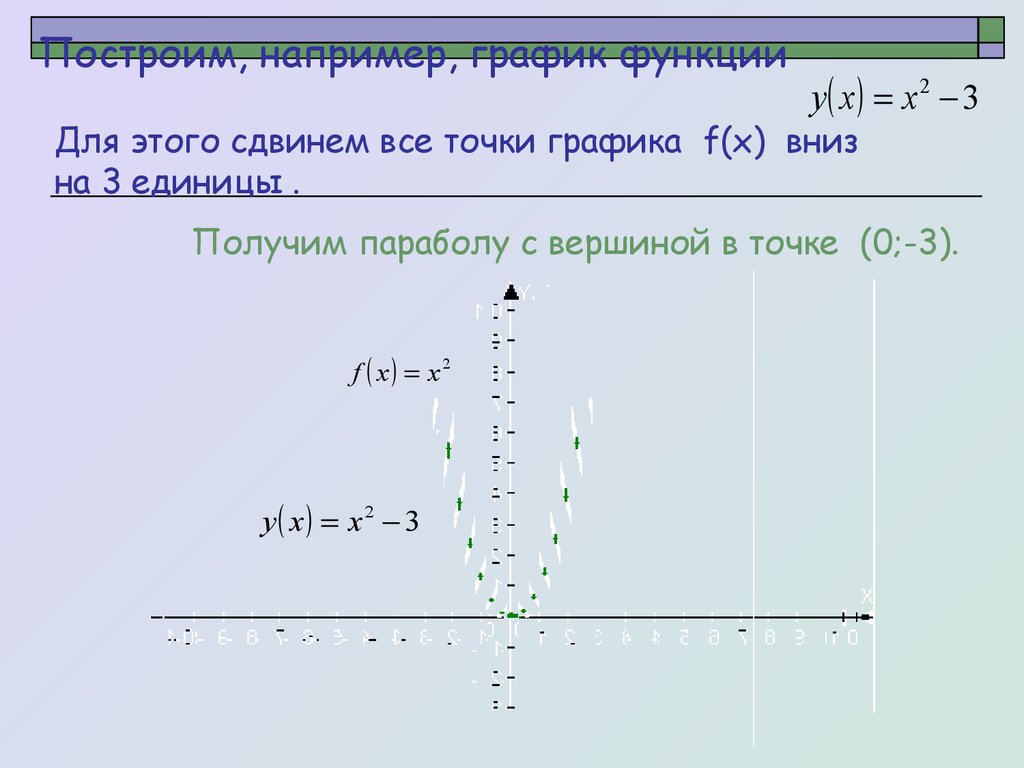
6. Построим, например, график функции

y x x 2 3
Для этого сдвинем все точки графика f(x) вниз
на 3 единицы .
Получим параболу с вершиной в точке (0;-3).
f x x2
y x x 2 3

7. Рассмотрим графики построенных функций в одной системе координат

y x x 2 2
f x x2
y x x 2 3

8. Построение графика функции с помощью графика функции .

Построение графика функции
2
s
x
x
m
n
с помощью графика
f x x
функции
.
2
График функции s(x) может быть получен из графика функции f(x) с
помощью последовательно выполненных двух параллельных
переносов : сдвига графика f(x) вдоль оси x на m единиц и сдвига
полученного графика вдоль оси y на n единиц. График является
параболой с вершиной в точке (m;n) .
2
Построим, например, график функции y x x 3 1.
Алгоритм построения :
2
1.Построим график f x x
2.Построим график y x x 3
2
3.Построим график y x x 3 1
2
Получили параболу с
вершиной в точке (-3;-1).

9. Построение графика функции с помощью графика функции .

Построение графика функции
2
y
x
x
с помощью графика функции
2
f
x
x
.
График функции y=-f(x) симметричен графику функции f(x)
относительно оси абсцисс.
f x x2
y x x 2

10. Построение графика функции с помощью графика функции .

2
g
x
ax
Построение графика функции
с
помощью графика функции f x x 2 .
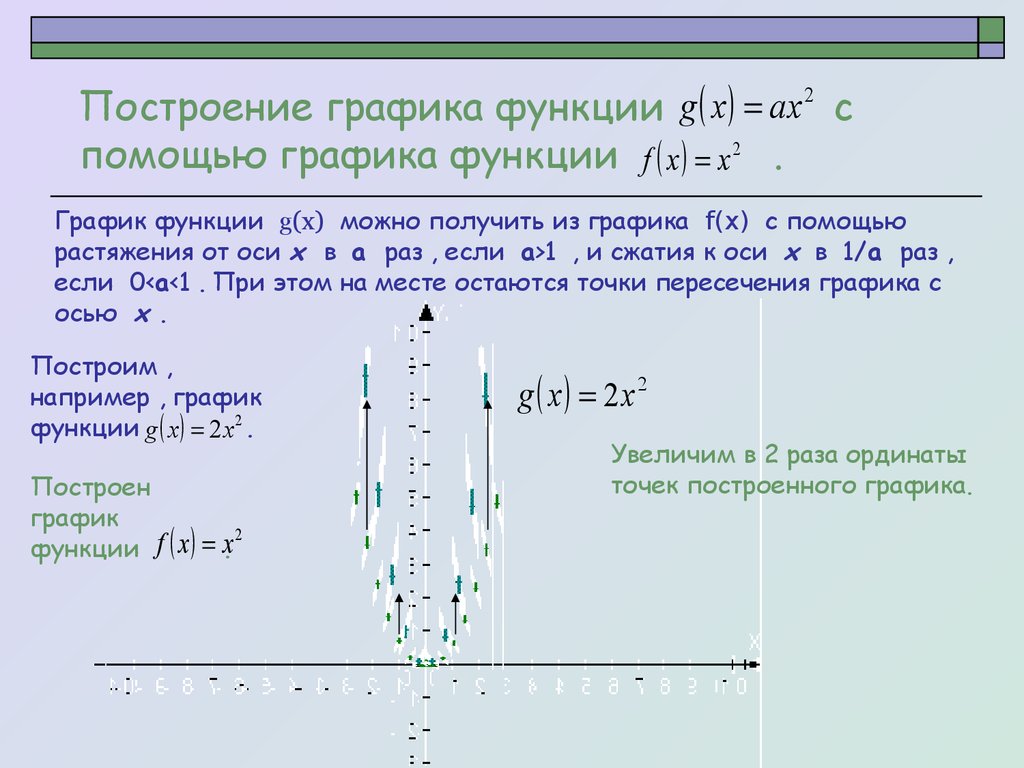
График функции g(x) можно получить из графика f(x) с помощью
растяжения от оси x в а раз , если а>1 , и сжатия к оси x в 1/а раз ,
если 0<а<1 . При этом на месте остаются точки пересечения графика с
осью x .
Построим ,
например , график
функции g x 2x 2 .
Построен
график
2
функции f x x.
g x 2x 2
Увеличим в 2 раза ординаты
точек построенного графика.

11.

Если а <0, то растянутый в |а| раз (для |а| >1 ) , или
сжатый в 1/|а| раз (для 0<|а|<1 ) график подвергают
преобразованию симметрии относительно оси x.
Построим , например , график функции
у ( x) 2 x 2
Алгоритм построения :
1. Построим график
функции f x x 2 .
f x x2
2.Построим график
2
функции g x 2x.
3.Выполним
преобразование
симметрии
относительно
оси x .
у ( x) 2 x 2
.
g x 2x 2

12.

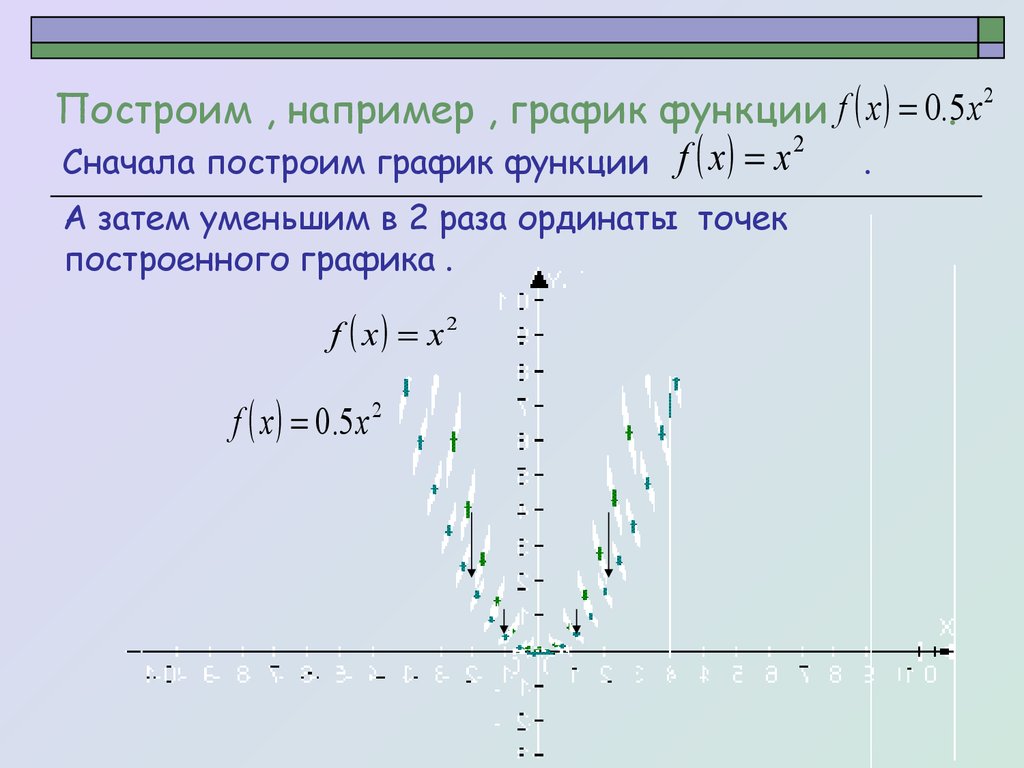
Построим , например , график функции f x 0..5 x
2
f
x
x
Сначала построим график функции
.
А затем уменьшим в 2 раза ординаты точек
построенного графика .
f x x2
f x 0.5 x 2
2

13. Проверите себя ?

да
нет
Дополнительно:
y ax 2 bx c

14.

Для построения графика функции
f x x2
график функции
переносят
y х 2 4,5
На 4,5 масштабных единицы вниз .
На 4,5 масштабных единицы вверх .
На 4,5 масштабных единицы влево .
На 4,5 масштабных единицы вправо .
теория

15.

Не правильно
назад

16.

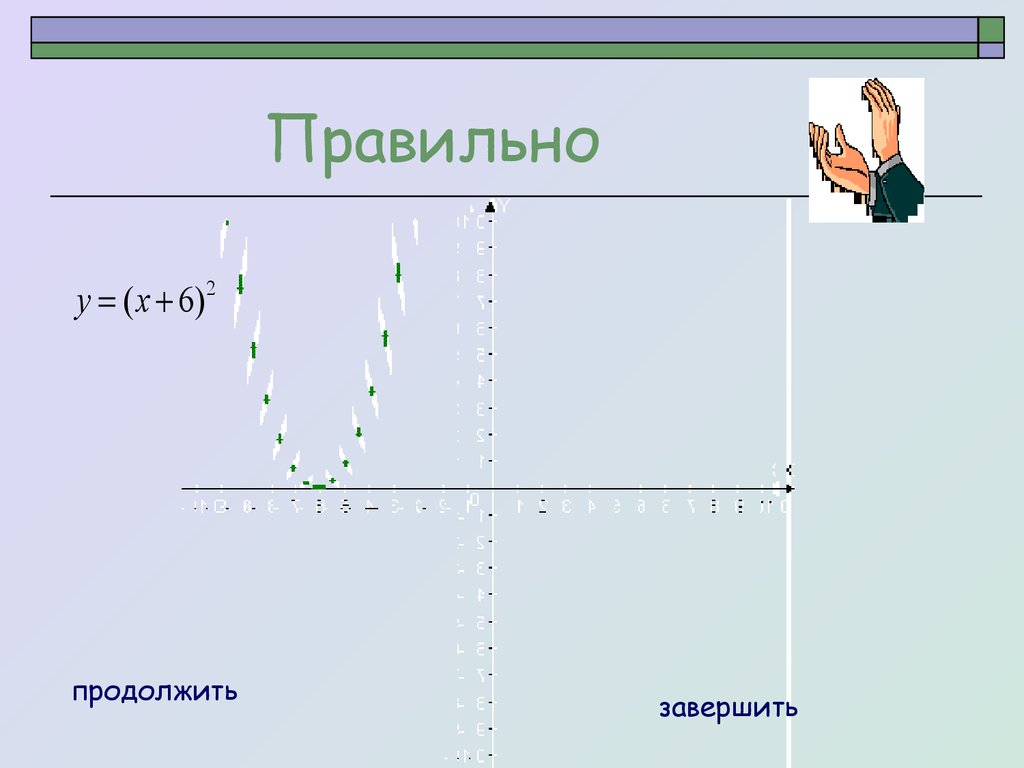
Правильно
y х 2 4,5
продолжить
завершить

17.

Для построения графика функции y x 2 3,8
f x x2
график функции
переносят
На 3,8 масштабных единицы вправо .
На 3,8 масштабных единицы вверх .
На 3,8 масштабных единицы вниз .
На 3,8 масштабных единицы влево .
теория

18.

Не правильно
назад

19.

Правильно
y x 2 3,8
продолжить
завершить

20.

2
y
(
x
7
)
Для построения графика функции
2
f
x
x
график функции
переносят
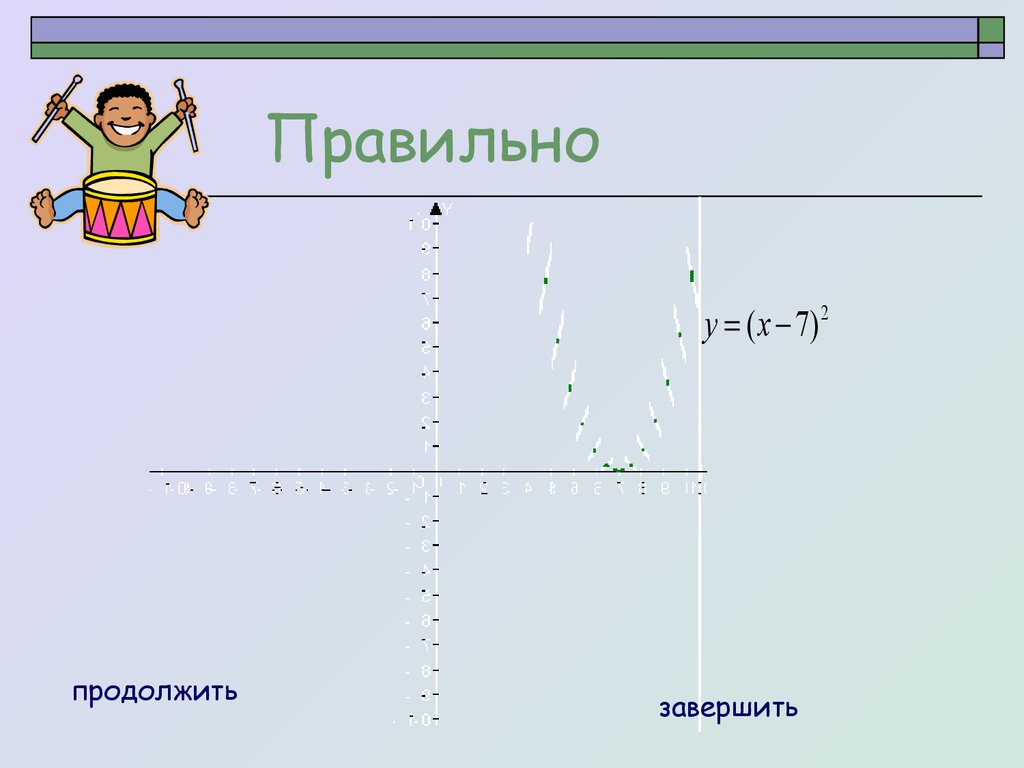
На 7 масштабных единиц вправо.
На 7 масштабных единиц вверх .
На 7 масштабных единиц вниз .
На 7 масштабных единиц влево .
теория

21.

Не правильно
назад

22.

Правильно
y ( x 7) 2
продолжить
завершить

23.

2
y
(
x
6
)
Для построения графика функции
f x x2
график функции
переносят
На 6 масштабных единиц вправо .
На 6 масштабных единиц вверх .
На 6 масштабных единиц вниз .
На 6 масштабных единиц влево .
теория

24.

Не правильно
назад

25.

Правильно
y ( x 6) 2
продолжить
завершить

26.

Для построения графика функции y x x 5 2
f x x2
график функции
переносят
2
На 5 масштабных единиц вправо и на 2 единицы вниз .
На 5 масштабных единиц вправо и на 2 единицы вверх .
На 5 масштабных единиц влево и на 2 единицы вниз .
На 5 масштабных единиц влево и на 2 единицы вверх .
теория

27.

Не правильно
назад

28.

Правильно
y x x 5 2
2
продолжить
завершить

29.

2
y
(
x
3
)
4
Для построения графика функции
2
f
x
x
график функции
переносят
На 3 масштабных единицы вправо и на 4 единицы вниз .
На 3 масштабных единицы вправо и на 4 единицы вверх .
На 3 масштабных единицы влево и на 4 единицы вниз .
На 3 масштабных единицы влево и на 4 единицы вверх .
теория

30.

Не правильно
назад

31.

Правильно
y ( x 3) 2 4
продолжить
завершить

32.

Выберите функцию график которой изображен :
2
y
3x
1.
2
y
3x
2.
1 2
3. y x
3
1 2
4. y x
3

33.

Не правильно
назад

34.

Правильно
продолжить
завершить

35.

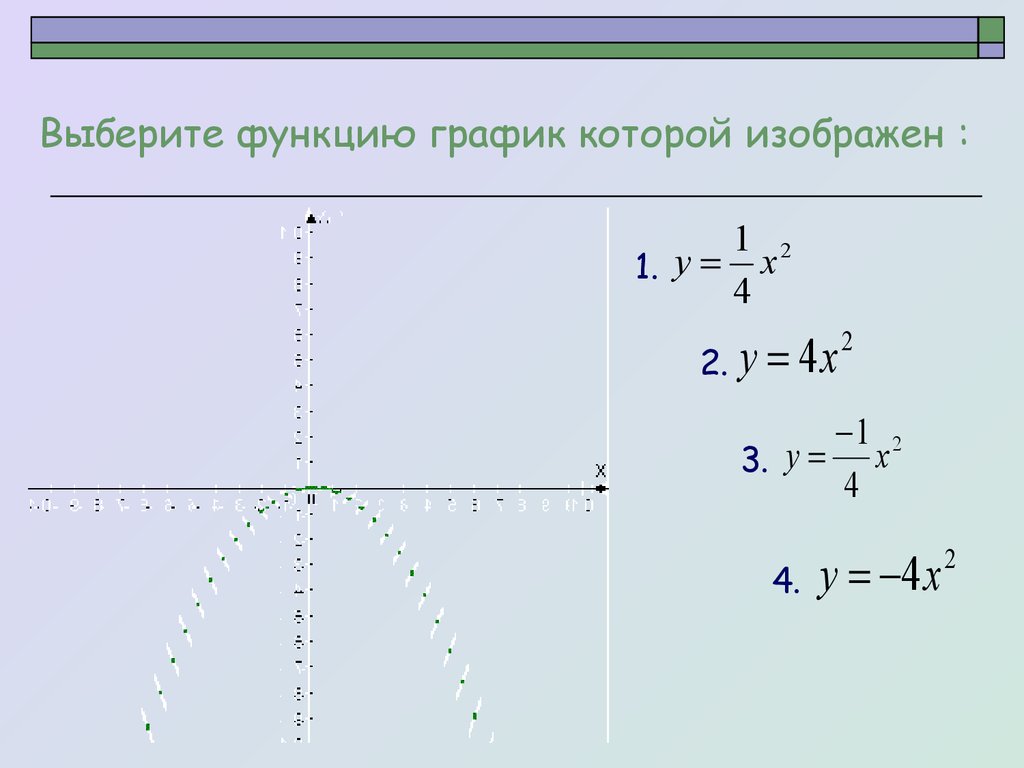
Выберите функцию график которой изображен :
1 2
1. y x
4
2.
y 4x
2
1 2
3. y x
4
4.
y 4x
2

36.

Не правильно
назад

37.

Правильно
продолжить
завершить

38.

Выберите функцию график которой изображен :
1.
y 2( x 2) 2 2
2.
y 2( x 2) 2
2
3.
y 2( x 2) 2 2
4.y 2( x 2)
2
2

39.

Не правильно
назад

40.

Правильно
продолжить
завершить

41.

Выберите функцию график которой изображен :
1
2
y
(
x
3
)
3
1.
2
1
2
y
(
x
3
)
3
2.
3
1
2
3. y ( x 3) 3
2
1
4. y ( x 3) 2 3
7

42.

Правильно
продолжить
завершить

43.

Не правильно
назад

44. Построение графика функции с помощью графика функции

f x x 2
h( x ) x 2 n
Пусть построен график квадратичной функции f(x) . График функции
h(x) можно построить из графика f(x) путем его сдвига вверх на n
единиц если n>0 , или вниз на |n| единиц, если n<0. График функции
h(x) является параболой с вершиной в точке (0;n).
y ( x) x 2 2
Построим , например, график
функции
. Для этого сдвинем все точки
графика f(x) вверх
на 2 единицы.
Получим параболу с
вершиной в точке (0;2).
назад
f x x2
y ( x) x 2 2

45. Построение графика функции с помощью графика функции

f x x 2
h( x ) x 2 n
Пусть построен график квадратичной функции f(x) . График функции
h(x) можно построить из графика f(x) путем его сдвига вверх на n
единиц если n>0 , или вниз на |n| единиц, если n<0. График функции
h(x) является параболой с вершиной в точке (0;n).
y ( x) x 2 2
Построим , например, график
функции
. Для этого сдвинем все точки
графика f(x) вверх
на 2 единицы.
Получим параболу с
вершиной в точке (0;2).
назад
f x x2
y ( x) x 2 2

46. Построение графика функции с помощью графика функции .

Построение графика функции g x x m 2 с
помощью графика функции f x x 2 .
Пусть построен график квадратичной функции f(x) . График функции g(x)
можно получить из графика функции f(x) путем его сдвига на |m| единиц
вдоль оси x вправо , если m>0 или влево , если m<0 . График функции
g(x) является параболой с вершиной в точке (m,0) .
2
Построим , например , график функции y x x 4 . Для этого сначала
построим график функции f x x 2
.
А затем сдвинем все точки графика вправо на 4 единицы .
y x x 4
2
Получим
параболу с
вершиной в
точке (4;0).
назад

47. Построение графика функции с помощью графика функции .

Построение графика функции g x x m 2 с
помощью графика функции f x x 2 .
Пусть построен график квадратичной функции f(x) . График функции g(x)
можно получить из графика функции f(x) путем его сдвига на |m| единиц
вдоль оси x вправо , если m>0 или влево , если m<0 . График функции
g(x) является параболой с вершиной в точке (m,0) .
2
Построим , например , график функции y x x 4 . Для этого сначала
построим график функции f x x 2
.
А затем сдвинем все точки графика вправо на 4 единицы .
y x x 4
2
Получим
параболу с
вершиной в
точке (4;0).
назад

48. Построение графика функции с помощью графика функции .

Построение графика функции
2
s
x
x
m
n
с помощью графика
f x x
функции
.
2
График функции s(x) может быть получен из графика функции f(x) с
помощью последовательно выполненных двух параллельных
переносов : сдвига графика f(x) вдоль оси x на m единиц и сдвига
полученного графика вдоль оси y на n единиц. График является
параболой с вершиной в точке (m;n) .
2
Построим, например, график функции y x x 3 1.
Алгоритм построения :
2
1.Построим график f x x
2.Построим график y x x 3
2
3.Построим график y x x 3 1
2
Получили параболу с
вершиной в точке (-3;-1).
назад

49. Построение графика функции с помощью графика функции .

Построение графика функции
2
s
x
x
m
n
с помощью графика
f x x
функции
.
2
График функции s(x) может быть получен из графика функции f(x) с
помощью последовательно выполненных двух параллельных
переносов : сдвига графика f(x) вдоль оси x на m единиц и сдвига
полученного графика вдоль оси y на n единиц. График является
параболой с вершиной в точке (m;n) .
2
Построим, например, график функции y x x 3 1.
Алгоритм построения :
2
1.Построим график f x x
2.Построим график y x x 3
2
3.Построим график y x x 3 1
2
Получили параболу с
вершиной в точке (-3;-1).
назад

50.

Графиком квадратичной функции y ax 2 bx c
является парабола , которая получается из
параболы y ax 2 параллельным переносом .
Применив метод выделения полного квадрата
2
для преобразования трехчлена ax bx c
2
b 2 4ac b
y a( x )
a( x l ) m
2
a
4
a
2
b
к виду
:
4acполучим
b
2
l
m
2a
4a
2
Чтобы построить график функции y ax bx c
где
,
.
необходимо выполнить
2
y
ax
параллельный перенос параболы
так
, чтобы вершина параболы оказалась в точке
(-l ; m) .
назад
подробнее
завершить

51. Построение графика функции с помощью графика функции .

Построение графика функции
2
s
x
x
m
n
с помощью графика
f x x
функции
.
2
График функции s(x) может быть получен из графика функции f(x) с
помощью последовательно выполненных двух параллельных
переносов : сдвига графика f(x) вдоль оси x на m единиц и сдвига
полученного графика вдоль оси y на n единиц. График является
параболой с вершиной в точке (m;n) .
2
Построим, например, график функции y x x 3 1.
Алгоритм построения :
2
1.Построим график f x x
2.Построим график y x x 3
2
3.Построим график y x x 3 1
2
Получили параболу с
вершиной в точке (-3;-1).
вернуться

52.

Презентация выполнена с использованием
учебно- методического комплекта :
А.Г. Мордкович.Алгебра-8.Учебник.
А.Г. Мордкович.Алгебра-8.Задачник.