Графики функций, содержащие знак модуля

1. Построение графиков функций, содержащих знак модуля

Десятниченко В. И.

2. ОПРЕДЕЛЕНИЕ МОДУЛЯ

f ( x), где f ( x) 0
f ( x)
f ( x), где f ( x) 0

3. Алгоритм построения графика функции

1.Строим график функции y=f(x).
2. Участки графика, лежащие выше
оси абсцисс, оставить без изменения.
3. Участки, лежащие ниже оси
абсцисс, зеркально отобразить
относительно этой оси.

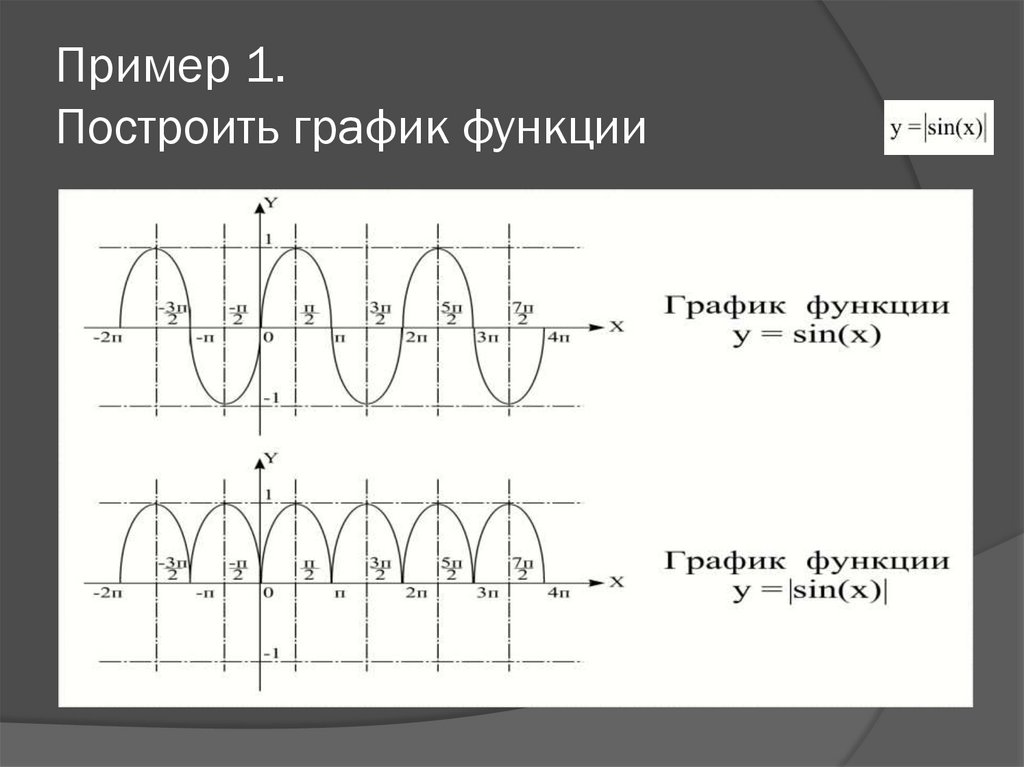
4. Пример 1. Построить график функции

5. Алгоритм построения графика функции

1. Построим график функции y=f(x).
2. Удалим точки графика y=f(x),
находящиеся слева оси OY.
3. Все точки, лежащие на оси OY и
справа от неё, отразим симметрично
относительно оси OY.

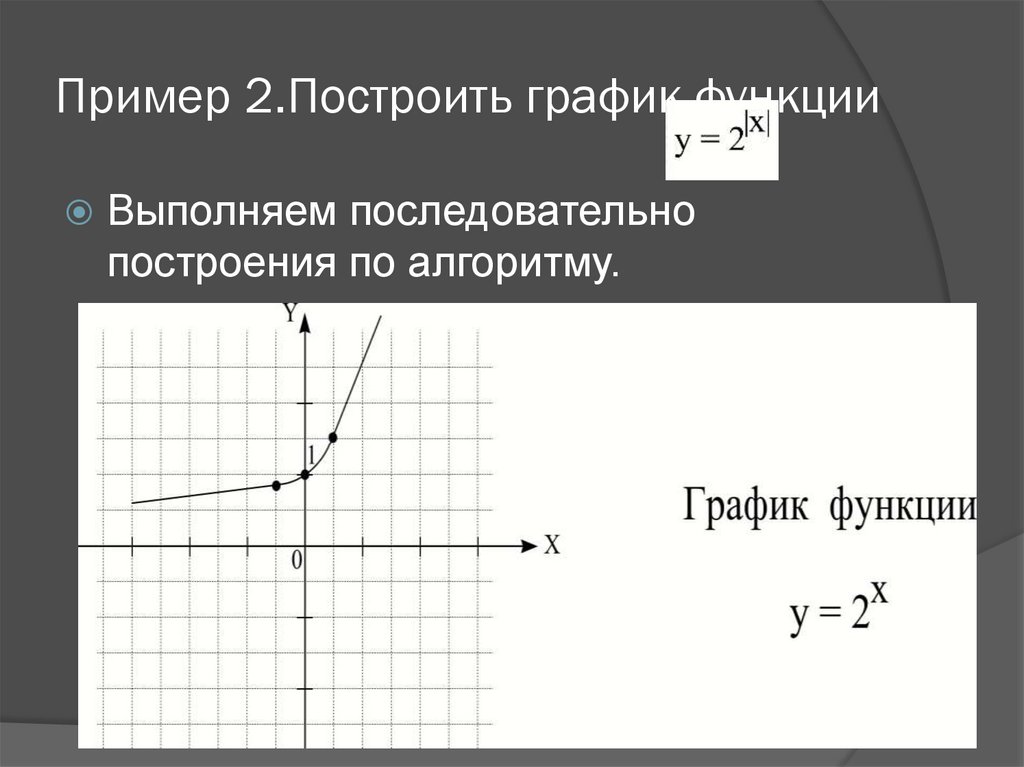
6. Пример 2.Построить график функции

Выполняем последовательно
построения по алгоритму.

7. Пример 2.

Получим в итоге график.

8. Алгоритм построения графика функции

1. Построить график функции y=f(x) для
x>=0.
2. Отобразить построенную часть
графика симметрично относительно оси
ординат.
3. Участки полученного графика,
лежащие ниже оси абсцисс, зеркально
отобразить относительно этой оси.

9. Пример3. Построить график функции

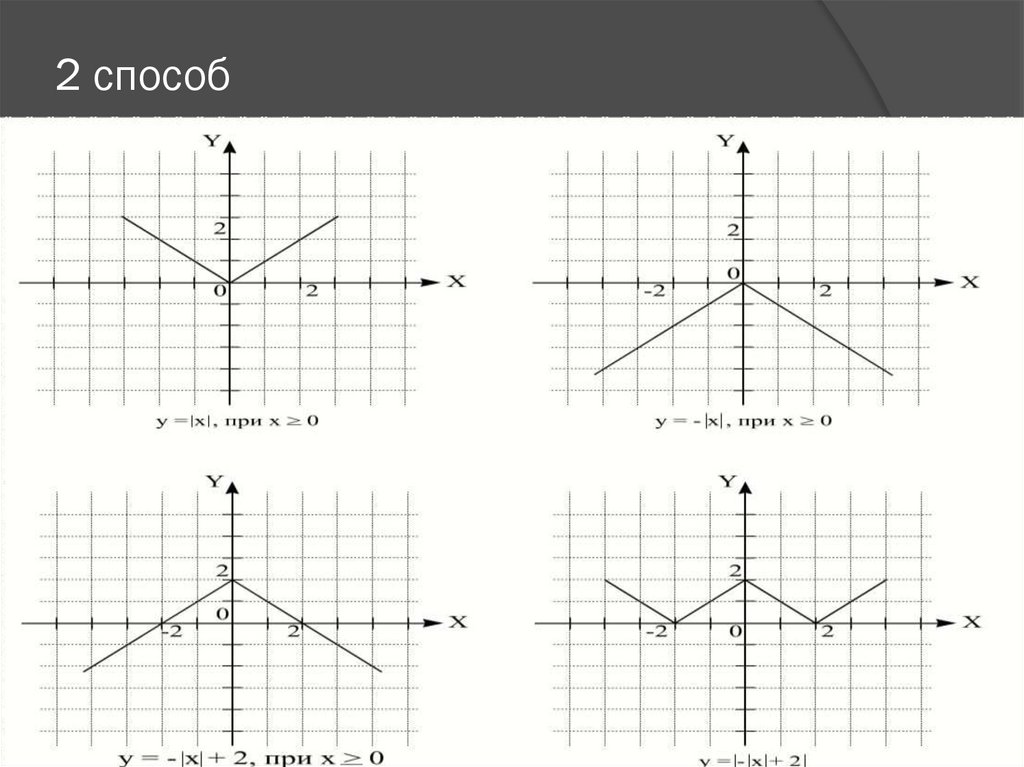
1 способ.

10. 2 способ

11. Алгоритм построения графика

1. Строим график функции y=f(x).
2. Строим график функции
3. Осуществить его зеркальное
отображение относительно оси Ox.

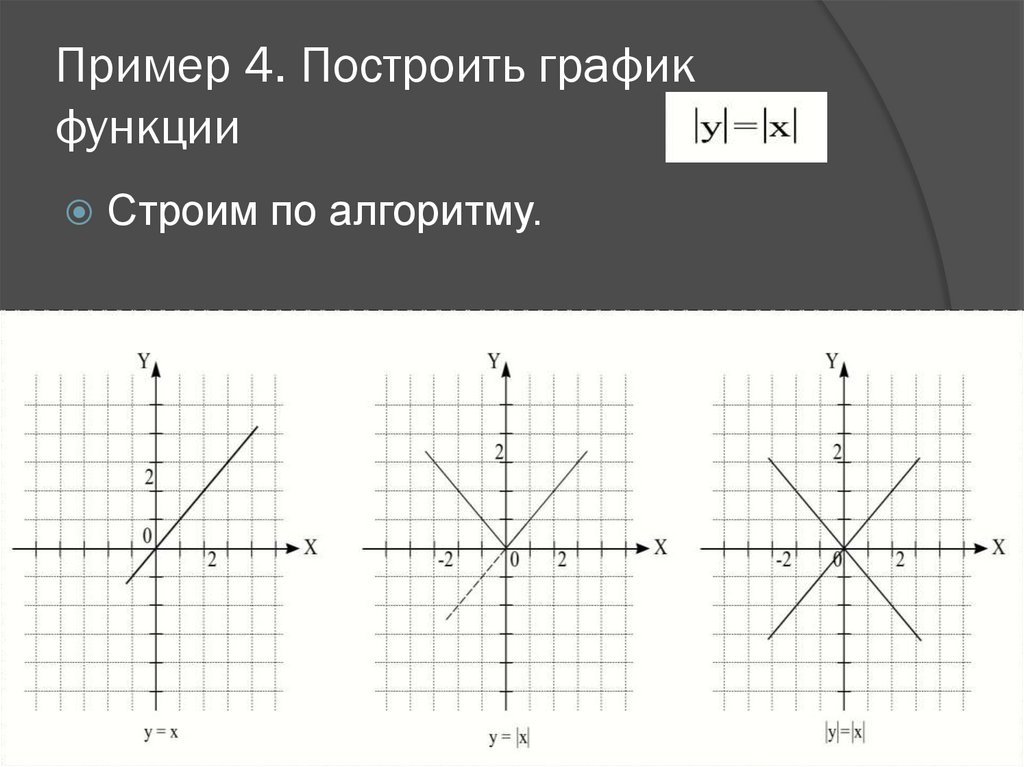
12. Пример 4. Построить график функции

Строим по алгоритму.

13. Пример 5

Построить график

14. Алгоритм построения графика

1. Найдите абсциссы точек
«перелома» графика функции: x=x1,
x=x2,x=x3,…,x=xn.
2.Рассмотреть функцию на каждом из
полученных промежутков.

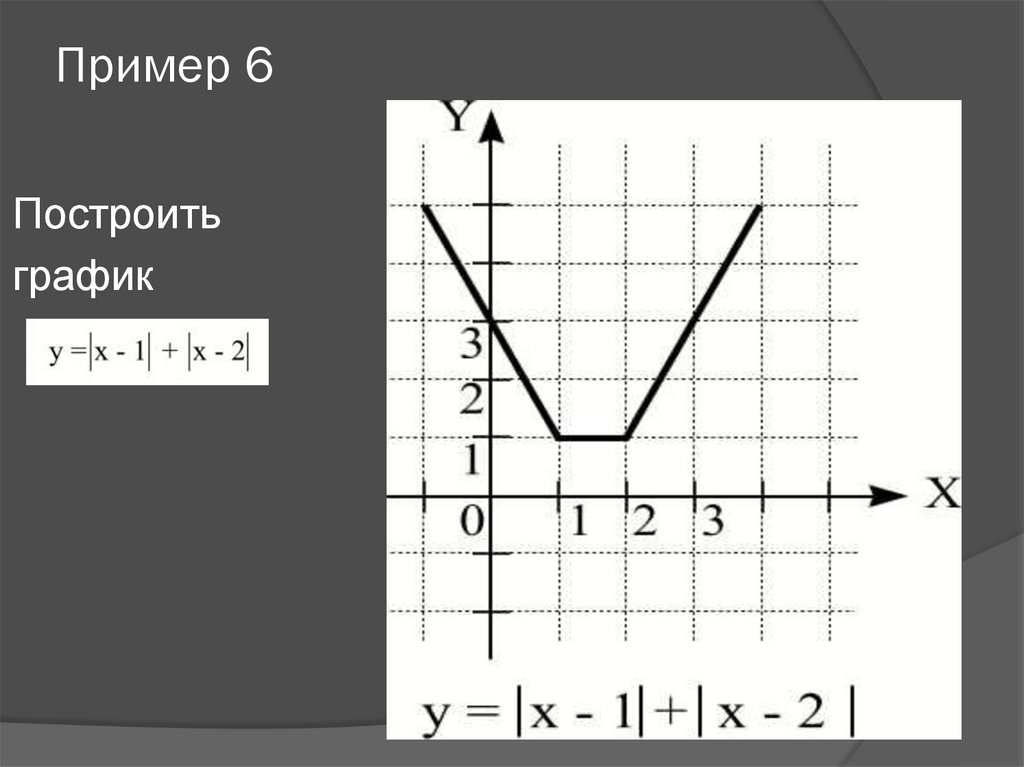
15. Пример 6

Построить
график

16. Алгоритм построения графика функции

1.
2.
Найти абсциссы точек «перелома»
графика функции.
Использовать способ, связанный с
геометрическими преобразованиями.

17. Пример 7

Построить
график
функции
k=2
b=1
c=2

18. Построение графиков функций аналитические выражения которых содержат знак модуля, выраженных неявно.

Рассмотрим пример. Построить график
функции
.По определению
абсолютной величины
. График этой
«функции» симметричен как относительно оси
Ох, так и относительно оси Oy. Построим его
лишь для первой координатной четверти, а
затем посредством двух зеркальных
отражений получим окончательный график.

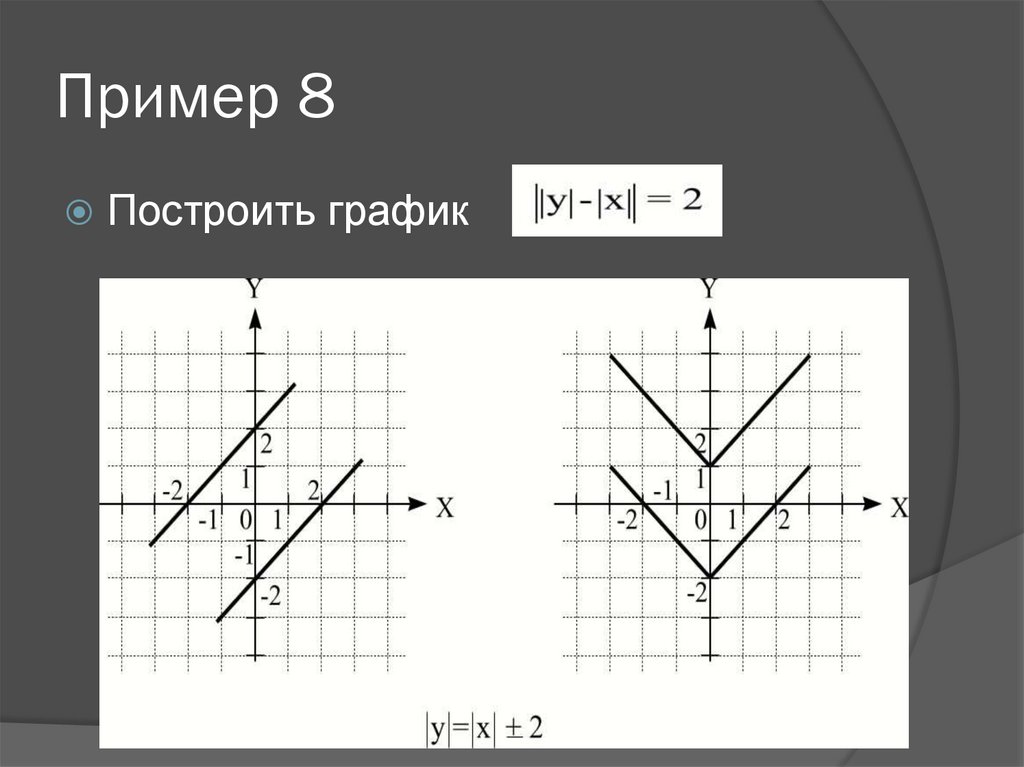
19. Пример 8

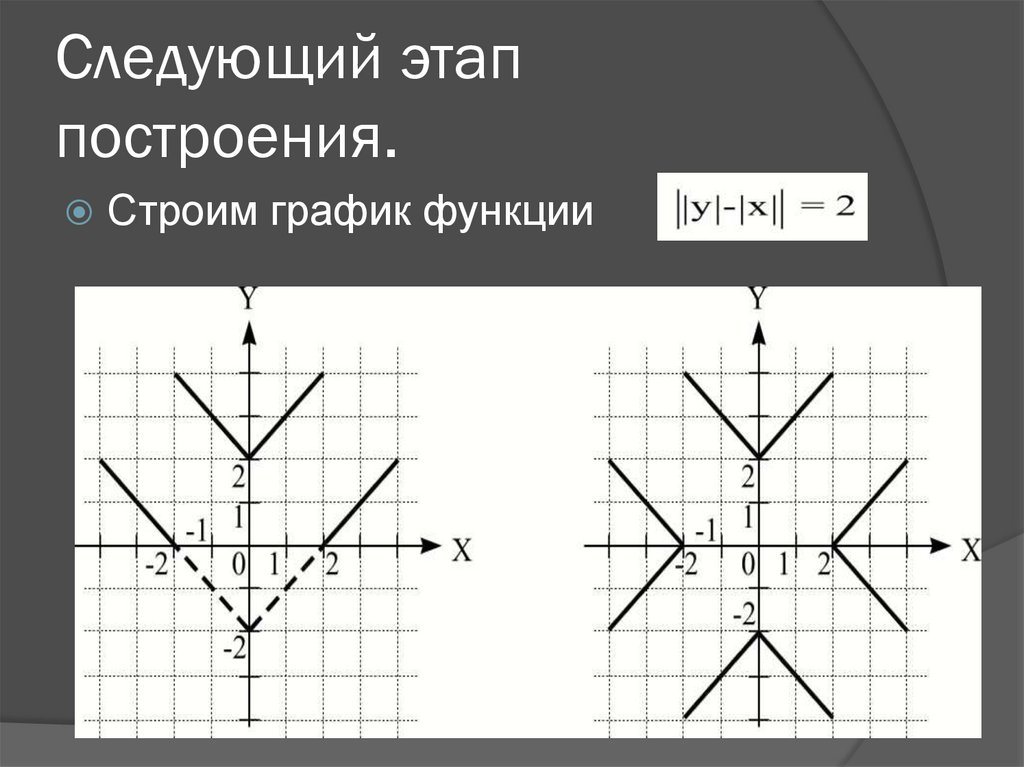
Построить график

20. Следующий этап построения.

Строим график функции

21. Пример 9. Построить график функции

По определению модуля
Так как график «функции»
симметричен относительно двух осей,
построим его сначала для первой
координатной четверти. При этом
уравнение функции примет вид

22. Второе уравнение имеет решение х=2, y=0.

Рассмотрим первое уравнение.
а) y=x+2, при 0≤x≤2 и x-2≤0
б) y=6-x, при x>2 и x-2>0.
Строим графики полученных прямых
в первой четверти.

23. График функции

Строим в первой координатной
четверти.
x 2 y 4

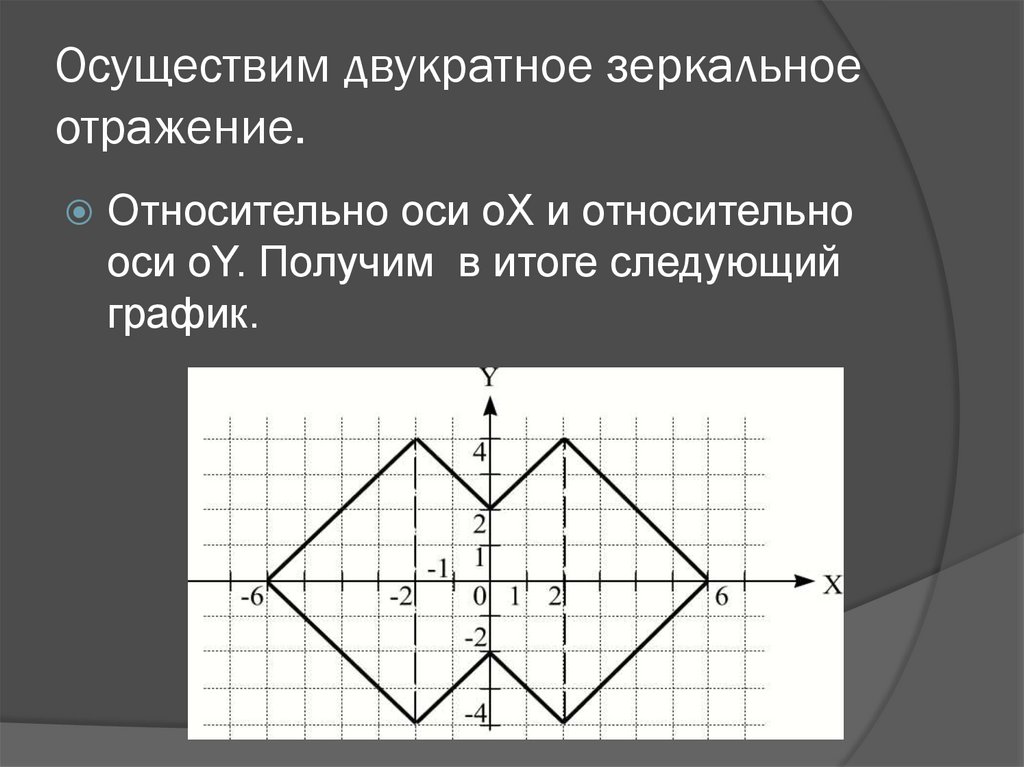
24. Осуществим двукратное зеркальное отражение.

Относительно оси оX и относительно
оси оY. Получим в итоге следующий
график.

25. Итог работы.

В работе рассмотрены основные
случаи построения графиков
функций, которые содержат знак
модуля.