Similar presentations:
Построение графика функции, содержащей модуль
1.
МБОУ СОШ №11пгт.Шерегеш
Материалы к ШМО
Учитель математики Белоусова М.А.
14.10.2019
2.
Математика является одним изнаиболее важных предметов школьного
курса.
Статус математики как обязательного
государственного экзамена подтверждает
необходимость изучения
математики
каждым учащимся
14.10.2019
2
3.
Каждый школьник в процессе обучениядолжен иметь возможность получить
качественную подготовку к выпускным
экзаменам, освоить тот объём знаний,
умений и навыков, который необходим
для успешной сдачи ОГЭ в 9 классе,
дальнейшего обучения в 10-11 классах,
сдачи ЕГЭ и последующего обучения в
вузе.
14.10.2019
3
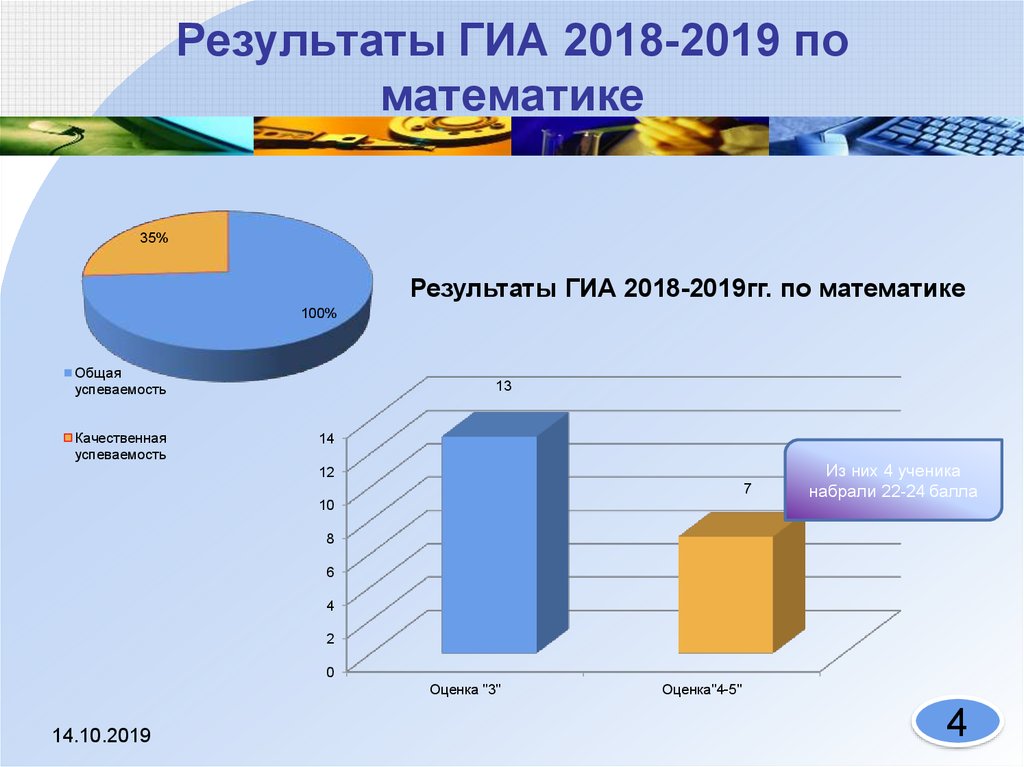
4. Результаты ГИА 2018-2019 по математике
35%Результаты ГИА 2018-2019гг. по математике
100%
Общая
успеваемость
Качественная
успеваемость
13
14
12
7
10
Из них 4 ученика
набрали 22-24 балла
8
6
4
2
0
Оценка "3"
14.10.2019
Оценка"4-5"
4
5. «Западающие темы»
Геометрическиезадачи
Текстовые
задачи
Графики функций
Неравенства
14.10.2019
Формулы
сокращенного
умножения
5
6.
Цели и задачиЦели:
– Подготовка учащихся к успешной сдачи ОГЭ по
математике
Задачи:
– Обучить строить графики функции, содержащей
модуль, посредством алгоритмизации шагов;
– Углубить знания по математике, предусматривающие
формирование у учащихся устойчивого интереса к
предмету;
– Расширить математические представления учащихся о
приёмах и методах решения задач с модулями;
6
14.10.2019
7. Краткое описание работы
Презентациясодержит
алгоритмы
построения графиков функций, содержащих
модуль, семь примеров построения графиков
функции.
Формат презентации дает возможность
учителю обсудить шаги выполнения задания с
обучающимися, дать возможность самим
обучающимся выполнить действие, а потом
уже проконтролировать, используя анимацию.
14.11.2017
7
8. Построение графиков функций с выражениями под знаком модуля
Построениеграфиков,
содержащих
осуществляется двумя способами:
модуль,
На основании определения модуля;
На основании правил геометрического
преобразования графиков функций.
По определению модуля числа:
14.11.2017
8
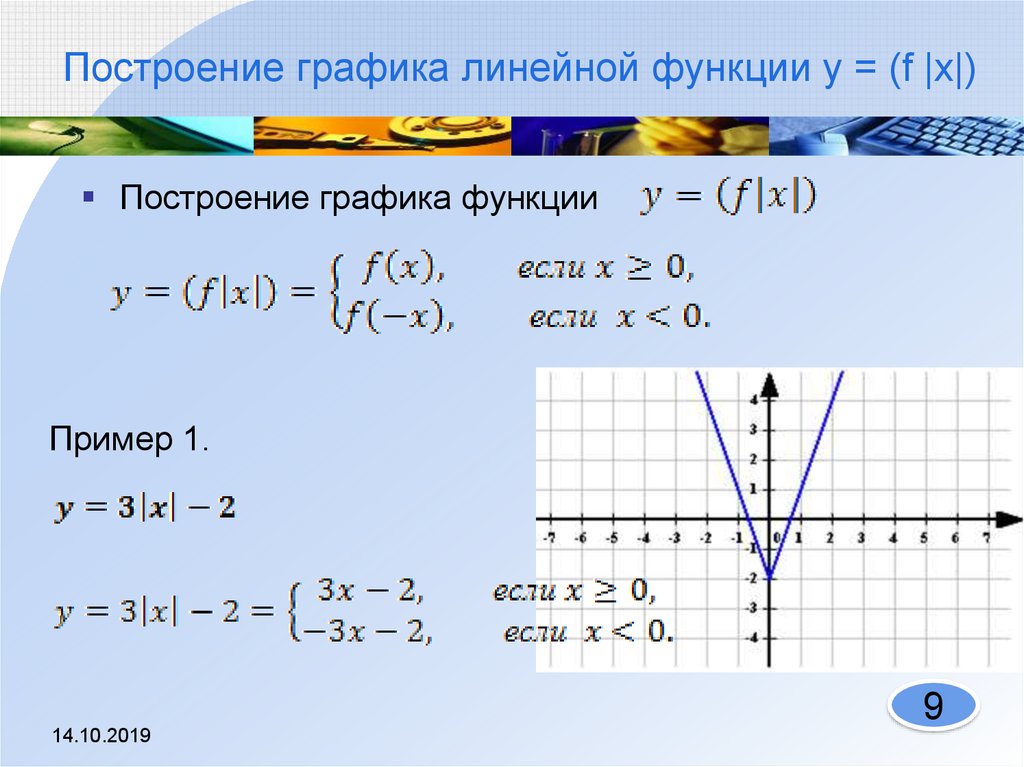
9. Построение графика линейной функции y = (f |x|)
Построение графика функцииПример 1.
14.10.2019
9
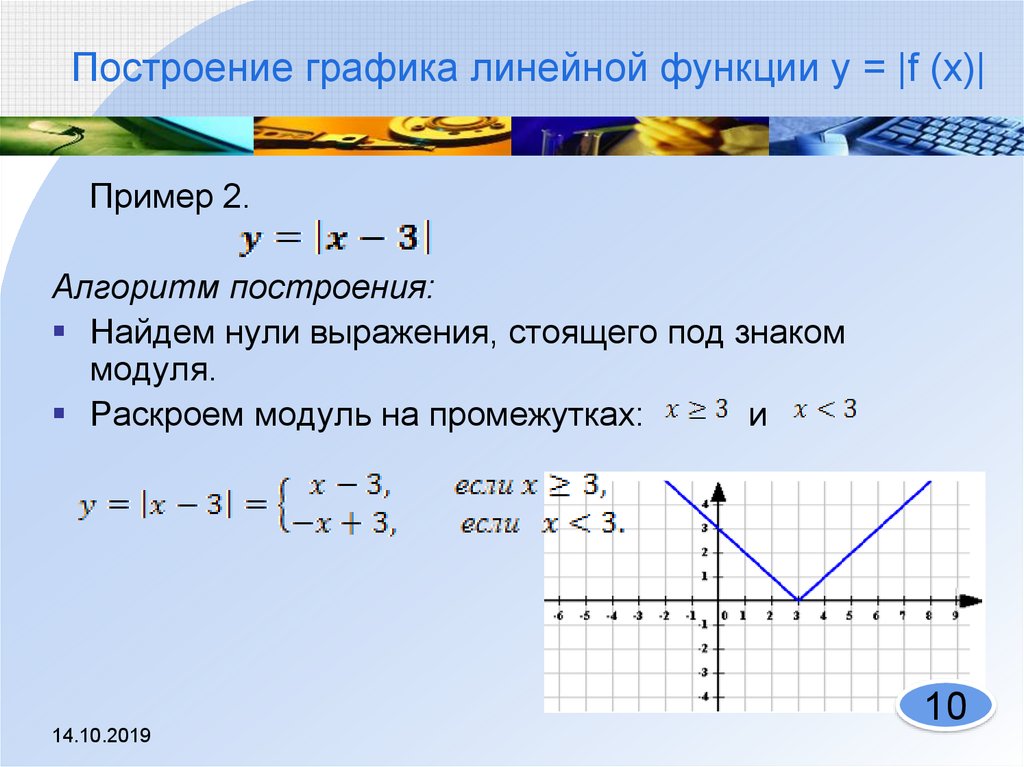
10. Построение графика линейной функции y = |f (x)|
Пример 2.Алгоритм построения:
Найдем нули выражения, стоящего под знаком
модуля.
Раскроем модуль на промежутках:
и
14.10.2019
10
11. Построение графика линейной функции y = |f (x)|
Пример 3.Построить график функции
Найдем нули выражений, стоящих под знаком
модуля.
Получим три промежутка:
Расставим знаки для подмодульных выражений на
координатной прямой:
14.10.2019
11
12. Пример 3. Построение графика линейной функции y = |f (x)|
Раскроем знаки модуля на промежутках:Раскрыв скобки и выполнив тождественные
преобразования, получим:
Строим график:
0
х
-7
14.10.2019
12
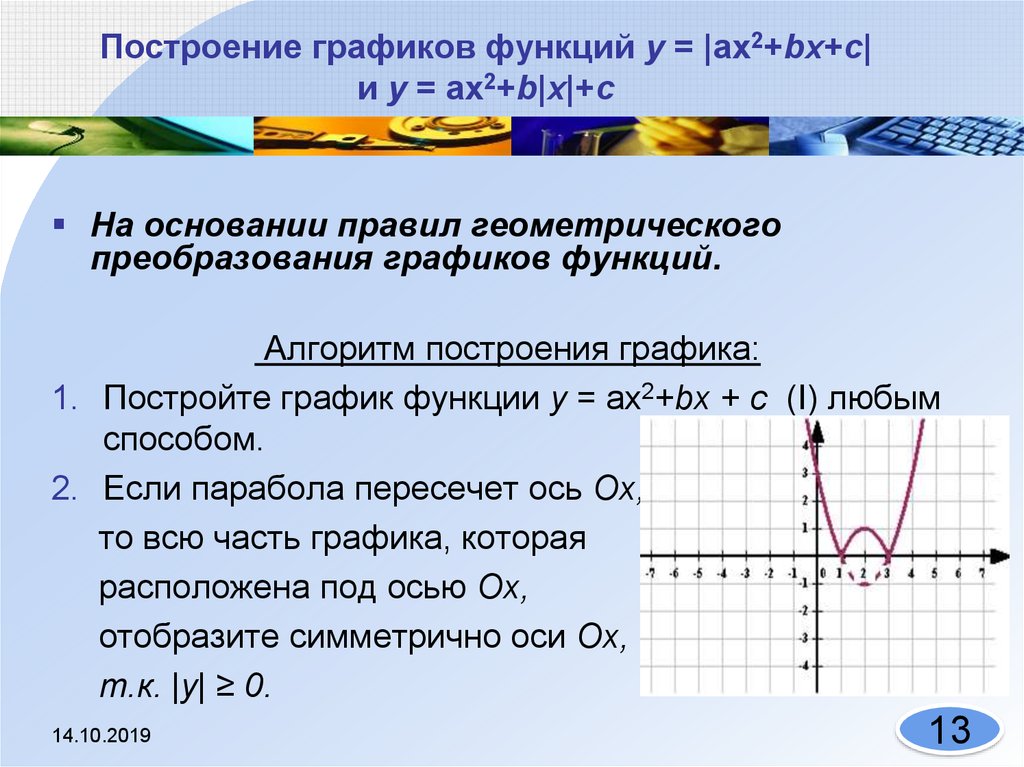
13. Построение графиков функций у = |ах2+bх+с| и у = ах2+b|х|+с
На основании правил геометрическогопреобразования графиков функций.
Алгоритм построения графика:
1. Постройте график функции у = ах2+bх + с (I) любым
способом.
2. Если парабола пересечет ось Ох,
то всю часть графика, которая
расположена под осью Ox,
отобразите симметрично оси Ox,
т.к. |y| ≥ 0.
14.10.2019
13
14. Построение графиков функций у = |ах2+bх+с| и у = ах2+b|х|+с
3. Если парабола расположена над осью Ох,то |ах2+bх+с| = ах2+bх+с при всех значениях х,
а значит, весь график сохранит свое положение.
4. Если вся парабола (I) расположена под осью Ох,
( а < 0; D < 0), то графиком функции у = |ах2+bх+с| будет
парабола,
расположенная
над
осью
Ох
симметрично параболе (I) относительно оси Ох.
5. Если надо построить график функции у = ах2+b|х| + с ,
то всю часть графика (I), которая справа от оси Оу,
отобразите симметрично оси ОУ, а левую часть
графика (I) относительно оси ОУ стройте пунктиром.
14.10.2019
14
15. Пример 4. Построение графика функции у = |ах2+bх+с|
.-Пример 4. Построение графика функции
у = |ах2+bх+с|
Построение
1) Найдем координаты вершины
параболы:
1) Постройте график
функции
у =ах2+bх+с (I) любым
способом.
Подставим
в трехчлен и найдем
- вершина параболы
14.11.2017
15
16. Пример 4. Построение графика функции у = |ах2+bх+с|
2)- ось симметрии;
3) Точки пересечения с осью Ох:
- точки пересечения с осью Ох.
14.11.2017
16
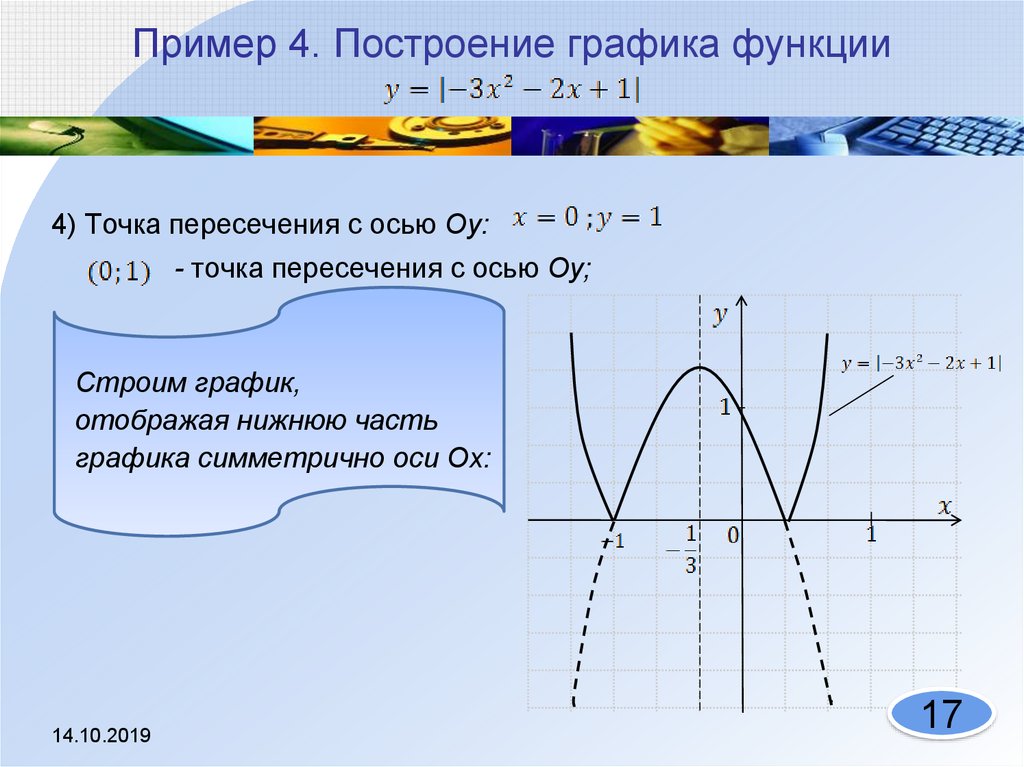
17. Пример 4. Построение графика функции
4) Точка пересечения с осью Оу:- точка пересечения с осью Оу;
Строим график,
отображая нижнюю часть
графика симметрично оси Ох:
14.10.2019
17
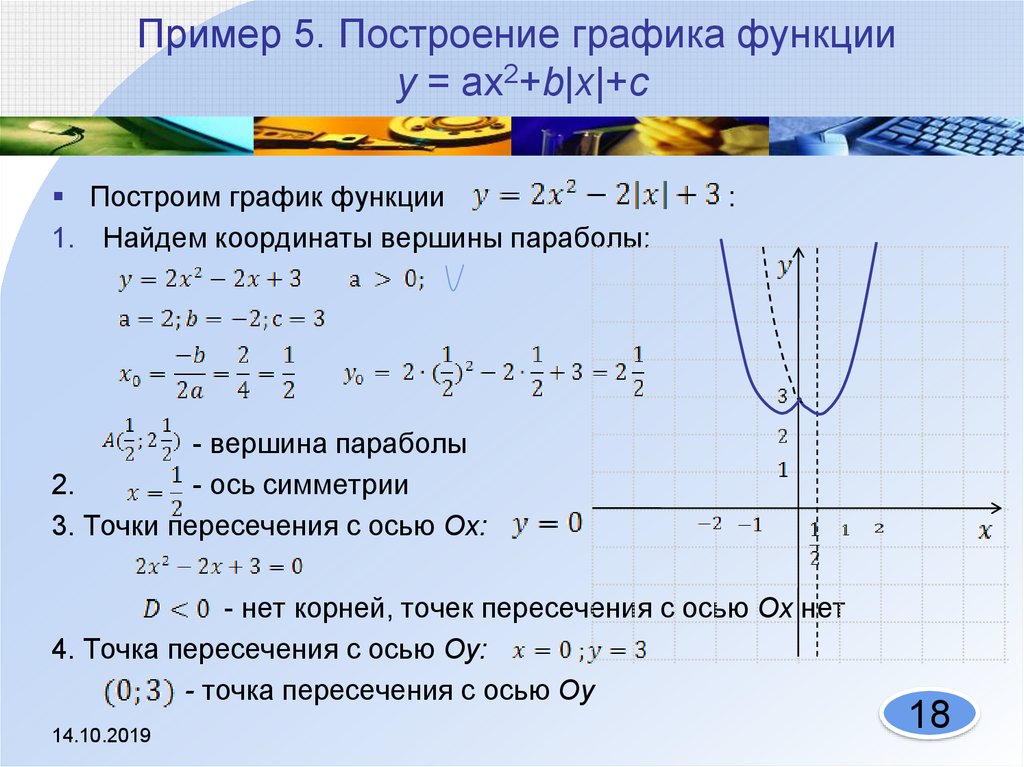
18. Пример 5. Построение графика функции у = ах2+b|х|+с
Построим график функции1. Найдем координаты вершины параболы:
:
- вершина параболы
2.
- ось симметрии
3. Точки пересечения с осью Ох:
- нет корней, точек пересечения с осью Ох нет
4. Точка пересечения с осью Оу:
- точка пересечения с осью Оу
14.10.2019
18
19. Алгоритм. Построение графика функции у = |ах2+b|х|+с|
1. Постройте график функции у = ах2+bх+с .2. Постройте график функции у = ах2+b|х|+с.
Для этого постройте симметрично оси Оу ту
часть графика, которая справа от оси Оу.
3. Постройте симметрично оси Ох ту часть
графика, которая находится под осью Ох.
Построенный график является графиком
функции у = |ах2+b|х|+с|
14.10.2019
18
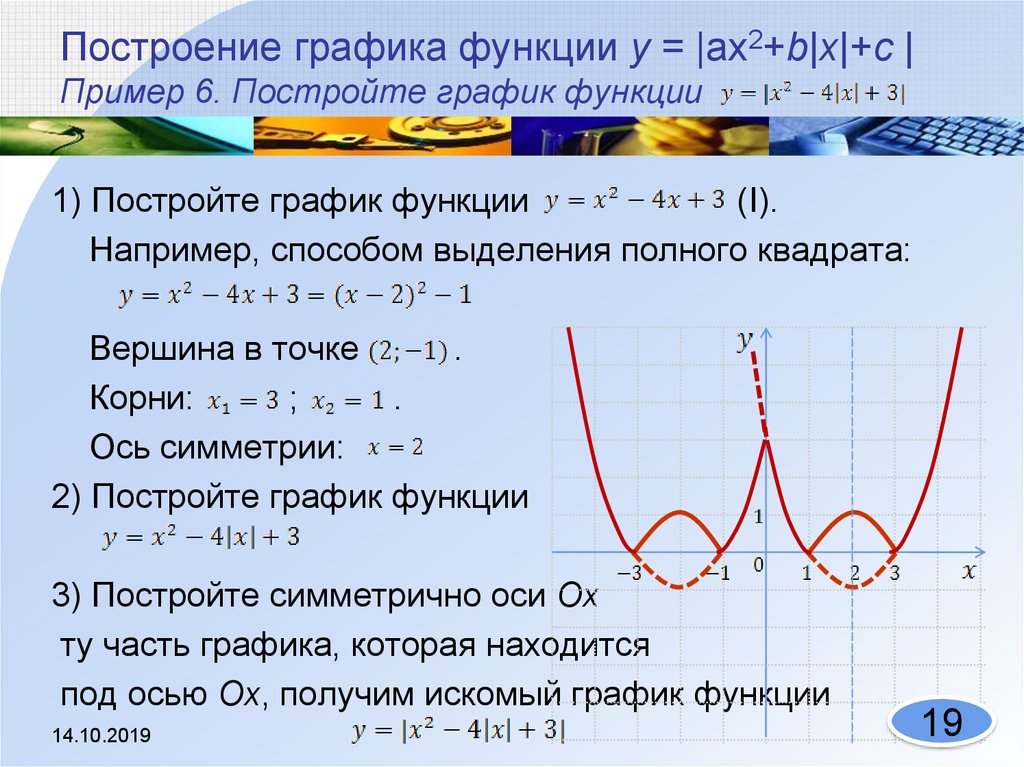
20. Построение графика функции у = |ах2+b|х|+с | Пример 6. Постройте график функции
1) Постройте график функции(I).
Например, способом выделения полного квадрата:
Вершина в точке
.
Корни:
;
.
Ось симметрии:
2) Постройте график функции
3) Постройте симметрично оси Оx
ту часть графика, которая находится
под осью Ох, получим искомый график функции
14.10.2019
19
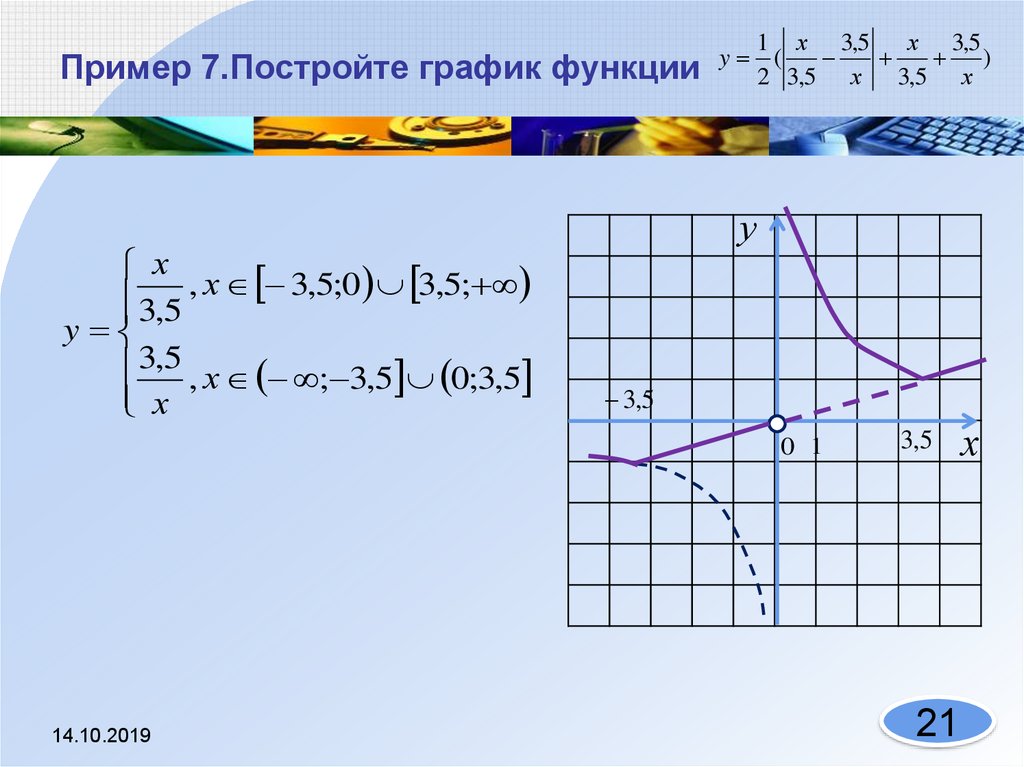
21. Пример 7.Постройте график функции
1 х 3,5х 3,5
y (
)
2 3,5 х 3,5 х
1 х 3,5
х 3,5 1 х 2 3,52 х 2 3,52
y (
) (
)
2 3,5 х 3,5 х
2
3,5х
3,5х
х 2 3,52
( х 3,5)( х 3,5)
3,5 х
3,5 х
y
-
+
-3,5
0
+
3,5
1
х
3,5
х
3,5
(
)
2 3,5
х
3,5
х
1 х 2 3,5 2
х 2 3,5 2
(
)
2
3,5 х
3,5 х
1 2х2
х
, х 3,5;0 3,5;
3,5
2 3,5 х
2
1 2 3,5 3,5 , х ; 3,5 0;3,5
3,5 х
х
2
14.10.2019
20
22. Пример 7.Постройте график функции
х, х 3,5;0 3,5;
3,5
y
3,5 , х ; 3,5 0;3,5
х
1 х 3,5
х 3,5
y (
)
2 3,5 х 3,5 х
у
3,5
0 1
14.10.2019
3,5
21
х
23. Использованные материалы и литература:
1.Алгебра.7-9 класс: учеб.для общеобразоват.
организаций/Ю.Н.Макарычев, Н.Г.Миндюк,
К.Нешков,С.Б.Суворова; под ред.С.А.Теляковского.-4-е
изд.-М.:Просвещение, 2015
2.
Башмаков М.И. Уравнения и неравенства.
3.
Михайлова Ж.Н. Алгоритмы - ключ к решению задач:
Алгебра. 7-9 классы.-СПб.:Издательский дом
«Литера»,2014. - 448 с.: ил..-(Серия «Средняя школа»)
4.
http://www.fipi.ru/ http://reshuege.ru/ Сайт Федерального
института педагогических измерений (ФИПИ)
14.10.2019
23
















 mathematics
mathematics








