Модуль. Графики функций, содержащих переменную под знаком модуля

1. Урок-презентация на тему: «Модуль»

Учитель: Матюшева В.И.

2. Графики функций, содержащих переменную под знаком модуля

1. Преобразование графиков
2. Построение графиков
3. Решение уравнений
4. Дидактический материал

3. 1.Преобразование графиков функций, содержащих переменную под знаком модуля

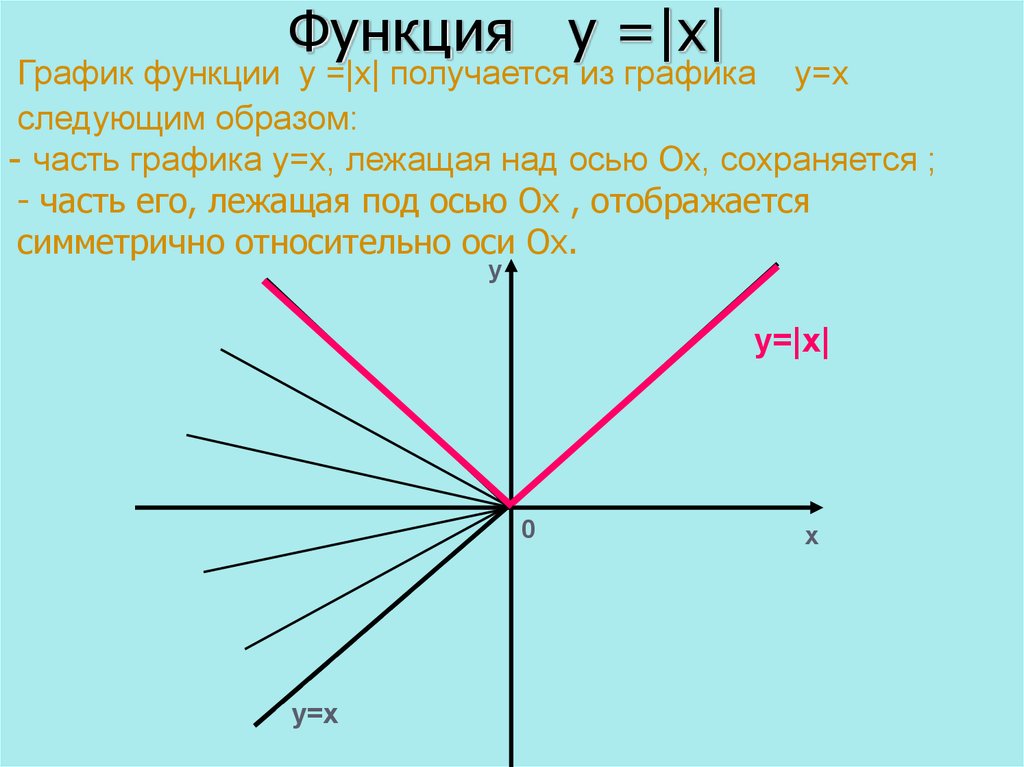
4. Функция у =|х|

График функции у =|х| получается из графика у=х
следующим образом:
- часть графика у=х, лежащая над осью Ох, сохраняется ;
- часть его, лежащая под осью Ох , отображается
симметрично относительно оси Ох.
у
у=|x|
0
у=х
х

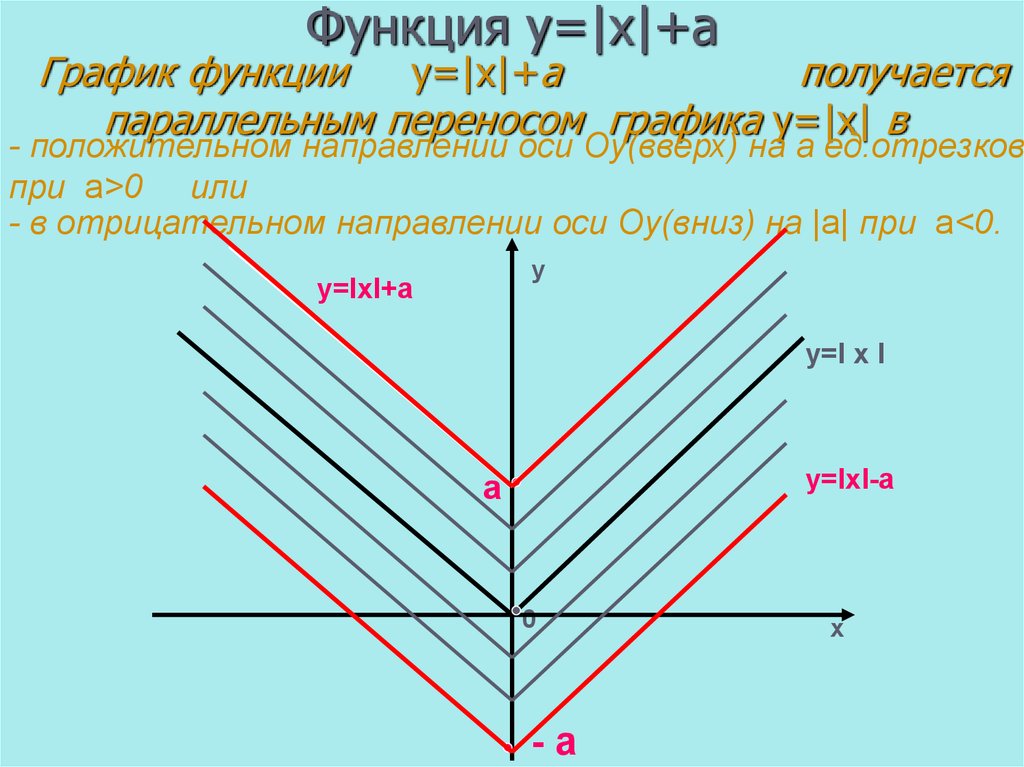
5. Функция у=|х|+а

График функции
у=|х|+а
получается
параллельным переносом графика у=|х| в
- положительном направлении оси Оу(вверх) на а ед.отрезков
при а>0 или
- в отрицательном направлении оси Оу(вниз) на |а| при а<0.
y
у=IxI+a
у=I x I
у=IxI-a
a
0
-a
x

6. y

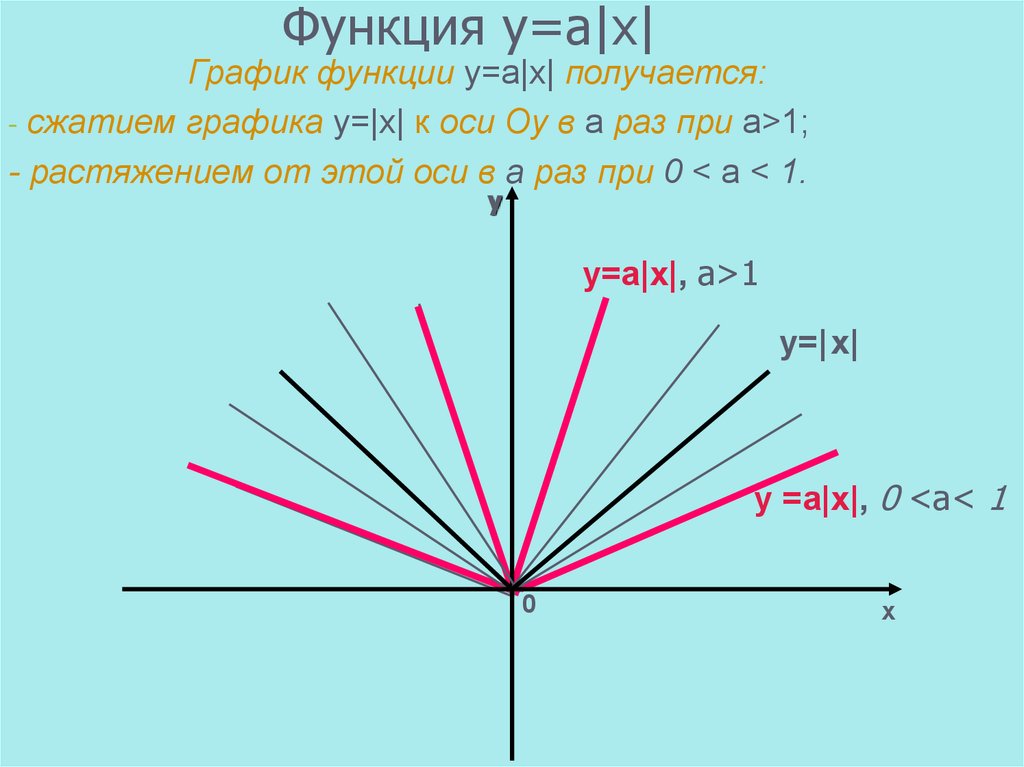
Функция у=а|х|
График функции у=а|х| получается:
- сжатием графика у=|х| к оси Оу в а раз при а>1;
- растяжением от этой оси в а раз при 0 < a < 1.
y
у=a|x|, а>1
у=| x|
у =а|x|, 0 <a< 1
0
x

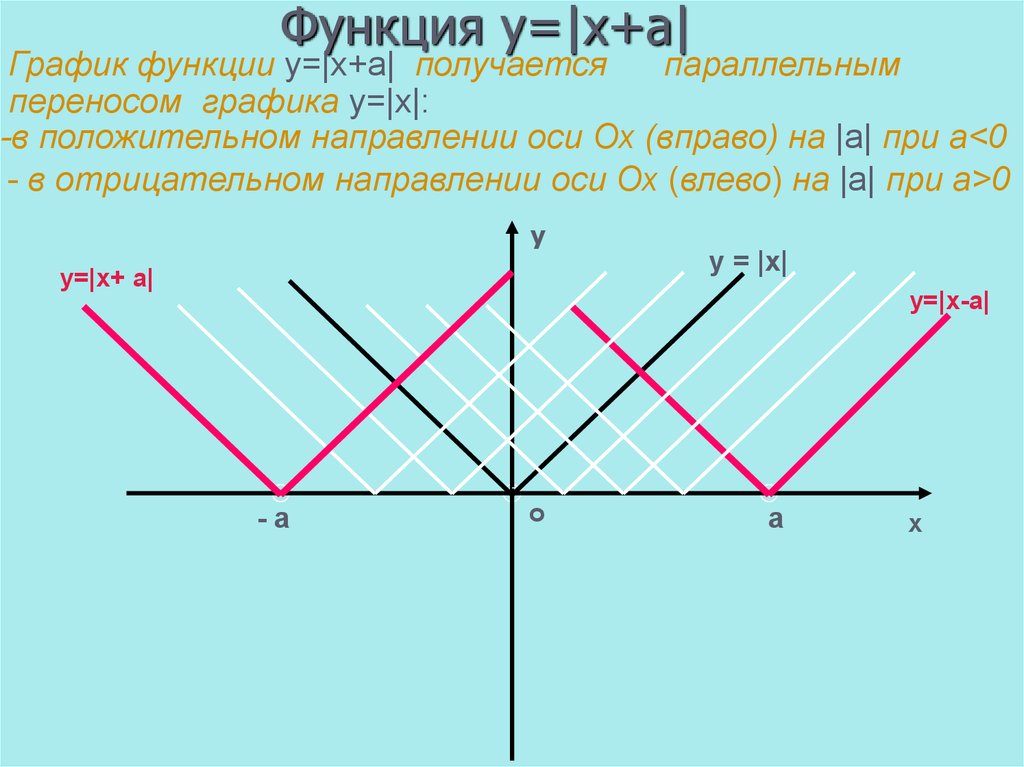
7. Функция у=|x+a|

График функции у=|x+a| получается
параллельным
переносом графика y=|x|:
-в положительном направлении оси Ох (вправо) на |a| при a<0
- в отрицательном направлении оси Ох (влево) на |а| при а>0
y
у=|x+ a|
у = |x|
у=|x-a|
о
-a
a
х

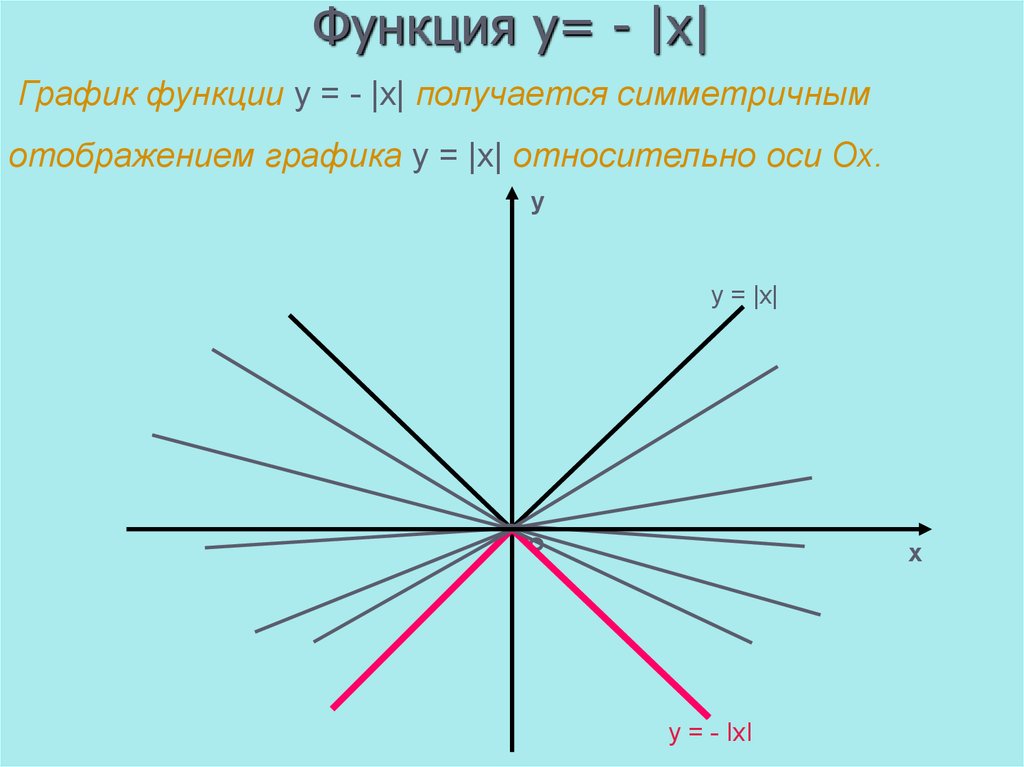
8. Функция y= - |x|

График функции y = - |x| получается симметричным
отображением графика y = |x| относительно оси Ох.
у
у = |x|
о
х
у = - IxI

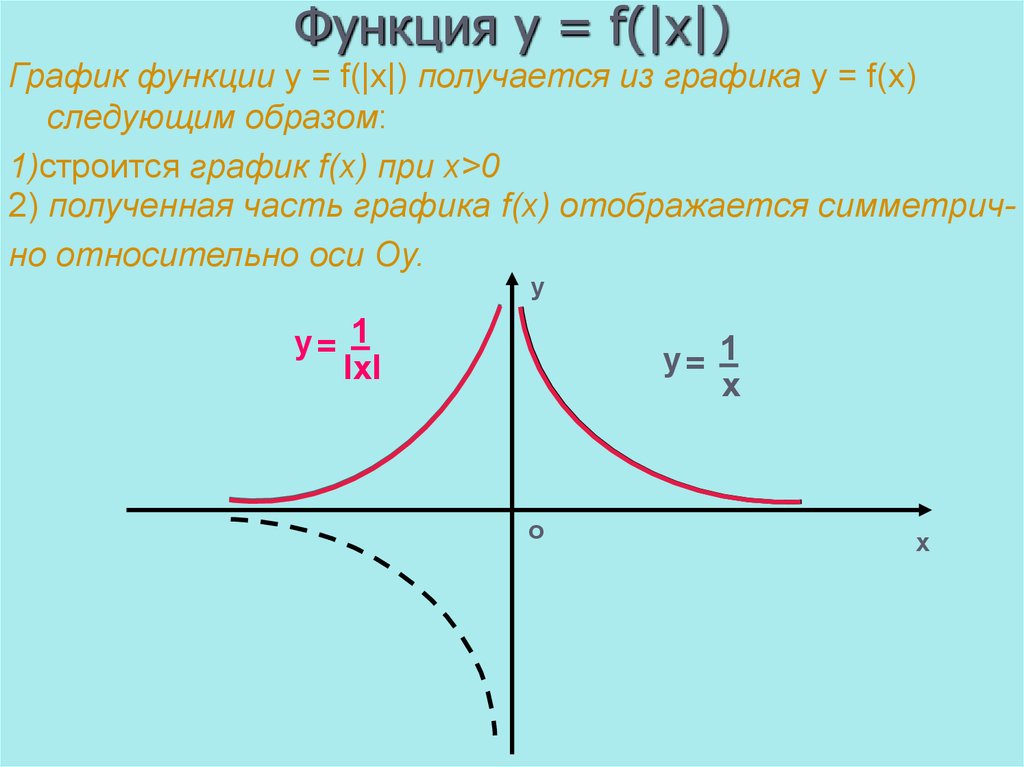
9. Функция y = f(|x|)

График функции y = f(|x|) получается из графика y = f(x)
следующим образом:
1)строится график f(x) при х>0
2) полученная часть графика f(x) отображается симметрично относительно оси Оу.
у
у= 1
IxI
у= 1
x
х
о

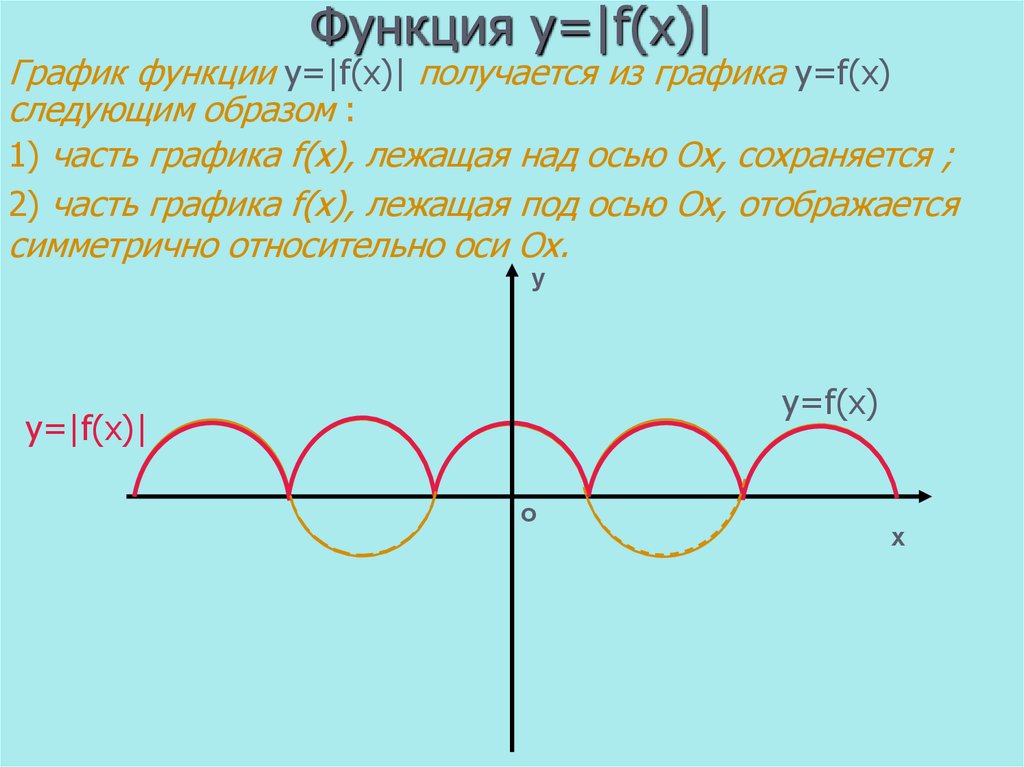
10. Функция y=|f(x)|

График функции y=|f(x)| получается из графика y=f(x)
следующим образом :
1) часть графика f(x), лежащая над осью Ох, сохраняется ;
2) часть графика f(x), лежащая под осью Ох, отображается
симметрично относительно оси Ох.
у
y=f(x)
y=|f(x)|
х
о

11. 2.Построение графиков функций, содержащих переменную под знаком модуля

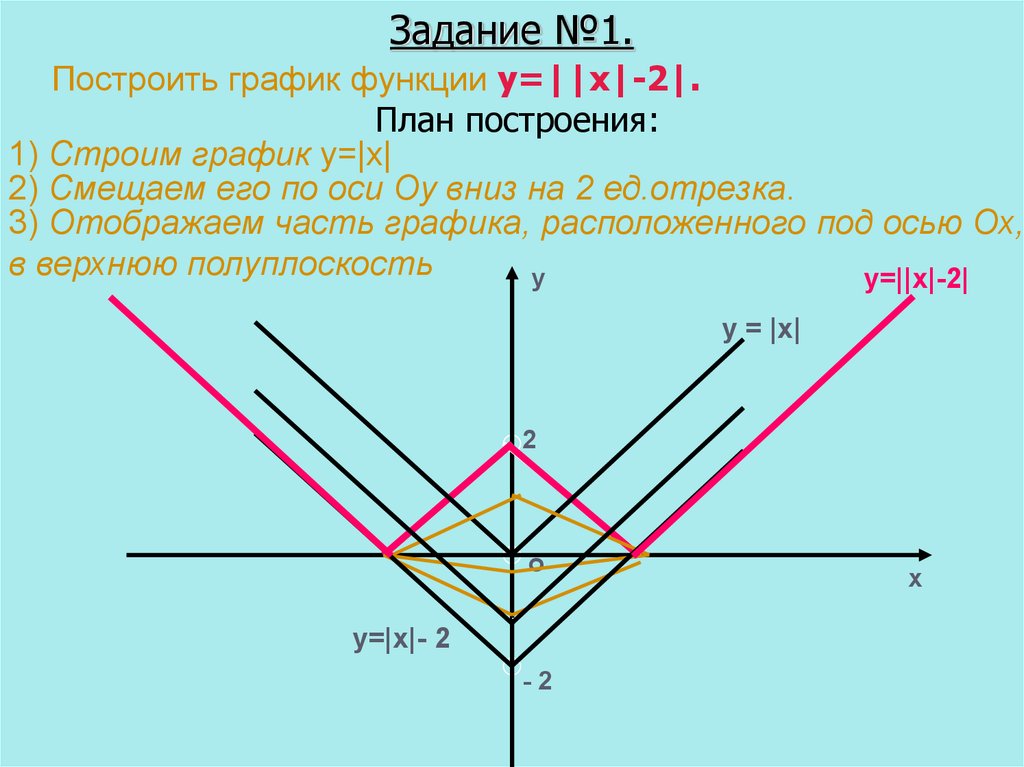
12. Задание №1.

Построить график функции у=||x|-2|.
План построения:
1) Строим график y=|x|
2) Смещаем его по оси Оу вниз на 2 ед.отрезка.
3) Отображаем часть графика, расположенного под осью Ох,
в верхнюю полуплоскость
у
у=||x|-2|
у = |x|
2
о
у=|x|- 2
-2
х

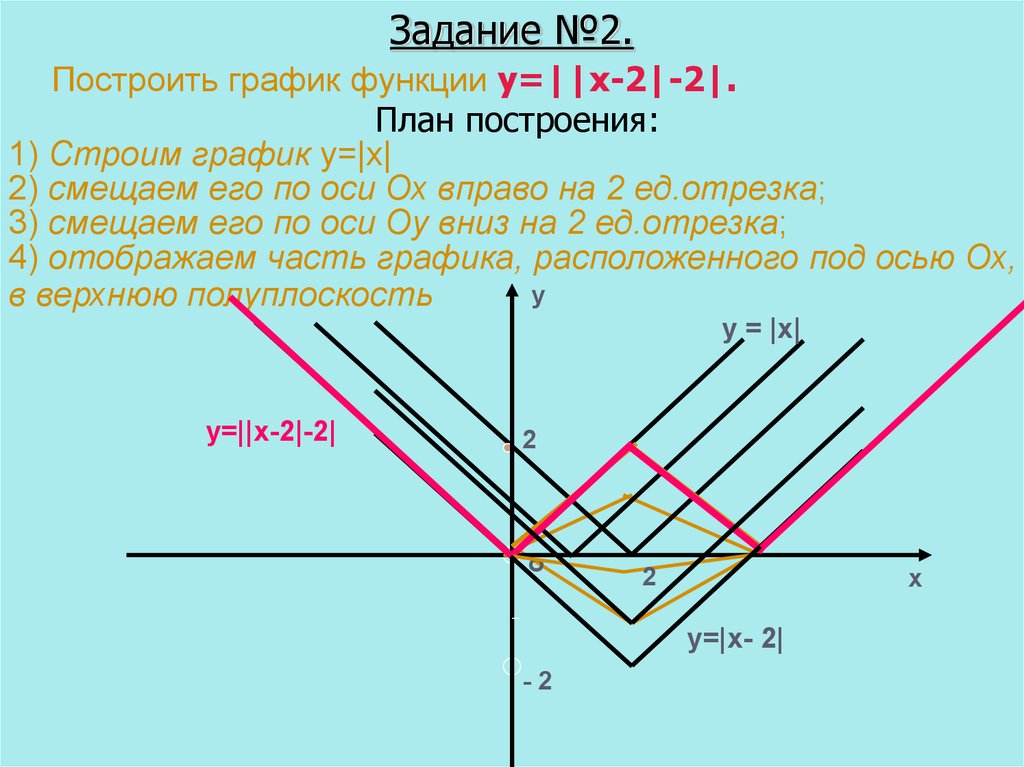
13. Задание №2.

Построить график функции у=||x-2|-2|.
План построения:
1) Строим график y=|x|
2) смещаем его по оси Ох вправо на 2 ед.отрезка;
3) смещаем его по оси Оу вниз на 2 ед.отрезка;
4) отображаем часть графика, расположенного под осью Ох,
у
в верхнюю полуплоскость
у = |x|
2
о
у=||x-2|-2|
х
2
у=|x- 2|
-2

14. 3.а)Решение уравнений, содержащих переменную под знаком модуля; б)решение уравнений с параметром.

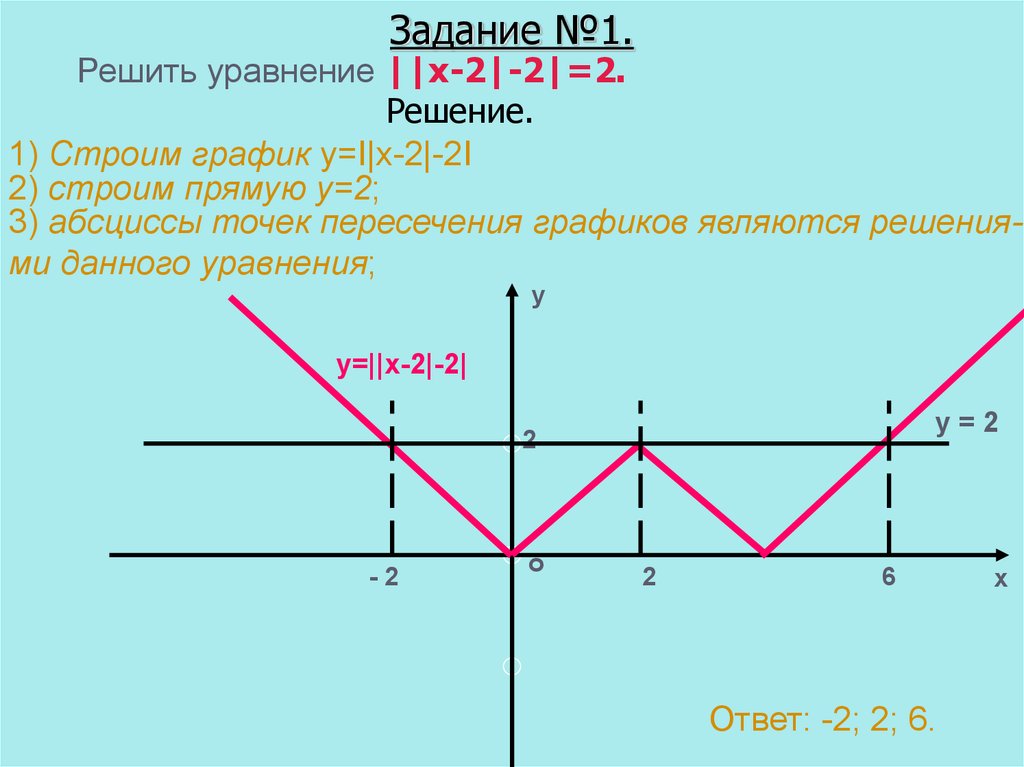
15. Задание №1.

Решить уравнение ||x-2|-2|=2.
Решение.
1) Строим график y=I|x-2|-2I
2) строим прямую у=2;
3) абсциссы точек пересечения графиков являются решениями данного уравнения;
у
у=||x-2|-2|
у=2
2
о
-2
2
6
Ответ: -2; 2; 6.
х

16. Задание №2.

В зависимости от параметра а определить количество
корней уравнения
||x|-2|=а.
Решение.
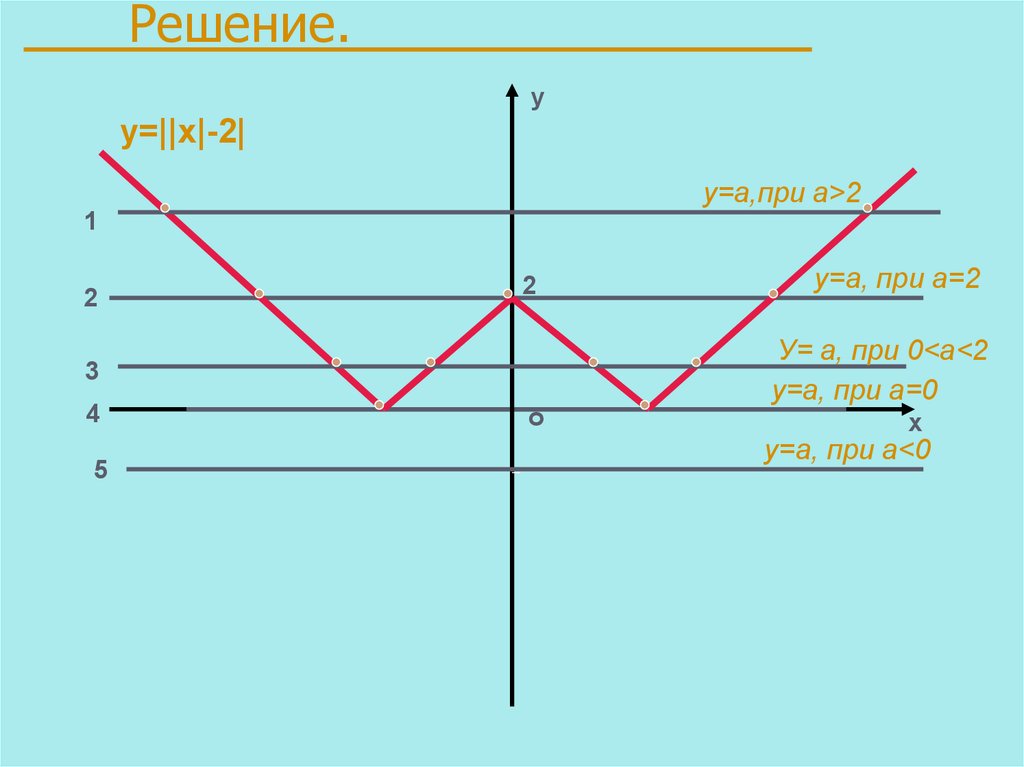
1) Строим график y= ||x|-2|;
2) Строим прямые:
у = а, при а > 2 ;
у = а, при а = 2 ;
у = а, при 0 < a < 2 ;
y = a, при а = 0 ;
у = а, при а < 0 .
3) Определяем число корней по количеству точек
пересечения прямой у=а и графика функции y= ||x|-2|.

17.

Решение.
у
у=||x|-2|
у=а,при а>2
1
2
2
У= а, при 0<a<2
y=a, при а=0
3
5
о
4
у=а, при а=2
х
у=а, при а<0

18. 4. Дидактический материал

19.

A. Построить график функции:
а) у=IxI+2; б) y=Ix+2I; в) y=-Ix+2I-1.
Б. a) y= 1/ Ix-2I+3;
б) y=- IIIxI-2I-3I;
в) у=IIII2xI-1I-1I-2I.
В. Решить уравнение: IIх+4I-3I = 2
Г. В зависимости от параметра а определить количество
корней уравнения
а)
IIIxI-2I-3I=a;
б) III2xI-1I-1I=a;
в) при каких k уравнение IIII4xI-2I-1I-1I=k имеет
наибольшее количество корней?