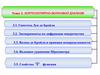
Опыт Франка и Герца (1914)

1.

Опыт Франка и Герца (1914).
K
C
Результат
эксперимента:
A
I
Hg
G
v
U З 0,5В
Ускоряющее напряжение, В
1.Пары
Hg в откаченном объёме;
2.Катод-сетка: ускор. разность потенциалов
3.Сетка-анод: задерживающая разность
потенциалов
Атом поглощает
энергию (механическую)
дискретно!
Начало
неупругих
взаимодействий
Начало 2-х
возможных
неупругих …
…3-х…
Доказательство
1-го постулата
Бора.
Комптон 1925. При U>4.9 В атомами ртути излучается свет с λ=0.2537мкм (УФ)
λ=0.2537мкм
Фотон hν = 4.9 эВ
Доказательство второго
постулата Бора

2.

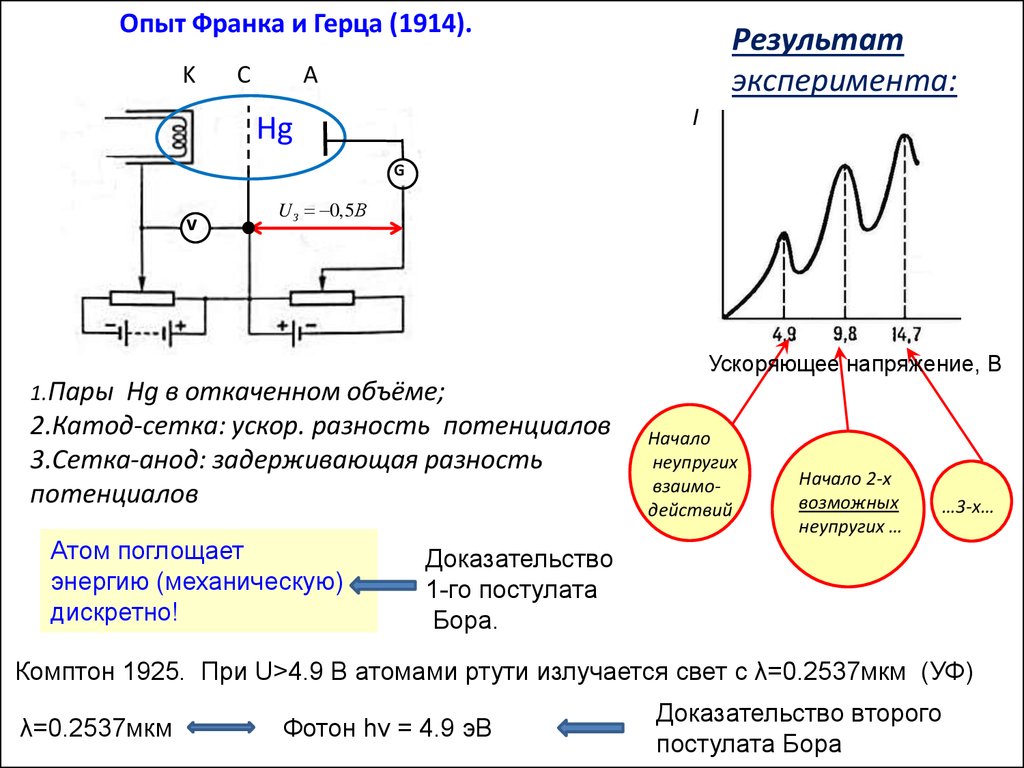
Боровская модель атома водорода, водородоподобного иона
Fe
e
1-ый п-т.Бора
me
Ze
2-ой з-н Н.
Скорость
электрона на
боровских
орбитах
Энергия
me r n
Ze
(n 1,2,3,...)
r
Радиусы
боровских
орбит
1 ЭЛЕКТРОН В
ПОЛЕ ЯДРА С
ЗАРЯДОМ
h 2 0
2
rn
n
me Ze2
,r
me 2
Ze2
r
4 0 r 2
Атом Н , Z=1
r1=0.53∙10-10 м=0.53 Å
v1=2∙106 м/сек
Ze2 1
n
2h 0 n
me Z 2e 4 1
En 2 2 2
8h 0 n

3.

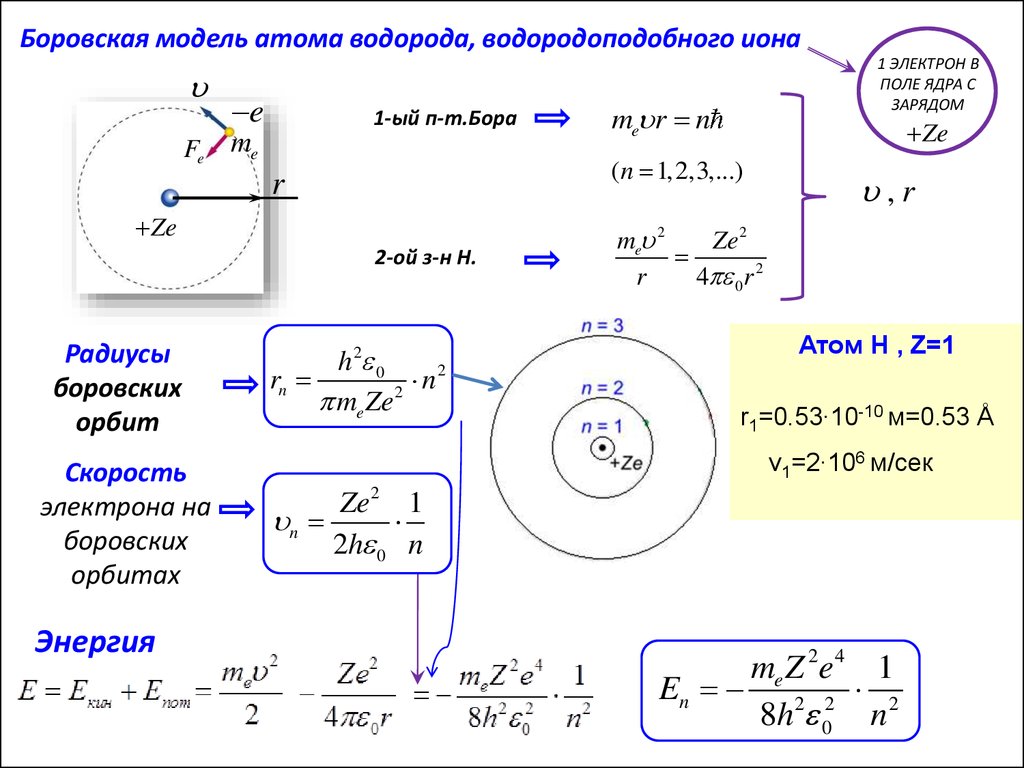
Энергетические уровни атома
водорода в модели Бора
me Z 2e 4 1
En 2 2 2
8h 0 n
2-ой постулат
Бора
En Em h
Обобщенная
формула Бальмера
?
1
1
2
2
m
n
R
n m
R 2,07 1016 рад
с

4.

2-ой постулат
Бора
En Em h
me Z 2e4 1
En 2 2 2
8h 0 n
me Z 2e4 1
1
1
En Em
h
8h3 02 m2 n 2
me Z 2e4 1
Em 2 2 2
8h 0 m
n m
Постоянная
Ридберга
me Z 2e4 1
1
1
1
2
R
2
2
4h3 02 m2 n 2
m n
Формула
Бальмера!!
Формула Бальмера
1 1
R 2 2
2 n
Теория
Бора
(!!)
n 3,4,5,...
R 2,07 1016 рад
me Z 2e4
R
4h3 02
с
Эксперимент

5.

E>0 Соответствует
свободному электрону.
m=3 – серия Пашена
E 0
E4
E3
E2
m=2 – серия Бальмера
(красное свечение)
3,40 eV
m=1 – серия Лаймана
E1
13,6 eV

6.

Недостатки теории Бора
Не удаётся рассчитать атомы с двумя (атом Не) и более электронами.
Ничего не говорит об интенсивности линий излучения (а она разная для
разных линий (например, водород светится красным, а почему не зелёным?).
Основной недостаток непоследовательность:
вычисление орбит на основе законов классической механики, считая при
этом неприменимой классическую электродинамику.
МОДЕЛЬ АТОМА БОРА промежуточный этап в поисках адекватной теории,
получившей название квантовой физики.

7.

1924 г.
Де-Бройль
1927 г.
Дэвиссон и
Джермер

8.

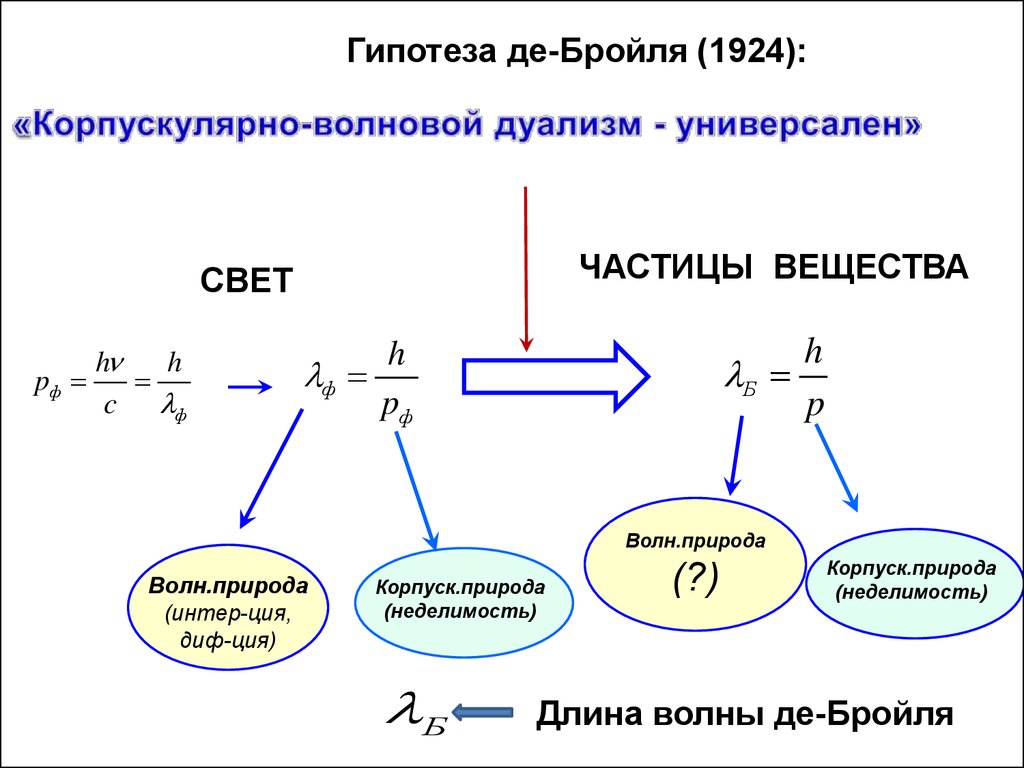
Гипотеза де-Бройля (1924):
ЧАСТИЦЫ ВЕЩЕСТВА
СВЕТ
h
h
pф
c ф
h
Б
p
h
ф
pф
Волн.природа
Волн.природа
(интер-ция,
диф-ция)
Корпуск.природа
(неделимость)
Б
(?)
Корпуск.природа
(неделимость)
Длина волны де-Бройля

9.

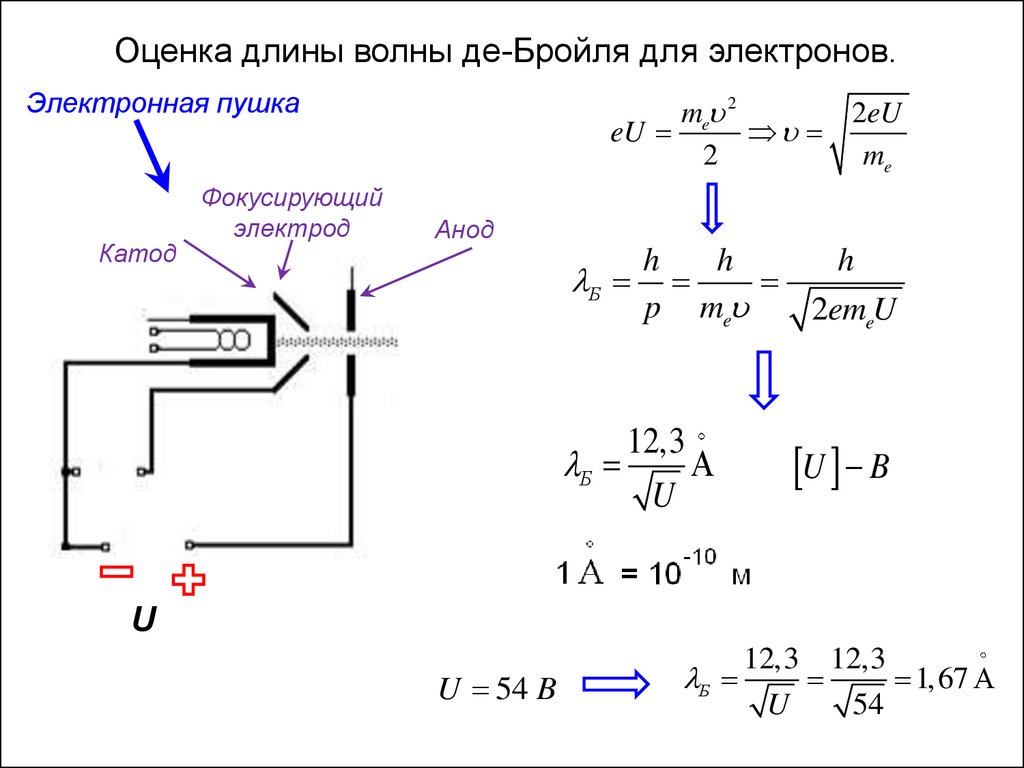
Оценка длины волны де-Бройля для электронов.
Электронная пушка
Катод
Фокусирующий
электрод
me 2
2eU
eU
2
me
Анод
h
h
h
Б
p me
2emeU
12,3
Б
U
U B
U
U 54 B
Б
12,3 12,3
1,67
U
54

10.

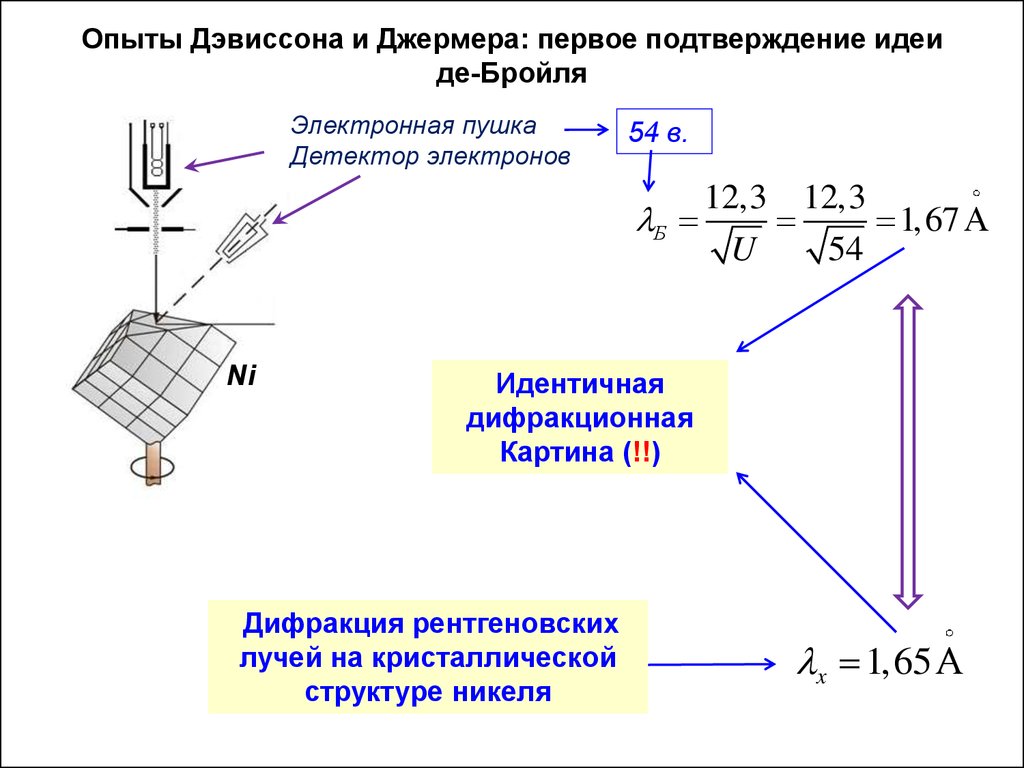
Опыты Дэвиссона и Джермера: первое подтверждение идеи
де-Бройля
Электронная пушка
Детектор электронов
54 в.
12,3 12,3
Б
1,67
U
54
Ni
Идентичная
дифракционная
Картина (!!)
Дифракция рентгеновских
лучей на кристаллической
структуре никеля
x 1,65

11.

Дальнейшие опыты по дифракции микрочастиц.
Томсон и одновременно Тартаковский: дифракция при прохождении
электронного пучка через металлическую фольгу (1927).
Эл.пушка фольга фотопластинка
Электронограмма
Полная аналогия с
рентгенограммой
при λx-ray= λe
Штерн & K.: дифракционные явления
в опытах с атомными и
молекулярными пучками.
Доказаны волновые свойства
частиц!
Каждой ? Или совокупности ?
h
1
Б
m
mEk
Длина волны де Бройля для
атомов имеет тот же масштаб, что
и для электронов, благодаря малой
(тепловой) скорости.

12.

Биберман, Сушкин и Фабрикант (1949): Опыты по дифракции
электронов с пучками слабой интенсивности
Электрон
регистрировался как
одно целое
Место прихода электрона на
фотопластинку имело случайный
характер. При достаточной
экспозиции получалась
дифракционная картина.
Вывод. Единичная частица обладает волновыми свойствами. А именно, её
положение в пространстве определяется вероятностным законом и этот
вероятностный закон таков, что при усреднении (по времени или по большому
числу частиц) реализуется волновая картина.
Усреднение по времени (пускаем электроны по одному и ждём пока их не придёт
достаточно много) или по большому числу частиц в потоке (много электронов
одновременно, видим мгновенную картину) эквивалентно.
В то же время микрочастицы обладают свойствами корпускулярности:
масса, размеры, заряд - неделимы.

13.

Гейзенберг, Вернер Карл
(1901-1976)

14.

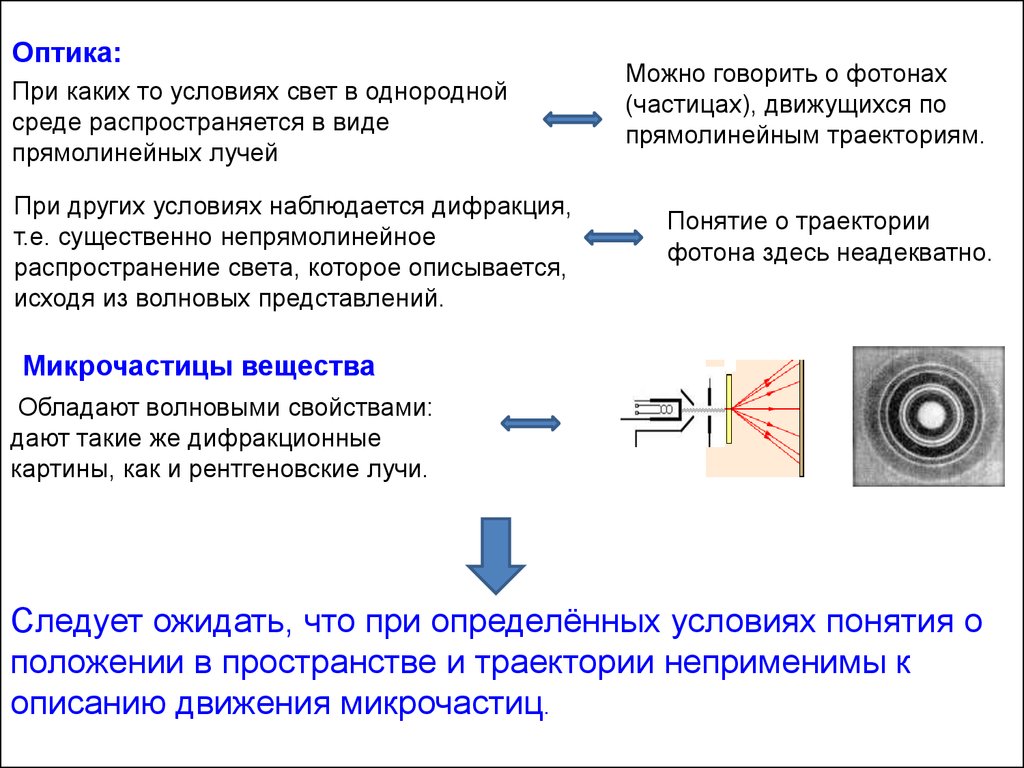
Оптика:
При каких то условиях свет в однородной
среде распространяется в виде
прямолинейных лучей
При других условиях наблюдается дифракция,
т.е. существенно непрямолинейное
распространение света, которое описывается,
исходя из волновых представлений.
Можно говорить о фотонах
(частицах), движущихся по
прямолинейным траекториям.
Понятие о траектории
фотона здесь неадекватно.
Микрочастицы вещества
Обладают волновыми свойствами:
дают такие же дифракционные
картины, как и рентгеновские лучи.
Следует ожидать, что при определённых условиях понятия о
положении в пространстве и траектории неприменимы к
описанию движения микрочастиц.

15.

Принцип неопределённости Гейзенберга
Степень точности, с которой к частице может
быть применено представление об её
определённом положении в пространстве
Частица не может иметь одновременно
точного значения координаты x и
проекции импульса на направление x.
ДО СИХ
Соотношения неопределённости Гейзенберга
p x x , p y y , p z z
2
2
2
Соотношение
неопределённости
Гейзенберга
p x x
2
степень неточности

16.

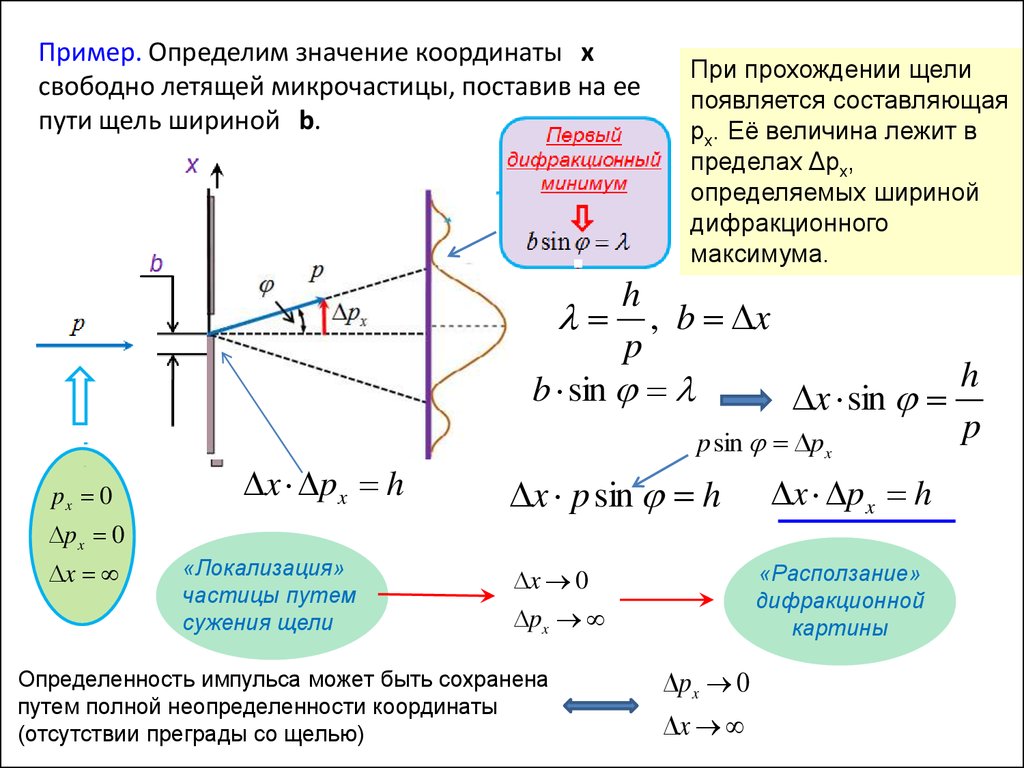
Пример. Определим значение координаты x
cвободно летящей микрочастицы, поставив на ее
пути щель шириной b.
При прохождении щели
появляется составляющая
px. Её величина лежит в
пределах Δpx,
определяемых шириной
дифракционного
максимума.
h
, b x
p
h
b sin
x sin
p
p sin p
px 0
x px h
x
x p sin h
p x 0
x
«Локализация»
частицы путем
сужения щели
«Расползание»
дифракционной
картины
x 0
px
Определенность импульса может быть сохранена
путем полной неопределенности координаты
(отсутствии преграды со щелью)
x px h
px 0
x

17.

Соотношение неопределенности указывает, насколько корректно
применять классическую механику к объектам микромира
Пример. Электрон в модели
атома водорода Бора.
x px
x
2 px
Атом Н , Z=1
r1=0.53∙10-10 м=0.53 Å
v1=2∙106 м/сек
2
2m x
x 0.5 x
x 2 106
6.6 10 34
10 м
x
0.5 10
0.5
31
6
m x 9.1 10 2 2 10
сек
м
сек
Неопределенность координаты масштаба линейных размеров самого
атома. Понятие круговой орбиты в атоме Бора теряет смысл!
Применение классической механики (Бор) – некорректно.

18.

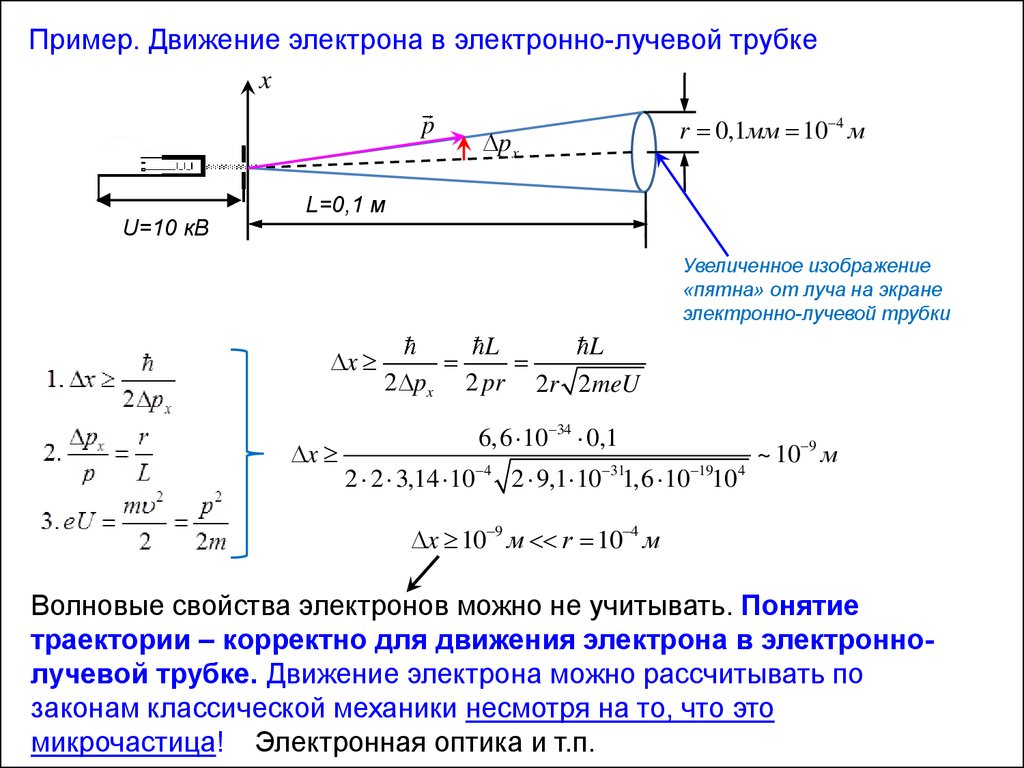
Пример. Движение электрона в электронно-лучевой трубке
x
p
U=10 кВ
px
r 0,1мм 10 4 м
L=0,1 м
Увеличенное изображение
«пятна» от луча на экране
электронно-лучевой трубки
x
x
2 px
L
L
2 pr 2r 2meU
6,6 10 34 0,1
2 2 3,14 10 4 2 9,1 10 311,6 10 19104
~ 10 9 м
x 10 9 м r 10 4 м
Волновые свойства электронов можно не учитывать. Понятие
траектории – корректно для движения электрона в электроннолучевой трубке. Движение электрона можно рассчитывать по
законам классической механики несмотря на то, что это
микрочастица! Электронная оптика и т.п.

19.

Пример. Движение электрона в электронно-лучевой трубке
Пятно, которое даёт электронный луч на экране, должно восприниматься глазом.
Соответственно, его радиус не должен быть меньше быть ≈0.1 мм.
Пусть этот размер пятна полностью определяется неопределённостью импульса.
x
p
px
r 0,1мм 10 4 м
L=0,1 м
U=10 кВ
x
x
2 px
L
L
2 pr 2r 2meU
Увеличенное изображение
«пятна» от луча на экране
электронно-лучевой трубки
6,6 10 34 0,1
2 2 3,14 10 4 2 9,1 10 311,6 10 19104
~ 10 9 м
x 10 9 м r 10 4 м
Волновые свойства электронов можно не учитывать. Понятие
траектории – корректно для движения электрона в электроннолучевой трубке. Движение электрона можно рассчитывать по
законам классической механики несмотря на то, что это
микрочастица! Электронная оптика и т.п.

20.

Пример. Пылинка
Линейный размер:
r ≈10-4 см = 1мкм
Будем определять координату пылинки x с точностью
∆x<<r и ∆x<<λ (длины волны
видимого света, ≈5∙10-5 см)
.
Очень высокая точность!
Какова неопределённость определения скорости?
x px
2
6,6 10 34
11 м
x
0,5
10
с
2m x 2 3,14 2 10 15 10 8
Пылинка – большая; у нее большая масса; она объект макромира и к
ней применимы законы классической физики !!

21.

ВОЛНОВАЯ ФУНКЦИЯ
Микрочастицы обладают волновыми свойствами. А именно, их
положение в пространстве задаётся определённым
вероятностным законом и этот вероятностный закон таков, что
при усреднении (по времени или по большому числу частиц)
реализуется волновая картина.
Необходимо создать математический формализм, описывающий наблюдаемые в
микромире явления и правильно предсказывающий поведение микрочастиц.
Описание поведения (состояния)
Такой формализм был создан
микрочастиц с помощью волновой
функции Ψ.
Вводится комплексная волновая функция Ψ, квадрат модуля которой даёт
вероятность обнаружения частицы в пределах объёма dV
Вероятность обнаружения
частицы в объёме dV
Нобелевская
премия за
истолкование
статистического
смысла Ψ
dW dV dV
Плотность вероятности
обнаружения частицы в данной
точке пространства.
2
dW
2
w
dV
*
Макс Борн
(1882-1970)
Для волновой функции Ψ должно быть найдено такое уравнение, чтобы найденная
из него Ψ описывала поведение микрочастиц с учётом их волновых свойств.

22.

U i
2m
t
2
Эрвин Шредингер
(1887-1961)

23.

Уравнение Шредингера
Потенциальная
энергия
2 2 2
( 2 2 2 ) U i
2m x
y
z
t
2
2 2 2
2 2 2
2
x
y
z
2
2m
U i
t
Дифференциальное ур-ие 2-го
порядка в частных производных –
основное ур-ие нерелятивисткой
квантовой механики.
Не выводится – физический закон
Оператор Лапласа
Стационарное уравнение Шредингера.
Если силовое поле, в котором движется частица, стационарно, т.е. не зависит
от времени (U не зависит от t), то уравнение Шредингера имеет вид
Полная энергия
системы
2
2m
( x, y, z ) ( E U ) ( x, y, z ) 0
Стационарное уравнение
Шредингера.
Не зависит от времени

24.

3.
Стационарное уравнение Шредингера.
Если силовое поле, в котором движется частица, стационарно, т.е. не
зависит от времени, то решение ур-ия Шредингера ищут в виде:
( x , y , z , t ) ( x, y , z ) e
2
2m
2
2m
U i
( x, y, z ) e
2
2m
2
2m
( x, y, z )
t
E
i t
E
U ( x, y, z ) e
E
i t
- Координатная часть
волновой функции
- Полная энергия
частицы
i ( x, y, z ) ( i
E
)e
E
i t
( x, y, z ) U ( x, y, z ) ( x, y, z ) E
( x, y, z ) ( E U ) ( x, y, z ) 0
2
E
i t
2
Не зависит от времени
Стационарное
уравнение Шредингера.

25.

2
2m
( x, y, z ) ( E U ) ( x, y, z ) 0
Уравнение Шредингера имеет решения при определенных значениях Е
– «собственные значения».
En
«Собственным значениям» соответствуют «собственные
функции», характерные для определенного состояния частицы
(квантово-механической системы).
n
Квадрат модуля «собственной функции» определяет вероятность
этого состояния.