Similar presentations:
Элементы квантовой механики
1.
ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ1. Гипотеза де Бройля. Физический смысл волн де Бройля
2. Дифракция электронов
3.
Корпускулярно-волновой
дуализм
микрочастиц
вещества
4. Соотношение неопределенности Гейзенберга
5. Понятие о волновой функции
6. Уравнение Шредингера
2.
1. Гипотеза де БройляНедостатки теории Бора указывали на необходимость
пересмотра основ квантовой теории и представлений о
природе микрочастиц.
Электрон представляется в виде малой механической
частицы,
характеризующейся
определенными
координатами и определенной скоростью.
В оптических явлениях наблюдается своеобразный
дуализм.
Дифракция, интерференция – волновая природа света
Фотоэффект, эффект Комптона - корпускулярная природа
света
3.
В 1924 г. Луи де Бройль выдвинул смелую гипотезу, чтодуализм не является особенностью только оптических
явлений, а имеет универсальный характер:
частицы вещества также обладают волновыми
свойствами.
Допуская,
что
частицы
вещества
наряду
с
корпускулярными свойствами имеют также и
волновые, де Бройль перенес на случай частиц вещества
те же правила перехода от одной картины к другой, какие
справедливы в случае света.
4.
Луи де Бройль (1892 – 1987),французский
физик,
удостоенный
Нобелевской
премии 1929 г. по физике за
открытие волновой природы
электрона.
Предположил, что поток материальных частиц должен
обладать и волновыми свойствами, связанными с их
массой и энергией (волны де Бройля).
Экспериментальное подтверждение этой идеи было
получено в 1927 в опытах по дифракции электронов в
кристаллах.
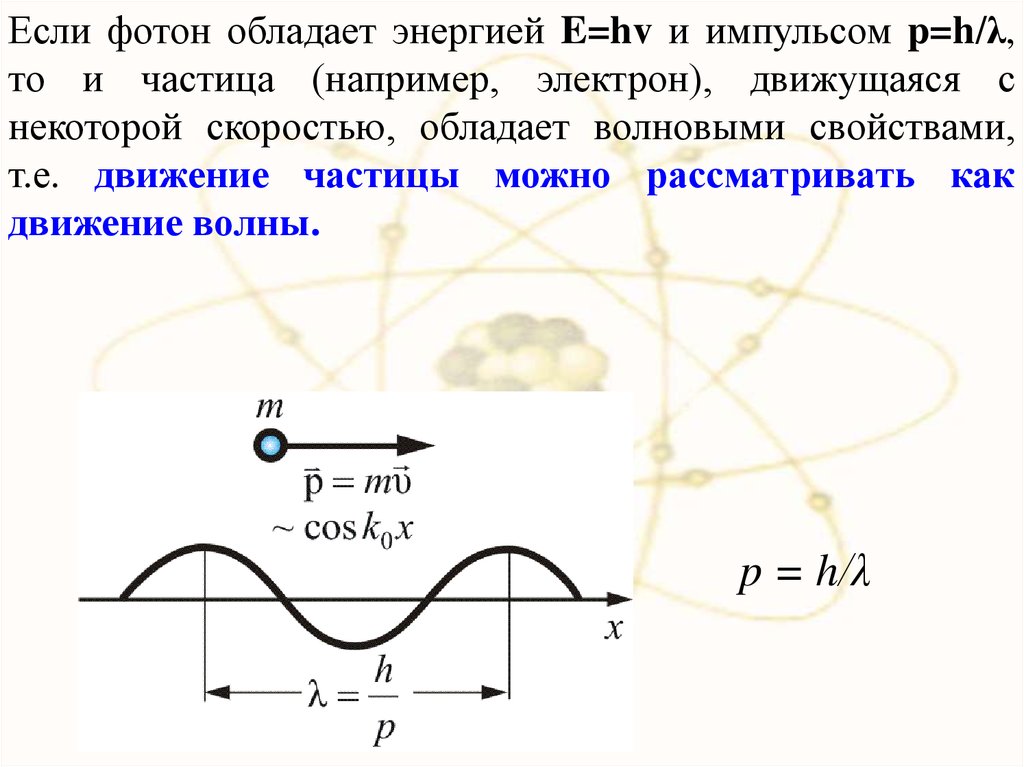
5.
Если фотон обладает энергией E=hv и импульсом p=h/λ,то и частица (например, электрон), движущаяся с
некоторой скоростью, обладает волновыми свойствами,
т.е. движение частицы можно рассматривать как
движение волны.
p = h/λ
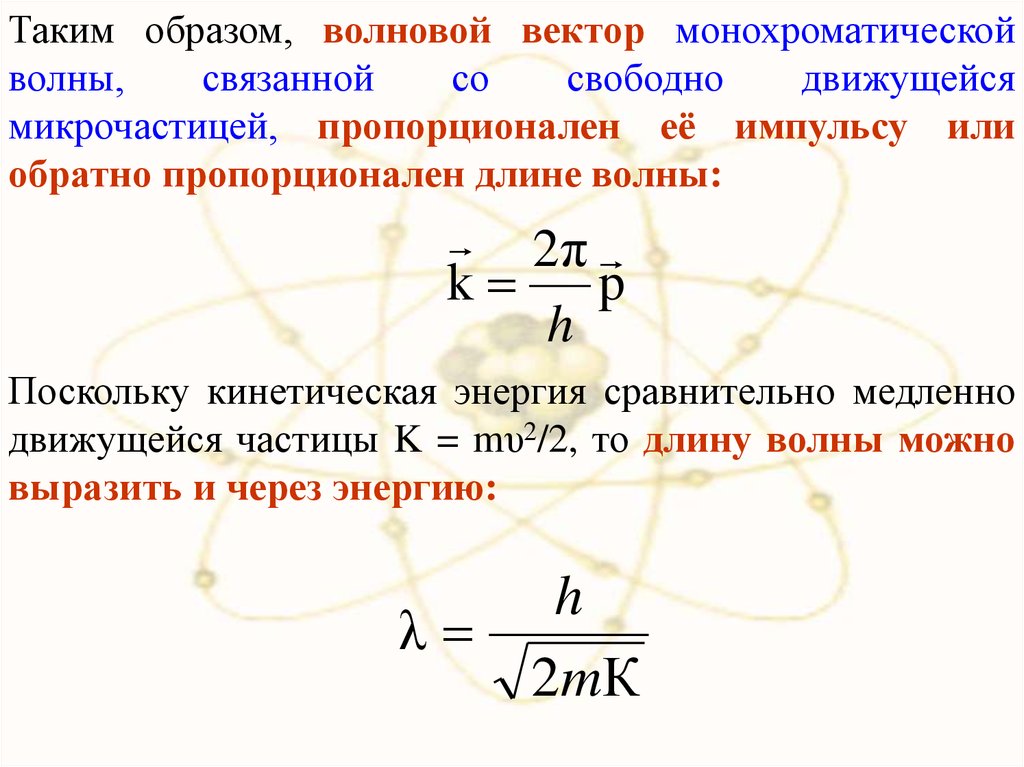
6.
Согласно квантовой механике, свободное движениечастицы с массой m и импульсом p = mυ можно
представить как плоскую монохроматическую волну Ψ0
с длиной волны λ h/p
Ψ0 ~ cos( k x) - волна де Бройля
где k – волновое число,
2π
волновой вектор: k
p
h
- направлен в сторону распространения волны, или вдоль
движения частицы.
7.
Таким образом, волновой вектор монохроматическойволны,
связанной
со
свободно
движущейся
микрочастицей, пропорционален её импульсу или
обратно пропорционален длине волны:
2π
k
p
h
Поскольку кинетическая энергия сравнительно медленно
движущейся частицы K = mυ2/2, то длину волны можно
выразить и через энергию:
λ
h
2 mК
8.
При взаимодействии частицы с некоторым объектом(кристаллом, молекулой) её энергия меняется: к ней
добавляется потенциальная энергия этого взаимодействия.
Соответственно, меняется характер распространения
связанной с частицей волны.
Поэтому, основные геометрические закономерности
дифракции частиц, ничем не отличаются от
закономерностей дифракции любых волн.
Общим условием дифракции волн любой природы
является соизмеримость длины падающей волны λ с
расстоянием d между рассеивающими центрами: λ ≤ d
9.
Физический смысл волн де БройляИдея де Бройля о наличии у частиц вещества волновых
свойств получила экспериментальное подтверждение.
Обнаружить волновые свойства у макроскопических
тел не представляется возможным из-за присущей им
малой длины волны.
Волны, связанные с движущимися частицами, не имеют
никакого отношения к распространению какого-либо
электромагнитного поля, к электромагнитным волнам.
10.
Было выяснено, что квадрат амплитуды световой волныв какой-либо точке пространства пропорционален
числу фотонов, попадающих в эту точку.
Вопрос о природе волн, связанных с движущимися
частицами вещества, можно сформулировать как вопрос о
физическом смысле амплитуды или интенсивности этих
волн.
11.
Интенсивностьамплитуды.
пропорциональна
квадрату
Эксперименты по отражению электронов и др. частиц от
поверхности
показывают,
что
по
некоторым
направлениям обнаруживаются максимумы числа
отраженных частиц.
Это означает, что в указанных направлениях отражается
большее число частиц, чем в других направлениях.
С волновой точки зрения наличие максимумов в
некоторых направлениях означает, что эти направления
соответствуют наибольшей интенсивности волн,
связанных с отражающимися частицами.
12.
Интенсивность дебройлевской волны оказываетсябольшей там, где имеется большее число частиц.
Другими словами, интенсивность волн де Бройля в данной
области пространства определяет число частиц,
попавших в эту область. В этом заключается
статистическое,
вероятностное
толкование
волн,
связанных с движущимися частицами.
Квадрат амплитуды дебройлевской волны в данной
точке пространства является мерой вероятности того,
что частица находится в этой области.
13.
2. Дифракция частицДифракция
частиц,
рассеяние
микрочастиц
(электронов, нейтронов, атомов и т.п.) кристаллами
или молекулами жидкостей и газов, при котором из
начального пучка частиц данного типа возникают
дополнительно отклонённые пучки этих частиц.
Направление и интенсивность таких отклонённых пучков
зависят от строения рассеивающего объекта.
14.
Квантовая механика устранила абсолютную грань междуволной и частицей.
Основным
положением
квантовой
механики,
описывающей поведение микрообъектов, является
корпускулярно-волновой дуализм, т.е. двойственная
природа микрочастиц.
15.
Опыты по дифракции частици их квантовомеханическая интерпретация.
Первым
опытом
по
дифракции частиц, блестяще
подтвердившим
исходную
идею квантовой механики –
корпускулярно-волновой
дуализм,
явился
опыт
американских
физиков
К.
Дэвиссона и Л. Джермера
проведенный
в
1927
по
дифракции
электронов
на
монокристаллах никеля:
15
16.
Кристаллы обладают высокой степенью упорядоченности.Атомы в них располагаются в трёхмерно-периодической
кристаллической
решётке,
т.е.
образуют
пространственную дифракционную решётку для
соответствующих длин волн.
17.
Если ускорять электроны электрическим полем снапряжением U, то они приобретут кинетическую
энергию K = eU, (е – заряд электрона), что после
подстановки в равенство
λ
h
2 mК
числовых значений даёт
12,26
λ
U
Здесь U выражено в В, а λ – в Å (1 Å = 10–10 м).
18.
При напряжениях U порядка 100 В, получаются такназываемые «медленные» электроны с λ порядка 1 Å.
Эта величина близка к межатомным расстояниям d в
кристаллах, которые составляют несколько Å и менее, и
соотношение λ ≤ d, необходимое для возникновения
дифракции, выполняется.
19.
Дифракция волн на кристаллической решётке происходитв результате рассеяния на системах параллельных
кристаллографических плоскостей, на которых в строгом
порядке расположены рассеивающие центры.
Условием наблюдения дифракционного максимума при
отражении от кристалла является условие Вульфа –
Брэггов - :
2d sin θ nλ
В опыте Дэвиссона и Джермера при «отражении»
электронов от поверхности кристалла никеля при
определённых углах отражения возникали максимумы.
20.
Эти максимумы отражённых пучков электроновсоответствовали условию Вульфа – Брэггов :
2d sin θ nλ
и их появление не могло быть объяснено никаким другим
путём, кроме как на основе представлений о волнах и их
дифракции;
таким образом, волновые свойства частиц –
электронов – были доказаны экспериментом.
21.
При более высоких ускоряющих электрическихнапряжениях (десятках кВ) электроны приобретают
достаточную кинетическую энергию, чтобы проникать
сквозь тонкие плёнки вещества (толщиной порядка 10–5
см, т. е. тысячи Å).
Тогда возникает так называемая дифракция быстрых
электронов
на
прохождение,
которую
на
поликристаллических плёнках алюминия и золота
впервые исследовали английский учёный Дж. Дж. Томсон
и советский физик П. С. Тартаковский.
22.
Вскоре после этого удалось наблюдать и явлениядифракции атомов и даже молекул!
Атомам с массой М, находящимся в газообразном
состоянии в сосуде при абсолютной температуре Т,
соответствует длина волны:
h
λ
3MkT
где k –постоянная Больцмана, k = 3/2kT - средняя
кинетическая энергия атома
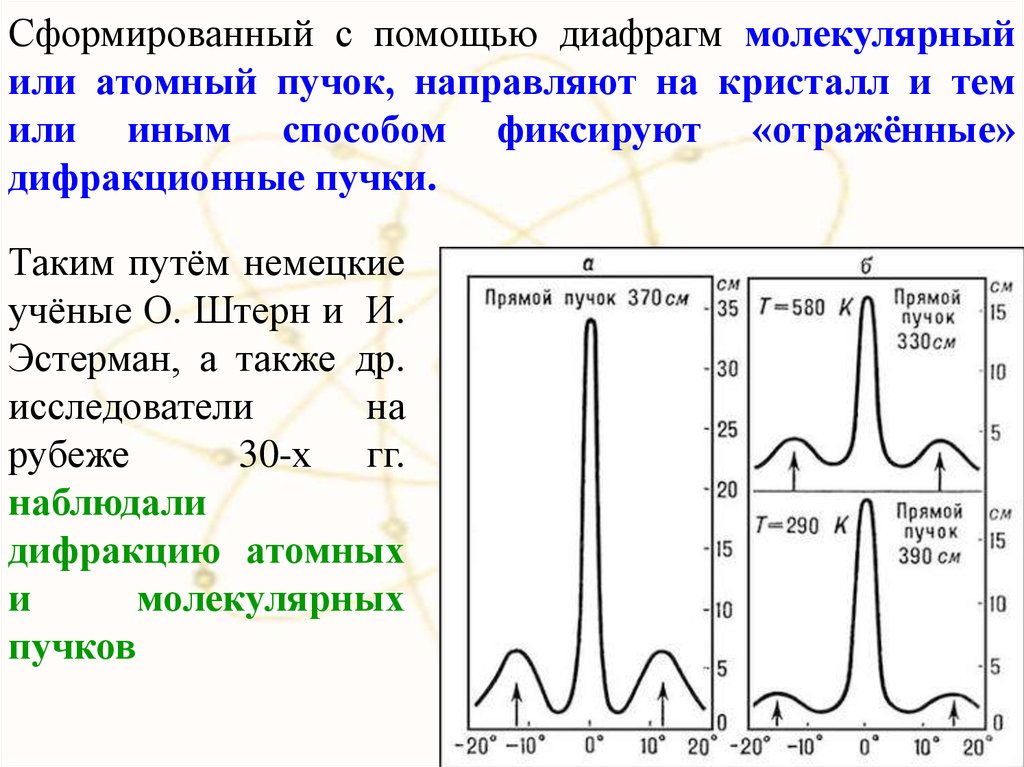
23.
Сформированный с помощью диафрагм молекулярныйили атомный пучок, направляют на кристалл и тем
или иным способом фиксируют «отражённые»
дифракционные пучки.
Таким путём немецкие
учёные О. Штерн и И.
Эстерман, а также др.
исследователи
на
рубеже
30-х гг.
наблюдали
дифракцию атомных
и
молекулярных
пучков
23
24.
Позженаблюдалась
дифракция протонов, а
также
дифракция
нейтронов , получившая
широкое
распространение
как
один
из
методов
исследования структуры
вещества.
Так было доказано экспериментально, что волновые
свойства
присущи
всем
без
исключения
микрочастицам.
25.
Картина дифракцииэлектронов на слюде
26.
Картина дифракциинейтронов на кварце
26
27.
В 1927 г. Дж.П. Томпсон и независимо от него П.С.Тартаковский получили дифракционную картину при
прохождении электронного пучка через металлическую
фольгу.
В 1949 г. советские ученые Л.М. Биберман, Н.Г. Сушкин,
В.А. Фабрикант поставили такой же опыт, но
интенсивность электронного пучка была настолько
слабой, что электроны проходили через прибор
практически поодиночке. Однако картина после
длительной экспозиции была точно такой же. Т.е. было
доказано, что волновыми свойствами обладает каждый
отдельный электрон.
28.
Дифракция частиц, сыгравшая в своё время стольбольшую роль в установлении двойственной природы
материи – корпускулярно-волнового дуализма стала
одним из главных рабочих методов для изучения
строения вещества.
На дифракции частиц основаны два важных современных
метода анализа атомной структуры вещества –
электронография и нейтронография.
29.
3. Корпускулярно- волновой дуализм микрочастицвещества
Микрочастицы обладают необычайными свойствами.
Микрочастицы – это элементарные частицы (электроны,
протоны, нейтроны и т.д.), а также сложные частицы,
образованные из небольшого числа элементарных (пока
неделимаых) частиц (атомы, молекулы, ядра атомов).
Называя эти микрочастицы частицами, мы подчеркиваем
только одну сторону, правильнее было бы назвать
«частица – волна».
30.
Волны де Бройля не являются электромагнитными, этоволны особой природы.
Вычислим дебройлевскую длину волны мячика массой
0,20 кг, движущегося со скоростью 15 м/с.
h
6,67 10 34 Äæ ñ
2,2 10 34 ì
m
0,2 15
При скорости 10–4м/с, дебройлевская длина волны
составляла бы примерно 10–9м.
31.
Дебройлевская длина волны обычного тела слишком мала,чтобы ее можно было обнаружить и измерить.
Волновые свойства – интерференция и дифракция –
проявляются только тогда, когда размеры предметов или
щелей сравнимы по своей величине с длиной волны.
Поэтому волновые свойства обычных тел обнаружить
не удается.
32.
Определим дебройлевскую длину волныускоренного разностью потенциалов 100 В.
электрона,
h
m
1
m 2 eU
2
2eU
5,9 106 ì / c
m
34
h
6,6 10
10
λ
1,2 10 м
31
6
mυ 9,1 10 5,9 10
33.
Электрон может соответствовать длине волны 10–10м.Это очень короткие волны, но их можно обнаружить
экспериментально: межатомные расстояния в кристалле
того же порядка величины (10–10м) и регулярно
расположенные атомы кристалла можно использовать в
качестве дифракционной решетки, как в случае
рентгеновского излучения.
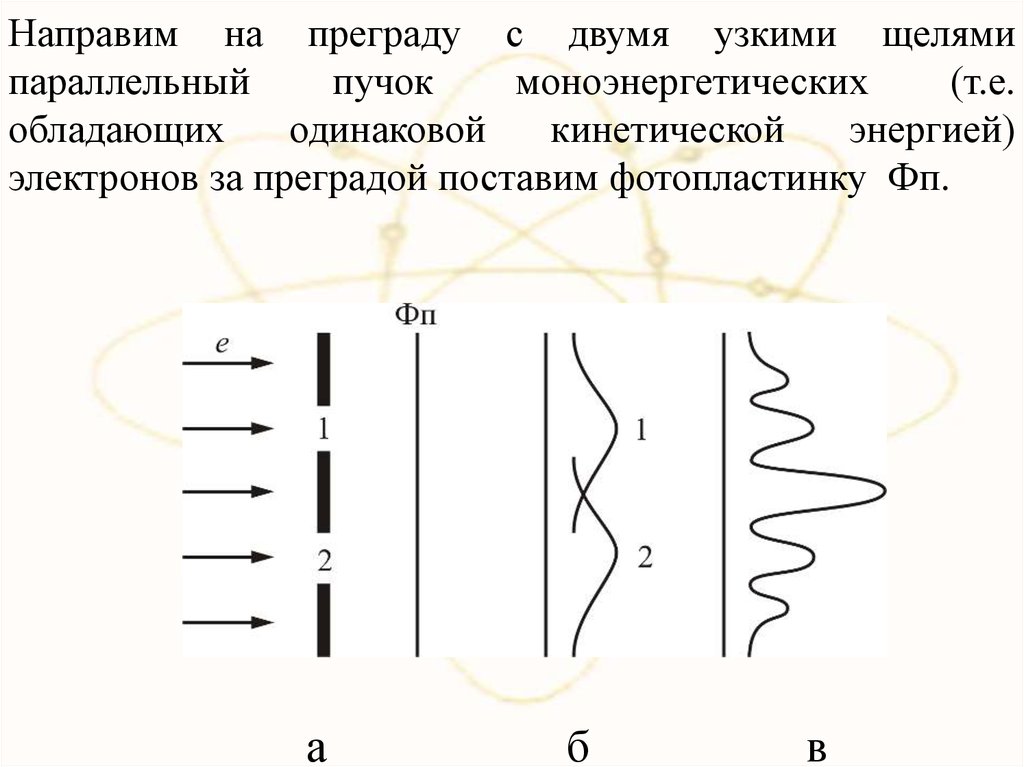
34.
Направим на преграду с двумя узкими щелямипараллельный
пучок
моноэнергетических
(т.е.
обладающих
одинаковой
кинетической
энергией)
электронов за преградой поставим фотопластинку Фп.
а
б
в
35.
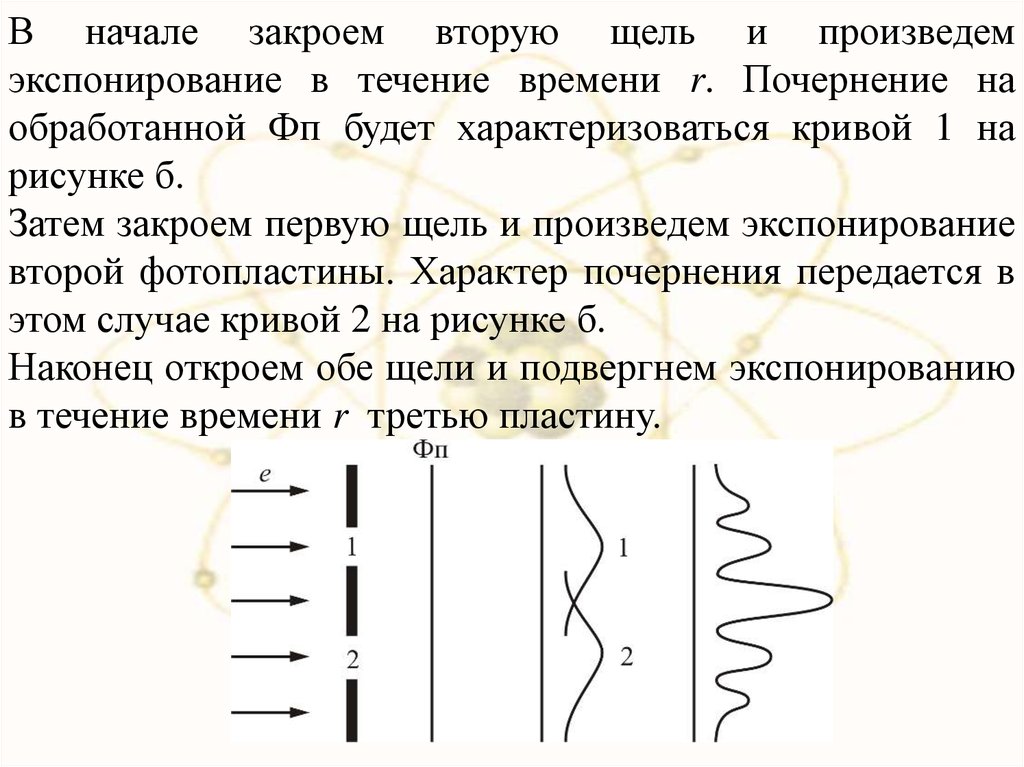
В начале закроем вторую щель и произведемэкспонирование в течение времени r. Почернение на
обработанной Фп будет характеризоваться кривой 1 на
рисунке б.
Затем закроем первую щель и произведем экспонирование
второй фотопластины. Характер почернения передается в
этом случае кривой 2 на рисунке б.
Наконец откроем обе щели и подвергнем экспонированию
в течение времени r третью пластину.
36.
Распределение интенсивности электронов согласноклассической физике
37.
Распределение интенсивности электронов согласноквантовой теории
38.
а – интерференционнаякартина от двух щелей в
случае электронов, каждое
из
зерен
негатива
образовано
отдельным
электроном;
б – интерференционная
картина от двух щелей в
случае света, на этом фото
каждое из зерен негатива
образовано
отдельным
фотоном.
39.
Результатымоделирования
эксперимента с двумя
щелями.
Распределения
отвечают экспозициям
с малым числом
электронов:
а – 27 электронов;
б – 70 электронов;
в – 735 электронов
40.
Картина почернения, получающаяся в последнем случае,изображена на рисунке.
Эта картина не эквивалентна положению первых двух.
Полученная картина оказывается аналогичной картине,
получающейся при интерференции двух когерентных
световых волн.
41.
Характер картины свидетельствует о том, что надвижение каждого электрона оказывает влияние оба
отверстия.
Явление дифракции доказывает, что в прохождении
каждого электрона участвуют оба отверстия – и
первое, и второе.
Таким образом, дифракция электронов и других
микрочастиц доказывает справедливость гипотезы де
Бройля и подтверждает корпускулярно-волновой
дуализм микрочастиц вещества.
42.
4. Соотношение неопределенностей ГейзенбергаСогласно двойственной корпускулярно-волновой природе
частиц
вещества,
для
описания
микрочастиц
используются то волновые, то корпускулярные
представления.
Необходимо внести некоторые ограничения в применении
к объектам микромира понятий классической механики.
43.
В классической механике состояние материальной точки(классической частицы) определяется заданием значений
координат, импульса, энергии и т.д. перечисленные
величины называются динамическим переменными.
Для макрообъектов можно одновременно задать r(t) и P(t)
Микрообъекту не могут быть приписаны указанные
динамические переменные.
Для микрочастиц нельзя одновременно знать x и P
44.
Pm
Z
r
Y
X
45.
Можно записать уравнение движения2
dP
d r
ma m 2
dt
dt
Решение уравнения дает траекторию движения –
непрерывную линию в пространстве
46.
Корпускулярно-волноваядвойственность
свойств
частиц, изучаемых в квантовой механике, приводит к
тому, что оказывается невозможным одновременно
характеризовать частицу ее положением в пространстве
(координатами) и скоростью (или импульсом).
Так, например, электрон (и любая другая микрочастица)
не может иметь одновременно точных значений
координаты x и импульса px.
Неопределенности значений x и px удовлетворяют
соотношению
ΔxΔp x h
где h – постоянная Планка.
47.
Из формулы следует, что чем меньше неопределенностьодной величины (x или px), тем больше неопределенность
другой. Если Δx=0, то Δp→∞.
Для микрочастицы не существует состояний, в
которых ее координаты и импульс имели бы
одновременно точные значения.
Отсюда вытекает и фактическая невозможность
одновременного с любой наперед заданной точностью
изменить координату и импульс микрообъекта.
48.
Соотношение, аналогичноеΔxΔp x h
имеет место для y и py, для z и pz, а также для других пар
величин.
В классической механике такие пары называются
канонически сопряженными. Обозначив канонически
сопряженные величины буквами A и B, можно написать
ΔAΔB h
Это соотношение неопределенности Гейзенберга для
величин A и B.
Это соотношение открыл в 1927 году Вернер Гейзенберг.
49.
hΔPΔX
2π
50.
51.
Энергия и время являются канонически сопряженнымивеличинами. Поэтому для них также справедливо
соотношение неопределенностей
ΔEΔt h
это соотношение означает, что определение энергии с
точностью ΔE должно занять интервал времени,
равный, по меньшей мере
h
Δt ~
ΔE
52.
Соотношениенеопределенностей
получено
при
одновременном
использовании
классических
характеристик движения частицы (координаты, импульса)
и наличии у нее волновых свойств.
Соотношение неопределенностей является квантовым
ограничением применимости классической механики
к микрообъектам.
53.
Соотношение неопределенностей указывает, в какой мере,возможно,
пользоваться
понятиями
классической
механики применительно к микрочастицам, в частности, с
какой степенью точности можно говорить о траекториях
микрочастиц.
Движение по траектории характеризуется вполне
определенными значениями координат и скорости в
каждый момент времени.
Подставив в (1) вместо px произведение mυy, получим
соотношение
ΔxΔυ x h / m
54.
Чембольше
масса
частицы,
тем
меньше
неопределенность
ее
координаты
и
скорости,
следовательно, с тем большей точностью можно
применять к этой частице понятие траектории.
Для пылинки массой 10–12кг и линейным размерами 10–6м,
координата которой определена с точностью до 0,01 ее
размеров (Δx=10–8 м), неопределенность скорости
34
6,62 10
14
Δυ x
м/с 6,62 10 м/с,
8 12
10 10
55.
Δυ x 6,62 1014
м/с,
Для макроскопических тел их волновые свойства не
играют ни какой роли; координаты и скорости могут
быть измерены достаточно точно.
Это означает, что для описания движения макротел с
абсолютной
достоверностью
можно
пользоваться
законами классической механики.
56.
Пучок электронов движется вдоль оси x со скоростьюυ=108 м/с, определяемой с точностью до 0,01
(Δυx≈104м/с). Точность определения координаты электрона
равна:
h
6,62 10 34
6
Δx
7,27 10 м
34
4
mΔυ x 9,11 10 10
Положение электрона может быть определено с точностью
до тысячных долей миллиметра.
Такая точность достаточна, чтобы можно было говорить о
движении электронов по определенной траектории,
иными словами, описывать их движения законами
классической механики.
57.
Применимсоотношение
неопределенностей
к
электрону, двигающемуся в атоме водорода.
Допустим, что неопределенность координаты электрона
Δx≈10–10 м (порядка размеров самого атома), тогда
34
6,62 10
7
Δυ
7,27 10 м/с
31
10
9,11 10 10
Так как скорость электрона вокруг ядра по круговой
орбите радиуса 0,5∙10–10 м равна υ≈2,3∙106 м/с, то
очевидно, что в данном случае нельзя говорить о
движении электронов в атоме по определенной
траектории, иными словами, для описания движения
электронов в атоме нельзя пользоваться законами
классической физики.
58.
5. Понятие о волновой функцииЭкспериментальное подтверждение идеи де Бройля,
ограниченность применения классической механики к
микрообъектам, а также противоречия ряда экспериментов
привели к созданию квантовой механики, описывающей
законы движения и взаимодействия микрочастиц с учетом
их волновых свойств.
Ее создание и развитие охватывает период с 1900 г. до 20х годов XX века и связано, прежде всего, с работами
австрийского физика Э. Шредингера, немецкого физика В.
Гейзенберга и английского физика П. Дирака.
59.
Необходимость вероятностного подхода к описаниюмикрочастиц,
является
важнейшей
отличительной
особенностью квантовой теории.
Немецкий физик М. Борн в 1926 г. предположил, что по
волновому закону меняется не сама вероятность, а
величина, названная амплитудой вероятности и
обозначаемая
Ψ(х, y, z, t).
Эту величину называют также волновой функцией (или
Ψ – функцией).
60.
Амплитуда вероятности может быть комплексной, ивероятность W пропорциональна квадрату ее модуля:
2
W ~ Ψ( х, y, z, t ) ,
где |Ψ|2=ΨΨ` , где Ψ` – функция комплексно-сопряженная
с Ψ.
Таким образом, описание микрообъекта с помощью
волновой
функции
имеет
статистический,
вероятностный характер:
квадрат модуля волновой функции (квадрат модуля
амплитуды волн де Бройля) определяет вероятность
нахождения частицы в момент времени в области с
координатами x и dx, y и dy, z и dz.
61.
В квантовой механике состояние частицы описываетсяпринципиально по-новому – с
помощью
волновой
функции, которая является основным носителем
информации об их корпускулярных и волновых свойствах.
Вероятность нахождения частицы в объеме V равна:
2
dW Ψ dV
62.
Величина |Ψ2|=dW/dV (квадрат модуля Ψ – функции)имеет смысл плотности вероятности, т.е. определяет
вероятность нахождения частицы в единице объема в
окрестности точки, имеющей x, y, z.
Таким образом, физический смысл имеет не сама Ψ–
функция, а квадрат ее модуля |Ψ2|, которым определяется
интенсивность волн де Бройля.
63.
Вероятность найти частицу в момент времени t вконечном объеме V, согласно теореме о сложении
вероятностей, равна:
W dW Ψ dV
2
υ
υ
Т.к. |Ψ|2dV определяется как вероятность, то необходимо
волновую функцию Ψ представить так, чтобы вероятность
достоверного события обращалась в единицу, если за
объем V принять бесконечный объем всего пространства.
Это означает, что при данном условии частица должна
находиться где-то в пространстве.
Условие нормировки вероятности:
2
| Ψ |
dV 1
64.
Условие нормировки вероятности:| Ψ |
2
dV 1,
где данный интеграл вычисляется по всему бесконечному
пространству, т.е. по координатам x, y, z от –∞ до ∞.
Таким образом, условие нормировки говорит об
объективном существовании частицы во времени и
пространстве.
65.
Чтобы волновая функция являлась объективнойхарактеристикой состояния микрочастицы, она должна
удовлетворять ряду ограничительных условий
Функция Ψ, характеризующая вероятность обнаружить
действия микрочастицы в элементе объема, должна быть:
• конечной (вероятность не может быть больше
единицы);
• однозначной
(вероятность
не
может
быть
неоднозначной величиной);
• непрерывной (вероятность не может меняться
скачком).
66.
Волноваяфункция
удовлетворяет
принципу
суперпозиции: если система может находиться в
различных
состояниях,
описываемых
волновыми
функциями Ψ1, Ψ2, … Ψn, то она может находиться в
состоянии, описываемом линейной комбинацией этих
функций
Ψ Cn Ψn
n
где Cn (n = 1, 2, 3…) – произвольные, комплексные числа.
67.
Волноваяфункция
Ψ
является
основной
характеристикой состояния микрообъектов.
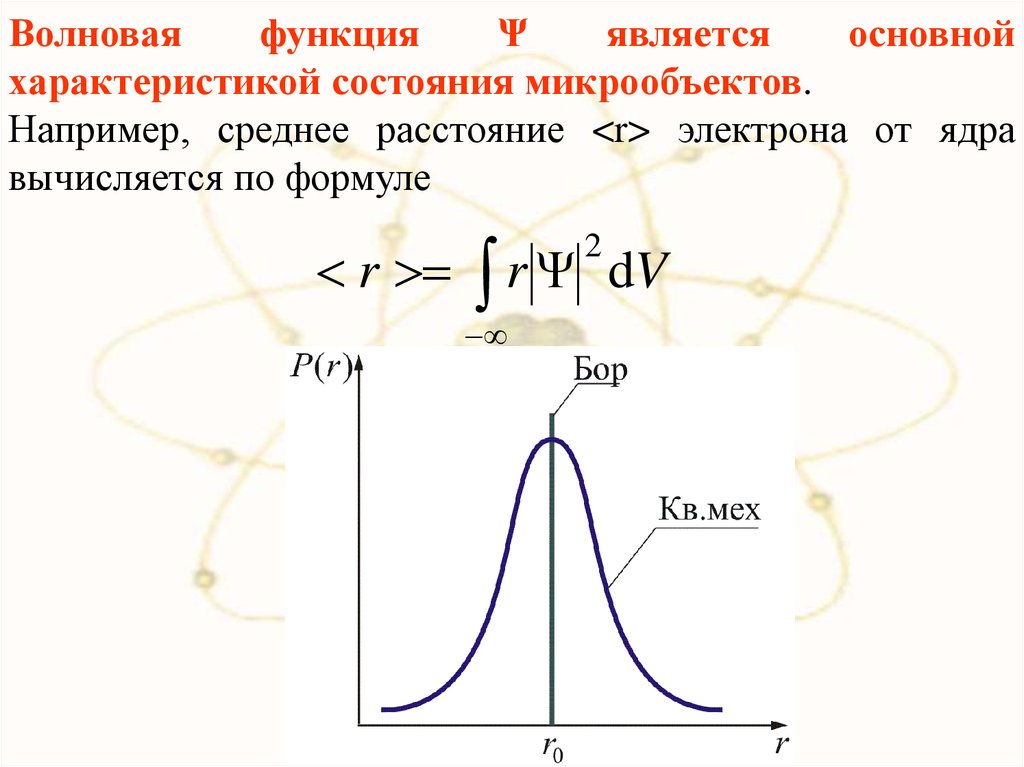
Например, среднее расстояние <r> электрона от ядра
вычисляется по формуле
r
rΨ
2
dV
68.
69.
6. Уравнение ШредингераТолкование
волн
де
Бройля
и
соотношение
неопределенностей Гейзенберга привели к выводу, что
уравнением
движения
в
квантовой
механике,
описывающей движение микрочастиц в различных
силовых полях, должно быть уравнение, из которого бы
вытекали наблюдаемые на опыте волновые свойства
частиц.
70.
Основное уравнение должно быть уравнениемотносительно волновой функции Ψ(х, y, z, t), т.к. именно
величина |Ψ|2, осуществляет вероятность пребывания
частицы в момент времени t в объеме dV, т.е. в области с
координатами x и x+dx, y, и y+dy, z и z+dz.
Т.к. искомое уравнение должно учитывать волновые
свойства частиц, то оно должно быть волновым
уравнением,
подобно
уравнению,
описывающему
электромагнитные волны.
Основное уравнение нерелятивистской квантовой
механики сформулировано в 1926 г. Э.Шредингером.
71.
Шредингер Эрвин (1887 – 1961) –австрийский физик-теоретик, один из
создателей квантовой механики.
Основные
работы
в
области
статистической физики, квантовой
теории, квантовой механики, общей
теории относительности, биофизики.
Разработал теорию движения микрочастиц –
волновую механику, построил квантовую теорию
возмущений – приближенный метод в квантовой
механике. За создание волновой механики
удостоен Нобелевской премии.
72.
Уравнение Шредингера не выводится, а постулируется.Правильность этого уравнения подтверждается согласием
с опытом получаемых с его помощью результатов, что в
свою очередь, придает ему характер закона природы.
73.
Уравнение Шредингера в общем виде:2
Ψ
Ψ U ( x, y, z, t )Ψ i 2 ,
2m
t
2
где
h
2π
2
- постоянная Планка,
– оператор Лапласа
2
2
2
2
2
Ψ Ψ Ψ
Ψ 2 2 2 ,
x
y
z
i – мнимая единица,
U(x, y, z, t) – потенциальная функция частицы в силовом
поле, в котором она движется,
Ψ – искомая волновая функция.
m – масса частицы.
74.
Если силовое поле, в котором движется частицапотенциально, то функция U не зависит явно от
времени и имеет смысл потенциальной энергии.
В этом случае решение уравнения Шредингера
распадается на два сомножителя, один из которых зависит
только от координаты, а другой – только от времени.
Ψ( x, y, z, t ) Ψ( x,
E
i t
y, z )e
E – полная энергия частицы, которая в случае
стационарного поля остается постоянной.
75.
Уравнение Шредингера для стационарных состояний2m
Ψ 2 ( E U )Ψ 0
2
Е - полная энергия электрона
U - потенциальная энергия
-волновая функция электрона
( x , y, z )
76.
Уравнение Шредингера для стационарных состояний2m
Ψ 2 ( E U )Ψ 0
2
можно переписать в виде:
H Ψ EΨ
2
U H
2m
– оператор Гамильтона
Гамильтониан является оператором энергии E.
77.
Любое движениемикрочастиц
можно
уподобить
движению
особых волн
78.
79.
Для стационарных состояний при движении поодной оси x
d Ψ 2m
[
E
U
(
x
)]
Ψ
0
2
2
dx
2
80.
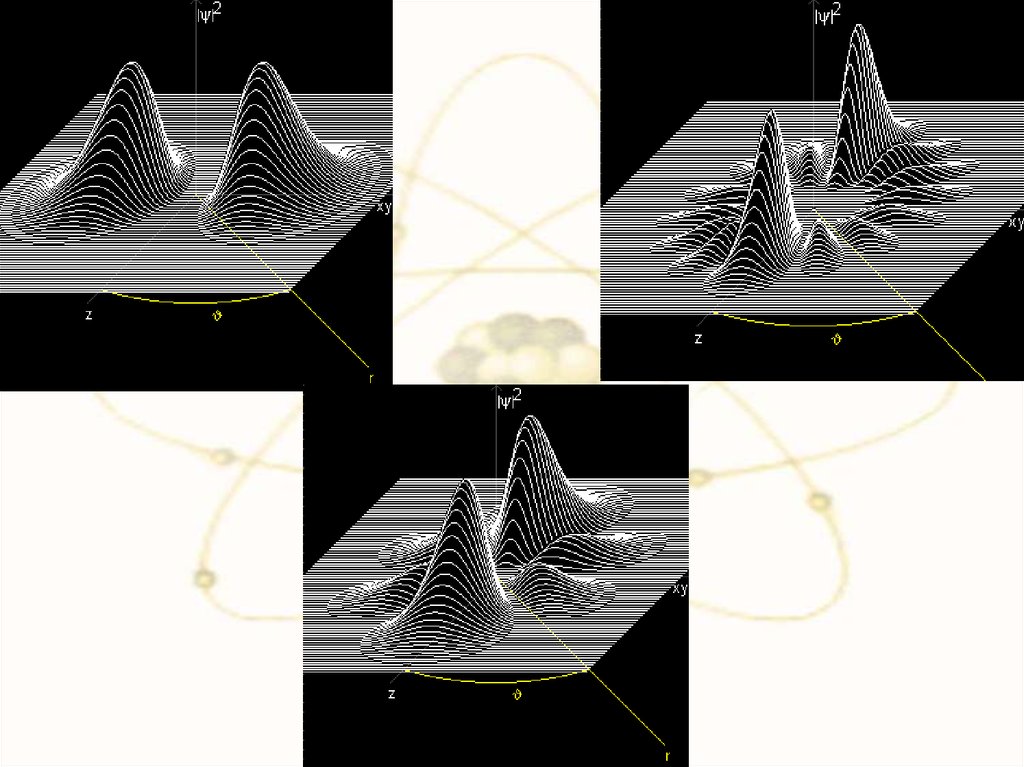
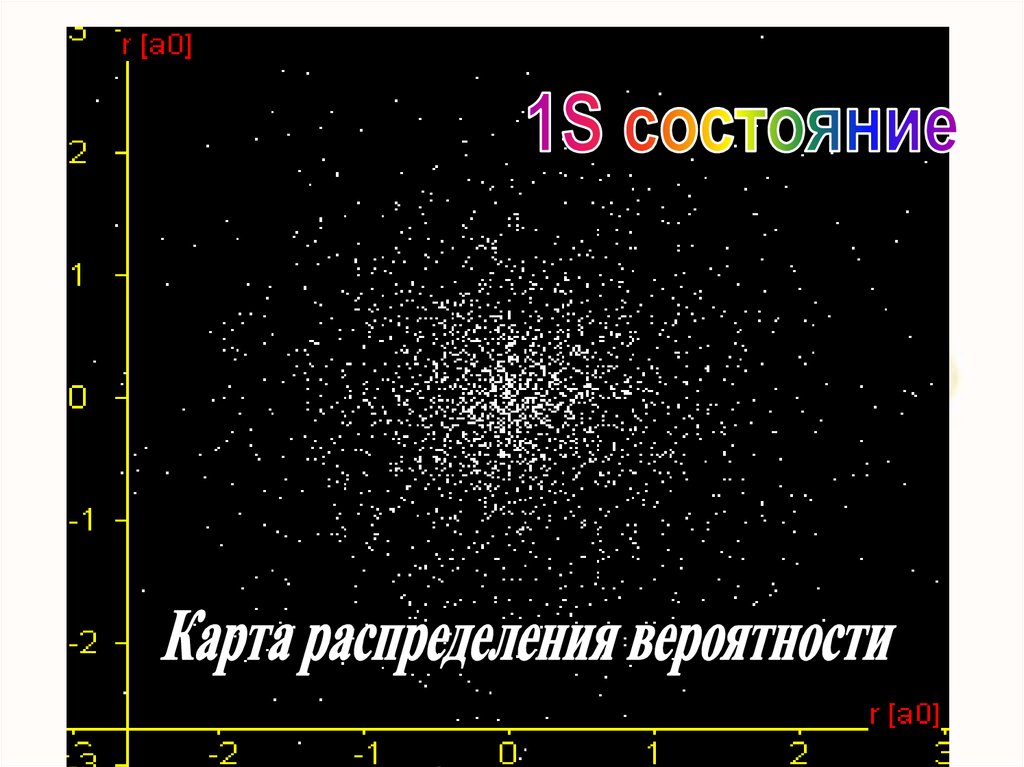
В самом простом случае для 1S состояния:1
r
3
0
e
r
r0









































































 physics
physics








