Similar presentations:
Фотоэффект объяснение Эйнштейна
1.
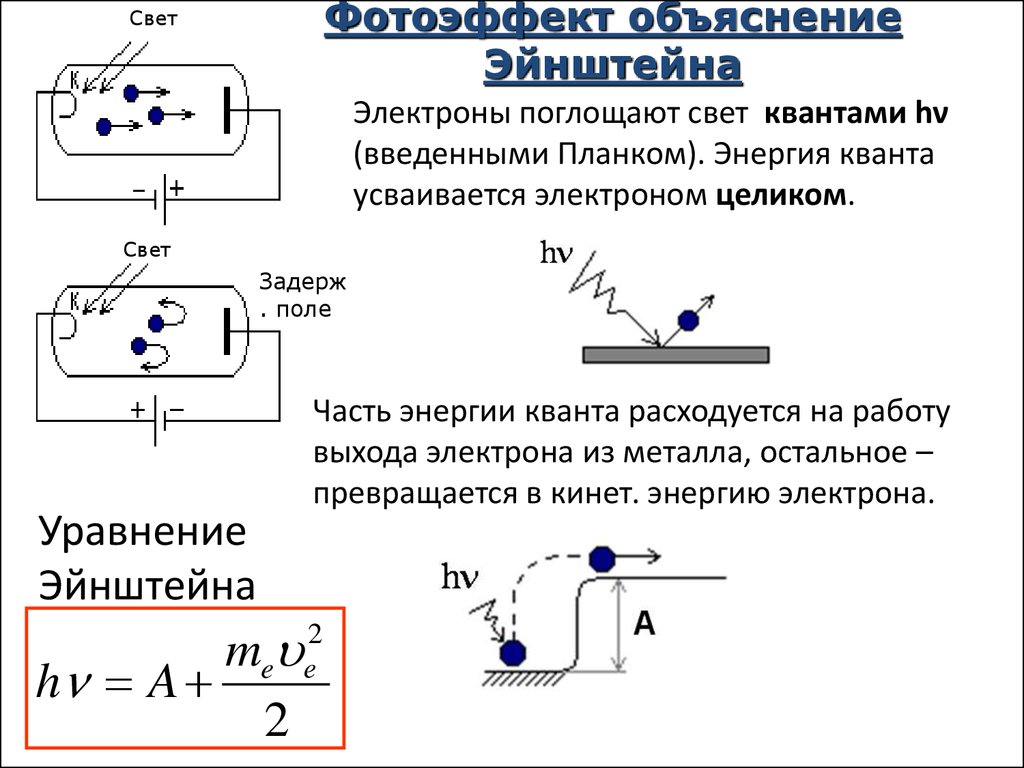
Фотоэффект объяснениеЭйнштейна
Свет
Электроны поглощают свет квантами hν
(введенными Планком). Энергия кванта
усваивается электроном целиком.
Свет
Задерж
. поле
Уравнение
Эйнштейна
Часть энергии кванта расходуется на работу
выхода электрона из металла, остальное –
превращается в кинет. энергию электрона.
me е2
h A
2
2.
Фотоэффект - объяснение Эйнштейнаme е2
h A
2
Уравнение
Эйнштейна
Часть энергии кванта расходуется на работу
выхода электрона из металла, остальное –
превращается в кинет. энергию электрона.
hν < A – фототок =0
me е2
h A
2
Характерная для
данного металла
hν = A/ h - красная граница фотоэффекта
Кинетическая энергия электрона линейно зависит от
частоты света и не зависит от его интенсивности
Число выбитых электронов (ток насыщения) –
пропорционально числу квантов, т.е.
интенсивности света - закон Столетова
3.
ВНУТРЕННИЙ ФОТОЭФФЕКТ В ПОЛУПРОВОДНИКАХФотоприёмники электронно-оптические
преобразователи оптическая связь и др.
Фотовольтаика –
солнечные батареи возобновляемая
энергетика.
4. Фотон Альберта Эйнштейна (1905 г.)
Альберт ЭйнштейнАльберт Эйнштейн (1879-1955) – один из
создателей современной физики, создатель
специальной и общей теории относительности.
В 1905 г. ввёл представление о дискретной
квантовой структуре светового излучения,
рассматривая последнее, как поток квантов света,
или фотонов – фотонная теория света.
Нобелевская премия 1921 г. за открытие
законов фотоэлектрического эффекта.
5.
Фотон Альберта Эйнштейна(1905)
Эйнштейн: свет не только испускается квантами (Планк, излучение
АЧТ), и не только поглощается квантами (Эйнштейн, фотоэффект)
но и распространяется в виде квантов – фотонов.
Свет состоит из частиц – фотонов, несущих энергию
E mc 2
E h Pф h h
c
c
P mc
1
m m0
2
m0 0
1 2
c
с
PФ
h
Фотон обладает
импульсом
Масса покоя фотона равна 0
h
6.
Свойства фотонаФотон обладает:
а) корпускулярными св-вами
– он неделим при любых взаимодействиях
- он обладает импульсом
б) волновыми св-вами
- ему соответствует определённая частота ν
(длина волны λ)
- он проявляется в явлениях интерференции
и дифракции
Корпускулярно-волновой дуализм. Статистическое объяснение
непротиворечивости корпускулярных и волновых свойств.
7.
Световое давлениеЕсли фотоны имеют импульс, они должны оказывать давление на
поверхность.
E mc2
Е
P
с
P mc
Если n – концентрация фотонов, то
nc – число фотонов , падающих в единицу времени на единицу
площади
E
давление p nc En w
c
энергия фотонов в ед объёма
Если все упавшие фотоны поглотятся p=w
Если все фотоны отразятся, p=2w
8.
B const.1871 – 1937
9.
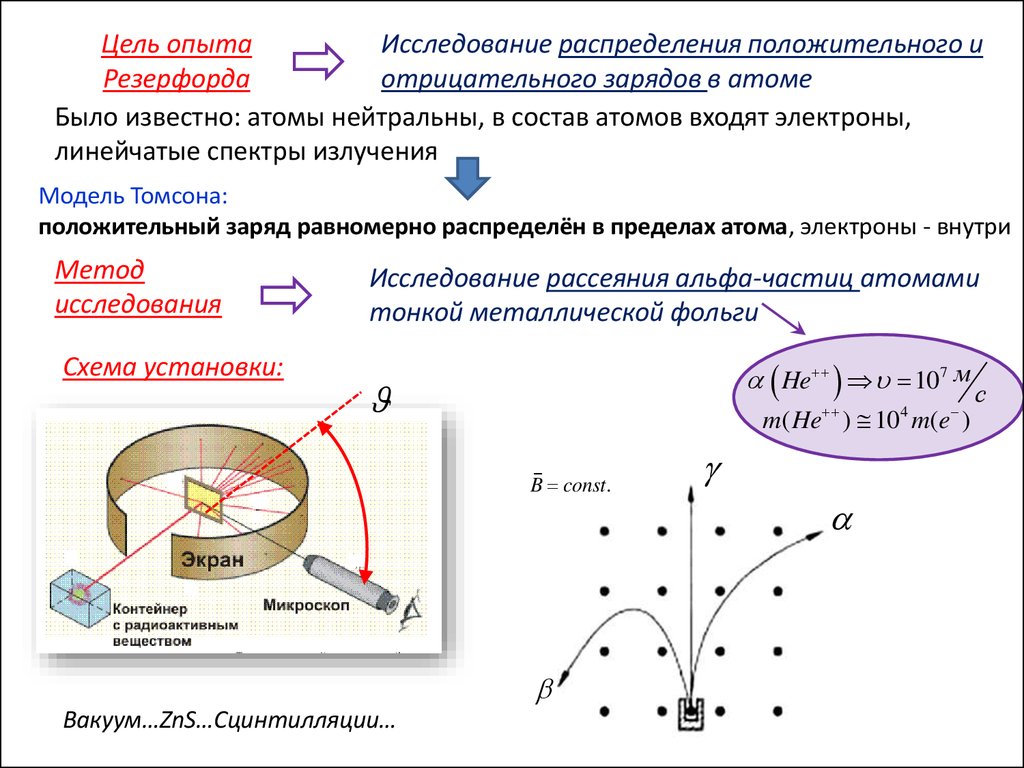
Цель опытаИсследование распределения положительного и
Резерфорда
отрицательного зарядов в атоме
Было известно: атомы нейтральны, в состав атомов входят электроны,
линейчатые спектры излучения
Модель Томсона:
положительный заряд равномерно распределён в пределах атома, электроны - внутри
Метод
исследования
Схема установки:
Исследование рассеяния альфа-частиц атомами
тонкой металлической фольги
He 107 м с
m( He ) 104 m(e )
B const.
Вакуум…ZnS…Сцинтилляции…
10.
Результаты исследований:Относительное
число частиц
dN
f ( )
N
Вакуум…ZnS…Сцинтилляции…
0,9
0
Линейные размеры ядра составляют 1/10 000 линейных
размеров атома; почти вся масса атома сосредоточена в ядре
Атом пуст
Оценка линейного размера ядра
5·10-12 см
11.
Линейные размеры ядра составляют 1/10 000 линейныхразмеров атома; почти вся масса атома сосредоточена в ядре.
1911 г.
Планетарная (ядерная) модель атома:
«Атом состоит из положительно-заряженного ядра, вокруг
которого перемещаются по замкнутым траекториям, подобно
планетам вокруг Солнца, электроны».
Недостатки планетарной модели атома.
1. Неустойчивость: криволинейное движение заряжененой
частицы (электрона)
Излучение ЭМВ
Электрон должен в конечном счете упасть на ядро
2. Нет объяснения дискретности спектров испускания.
12.
13.
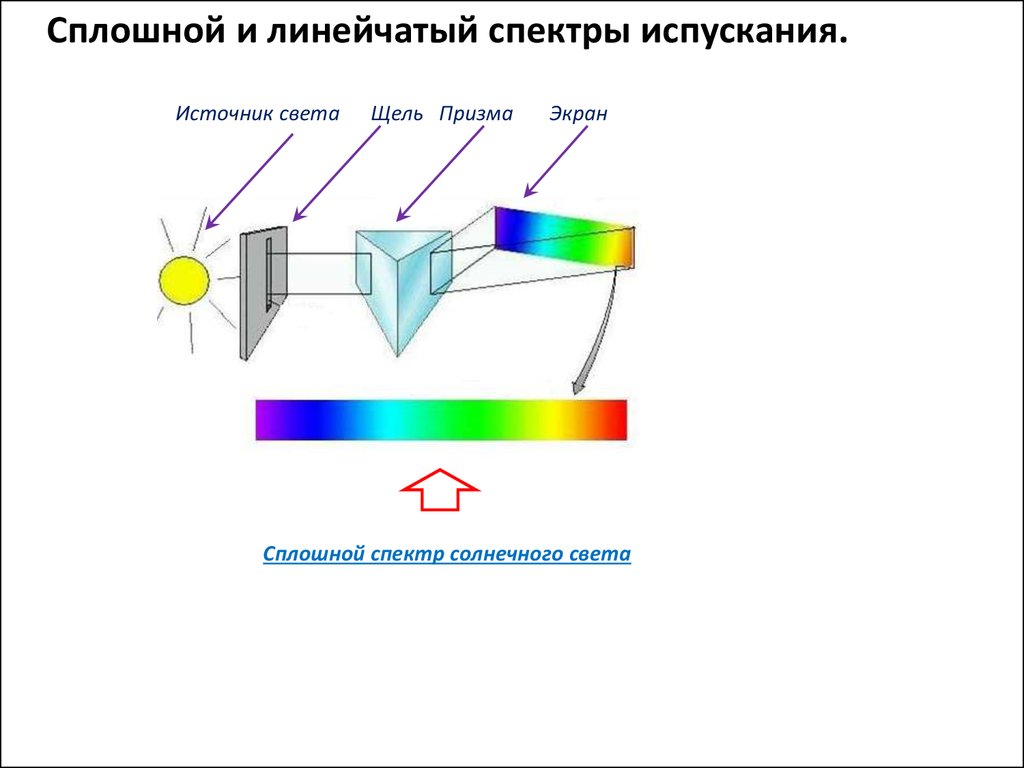
Сплошной и линейчатый спектры испускания.Источник света
Щель Призма
Экран
Сплошной спектр солнечного света
14.
Излучение индивидуальных атомов (разреженного газа) состоитиз отдельных узких спектральных линий
линейчатый спектр
Na
H
Ge
Hg
Ne
Для атомов каждого
вещества характерен
Линейчатые спектры испускания
свой спектр.
атомов
(окрашенные изображения щели)
15.
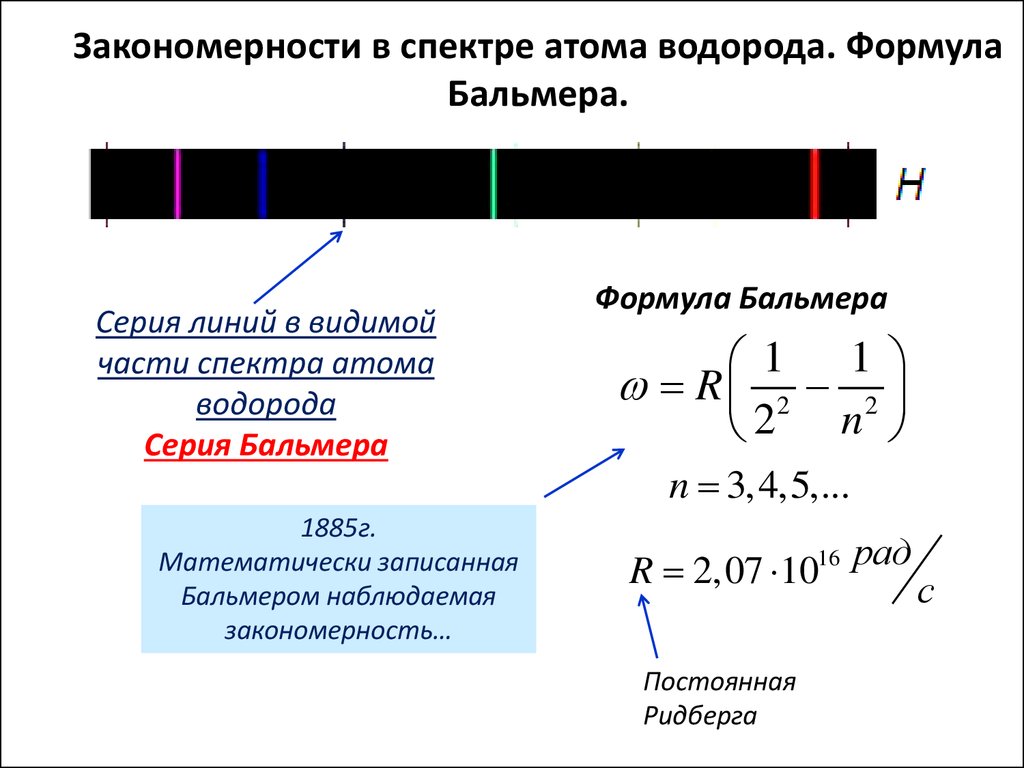
Закономерности в спектре атома водорода. ФормулаБальмера.
Серия линий в видимой
части спектра атома
водорода
Серия Бальмера
1885г.
Математически записанная
Бальмером наблюдаемая
закономерность…
Формула Бальмера
1 1
R 2 2
2 n
n 3,4,5,...
R 2,07 1016 рад
Постоянная
Ридберга
с
16.
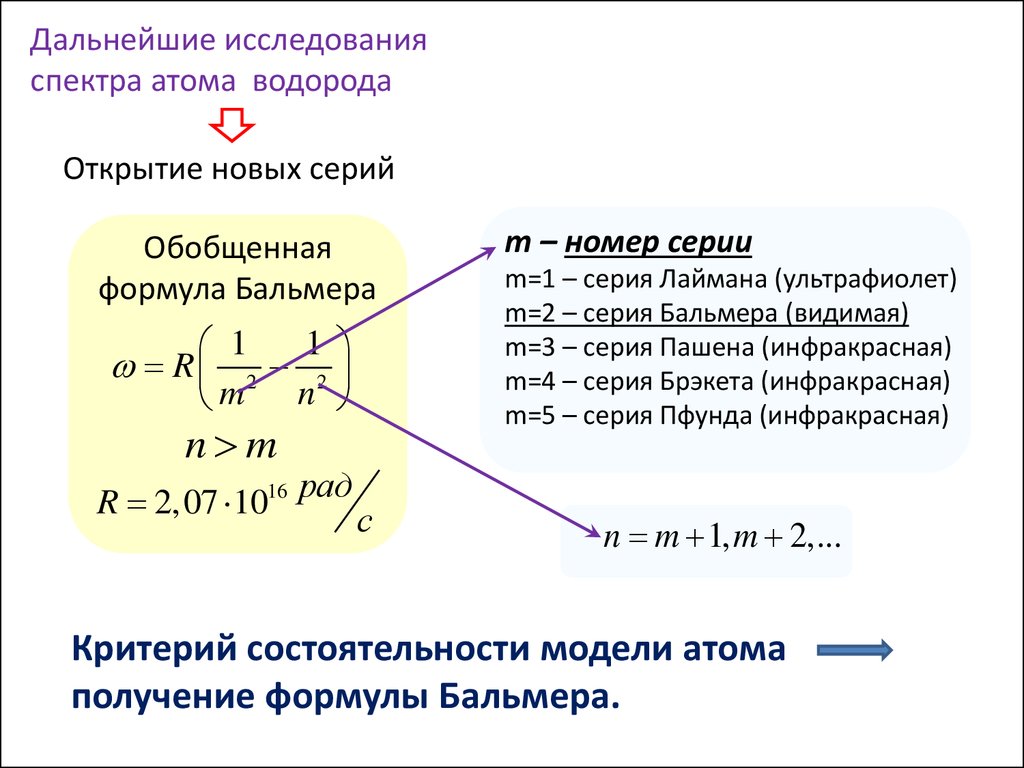
Дальнейшие исследованияспектра атома водорода
Открытие новых серий
Обобщенная
формула Бальмера
1
1
R 2 2
m n
n m
R 2,07 1016 рад
с
m – номер серии
m=1 – серия Лаймана (ультрафиолет)
m=2 – серия Бальмера (видимая)
m=3 – серия Пашена (инфракрасная)
m=4 – серия Брэкета (инфракрасная)
m=5 – серия Пфунда (инфракрасная)
n m 1, m 2,...
Критерий состоятельности модели атома
получение формулы Бальмера.
17.
Нильс Бор(1913г.)
18.
Первый постулат Бора.Атом может находится только в особых
стационарных, или квантовых (дискретных)
состояниях, каждому из которых соответствует
определенная энергия En. Находясь в любом из
стационарных состояний атом не излучает.
Стационарным состояниям соответствуют дискретные
круговые орбиты, для которых момент импульса
принимает определенные значения.
E3 E2 h
me r n
(n 1,2,3,...)
Второй постулат Бора.
Переход атома из одного стационарного
состояния в другое сопровождается поглощением
или излучением кванта энергии (фотона), равного
разности энергий стационарных состояний.
En Em h
19.
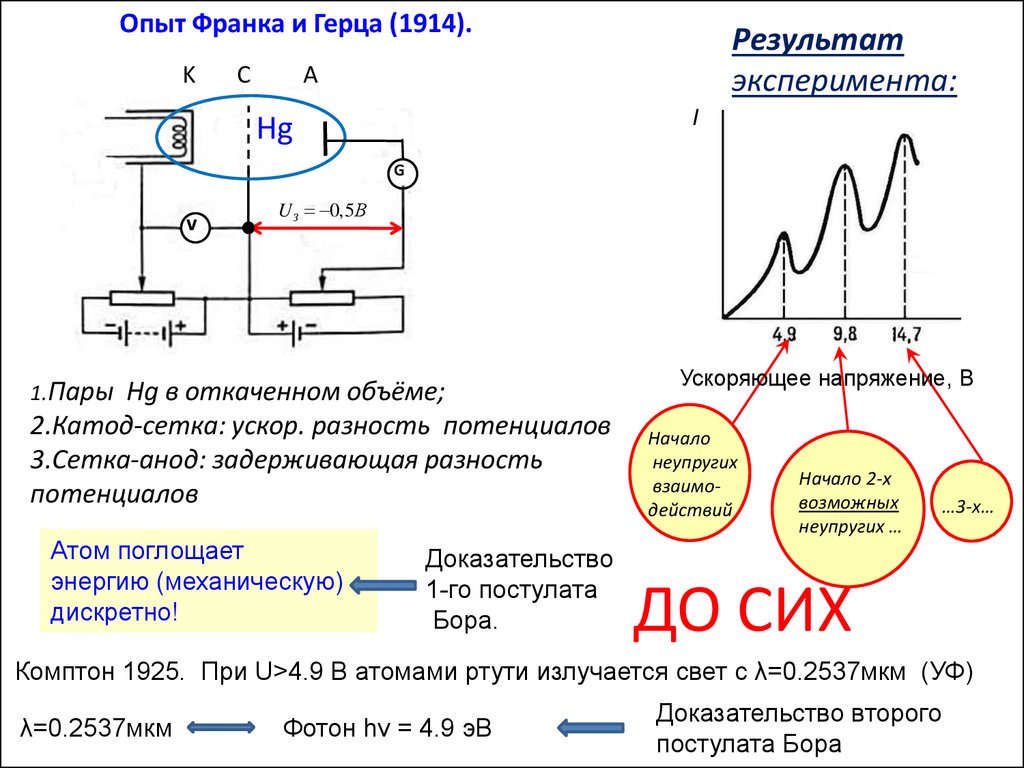
Опыт Франка и Герца (1914).Цель опыта: экспериментальное доказательство существования
дискретных энергетических состояний в атоме ( 1-ый постулат Бора ).
Идея опыта: свободный электрон при
столкновении с атомом не может передать ему свою
энергию путём изменения кинетической энергии
атома из-за огромной разницы масс.
Упругое столкновение.
Но электрон может передать свою энергию электронам, принадлежащим
атому. При этом изменится внутренняя энергия атома.
Неупругое
столкновение.
Если внутренняя энергия атома может изменяться непрерывно, электрон в
неупругих столкновениях может передать атому любую порцию энергии.
Если внутренняя энергия атома может изменяться лишь дискретно ( 1-ый
постулат Бора , электрон в неупругих столкновениях может передать атому
лишь определённые (дискретные) порции энергии.
20.
Опыт Франка и Герца (1914).K
C
Результат
эксперимента:
A
I
Hg
G
v
U З 0,5В
1.Пары
Hg в откаченном объёме;
2.Катод-сетка: ускор. разность потенциалов
3.Сетка-анод: задерживающая разность
потенциалов
Атом поглощает
энергию (механическую)
дискретно!
Доказательство
1-го постулата
Бора.
Ускоряющее напряжение, В
Начало
неупругих
взаимодействий
Начало 2-х
возможных
неупругих …
…3-х…
ДО СИХ
Комптон 1925. При U>4.9 В атомами ртути излучается свет с λ=0.2537мкм (УФ)
λ=0.2537мкм
Фотон hν = 4.9 эВ
Доказательство второго
постулата Бора
21.
Боровская модель атома водорода, водородоподобного ионаFe
e
1-ый п-т.Бора
me
Ze
2-ой з-н Н.
Скорость
электрона на
боровских
орбитах
Энергия
me r n
Ze
(n 1,2,3,...)
r
Радиусы
боровских
орбит
1 ЭЛЕКТРОН В
ПОЛЕ ЯДРА С
ЗАРЯДОМ
h 2 0
2
rn
n
me Ze2
,r
me 2
Ze2
r
4 0 r 2
Атом Н , Z=1
r1=0.53∙10-10 м=0.53 Å
v1=2∙106 м/сек
Ze2 1
n
2h 0 n
me Z 2e 4 1
En 2 2 2
8h 0 n
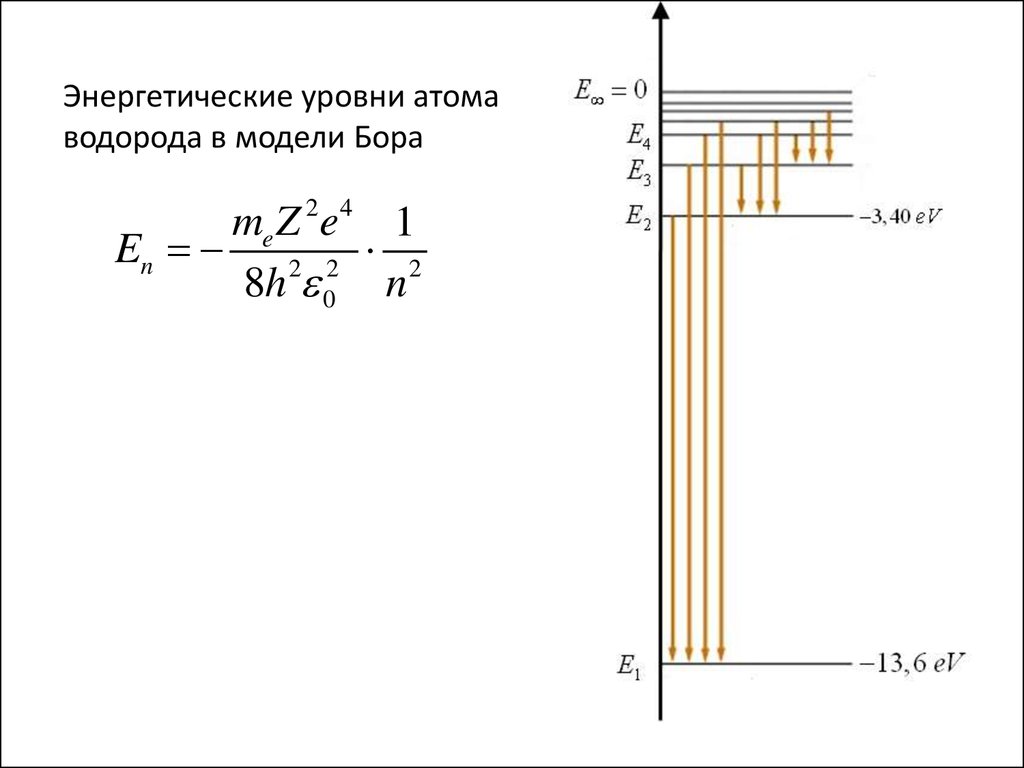
22.
Энергетические уровни атомаводорода в модели Бора
2 4
me Z e 1
En 2 2 2
8h 0 n
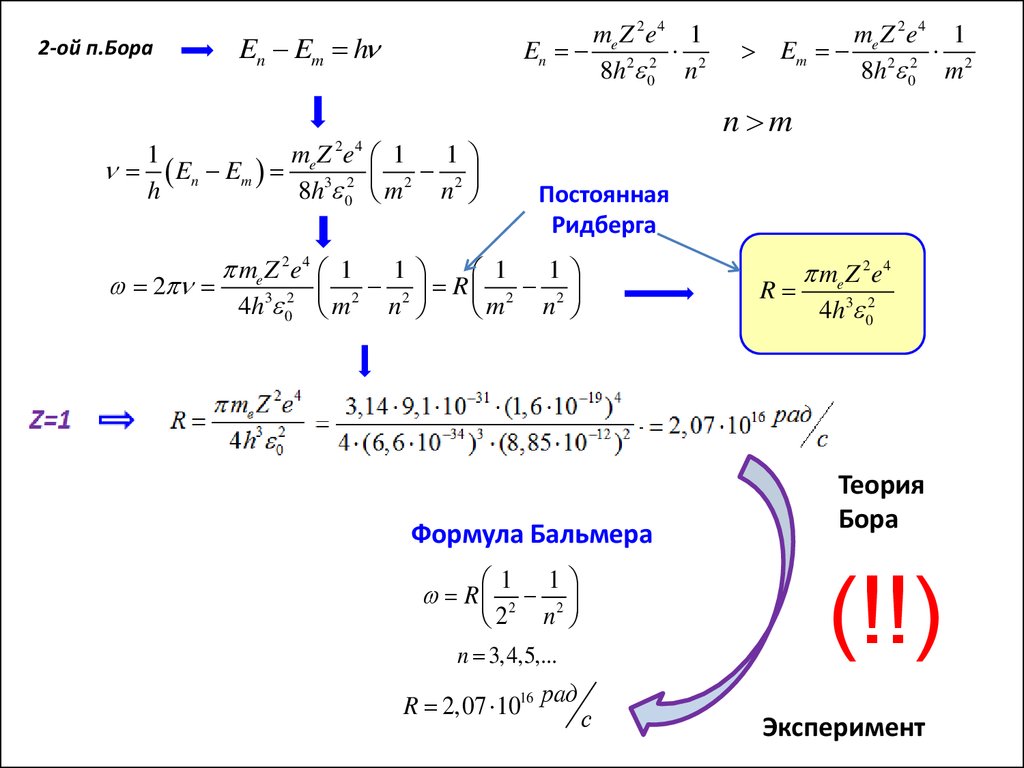
23.
2-ой п.Бораme Z 2e4 1
En 2 2 2
8h 0 n
En Em h
me Z 2e4 1
Em 2 2 2
8h 0 m
n m
mZ e 1
1
1
En Em e 3 2 2 2
h
8h 0 m n
2 4
Постоянная
Ридберга
me Z 2e4 1
1
1
1
2
R
2
2
4h3 02 m2 n 2
m n
Формула Бальмера
1 1
R 2 2
2 n
Теория
Бора
(!!)
n 3,4,5,...
R 2,07 1016 рад
me Z 2e4
R
4h3 02
с
Эксперимент
24.
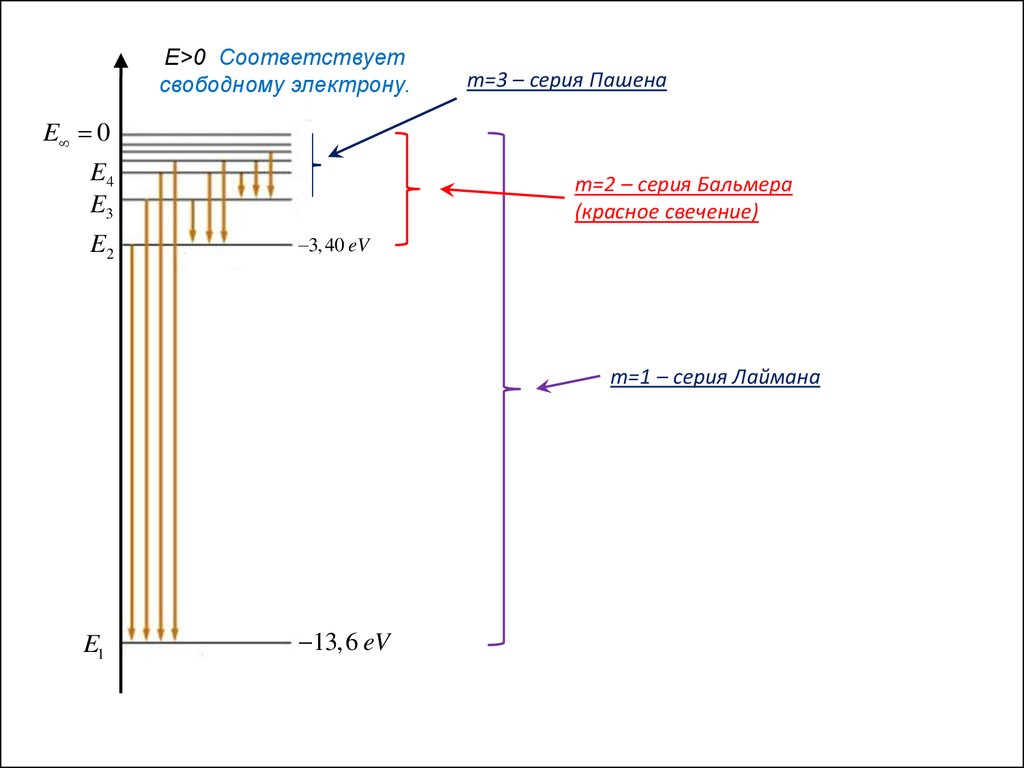
E>0 Соответствуетсвободному электрону.
m=3 – серия Пашена
E 0
E4
E3
E2
m=2 – серия Бальмера
(красное свечение)
3,40 eV
m=1 – серия Лаймана
E1
13,6 eV
25.
Недостатки теории БораНе удаётся рассчитать атомы с двумя (атом Не) и более электронами.
Ничего не говорит об интенсивности линий излучения (а она разная для
разных линий (например, водород светится красным).
Основной недостаток непоследовательность:
вычисление орбит на основе законов классической механики, считая при
этом неприменимой классическую электродинамику.
Промежуточный этап в поисках адекватной теории, получившей название
квантовой физики.
26.
1924 г.Де-Бройль
1927 г.
Дэвиссон и
Джермер
27.
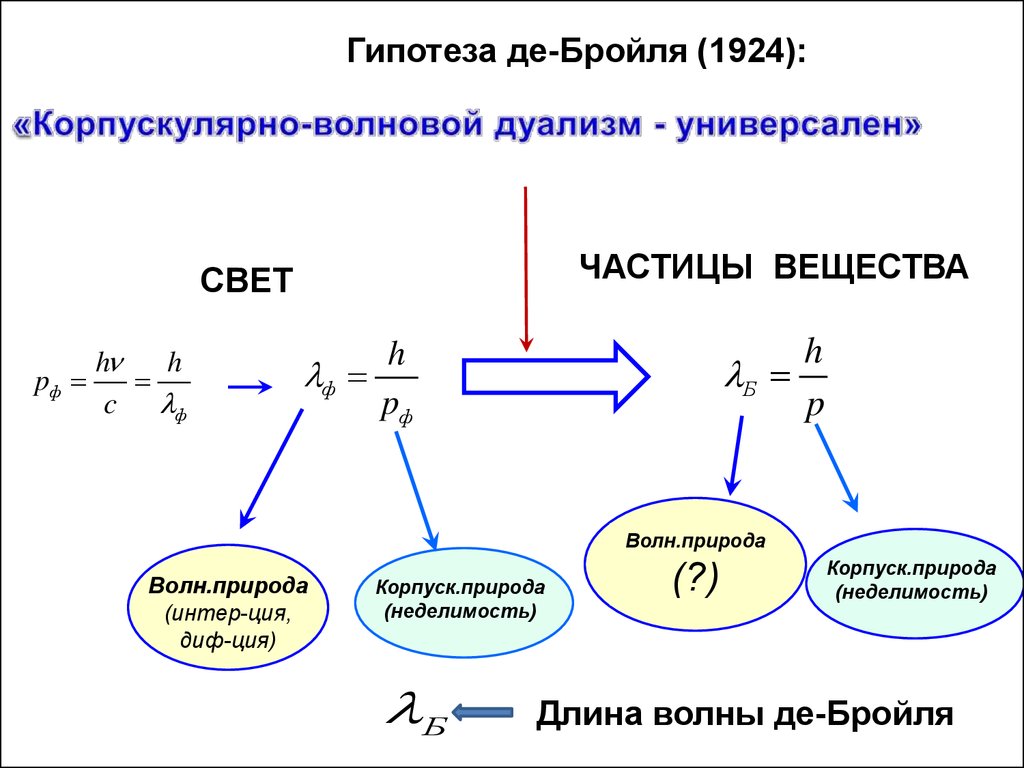
Гипотеза де-Бройля (1924):ЧАСТИЦЫ ВЕЩЕСТВА
СВЕТ
h
h
pф
c ф
h
Б
p
h
ф
pф
Волн.природа
Волн.природа
(интер-ция,
диф-ция)
Корпуск.природа
(неделимость)
Б
(?)
Корпуск.природа
(неделимость)
Длина волны де-Бройля
28.
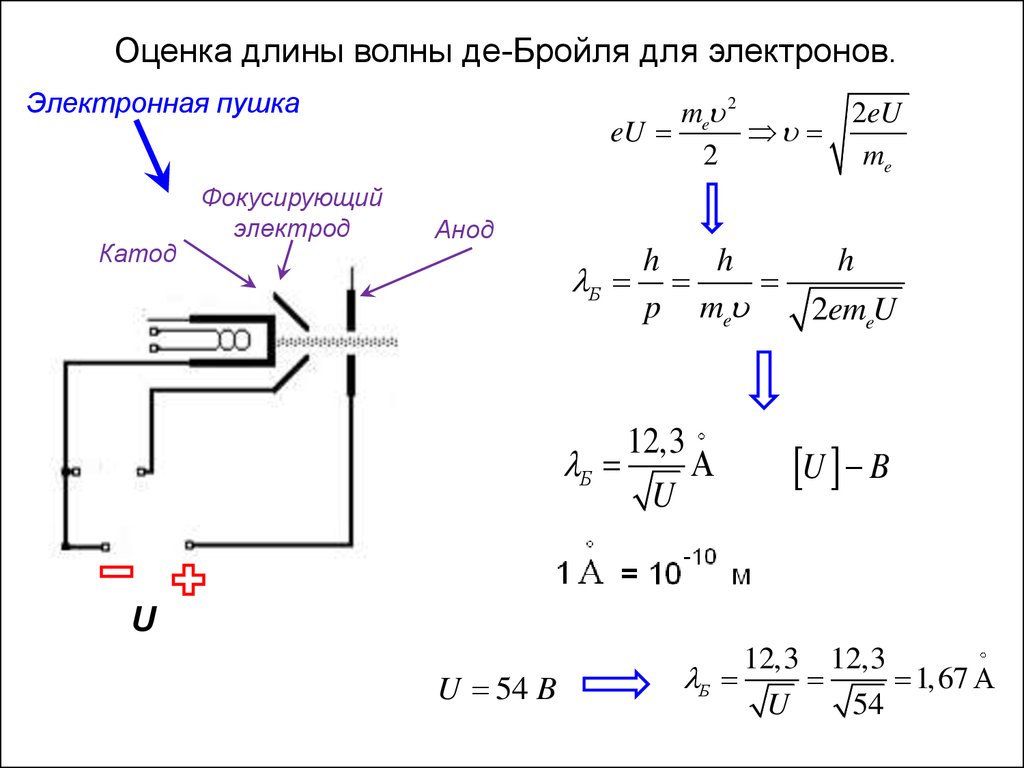
Оценка длины волны де-Бройля для электронов.Электронная пушка
Катод
Фокусирующий
электрод
me 2
2eU
eU
2
me
Анод
h
h
h
Б
p me
2emeU
12,3
Б
U
U B
U
U 54 B
Б
12,3 12,3
1,67
U
54
29.
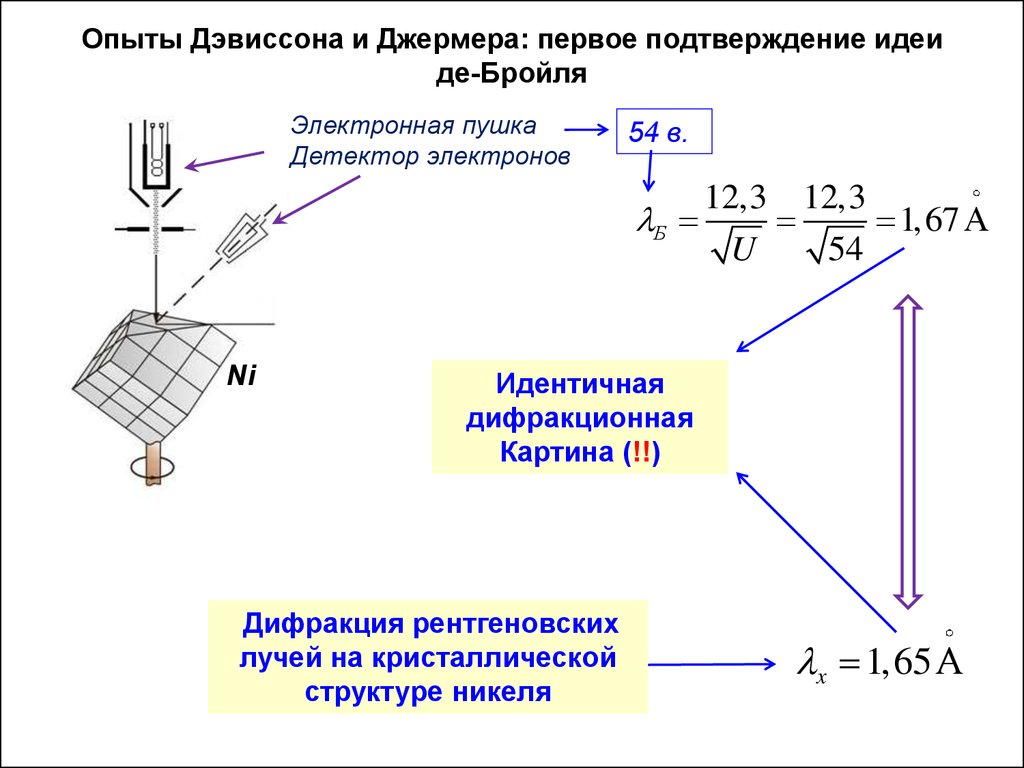
Опыты Дэвиссона и Джермера: первое подтверждение идеиде-Бройля
Электронная пушка
Детектор электронов
54 в.
12,3 12,3
Б
1,67
U
54
Ni
Идентичная
дифракционная
Картина (!!)
Дифракция рентгеновских
лучей на кристаллической
структуре никеля
x 1,65
30.
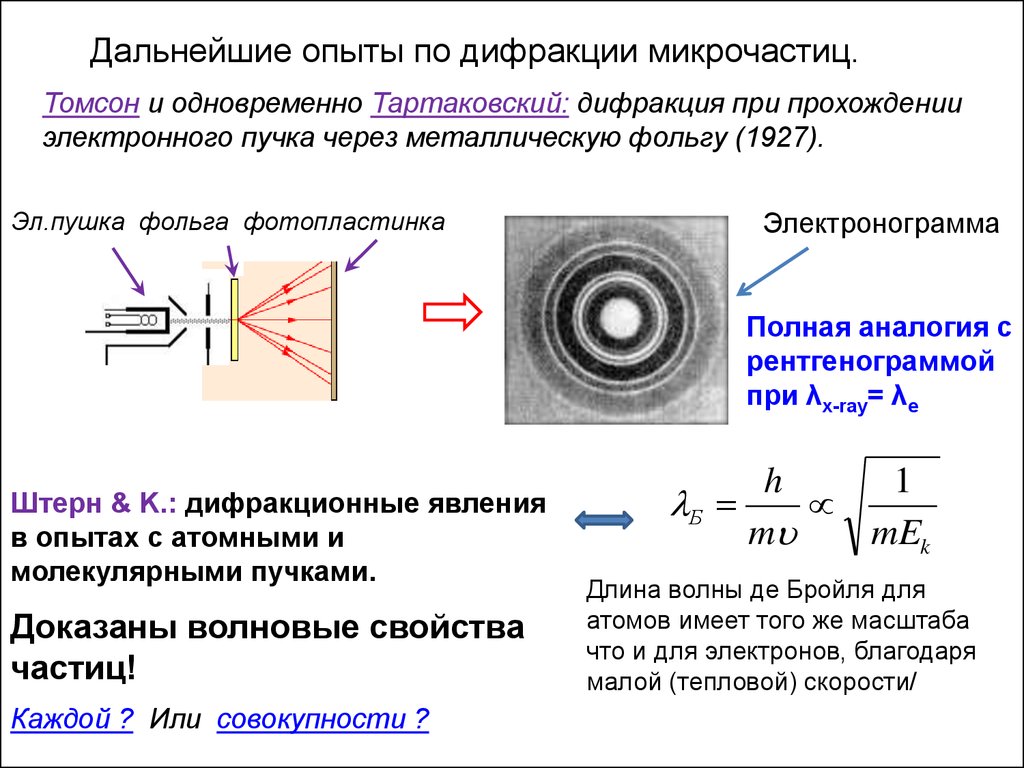
Дальнейшие опыты по дифракции микрочастиц.Томсон и одновременно Тартаковский: дифракция при прохождении
электронного пучка через металлическую фольгу (1927).
Эл.пушка фольга фотопластинка
Электронограмма
Полная аналогия с
рентгенограммой
при λx-ray= λe
Штерн & K.: дифракционные явления
в опытах с атомными и
молекулярными пучками.
Доказаны волновые свойства
частиц!
Каждой ? Или совокупности ?
h
1
Б
m
mEk
Длина волны де Бройля для
атомов имеет того же масштаба
что и для электронов, благодаря
малой (тепловой) скорости/
31.
Биберман, Сушкин и Фабрикант (1949): Опыты по дифракцииэлектронов с пучками слабой интенсивности
Электрон
регистрировался как
одно целое
Место прихода электрона на
фотопластинку имело случайный
характер. При достаточной
экспозиции получалась
дифракционная картина.
Вывод. Единичная частица обладает волновыми свойствами. А именно, её
положение в пространстве определяется вероятностным законом и этот
вероятностный закон таков, что при усреднении (по времени или по большому
числу частиц) реализуется волновая картина.
Усреднение по времени (пускаем электроны по одному и ждём пока их не придёт
достаточно много) или по большому числу частиц в потоке (много электронов
одновременно, видим мгновенную картину) эквивалентно.
В то же время микрочастицы обладают свойствами корпускулярности:
масса, размеры, заряд - неделимы.
32.
Гейзенберг, Вернер Карл(1901-1976)
33.
Оптика:При каких то условиях свет в однородной
среде распространяется в виде
прямолинейных лучей
При других условиях наблюдается дифракция,
т.е. существенно непрямолинейное
распространение света, которое описывается,
исходя из волновых представлений.
Можно говорить о фотонах
(частицах), движущихся по
прямолинейным траекториям.
Понятие о траектории
фотона здесь неадекватно.
Микрочастицы вещества
Обладают волновыми свойствами:
дают такие же дифракционные
картины, как и рентгеновские лучи.
Следует ожидать, что при определённых условиях понятия о
положении в пространстве и траектории неприменимы к
описанию движения микрочастиц.
34.
Принцип неопределённости ГейзенбергаСтепень точности, с которой к частице может
быть применено представление об её
определённом положении в пространстве
Частица не может иметь одновременно
точного значения координаты x и
проекции импульса на направление x.
Соотношение
неопределённости
Гейзенберга
p x x
2
степень неточности
Соотношения неопределённости Гейзенберга
p x x , p y y , p z z
2
2
2
35.
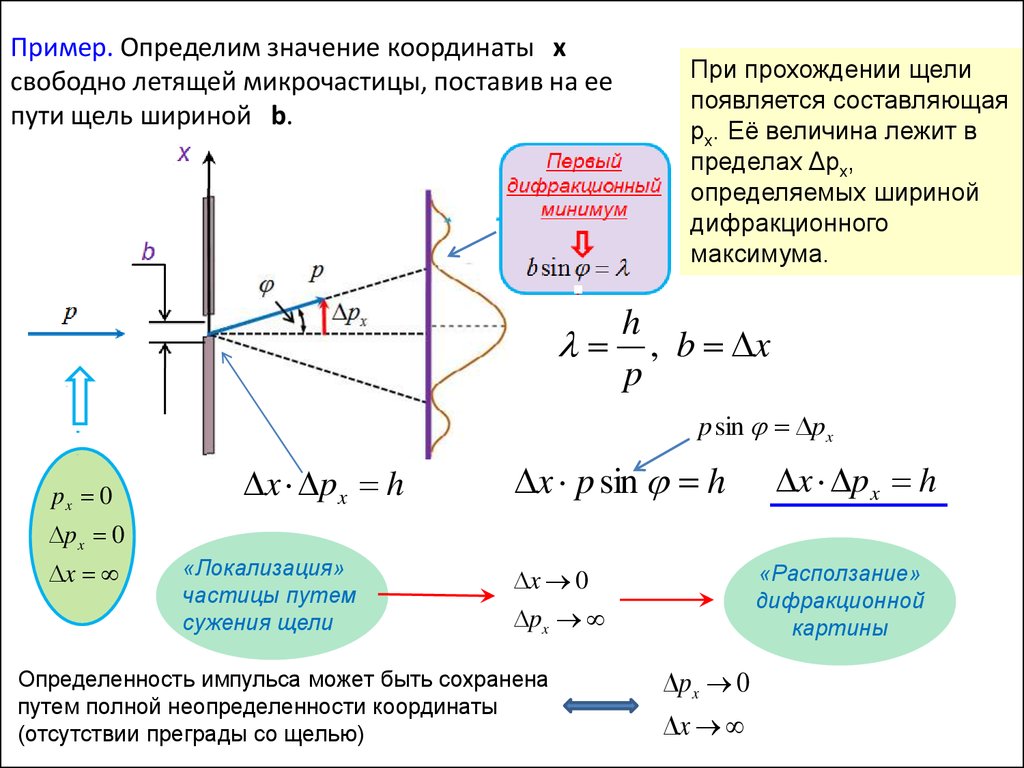
Пример. Определим значение координаты xcвободно летящей микрочастицы, поставив на ее
пути щель шириной b.
При прохождении щели
появляется составляющая
px. Её величина лежит в
пределах Δpx,
определяемых шириной
дифракционного
максимума.
h
, b x
p
p sin px
px 0
x px h
x p sin h
x px h
p x 0
x
«Локализация»
частицы путем
сужения щели
«Расползание»
дифракционной
картины
x 0
px
Определенность импульса может быть сохранена
путем полной неопределенности координаты
(отсутствии преграды со щелью)
px 0
x





















 physics
physics








