Similar presentations:
Гипотеза и формула де Бройля
1.
Гипотеза и формула де Бройля• Де Бройль предположил, что корпускулярноволновым дуализмом (двойственными корпускулярноволновыми свойствами) обладает не только свет, но и
любые частицы вещества – электроны, протоны, атомы
и т.д.
• Связь между корпускулярными и волновыми
характеристиками для микрочастиц такая же, как и
для фотонов:
- формула де Бройля
h
h
для υ<<с.
p
m
2.
Экспериментальное подтверждениегипотезы де Бройля
• Гипотеза де Бройля получила подтверждение в опытах по
дифракции пучка электронов, прошедших через тонкие
металлические фольги (опыты Дэвиссона и Джермера,
Томсона, П.С.Тартаковского и др.)
сравнить:
дифракция электронов
дифракция
рентгеновских лучей
Пример: электроны, прошедшие ускоряющую разность
потенциалов U =1 В, имеют длину волны λ = 1,225 нм
3.
Соотношения неопределённостей• Так как микрочастица обладает одновременно и
свойствами волны и свойствами частицы, то она не
является ни волной, ни частицей в обычном
понимании. Поэтому характеристики частицы,
введённые в классической механике (координаты,
импульс, траектория и т.д.), для них применимы с
некоторыми ограничениями.
Эти ограничения установлены Гейзенбергом и
называются соотношениями неопределённостей или
соотношениями Гейзенберга:
ΔxΔрх ≥ ħ
Чем более точно заданы координаты
ΔуΔру ≥ ħ
микрочастицы, тем менее определённым
ΔzΔрz ≥ ħ
становится её импульс, т.е. тем больше
ошибка в определении импульса.
Одновременно одинаково точно определить и
координату и импульс микрочастицы невозможно.
4.
Аналогичное соотношение существует для энергии Емикрочастицы и времени t пребывания её в состоянии
с данной энергией:
ΔE.Δt ≥ ħ
ΔE – ошибка в определении энергии;
Δt – неопределённость во времени;
ħ = h /2π – приведённая постоянная Планка.
5.
Волновая функция• Согласно опытным данным, параллельный пучок
микрочастиц обладает свойствами плоской волны,
распространяющейся в направлении движения частиц
со скоростью υ. Уравнение плоской волны в общем
виде:
i t kr
Ψ=Ψ0соs(ωt-kr) или
Ψ= Ψ0 e
.(*)
• Чтобы
это
уравнение
описывало
процесс
распространения
волн
де
Бройля
(движения
микрочастиц),
необходимо
ввести
в
него
характеристики частицы:
Е = ħω, след.: ω = Е / ħ; k = 2π/λ, λ = h / p, k = p/ħ,
Подставим выражения ω и k в формулу (*):
i
- это волновая или
Et pr
пси-функция
0 е
6.
Физический смысл волновой функцииСама волновая функция физического смысла не имеет.
Имеет смысл квадрат модуля её амплитуды,
пропорциональный интенсивности волны.
Дифракционная картина потока микрочастиц
Представляет собой чередование светящихся и тёмных
колец (экран покрыт сцинтиллирующим веществом).
Рассмотрим дифракцию с двух позиций – волновой и
корпускулярной.
• С волновой точки зрения светящиеся кольца
соответствуют тем местам, где квадрат модуля амплитуды
волновой функции достигает максимума:
|Ψ0|2 = |ΨΨ*| = | Ψ|2 - максимально.
7.
• С корпускулярной точки зрения светящиеся кольцасоответствуют тем местам, куда чаще попадают
микрочастицы, т.е. в этих местах наибольшая вероятность
обнаружения частицы.
• Таким образом, квадрат модуля амплитуды волновой
функции (волн де Бройля) в данной точке пространства
определяет вероятность обнаружения микрочастицы в этой
точке.
• Вероятность обнаружения микрочастицы в элементе объёма
dV:
dW = |Ψ0|2dV.
Тогда имеем:
|Ψ0|2 = dW/dV = ρw
ρw - плотность вероятности обнаружения микрочастицы в данном
объёме в момент времени t.
8.
Квадрат модуля амплитуды волновой функцииопределяет плотность вероятности ρw обнаружения
микрочастицы в данном объёме в момент времени t.
• Так как частица существует, она обязательно будет
обнаружена в какой-либо точке пространства – это
достоверно. Вероятность достоверного события равна
1, поэтому:
dV 1
2
Этот интеграл – условие нормировки волновой функции.
Все волновые функции должны быть нормированы.
9.
Уравнение Шредингера• Уравнение Шредингера играет в нерелятивистской
квантовой механике такую же роль, что и 2-ой закон
Ньютона в классической механике. Как и второй закон
Ньютона это уравнение не выводится, а постулируется.
Уравнение Шредингера имеет вид:
2
i
U x, y, z , t
t
2m
где: U(x,y,z,t) – потенциальная энергия частицы в
силовом поле, в котором она движется ;
m – масса микрочастицы;
2
2
2
2 2 2
х у z
- оператор Лапласа;
Ψ(x,y,z,t) – искомая волновая функция;
i =√-1 - мнимое число.
10.
• Рассмотренное уравнение называют временным уравнениемШредингера, т.к. Ψ и U зависят от времени. Уравнение
Шредингера дополняется следующими важными условиями:
1) функция Ψ должна быть непрерывна, однозначна,
конечна;
2) ∂Ψ /∂x, ∂Ψ/∂y, ∂Ψ/∂z, ∂Ψ/∂t – должны быть
непрерывны;
2
2
dV
3) функция |Ψ| должна быть интегрируема, т.е.
должен быть конечным. В частном случае это условие
нормировки.
• Если во временном уравнении Шредингера произвести
разделение переменных: Ψ(x,y,z,t)=ψ(x,y,z)·φ(t), то
можно получить уравнение Шредингера не зависящее
от времени, которое называется стационарным
уравнением Шредингера .
11.
• Стационарное уравнение Шредингера имеет вид:2m
2 ( E U ) 0
(*)
где ψ(x,y,z) – искомая волновая функция;
Е – полная энергия частицы, движущейся в силовом поле
и обладающей потенциальной энергией U(x,y,z).
• Функции ψ, являющиеся решением уравнения (*),
называются собственными функциями , а значения
энергий, при которых уравнение (*) имеет решения,
называются собственными значениями энергий.
Например, при решении задачи о свободной частице,
стационарное уравнение Шредингера имеет решения при
любых значениях энергий, т.е. энергия свободной частицы не
квантована.
12.
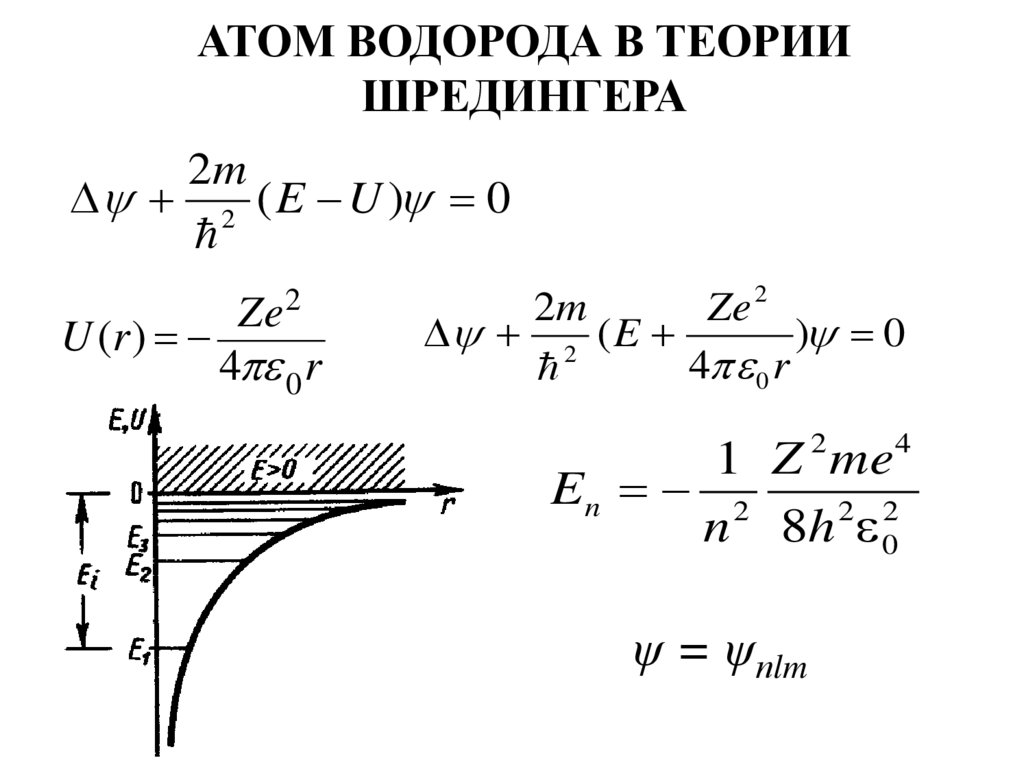
АТОМ ВОДОРОДА В ТЕОРИИШРЕДИНГЕРА
2m
2 ( E U ) 0
2
Ze
U (r )
4 0 r
2m
Ze 2
2 ( E
) 0
4 0 r
2
4
1 Z me
En 2
2 2
n 8h 0
ψ = ψпlm
13.
n=1, 2, 3,…….-главное квантовое число;Ll l( l 1 ) , l = 0, 1, ... , (n - 1) -,
орбитальное квантовое число
Llz = m
LS s( s 1)
n 1
ml = 0, ±1, ±2,..., ±l магнитное квантовое число
s = ms = 1/2 – cпиновое
квантовое число
2
2
(
2
l
1
)
2
n
- число состояний с заданным
l 0
значением энергии (п)
14.
АТОМ БОРА1
1
1
R 2 2 ;
n
m
R=1,097373.107 м-1
Ze2
1
mv
4 о r 2
r
m r n
При п = 1
2
с
1
1
R 2 2
n
m
R*=3,3.1015 c-1
Решая эту систему уравнений,
можно получить r и υ:
rn
4 0
mZ е
2
2
n
,
2
где п = 1, 2, 3,… - главное
квантовое число
4 0 2
r1
53nм;
2
mZ e
rn = r1 n2
15.
Z e2n
;
4 0 n
При п = 1
1
Z e2
4 0
2,2 10 6 м / с
υn=υ1 /n
Зная rп и υп , можно определить кинетическую,
потенциальную и полную энергии электрона в атоме
водорода на п – ой орбите (Ек, Ер и Еп).
16.
24
2
1 Z me
Eк 2
2 2
n 8h 0
1 Z me
Eр 2
2 2
n 4h 0
2
4
1 Z me
En 2
n 8h 2 02
п =1
4
Z 2 me4
E1
13,6 эВ
2 2
8h 0
Е1
Еп 2
п
Z me
Ei Е1 2 2 13,6эВ - энергия ионизации
8h 0
атома водорода
2
4
hν = Еп – Ет ;
1
1
h Ei 2 2 ,
n
m
Еi
1
1
R 2 2
h
n
m
17.
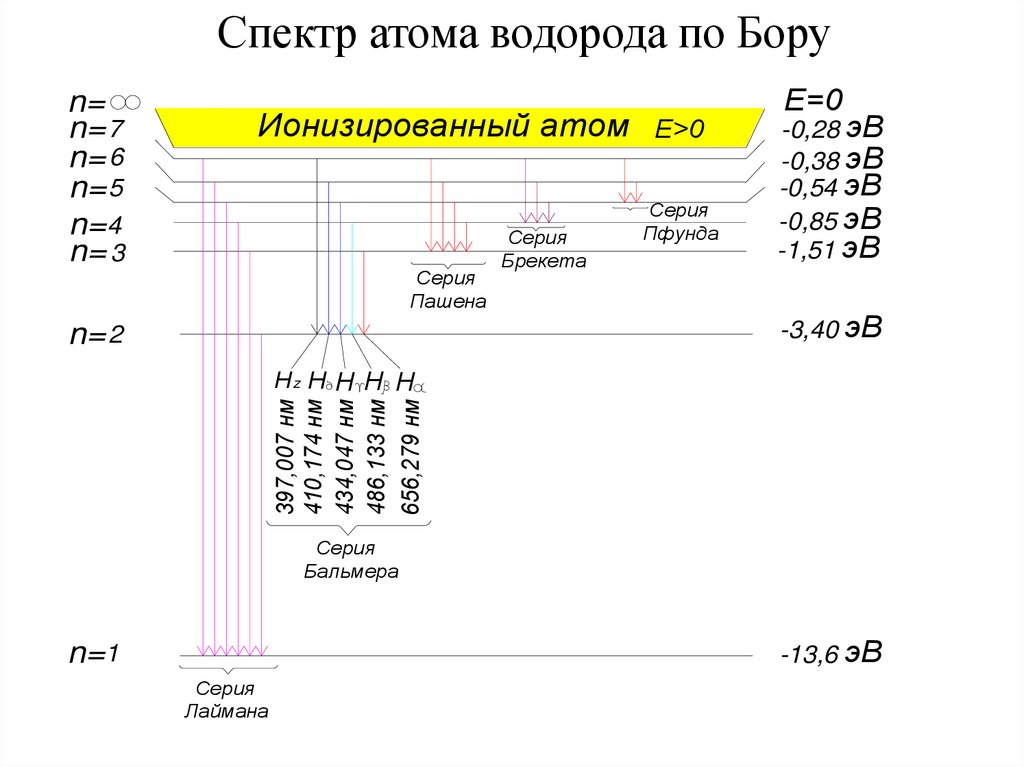
Спектр атома водорода по Боруn=
n= 7
n= 6
n= 5
n= 4
n= 3
Ионизированный атом
Серия
Пашена
n= 2
Серия
Брекета
Е>0
Серия
Пфунда
Е=0
-0,28 эВ
-0,38 эВ
-0,54 эВ
-0,85 эВ
-1,51 эВ
-3,40 эВ
397,007 нм
410,174 нм
434,047 нм
486,133 нм
656,279 нм
Нz Н Н Н Н
Серия
Бальмера
-13,6 эВ
n=1
Серия
Лаймана















 physics
physics








