Квантовая механика. Гипотеза де Бройля и соотношения неопределенностей Гейзенберга. Волновая функция и уравнение Шредингера

1.

Лекция 14
ПОНЯТИЕ
О КВАНТОВОЙ МЕХАНИКЕ
Вопросы:
1. Гипотеза де Бройля и соотношения
неопределенностей Гейзенберга.
2. Волновая функция и уравнение
Шредингера.

2.

Возникновение квантовой механики
Теория Бора является внутренне противоречивой, т.к. сочетает в себе и классические, и квантовые представления. Она
не может объяснить строение многоэлектронных атомов.
Основы квантовой (волновой)
механики, последовательно
объясняющей строение микромира, были созданы в 1923 –
– 1931 г.г.
Вернер Гейзенберг
(1901 – 1976)
Эрвин Шредингер
(1887 – 1961)
Квантовая механика раскрывает три основных свойства
микрообъектов (микрочастиц):
• их волновую природу («частица-волна»);
• вероятностный (статистический) характер явлений микромира;
• квантованность внутриатомных процессов и характеристик.

3.

Гипотеза де Бройля
В 1923 г. французский физик Л. де Бройль
выдвинул гипотезу: с движением электрона
или какой-либо другой микрочастицы связан
волновой процесс, длина волны которого
Луи де Бройль
(1892 – 1987) (длина волны де Бройля) равна
– импульс частицы.
Движущуюся микрочастицу
следует рассматривать как
объект «частица-волна».
Таким образом, по де Бройлю, дуализм присущ не только
оптике, но имеет универсальное значение.

4.

Формулы де Бройля
1. Нерелятивистский случай:
2. Релятивистский случай:
– энергия покоя (для электрона 0,511 МэВ).

5.

Экспериментальное подтверждение гипотезы де Бройля
Опыты Дэвиссона и Джермера
(1927 г.) – опыты по дифракции
электронов на монокристаллах
никеля.
Клинтон Джозеф
Дэвиссон
(1881 – 1958)
Лестер Халберт
Джермер
(1896 – 1971)

6.

Оценка длины волны де Бройля
для макрообъектов и микрообъектов
Пример 1. Пуля массой т = 10 г, летящая со скоростью
υ = 100 м/с.
Пример 2. Электрон в атоме водорода (для п = 4).

7.

Соотношения неопределенностей
(сформулированы В. Гейзенбергом в 1927 г.)
Вследствие корпускулярно-волнового дуализма в квантовой
механике теряет смысл понятие «траектории частицы».
Чем точнее определена координата микрочастицы (Δх → 0),
тем менее точно определен ее импульс (Δрх → ∞) и наоборот.
1. Соотношения неопределенностей для координат и импульсов:
Здесь Δх, Δy, Δz, Δрх, Δpy, Δpz – неопределенности координат
частицы и соответствующих проекций ее импульса.
2. Соотношение неопределенностей для энергии и времени:
где ΔW – неопределенность энергии состояния; Δt – время
пребывания системы в данном состоянии.

8.

Практические применения
соотношений неопределенностей
1. Доказательство того, что в ядрах атомов не могут находиться электроны.
2. Оценка величины размытости спектральных линий.
(Δt ~ 10 нc – характерное время возбужден. состояния атома).

9.

Прохождение микрочастицы через две щели
Физическая картина для электронов идентична картине
дифракции для фотонов.

10.

Волновая функция и ее статистический смысл
Вывод из опыта с электронами: поскольку электрон неделим
и локализован в одной точке при попадании на фотопластинку,
то движение частиц подчиняется статистической (вероятностной) закономерности, согласно которой они попадают в те точки, где интенсивность волн де Бройля наибольшая.
( r , t ) ( x, y , z , t )
– волновая функция.
– вероятность нахождения частицы в
объеме dV.
Физический смысл волновой функции состоит в том, что квадрат ее модуля задает плотность вероятности обнаружения
частицы в данный момент времени в данной точке:

11.

Свойства волновой функции
1. Конечность (волновая функция не может обращаться в
бесконечность, т.к.
2. Однозначность (вероятность не может быть неоднозначной величиной).
3. Непрерывность (вероятность не может изменяться
скачком).
– условие нормировки волновой функции
(физич. смысл: условие объективного
существования частицы).

12.

Уравнение Шредингера
Уравнение, определяющее поведение микрообъектов, должно
выполнять ту же роль, что и законы Ньютона для макроскопических тел. Оно должно быть уравнением относительно
волновой функции
Если задача не зависит от времени:
то выполняется уравнение Шредингера для стационарных
состояний:
Здесь
– оператор Лапласа;
– потенциальная энергия частицы
в силовом поле.

13.

Задача о частице в одномерной
прямоугольной потенциальной яме
d 2m
2 W U 0
2
dx
, x 0, x l
U x
0, 0 x l
2
U=
0
U=0
U=
l
x
Граничные условия:
d 2 2m
2 W 0
2
dx
Общее решение:
0 l 0
(вытекают из св-ва
непрерывности ψ).
d
2
k 0,
2
dx
2
2mW
k
2
2
x Asin kx Bcos kx

14.

0 0 B 0
l Asin kl 0
2 2
2 2
k
2
Wn
n
2m
2
n x sin
l
2ml
n
l
2
n
k
, n = 1, 2, 3, …
l
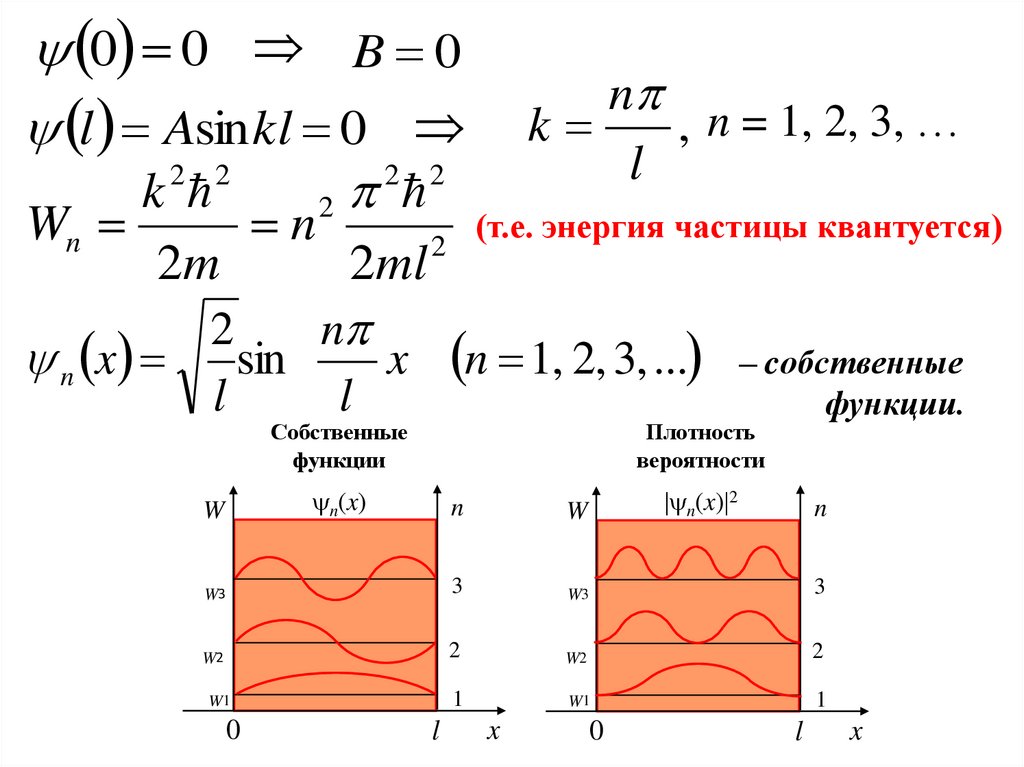
(т.е. энергия частицы квантуется)
n 1, 2, 3, ...
x
Собственные
функции
– cобственные
функции.
Плотность
вероятности
n(x)
n(x) 2
n
W
W3
3
W3
3
W2
2
W2
2
1
W1
1
W
W1
0
l
x
0
n
l
x