Similar presentations:
Оптика полупроводников
1. Оптика полупроводников
2.
Диэлектрическая проницаемость в быстропеременном поле.Соотношения Крамерса-Кронига
Нужно рассмотреть быстропеременное электромагнитное поле с частотой
ω> ωp=1/tp (tp – время установления поляризации).
Можно ли в этом случае пользоваться соотношениями электродинамики
сплошных сред?
1
a
Поляризация вызвана перераспределением электронов в атомах t p
p va
p
c
p
c
c
a a
10 2
va
va
В случае быстропеременного поля (ω> ωp) длина волны может существенно
превышать атомные размеры => можно ввести понятие сплошной среды и
использовать соотношения электродинамики сплошных сред (есть
локальность).
3.
Есть локальность, однако нет синхронности => Нет пространственной дисперсии,однако есть временная (частотная) дисперсия.
p поляризаци я не успевает устанавливаться
электрическая индукция определяется электрической
напряженностью в предшествующие моменты времени
t
D(t ) E(t ) dt f (t t )E(t )
f (t ) функция , определяемая только свойствами среды
Доопрелелим f так, чтобы f (t t ) 0 при t t
D(t ) E(t ) dt f (t t )E(t )
4.
d2 D( ) exp i t
D(t )
d
E(t )
E( ) exp i t D(t ) E(t ) dt f (t t )E(t )
2
d
2 f ( ) exp i t
f (t )
d
d
D
(
)
exp
i
t
2
2 E( ) exp i t
d
d
dt
f ( ) exp i t
E( ) exp i t
2
2
d
d
d
t
f
(
)
exp
i
t
t
2
2 E( ) exp i t
d
d
d
f ( ) exp i t
E( ) dt exp i ( )t
f ( )E( ) exp i t
2
2
2
dt exp i( )t 2
d
2 E( ) dt exp i( )t E( )
5.
d2 D( ) 1 f ( ) E( ) exp i t 0
D( ) E( )
t
1 f ( ) 1 dtf (t ) exp i t
0
f (t ) вещественная комплексна я
В случае быстропеременного поля связь между фурье-компонентами
электрической индукции и напряженности формально остается такой же. Однако
коэффициент пропорциональности (по аналогии – диэлектрическая
проницаемость) зависит от частоты и является комплексной
6.
1 i 21 dtf (t ) exp i t
0
t
t
t
0
0
1 dtf (t ) exp i t 1 dtf (t ) exp i t
1 1
2 2
7.
Продолжим f ( ) в верхнюю половину комплексно й плоскости1 i 2 ; 1 ; 0 2
0
0
1 dtf (t ) exp i t dtf (t ) exp i 1t exp 2t cхходитс
во всех точках верхней полуплоскости из за наличия затухающей
экспоненты в верхней полуплоскости 1 не имеет особенностей
и 1 0
Th Коши d
Г
R
ρ
ω0
1
0
0
1
0 d
0
Г
CR
0
R
R 0
0
C
CR
0
R
C : 0 exp i , 0
C
0 exp i 1 0
i d exp i
i d 0 exp i 1 ( i ) 0 1
0
exp
i
0
8.
1i 0 1
0
x; 0
1
d
Cоотношения Крамерса-Кронига
x 1
dx
i 1
x
1
2 x
1
1 x 1
1 i 2 1 1 dx
; 2 dx
x
x
1
2 x 0 2 x 2 x
dx x dx x 0 dx x
2 x
2 x 2 x
2 x 2 x dx
x x dx
dx
x
x 0 x
0
0
2 x 2 x 2 x x 2 x
dx x 0 dx x 0 dx x 2 0 dx x 2 2
2 x 2 x 2 x
1 1 dx
dx 2
x 0 x 2
1
9.
1 x 1 0 1 x 1 1 x 1dx x dx x 0 dx x
1 x 1
1 x 1
1 x 1
1 x 1 x dx
x x dx
dx
x
x
x
0
0
0
1 x 1 1 x 1 1 x 1
1 x 1
dx x 0 dx x 0 dx x 2 0 dx x 2 2
1 x 1 2 1 x 1
2 dx
dx 2
x
0 x 2
1
Cооотношеня Крамерса Кронига
2 x 2 x 2 x
1 1 dx
dx 2
x 0 x 2
1
1 x 1 2 1 x 1
2 dx
dx 2
x
0 x 2
1
10.
Рассмотрим распространение света в немагнитной среде с комплекснойдиэлектрической проницаемостью. .
Введем комплексны й показатель преломления n~ n ik , определив
его так, чтобы выполнялось обычное соотношение Максвелла n~ 2 ,
но с комплексны ми диэлектической проницаемостью и показателем
преломления
1 i 2
2
n~ 2 n ik
1 n 2 k 2
2
2
n k i 2nk
2 2nk
Какой физический смысл у комплексной диэлектрической проницаемости?
Рассмотрим распространение плоской монохроматической световой волны в
отсутствие сторонних токов
E E 0 exp iκr i t 2 E
2E
с 2 t 2
11.
1 B, E c t
B 0
D E; B H;
, H 4 j 1 D
c
c t
D 4
1 B
, E c t
B 0
4
E
, B c j c t
E 4
12.
Cеед немагнитная 1, незаряженн ая 0; Полный ток j 01 B
,
E
(1)
c t
B 0 (2)
, B E (3)
c t
E 0 (4)
B
B
(3) , B e
, B ,
t
x
t
t
, ,
2
B E
, t c t 2
2
1 B
2E
B E
(1)
c , E ,
, , E 2 2
2
c t
c t
t c t
13.
, , E k i , j ,ki, j
, E j
xi
i , j ,k
i, j
xi
,m , j
,m
Em
x
E
m
i , j ,k ,m , j
xi x
i , , m j
i , j ,k i ,k , j
i , j ,k
,m, j
j
i , , m
i , k ,m i ,m k ,
j
, , E k i , k ,m
i ,k , j ,m, j
2 Ek
2
x
Ek
m
Em
Em
i ,m k ,
xi x i , ,m
xi x
Em
Ek
xm xk
xk
m
Em
xm
E
xk
Есть квазиэлект ронейтральность E
, , E E, где E e E
4
0
14.
, , E E , , EE
2E
c 2 t 2
2E
волновое уравнение
c 2 t 2
Плоская монохроматическая волна E E 0 exp iκr i t элементарное
решение волнового уравнения
n~ 2 2 E
E E 0 exp iκr i t E 2 2 ; n~ 2
c t
2 E
2
E e E
e E0, exp i t 2 exp( iκr )
2
x
x
κr x
exp( iκr ) exp( iκr )
x
x
exp( iκr ) i
x
x
i x i exp( iκr)
exp( iκr ) i , i exp( iκr )
2
2
exp(
i
κr
)
exp( iκr )
2
x
E e 2 E0, exp iκr i t e 2 E
(i x )
x
15.
n~ 2 2 EE E 0 exp iκr i t E 2 2
c t
E e 2 E
n~ 2 2 E
E 2 2
c t
2E
2 exp i t
2
E
exp
i
κr
E
0
2
2
t
t
~2
~2
2
2 n
2
2 n
e E 2 0 2 0
c
c
~
n
n i
k
c
c
c
Направим ось х вдоль распространения волны κ e x
x
c
E E 0 exp iкк i t E 0 exp k exp i t ; c1
n
c
c1
16.
xc
E E 0 exp iкк i t E 0 exp k exp i t ; c1
n
c
c1
x
( x, t ) t
c1
0 ( x0 , t 0)
x0
c1
x
0 t x(t ) x0 c1t
c1
c
c1 фазовая скорость электромагнитной волны в веществе
n
n Re n~ обычный показатель преломления
k коэффициен т экстинкции характеризует затухание волны
17.
Коэффициент поглощения – часть интенсивности (доля фотонов),поглощенных в единицу времени в единице объема
1 dI ( x)
I ( x) dx
dI ( x)
1 dI ( x)
0
I ( x) I (0) exp( x)
dx
I ( x) dx
I Π
c
E, B
cn
E, e x , E cn E 2 e x
Π
4
4
4
B n e x , E
Π
I Π
cn 2
E
4
x
E E 0 exp k sin t
c c1
E
2
I
x
1
2
2
E exp
kx sin t E02 exp k
2
c
c
c1
2
0
cn 2
cn 2
2
E
E0 exp k
k
4
8
c
c
18.
Оптические константы среды часто определяют, измеряя отражение света отповерхности. При нормальном падении света коэффициент отражения
2
n~ 1 n 1 k 2
R ~
n 1 n 1 2 k 2
1 n 2 k 2
2 2nk
2 x 2 x 2 x
1 1 dx
dx 2
x 0 x 2
1
1 x 1 2 1 x 1
2 dx
dx 2
x
0 x 2
1
19.
Потенциалы электромагнитного поля.B 0
, A 0 A
B , A , A векторный потенциал
B , A , E
, E 1 , A 0
1 B
c t
c t
1 , A
1
, A
c t
t
c t
e
, ,
,
A
x
, E 1 , A 0 , E , 1 A 0
c
t
e
,
, ,
x
c t
1 A
,
E
0
1 A
E
, скалярный потенциал
c t
c t
, f 0
1 A
c t
1 A
,
c t
20.
4n 2 E
B , A
j
, B
c
c t
1 A
E с t
E 4
n2
n2 2A
4
n 2
j A
A 2 2
c t
c
c t
1
4
A
c t
n2
Уравнения для потенциалов взаимосвязанны. Однако их можно развязать
воспользовавшись калибровочной инвариантностью (неоднозначностью в
выборе потенциалов поля)
, f 0 A A f
rotA rotA B A векторный потенциал тогоже поля
Векторный потенциал определен неоднозначно – с точностью до градиента
произвольной гладкой функции. Однако изменив только векторный
потенциал, и оставив неизменным, мы меняем электрическую
напряженность=> Одновременно с векторным потенциалом также нужно
менять и скалярный потенциал
1 A
1 A
1 A
1 f
1 A
c t
c t
c t
c t
c t
1 f
c t
21.
A A f1 f
с t
n2 2A
4
n 2
j A
A 2 2
c t
c
c t
1
4
c t A n 2
Функцию f всегда можно подобрать так, чтобы
n 2
A
0 калибровка Лоренца
c t
n2 2A
4
A
j
2
2
c t
c
уравнения Даламбера
2
2
n 4
c 2 t 2
c
22.
В случае электронейтральной среды скалярный потенциал можно исключитьиз рассмотрения, положив его равным нулю. Тогда
1 B
, E
c t
B , A
1 A
B 0
E
2
c
t
n
E
, B
A 0
c t
E 0
1 B
1
1
, E
, A , A выполнено
c t
с t
c t
B 0 , A 0 выполнено
1 A
E 0
0 выполнено
c t
n 2 E
n2 2A
, B
A 2 2 0 волновое уравнение
c t
c t
23.
В случае электронейтральной среды всегда можно положить скалярныйпотенциал равным нулю.
B , A
E 1 A
c t
A 0
n2 2A
A 2 2 0
c t
Плоской монохроматической волне отвечает векторный потенциал
A A0e exp i x i t E
1 A
i A0e exp i x i t ; e вектор порляризац ии
c t
c
E E0e exp i x i t E0
c
A0
Плотность энергии
w
n2 E 2 B
2
8
Плоская волна B nE w
n2 E 2
4
n 2 E0
8
2
n2
2
A0
8 c
2
8 c 2
8 N
c
A0
w
A0
c1 ; c1
2n2
n
w N , N концентр.фотонов
24.
Гамильтониан электрона в периодическом поле V (r ) кристалла2
1
e
1
e
e
ˆ
ˆ
ˆ
Hˆ
p
A
V
(
r
)
p
A
p
A
V (r )
2m0
c
2m
c
c
1 2
e
e
e2 2
pˆ pˆ A Apˆ 2 A V (r )
2m0
c
c
c
pˆ A Apˆ i A A i A 2 A 2 Apˆ
2
1
2
e
e
2
pˆ Apˆ 2 A 2 V (r )
Hˆ
2m0
c
c
e A0 e E0
e 2 2 2e
e 8
A / Ap
1 как правило
2
c
c
cp
p p c
Hˆ Hˆ Hˆ
0
2
ˆ
p
Hˆ 0
V (r ) гамильтониан в отсутствие света(нулевое приближение)
2m0
e
Hˆ
Apˆ возмущение, связанное с наличием излучения
m0 c
25.
A A0e cos iκr i tA0
A
e
e exp iκr i t 0 e exp iκr i t Hˆ
Apˆ
2
2
m0 c
Hˆ исп
Hˆ Hˆ погл
eA0
Hˆ погл
exp iκr i t epˆ описывает поглощение фотонов
2m0 c
eA0
Hˆ погл
exp iκr i t epˆ описывает испускание фотонов
2m0 c
Рассматриваем поглощение
Нулевая задача задача о Блоховском спектре
i
k , exp (k )t uk , (r ) exp ikr
eA0
i
k 1 , v dr k* 2 ,c Hˆ погл
k 1 ,v
k 2 , c Hˆ погл
Pv ,c (k 1 , k 2 ) exp c (k ) v (k )
2m0 c
Pv ,c (k 2 , k 1 ) dr uk* 2 ,cepˆ uk1 ,v i k 1e uk* 2 ,cuk1 ,v exp k 1 k 2 κ r
26.
Pv ,c (k 2 , k 1 ) dr f (r ) exp k 1 k 2 κ rf (r ) uk* 2 ,cepˆ uk1 ,v i k 1e uk* 2 ,cuk1 ,v
u (r m) u (r ) f (r m) f (r )
Разбиваем область интегрированя на элементарные ячейки ,
заменой переменных r r m сводим интегрирование по ячейке m
к интегрированию по ячейке m 0 и используем решеточную сумму
Pv ,c (k 2 , k 1 ) drf (r ) exp k 1 k 2 κ r
m m
dr f (r m) exp k 1 k 2 κ r m
m 0
exp k 1 k 2 κ m dr f (r ) exp k 1 k 2 κ r
0
m
dr f (r ) exp k 1 k 2 κ r exp k 1 k 2 κ m
0
m
N k1 k 2 κ , 0 dr f (r ) exp k 1 k 2 κ r N k1 k 2 κ , 0 dr f (r )
0
0
27.
V*
*
Pv ,c (k 2 , k 1 )
k k κ ,0 druk 2 ,cepˆ uk1 ,v i k 1e druk 2 ,cuk1 ,v
0 1 2 0
0
P 0 k 1 κ k 2 закон сохранения импульса
Практически всегда, κ k электрон при переходе остается практически
в одной и тойже точке зоны Бриллюэна прямые переходах
Ложим κ 0 дипольное приближение
V
*
*
ˆ
Pv ,c (k 2 , k 1 )
k ,k druk1 ,cepuk1 ,v i k 1e druk1 ,cuk1 ,v
0 1 2 0
0
*
druk1 ,cuk1 ,v 0 Pv,c (k 2 , k1 ) V k1 ,k 2 epcv ; p cv
0
V
0
dru
*
k1 ,c
pˆ uk1 ,v
0
i
k 1 , v dr k* 2 ,c Hˆ погл
k1 ,v v ,c (k 1 , k 2 ) exp c (k 2 ) v (k 1 )
k 2 , c Hˆ погл
eA0
v ,c (k 1 , k 2 )
k1 ,k 2 epcv
2m0 c
2
v ,c (k 1 , k 2 )
e 2 A0
2
2 2
0
4m c
epcv (k 1 ) k1 ,k 2 A0
2
2 e 2 N phot
2
v ,c (k 1 , k 2 ) 2
ep
(
k
)
k 1 ,k 2
cv
1
m0 n 2
2
2
8 c 2 N phot
n 2
28.
Ограничимся приближением правила Ферми первым порядком временной теории возмущенияЧисло переходов в единицу времени число фотонов, поглощенных в ед.времени
Wcv
2
v,c (k1 , k 2 ) c (k 2 ) v (k1 ) N e,v (k1 ) 1 N e,с (k 2 )
2
k 1 ,k 2
Для простоты считаем валентную зону полностью заполненной , а зону проводимости
полностью пустой
2
Wcv 2
2 e 2 N phot
2
v ,c (k 1 , k 2 ) c (k 2 ) v (k 1 ) v ,c (k 1 , k 2 ) 2
ep
(
k
)
k 1 ,k 2
cv
1
2
m0 n
k 1 ,k 2
2
2
2 2 e 2 N phot
2
Wcv 2
ep
(
k
)
cv 1 k1 ,k 2 c (k 2 ) v (k1 )
m02 n 2 k1 ,k 2
2
V
2 2 e 2 N phot
m02 n 2
e 2 N phot
m02 n 2
epcv (k ) c (k ) v (k )
2
k
dk epcv (k ) c (k ) v (k )
2
29.
Распространяется плоская световая волнаc
Плотность потка фотонов I 0 N phot
n
2
e
N phot
Wcv
2
dk epcv (k ) c (k ) v (k )
2
2
V
m0 n
Коэффициент поглощения
Wcv
e2
2
dk epcv (k ) c (k ) v (k )
2
VI 0 m0 cn
30.
Пусть минимум зоны проводимости и максимум валентной зоны расположены водной и той же точке k=0. Оба экстремума считаем простыми
(невырожденными и параболическими)
e2
2
2
d
k
ep
(
k
)
c (k ) v (k )
cv
m0 cn
2k 2
2k 2
c (k ) c
; v (k ) v
2mc
2m p
2k 2
1
1
1
c (k ) v (k )
0 ;
; 0 c ( 0) v ( 0)
2
mc m p
Для k 0
epcv (k ) epcv (0)
epcv (k )
k
k
k 0
epcv (0) 0 разрешенные переходы
epcv (0) 0 запрещенные переходы
Рассмотрим разрешенные переходы epcv (k ) epcv (0)
2k 2
e2
2e 2
2
2 2
2
epcv (0) dk
0 2
epcv (0) 2
m0 cn
2
m0 cn
3/ 2
0 1/ 2
31.
Рассмотрим запрещенные переходы epcv (k )epcv (k )
e2
2
m0 cn
k
k 0
2
epcv (k )
k
k
k 0
2
2 2
2e 2 epcv (k )
2
2 k
d
k
k
2
0
2
2
m
cn
k
k 0
0
5/ 2
0 3 / 2
32.
eA0i
k , v dr k* ,c Hˆ погл
k ,v
k , c Hˆ погл
Pv ,c exp c (k ) v (k )
2m0 c
Pv ,c e dr k* ,cpˆ k ,v
vˆ
1 dr
1 i ˆ
pˆ
H 0rˆ rˆHˆ 0
m0 m0 dt m0
Pv ,c
1 i
e dr k* ,c Hˆ 0rˆ k ,v dr k* ,crˆHˆ 0 k ,v
m0
1 i
ˆ
e dr H 0 k ,c rˆ k ,v v (k ) dr k* ,crˆ k ,v
m0
1 i c (k ) v (k )
1 i c (k ) v (k )
*
ˆ
dr k ,cer k ,v
d v ,c
m0
m0
d v ,c dr k* ,cer k ,v дипольный матричный элемент
k , v d v ,c
k , c Hˆ погл





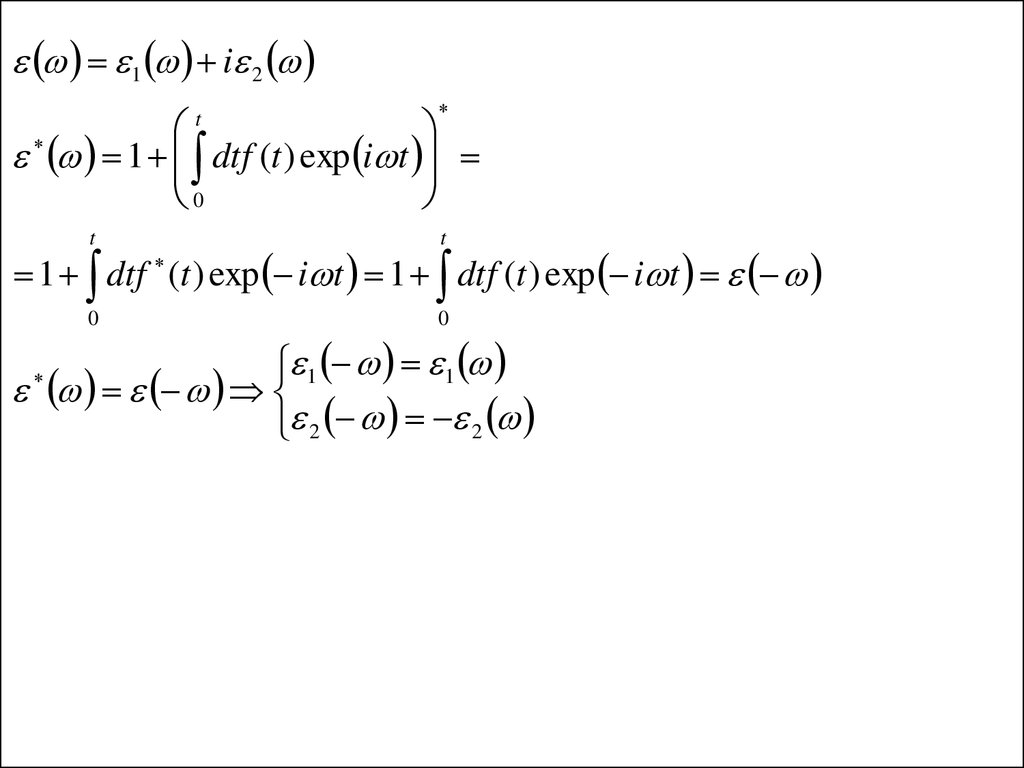


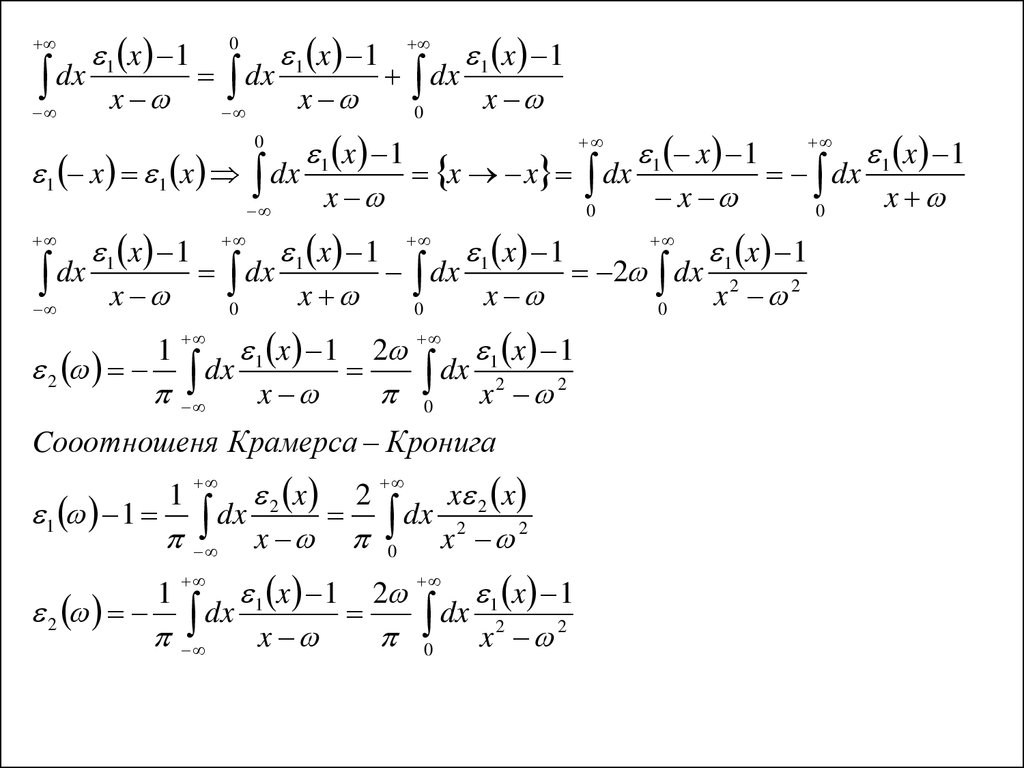























 physics
physics








