Similar presentations:
Взаимодействие излучения с веществом (силовая оптика)
1.
ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ СВЕЩЕСТВОМ (СИЛОВАЯ ОПТИКА)
Поляков Дмитрий Сергеевич
polyakovdmitry1988@gmail.com
2.
Литература1. В.П. Вейко, М.Н. Либенсон, Г.Г. Червяков, Е.Б. Яковлев. Взаимодействие
лазерного излучения с веществом (силовая оптика). Под редакцией чл.-корр. РАН
В.И. Конова. Физматлит. М.: 2008 г. 348 с.
2. М.Н. Либенсон, Е.Б. Яковлев, Г.Д. Шандыбина. Взаимодействие лазерного
излучения с веществом (силовая оптика). Конспект лекций под редакцией Вейко
В.П. Часть I. Поглощение лазерного излучения в твердых телах. СПб: СПб НИУ
ИТМО, 2008. 141 с.
3. М.Н. Либенсон, Е.Б. Яковлев, Г.Д. Шандыбина. Взаимодействие лазерного
излучения с веществом (силовая оптика). Конспект лекций под редакцией Вейко
В.П. Часть II. Лазерный нагрев и разрушение материалов. СПб: СПб НИУ ИТМО,
2011. 184 с.
4. Дж. Реди. Действие мощного лазерного излучения. М.: Мир, 1974, 468 с.
5. Либенсон М.Н. Лазерно-индуцированные оптические и термические процессы в
конденсированных средах и их взаимное влияние. СПб.: Наука, 2007. 423 с.
6. .....
3.
Предмет курсаВзаимодействие лазерного излучения с веществом имеет множество направлений
и оттенков:
- распространение низкоинтенсивного излучения в оптических средах (отражение,
преломление, дисперсия) – линейная оптика
- распространение высокоинтенсивного излучения в прозрачных средах
(самофокусировка, фазовая самомодуляция, генерация гармоник и т.п.) –
нелинейная оптика
- взаимодействие света с веществом в самой активной среде лазеров (спонтанное и
вынужденное излучение света, процессы рассеяния) – квантовая электроника и
лазерная техника
- взаимодействие излучения с поглощающими (и слабопоглощающими) средами,
вызывающее в них необратимые изменения (нарушения целостности и т.п.) –
силовая оптика.
Именно эта дисциплина (силовая оптика) является ключевой дисциплиной,
находящейся на стыке лазерной физики и техники со всевозможными лазерными
технологиями обработки материалов, и изучается в данном курсе.
При этом акцент делается на физике и физико-математическом описании
соответствующих процессов.
4.
План курса1 семестр
- введение во взаимодействие лазерного излучения с веществом
- поглощение лазерного излучения в металлах, оптические свойства металлов
- поглощение лазерного излучения в полупроводниках, оптические свойства
полупроводников
- элементы нелинейной оптики, нелинейно-оптические эффекты в задачах лазерной
обработки материалов
- оптические свойства неоднородных (композитных) сред
- «пондеромоторное» действие лазерного излучения
2 семестр
- теплофизика лазерного нагрева
- тепловые эффекты инициированные лазерным нагревом (фазово-структурные
переходы, химические реакции, микроструктурирование поверхности, абляция и т.д.)
- взаимодействие импульсов сверхкороткой длительности с конденсированными средами
5.
Введение во взаимодействие лазерногоизлучения с веществом
6.
Тепловая модель взаимодействия лазерногоизлучения с веществом
В настоящем курсе рассмотрение вопросов взаимодействия лазерного излучения с
веществом будет вестись с позиций анализа теплового действия лазерного излучения на
поглощающие материалы, как представляющего наибольший интерес для различных
лазерных технология обработки материалов.
В рамках тепловой модели выделяют 4 основных стадии:
- поглощение света и переход поглощенной энергии в тепловую
- нагрев материала без разрушения
- инициирование лазерным нагревом различных тепловых процессов (фазовые
переходы, химические реакции, эмиссионные процессы и т.д.)
- остывание материала (последействие лазерного импульса)
В общем случае эти стадии нельзя рассматривать независимо друг от друга.
Например, нагрев материала может вызывать изменения его оптических свойств и,
соответственно, оказывать влияние на процесс поглощения лазерного излучения.
В целом же, в рамках «тепловой модели» можно дать адекватное объяснение
большинству наблюдаемых в экспериментах явлений.
7.
Подходы к описанию взаимодействиялазерного излучения с веществом
классический
полуклассический
квантовомеханический
При классическом подходе В полуклассическом подходе При
квантовоизлучение
описывают
с излучение
по
прежнему механическом
помощью
уравнений описывается
уравнениями описании излучение и
Максвелла, а свойства среды Максвелла,
но
при среда рассматриваются
(диэлектрическая
вычислении
оптических как единая квантовая
проницаемость)
считаются свойств среды используются система.
известными из эксперимента квантово-механические
(либо для их вычисления модели.
используются
простые
феноменологические модели
на
основе
классической
механики).
В дальнейшем как правило, будем работать в рамках классического подхода, либо, в
некоторых случаях, будем использовать упрощенное представление об электромагнитном
излучении как о потоке фотонов.
8.
Некоторые сведения из векторного анализа.Скалярные и векторные поля
Если каждой точке некоторой области пространства (мы будем иметь ввиду
трехмерное эвклидово пространство) по некоторому правилу поставлено в
соответствие действительное число U, то говорят, что в этой области пространства
задано скалярное поле.
U U r
U U x, y , z
r – радиус вектор точки
x, y, z – декартовы координаты точки
Примеры скалярных полей в физике: поле температур, поле концентраций,
скалярный потенциал э-м поля, поле давлений (в газах).
Если каждой точке некоторой области пространства по некоторому правилу
поставлен в соответствие вектор a, то говорят, что в этой области пространства
задано векторное поле.
a a r
a a x x, y , z e x a y x , y , z e y a z x , y , z e z
ax, ay, az – компоненты а в базисе ex, ey, ez
Примеры векторных полей в физике: напряженности электрического и магнитного
поля, поле скоростей в жидкости.
В физике рассматриваются поля зависящие от времени.
9.
Некоторые сведения из векторного анализа.Производная по направлению и градиент скалярного
поля
Пусть скалярное поле U в некоторой точке S0
имеет значение U(S0) и задан вектор s,
определяющий направление вдоль которого мы
хотим определить производную. Выберем
точку S отстоящую от точки S0 на расстояние
Δs по направлению s, тогда производной
скалярного поля U по направлению s
называется предел:
U S U S0
U
lim
s s 0
s
Производная по направлению, очевидно, существенно зависит от выбора
направления s, т.е. для заданной точки существует бесконечно много различных
производных вдоль разных направлений.
Можно ли исследовать производные по направлениям с помощью единственной
величины, вычисляемой по заданному скалярному полю?
10.
Некоторые сведения из векторного анализа.Производная по направлению и градиент скалярного
поля
Рассмотрим поверхность задаваемую уравнением U(x, y, z) = U0 (U0 = U(S0)) –
поверхность уровня. Построим нормаль n к этой поверхности в точке S0. Отступив
вдоль нормали на некоторое малое расстояние Δn, построим м ещё одну поверхность
уровня U(x, y, z) = U0 + ΔU (U0 + ΔU = U(N)) (см. рис.)
Uнаправлений,
U
SS UU SS00 направления,
U
в U
U U
n
Последовательно
выбирая
качестве
Из рисунка
ясно,
что
lim
тогда
lim
gradU
cos ss, n
s
00
ss
ss координат
ss
s
n
cos sосями
, n декартовых
задаваемые
получим:
U
Вектор численно
равный производной
и направленный
к поверхности
U
U
U
N U S
n
U cos gradU
U gradU
gradU z
x 0
y
cos s, n lim
s
,
n
x
yn
z
n 0
n
уровня в сторону
возрастания
U называется
градиентом скалярного поля U.
U
U
U поля по
U
Из изложенного следует, что
производная
скалярного
gradU
e
e
ez
gradU
n
Соответственно, в декартовых координатах
x
y
x
y
z
направлению
s
равна
проекции
градиента
на
это
направление.
n
11.
Пример вычисления градиентаВычислим градиент скалярного поля, задаваемого соотношением:
A
U r r r
r
1 способ (по определению): Из вида поля U следует, что поверхности уровня
представляют собой сферы с центром начале координат. Направление нормалей к
этим поверхностям совпадает с радиальными направлениями, а приращение вдоль
нормали равно приращению dr.
Соответственно: gradU
U r
Ar
r
2 A 3
r r
r r
r
В общем случае ясно, что если U(r) есть функция только от r, то gradU
2 способ (в декартовых координатах):
U x, y , z
U r r
r r
A
x2 y 2 z 2
U
U
1
xe x xye y ze z
U
U2 x
r
A e x
gradU
e
e
A
A
3
y
zz
3
x 2
2 2 2 2 2 23 3
x
2 y 2 z
r
x
y
x
y
z
2 x y z
x y z
U
A
x
x
x y z
2
2
2
3
U
A
y
y
x y z
2
2
2
3
U
A
z
z
x y z
2
2
2
3
12.
Некоторые сведения из векторного анализа.Поток и дивергенция векторного поля
Пусть задано векторное поле a, выделим малую плоскую
площадку (с площадью dS) и построим единичную
нормаль n к этой площадке.
Введем вектор dS ndS
Потоком поля a через площадку dS называется величина
d a, dS an dS
( , ) – означает скалярное произведение
Поток вектора через произвольную поверхность складывается из потоков через
элементарные площадки на которые можно разбить поверхность:
Ф a, dS
Ф a, dS
- поток через замкнутую поверхность (при
вычислениях будем выбирать внешние
S
S
нормали)
Выделим около некоторой точки замкнутую поверхность и вычислим поток через эту
поверхность и разделим на объем который ограничивает эта поверхность. Будем
стягивать эту поверхность к точке, то указанное отношение будет стремиться к
некоторому пределу, который и называется дивергенцией поля в этой точке (если он
существует и не зависит от способа стягивания объема в точку).
a, dS
Итак, дивергенцией поля a называется предел:
(можно сказать, что дивергенция
объемная плотность потока)
есть
diva = lim
V 0
S
V
13.
Некоторые сведения из векторного анализа.Вычисление дивергенции в декартовых координатах
Около точки с координатами x, y, z выделим объем в прямоугольного параллелепипеда,
грани которого перпендикулярны осям координат.
Пусть задано поле
a ax e x a y e y az e z
Поток
поля
а
перпендикулярные оси x:
через
грани,
x ax x x, y , z y z
ax x, y , z y z
Аналогично для потоков через грани, перпендикулярные осям y и z:
y a y x , y y, z x z a y x , y, z x z x , y , z - некоторые значения
координат на гранях куба
z az x , y , z z x y az x , y , z x y
x y y
Составим
ay,y z x , yaпри
y xy,, yz,x z, xy , z z
a y 0x , y, z x z
axy x a z x, y , z ya x z x , ayx, zx и, yвычислим
,azy xy, yz предел
ax отношение
x
y
z
divdiv
a =a = lim
x ,
y ,x
z 0 y
z
x поля
x y azв точке x.
y
x y z
т.е. вычислим
дивергенцию
aazz xx,,yy,,zz zz x
azy x ,ayz , zx , y , z axx y a y az
z x y z
x y z
14.
Пример вычисления дивергенцииВычислим дивергенцию поля задаваемого соотношением: a
Проведем вычисления в декартовых координатах.
ye y
xe x
ze z
a
3
3
3
2
2
2 2
2
2
2 2
2
2
2 2
x y z x y z x y z
3
5
3 2
ax
2
2
2 2
2
2 2
x y z x x y z 2x
x
2
a y
y
1
3
2 2
az
z
3y2
5
2 2
x y z x y z
2
2
2
a a a
diva xx yy zz
x
y
z
2
3
3
2 2
1
3
2 2
2
2
1
3
2 2
2
2
5
2 2
3z 2
5
2 2
x y z x y z
2
2
3 x 2 y 2 z 2
5
2 2
2
2
2
0
Вычислим дивергенцию в начале координат по определению
11
22
4
R
4
R
2
2
3
divaa lim
lim RR
lim 3
div
00 4
R 0 R
RR
4 33
RR
33
3x 2
x y z x y z
2
x y z x y z
2
r
r3
2
15.
Некоторые сведения из векторного анализа.Теорема Гаусса-Остроградского
Теорема Гаусса-Остроградского: Поток векторного поля a через произвольную
замкнутую поверхность S равен интегралу от дивергенции по объему V,
ограниченному этой поверхностью.
a, dS divadV
S
V
Поясним данную теорему следующим
образом.
Разобьем
объем
V
на
бесконечно малые кубические элементы,
вычислим поток поля a через каждый из
кубиков dФ и просуммируем:
d divadV divadV
i
i
V
Грани всех кубиков либо граничат с соседними кубиками, либо находятся на границе
области S. При подсчете суммарного потока поток через внутренние грани будет
входить дважды причем с разными знаками (т.к. для соседних кубиков нормали к
одной грани направлены в противоположные стороны). Т.о. суммарный поток через
внутренние грани будет равен 0, а поток через внешние грани будет стремиться к
потоку через поверхность S. Таким образом, с другой стороны
16.
Некоторые сведения из векторного анализа.Циркуляция и ротор векторного поля
Пусть в поле вектора a имеется кривая L и задано
направление
обхода
кривой,
считающееся
положительным. Разобьем кривую L множество
ориентированных элементов dl, умножим dl скалярно
на a и просуммируем по всем элементам. Предел это
суммы при уменьшении элементов dl называется
криволинейным интегралом по контуру L и
обозначается:
Если контур L замкнутый то интеграл
- криволинейный интеграл
a, dl по контуру L
называется циркуляцией
a
,
d
l
L
векторного поля a по
L
контуру L.
Выделим около некоторой точки замкнутый плоский контур L и вычислим
циркуляцию поля a. Составим отношение циркуляции к площади поверхности,
ограничиваемой контуром. Предел указанного отношения при стягивании контура в
точку даст проекцию ротора на нормаль к площадке, ограниченной контуром (при
этом считается, что направление нормали и направление обхода контура связаны
правилом правого винта).
a, dl
L
rota, n lim
S 0
S
Для полного задания ротора нужно вычислить
указанный предел для трех различным образом
ориентированных площадок.
17.
Некоторые сведения из векторного анализа.Вычисление ротора в декартовых координатах
Вычислим проекцию ротора на ось x, выбрав в качестве контура квадрат со сторонами
Δy, Δz, находящийся в плоскости, перпендикулярной оси х.
Циркуляция поля а через выбранный контур будет
Складываться из интегралов взятых по участкам
параллельным осям y и z.
Вклад в циркуляцию от участков параллельных оси y:
С y a y x, y , z y a y x, y , z z y
Вклад в циркуляцию от участков параллельных оси z:
Сz az x, y dy, z z az x, y, z y
Составим отношение циркуляции к площади контура:
С y Cz
y z
.
Предел этого отношения при Δy, Δz →0 согласно определению даст проекцию ротора
на ось x.
aa yy x, y , z y a y x, y , z z y az x, y dy
y,,zz zz aazz xx,, yy,,zz yy
a
z
rot
rotaa xx
ylim
Рассуждая
аналогичным образом
можно показать,
что
, z 0
y
z
y
z
y z
a a
a a
a a
ax az
rota = z y e x x z e y y x e z
rota y a y x, y , z z ayy x, yz, z az x ,zy yx, z az x ,xy, z y az a y
z x
lim
y
,
z
0
z
y
y
z
a y ax
rota z
x
y
18.
Некоторые сведения из векторного анализа.Теорема стокса
Теорема Стокса: Циркуляция векторного поля a по некоторому замкнутому контуру
равна потоку ротора этого векторного поля через поверхность S, опирающуюся на
контур L.
a, dl rota, dS
L
S
Поясним теорему следующим образом. Будем
приближать
поверхность
S
маленькими
прямоугольными
контурами.
Вычислим
циркуляции по каждому из контуров, умножим
на площадь контура и просуммируем.
dC rota, dS rota, dS
i
i
i
S
Участки контуров могут быть либо внешними, либо внутренними. Сумма
циркуляций по всем внутренним участкам даст 0, т.к. направления проходов этих
участков
при
вычислении
циркуляции
соседних
контуров
будут
противоположными. Оставшаяся часть суммы по внешним границам будет
стремиться к циркуляции по внешнему контуру L все более мелком разбиении.
dC a, dl
i
i
L
19.
Пример вычисления ротораВычислим ротор поля скоростей равномерно вращающегося твердого тела c угловой
скоростью ω.
Ось z направим вдоль оси вращения, т.ч.
направление и направление оси связаны правилом
правого винта.
Ясно, что
v v r
(r – расстояние от точки до оси вращения)
x
x
r
y
vx v cos r y
r
2
v yy v cos r
vz 0
v v
v v
v v
v v
2 ezz y e x x z e y y x e z y x e z 2 e z
rotv =
z x
y z
x y
x y
Ротор линейной скорости точек вращающегося твердого тела постоянен и равен
удвоенной угловой скорости его вращения.
20.
Некоторые формулы векторного анализаФормулы векторного анализа удобно записывать и преобразовывать с помощью
оператора набла.
В декартовых координатах вектор набла представляется вектором c компонентами
следующего вида:
, ,
x y z
т.е.
ex e y
ez
x
y
z
Под «произведением» оператора
x
U
и функции U следует понимать
.
x
Операции взятия градиента, дивергенции и ротора с помощью оператора набла
могут быть записаны следующим образом.
gradU e x
U
U
U
ey
ez
U Градиент U – умножение вектора набла на
x
y
z
скаляр U.
ax a y az
diva
, a
x
y
z
Дивергенция a – скалярное произведение
вектора набла на a.
Ротор a – векторное
az a y
a y ax
ax az
rota =
ey
ex
e y , a произведение
вектора
z
x
y
z
y
x
набла на a.
21.
Некоторые формулы векторного анализаДля выражений содержащих вектор набла оказываются
ограничениями) справедливы формулы векторной алгебры.
Тождество из векторной алгебры
b, bC b, b C b C
2
(с
некоторыми
Тождество с оператором набла
2U 2U 2U
, U div gradU U U 2 2 2
x
y
z
2
Δ – оператор Лапласа
b, bC 0
, U rot gradU 0
Ротор градиента равен 0.
b, b, a 0
, , a div rota 0
Дивергенция ротора равна 0.
b, b, a b b, a b, b a
, , a rot rota
, a 2a grad diva a
Ротор ротора равен градиенту от дивергенции
минус лапласиан.
22.
Некоторые формулы векторного анализаПроверим тождество
rot rota grad diva a непосредственной выкладкой.
Вычислим проекцию левой части на ось x:
rota rota y 2 a y 2 ax 2 ax 2 az
rot rota x y z z x y y 2 z 2 x z
rota y
ax az
z
x
rota z
a y
x
ax
y
Вычислим проекцию правой части на ось x:
ax a y az 2 ax 2 ax 2 ax
grad diva x a x x x y z x 2 y 2 z 2
2
2 ax a y 2 az 2 ax 2 ax 2 ax
2
2 2 2
x
x y x z x
y
z
2a y
2 az 2 ax 2 ax
2
x y x z y 2
z
Для
остальных
проверка
аналогично.
компонент
проводится
23.
Некоторые формулы векторного анализаОператор набла сочетает в себе свойства вектора и производной, если он действует
на произведение двух иди более истинных векторных или скалярных полей.
Например:
grad UV UV U V V U UgradV VgradU
div Ua ,Ua a, U U , a agradU Udiva
rot Ua ,Ua U , a a , U Urota gradU , a
div a, b , a, b b, , a a, , b b, rota a , rotb
Эти формулы можно проверить непосредственным вычислением в декартовых
координатах.
24.
Описание электромагнитного поля вклассической электродинамике
Электромагнитное поле можно описывать с помощью векторов, определяющих
направления и величины сил действующих на заряды.
1. Напряженность электрического поля, E, определяет силу, действующую на
заряд со стороны электрического поля.
FE qE
[E]=Н/Кл=В/м
2. Индукция магнитного поля, B, определяет силу, действующую на движущийся
заряд со стороны магнитного поля.
FM q[v , B ]
[B] = Н·с/(Кл·м)=Тл
(v – скорость заряда)
3. Индукция электрического поля, D.
D 0E P
P
dp
dV
[D] = Кл/м2
- поляризованность (дипольный момент единицы объема среды)
p – дипольный момент
25.
Описание электромагнитного поля вклассической электродинамике
4. Напряженность магнитного поля, H.
H
M
B
0
M
dm
dV
[H] = A/м
- вектор намагниченности (магнитный момент единицы объема среды)
m iSn
- магнитный момент
(S – площадь контура, i - ток)
26.
Уравнения максвелла в вакуумеВ дифференциальной форме
rotE
rotB
0
B
t
S
S
, dS
S
dV
V
divB 0
B
t
S S
B, dS
E
,
d
l
rot
E
,
d
S
t , dS
, dS
E
0
j
t
0 divE e
В интегральной форме
L
B, dl 0 0 t E , dS 0 j, dS
L
S
S
S ee dV
EE, ddV
0
0 div
VS
V
V
B, dS 0
S
E E , dS - поток напряженности электрического поля
В магнитостатике
S
- поток вектора магнитной индукции через поверхность
B
B, dS
Q
B, dSeldV
0- заряд
j, dSвнутри
0 Iобъема V
L V
S
indQ E , dl - работа по перемещению единичного заряда по замкнутому
- поток напряженности
эл. индукции.
поля через замкнутую
E
контуру – ЭДС
L
0 поверхность пропорционален сумме зарядов
0 I - магнитное поле
внутри
Гаусса).
B неё (теорема
B
,
d
l
2
rB
B
I
0
ind
- L закон электромагнитной
индукции
2 Фарадея
r линейного тока
Q
1 Q
2
2t
EE E 4 r
E
- закон Кулона
0
4 0 r 2
27.
Закон сохранения зарядаИз уравнений Максвелла следует закон сохранения заряда:
rotB
0
0
div rotB
E
j
t
div
0
divE divj
t
e
divj 0
t
dV
0
divE
e
0
- локальная форма закона сохранения заряда
V
e dV divjdV 0
t V
V
Q
j , dS
t
S
скорость изменения заряда
внутри поверхности S
Аналогичные по форме уравнения,
выражающие
закон
сохранения
справедливы
и
для
других
сохраняющихся величин – массы,
энергии, импульса.
(Q – заряд
поверхности S)
внутри
полный ток, втекающий через
поверхность S
dI jdS j , dS
28.
Уравнения максвелла в средеВ дифференциальной форме
rotE
В интегральной форме
B
t
E , dl t B, dS
L
S
D
rotH
j
t
H , dl t D, dS j, dS
divD e
D, dS dV
divB 0
L
S
S
e
S
V
B, dS 0
S
j – плотность токов проводимости и токов свободных зарядов
ρe – плотность свободных зарядов
В уравнениях Максвелла в среде под E и B следует понимать усредненные по
физически малым объемам среды поля.
Под физически малыми объемами понимается следующее:
1. Они велики по сравнению с расстояниями м/у атомами, молекулами и т.п., т.е.
велики по сравнению с микроскопическими неоднородностями среды и поля.
2. Они малы по сравнению с макроскопическими неоднородностями среды и поля.
29.
Взаимосвязь между уравнениями максвелла ввакууме и в среде
rot BB
E
E P
D 0E P
M+
rot 0M rot
j
0
0 0
t
t
t
B
H
M
div
E
div
P
div
0
divD e
0 0 E P
e e
Из сопоставления полученных уравнений с уравнениями Максвелла для пустого
пространства следует, что:
rotH
D
j
t
P
, rotM
t
- есть некоторые токи, создаваемые связанными зарядами среды.
divP
- есть объемная плотность связанных зарядов
Покажем, что это действительно так.
Запишем
сохранения
связанных зарядов.
Выделим закон
поверхность
S, ограничивающую
макроскопический объем V материала.
P
e
l
(n – концентрация атомов-диполей)
l P
divj P nq
div
nq
e
t
Если центр диполя расположен в прилегающем к элементу поверхности
divP divj dS слое толщиной l|cos(P, l)| , диполь рассекается поверхностью. Объем
t
этого слоя равен dS l|cos(P, l)|, величина некомпенсированного заряда
внутри V равна
P
- плотность
тока, создаваемого смещением связанных зарядов равна
j
производной
от поляризации
dq nqldS
cos P , n среды
P ,по
dSвремени.
t
Можно также Полный
показать,заряд:
что ротор
оказывается
q намагниченности
P dV равен
e dV плотности
P , dS div
V движением электронов
V
т.н. молекулярных токов, связанных Sорбитальным
( а также
Дивергенция поляризации среда равна объемной плотности
их спином).
divP e связанных зарядов, взятой с обратным знаком.
30.
Граничные условия для электромагнитного поляУравнения Максвелла в дифференциальной форме справедливы во всех точках объема
сплошных сред, однако теряют смысл в точках на границах раздела сред, при переходе
через которые свойства сред меняются скачком.
Условия которым удовлетворяют поля на границах раздела сред можно получить из
уравнений Максвелла в интегральной форме.
Рассмотрим условия для векторов E и D.
dV ,
nD
S D D , n S h
D
, nD
DD, dnS Q
2
S
12
1
e12 1
1
2n
1n 2
2e
D
V
через боковые стенки(Ф (Δh)→0
Ф
(Δh)
–
поток
D
D
E
,
d
l
E 2 , E1, t EB2 , d SE 1 0
при
Δh →0)
L
S
B
2 , n l ED , nh
l, nh
QE1, 1 l e E 2 ,D
D2, s D
2
12
1 12
t 1 12
S h 0
ΘE(Δh) – вклад в циркуляцию от боковых концов
Рассуждая
аналогичным
образом
можно показать,
σe – поверхностная
плотность
свободных
зарядовчто
контура(Θ
(Δh)
→0
при
Δh
→0)
E
B,2 , n 12нормальная
E ,B 1 , n120 Bкомпонента
2 n B1n 0
E
вектора D
Т.о.
2
1
испытывает
скачок
при переходе через границу
H
,
H
,
j
2
1
Т.о. тангенциальнаяS составляющая векnора E
раздела сред равной поверхностной плотности
непрерывна
при
переходе
границы
jS – плотность
поверхностных
токовраздела двух
свободного
заряда
на этой границе.
сред.
σe – поверхностная плотность свободных зарядов
31.
Материальные уравненияМатериальные уравнения устанавливают взаимосвязь между векторами D, H и E, B.
Для медленноменяющихся в пространстве и времени полях для линейной изотропной
среды справедливы следующие материальные соотношения:
D 0 E
B 0 H
j E
ε – диэлектрическая проницаемость
μ – магнитная проницаемость
σ – удельная проводимость
Здесь ε, μ, σ положительные вещественные константы.
В дальнейшем нас главным образом будут интересовать поля быстроменяющиеся
меняющиеся со временем по гармоническому закону:
E E e i t D D e i t B B e i t H H e i t
Для таких полей оказываются справедливы материальные соотношения следующего
вида (для изотропной линейной среды):
D 0 E
B 0 H
j E
Здесь величины ε, μ, σ являются комплексными функциями частоты электромагнитного
поля.
32.
Поток энергии электромагнитного поляSP E , H
Модуль вектора Пойнтинга численно равен энергии которая переносится через
единичную площадку перпендикулярную Sp в единицу времeни.
B D
divS p div E , H H , rotE E , rotH H ,
E,
E, j
t
t
divE a , b B b, rot
rot
w
w a a, rot
B b D
Обозначим
W
wdV
E, j
H
,
E
,
t
t
t
t
V
D t
rotH
j
t
W
w
j , E dV
E , EH, H, d SdV
div
E , j div E , H dV
t
V
t
V
V
S
W
j2
j , E dV dV - но это есть джоулево тепло, выделяющееся в
t
V
V
единицу времени.
Если в объеме V тепло выделяется только за счет токов проводимости, то резонно
считать, что W – есть энергия электромагнитного поля внутри этого объема, a w –
объемная плотность энергии.
Если токов проводимости нет, а объем V недостаточно велик, то изменение энергии
поля внутри поверхности S происходит за счет её потока через границу и Sp
действительно уместно отождествить с потоком энергии электромагнитного поля.
33.
Энергия электромагнитного поляПусть выполнены материальные соотношения:
D 0 E
B 0 H
ε, μ – постоянные вещественные числа, среда без дисперсии, медленно
меняющиеся поля.
Согласно нашему предыдущему рассмотрению
w D B 1 D E B H
E,
D,
H , B,
H,
E,
t
t
t 2 t t
t t
1
E , D B, H
2 t
Таким образом объемная плотность энергии электромагнитного поля:
1
0 E 2 P, E B2
(немагнитная среда)
w D, E B , H
2
2
2
2 0
Для вакуума (ε = 1, μ = 1):
0E2
B2
w
2
2 0
Объемная плотность энергии в среде (диэлектрике) складывается из энергии поля в
вакууме и энергии элементарных диполей (слагаемое (P,E)/2), составляющих среду.
Для быстроменяющихся в диспергирующих средах ситуация иная.
34.
Усреднение периодически меняющихсяфизических величин по времени
Под средним по времени периодически меняющейся величины A будем понимать:
T
1
A A t dt (T – период колебаний)
T
T0
T
22 TT
2
TT
sin 2 t 0
1 222 222
A00 cos 2 t 00 1
A0
222
dt
T
Вычислим A A000 cos t 000 dt
T 000
T 00
2
2T
2
0
A A0 cos t 0
0.5 A02
Для гармонически меняющихся полей используют комплексное представление:
- физический смысл тогда имеет вещественная
A A0 cos t A A A0e i A e i t
часть ReA
i A если
Ясно,
вещественные и мнимые части
A A0eчто
e i t при проводимых операциях
1
* то вычисления можно проводить в
преобразуются независимо
(операции
линейны),
Re
A
Re
B
Re
AB
i t
2
B B0e i B eформе,
комплексной
вещественную часть брать
от конечного результата.
T
1
Для
выделять вещественные части.
Re нелинейных
A Re B операций
A0 cos надо
t сразу
A B0 cos t B dt
T0
Однако, если нас интересуют
среднее по времени от произведения двух величин (A , B ~
T
B
A0 B0 меняющихся со временем, то можно Aсохранить
0 B0 cos A комплексное
e-iωt), гармонически
cos
2
t
cos
dt
A
B
0 среднее A от Bпроизведения
2T этом
2
представление, при
можно вычислить
по формуле
*)/2 (* означает комплексное сопряжение).
Re(AB
1
1
1
AB
i
Re AB* Re A0e i A e i t B0ei B ei t Re A0 B0e A B 0 0 cos A B
2
2
2
2
35.
Поглощение энергии монохроматическогоэлектромагнитного поля в диспергирующих средах
Рассмотрим монохроматическое поле в среде с материальными соотношениями:
D 0 E
i
B 0 H
i
E , B, D, H ~ e i t
комплексная
диэлектрическая
проницаемость
комплексная
магнитная
проницаемость
B D
divS p H ,
E,
t
t
B
D
Для усредненных величин:
div S p H ,
E,
t
t
1 D 1 B
2
21
*
div S p Re E ,
Re
H
,
E
H
0 Re
A Re 0B Re AB
2
t 2
t 2
2
Из уравнений Максвелла следует, что при j = 0:
Энергия монохроматического
При постоянной
электромагнитного
амплитуде поля
поля,этапоглощаемая
величина и в единицу
D 1
1
E времени
E e i tв единице1 объема
iii
ttt среды
определяется
iii
ttt энергии
будет
q
равна
диспергирующей
потерям
электромагнитной
мнимой
в 0 частью
Re
E
,
Re
E
e
,
i
E
e
Re
i
E
,
E
v
0
00
0
2 единицу
t
Dкомплексной
0 E e i t диэлектрической
2
2
проницаемости
времени
в единице
и равна:
объема.
22
2
D qv
0 E e0 i Et 2 0 0 E
0
E
H
Эта энергия
и выделяется
в виде тепла в среде.
Re
i
2
D
i t
2
2
i 0 E e
t
36.
Оптические свойства металлов37.
Уравнение для комплексной амплитудымонохроматического поля (уравнение Гельмгольца)
E E e i t
rotE
B B e i t
ee ii ttrotE
E B
rotE i B
B
t
ii tt
e i B e i t
t
D D e i t
rotH
H H e i t
D
j
t
rotH i D + j
С учетом материальных уравнений
получаем
или
rotB
0
B 0 H
i 0 E E
rotB i 0 0 E 0 E
D 0 E
j E
38.
Уравнение для комплексной амплитудымонохроматического поля (уравнение Гельмгольца)
rotB i 0 0 0 E
rotE i B
rot (rota ) grad (diva ) a
rot
rot rotE i rotB
grad (divE ) E i i 0 0 0 E
D 0 E
Вспомним, что
divE 0
divD e 0
тогда
E
22 00 00 i 00 E 0
E
2
c
i
2
E 0
0
Обозначим i
Тогда E
2
c
2
0
E 0
c
1
0 0
- скорость света в вакууме
- комплексная диэлектрическая проницаемость металла
уравнение
для
комплексной
амплитуды
монохроматической волны (уравнение Гельмгольца)
39.
Решение уравнения для комплексной амплитудымонохроматического поля
Рассмотрим случай линейной поляризации излучения, т.е. E 0, E ,0
Будем также полагать, что E E x тогда
2 E 2
2 E 0
x 2
c
Несложно понять, что решение будет иметь вид E E0e
ikx
k k is
, где
- комплексное волновое число
k
2
2
2
c
2
c
2
n2 .
n2 , n n ik p - комплексный показатель преломления (kp – коэффициент
экстинкции)
i t kx
С учетом временной зависимости E E0 e
Абсолютно аналогично для магнитного поля B B0 e
i t kx
но B 0, 0, B .
,
Получим соотношение амплитуд электрического и магнитного поля для плоской
монохроматической волны:
eexxx eeyyy eezzz
.i t kx
nE
cB
B
B
E
E y 0 E0e0
rotE
E
det
rot
det
xx yy zz
tt
i t kx
B
Bz B0e электрического и магнитного полей
пропорциональны
Амплитуды
друг другу, но их
E
E
E
E
E
E
yyy
zzz
xxx друг
колебания сдвинуты по фазе относительно
друга,
если мнимая часть
комплексного
не
равна
EEEzzzz EEEyyyy показателя
EEE
EEEzzzz
EEExxxx 0. EEyyy
i i
EEExxxx преломления
i t kx
yyyy
t t kxkx e
e
e
e
eeexxxx
e
e
e
e
e
ikE
e
ikE
e
e
i
B
e
ez
00
zz
zzzz
yyyy z
x zzz
0
y
z
x
x
y
y
y
z
z
z
z
x
x
x
x
y
y
x
40.
Поглощение электромагнитных волнК чему приводит комплексность параметров k , n, ?
k k is
E ( x, t ) E0eikx e i t
ikx sx
sx ii tt
E00 eii kk isis xx e ii tt E00eikx
e
E0e sx e i t kx
i k is x
E x, t E0e sx e i t kx
т.е. амплитуда поля экспоненциально убывает вдоль
направления распространения волны.
Интенсивность волны I – это средняя по времени величина вектора Пойнтинга (Sp = [E,H]).
H~E
E ~ e sx
s
c
kp
I ~ e x
2 k p
c
(α – коэффициент поглощения)
Коэффициент поглощения определяется мнимой часть комплексного показателя
преломления (коэффициентом экстинкции).
1
- глубина проникновения излучения (расстояние на котором
интенсивность излучения спадает в e раз).
Слой металла, в котором происходит поглощение называется скин-слоем.
41.
Отражение электромагнитных волн от границыраздела 2-х сред при нормальном падении
Падающая волна (i):
E yi E0i exp i t x
c
Bzi B0i exp i t x
c
Отраженная волна (r):
Воспользуемся
условием
непрерывности
тангенциальных
компонент
электрического
и
магнитного поля при x=0:
E0t E0i E0r
nE
B BE BE
tt
00
ii
00
rr
00
nE0t E0i E0r
kE0 B0
E yr E0r exp i t x
c
Bzr B0r exp i t x
c
Прошедшая волна
n
E yt E0t exp i t
x
c
n
Bzt B0t exp i t
x
c
42.
Отражение электромагнитных волн от границыраздела 2-х сред при нормальном падении
E0t E0i E0r
: E0i и обозначим
nE0t E0i E0r
t 1 r
nt 1 r
E0r
r i
E0
n 1
r
n 1
n 1 r 1 r
Отношение интенсивностей отраженной
коэффициентом отражения металла R.
R
E0r
2
i 2
0
n n 1 1 ik p k p2
2
r
2
r
R
E
n n 1 1 ik p k
2
E0t
t i
E0
2
p
и
падающей
волн
называют
n 1 k p2
2
n 1 k p2
2
r
Всегда имеет место соотношение R + A + T = 1. Для металлов T = 0, поэтому
поглощательная способность А равна:
A 1 R
A
4n
n 1 k p2
2
Поглощательная способность определяет долю
энергии электромагнитной волны, поглощенной
средой.
43.
Теория Друде оптических свойств металловДля определения зависимостей n(ω, T) и kp(ω, T) будем использовать классическую
модель Друде. В модели Друде для рассмотрения электронного газа в металлах
практически без изменений применяются методы кинетической теории разреженных
газов.
Основные положения теории Друде:
1. В интервале между столкновениями не учитывается взаимодействие электрона с
другими электронами и ионами. (приближение свободных и независимых
электронов).
2. Столкновения - внезапные события, меняющие скорость электрона. Столкновения
поддерживают локальное термодинамическое равновесие: скорость электрона не
связана со скоростью до столкновения, её величина соответствует температуре
области где произошло столкновение.
3. Для электрона вероятность испытать столкновение за время dt равна dt/τ. (τ – время
свободного пробега).
Покажем, что
время τ введенное
в 3-м предположении действительно есть время
t
t
t
1
dt
dt
dt dt dt
свободного
dP
1 пробега.
1 z z
e
момент
t = 0 произошло столкновение электрона, вычислим
в некоторый
времени
Пусть
1
вероятность
dP,
того,
что
следующее
e lim 1 z z столкновение произошло в промежуток времени
Обозначим z = -dt/τ
z 0
t
от t до t+dt.
dt
t
t
t
dt dt
t
на
промежутков,
dt
t/dt малых
Время
t
разобьем
тогда
dP
1
t te
te
e dt e
t
0
0
0
0
dt dt dt
- вероятность
вероятность,того,
того что столкновение не
произошло
произошло
за время
за время
dt. t .
1
44.
Уравнение для среднего импульса электроновp(t) – средний импульс электронов в момент времени t.
Доля электронов не испытавших столкновение за промежуток времени dt равна 1
dt
Если электроны движутся в силовом поле, то вклад от этих электронов в средний
dt
импульс в момент времени t + dt будет равен 1 p(t ) F (t )dt
Рассмотрим вклад в средний импульс электронов от электронов испытавших
столкновений за время dt.
Доля таких электронов равна dt/τ, при этом приращение импульса полученное
этими электронами от внешнего поля не может превышать F(t)dt.
Таким образом, вклад от этих электронов в средний импульс не больше
F (t )
dt 2 .
Т.е. этой поправкой (квадратичной по dt) можно пренебречь.
Окончательно имеем:
p(t dt ) p(t ) F (t )dt
dt
p(t )
или
dp
p(t )
F (t )
dt
Действие отдельных столкновений эффективно сводится к тому, что
электроны как бы движутся в среде с вязким трением.
.
45.
Связь проводимости с микро-характеристикамиметалла
Изменение среднего импульса, приходящегося на один электрон, во внешнем
переменном электрическом поле подчиняется уравнению:
dp
p
eE (t )
dt
(знак заряда электрона будем учитывать в явном виде)
Для гармонических воздействий
p y (t ) p0e i t .
После подстановки получаем:
E y (t ) E0e i t
будем искать решение в виде:
eEpy (yt )t
pi y (pt )y
t 1 i eE y t
enee p yy t e 2 ne E y t
Определим
плотностью
j t связь между
E yтока
t и py(t)
mee
me 1 i
За время dt через 2площадку S пройдет число электронов
равное
2
n
e
nee
0 e
при ω = 0
ne Sv y dt(
. )
Соответственно
ene p y me
(1 i )me eneeSv yydt
j
Плотность тока
Sdt
m
e
46.
Дисперсия комплексной диэлектрическойпроницаемости
nee2
( )
(1 i )me
( ) ( )
i ( )
0
Будем полагать,
= 1p2 (т.е. пренебрежем вкладом связанных электронов).
p2 что ε(ω)
формула
Друде
для
комплексной
( ) 1 2 12 i
2
2
столкновений
Обозначим
- частота
диэлектрической проницаемости металла
2
2
2
e2 ne e 22nee 1 i
i
i
p
p
(p ) 1 m
частота
1 p 2 γ –2 частота
1 столкновений
i
- плазменная
0 e 00mee i
2 2 2 2
1
e 2 ne
~ 1013 1014 с 1
Для металлов
p
- плазменная
частота
0 me
p ~ 1016 c 1
Параметры γ и ωp играют роль граничных параметров, определяющих
дисперсионные зависимости оптических свойств металлов.
47.
Частотные зависимости оптических свойств металлаЗависимость глубины скин-слоя
от длины волны
Частотные зависимости n и kp
( ) 1 2
i
2
2 2
2
p
2
p
( ) 1 b i
или
b
p2
b 2
2
n2
Частотная зависимость поглощательной способности
2
1
2
b
n( )
1
b
1 b
2
1
k p ( )
2
c
2 k p
2
b
4n
1
b
1 b A 1 R
2
n 1 k p2
2
48.
Классическая теория Лоренца дисперсии оптическихсвойств диэлектриков
Теория Лоренца описывает оптические свойства сред, обусловленные наличием
связанных электронов.
В теории Лоренца полагается, что среда представляет собой набор линейных
квазиупругих затухающих дипольных осцилляторов.
Уравнение движения электрона
(2-ой закон Ньютона):
d2y
dy
me 2 ky
eE y t
dt
dt
d2y
dy
eE0 i t
2
k
2
2
y
e
L
0
2
Обозначим
- собственная частота колебаний
0
dt
dt
me
Поляризация среды
m
e
i t
2
e
E
e
Общее
решение
неоднородного
уравнения
–
сумма
общего
однородного
Eрешения
0
n
e
y t
y t
e
2
2
Py t neey уравнения:
Lt - постоянная
уравнения
me и частного
0 i 2 Lрешения неоднородного
2
2
m
i 2затухания
L
e
0
2
m
e
yn et– концентрация
yOO t yЧН t диполей
2
d
y 2 d 2 y dy dy
eE0 i t
2
t
2
i
t
Найдем yОО
(t):
2
y
0
n
e
1
2
y
e
e
y0Pe t 1 dt e2 dt 2L dt L dt0
0
Dy t ЧН
E
t
E
t
m
0 2 y e 4 2 4 2
0 y
y
2
2
2 L 2
m
i
2
L
0
2 0 2e 0
eE
2
2 L
0
L
L
0
1,2
2
Li
2 L 0y0 0 0 y0 2
y
2
2
p m
Диэлектрическая проницаемость0
e
ne
e
общее
1 решение
p уравнения
-eE
однородного
2
2
1 0 i 2 L
0 me
0
t
t
к
yOO t С1e t e
C2e t e y0 стремится
2
2 0 при больших t и при рассмотрении
me 0 i 2 Lполей нас не интересует.
монохроматических
L
2
L
2
0
L
2
L
2
0
49.
Классическая теория Лоренца дисперсии оптическихсвойств диэлектриков
Зная комплексную диэлектрическую проницаемость, можно рассчитать вещественную
и мнимую части комплексного показателя преломления:
2
n
2
2
2
k p
2
2
Мнимая часть комплексного показателя
преломления отлична от 0 в области
шириной ~ 2γL – область (линия)
поглощения.
Вне линии поглощения вещественная
часть показателя преломления возрастает
с ростом частоты – область нормальной
дисперсии; внутри линии поглощения
ситуация обратная – область аномальной
дисперсии.
Коэффициент отражения:
R
n 1 k p
2
2
n 1 k
2
2
p
50.
Оптические свойства реальных диэлектриковРеальные диэлектрики имеют множество линий поглощения и их свойства могут быть
описаны суммой вкладов, полученных в теории Лоренца:
fj
nee 2
1
0 me j 02 j 2 i 2 Lj
fj – силы осцилляторов, при этом
f 1.
j
j
В рамках классической теории параметры fj, ω0j, γLj являются феноменологическими и
подбираются из условия наилучшего согласия с экспериментом.
Строгий расчет этих параметров становится возможным только в рамках квантовой
теории (сама формула для диэлектрической проницаемости при этом сохраняет свой
вид):
nej f jk
e2
1
0 me j k 2jk 2 i 2 Ljk
Но теперь резонансные частоты, определяются разностью энергий между j-м и k-м
уровнями:
E Ek
jk j
Ej,k – энергетические уровни атома (молекулы и т.п.)
nej - населенности уровней
f jk f kj
Возможна ситуация, когда nej > nek (Ej > Ek). В этом случае kp для
соответствующей частоты будет отрицательным, тогда излучение будет
усиливаться средой.
51.
Оптические свойства реальных металловВ реальных металлах будут иметься вклад как от свободных электронов (теория Друде)
так и от связанных электронов (теория Лоренца).
nej f j
e2
e 2 ne
1
1
0 me j 02 j 2 i 2 Lj 0 me 2 i D
вклад от связанных
электронов
вклад от свободных
электронов
Влиянием связанных электронов объясняется цвет металлов (медь, золото).
Рассмотрим ситуацию на примере меди.
Переходы из d-зоны в s-зону возможны при энергии кванта свыше 2 эВ.
52.
Экспериментальные методы определенияоптических констант металла
Способы определения n(ω) и kp(ω) :
1. Спектр отражения + соотношения Крамерса-Кронига
Формулы Крамерса-Кронига – фундаментальные соотношения, связывающие
(посредством некоторых интегральных соотношений) вещественную и мнимую части
комплексной диэлектрической проницаемости.
2. Измерения отражения при нормальном падении на поглощающий материал в двух
различных средах с известными показателями преломления.
n1,2 – заранее известные показатели
2
2
n n1 k p 2
n n2 k p 2 преломления
двух различных материалов
R1
R2
2
2
2
2
n n1 k p
n n2 k p Метод дает хорошие результаты если kp < 1.
3. Наиболее употребительные методы основаны на анализе поляризации отраженного
излучения, падающего под некоторым углом.
Если на металл под некоторым углом падает линейно поляризованная (под
некоторым углом к плоскости падения) волна, то отраженное излучения будет
вообще говоря эллиптически поляризованным. Измерив элементы эллиптической
поляризации можно вычислить оптические константы металлов.
52
В отличии от слабо поглощающих материалов данные по спектральным зависимостям
n и kp для металлов можно извлечь только из спектров отражения.
Для нормального падения:
2
2
- очевидно, что для определения 2-х функций n(ω) и
n
1
k p
R
kp(ω) не достаточно знать спектр отражения при
2
2
n 1 k p нормальном падении.
53.
Температурные зависимости оптическихсвойств металла
Сопротивление металлов увеличивается с ростом температуры. Это увеличение
связано с увеличением частот столкновений электронов с решеткой.
nee 2 1
Из эксперимента известно, что статическая проводимость 0
me T
T
- частота столкновений пропорциональна
справедливо при температурах выше дебаевской)
температуре
(это
Для
: p :
Для металла,
металла, свойства
свойства которого
которого описывается
описывается теорией
теорией Друде
Друде при
при
2 2
A
соответственно,
соответственно,
поглощательная
A ~ T . способность пропорциональна температуре.
p p
записать, что A T A0 T T0 .
Тогда,c можно
p 2
Параметр
χ ~ 10-5 – 10-4 K-1 может быть определен по температурным зависимостям
проводимости.
Для металлов, оптические свойства которых определяются связанными электронами
При
нагреве на зависимости
1000 К температурная
поглощательной
температурные
оптическихдобавка
свойствк выражены
слабее.способности может
составлять несколько процентов, что может быть существенно, ввиду её низкого
первоначального значения.
c
- глубина скин-слоя не зависит от частоты столкновений и соответственно,
2 p от температуры.
54.
Оптические свойства полупроводников55.
Особенности поглощения излучения вполупроводниках
По величине проводимости полупроводники занимают промежуточное положение
между диэлектриками и металлами.
В собственных полупроводниках концентрация свободных носителей на много
порядков ниже чем в металлах, соответственно, в этом случае основные механизмы
поглощения обусловлены связанными электронами.
При поглощении связанный электрон из
валентной
зоны
переводится
в
зону
проводимости – такой тип поглощения
называется собственным или межзонным.
Необходимо выполнение условия:
Eg
(Eg – ширина запрещенной зона полупроводника)
Данный механизм поглощения является
преобладающим в указанной спектральной
области.
Для сильнолегированных полупроводников вне
области собственного поглощения, либо для
полупроводников в условиях интенсивного
фотовозбуждения существенную роль может
начать
играть
поглощение
свободными
носителями
(внутризонное поглощение),
которое в общем случае осуществляется электронами и дырками.
56.
Виды межзонного поглощенияС квантовомеханической точки зрения на процесс поглощения кванта излучения
должны совместно выполняться законы сохранения энергии и импульса (точнее
квазиимпульса), при этом можно считать, что импульс фотона много меньше импульса
электрона.
В зависимости от типа зонной структуры полупроводника в процессах межзонного
поглощения имеется ряд особенностей.
Различают
т.н. разрешенные полупроводниках
и запрещенные
В
прямозонных
прямые
переходы:
квазиимпульс
электрона практически не
1
такие
переходы переходов
называются
изменяется
~ Eg –2 - для
разрешенных
прямыми. 3
~ Eg 2 - для запрещенных переходов
Для
непрямых переходов:
В непрямозонных
полупроводниках
2
поглощение
происходит
при участии
~ Eg
3ей
частицы
(фонона),
ħΩ – энергия фонона
обеспечивающей
выполнение закона
сохранения квазиимпульса.
57.
Вклады межзонного и внутризонного поглощенияПредставим комплексную диэлектрическую проницаемость полупроводника в виде:
i 1 L D i L D
Индексами L, D обозначены вклады Друде (свободных носителей) и Лоренца
(связанных электронов).
mopt – приведенная оптическая масса
2
p2
e
n
e
носителей (вводится для учета того, что
D
~
n
e
p
2
2
0 mopt вклад
в
диэлектрическую
проницаемость
дают
оба
типа
ne
–
концентрация 1
1
1
носителей).
свободных носителей
m
m m
opt
e
h
Для полупроводника в отсутствии сверхсильного фотовозбуждения
~ 10 .
2
1
1
1
2
2
2
2
2
2
2
2
kp
Коэффициент поглощения
22
kkpp
cc
L D
vc e
c c c
Коэффициент поглощения полупроводника складывается из коэффициента
межзонного поглощения (αvc) и коэффициента поглощения свободными носителями
(αe), которые определяются мнимыми частями вкладов в диэлектрическую
проницаемость от связанных (валентных электронов) и свободных электронов .
58.
Вклады межзонного и внутризонного поглощенияИтак, в условиях
D
e
c
p2
D
2 2
vc e
p2p2
e2
ne
ee
e ne
2
22
c 0 mopt
cc
e
c 0
e2
mopt 2
- сечение поглощения на
свободных носителях
2
однако это не всегда так, более строгая квантовая
По теории Друде e
теория внутризонного поглощения дает немного другой результат αe ~ ω-g (1.5<g<2.5).
Вклад Друде в вещественную часть диэлектрической проницаемости отрицательный и
растет по абсолютной величине при увеличении концентрации свободных носителей:
D
p2
2
2
Несложно увидеть, что при ne n
*
e
0 mopt
e2
n 02 L 21 22 2
вещественная часть диэлектрической проницаемости обратится в 0 (n0 – показатель
преломления невозбужденного полупроводника).
В условиях ne > ne* вклад свободных электронов становится определяющим и
полупроводник по оптическим свойствам становится близок металлу (происходит
металлизация полупроводника).
59.
Влияние концентрации свободных носителей наоптические свойства полупроводника
При
малых
уровнях
фотовозбуждения
коэффициент
поглощения
полупроводника
определяется межзонным поглощением.
Далее по мере роста ne становится существенным
поглощение свободными носителями, при этом
добавка линейна по ne.
При переходе через ne* ~ 1021 см-3 полупроводник
металлизируется и его оптические свойства
становятся близки к оптическим свойствам
металлов.
Коэффициент отражения полупроводника при
малых уровнях фотовозбуждения слабо зависит
от концентрации фотовозбужденных носителей.
При приближении ne к ne* наблюдается снижение
R c последующим переходом к металлическому
отражению при ne > ne*.
Достичь концентраций ne ~ ne* в видимом или
ближнем ИК диапазоне спектра без разрушения
поверхности полупроводника возможно только
при воздействии фемтосекундными лазерными
импульсами.
60.
Температурные зависимости оптических свойствполупроводника
Ширина запрещенной зоны полупроводников уменьшается с повышением температуры.
Для большинства полупроводников справедливо феноменологическое соотношение
Варшни:
1T 2
α1,2
–
некоторые
константы,
определяемые
по
Eg T E g 0
2 T экспериментальным данным.
Соответственно, при повышении температуры изменяется граница области
межзонного поглощения и происходит увеличение
коэффициента межзонного
поглощения (как в случае прямых, так и в случае непрямых переходов), т.к:
vc , T Cd Eg T
1
2
- для (разрешенных) прямых переходов
vc , T ~ Cind T Eg T
2
- для непрямых переходов
Сd,ind – некоторые коэффициенты.
Для непрямых переходов в силу того, что поглощение происходит при участии
фононов, коэффициент Сind будет определяться концентрацией фононов, которая также
зависит от температуры. При температурах выше дебаевской можно считать её
пропорциональной T, соответственно, Сind ~ T.
Поглощение на свободных носителях определяется частотой столкновения носителей
γ. При рассеянии на фононах по аналогии с металлами γ ~ T, соответственно, αе ~ T.
61.
Насыщение межзонного поглощенияВ некоторых ситуациях может наблюдаться
уменьшение
коэффициента
межзонного
поглощения полупроводника при интенсивном
лазерном облучении. Эффект, благодаря
которому,
это
происходит,
называется
насыщением межзонного поглощения (или
динамическим эффектом Бурштейна-Мосса).
Его природа аналогична известному эффекту
насыщения поглощения в двухуровневой
системе: под воздействием интенсивного
светового поля происходит выравнивание
населенностей верхнего и нижнего уровня, что
приводит к просветлению среды.
Если энергия кванта ħω лишь незначительно превышает ширину запрещенной зоны и
интенсивность излучения достаточно велика, то состояния вблизи дна запрещенной
зоны будут быстро заполняться электронами, в то время как состояния у потолка
валентной зоны напротив будут обедняться. По мере выравнивания населенностей
процессы вынужденного излучения будут компенсировать поглощение квантов
излучения и коэффициент межзонного поглощения уменьшится.
Коэффициент межзонного поглощения можно приближенно принять равным:
ne
nmax – концентрация, при которой межзонные переходы
VC (ne ) VC (0) 1
полностью прекращаются
nmax
62.
Рекомбинация фотовозбужденных носителейСгенерированный в зоне проводимости при межзонном поглощении электрон может
перейти обратно в валентную зону – этот процесс называется рекомбинацией.
Из закона сохранения энергии следует, что при рекомбинации должна выделяться
энергия примерно равная Eg.
В зависимости от способа выделения энергии процессы рекомбинации разделяют на
различные категории.
Процессы рекомбинации
Излучательная рекомбинация
Безызлучательная рекомбинация
Испускается фотон с энергией ~ Eg
Скорость
изменения
концентрации носителей:
Ударная (Оже) рекомбинация
ne
2
2 ne
Энергия ~ Eg передается третьему
t
носителю (электрону или дырке)
Скорость
изменения
концентрации носителей:
ne
3ne3
t
Энергия
~
Eg
передается решетке
Скорость изменения
концентрации носителей:
ne
1ne
t
63.
Переход поглощенной энергии в тепловую вполупроводниках
С точки зрения классической электродинамики сплошных сред в металлах
индуцированные полем электромагнитной волны токи проводимости нагревают
материал. Соответственно, поглощенная энергия сразу же переводится в тепловую
(особого рассмотрения здесь требует случай воздействия ультракороткими лазерными
импульсами).
В полупроводниках (поскольку поглощение свободными носителями может не
являться преобладающим механизмом поглощения) ситуация иная.
При межзонном поглощении электрон, имеющий избыток энергии ~ Eg ,
передает её решетке за счет столкновений (электрон-фононного взаимодействия) за
время ~ 10-13 ~ 10-12 c (т.е. практически мгновенно для импульсов с существенно
большей длительностью).
Однако, оставшаяся часть энергии ~ Eg передается решетке за счет рекомбинации
(либо вообще переизлучается, если преобладает излучательная рекомбинация) за
время равное характерному времени рекомбинации, которое может лежать в
диапазоне 10-9 – 10-3 с.
Указанное обстоятельство может вызывать аномалии (задержку) в тепловом действии
лазерного излучения на полупроводник.
Также как и в металлах для энергии поглощенной свободными носителями допустимо
считать, что она переводится тепло практически мгновенно.
64.
Кинетика фотовозбуждения полупроводникалазерным излучением
Изменение концентрации носителей при лазерном фотовозбуждении полупроводника
происходит по следующим причинам:
1. Генерация электрон-дырочных пар
при межзонном поглощении.
2. Рекомбинация носителей
3. Процессы переноса (диффузия) носителей
Определим скорость генерации носителей:
1 q
q x
(при α = const q q0 e x )
(q – плотность мощности
(интенсивность) излучения)
vc n ...
(lD – длина диффузии)
αvc – коэффициент межзонного поглощения
αn – коэффициент поглощения на свободных носителях
1фотонов,
q
qпоглощенных
( x) q( x dx
)единицу времени в
q(1x) qq ( x qdx) Sdt
Определим
число
в
- число фотонов поглощенных в слое толщиной
Sdt dx за время dt
смысл величины:
x
dx
единице объема
x
Sdt
q((xx))только
q ( x фотоны,
dx) Sdt
qТ.к.
1 падающих
- число
фотонов
- при
число
нафотонов,
площадку
поглощенных
величинойприводят
Sвза
единицу
время
dt
времени
в точкевx.
поглощенные
межзонном
поглощении
к генерации
носителей,
то:
dxSdt единице объема
q ( xn dx) Sdt
фотонов падающих на площадку величиной S за время dt в
vc q --число
e
скорость
генерации носителей за счет поглощения излучения
точке
x+dx.
t
65.
Кинетика фотовозбуждения полупроводникалазерным излучением
Скорость изменения концентрации носителей за счет рекомбинации:
ne
2
3
1ne 2 ne 3ne
t
Определим скорость изменения концентрации носителей за счет диффузионных
процессов.
излучательная
Оже-рекомбинация
рекомбинация
Пусть
jn – вектор
потока носителей, равный по величине числу носителей,
пересекающих единичную площадку за единицу времени.
Для диффузионных процессов справедлив закон Фика:
jn Dgrad ne
- поток носителей пропорционален градиенту их концентрации с
обратным знаком (D - коэффициент диффузии)
Т.к. при диффузионных процессах полное число носителей сохраняется можем
написать закон сохранения в локальной форме:
ne
ne
ne
div
j
или
с
учетом
закона
Фика
для
одномерного
случая
D
n
t D
t D x x
При D = const
2 ne
ne
D 2
x
t D
66.
Кинетика фотовозбуждения полупроводникалазерным излучением
Полная скорость изменения концентрации носителей в некоторой точке будет равно
сумме вкладов от процессов генерации, рекомбинации и диффузии:
ne ne ne ne
t t t t D
ne
2ne vc q
D 2
1ne 2 ne2 3ne3
Соответственно
t
x
Начальные и граничные условия:
ne
0
x x 0
- отсутствие потока электронов на
границе
ne t 0 0
q
q q x 0 Aq0
Уравнение для плотности мощности:
x
При VC const (ne ) имеем q Aq0 exp vc x
Решение уравнения для концентрации устроено
таким образом, спустя некоторое время tst
устанавливается
стационарное
распределение
концентрации N(x).
2 N
Aq
D 2 vc 0 e vc x 1N 2 N 2 3 N 3
x
67.
Фотоиндуцированный эффект ДембераПоскольку
коэффициенты
диффузии электронов и дырок
вообще говоря различны (как
правило,
Dn
>
Dp),
то
разноскоростное
диффузионное
«растекание» носителей из более
освещенной части приводит к
появлению электрического поля.
Продольный эффект Дембера
Фотоиндуцированный эффект Дембера используется для генерации терагерцового
излучения при облучении полупроводников ультракороткими импульсами.
68.
Экспериментальные методы исследования процессовфотовозбуждения полупроводников лазерными
импульсами
Схема эксперимента
для исследования
кинетикивызывает
фотовозбуждения
полупроводника
Интенсивное
фотовозбуждение
полупроводника
изменение
его оптических
(германия)
наносекундными
лазерными импульсами.
свойств и, в частности,
коэффициента
отражения.
фотовозбуждения
Для фотовозбуждения следует использовать лазеры с Для
длиной волны
попадающий в
область межзонного поглощения (т.е. лазеры ближнего полупроводника
ИК или видимого используется
диапазона).
лазер на стекле с неодимом,
генерирующий импульсы с
Однако достичь уровней фотовозбуждения достаточных для изменения отражения
длительностью 80 нс на
(металлизации полупроводника) на этих длинах волн без разрушения поверхности
основной длине волны (1.06
оказывается возможным только для фемтосекундных воздействий.
мкм).
Для исследования динамики
В наносекундном диапазоне цлесообразно использовать
2 лазера: лазер ближнего
ИК
коэффициента
отражения
или видимого диапазона для собственно фотовозбуждения
и лазерв среднего
ИК
полупроводника
среднем ИК
диапазона для исследования динамики отражения поскольку
спектральной
диапазоне в этой используется
области коэффициент отражения более чувствителенимпульсный
к изменениям
CO2концентрации
-лазер (10.6
носителей в области концентраций ~ 1018 – 1020 cм-3 (см.
рис. на
слайде 53)
мкм),
синхронизированный
с
лазером на стекле с неодимом.
Рассмотрим схему и результаты одного из таких экспериментов.
Излучение, отраженное от фотовозбужденного полупроводника, регистрируется
Ge:Au детектором, соединенным с осциллографом. Также дополнительно
проводились измерения динамики коэффициента отражения излучения He-Ne лазера.
69.
Экспериментальные методы исследования процессовфотовозбуждения полупроводников лазерными
импульсами
Динамика изменения коэффициента отражения германия на длине волны 10,6 мкм при
возбуждении наносекундными импульсами различной интенсивности (пунктиром
показана форма возбуждающего импульса)
В случае невысоких интенсивностей,
наблюдается
спад
коэффициента
отражения с последующим возвратом к
первоначальному
значению
после
окончания импульса.
При
повышении
интенсивности
возбуждающего
импульса
первоначальный
спад
сменяется
быстрым
ростом
коэффициента
отражения с последующим спадом и
возвращением
к
первоначальному
значению после окончания импульса.
Рост
коэффициента
отражения
Спад коэффициента отражения на заднем соответствует концентрации носителей,
фронте импульса и его возврат к при которой плазменная частота
первоначальному значению связаны с превышает частоту излучения (ne > ne* полупроводник металлизируется).
рекомбинацией носителей.
Достигаемые значения ne ~ 1019 – 1020 cм-3.
70.
Элементы нелинейной оптики71.
Предмет нелинейной оптикиНелинейная оптика – раздел оптики, изучающий распространений интенсивных
световых волн и их взаимодействие с веществом, при котором характер протекания
оптических явлений зависит от интенсивности излучения.
В нелинейной оптике оптические характеристики среды зависят от интенсивности
излучения.
С микроскопической точки зрения это связано с тем, что напряженность поля световой
волны в нелинейной оптике становится сравнима с напряженностью внутриатомного
поля и смещение электрона (электронного облака) под действием светового поля
перестает линейно зависеть от напряжённости поля падающей волны.
Напряженность внутриатомного поля можно оценена из соотношения eEат a0 I
I ~ 10 эВ – потенциал ионизации, а0 ~ 10-10 – размер атома
Eат ~ 109 В/см
Интенсивность световой волны при которой напряженность светового поля имеет
сравнимые значения:
1 0 2
Вт
Эффекты нелинейной оптики проявляются по мере
q~
Eат ~ 1015 2
приближения интенсивности волны к этому значению.
2 0
см
Такие интенсивности легко достижимы на современных лазерных системах
генерации ультракоротких импульсов.
Многие нелинейные эффектны начинают проявляться уже при значительно
меньших интенсивностях.
72.
Основные нелинейно-оптические явления- нелинейная рефракция в оптически прозрачной среде, т.е. зависимость
показателя преломления от интенсивности световой волны.
- нелинейный характер рассеяния света в среде при больших интенсивностях
светового поля
- многофотонное поглощение интенсивного оптического излучения в веществе
- генерация высших гармоник при переизлучении световой волны
- тепловые самовоздейсвтия
В контексте задач лазерной обработки материалов наиболее важным нелинейным
эффектом является многофотонное поглощение, поскольку оно обуславливает
возможность обработки изначально прозрачных материалов.
Важную роль также могут играть процессы нелинейной рефракции, поскольку они
определяют характер фокусировки излучения.
73.
Нелинейное волновое уравнениеИсходный уравнения Максвелла для сплошной среды сохраняют свой вид:
B
t
D 0E P
D
j
t
B
(рассматриваем
оптические
проводимости)
H
M (в оптике
почтисреды
всегдабез
можно
считать, что H B )
0
0
rotE
rotH
divD 0 e
2
rot rotE 00 rot
rotH
H 0 2 0 E P
tt
t
divB 0
2 E
2 P
rot rotE 0 0 2 0 2
t
t
Однако теперь связь между поляризацией среды в отличие от линейной оптики носит
более сложный характер.
Обычно поляризацию среды представляют в виде суммы: P PЛ PНЛ
PЛ – линейный вклад в поляризацию (он пропорционален напряженности поля Е)
PНЛ – нелинейный вклад в поляризацию, именно наличие этого слагаемого отвечает
за протекание различного радо нелинейно оптических явлений
2 E
2 PЛ
2 PНЛ
rot rotE 0 0 2 0
0
t
t 2
t 2
- волновое уравнение для нелинейной среды
74.
Нелинейные восприимчивостиСвязь между поляризацией и напряженностью поля в линейной оптике:
PЛ 0 (1) E
χ(1) - линейная восприимчивость среды
- такая связь справедлива если параметр нелинейности E/Eат << 1.
Если по прежнему E/Eат < 1, но уже намного больше чем в области линейной
оптики, то зависимость поляризации может быть представлена в виде ряда по
степеням E:
P 0 (1) E (2) EE (3) E 2 E ... ( m ) E m 1 E ...
Коэффициенты χ(m) (m > 1) при членах разложения называются нелинейными
восприимчивостями m-го прядка.
В типичных оптических средах
м
B
(1) 1 (2) 10 13 10 11 (3) 10 23 10 21
м2
.
B2
В случае анизотропной среды:
3
3
3
3
3
3 (1)
нелинейные восприимчивости
(2)
(3)
Pi 0 ij E j ijk E j Ek ijkl E j Ek El ... порядка m – тензоры ранга
j 1 k 1
j 1 k 1 l 1
j 1
(m+1)
В общем случае компоненты тензоров нелинейной восприимчивости следует
рассматривать как комплексные величины:
( m ) Re ( m ) i Im ( m )
- мнимые части ответственны за процессы нелинейного
поглощения
75.
Генерация высших гармоникНелинейные восприимчивости приводят к появлению качественно нового эффекта,
радикально отличающегося от эффектов линейной оптики – генерации высших
гармоник.
Пусть падающее на среду поле представляет собой монохроматическую волну:
E t E cos t
При этом среда имеет отличную от нуля квадратичную восприимчивость:
P P (1) P (2) 0 (1) E 0 (2) E 2
Тогда:
P (1) 0 (1) E cos t
cos 2 2cos 2 1
1
1
22
(2) 22
(2) 2
P (2) 00 (2)
EE cos
t
cos t 0 E 0 (2) E 2 cos 2 t
2
2
появляется
постоянная
составляющая
поляризации – оптическое выпрямление
(используется для генерации импульсов
терагерцового излучения при облучении
нелинейных
сред
фемтосекундными
лазерными импульсами)
Аналогично для кубической поправки:
3
1
P (3) 0 (3) E 3 cos t 0 (3) E 3 cos 3 t
4
4
поляризация среды осциллирующая
с удвоенной частотой становится
источником
вторичных
волн
удвоенной частоты
76.
Модель нелинейной средыМоделью оптически нелинейной
(ангармонических) осцилляторов.
среды
служит
система
нелинейных
Зависимость возвращающей силы нелинейного осциллятора от смещения
оптического электрона из положения равновесия может быть представлена в виде
ряда:
me – масса электрона
F y ky me a2 y 2 me a3 y 3 ...
a2, a3 – коэффициенты разложения
Отметим, что, например, для изотропных сред (а также сред с центром инверсии) в
разложении должны отсутствовать слагаемые с четными степенями смещения.
Уравнение движения электрона будет иметь вид:
eE y t
d2y
dy
2
2
3
2 L
0 y a2 y a3 y ...
2
dt
dt
me
02
k - собственная частота
me колебаний линейного
осциллятора
Решение данного уравнения движения позволяет найти поляризацию среды и
вычислить нелинейные поправки:
Py t ene y t
(ne – концентрация осцилляторов)
Точное аналитическое решение указанного уравнения в общем случае затруднено.
Однако, возможно получить решение приближенными методами.
77.
Метод возмущений. Осциллятор с квадратичнойнелинейностью.
Основная идея метода возмущений состоит в том, что нелинейный эффект
рассматривают как малую поправку к движению системы в линейном режиме.
Т.е. y t yL (t ) y NL t
y NL yL
yL – решение уравнения движения без
нелинейных поправок, yNL – малая поправка
учета
Рассмотрим осциллятор с квадратичной нелинейностью и исследуем его отклик на
воздействие в виде монохроматического поля.
d2y
dy
eE Мы полагаем, что нелинейные поправки малы
2
2
2 L
0 y a2 y
2
2
2
2
y
a
y
или
0 a2 y
dt
dt
me
0
2
d 2 yL
dyL
d 2 y NL
dy NL
eE
2
2
2
2
2
y
2
y
a
y
2
y
y
y
L
0 NL
2 L
L NL
NL
2
yLD dty NL 0 L dt 2
dt y
dt
me
2
d 2 yL
dyL
eE
2
2
2
но
0 y NL 2a2 y L y NL
2
y
y
y
L
0
L
L
NL
dt 2
dt
me
y NL 02 2a2 yL 02 y NL
d 2 y NL
dy NL
2
2
Тогда
2
y
a
y
L
0 NL
2 L
dt 2
dt
Уравнение для нелинейной поправки представляет собой уравнение колебаний
линейного(!) осциллятора в котором роль вынуждающий силы играет член –a2yL2.
78.
Метод возмущений. Осциллятор с квадратичнойнелинейностью.
d 2 y NL
dy NL
2
2
Итак, необходимо решить уравнение
2
y
a
y
L
0 NL
2 L
dt 2
dt
i t
e
- это решение было получено ранее при
E
e
0
где y Re
рассмотрении модели линейной среды
L
2
2
m
i
2
0
L
e
e
E0
i y
yL
y
y
e
yL yL e i t
L
L
me 2 02 i 2 L
2
2
22
2 y
22
2
2
y
2
ii tt yy
L
22
L y
tt
ii
d y NL yy 2cos
dy NL
2
i 2t
t 2 y L
Re
y
e
Re
y
e
t
cos
2
L
Re
y
e
cos
t
LL
y a
LL
2L L L
0 yyNL
e
y 2
Окончательно
получаем
2
2
2
dt
dt
2
2
При подстановке полученного выражения в правую часть уравнения
удобно опять
Ясно, что решение
следует
искатьт.е.
в виде
вернуться
к комплексной
форме,
2
2
2
y NL y NL e i 2 t CNL
2
2
yL подстановки решения
yL в исходное
yL i 2 уравнение
y
y
После
получаем
i
2
t
L
y
L i 2 t
2
cos 2 t 2 y
e
e
e
2
2
2
2 22
y L i 2 t y L
2
i 2 t
i 2 t
2
i 2 t
2
4 y NL e
i 4 L y NL e
0 y NL e
0 C NL a2 e
yL
22
2
Откуда
a2 yL
a2 yL2
y NL
C
NL
2 02
2 02 4 2 i 4 L
2
2
79.
Частотные зависимости квадратичнойвосприимчивости.
Полученное решение позволяет определить поляризацию среды:
e
E0e i t
yL
me 2 02 i 2 L
P ene Re yL y NL
Получим
формулы
для
квадратичных
восприимчивостей
для случая когда затуханием можно
пренебречь (γL = 0).
a2 yL
a2 yL2
i 2 t
y NL
e
2
2
2 02
2 0 4 i 4 L
2
e 2 nee
yL
E0 cos - линейная
t
Re
восприимчивость
2
22
mm
0
0
e e0
2
2
2
2
3
2 e
E
cos
2
t
2a
a
e
n
a
e
E
(2)
0
2
e
2
2
0
- нелинейные восприимчивости,
ee
(1)
y2NL ,
Re
nn,e e
2E cos t
2
2 E
P
E
cos
t
cos
t
2
2
2
2
2
2
2
2 2
L
0 2
0 соответствующие
02 0 2 4
2
m
2m
22 2me22
колебаниям
e 0 0
00 e0 0 4 0
mee
0 0
поляризации на удвоенной и нулевой
a2e3ne
(2)
частотах
0, ,
2
2
2
2 2
2me 0 0 0
(1)
Метод возмущений может быть также применен для исследования восприимчивостей
более высоких порядков.
80.
СамофокусировкаЯвление самофокусировки связано с кубической нелинейностью восприимчивости
(напомним, что в изотропных средах именно она является первой нелинейной
поправкой, отличной от нуля ).
(1)
Для такой среды: P 00 (1)
EE 00 (3)(3)EE3 3 0 (1) E0 cos t 0 (3) E03 cos3 t
(1)
(3)
3
(1)
(3)
3
3
3
1
0 (1) E0 cos t 0 (3) E03 cos t 0 (3) E03 cos 3 t
4
4
Нас интересует составляющая поляризации, колеблющаяся на основной частоте:
3
P 0 (1) E0 cos t 0 (3) E03 cos t
4
Показатель преломления определяется в соответствии с соотношениями:
D 0 E P 0 E
n
2
n2
3
4
0 E0 cos t 0 (1) E0 cos t 0 (3) E03 cos t
0 E0 cos t
3
1 (1) (3) E02
4
(3)
3 (3)
3 (3) 2
333 (3)
(3)
22
(3) 222
EE000 n00 1
E0
Соответственно nn 11 E
E00 n0
22
8 n0
444
8n00
(1)
(1)
(1)
этом,(1)если
нелинейность
носит характер
поправки, т.е.
nПри
- линейный
показатель
преломления.
0 1
1 (1)
nформулой
n0 n2 q 1 x 1
Т.к.
можно
E02 ~воспользоваться
q (q – интенсивность)
приближенной
то
x
2
n2 – рефракционный индекс
3 (3) 2
E0
4
81.
СамофокусировкаРассмотрим излучение, распространяющееся в кубично-нелинейной среде, имеющее
куполообразное (например, гауссово) распределение интенсивности в поперечном
сечении.
Ввиду неоднородности распределения интенсивности по
n r n0 n2 q r сечению пучка показатель преломления также становится
зависящим от поперечной координаты.
Если параметр n2 > 0 и интенсивность излучения
убывает по мере удаления от центра пучка, то
показатель преломления также будет убывать (а
фазовая скорость возрастать) по мере удаления от
центра пучка. Соответственно, волновые фронты
будут изгибаться как показано на рисунке и
излучение будет фокусироваться.
Если n2 < 0, то наоборот будет наблюдаться
дефокусировка излучения.
Изменение радиуса светового пучка в
линейной (1) и нелинейной (2,3) средах.
Режим 3 соответствует самофокусировке,
режим 2 соответствует условиям, когда
самофокусировка
компенсирует
дифракционную расходимость.
82.
Многофотонное поглощениеЯвление многофотонного (нелинейного поглощения) связано с мнимыми частями
нелинейных восприимчивостей соответствующих порядков.
Однако более наглядно использовать представление о фотонах.
Вероятность поглощения фотона атомом пропорциональна плотности потока фотонов
(или интенсивности излучения):
w1 ~ q
Однако если интенсивность велика возможно одновременное поглощение нескольких
(k) фотонов.
Вероятность этого процесса
однофотонных переходов:
равна
произведению
вероятностей
отдельных
kk
wkk wii w1k ~ q k Вероятность поглощения k фотонов пропорциональна k-й
ii 11
степени интенсивности.
При многофотонном поглощении должно выполняться условие: E2 E1 k
E1, E2 – энергетические уровня, соответствующие начальному и конечному
состоянию.
При облучении полупроводников и диэлектриков порядок многофотонного процесса
для заданной частоты определяется из неравенства:
k Eg
(Eg – ширина запрещенной зоны)
83.
Нелинейные эффекты в лазерной обработкематериалов
Наличие нелинейных эффектов открывает новые возможности в лазерной обработке
материалов.
А именно возможность нелинейного (многофотонного) поглощения открывает
возможность модификации изначально-прозрачных материалов внутри объема.
Для этого, как правило, используются импульсы со сверхкороткой длительностью
(пико- и фемтосекундные) поскольку для них характера высокая интенсивность и
нелинейно-оптические эффекты сильно выражены.
Фемтосекундное лазерной излучение фокусируется в
объем прозрачного материала. Т.к. вероятность
многофотонного поглощения растет пропорционально
qk то в фокальной области вероятность поглощения
оказывается намного выше.
Поглощение излучения приводит к генерации
свободных носителей (электрон-дырочной плазмы),
которые в свою очередь также начинают поглощать
излучение.
В результате поглощение энергии лазерного излучения в фокальной области приводит
к различного рода локальной модификации материала внутри объема.
При этом на характер распространения импульса при фокусировке оказывают влияние
явления самофокусировки и дефокусировки в генерируемой плазме.
84.
Экспериментальные методы исследованияраспространения ультракороткого импульса при
фокусировке в объем прозрачного материала
Экспериментальные методы исследования распространения фемтосекундного импульса
в объеме прозрачного материала основаны на методике опрос-накачка (pump-probe) в
сочетании с фемтосекундной интерферометрией.
Рассмотримиз пример
такого
эксперимента
Вышедший
усилителя
импульс
разделяетсяв
излучение
на длине
волны ~ импульс.
1200 нм,
накотором
импульс
накачки
и пробный
фокусировалось
в объем кремния.
Импульс
накачки фокусируется
в объем образца.
Кремний импульс
является через
прозрачным
длины
Пробный
линию для
задержки
волны 1200 нм,
можно
направляется
на поэтому
образец излучение
перпендикулярно
фокусировать
в объем образца.
импульсу
накачки.
После прохождения образца излучение пробного
импульса
попадает
в
интерферометр,
интерференционная картина регистрируется
ССD камерой.
Изменения показателя преломления наведенные
импульсом накачки приводят к смещению полос
интерференционной картины. Регистрируя
интерферограммы для различных задержек
пробного
импульса
можно
исследовать
распространение импульса накачки.
85.
Экспериментальные методы исследованияраспространения ультракороткого импульса при
фокусировке в объем прозрачного материала
Основные процессы влияющие на распространение
Снимки,
полученные
импульса накачки
при
вобработки
объеме
кремния:
интерферограмм для различных временных
задержек,
иллюстрирующие
картину
1. Кубическая нелинейность среды (эффект
Керра).
распространения
ультракороткого
Т.к. n2 > 0 этот эффект приводит к увеличению
показателя
преломления. импульса.
На
рисунках
увеличение
яркости
2. Двухфотонное поглощение.
увеличениюплазмы.
показателя
Двухфотонное поглощение приводит ксоответствует
генерации электрон-дырочно
преломления, а снижение соответствует
3. Генерация электрон-дырочной плазмыуменьшению.
Формирование электрон дырочной плазмы приводит к снижению показателя
преломления согласно модели Друде. Видно светлое облако (увеличение показателя
преломления
связанное
с
керровской
нелинейностью), распространяющееся со
скоростью света.
В результате двухфотоннго поглощения
формируется электрон-дырочная плазма,
снижающая показатель преломления, что
приводит к формированию темного «хвоста»
на рисунках.
86.
Экспериментальные методы исследованияраспространения ультракороткого импульса при
фокусировке в объем прозрачного материала
Временная
динамика
изменения
относительного изменения яркости
интерференционной картины в центре
перетяжки импульса накачки. На
вставке разделение вкладов эффекта
Керра и генерации электрон-дырочной
плазмы.
Концентрация электрон-дырочной
плазмы,
сгенерированной
в
кремнии для различных плотностей
энергии импульса накачки.
Зависимость в целом носит квадратичный
характер,
что
характерно
для
двухфотонного поглощения.
87.
Некоторые приложения объемной лазерноймодификации прозрачных материалов
1. Двухфотонная полимеризация (лазерная стереолитография, 3D печать)
Двухфотонное поглощения в фокальной
области
инициирует
реакцию
полимеризации,
что
приводит
к
локальному отверждению.
Необлученные
участки
впоследствии
удаляется растворителем.
Примеры изготовленных структур:
3D спиральный фотонный кристалл
a = 1.8 μm, L = 2.7 μm, c = 3 μm
88.
Некоторые приложения объемной лазерноймодификации прозрачных материалов
2. Создание 3D фотонных чипов
Запись волноводов в объеме стекла
а – схема записи
b – изображение записанного волновода (без установкой маски)
с – изображение записанного волновода (с установкой маски)
89.
Некоторые приложения объемной лазерноймодификации прозрачных материалов
3. Создание 3D микрофлюидных устройств
Общая схема записи каналов в фоточувствительном стекле Foturan.
Лазерное облучение с последующим термическим отжигом формируют в
облученной области фазу, обладающую высокой скоростью травления в плавиковой
кислоте.
4. 3D память
5. Микросварка стекол
…
Подробнее см. обзор K. Sugioka, Y. Cheng. Femtosecond laser three-dimensional microand nanofabrication//Applied Physics Reviews, 1, 041303 (2014).
90.
Оптические свойства неоднородных(композитных) сред
91.
Неоднородные оптические среды в задачахлазерного воздействия на материалы
Предыдущее рассмотрение оптических свойств материалов касалось
однородных сред, т.е. таких сред свойства которых постоянны в пространстве.
случая
Однако на практике зачастую возникает необходимость лазерной обработки
неоднородных, композитных (составных) сред.
Оптические свойства композитных сред могут существенно отличаться от свойств сред
из которых они составлены.
Кроме того исходно однородная среда может стать неоднородной в процессе лазерной
обработки (например, из-за образования окисной пленки на поверхности
обрабатываемого материала и т.п.).
Установление основных закономерностей зависимостей оптических свойств
композитных сред от их состава и структуры важно в контексте задач лазерной
обработки материалов важно для осуществления оптимального выбора режимов
обработки таких сред.
В рамках данного курса мы коротко рассмотрим основные подходы к расчету
оптических свойств 2-х классов композитных сред:
1. Слоистые среды
2. Среды содержащие нановключения других материалов (например, прозрачные
матрицы с наночастицами металлов).
92.
Отражение, пропускание и поглощение однородногослоя
Прежде чем перейти к общему методу расчета оптических свойств слоистых сред
рассмотрим отдельно случай однородного слоя некоторого материала толщиной h в
воздухе (вакууме), что позволит просто проиллюстрировать некоторые характерные
особенности задачи.
Слева от слоя распространяются падающая
(i) и отраженная (r) волны:
E i E0i exp i t x
c
E r E0r exp i t x
c
Справа
от
слоя
распространяется
прошедшая волна:
E t E0t exp i t x
c
Внутри слоя бегут затухающие волны,
распространяющиеся в противоположных
направлениях:
На границах должны выполняться условия непрерывности
тангенциальных компонент электрического поля:
E E0 exp i t nx
i
r
c
при х = 0: E0 E0 E0 E0
E r E0r exp i t nx
c
при х = h:
E0t exp i h E0 exp i nh E0 exp i nh
c
c
c
93.
Отражение, пропускание и поглощение однородногослоя
Аналогичные условия непрерывности должны также выполняться и для
тангенциальных компонент магнитного поля:
Вспомним, что nE0 cB0
B0i B0r B0 B0
(при этом знак «-» соответствует
t
B0 exp i h B0 exp i nh B0 exp i nh волне, бегущей против оси х)
c
c
c
Тогда
E0i E0r n E0 E0
Мы получили 4 уравнения,
содержащие
4
неизвестных
амплитуды.
Амплитудные
коэффициенты
отражения
и
пропускания можно получить из
решения этой системы уравнений.
1 t
E0 exp i h E0 exp i nh E0 exp i nh
n
c
c
c
E0i E0r E0 E0
E0t exp i h E0 exp i nh E0 exp i nh
c
c
c
i
rE0 Eи0 третьего уравнений
Из первого
следует,
что
2
E
E
1
n
E
0
0
0 1 n
Из
второго
и
четвертого
уравнений
следует,
что
rh
E0 rE0
2 E r E 1 n E 1 n
0
0
0
1 nnE
E
11
nn nh rE
Eexp
EE i EEnh
E
E exp i nh Errr exp
i
nE
exp
i
nh
0
0
0
c
E 1 n E
11 ncn E0 rE0 c
EE cE
E
коэффициент отражения слоя
h
2
2 - амплитудный
2
2 2
E1
rexp
exp
i
nh
E
exp
i
nh
E
r
exp
i
nh E0
E0r 1 1 0 n r n
nh
E
exp
i
nh
1
n
0
- амплитудный
0
отражения
границы
слоя
cc c 0 коэффициент
c
c
1 n
rr
2 2 0 0
0 rrE1
r exp
E
соответственно
i i nh0hnh
0 exp
h h 0i i
c
c
00
rh
00
00
00
0
00
94.
Отражение, пропускание и поглощение однородногослоя
Итак,
для амплитудных
коэффициентов
отражения
и пропускания
слоя справедливы
Для того,
чтобы получить
выражение для
амплитудного
коэффициента
пропускания
формулы:
воспользуемся ранее полученными следствиями из рассматриваемой системы
уравнений:
1 n
2
exp
i
h
r
r 1 exp i
nh
4n
ci 2
nh E
i
1 n
c
E
r
exp
2rE 0 E0 1 n E 0 1 nth
2
0
0
h
c i nh
n 1 exp i nh r 2 exp
2
2
n n ik p
1 r exp i
nh
c
c
c
E0t E0 exp i nh E0 exp i nh exp i h
и четвертым уравнением
c нас энергетическим
c коэффициентам
c
Для того, чтобы перейти к интересующим
(T ) необходимо
отражения
(R
)
и
пропускания
взять iквадрат
h
h
E
exp
i
nh
E
r
exp
i nh
2exp
h exp модулей
i nh 1 от
r
t
0
00
E
c
c
c
c
коэффициентов.
thhсоответствующих
0i 2exp i hамплитудных
2
E0
2
c E 12 n E r exp
1 r 2 exp i
nh
i nh 12 n 1 n
r 1 exp0 i
nh 0 r * 1 exp
n *h
c i
c
c
c
*
1 n
2n
1R h r r1h r h 2
Таким
образом,
имеем
exp
2
i h
2
2
*
*
4
n
1 n1 1r exp
n i
c
nh 1 r exp
i n h
t
c
h c n 1 2 2
exp
i
nh
r
exp
i nh
2
h
h * *2
2
2
2
2 2 2
2
*
*
c
2 2cos
i r ) nh
2 2 2ck p
Im(
2i enhnh
2
nh h
e
2exp
*r
* n
1
r
exp
1
r
exp
i
1
R
exp
1
r
i
1
exp
i
2 2 h
R
1 r Rexp i c cnh 1
r exp i
n chc 1 2 R
exp
arctg
h cos
rexp
c 2 arctg
r
2
r R
h
h
n k p 1
Re r
e h c R 2e
2 R cos c 2 r
2 k p
2 * 2
2 **
2 ***
2 2 22 2 2 ***
r
1 exp
i
nh
r
1
exp
i
n
h
R
1
exp
i
nh
exp
i
n
h
exp
h n n c
2 nk p11n h
pip
2 n r k p R
ik
nexp
ik
h n n i
n 1 cik
1 cexp
2ik p i
1 ik
n pp R
pp
c
c
c
r 2
22 c 2
h
c
2
n
2
2
2
n 1 cik
1 c kkpp
h
n exp
n 1 k p
2 pp
*
R
R 1
2exp
h
cos
2 h
2
r
r
exp
i
rr
r
c
1 R exp h cos r2 R exp h cos 2 R exp 2 h
r
r
95.
Отражение, пропускание и поглощение однородногослоя
*
Теперь вычислим Th thth
exp i h
exp i h exp i nh
4n
4n
c
c
c
th
2
2
n 1 exp i nh r 2 exp i nh n 1 1 r 2 exp i 2 nh
c
c
c
2
exp i nh exp h
c
4n 4k pp
4k p2p2
4k p2
n 1 k p2p2
4n
22
2
1 R 4
1 R 4 R
2
22
22
22
2
2
22
22
22
22
22
n
1
k
n 1 2
n 1 k p2 n 1 k p2
pp
n 1 k
n 1 k
22
22
22
pp
Оказывается, что
22
pp
4k p2
n 1 k n 1 k
2
2
2
p
2
p
2k p
n 2 k 2 1
p
sin 2 r
r arctg
1
x2
sin arctg
arctg xx 11 cos
cos arctg
arctg xx 1 2
Действительно, т.к. sin
tg arctg x 1 x 2 1
4k p2
4k p2
1
2
Осталось показать, что
sin r
222
r
n2 k p2 1
2
22
4k p2
n k 1
2
2
p
4k p2 n 2 k p2 1
2 1
n 1 k p2 n 1 k p2 4k p2 n2 k p2 1
2
2
2
4k p2 n 2 k p2 1 4k p2 n 4 n 2 k p2 n 2 n 2 k p2 k p4 k p2 n 2
k p2p2 1 n 2 1 k p4 k p2 2n 2 2
2
2
n 1 k n 1 k n 1 n 1 k n 1 k n 1 k n 1 k k 2n 2
22
22
pp
22
22
pp
22
22
22
pp
22
22
pp
22
44
pp
2
2
4
p
2
p
2
2
2
h
2
1
R
4
R
sin
e
1
R
4 R sin 2 r
r
Таким образом T
h
1 R 2e 2 h 2 R cos 2 r e h e h R 2e h 2 R cos 2 r
2
2
96.
Отражение, пропускание и поглощение однородногослоя
Итак, мы получили, что
2 n
h
c
2 k p
c
e h e h 2cos
Rh R h
e R 2e h 2 R cos 2 r
1 R 4 R sin 2 r
Th h
e R 2e h 2 R cos 2 r
2
- коэффициент
отражения слоя
2k p
коэффициент
r arctg 2
пропускания слоя
n k 2 1
p
2
n 1 k p2
R
Ah 1 Rh Th - поглощательная способность слоя
2
2
n 1 k p
Пример экспериментально
Пример расчета спектров отражения
измеренного спектра оптической
пропускания и поглощения
плотности
(-lg(Th))
В спектр добавлена
линия поглощения
(по модели
Лоренца)
с
центральной
частотой
ω0,
соответствующей длине волны ~ 540 нм. При этом
в максимуме поглощения глубина проникновения
излучения δ(ω0) ~ 5.4 мкм.
Расстояние между максимумами в спектре
мкм
hh == 4216
8 мкм
мкм
пропускания Δλ определяется из соотношения:
2
Что после несложных преобразований дает:
1
Кристалл
MnS
(h ~ 6.3 мкм, n ~ 2, разрешение
1
спектрометра
2nh 2nh
δλ = 0.5 нм)
97.
Отражение, пропускание и поглощение однородногослоя
Если излучение нестрого монохроматическое и занимает некоторый спектральный
интервал δλ >> Δλ, то коэффициент пропускания такого пучка может быть получен
усреднением по спектральному диапазону δλ.
(1 RR))22ee hh
(1 R) 2 e h
1
(1 R)22
dd
(1
dd
T
TThhhdd
ee hh RR222ee hhh 22RRcos
0 0 CC BBcos
cos
2
cos
C 2 B2
Обычно когда рассматривают пропускание слоев (h > λ) kp << 1 (в то время как n ~ 1), в
этих условиях угол φ-r мал и коэффициент пропускания равен:
Th
1 R
2
e h R 2e h 2 R cos
Далее, если масштаб на котором меняются оптические характеристики среды из
которой сделан слой (n и kp, а вместе с ними R и α) слабо меняются на масштабе δω, то
при интегрировании по интервалу δω их можно считать константами.
c
2 n
d d
Достаточно усреднить по одному периоду.
h
2
nh
c
Введем обозначения C 1 R 2e 2 h Интеграл полученного вида можно найти в
справочниках:
B 2 Re h
h
2 C B
C B 1 1R
2 Re2 exp 2 h R 4 exp 4 hd 4 R 2 exp 2 2 h 1tg
R
h
2 exp 2
T
arctg
C 2 B2
2 2 h
C B cos
C B
1 R e
C 2 B2
2
2
2
2
2
98.
Отражение, пропускание и поглощение однородногослоя
Формулы для усредненных коэффициентов отражения,
поглощательной способности слоя можно получить проще.
пропускания,
и
Действительно, в этом приближении интерференционные эффектны «усредняются» и
вместо амплитуд (комплексных, учитывающих фазу волны) можно сразу
рассматривать интенсивности.
Коэффициент пропускания:
2 h
2
Th 1 R e h 1 R R 2e 3 h
Th
2 2 h
2
1
R
1 e R R 4e 5 h ...
2
Коэффициент отражения:
2 22 hh
Rh R 1
RR
Re
1 R R 3e 4 h
1
e
2
2
Rh R 1 2 52 62 hh
1 R1 RR ee ...
убывающей
Сумма бесконечно
2 2 h
1 R e прогрессии
геометрической
со
R 1
2 2 h
1
R
e
знаменателем
R2e-2αh и первым
слагаемым (1 - R)2e-αh.
Соответственно
1 R e h
T
2
h
1 R 2e 2 h
99.
Отражение, пропускание и поглощениемногослойной среды
Рассмотрим среду состоящую из слоев с различными оптическими свойствами
различной толщины, расположенных перпендикулярно некоторому направлению.
Пусть на такую среду по нормали падает плоская линейно-поляризованная
монохроматическая волна. Определим коэффициенты отражения, пропускания и
поглощательную способность такой среды.
Внутри каждого из слоев комплексные амплитуды
напряженности электрического и индукции
магнитного полей, подчиняются волновым
уравнениям.
2 E 2 2
2 B 2 2
x
2
c
2
nj E 0
x
2
c
2
nj B 0
Общее решение этих уравнений имеет вид
суперпозиции плоских волн, бегущих вдоль и
против оси х:
E x C1 exp i n j x C2 exp i n j x
c
c
cB x
n j C1 cC1B n j C2 cC2B
B
B
B x CC11 exp ii nnjjxx CC22exp
exp i i nnj xj x
nj
c
c
cc
E j C1 exp i n j x j C2 exp i n j x j
E j 1 C1 exp i n j x j 1 C2 exp i n j x j 1
c
c B x B
c
c
E x j E j
j
j
Обозначим
cB
cB j 1
j
C1 exp i n j xEj x j C1 2 exp
i
n
x
C1 exp i n j x j 1 C2 exp i n j x j 1
E j
B
x
j
j
j 1 B j 1
nj
nj
c
1 c
c
c
100.
Характеристическая матрица слояE j C1 exp i n j x j C2 exp i n j x j
c
c
E j 1 C1 exp i n j x j 1 C2 exp i n j x j 1
c
c
cB j 1
nj
C1 exp i n j x j C2 exp i n j x j
nj
c
c
cB j
C1 exp i n j x j 1 C2 exp i n j x j 1
c
c
Выразим Ej-1, Bj-1 через Ej и Bj.
cB j
1
С1 E j
exp i n j x j
2
n j
c
cB j
1
С2 E j
exp i n j x j
2
n j
c
h j x j x j 1
1 cB jj c
1 E cB jj exp i n h или в матричной форме
E j 1 E j cos
E jj n j h exp
i
n
h
B
sin
j
j j n h
j j
2 cn jj j j nc j j j c 2j j j n jj
c j j
c
cos
n
h
i
sin
n
h
j
j
j
j
E
n j
E j 1
c
n
c
j
j
B j 1 E jexp
i sin
B j cos
i nnjj hj hjj j exp
i n jj hnjj j h j
exp i n jj h jj
exp i n jj h jj
cB
cB
c c c
c c jj
c
c
j
E jj
E
cos
n
h
i
s
in
n
h
B
B
c jj j
j 1 2 i n j sin n h j ccosj j
2
n jj
n nhj
c
j
j
c
j
j
cBjj
cBjj
cB
cB
11
cB j
11
exp ii nnjjhhjj EEjj
exp ii nnjjhhjj E ji sin n j h j
cos n j h j
EEjj
exp
exp
nnjj 22 nnj cc c 22
nn j Квадратная
cc
c
n
2x2 матрица cMj называется
cBjj 11
cB
i sin n j h j
cos c n j h j
nj
c
Mj
nj
cos n j h j
i sin n j h j
c
c
c
Несложно убедиться, что det M j 1
c
характеристической матрицей j-го слоя, с её
помощью вычисляются амплитуды полей на
одной из границ слоя если заданы амплитуды
на другой границе.
101.
Характеристическая матрица слоистой средыРассмотрим последовательно слои составляющие среду начиная с первого:
E0
EN
M
M
...
M
1
2
N
B
B
0
N
E0
E1
M1
B1
B0
т.е. M M 1M 2 ...M N
E1
E2
M2
B1
B2
- есть характеристическая матрица среды составленной
из N слоев с характеристическими матрицами M1, M2,..
MN, соответственно.
:
Полученный результат можно обобщить на случай
среды с непрерывно меняющимися (вдоль некоторого
направления) оптическими свойствами.
EN 1
EN
MN
BN 1
BN
Необходимо разбить среду на множество малых слоев, в которых оптические
постоянные можно считать постоянными, и составить произведением матриц таких
слоев ( и формально перейти к пределу при N → ∞).
Т.е. для участка среды с непрерывно меняющимися оптическими свойствами
толщиной h:
c
cos
n
x
i
sin
n
x
j
j
N
h
c
n
c
j
x
Mj
M lim
Mj
N
nj
N
j 1
cos n j x
i sin n j x
c
c
c
102.
Коэффициенты отражения, пропускания ипоглощательная способность среды
Выразим коэффициенты отражения и пропускания слоистой среды через элементы
характеристической матрицы.
E0
EN
E0 M 11EN M 12 BN
M или B M E M B
0
21 N
22 N
B0
BN
n
c
Кроме того Bi 0 E i
n
B t N 1 E t
c
n
Br 0 E r
c
но, в силу граничных
условий к уравнениям
Максвелла
соответственно
Здесь индекс 0 относится к среде
из которой излучение падает на
слоистую среду, а индекс N + 1 к
среде в которую излучение
попадает пройдя, через слоистую
среду.
22n0
t
c
nN 1
nN 1nM
N 1
M
M 1M 22
nM0 11
M
M
cM
12 12
21
11 c
21 nN 22
n
n
c
0
0
или
E0 E i E r
B0 B i B r BN B t
nN 1
M 12 E t
c
n0 i n0 r
n
E E M 21E t N 1 M 22 E t
c
c
c
n
1 r t M 11 N 1 M 12
c
E i E r M 11E t
c
n
1 r t M 21 N 1 M 22
n0
n0
nN 1
nn
20n 0 MM1111 N N1 1MM1212 cM
n0 21M 11n N 1M
M cM 21 nN 1M 22
n
22 12
c
cc
r
n nN 1
M1211 cMM
cM2221 nN 1M 22
n0 M 11 Nn 01 M
nN 1 M
21 12
c
c
T
nN 1 2
t
n0
R r
2
A 1 R T
103.
Прозрачная пленка на металлической подложкеХарактеристическая матрица:
c
cos
n
h
i
sin
n
h
1
1
c
n
c
1
M
n1
cos n1h
i sin n1h
c
c
c
n2
M 11 M 12 cM 21 n2 M 22
c
r
n2
M 11 M 12 cM 21 n2 M 22
c
R r
2
- коэффициент отражения системы пленкаподложка
A 1 R - поглощательная способность системы
пленка подложка
Зависимость поглощательной способности от
Спектр поглощательной способности
пленки.
При расчетах толщины
полагалось,
что оптические
свойства металла описываются в приближении
h
Друде (ωp = 1016 c-1, γD = 1014 c-1), а показатель
2n1
преломления пленки n1 ≈ 2.36 – 2.6.
- расстояние
между максимумами (минимумами)
104.
Металлическая пленка на прозрачной подложкеХарактеристическая матрица:
c
cos
n
h
i
sin
n
h
1
1
c
n
c
1
M
n1
cos n1h
i sin n1h
c
c
c
n2
M 11 M 12 cM 21 n2 M 22
c
r
n2
M 11 M 12 cM 21 n2 M 22
c
R r
2
T n2 t
2
t
2
n2
M 11 M 12 cM 21 n2 M 22
c
A 1 R T
R, T, A – коэффициент отражения, пропускания и поглощательная способность системы
металлическая пленка/прозрачная подложка.
Зависимость
коэффициентов
отражения,
Спектры
отражения,
пропускания
и
пропускания
способности
поглощения и поглощательной
системы
металлическая
системы
металлическая
пленки/прозрачная
пленка/прозрачная
подложка
для различных
подложка
от
толщины
металлической
пленки
толщин пленки.
для фиксированной длины волны.
105.
Отражение излучения от неоднородновозбужденного полупроводника
В качестве примера применения рассмотренного метода расчета оптических свойств
неоднородной среды с непрерывно меняющимся показателем преломления рассмотрим
ситуацию отражения излучения от неоднородно возбужденного полупроводника.
Подобный анализ может быть важен при интерпретации экспериментов по
исследованию фемтосекундного фотовозбуждения полупроводников методом накачкаопрос (pump-probe).
Т.к. при лазерном возбуждении полупроводника ne = ne(x), то n n( x).
(ne – концентрация фотовозбужденных носителей, ось х направлена вглубь)
x
Для качественного анализа ситуации будем полагать, что ne x ne 0 e ne .
(ne(0) – максимальная концентрация у поверхности, δne – характерный масштаб
неоднородности распределения)
Зависимость
коэффициента
отражения
фотовозбужденного кремния (для λ = 1250 нм,
ne(0) = 3.5∙1021 см-3) от характерного масштаба
неоднородности. На графике также показаны
расчеты отражения по формуле Френеля в
случае
если
показатель
преломления
определяется концентрацией на поверхности
(пунктир)
и
для
невозбужденного
полупроводника (точки).
106.
Расчет отражения, пропускания и поглощения в случаенаклонного падения излучения на слоистую среду
Подробное рассмотрение этого вопроса приведено в книге М. Борн, Э. Вольф. Основы
оптики. М.: «Наука», 1973, 719 с.
В случае наклонного падения излучения нужно различать случаи s-поляризованной
(т.е. поляризованной перпендикулярно плоскости падения) и p-поляризованной волн
(т.е. поляризованной в плоскости падения).
s-поляризация
p-поляризация
i
sin n j h j cos j
cos c n j h j cos j
pj
c
Mj
cos n j h j cos j
ip j sin n j h j cos j
c
c
pj
p j n j cos j
cos j
nj
Углы βj могут быть последовательно
найдены исходя из закона преломления.
N
M M j
j 1
r
t
M11 M 12 pN 1 p0 M 21 M 22 pN 1 R r 2
M11 M 12 pN 1 p0 M 21 M 22 pN 1
2 p0
p
2
T N 1 t
p0
M11 M 12 pN 1 p0 M 21 M 22 pN 1
A 1 R T
107.
Среды с микро/нановключениями. Эффективнаядиэлектрическая проницаемость
Рассмотрим композитную среду, представляющую собой некоторую матрицу,
содержащую включения другого материала с характерными размерами (а) много
меньшими длины волны излучения (a << λ).
ε1 – диэлектрическая проницаемость
материала матрицы
ε2 – диэлектрическая проницаемость
материала включений
В
модели
эффективной
среды
(эффективной
диэлектрической
проницаемости)
исходно
неоднородная среда рассматривается
как
однородная
с
некоторой
эффективной
диэлектрической eff f
проницаемостью εeff.
1 , 2
Теория эффективной диэлектрической проницаемости оперирует с усредненными по
объемам содержащим большое количество включений величинами E, D, P.
Наиболее часто при описании оптических свойств подобных сред используются
подходы Максвелла-Гарнетта и Бруггемана.
108.
Формула Максвелла-Гарнетта для эффективнойдиэлектрической проницаемости
В рамках модели Максвелла-Гарнетта эффективная диэлектрическая проницаемость
может быть найдена из соотношения (для включений сферической формы):
eff 1
2 1
g2
eff 2 1
2 2 1
g2 – объемная доля включений
Для металлических частиц
(в приближении Друде)
p
0
2 1 1
ПЭМ изображение
наночастиц
Формула Максвелла-Гарнетта может быть применена к случаю неоднородной среды с
включениями в условиях когда объемная доля включений мала (g2 << 1).
Пример
вещественной испектра
мнимой
Пример расчета
экспериментального
части
эффективного
поглощения
водного комплексного
раствора
показателя
преломления
раствора
наночастиц
серебра,
полученного
металлических
наночастиц
в воде.
методом импульсной
лазерной
абляции.
Как видно в спектре поглощения
появляется
полоса,
которая
не
характерна для материалов из которых
составлена среда по отдельности.
Её появление связано с возбуждением
резонансных плазменных (дипольных)
колебаний в частицах.
Резонансная частота определяется из условия 2 2 1 0
(дисперсией в матрице пренебрегаем)
109.
Формула Бруггемана для эффективнойдиэлектрической проницаемости
В рамках модели Бруггемана эффективная диэлектрическая
двухкомпонентной среды может быть найдена из соотношения:
1 g 2
проницаемость
1 eff
g 2 2 eff 0
1 2 eff
2 2 eff
Формула Бруггемана относится к случаю двухкомпонентной смеси, в которой нельзя
провести четкого разделения на матрицу и включения: оба вещества рассматриваются
симметричным образом. Примером таких сред могут являться пористые среды с
высокой степенью пористости (нанопористый кремний, нанопористое стекло).
Рассмотрим пример применения формулы Бруггемана к описанию оптических свойств
нанопористого кремния.
Спектр пропускания пластины нанопористого кремния (слева), определенный по
измеренному спектру пропускания и рассчитанный показатель преломления (справа).
110.
Механическое (пондеромоторное) действиелазерного излучения на вещество
111.
Общая характеристика механического действиялазерного излучения
Механическое действие лазерного излучения на вещество может быть обусловлено
силами действующими со стороны электрического и магнитного полей на
элементарные заряды составляющие среду (мы будем называть действие лазерного
излучения, обусловленное этими силами пондеромоторным).
Как правило подобного рода эффекты в большинстве задачах лазерной обработки не
играют существенной роли из-за их относительной малости. Более существенную
роль играют механические эффекты обусловленные тепловыми эффектами (генерация
термоупругих напряжений, формирование ударных волн при абляции и т.п.).
Однако в ряде случаев (в частности, при воздействие на малые диэлектрические
частицы) такие эффекты не только можно легко наблюдать, но и использовать на
практике (оптическая ловушка).
В случае же воздействия мощных ультракоротких импульсов пондеромоторные силы
действующие на заряды среды (плазмы) могут приводить к разделению
разноименных зарядов и образованию электрических полей огромной напряженности
(~ 109 В/см), которые могут быть использованы для ускорения заряженных частиц
(т.н. кильватерное ускорение).
Вначале рассмотрим именно пондеромоторное действие, термомеханические будут
рассмотрены позднее в последующих лекциях.
112.
Световое давление при нормальном паденииплоской монохроматической волны на металл
Механизм возникновения светового давления в рамках классической электродинамики
объясняется следующим образом.
Электрическое
поле
электромагнитной
волны
раскачивает электроны, сила Лоренца, действующая со
стороны магнитного поля на движущиеся электроны
оказывает давление в направлении распространения
излучения.
Электрическое и магнитное поля плоской волны в
металле могут быть записаны в виде:
i t nx
t
c
E Ee
n t i t c nx
B Ee
c
(Et – амплитуда прошедшей волны, причем можно считать,
что Et вещественно)
Поле E индуцирует токи с плотностью
j eneve
j E
ve
E
ene
Нас интересует среднее значение силы Лоренца за период.
t
** ii tt nn**xx
nx
ii
t nx
1
1
n
n
**
t
c
tt
t
c
cc
Re
EB
ne FM
E
e
Re
E
e
E
e
M
2
2
c
c
i
2
1
2
2
1
t 2 x
n
k
i
2
nk
1
i
p
p
E e
0
0 0
Лоренца,Re
1 i 2 nна ikединицу
сила
действующая
объема
p
1 i 2
2c
2
Re 1 i 2 n ik p 1n 2 k p
1 2nk p 0 2 1 k p2 n 2 0
n 2 n ik
p
113.
Световое давление при нормальном паденииплоской монохроматической волны на металл
E tt e xx
E t 0 e x
2n 2 k p k p 1 k p2 n 2
neee FMMM
1n 2k p
2c
2c
22
2
1 2nk p 0 2 1 k p2 n 2 0
E t 0 e x
2
4
t i t n* t i t n E
1
Re E e
E e
2 00
c
2 0c
t 2
qqttt S tptp
ne FM
n k 1
2
2
p
S tp E , 0 1B
qt e x 2
n k p2 1
2cn
0 0
1
c2
Чтобы получить давление Pl (силу на единицу площади) нужно проинтегрировать
объемную плотность силы по глубине.
qt n k p 1
qtt 22
22
xx
Pll nee FMM dx
n k pp 1 e dx c 2n
2
cn
00
00
2
2
По закону сохранения энергии должно выполняться: qt 1 R q0
11 на
n kk света
n 22kk определяется
22 22nn 22nn интенсивностью
n 1 k
q n 1 k падающей
q4n - давление
q 2металл
q
P (1 R)
22
ll
00
0
22
pp
22
00
2
22
pp
c
c n c1 волны
22nn
k
и коэффициентом
отражения.
nn 11 kk
22
22
pp
22
22
pp
0
c
2
2
p
n 1 k p2
2
2
p
114.
Световое давление при нормальном паденииплоской монохроматической волны на диэлектрик
В диэлектрике токи проводимости отсутствуют, однако имеются поляризационные
токи связанных зарядов.
P
.
Эти токи определяются вектором поляризации среды и равны
t
P
eneve есть плотность токов
Действительно, P ene y соответственно
t
связанных зарядов.
(здесь y – проекция смещения электрона на ось y, ne – концентрация диполей)
Выражение для объемной плотности силы Лоренца, выраженной через плотность
токов сохраняется, соответственно:
**
nx n
ii tt nx
ii tt nn* xx
P *** 1
n
1 P
2
t
t
Re
Re
00 nn2 11 EEt ee cc EEt ee cc
BB Re ii
cc
2 tt 2
*
nee FMM
i
t
nx
E e
E
e
t
c
D 0 E 0 ERe
P
i nP 1 n 1 E 4 E En e k 1
2c
t 2
x
0
t
2
*
2
x
0
2
0
2
p
n t i t c nx
B Ee
c
i t nx
P выражение для tобъемной
Т.е.
плотности силы Лоренца имеет тот же вид, что и для
2
Re i in 2 10 n* 1 ERe
i 2nk p n 2 k p2 1 k p in n 2 k p2 1 k p 2n 2k p
e nc
металлов.
t
Соответственно, выражение для светового давления будет тем же:
q
Pl 1 R 0
c
115.
Квантовая трактовка светового давленияВ квантовой трактовке излучение рассматривается как поток фотонов с энергией
и импульсом k .
q0
- есть плотность потока фотонов, т.е. число фотонов проходящих
Величина
за единицу времен через единичную площадку перпендикулярную
лучу.
При падении на поверхность часть фотонов отражается, при этом импульс фотона
меняется на величину 2 k .
Поэтому импульс передаваемый единице площади среды в единицу времени будет
равен
2 Rq0 но по второму закону Ньютона это есть сила действующая на
Rq0
2 k
единицу площади среды, т.е. это и есть давление создаваемое
c
отражающимися фотонами.
Аналогично давление создаваемое поглощаемыми фотонами (их доля равна (1 - R), а
изменение импульса k ) будет равно
1 R q0 .
c
Суммируя оба вклада получим, что полное световое давление опять же равно:
q
Pl 1 R 0
c
116.
Силы, действующие на малые прозрачные частицы внеоднородном световом пучке. Случай крупных по
сравнению с длиной волны частиц
Пионерские работы по исследованию динамики поведения малых прозрачных частиц в
жидкости в неоднородном поле лазерного излучения были проведены А. Эшкиным. В
2018 г. за эти работы ему была вручена нобелевская премия.
При анализе сил действующих на прозрачные частица в неоднородном лазерном пучке
выделяют случай малых и крупных по сравнению с длиной волны частиц.
Рассмотрим механизм возникновения сил, действующих на сферическую частицу,
направленных в радиальных направлениях в неоднородном пучке.
Крупные
В
результате
по отражения
сравнению ис преломления
длиной волны
на
частицы можно
каждой
из границ
рассматривать
будут возникать
в приближении
силы
геометрической
светового
давления
оптики.
Fr и Fd соответственно.
При этом для каждого из лучей силы
В
силу симметрии
для качественного
анализав
связанные
с отражением
на разных границах
достаточно
два луча, проходящих
проекции рассмотреть
на
радиальное
направление
на
одинаковом
расстоянии
от
центра
частицы.
компенсируют друг друга.
Силы, связанные с преломлением для рассматриваемых двух лучей будут направлены
в противоположных направлениях. Однако, ввиду того, что для луча 1, проходящего
ближе к оси пучка интенсивность излучения выше, эти силы для луча 1 будут больше
по величине. Таким образом, частица будет приобретать ускорение, направленное к
центру пучка. Также, как видно из рисунка, на частицу будет действовать сила
светового давления, направленная вдоль направления распространения пучка
117.
Силы, действующие на малые прозрачные частицы внеоднородном световом пучке. Случай крупных по
сравнению с длиной волны частиц
Рассмотрим теперь механизм возникновения осевых сил, направленных к фокусу
пучка при острой фокусировке.
По прежнему можно
оптическое приближение.
использовать
геометро-
На рисунке показан ход двух лучей в ситуации когда
частица расположена оси пучка ниже фокуса.
Из рисунка видно, что силы обусловленные
преломлением лучей на границах направлены к фокусу.
При этом оказывается, что по величине эти силы
больше сил, связанных с отражением на границах.
Если образец расположен строго в фокусе, то
преломленные лучи направлены по радиусам, т.е.
преломления лучей на границах нет. Соответственно,
силы FD отсутствуют.
Таким образом, существует положение (чуть ниже фокуса) в котором силы FD
компенсируются силами FR (не указаны на рисунке), связанные с отражением, а также
силой тяжести.
Таким образом возможен оптический захват (optical trapping) частицы.
118.
О методе расчета силы действующий на малыепрозрачные частицы в неоднородном световом пучке.
Случай крупных по сравнению с длиной волны частиц
В простейшем методе расчета сил, действующих на крупные по сравнению с длиной
волны частицы, в неоднородном лазерном пучке используется синтез геометрооптических представлений и представлений о свете как потоке фотонов, обладающих
импульсом.
Задача разбивается на 3 этапа:
1. По законам геометрической оптики, определяются направления отраженных и
преломленных лучей. Исходя из закона сохранения импульса для системы «свет-тело»
находятся направления сил светового давления.
2. Используя формулы Френеля, вычисляются интенсивности отраженных и
преломленных элементарных пучков (лучей).
3. Используя соотношение между интенсивностью волны и плотностью потока
импульса (q/c) и зная рассчитанные в предыдущем пункте интенсивности
отраженных и преломленных пучков, определяется изменение полного импульса
света. Используя законы сохранения импульса для системы «свет-тело» и второй
закон Ньютона определяется сила действующая на частицу.
119.
Силы, действующие на малые прозрачные частицы внеоднородном световом пучке. Случай малых по
сравнению с длиной волны частиц
Малые по сравнению с длиной волны частицы могут рассматриваться как точечные
диполи.
Рассмотрим силы действующие на точечный диполь в неоднородном
электромагнитном поле.
dr
Силы действующая на заряды диполя: F1 qE r1 q 1 , B r1
dt
q > 0 – заряд диполя
dr
r1 – радиус вектор положительного F2 qE r2 q 2 , B r2
r1 x1 , y1 , z1
dt
заряда,
r
–
радиус
вектор
2
отрицательного заряда.
l r1 r2
l lx , l y , lx r2 x2 , y2 , z2
Т.к. пространственный масштаб на котором меняются поля E и B много меньше
расстояния между зарядами l, то поле в точке 2 можно представить в виде ряда,
ограничившись линейной поправкой.
Для каждой проекции вектора напряженности электрического поля можно записать
следующие приближенные равенства:
E y
E y
E y
Ex r2 Ex r1 lx
Ex
E
E
ly x
lz z
x x x1
y x x1
x x x1
E y r2 E y r1 lx
Ez r2 Ez r1 lx
Ez
E
E
ly z
lz z
x x x1
y x x1
x x x1
E r2 Ex r2 e x E y r2 e y Ez r2 e z
x x x1
ly
y x x1
lz
x x x1
120.
Силы, действующие на малые прозрачные частицы внеоднородном световом пучке. Случай малых по
сравнению с длиной волны частиц
E r2 Ex r2 e x E y r2 e yy Ezz r22 e zz E r1 l , E
r r
1
Действительно, поскольку оператор
l , есть
l , lx l y lz , то для каждой из проекций
x
y
z
напряженности поля E(r2) получаться равенства,
записанные на предыдущем слайде.
Таким образом для полей E(r2) и В(r2) имеем
x
y
z
- оператор набла
E r2 E r1 l , E r r
1
B r2 B r1 l , B r r
1
Полная сила действующая на диполь F = F1 + F2.
drr1
drr2
d
d
F
F
q
qE
E r11 q 1 , B r11 qE r22 q 22 , B r222
dt
dt
r1 r
d ql
dr dr dl
q l , E q , B , B l , B ql , E +
, B
dt
dt
dt
dt
Дипольный
момент частицы ql должен
быть пропорционален
напряженности
поля, т.е.
dr dr dl
dr
dl dl
dl
, B l , B частицы).
, l , Тогда
B , B , l , B , B
ql = α, B
pE (α p – поляризуемость
dt dt dt
dt
dt dt
dt
d
E
F p E, E + p
, B
dt
121.
Силы, действующие на малые прозрачные частицы внеоднородном световом пучке. Случай малых по
сравнению с длиной волны частиц
Итак, мы получили, что сила действующая на диполь равна F p E , E + p dE , B .
dt
Воспользуемся известным тождеством из векторного анализа
1
E 2 E , E + E , , E
2
тогда
С учетом первого уравнения Максвелла
F
pp
1
E
F p E 2 E , , E + p , B .
2
t
rotE , E
E B
E 22 + pp , B E , p E 2 + p E , B .
2
t
t 2
t
B
t
получим
но, E , B E , B E , B ~ S p
(Sp – вектор Пойнтинга)
t
t t
Если интенсивность световой волны постоянна по времени то среднее от модуля Sp за
период колебаний не изменяется, поэтому второе слагаемое обращается в ноль, а
среднее значение первого будет пропорционально градиенту квадрата амплитуды
поля, т.е. интенсивности световой волны.
Таким образом среднее значение силы, действующей на частицу
F ~ q.
Соответственно, частица будет двигаться из области с меньшей интенсивностью в
область с большей.
122.
Примеры использования оптических ловушек дляманипулирования микро/нанообъектами
В работе P.J. Pauzauskie et al. Optical trapping and integration of semiconductor nanowire
assemblies in water//Nature, 2006, V.5, pp. 97-101 показана возможность лазерной
манипуляции с протяженными объектами – полупроводниковыми наностержнями.
Примеры
собранных структур:
Схема
эксперимента:
Оптическое и РЭМ изображение GaN нанопровода,
a)
–
общая
схема
приваренного к SnO2 наноленте (сварка также
оптической ловушки
осуществлялась лазером).
Схематичное и темнопольное
б)
–
схематичное
оптическое
изображение
изображение
4-х этапного
сборки
из GaN наностержней
позиционирования
нано
и SnO
2 нанолент
стрежня
Схематическое
и
с) оптическое
–
схематичное
изображение
изображение
GaN
экспериментальной
наностержня, кюветы
закрепленного
на
клетке рака шейки
Под действием силы тяжести наностержни падают на нижнююматки.
поверхность кюветы,
где они могут быть захвачены в оптическую ловушку.
123.
Лазерное охлаждение атомовСуществует несколько методов лазерного охлаждения:
1. Доплеровское охлаждение
2. Сизифово охлаждение
3. Охлаждение методом боковой полосы
4. Антистоксово неупругое рассеяние света
5. ….
Рассмотрим более подробно механизм доплеровского охлаждения.
Доплеровскому охлаждению подвергается достаточно разреженный одноатомный газ.
Неподвижный
атом
хорошо
поглощает
на
некоторой
k
k
резонансной частоте ω12.
Частота излучения лазера выбирается
так, что ω < ω12.
Для атома, движущегося со скоростью vx
вдоль оси x, из-за эффекта Доплера
частота излучения сдвинется на величину
равную kvx.
Охлаждение
происходит
счет того,излучение
что при спонтанном
излучении
в
Таким образом
хорошо за
поглощать
будут только
атомы снаправление,
определённой
котором
проекциейизлучается
скорости на фотон,
ось x: случайно и равномерно распределено по всем
направлениям.
В результате, в среднем при переизлучении скорость атома не
12
В результате поглощения фотона скорость атома vx по абсолютной
0
меняется. vЭто
приводит
к понижению энергии системы атомов и соответственно к
x
величине уменьшится.
k
охлаждению.
T ~ 0.5 мK - предельные температуры охлаждения
124.
Движение свободной заряженной частицы внеоднородном световом поле
Рассмотрим характер движения электрона в
неоднородном гармонически меняющемся со
временем поле.
В результате того, что электрон при
колебаниях в области большей напряженности
разгоняется сильнее, чем потом тормозится в
области с меньшей напряженностью, на
колебательное
движение
накладывается
дрейфовое движение направленной в сторону
E x, t E0 x cos t
уменьшения амплитуды поля.
(действием
d2y
Уравнение движения электрона имеет вид: me 2 eE0 y cos t магнитной силы
dt
пренебрегаем)
Искать решение будем в виде
y y0 y1
При этом можно считать, что
d 2 y0
d 2 y1
но
y1 y0 ,
.
2
2
dt
dt
Т.к. мы полагаем, что амплитуда поля E0 мало меняется на при изменении
координаты электрона, обусловленного быстрыми осцилляциями, то
E0 y E0 y0 y1
E0
y y y0
125.
Движение свободной заряженной частицы внеоднородном
Таким образом уравнение движения будет иметь вид:
d 2 y0
d 2 y1
E
me 2 me 2 eE0 y0 cos t ey1 0
cos t
dt
dt
y y y0
Попытаемся отыскать решение полученного уравнения, разбив его на два уравнения
следующего вида:
d 2 y1
me 2 eE0 y0 cos t
dt
d 2 y0
E
me 2 ey1 0
cos t
dt
y y y0
Несложно увидеть, что решением первого уравнения является функция:
y1
eE0 y0
cos t
2
me
После подстановки полученного решения во второе уравнение для средней за
период колебаний силы, действующей на электрон получим:
2
2
e 2 E02
de 22 y00 E0 -e 22видно,
E0что
22
0
сила
пропорциональна
градиенту интенсивности
F mee 222
E
cos t
2
22 00
y
4mdt
y m
волны
с обратным
знаком 4me y
ee
e
Отметим, что направление силы не зависит от знака заряда, т.е. как положительные
заряды, так и отрицательные будут выталкиваться из области с большей
интенсивностью.
126.
Лазерное кильватерное ускорение заряженныхчастиц
Эффект дрейфового смещения заряженных частиц в неоднородном поле мощного
фемтосекундного импульса используется для ускорения заряженных частиц.
Пример
численного
расчета прохождения
Схема
лазерного
кильватерного
ускорения (в т.н.
мощного ультракороткого
импульса через
bubble-режиме)
плазму.
Распространяясь в плазме мощный
a,b
–
распределение
фемтосекундный
импульс
(q ~ 1017
19 Вт/см2) за счет
концентрации
электронов
– 10
действия
плазмы
и
интенсивности
пондеромоторной
силы
лазерного электроны
импульса,из той
в
выталкивает
плоскости
содержащей ось
области,
где распространяется.
пучка.
В с результате
импульсом
–
3D за изображение
формируется
распределения область
плотностис
избыточным
электронов в положительным
окрестности
зарядом,
которая распространяется
«пузыря».
вслед за импульсом.
На задней границе этой области (см. рисунок) электрическое поле разделения зарядов
максимально. Электроны захваченные в эту область будут ускоряться вслед за
импульсом.
Таким методом удается разогнать электроны до энергий ~ 100 МэВ и выше.
127.
Теплофизика лазерного нагрева128.
Общая характеристика лазерного нагреваЛазерный нагрев по своей физической сущности в большинстве случаев не отличается
от других видов нагрева.
Однозначной характеристикой теплового действия является температура, а сам нагрев
состоит в увеличении амплитуды тепловых колебаний решетки (особого рассмотрения
в этом отношении заслуживает нагрев импульсами ультракороткой длительности).
Перенос тепла в твердом теле осуществляется механизмами теплопроводности.
Для металлов и сильно вырожденных полупроводников основным является
электронная теплопроводность, а для неметаллов – решеточная.
Особенности лазерного нагрева:
1. Высокие градиенты температуры
T
~ 109 / м
x
2. Высокие скорости нагрева и охлаждения
T
~ 1013 K / c
t
Высокие скорости нагревания и охлаждения и большие пространственные градиенты
температуры обуславливают особенности лазерного нагрева и могут привести и
приводят к значительным отличиям в протекании тепловых процессов,
стимулированных лазерным воздействием.
129.
Общая характеристика лазерного нагреваРезультат теплового действия лазерного излучения будет определяться следующими
группами параметров:
1. Параметры нагревающего излучения
Плотность мощности q
Длительность импульса τ
Форма и размер зоны облучения (радиус пучка в зоне обработки r0)
….
2. Оптические характеристики материала
Поглощательная способность A
Коэффициент поглощения α
3. Теплофизические характеристики материала
Удельная теплоемкость c
Коэффициент теплопроводности k
Целью нашего дальнейшего анализа будет являться установление количественных
взаимосвязей между указанными параметрами и температурой лазерного нагрева.
130.
Основные теплофизические понятия1. Удельная теплоемкость – показывает количество теплоты, которое необходимо
сообщить единице объема (массы) материала, чтобы нагреть его на один градус.
сV
dQ
dVdT
- теплоемкость единицы объема [ Дж/(м3·K)].
сm
dQ
dmdT
- теплоемкость единицы массы [Дж/(кг·K)].
сV cm
(ρ - плотность)
В дальнейшем c = cV.
2. Тепловой поток – количество тепла проходящее в единицу времени и отнесенное к
единице площади изотермической поверхности.
jQ n
dQ
dtdS
n – единичная нормаль к изотермической поверхности,
направленная в сторону уменьшения температуры.
Необходимым условием наличия теплового
потока
является
наличие
температурного
градиента. Опыт показывает, что передача тепла
теплопроводностью происходит по нормали к
изотермической поверхности от мест с большей
температурой к местам с меньшей температурой.
131.
Основные теплофизические понятия3. Коэффициент теплопроводности
Закон Фурье: величина теплового потока в некоторой точке прямо
пропорциональна градиенту температур в этой точке, взятому с обратным
знаком.
Коэффициент
пропорциональности
называется
коэффициентом
теплопроводности.
k – коэффициент теплопроводности [Вт/(м·K)]
jQ k gradT
Для быстропротекающих процессов иногда используется обобщенный закон
Фурье:
jQ kgradT q
jQ
t
(τq – время релаксации теплового потока)
В дальнейшем при анализе задач лазерного нагрева мы будем использовать
классический закон Фурье.
4. Коэффициент температуропроводности
k
- коэффициент температуропроводности [м2/с]
a
c
В отличие от теплопроводности k , которая характеризует способность
материала проводить тепло, температуропроводность a
характеризует
распространение по веществу температуры.
132.
Основные теплофизические понятия5. Плотность мощности объемных источников тепла (объемная плотность
мощности тепловых источников) – энергия, выделяемая в виде тепла за единицу
времени в единице объема среды.
qv
dQ
dtdV
- плотность мощности объемных источников тепла [Вт/м3]
В общем случае действие теплового источника может быть обусловлено протеканием
электрического тока, поглощением лазерного излучения, протеканием химических
реакций и т.п.
Выясним чему равна плотность мощности теплового источника при поглощении
лазерного излучения.
Пусть излучение распространяется вдоль оси х. Энергия лазерного излучения
проходящая через площадку S в точке x за время dt равна q(x)Sdt.
Аналогично, q(x+dx)Sdt - энергия лазерного излучения проходящая через площадку
S в точке x+dx за время dt.
Разность между этими величинами равна энергии которая поглотилась в слое,
зажатом между плоскостями x и x+dx, за время dt. Если при этом поглощенная
энергия сразу переводится в тепловую, то
dQ q ( x) q ( x dx) Sdt
: Sdxdt
Для поглощения по закону Бугера
qv
q
x
qv A q0e x
q Aq0 e x
- т.е. объемная плотность мощности тепловых
источников
также
убывает
по
экспоненциальному закону.
133.
Экспериментальные методы определениякоэффициента теплопроводности
Стационарные методы:
1. Абсолютный метод
В данном методе на концах образца имеющего
прямоугольную или цилиндрическую форму поддерживается
постоянная разность температур.
Коэффициент
теплопроводности
вычисляется
непосредственно из закона Фурье:
k
Q0 Qloss L
S T1 T2
Q0 – мощность источника тепла, Qloss –
мощность потерь, L – длина образца, S –
поперечное сечение, T1 – T2 – разность
температур
2. Сравнительные метод
В сравнительном методе между источником тепла и образцом
помещается
эталонный
образец
с
известной
теплопроводностью.
При этом:
Индекс 1 относится к исследуемому
S T L
k1 k2 2 2 1
образцу, 2 – к эталонному
S1 T1L2
134.
Экспериментальные методы определениякоэффициента теплопроводности
3. Метод радиального теплового источника
В данном методе используется цилиндрический
образец, в котором нагревают ось, а тепло
распространяемся в радиальных направлениях
от центра к периферии.
Коэффициент теплопроводности определяется
из соотношения:
r
P0 ln 2
r1
k
2 H T
r1, r2 – расстояния от оси цилиндра до места расположения термопар
H – высота образца
ΔT – разница температур
Данный метод используется для определения коэффициента теплопроводности при
высоких температурах, т.к. позволяет минимизировать тепловые потери на открытых
поверхностях.
4. Метод параллельной проводимости
5. …
135.
Экспериментальные методы определениякоэффициента теплопроводности. Метод лазерной
вспышки
Нестационарные методы:
1. Метод импульсной мощности
2. Метод горячей проволоки
3. Метод лазерной вспышки
В методе лазерной вспышки образец облучают лазерным лучом, а с другой стороны
измеряют динамику повышения температуры.
Схема
облучения
и
зависимость температуры
от времени для тыльной
стороны пластины. (τ0.5 –
за которое поверхность
нагреется до половины
максимального значения)
Относительное изменение температуры на Температуропроводность
тыльной стороне образца:
определена по формуле:
T h, t T0
n 2 2 at
n
1 2 1 exp
Th max T0
h2
n 1
a 1.26976
h2
2 0.5
может
быть
136.
Уравнение теплопроводностиУравнение теплопроводности является следствием закона сохранения энергии закона
Фурье.
Запишем закон сохранения тепловой энергии:
S – произвольная (неподвижная) замкнутая
Q
jQ , dS
qv dV поверхность, V – объем, ограниченный этой
t
S
V
поверхностью
По теореме Гаусса-Остроградского:
j , dS divj dV
Q
S
Q
V
вклад
в изменение
вкладизменения
в тепловой
изменение тепловой
Q
T
скорость
c
dV
Скорость изменения
тепловойс энергии в объеме
V:
энергии,
энергии,
связанный
с
тепловой
энергии
в объеме связанный
V
t
t
V
переносом действием
энергии через теплового
границу объема
источника
T
- это равенство должно выполняться
Тогда
c
div
j
q
dV
0
Q
v
для любого объема
t
V
c
T
divjQ qv 0
t
T
c
div kgradT qv
t
но, по закону Фурье
jQ kgradT
- уравнение теплопроводности
Здесь T = T(r, t) – поле температуры, а с, k и qv в общем случае могут являться
функциями координат и/или температуры.
137.
Начальные и граничные условияУравнение теплопроводности является дифференциальным уравнением в частных
производных второго порядка (параболического типа).
Чтобы решение было однозначным необходимо задать дополнительные условия.
Начальные условия
Начальное условие для уравнения теплопроводности обычно состоит в задании
температуры в начальный момент времени во всех точках облучаемого лазерным
излучением образца.
T r ,0 T0 (r )
T0(r) – некоторая известная функция координат
Граничные условия
1. Граничные условия первого рода
Граничные условия первого рода заключаются в задании распределения температуры
тела на его поверхности во все моменты времени.
T r , t r T t
(TГ(t) – некоторая известная функция времени, заданная во всех
точках поверхности тела)
2. Граничные условия второго рода
Граничные условия второго рода заключаются в задании теплового потока в каждой
точке поверхности тела во все моменты времени.
T r , t
(n – внешняя нормаль к поверхности, qГ(t) – заданная во всех
k
q
t
точках поверхности функция времени)
n r Г
138.
Начальные и граничные условияИменно граничные условия второго рода представляют наибольший интерес в
контексте задач лазерного нагрева.
Если поверхность теплоизолирована, т.е. отсутствует приток или отток энергии извне,
то qГ = 0.
Если лазерное излучение поглощается в тонком поверхностном слое, то можно считать
объемный источник тепла равным 0, а источник перенести на поверхность.
Т.е. можно считать, что поглощаемая плотность мощности излучения сразу на
поверхности преобразуется в тепловой поток, тогда
(q0 – плотность мощности падающего излучения, A – поглощательная
q Aq0
способность)
На поверхности также могут иметь место потери тепла, связанные например с
конвективным или радиационным теплообменом.
Например, для случая потерь на тепловое излучение
q SB T 4 r , t
r
3. Граничные условия третьего рода
Если заданы температура окружающей среды Tcр и закон теплообмена между
окружающей средой и поверхностью обрабатываемого материала, то говорят, что в
тепловой задаче заданы граничные условия 3 рода
T r , t
k
T r , t r Г Tср
n r Г
β
–
коэффициент
теплообмена [Вт/(м2·K)]
конвективного
139.
Линейное уравнение теплопроводности дляоднородной среды
Наиболее просто анализу поддается ситуация, когда коэффициент теплопроводности и
удельная теплоемкость не зависят от координат и температуры, а объемный источник
тепла не зависит от температуры.
В этом случае уравнение теплопроводности можно преобразовать к виду
T
q
a T v
t
c
(Δ – оператор Лапласа, а - температуропроводность)
Это уравнение называется линейным уравнением теплопроводности.
В декартовых координатах (x, y, z) уравнение примет вид
2T 2T 2T qv
T
a 2 2 2
t
y
z c
x
Если температура зависит только от одной из координат, то уравнение примет вид
T
2T qv
a 2
t
x
c
- линейное одномерное уравнение теплопроводности
Отметим, что для решения ряда задач использование декартовых координат не
является удобным.
Более естественным может оказаться выбор криволинейных систем координат.
140.
Некоторые сведения из математики. Касательныйвектор к кривой в пространстве
Кривую в пространстве можно задать параметрически:
x x p y y p z z p p – параметр, непрерывно
некотором диапазоне значений
Дифференциал дуги:
2
2
dx dy dz
ds dx 2 dy 2 dz 2 dp
dp dp dp
dx
cos x
ds
cos y
cos z
dx
dp
dp
меняющийся
в
- иллюстрация для
случая
плоской
кривой
2
dx
dp
- проекция единичного
2
2
2
2
2
2 касательного вектора к
dx dy dz
dx dy dz кривой на ось x.
dp
dp dp dp
dp dp dp
dy
dp
2
2
2
dx dy dz
dp dp dp
dz
dp
2
2
dx dy dz
dp dp dp
2
2
2
Обозначим: H dx dy dz
dp dp dp
2
единичный
1 dx dy dz , , касательный вектор
Тогда:
H dp dp dp к кривой
141.
Некоторые сведения из математики. Криволинейныекоординаты
Положение точки в пространстве можно задать тройкой чисел p1, p2, p3 взаимно
однозначным образом связанными с декартовыми координатами.
p1 p1 x, y, z p2 p2 x, y, z p3 p3 x, y , z
x x p1 , p2 , p3 y y p1 , p2 , p3 z z p1 , p2 , p3
Вычислим расстояние между двумя близкими точками:
22
22
Фиксируя
координату
p
получим
1
yy
xx
xx
xx
yy
yy
ds22 dx
dx22 dy
dy22 dz
dz22
dp11
dp22 некоторую
dp33 координатную
dp11
dp22 поверхность
ds
dp
dp
dp
dp
dp
dp33
p
p
p
p
p
p
p
p
p
p
p
p
22
33
11
22
33
11
которой
внутри
меняются
только
22
22
22
22
координаты
p
,
p
.
zz
xx
xx
2 3 xx
zz
zz
dp11
dp22
dp33
dp11
dp22
dp33
dp
dp
dp
dp
dp
dp
2
другие
pp22
pp33
pp33
Аналогично,
pp22
фиксируя
pp11
pp11
координаты
координаты
получим
ещё две
22
22
22
22
22
22
zz координатные
yy
yy
yy
zz поверхности.
zz
dp11
dp22
dp33
dp11
dp22
dp33
dp
dp
dp
dp
dp
dp
pp22 получается
pp11
pp22
pp33
точка
pp33 на пересечении
pp11 Искомая
поверхностей.
x x
x x
x x трех координатных
2
dp1dp2
dp2 dp3
dp1dp3
Координатные
поверхности
кривым, вдоль которых
p2 p3 пересекаются
p1 p3 по некоторым
p1 p2
22
2
2
2если, например,
меняется
только
одна
из
координат.
Действительно,
кривая получена
xx y y xx
xy y x y y x
x
координатных
плоскостей
которых
dp11 dp1dp
dp
2 dp3 dp1 внутри
dp1dp
dp32 фиксированы
dp3 координаты p2 и
пересечением
dp222 dp33 dq
2 dp
pp332 p 3 может
p2 pp22 их пересечения
p 1 p 3 p2только
1
1 pна
p1 меняться
p3
p1.
p 3 , ppто
1 линии
координата
x z xz
x z x z
x x
линии
x x
z x dp
z 1называются
Такие
координатными.
dx
dp
dp
2
3
2
dp
dp
dp
dp
dp
dp
2 p dp1dp
dp2 dp 3
1dp12dp3
2
3
1
3
2
p
p
1
2
3
p
p
p
p
p
p
p2 p3
1
3
1 p1 2 p3
p1 p2
2 3
142.
Некоторые сведения из математики. Криволинейныекоординаты
Потребуем, чтобы выражение для ds2 не содержало слагаемых со множителями dp1dp2,
dp2dp3 и dp1dp3.
x x
y y
x x
x x
y y
y y
0 2
dp1dp2
dp2 dp3
dp1dp3 2
dp1dp2
dq2dp3
dp1dp3
p2 p3
p1 p3
p2 p3
p1 p3
p1 p2
p1 p2
z z
z z
z z
x x y y z z
2
dp1dp2
dp2 dp3
dp1dp3 2dp1dp2
p2 p3
p1 p3
p
p
p
p
p
p
p1 p2
1 2
1
2
1
2
x x y y z z
x x y y z z
2dp2 dp3
2dp1dp3
p
p
p
p
p
p
p
p
p
p
p
p
2
3
2
3
1
3
1
3
2 3
1 3
1 x y z
e p1
,
,
H1 p1 p1 p1
2
2
1 x y z
1 вектор
x yкасательный
z
- единичный
к
координатной
e p3
, линии,
,
вдоль
e p2
,
,
H 3 p3 p3 p3
H 2 p2 координата
p2 p2 p1
которой меняется
x y z
H
p
p
1 1 p1
2
1
2
2
2
x y z
H 22
p
p
2 2 p2
2
2
x y z
H
p
p
3 3 p3
2
2
2
3
ep1, ep2, ep3 – единичные вектора касательные к координатным линиям; Н1, Н2, Н3 коэффициенты Ламе.
e p1, e p 2
1 x x y y z z
H1H 2 p1 p2 p1 p2 p1 p2
e , e H 1H px px py py pz pz
p1
p3
1
e , e H 1H px px py py pz pz Таким
3
1
3
1
3
1
3
образом,
для
того
чтобы
удовлетворить
нашему
требованию
2 3
2
3
2
3
2
3
необходимо и достаточно, чтобы вектора ep1, ep2, ep3 были взаимно ортогональными.
Такие системы криволинейных координат называются ортогональными.
p2
p3
143.
Некоторые сведения из математики. Элемент объемав ортогональных криволинейных координатах
Итак для криволинейных ортогональных координат
x 22 y 22 z 22
x 22 y 22 z 22
x 22 y 22 z 22
dp2222
dp3232
ds 22 dp1122
p11 p11 p11
p22 p22 p22
p33 p33 p33
H12 dp12 H 22 dp22 H 32 dp32
Для малых приращений
s1 ds1 H1dp1
s2 ds2 H 2 dp2
s3 ds3 H 3dp3
Тогда элемент объема
dV ds1ds2 ds3 H1H 2 H 3dp1dp2 dp3
Для того, чтобы записать уравнение теплопроводности в криволинейных координатах
необходимо знать выражения для вычисления дивергенции и градиента в этих
координатах.
Векторное поле в криволинейных координатах задается в виде разложения по
векторам локального базиса (т.е. по векторам ep1, ep2, ep3).
Т.е. например, для некоторого векторного поля а:
a a p1 p1 , p2 , p3 e p1 a p 2 p1 , p2 , p3 e p 2 a p 3 p1 , p2 , p3 e p 3
144.
Некоторые сведения из математики. Дивергенция иградиент в криволинейных координатах
a, dS
diva lim
S
V
Поток через 2 грани, перпендикулярные
координатной линии q1
d pp11 a p1ds2 ds3
a p1ds2 ds33 p
p dp
V 0
p1 dp1
dp2 dp3 a p1H 2 H 3
p11
p1 dp1
a p1H 2 H 3
Аналогично d p 2 dp1dp3 a p 2 H1H 3
p1
p2 dp2
a p 2 H1 H 3
p2
d dp dp a H H
p3
1
2
p3
1
2
p3 dp3
a p 3 H1 H 2
p3
dp2 dpa
aH
dpa1dp3p a
appp22 H
pp a pdd1H
3 aH
p1 H
2H3
p1 H
2 H 3
p2H
1H
3
1H,33p e
3e
1p
p1p11 dd
H
H
a
H
dd
a
,
p
,
p
a
,
p
2
3
p
2
1
3
p
3
1
2
p
dp
p
p
dp
p
p
1
1
2
3
p
1
p
2
1
2
322
p2
p
dp
p
p
dp
pp
1
1
1
2
2
2
3
33
2
2
1
22
1
div
1 1
diva
a p 3 pH
dV
H H dp dp dp33
H1H 2 H 3dV
p1
H
p21H 2 H 3dp1dp2 dp
p33
1 , 1p2 ,2 p333 e p113 22
1 a H H ae Hесть
H a H H
Проекция градиента скалярного поля U на направление
производная по этому
Получим
dp dp a теперь
H H выражение
a H H для градиента в криволинейных координатах.
1
2
p3
1
2
p3 dp3
p3
1
H1H 2 H 3dp1dp2 dp3
направлению.
gradU p lim
s 0
1
т.е.
1
U
1 U
s1 H1 p1
gradU
2
p3
p1
2
3
H1 H 2 H 3
p1
gradU p
1 U
H 2 p2
2
1 U
1 U
1 U
e p1
e p2
e p3
H1 p1
H 2 p2
H 3 p3
p2
p1
p
1
3
p3
1
p3
2
gradU p
3
2
1 U
H 3 p3
145.
Уравнение теплопроводности в криволинейныхкоординатах
Вычислим теперь div gradU
a p1H 2 H 3 a p 2 H1H 3 a p 3 H1H 2
1
diva
H1 H 2 H 3
p1
p2
p3
gradU
1 U
H1 p1
1 U
ap2
H 2 p2
1 U
a p3
H 3 p3
a p1
Тогда
1 U
1 U
1 U
e p1
e p2
e p3
H1 p1
H 2 p2
H 3 p3
H 22H 33 U H1H 3 U H1H 2 U
1
div gradU
U
H11H 22H 33 p11 H11 p11 p2 H 2 p2 p3 H 3 p3
2
2
x y z
H1
p
p
1 1 p1
2
2
2
x y z
H2
p
p
2 2 p2
2
2
2
x y z
H3
p
p
3 3 p3
2
Сферические координаты
Цилиндрические
координаты:
Лапласа:
Лапласа:
x rcos
cos H1 1 H1 Оператор
1 Оператор
p1 r x r sin
2
y r sin sin H r H 1 1 12 1 2 1 2
1
p
z
2
y r sin
2
2
r
r 2 2 sin2 2 2 2
2
2
r
r
r
r
sin
r
sin
p z r cos
H
r
sin
r
r
r
z
r
H
r
3
3
3
z z
Линейное уравнение теплопроводности:
T
1 2 T T 2T 1 1 2T q vT
1
2T qv
a 2 rr 2 2 2sin
2 2
2
t
r
r
r
z
r
c
r r r r sin r sin c
146.
Уравнение теплопроводности в движущихсякоординатах
В некоторых задача лазерного нагрева удобнее использовать подвижную систему
координат.
Выясним какой вид будет иметь уравнение теплопроводности в системе координат
движущейся относительно рассматриваемого тела.
x, y, z - неподвижные относительно тела
координаты
система
координат,
x , y , z движущаяся со скоростью v
относительно тела
Пусть T(x, y, z, t) – распределение температур
в неподвижных координатах, а Tˈ(xˈ, yˈ, zˈ, t)
– в подвижных.
Ясно, что должно быть выполнено:
При этом для неподвижных координат x x vxt
d
dt
2T 2T 2T qv
y y v y t
T
a 2 2 2
t
y
z c
x
z z vz t
Тогда
для
подвижных
координат
получим:
dT T T dx T dy T dz T
Производные по пространственным
dt
T t x dt y dt qv -z уравнение
dt
t теплопроводности
в подвижных координатах
v , gradT a T
координатам
при
этом
t
c
T
T T
T T T
v
v
v
v , gradT преобразовываться не будут.
x
y
z
Уравнение
координатах используется при анализе
x
y
z в движущихся
t
t
t теплопроводности
задач лазерного нагрева движущимся пучком, а также при анализе задач лазерного
испарения поверхности.
T x, y, z , t T x , y , z , t
147.
Методы решения уравнения теплопроводности1. Метод интегральных преобразований (операционный метод).
Операционный метод основан на преобразовании искомой функции T(x, t) по одной
из переменных, причем это преобразование (обычно используется преобразование
Лапласа по времени, преобразование Ганкеля и др.) выбирается с таким расчетом,
чтобы уравнение для новой (преобразованной) функции было значительно проще
исходного. Находят решение преобразованного уравнения, а затем, применяя к
нему обратное преобразование, определяют решение исходного уравнения.
2. Метод источников (метод функций Грина)
Идея метода состоит в том, что сначала находят специальное решение краевой задачи
теплопроводности того же типа (так называемую функцию Грина) , но более простое.
Через него определяют интегральное представление решения исходной задачи.
Функция Грина описывает влияние мгновенного точечного теплового источника на
температурное поле. Решение задачи для произвольного источника получается
суммированием (интегрированием) вкладов от точечных источников.
3. Численные методы решения
Несмотря на то, что большинство реальных задач, как правило, решаются с помощью
численного анализа весьма полезно ознакомиться с аналитическими решениями
задач теплопроводности, поскольку они легко позволяют проиллюстрировать
наиболее характерные особенности лазерного нагрева материалов, знание которых
необходимо для специалиста в области лазерной обработки материалов.
148.
Некоторые специальные функции, использующиесяв теории теплопроводности. Интеграл вероятностей
и дополнительный интеграл вероятностей
x
2
t
erf x
e
dt - интеграл вероятностей
2
0
erfc x
2
t
e
dt 1 erf x - дополнительный интеграл вероятностей
2
x
erf ( ) 1
erf (0) 0
erfc( ) 0
erfc(0) 1
2
2
d
2 x2 yy22
xx2 yy2
xx22
- эти
вытекают
erf x e dxe ee dy
dx
dy
равенства
e
dxdy
e dxdx
непосредственно
из
2 определения
d
2
erfс rx2 e xa
dx
2 re dr e da
22
xx22
00
00
n 2 n 1
1
r 2 t 2a
3
5
t 2 1 x
2
2
x
x
e
dt
e
dt
erf
x
x
...
Т.о. справедливо
разложение
Получим
разложение
для erf(x) виде
степенного
2 ряда.
21 n!
da
0 2rdr
2
n
3
10
n
0
x
n 2n
n
2
2
2
1
t
t
t
Полученный
ряд является
при
x можно
t
erf сходится,
e малых
dt
x
e t знакопеременным и быстро
eограничиться
0
nслагаемым:
!
n 0
n! только линейным
n 0
2
n 2
nn 22nn
n 2 n 1
xx
11 nnt 222nnn x
xx
erf x 22 xx x
erfc
x
2
1
t
2
2
1
t
1
t
1
2
dt
2
dtdt 2 x .
t
erf
dt
erf xx ee t dt
dt
dt
0 nn!!
0 0 n
n
!
00
n
!
0
n
0
n 0
n 0 00
n 0 2n 1 n!
22
149.
Некоторые специальные функции, использующиесяв теории теплопроводности. Кратные
дополнительные интегралы вероятностей
Кратные дополнительные интегралы вероятности определяются с помощью
следующих рекуррентных соотношений:
i erfc x erfc t dt
1
x
i erfc x i1erfc t dt
2
x
.......................................
i erfc x i n 1erfc t dt
n
x
1
В дальнейшем нам понадобится только i erfc x ierfc x .
2 2
t 2
x
При
xerfc
x
x
1
x
terfc
t
td
erfc
t
ierfcмалых
erfc tt dt
dt
terfc
t
te
dt
x x:erfc
e 1 x
x
x
xx
xx
1 2
2
1 t 2 1 1 x2
ierfc
x
x te иt dt ierfc
terfc
t x xerfc x
Соответственно
fdg
gdf e0 e
проинтегрируем по частям
fg
x
x
2
2
x
149
1 x2
Получим разложение для ierfc(x):
Таким образом, справедливо рекуррентное соотношение: ierfc x
e xerfc x
150.
Интегральное преобразование ЛапласаПреобразование Лапласа некоторой функции вещественного аргумента f(t) задается
следующим образом:
s – комплексная переменная
st
f
t
e
dt L f t f L s
0
f(t) - оригинал
fL(s) - изображение
Полагается, что f(t) такова, что интеграл сходится (по крайней мере для некоторой
области значений s), кроме того обычно считается, что f(t) = 0 при t < 0.
Обратное преобразование Лапласа позволяет по изображению восстановить оригинал
функции, т.е. если L[f(t)] = fL(s), то L-1[fL(s)] = f(t), где L-1 означает обратное
преобразование Лапласа.
Можно показать, что обратное преобразование дается формулой
i
1
st
L 1 f L s f t
f
s
e
ds
L
2 i i
здесь σ – вещественное число, такое, что все особые точки функции fL(s) имеют
вещественную часть меньшую σ, сама же функция fL(s) должна равномерно
стремиться к 0 при s .
151.
Примеры нахождения изображений некоторыхфункций. Свойства преобразования Лапласа
Приведем несколько примеров вычисления изображений:
A
1. Lf At A const
s
Res > 0
t At 2
2. Lf At
Res > 0
A
s
t kte
3. Lf Ae
kt
A
s k
Res > -k
A st A
L A Ae dt e
0
s
s
0
st
e st
e
A
A
st
L At A te dt A t
dt 2 e st 2
0
s 0 0 s
s
s
0
1
kt
L e e s k t dt
s k
0
st
Более полная таблица оригиналов и изображений по Лапласу может быть найдена в
книге А.В. Лыков. Теория теплопроводности. М.:”Высшая школа”, 1967, 599 с.
Свойства преобразования Лапласа:
1. Свойство линейности
L Af t Bg t AL f t BL g t
L 1 Af L s Bg L s AL 1 f L s BL 1 g L s
здесь А, В – некоторые константы, fL, gL – изображения функций f и g соответственно.
Свойство линейности прямого и обратного преобразования Лапласа является
прямым следствием линейности операции интегрирования.
152.
Свойства преобразования Лапласа2. Изображение производной (!)
дифференцирование
оригинала
функции
df
df t df t st
LL
sf L s e f dt0 f соответствует
t e st dt sf Lизображения
t e st s f домножению
s f 0 на s и
0
dt 00 dt
добавлению
константы
f(0)
0
Также ясно, что
d 2 f t
df df
df
2
L
sL
s
f
s
sf
0
2
L
dt dt
dt
dt t 0
t
0
Рассуждая аналогичным образом, для производной n-го порядка получаем:
d n f t
d n 1 f t
n
n 1
n 2 df t
L
...
s fL s s f 0 s
n
dt t 0
dt n 1 t 0
dt
3. Интегрирование оригинала функции.
t
d
t
fL s
LМожно
dt что f t dt f t dt
f t записать,
s
0
0
t
2
2
dA t
t
t 2
2
t
Пример:
L
At
A
или
dt A L Lf tA L 3 f t dt sL f t dt 3
f t свойство
At
Тогда, используя
(2)
0 Atполучим
2
2 dts 0
0
s
t
f s
или L f t dt L
n!
Несложно
увидеть, что s L At n A n 1 (n 0,1,2,...)
0
s
153.
Свойства преобразования Лапласа4. Теорема подобия
ss
- замена
переменной
tt
1 s t на At в оригинале функции
1 stst s
dt
dt
A
A
L f At e f L ff ((At
e f ((tt )) замене
f L в изображении
At
dt соответствует
функции переменной
))dt
A
A
A
A
A
A
00
s 00на (s/A) и делению
изображения
на A.
t At
5. Теорема смещения
s A tt
- замена
на (s - А)
L e At f t f eL stse AtAf t dt
e s A переменной
f t dt f L ss вA изображении
соответствует умножению оригинала на eАt.
0
00
6. Производная изображения
df
f L L ss e st f t dt
L tf t
ds 0
d
ds
n
d
fL s
n
st
Для
производных
более
высоких
порядков:
L
t
f t
df L s
d e
df L s
st
n
tf t
te ds
f t dt L
f t dt
ds
ds
ds
0
0
0
7. Интегрирование оригинала
s t
f t st
f t
e
f t ss tt
f
s
ds
f
t
e
dtds
f
t
dt
ds L f t
e dt L
s f LLL s ds
t
t
t
t
s
ss
ss 00
0
0
8. Умножение изображений
t
t
(здесь fL1 и fL2 –
f L1 f L 2 L f1 t f 2 t t dt L f1 t t f 2 t dt изображения функций
0
0
f1 и f2 соответственно)
154.
Применение метода интегральных преобразований крешению задач теплопроводности
Для того, чтобы решить задачу теплопроводности
преобразования Лапласа по времени необходимо:
методом
интегрального
1. К уравнению теплопроводности применяем преобразование Лапласа по времени.
Вместо уравнения для оригинала функции получаем уравнение для изображения.
2. Полученное уравнение (являющееся более простым по отношению к исходному)
решается относительно изображения функции.
3. Используя известные соотношения между изображением функции и её оригиналом
находится искомое решение.
Восстановление функции по её изображению осуществляется с использованием
таблиц преобразования Лапласа в сочетании с рассмотренными ранее свойствами.
Применение интегрального преобразования Лапласа по времени позволяет исключить
производную по времени в уравнении для изображения температуры.
Проще всего анализу подаются задачи, в которых температура зависит только от
одной из пространственных координат.
155.
Нагрев полупространства экспоненциальноспадающим с глубиной источником
Во многих случаях лазерного воздействия можно считать, что излучение затухает по
экспоненциальному закону, соответственно, объемный источник тепла также будет
спадать по экспоненте.
Рассмотрим одномерную задачу теплопроводности.
Одномерное
линейное
уравнение
Точные границы применимости одномерного
рассмотрения мы
установим позднее.
теплопроводности:
Однако, интуитивно ясно, что оно применимо,
когда поперечный размер пучка
x
достаточно большой, а нагрев не слишком T
продолжительный
импульсы).
2T Aq0 e(короткие
t
a
x 2
c
Граничные условия:
Начальное условие:
T
2T Aq0 e x
a 2
t
x
c
2TL Aq0 e x
sTL T0 a 2
x
cs
2TL
Aq0 e x
a 2 sTL
T0
x
cs
L
T x,0 T0
Необходимо
также преобразовать граничные
T
L sTL T0
(см. свойство (2))
условия:
t
T
k 22T 0 L st 2T T , t 2T LT0 L
TL TL x, s
L ax x 202 a e
dt a 2
2
x
x
x
0
T0
T
LAq0 e 0 x Aq0 e TxL
x
L x
s
x 0c
cs
156.
Нагрев полупространства экспоненциальноспадающим с глубиной источником
T0
TL
TL x
0
x x 0
s
Найдем общее решение
неоднородного уравнения – сумма общего решения
однородного уравнения и частного решения неоднородного.
2TL
Aq0 e x
a 2 sTL
T0
x
cs
Найдем общее решение однородного уравнения:
Обыкновенное
линейное неоднородное
2TL
x
2
a(с правой
sT
0
e
частью
специального
вида)
a
s 0
L
2
x
дифференциальное
уравнение
второго
s
s
s
x
x
oo
a
1,2
Tпорядка
сC2e a постоянными
a
L C1e
коэффициентами.
Частное решение неоднородного уравнения следуют искать в виде С3e x C4 .
x
TLобщее решение
Aq0 неоднородного
e
Тогда
уравнения будет
иметь вид:
x
2
С3e C4 .
T0
x s x
s cs
x
Aq0 e x
1 x T0
a
a
TL C21e x C2e x
2
Aq
e
2
0
Aq
a
1
0
aC3 e s C3e C4c s s a Ts0
С
Aq0
1
1
2
cs
C
c
s
s
a
s
T0
3
2
Решение,
удовлетворяющее
граничным
условиям
имеет
вид:
TL x
c
x
С
0
s
s
a
Из условия
2
Aq0 e
2
x
s
s
C3 a s2 e sC 4 a x
T 0 x
cs
Aq0 a
e
Aq0 e
12
T0 T0
C
TL
TL
s
Aq0
1 4
2
2
0
C
c
c 1 s s a s 2 s 0
s s a s
Из условия
a
c s s a
x x 0
a
2
sTL
157.
Нагрев полупространства экспоненциальноспадающим с глубиной
источником
s
Aq
TL 0
c
2
a
x
изображение
-
e
Aq0 e x
1
T0
распределения температур
2
2
c
s s a s
s s a s
a
Чтобы найти распределения температуры нужно по изображению восстановить
оригинал.
x
Aq e x
1
1 T0
1 Aq0 e
2 at
0
L
e
1
L T0
2
c
k
s s a
s
x s
2
xx
Aq e2 2 xx
1 aaxx Aq e x 1
x
a
1
Aq
e
1
e x 0
1 1
00 0
Aq000 0 a a e e 22a Aq
Aq0 aLa L11 11
L
LLL 11 1 1 Aq
L
s a 2
2222
2
L ccc
2
tierfc
c
ca
s
s s a
c
s aa
s
s s s
c s s s sa a 2 s s
k
2
at
Aq 01e x at1 s 1
1
s
s
e
1
x
x
x
2
2
2
2
2
a
a
a
Aq
x
Aq
x
k
x 1
at s
1
Aq
e 0s e a
e at 10 e x e eat erfc
s
s 0 a a 1 a
at .
e
erfc
L
L
L
k s2ks 2 a 2 s at s a 2k s s a2 at
s
ss
2
И окончательно получим, что
1
1 1
1 1 1
1 x
1
1
0e a
a 20 sat ierfc
s a 2 xa 2 s Aq2
sT a x,2 t s 2 Aq
s
a
s
a
k
2 at
k
По таблице найдем, что
e A s Aq0 2at A x
e xA s x Ab b t x
A
1
1
e e erfc Lat
e erfc
L
2 tierfc
T0
b e e erfc
b t 2 t at
2
k
s
s
2 at
2 at
2 t
s s
2
158.
Нагрев полупространства экспоненциальноспадающим с глубиной источником
Итак, мы получили, что нагреву полупространства постоянным во времени тепловым
источником, экспоненциально спадающим с глубиной, соответствует распределение
температуры:
2 Aq0 at
x Aq0e x
T x, t
ierfc
k
k
2 at
Aq0 2at x
x x
x
e e erfc at
e
erfc
at
T0
2k
2
at
2
at
Для температуры на поверхности:
2Aq
Aq0 0 2at
atAq0 atAq0 e 2at erfc at
T 0, t
e erfc at 1 T 0 T0
k
k k
k
2
Рассмотрим 2 предельных случая
(
at 1
1.
видно,
что
характер
зависимости
определяется
следующей
комбинацией
величин at .
δ – глубина проникновения излучения
at )
Воспользуемся разложениями справедливыми при малых значениях аргументов
e at 1 2at
2
erfc at 1
2
Тогда
2 at
e at erfc at 1
1
2 at
at
2 at
at
at
at
22
2
22 at
at
33
159.
Нагрев полупространства экспоненциальноспадающим с глубиной источником
2
Aq 2 at
T 0, t 0
e at erfc at 1 T0
k
2 at
e
erfc at 1
2 at
at
2
2
Aq0 t
T 0, t
Tat0 T0 - температура поверхности при адиабатическом нагреве
k c
В полученное выражение не входят величины, характеризующие теплопроводность
материала.
Это означает, что сделанное допущение at 1 соответствует ситуации, когда
теплопроводностью можно пренебречь.
Действительно, если сразу пренебречь теплопроводнотсью в
T Aq0 e x
t
c
2. at 1
то сразу получим
(
В этом случае T 0, t
T x, t
исходном
уравнении
Aq0 e x
T x, t
t T0
c
at )
2 Aq0 at
T0
k
2 Aq0 at
x
ierfc
T0
k
2 at
- пространственно-временное распределения
температуры в случае когда нагрев,
определяется теплопроводностью.
160.
Нагрев полупространства поверхностнымисточником с постоянной плотностью мощности
Можно показать, что решение
T x, t
2 Aq0 at
x
ierfc
T0
k
2 at
соответствует задаче о нагреве полупространства поверхностном источником с
постоянной плотностью мощности, т.е. является решением задачи вида
160
T
T
2T
k
Aq0 T , t T0
T x,0 T0
a 2 0
x
t
x
x 0
Условие поверхностного поглощения обычно хорошо выполняется для металлов.
Действительно, для металлов a ~ 10-4 м2/с , а δ ~ 10-8 м, соответственно для
длительностей tp > δ2/a ~ 10-12 c поглощение можно считать поверхностным.
Распределение температуры по глубине
определяется функцией ierfc, которая
отлична от нуля при значениях аргумента
меньших 1.
Соответственно, за глубину прогретого
слоя за время tp можно взять величину lT
= (atp)1/2 (lT - длина теплопроводности)
Распределение температуры по глубине в
момент окончания лазерного воздействия
импульсами различной длительности (0.1
и 1 мс)
161.
Остывание полупространства после нагреваповерхностным источником постоянной мощности
В ряде случаев оказывается важным исследование не только стадии лазерного нагрева
материала, но также и стадии остывания материала после окончании лазерного
воздействия .
Для исследования стадии остывания материала после нагрева поверхностным
источником воспользуемся следующим приемом.
T
2T
a 2 0
Рассмотрим одномерное уравнение теплопроводности
t
x
с граничными условиями
Ясно, что если
T1 t , x
и
T2 t , x
то,
T1 t , x T2 t , x
k
T
A q1 q2 T , t T0
x x 0
- решение соответствующее условию
- решение соответствующее условию k
k
T
Aq1 ,
x x 0
T
Aq2 ,
x x 0
решение соответствующее условию
k
T
A q1 q2 .
x x 0
Воспользуемся этим фактом при анализе задачи остывания полупространства.
162.
Остывание полупространства после нагреваповерхностным источником постоянной мощности
0, t t p
q1 q0 q2
Для этого будем полагать, что
q0 , t t p
Т.е.
зависимость
плотности
Но соответствующие решения T1(x, t) и T2(x, t)
мощности от времени будет иметь
уже фактически были получены нами ранее.
вид:
Действительно:
2 Aq0 at
x
ierfc
T0
k
2 at
0, 0 t t p
T2 x, t 2 Aq0 a t t p
x
, t t
ierfc
p
2 a t t
k
p
T1 x, t
(решение T2(x, t) имеет знак «-» перед q0 и
сдвинуто во времени на величину tp при t > tp)
Для
температуры поверхности:
Тогда:
2 Aq0 at
x
2 Aq0 aierfc
T0 , 0 t t p
k
t
T
,
0 t tp
2
at
0
k
T
T x0,, tt
2
Aq
a
x
x
2 Aq0 0 a tierfc
T , t t
T t,
t p ierfc
p
t
t
t
t
t
k
p
0
p
0
2
at
2
a
t
t
p
k
163.
Метод источниковВ ряде задач решение линейного уравнения теплопроводности можно сравнительно
легко получить методом источников.
2T 2T 2T qv
T
Рассмотрим уравнение теплопроводности
a 2 2 2
t
y
z c
x
и выясним какой вид должна иметь его правая часть, чтобы функция G являлась
решением.
1 t t - функция
E0
G x, y, z , t t t g x x , y y , z z , t t t t
0 t t Хевисайда
c
E0 – константа [Дж]
x x 2 y y 2 z z 2
g x x , y y , z z , t t
exp
3
4
a
t
t
2
4
a
t
t
1
22 2
22
22
2
2
55
x
x
y
y
z
z
x
x
y
y
z
z
g
1
3
g
1
3
x
x
y
y
z
z
G E0
E0 g
3
1
2
2
2
exp
g 333 t t tt t t exp
g
t t
t
2
4
a
t
t
t
2
4
a
t
t
t
c t
c t
t 44 aa 2222
4a
2
2
2
x
E x22 1 x 22
G
2x
2
22
22
x
x
G E
E
2 22 01
0
30
3
Аналогично
для
производных
по y и z
g
x
x
y
y
z
z
x
x
y
y
z
z
g
22
t t
g
t
t
2
2
2
xt t cc exp
tt tt
t
a 4a4 at t 4 a t t c2 2a t
4
a
2
2
2G12 E0 2 x 2 x 2 y xy 2 x z z 22
E0 3 2x 5 x x x2 2 2 y 1y 2 z 1 z 2
7
x
x
y
y
z
z
G
G
G
E
3
2
1
g
g
g
t
t
t
t
2
0
a 2 3 exp
t t
t t 2
t
t
t
t
x 2 c 22a t t2 4a 2t
a g tt t
c
a
4
a
2
2
4a 2
4
a
4 xa 2 y z c
164.
Метод источниковИтак, мы видим, что функция G решением уравнения теплопроводности если qv = qG, где
qG E0
d
g.
dt
d
t t
Но
dt
вид функции
x x 2
1
exp
1
4
a
t
t
4 a t t 2
, а при t t
при различных t – tˈ
x x 2 y y 2 z z 2
g
exp
x x y y z z
3
4a t t
2
4
a
t
t
Итак, мы показали,
что
справедливо
равенство
q
E
t
t
x
x y y z z - соответствует
Таким образом
G 2 0
2
2
G G G E
G
0
, t zˈ),
dy dz
qv x ,(xˈ,
y , zyˈ,
dt dxт.е.
мгновенному
в точке
a 2 выделению
2 энергии
t t E 0 xв момент
x y времени
y z ztˈ
2
t
y
z c
xмгновенного
действию
точечного источника.
x x x dx f x , соответственно
ВспомнимG,свойство
дельта-функции
f мгновенного
Функция
соответствующая
действию
точечного источника называется
функцией
q x , y ,Грина.
z , t t t x x y y z z dt dx dy dz q x, y , z , t
1
v
v
Тогда мы получаем исходное уравнение теплопроводности с объемным источником
2T 2T 2T qv
T
a 2 2 2
но при этом
t
x
y
z
c
2
2
2
2
2
2
t
11 t qtv qxv , yx ,,zy , ,t z , t x x x y y y z zz z
dx dy dz
T x, y, z , t dt
exp
dt dz
dx dy
3 3 exp
cc
4a 4t a tt t
4
4 aa t t t t 2 2
165.
Нагрев полупространства поверхностнымисточником круглой формы
Применим метод источников к задаче нагрева полупространства поверхностным
источником круглой формы.
Для того чтобы применить метод источников к данной
задаче нужно рассмотреть эквивалентную задачу нагрева
всего пространства источником вида
2 Aq0 x y 2 z 2 r02
qv
2
2
2
0 y z r0
Тогда распределение температур можно найти из выражения (считаем, что источник
включился в момент времени t = 0):
t
x x 2 y y 2 z z 2
x
2 Aq0
T x, y , z , t
dt dy dz
exp
dx
3
c 0 y 2 z 2 r 2
4a t t
4 a t t 2
0
Будем искать решение на оси пучка (при y = 0, z = 0)
t
xx xx 22 yy 22 zz 22
x
2 Aq0
dx
T x,0,0, t
dt dy dz
exp
dx
33
c 0 y 2 z 22 r022
44aa tt tt
0
4 a t t 22
y 2 z 2
x2
exp
dt exp
dy dz
3
3
4a t t y 2 z 2 r02
4a t t
c 4 a 2 0 t t 2
2 Aq0
t
1
166.
Нагрев полупространства поверхностнымисточником круглой
формы
t
y 2 z 2
x2
T x,0,0, t
exp
dt exp
dy dz
3
3
4a t t y 2 z 2 r02
4a t t r 2
c 4 a 2 0 t t 2
2 Aq0
1
y 22 z 22
r 22
exp
dr 4 a t t
dy dz 2 exp
rr dr
00
4a t t
4a t t
y 22 zz 22 rr0022
rr00
0
4 a t t
exp d
0
2
2
r
0
r
4 a t t 1 expr dr 2a t t d
4a t t
4a t t
t
aAq00 t
x22
r02
88 aAq
11
,0,0,tt
exp
TT xx,0,0,
exp
1 exp
dt
33
11
4
a
t
t
4
a
t
t
cc 44 aa 22 00 tt tt 22
t
t
x 2 r02
Aq0
1
x2
1
exp
exp
dt
dt
1
1
4
a
t
t
4
a
t
t
c a 0 t t 2
0 t t 2
222
tttt
2
1
3
1
3
x 2 2 222
4x a a 11 11 22 22 22
22 222
xxx
11 exp xx
22 x4
2
2 2 2222
dt
t
t
exp
t
t
d
exp
d
t
t
exp
t
t
d
e
d
e
d
exp
e
2
e
d
dt
e
d
e
2
e
d
x
x
x
00 t 112212 44aa tt tt
x
x
x
a
a
a
aa xxxx
a
2
at
xx xx
00 tt t 2
at at
22 2at
2
at
2 at
at
1
22 at
atat 3
2
at
2
2
2
at
2
x
x
x
2
t t d 11
t t 2 dt t t
11
222
4 axx
x 22
xx 2 a 1 x
x
xx x 4a 2x 1
x
exp erfc
erfc
exp
a 2 at exp 4at 2 at erfc 2 at
2
at
4
at
4
at
aa 2 at
2
at
по частям
интегрируем
x
2 tierfc
2 at
167.
Нагрев полупространства поверхностнымисточником круглой формы
t
t
x 2 r02
Aq0
1
x2
1
T x,0,0, t
exp
exp
dt
dt
1
1
4
a
t
t
4
a
t
t
c a 0 t t 2
0 t t 2
t
1
x2
x
exp
dt
2
tierfc
1
0
4
a
t
t
2
at
Aq
Aq00 Aq0 a
2
t t
x2 r 2
x 2 r02
1
0
exp
dt 2 tierfc
1
0
2 at
t t 2 4a t t
t
c aa
k
- зависимость температуры
2
2 от времени и глубины в
x
r
2 Aq0 at
x
0
пучка
при
ierfc
центре
T x,0,0, t
ierfc
2 at поверхностям
k
2 at
нагреве
пучком круглого сечения
2 Aq0 at 1
r0
На поверхности (x = 0): T x,0,0, t
ierfc
T0
k
2 at
При
При
at r0 T ( x, 0, 0, t )
at r0
2 Aq0 at
T0
k
Aq r
T (ierfc
x, 0, 0, tr)0 010 T0r0
2 at k 2 at
- решение то же, что и для одномерного
случая
- температура поверхности не зависит от
времени, т.е. нагрев выходит на
стационарный режим
168.
Режимы лазерного нагреваСуммируем основные полученные результаты.
1. Источник тепла поверхностный, одномерный теплоотвод. at
T
r0 at
2Aq0 at
T0
k
q
q ~
k T T0
- пороговая плотность мощности – минимальная
плотность
мощности,
необходимая
для
нагрева
поверхности до заданной температуры (T*).
2A
at p
1
tp
Q q ~ t p
- пороговая плотность энергии пропорциональна
корню из длительности импульса
2. Источник тепла поверхностный, трехмерный теплоотвод.
T
Aq0 r0
T0
k
- стационарный режим
Зависимость пороговой плотности
мощности от длительности воздействия
→
at
r0 at
169.
Режимы лазерного нагреваПроиллюстрируем на конкретном примере переход между рассмотренными режимами
лазерного нагрева при уменьшении размера пучка (Q = 175 Дж/см2, τ = 100 мкс, Al).
Распределение температуры к
концу импульса
Зависимости температуры от времени и от глубины
T
2Aq0 at
T0
k
r0 3 a
r0 a
r0
a
3
x
T ~ ierfc
2 a
r0 3 a
r0 a
r0
a
3
170.
Режимы лазерного нагрева3. Источник тепла объемный, теплоотвод мал.
at
r0 at
at
r0 at
Температура поверхности T Aq0t T0
c
4. Источник тепла объемный, трехмерный теплоотвод.
Температура поверхности
Aq0 r02
a
T
ln 19.4 2 T0
4 k
r0
Для металлов характерно поверхностное поглощение, толщина прогретого cлоя при
этом определяется характерным размером теплопроводности (at)1/2.
171.
Режимы лазерного нагреваРассмотрим задачу нагрева полупространства движущимся с постоянной скоростью
поверхностным источником тепла.
Для получения качественных
оценок можно считать, что
действие движущегося пучка для
точки, находящейся на оси пучка
сходно с воздействием импульса
длительностью tp = 2r0/v.
Тогда, условие
2ar0
2 Aq0
Aq r
T 0 0 Tv0 T0
kk
at p r0
Распределение температуры по поверхности при
поверхностном нагреве движущимся источником
(r0 = 0.7 мкм, v = 3 м/с, a ~ 10-6 м2/с).
2a
и, соответственно
примет вид v
r0
Динамика
температуры для точки,
2a
2a
v
v
rr00
находящейся на линии сканирования.
(медленнодвижущийся
(быстродвижущийся источник)
источник)
172.
Лазерный нагрев тонкой пленки на подложкеРассмотрим лазерный нагрев пленки на подложке.
В условиях когда r0 at
распределение
температур может быть найдено как решение
системы
2-х
одномерных
уравнений
теплопроводности:
T1
2T1 qv1
a1 2
t
x
c1
T2
2T2 qv 2
a2 2
t
x
c2
(индекс 1 относится к пленке, 2 – к подложке)
На границе пленки с подложкой задаются граничные условия следующего вида:
k1
T1
T
- непрерывность теплового потока при переходе через границу
k2 2
x x h
x x h раздела
T1 x h T2 x h
- непрерывность температуры при переходе через границу
Выписанные граничные условия соответствуют т.н. идеальному тепловому контакту.
Для оставшихся границах могут, например, выполняться условия следующего вида:
T
k1 1
0 (отсутствует теплообмен м/у
T2 x T0
пленкой
и
окружающей
средой)
x x 0
Объемные тепловые источники qv1 и qv2 определяются характером поглощения
излучения в пленке и подложке.
173.
Лазерный нагрев тонкой пленки на подложкеРассмотрим нагрев системы пленка-подложка при выполнении следующих
дополнительных условий
1. Все излучение поглощается в пленке
qv1 A1q0 1e 1x
qv 2 0
тогда
1 h
2. Пленка достаточно тонкая для того, чтобы считать, что она прогревается равномерно
h a1t
T2 x h будет
Решение
для T1 условия
иметь выполняются
вид:
Перечисленные
хорошо
для практически важного случая
импульсного лазерного нагрева
тонкой металлической
пленки на диэлектрической
c2 a2t
c22 a2t
A1q0 h 2 a2t c1
подложке.
T1 t
exp 2 2 erfc
1 T0
k2
c2
c1 h
c1h -4 2
h
c2 aусловие
Действительно, для металлов δ ~ 10 нм, a ~ 10 м /с, и при h > 100 нм второе
2t
.
Видно, что результат воздействия определяется комплексом параметров
выполняется для длительностей импульса tp > h2/а ~ 10-10 c.
c1h
h
Рассмотрим
случая:
T1
T2
T1
2T1 дваA1предельных
q0 e x
k
k
T1 T2 x h
a1 2
1
2
dx
x
x
x h
x h
затраты на нагрев
подложки,
пленка термически тонкая)
1. t c2 a 2xt c1h c(преобладают
1
0
h
T2
свойства
T1системы
2A1q 0 a2t T 1 T1
T 1 T1 - оптические
A1q0
пленка подложка
h
T
dx
h
cT11 T 1dx
T1dx
k
A
q
a
т.к.
T
(x)
≈ const
1
1 1 T0
1 0
1
t x h
t
t
пленкой,
а
теплофизические
подложкой
t t0 0 k x xx hx h x xx 0определяются
c
0
x 0
1
h h
2
- новое
граничное
условие
для
затраты
на нагрев
подложки)
2. cT2 2 a2t c1 hT2 (преобладают
T2
2T2
a2 2 0
c1h
k2
A1q0 уравнения теплопроводности
At qx th
x x h
t
x
1 0
для
пленки
T1
T0
- пленка греется адиабатически
hc1
Такую задачу
несложно решить методом преобразования Лапласа по времени.
174.
Лазерный нагрев импульсом произвольнойвременной формы
До настоящего момента мы полагали, что плотность мощности излучения в течение
импульса постоянна во времени.
Рассмотрим задачу лазерного нагрева полупространства импульсом произвольной
формы для случая одномерного нагрева поверхностным источником.
t
Задача нагрева
импульсом с плотностью мощности q0 эквивалентна
A a q0полупространства
t dt T - зависимость
температуры поверхности от времени
T 0, t
0
задаче оkнагреве
всего
пространства
удвоенной
плотностью мощности, с учетом того,
0 t t
что задача одномерная и источник поверхностный (действует в плоскости x = 0)
Рассмотрим несколько примеров:
функция qv будет иметь вид:
Более реалистичной
оказаться
форма импульса
задаваемая соотношением:
Сравним
действие может
импульсов
прямоугольной
и треугольной
временной формы,
t
имеющих
одинаковую
энергию.
(Q
Q
q
2
Aq
t
0 – плотность энергии импульса, t0 – длительность переднего
0
q0v t 20 te t 0 x .
фронта импульса)
t0
В этом случае можно показать, что для максимальных
Тогда
22
t
температур
соотношение:
x x справедливо
y y 22 z z 22
1 t 2 Aq0 t
1
T x, t
dt x exp
exp
dy dz
Tmax 4Ta0 t t 8
c 0 2 a t t
4
a
t
t
4
a
t
t
1.09
П
T
max T0
3 6
2 Aq0 t
1
x
exp
dt
А
c 0 2 a t t
4
a
t
t
для времени достижения максимальной температуры
t
2
для импульса треугольной формы:
На поверхности (x = 0):
2
tmax t p
3
- зависимость
температуры поверхности сильноtt
A Aa qq00 t t
нагрева телаи приохлаждения,
T 0, t
dtdt TT00 поглощающегоДинамика
полубесконечного
нагреве
ck a 00 tt
tt
Прямоугольная
(синяя
линия)
и соответствующая действию прямоугольного
лазерным импульсом с произвольной временной формой.
куполообразная (красная линия) формы
(синяя кривая) и куполообразного (красная
кривая) импульса.
175.
Лазерный нагрев с учетом температурнойзависимости поглощательной способности
Для металла, описываемого моделью Друде поглощательная способность при γ < ω < ωp:
при этом
~ (1 5) 10 5 K 1
A A0 T T0
Рассмотрим одномерную задачу нагрева металла в таких условиях изменения
поглощательной способности:
T
2T
T
k
A T q0 A T A0 T T0
a 2 0
T , t T0 T x,0 T0
x x 0
t
x
Решение такой задачи несложно получить методом преобразования Лапласа по времени:
T x, t
A0 x 2at
x
x
e
e
erfc
at
erfc
T0
2
at
2
at
На поверхности:
A0 2at
T 0, t
e erfc at 1 T0
при
при
at 1
T 0, t
2 Aq0 at
T0
k
at 1
T 0, t
2 A0 2at
e T0
*
Время возникновения неустойчивости t
1
2a
q0
k
Пример расчета для меди:
176.
Экспериментальные методы исследования лазерногонагрева
Экспериментальные методы измерения температуры можно разделить на
1. Контактные методы (например, с использованием термопары)
Для исследования задач лазерного нагрева этот метод обладает рядом недостатков,
связанных с тем, что размеры области, подвергающейся нагреву могут быть сравнимы
с размером самой термопары.
Соответственно, она может служить стоком тепла, поглощать часть излучения, т.е. её
наличие будет искажать условия эксперимента.
2. Бесконтактные методы
- анализ теплового излучения нагреваемого тела
Используемые в настоящее время высокоскоростные ИК камеры имеют частоты
обновления кадров до нескольких десятков килогерц и выше, а также обладают
высоким пространственным разрешением (до нескольких десятков микрон)
- методы основанные на исследовании изменения интенсивности рамановского
рассеяния
Интенсивность рамановского (комбинационного) рассеяния зависит от температуры,
что позволяет использовать это явление для диагностики температуры.
Использование бесконтактных методов позволяет исследовать динамику лазерного
нагрева с достаточно высоким временным и пространственным разрешением.
177.
Экспериментальные методы исследования лазерногонагрева
Рассмотрим эксперимент измерению температуры кварцевого стекла при лазерном
нагреве с помощью ИК-камеры (см. Selim Elhadj, Manyalibo J. Matthews & Steven T.
Yang. Combined Infrared Thermal Imaging and Laser Heating for the Study of Materials
Thermophysical and Processing Properties at High Temperatures// Critical Reviews in Solid
State and Materials Sciences, 2014, 39:3, 175-196.).
Схема эксперимента:
f1, f2, Cf1 и Cf2 - линзы
Излучение CO2 лазера
фокусируется
на
образец плавленого
кварца и нагревает
его.
Тепловое излучение нагретого материала с помощью ZnSe клина, расположенного под
углом Брюстера (это позволяет избежать попадания в камеру p-поляризованного
излучения CO2 лазера, отраженного от образца), направляется на HgCdTe ИК камеру,
перед которой установлен узкополосный фильтр, который из широкого спектра
теплового излучения пропускает излучение с определенной, оптимальной для анализа
длиной волны (в рассматриваемом случае - 8.9 мкм).
Выясним, из каких соображений выбирается оптимальная длина волны для анализа
теплового излучения в данном эксперименте.
178.
Экспериментальные методы исследования лазерногонагрева
При лазерном нагреве материал будет прогрет по глубине неоднородно.
Подповерхностные слои, имеющие меньшую температуру, в общем случае также будут
вносить вклад в сигнал теплового излучения, регистрируемого камерой, что может
искажать оценку температуры поверхности.
Максимум поглощения плавленого кварца в ИК
диапазоне приходится на длину волны ~ 9 мкм.
Чтобы минимизировать это искажение длину волны для анализа следует выбирать из
условия её максимального поглощения исследуемым материалом.
Глубина проникновения излучения на этой длине волны ~ 9 мкм составляет ~ 0.1 – 1
мкм, что намного меньше, чем ожидаемый масштаб неоднородности нагрева
материала по глубине в рассматриваемом эксперименте (т.е. можно считать, что
температура внутри слоя, от которого регистрируется сигнал, практически
одинакова).
179.
Экспериментальные методы исследования лазерногонагрева
В эксперименте радиус пучка излучения r0 ~ 350 мкм, время облучения t ~ 5 c.
В этом случае at r0 . (для плавленого кварца a ~ 10-4 м2/с, δ = 10 мкм)
Зависимость
температуры
плавленого кварца от времени при
нагреве излучением СО2-лазера с
различной мощностью
P (P – мощность
Aq0 r0
q
0
T
T0
r02 излучения)
k
Лучшего согласования можно добиться,
если учесть, что пучок имеет гауссово
распределение
интенсивности
в
поперечном сечении.
Зависимость
максимальной
температуры
поверхности
от
отношения
мощности
излучения к радиусу пучка при облучении
плавленого кварца на различных длинах волн.
Для случая облучения на длине волны 4.6 мкм
экспериментальные точки не слишком хорошо
ложатся на прямую. Это связано тем, что для этой
длины волны источник будет объемным (и
зависящим от температуры).
180.
Термохимическое действие лазерногоизлучения
181.
Химическое действие лазерного излученияАктивация химических реакций под действием лазерного излучения может
происходить по двум механизмам:
1. Фотохимический механизм (резонансная лазерохимия).
Химическая реакция инициируется за счет резонансного возбуждения электронных
уровней атомов или молекул.
В зависимости от величины энергетического возбуждения различают фотохимические
процессы УФ диапазона, видимого диапазона а также ИК фотохимические процессы,
в которых существенно возбуждение колебательно-вращательных уровней молекулы.
Обычно (в условиях однофотонного возбуждения) скорость инициированной светом
реакции растет пропорционально интенсивности излучения.
2. Термохимический механизм (нерезонансная лазерохимия).
При термохимическом механизме активации реакция инициируется за счет
повышении температуры.
В этом случае скорость реакции зависит от температуры по т.н. активационному
закону (закону Аррениуса):
T
vR – скорость реакции, Ta – температура активации
vR ~ exp a
T
Многие особенности термохимического действия лазерного излучения обусловлены
аррениусовским характером зависимости скорости реакции от температуры.
182.
Общая характеристика термохимического действиялазерного излучения
Особенности термохимического действия лазерного излучения:
1. Активационный (аррениусовкий) закон инициирования химической реакции
обуславливает ряд особенностей в характере протекания химической реакции в
пространстве и во времени при лазерном воздействии.
2. Сильно-нелинейный характер термохимического действия лазерного излучения,
обусловлен возможностью формирования сложных опто-термо-химических обратных
связей.
Например, увеличение концентрации продуктов реакции может приводить к росту
поглощения нагревающего излучения в системе – возникает положительная обратная
связь (термохимическая неустойчивость), в противном случае обратная связь
отрицательная. В некоторых случаях положительная обратная связь периодически
может сменяться на отрицательную.
3. Возможность управления скоростью химической реакцией при изменении режимов
лазерного воздействия.
Примеры термохимических процессов, активированных лазерным облучением:
1. Лазерное окисление металлов на воздухе (железо, титан, хром)
2. Разложение металлоорганических соединений (формиаты Me(HCOO)n, карбонилы
Me(CO)n и т.п.)
3. Диссоциация составных полупроводников (GaAs).
183.
Лазерное окисление металлов на воздухеОсновные стадии лазерного окисления металлов на воздухе:
1. Адсорбция кислорода на поверхности.
2. Перенос атомов кислорода и/или ионов металла сквозь слой растущего окисла к
межфазным границам.
3. Собственно химическая реакция с образованием окисла.
Скорость роста окисла лимитируется наиболее медленной из перечисленных стадий.
При относительно невысоких температурах этой стадией является перенос реагентов
через слой окисла. При высоких температурах процесс роста окисла может
лимитироваться подводом кислорода из воздуха к окисляющейся поверхности.
При теоретическом анализе лазерного окисления
следующие типы процессов:
1. Теплофизические (уравнение теплопроводности)
приходится
рассматривать
2. «Химические» (уравнения химической кинетики, обобщенный активационный
закон)
3. Оптические (оптика слоисто-неоднородных сред)
Под «химическими» в данном случае также может пониматься анализ диффузионных
процессов в обедненном кислородом слое воздуха.
184.
Обобщённый активационный законКинетика изотермического окисления металлов на воздухе подчиняется обобщенному
активационному закону (исключая случай, когда лимитирующей стадией является
приток кислорода из газовой фазы):
B
db
T
n mm exp a
dt T b
T
b – толщина окисла
Bm – некоторая константа
Та – температура активации
m, n – целочисленные параметры. При различных m и n из него следуют известные
законы окисления: линейный, параболический, кубический и т.д.
При неизотермическом (лазерном) окислении в обобщенном активационном законе
просто полагают температуру зависящей от времени (T → T(t)).
b t
Т.е. если известна
температуры
окисляемой
поверхности
от времени то
t
зависимость
Ta
Bm
Ta
db
n
m
exp
db Bmбыть
exp из соотношения:
зависимость
окисла
от времени
dt
n m толщины
b может
T t найдена
dt
b t
T t b
m 1
T t
m 1 Bm I n t b0m 1
Ta
exp
dt
n
T
t
окисла
T t
b0 – начальная
толщина
b m db
Bm
T t
T a
I n t T t exp
dt
tT t
n T
0
b m 1 b0m 1 m 1 Bm T t exp a dt
0
T t
t
b0
0
n
Например, для Вагнеровского закона окисления (n = 0, m = 1):
b t 2 B1 I 0 t b
2
0
T
I 0 t exp a dt
0
T t
t
185.
Особенности окисления по активационному законупри лазерном нагреве
Итак, мы показали, что толщина окисла определяется величиной In(t).
Обычно Ta >> T(t), поэтому активационная экспонента
t
Ta
n
I n t T t exp
очень резко возрастает с температурой.
dt
0
T t
Ta ~ 104 – 105 K, T(t) ~ 103 K
Зависимость активационной экспоненты
от температуры
Поперечное распределение температуры
поверхности при гауссовом распределении
интенсивности и толщины окисла
Вследствие резкой зависимости скорости реакции окисления от температуры окисел
преимущественно будет формироваться в области, где температура максимальна, т.е.
в центре пучка (т.н. «термохимическое обострение»).
При определенных условиях «термохимическое» изображение может быть уже
оптического.
186.
bОценка интегралов вида f t e dt
g t
a
Для получения простых формул, позволяющих рассчитывать толщины окисла,
растущего в соответствии с обобщенным активационным законом, необходимо оценить
интеграл вида:
T
n
I n t T t exp a dt
0
T t
t
Для его оценки воспользуемся приближенными
методами.
b
Рассмотрим интегралы вида (интегралы Лапласа)
поведение при больших положительных λ.
f t e
g t
dt
и
изучим
его
a
Пусть функция g(t) при a ≤ t ≤ b имеет единственный максимум в точке t = t0, тогда
функция eλg(t) также будет иметь максимум в этой же точке, который будет тем резче чем
больше λ.
Тогда интеграл по промежутку a ≤ t ≤ b можно
заменить на интеграл по некоторой ε - окрестности
точки t0.
При этом в подынтегральном выражении можно
заменить f(t) на f(t0), а функцию g(t) в ε-окресности
точки t0 разложить в ряд Тейлора, ограничившись
первой ненулевой поправкой к значению g(t0).
187.
bОценка интегралов вида f t e dt
g t
a
Рассмотрим случай когда максимум g(t) достигается внутри промежутка (a < t0 < b).
Соответственно, полагаем, что f t f t0 и
Тогда
b
f t e
g t
dt f t00 e
g t t
2
0
g t00
t t00
2
tt0
0
a
a
f t0 e
t00
g t0
0.5 g t t
2
g t t 0.5 g
0
0
e
t t0
2
g t g t0
dt f t0 e
d f t0 e
g t0
t0
g t t
t t0 .
2
0
2
e
g tt tt
00
2
t t00 2
dt
t00
2
g t0
g t t
0
Соответственно, при больших λ можем считать, что в этом случае
g t t
t ft0 t e
f
t
e
dt
2
0
b
g t
0
a
g t0
2
g t t
0
Рассуждая аналогичным образом можно показать, что в случае когда максимум
достигается на краю промежутка (пусть для определенности при t = a)
асимптотическая оценка интеграла будет выглядеть следующим образом:
g t
b
f t0 e 0
g t
a f t e dt g
t t
0
188.
Эквивалентное время изотермического окисленияb
f t e
g t
dt f t0 e
g t0
g t t
a
Положим
1
g t
T t
Ta
2
b
f t e
dt
a
0
tt
f t T n t
g t
и вычислим I n t T t
nn
00
f t0 e
g t0
g t t
0
a
Taa
n
exp
dt Tmax e Tmax te
dt
T t
T
te – эквивалентное время изотермического окисления
Tmax – максимальная температура на рассматриваемом временном промежутке
Процесс неизотермического окисления можно представить как процесс
изотермического окисления при максимальной температуре, поддерживаемый в
течение некоторого эквивалентного времени.
Оценим эквивалентное время окисления в ситуациях когда максимум температуры
достигается различными способами.
2
T
T
2
T
1
1
2
2
1.
T 2 T max
T T 2 T 3
te
2
T
t
1
Ta T
2.
e
t t0
Ta T t t T
0
t t
1
T
t t0
0
2
max
T
2
11
T
1
te
te max
T 1 T 2
T
TaT TT 1
T
Ta T 1
a
t t0 0
t t0t t0 0
t t 0
1
0
0
T
1
t t0 0
T t t 0
0
2
max
T
189.
Лазерное окисление при облучении импульсомпрямоугольной временной формы
Если по каким либо причинам можно считать, что растущий окисел не влияет
существенным образом на оптические свойства системы пленка-металл и сама пленка
является термически тонкой, то для оценки динамики температуры можно
использовать формулы полученные в предыдущем разделе.
Например, при воздействии прямоугольного импульса (в условиях одномерного
теплоотвода):
T (t )
2 Aq0 at
T0
k
В этом случае эквивалентное время окисления за импульс длительностью tp:
2
Tmax
te
Ta Tmax T0
Tmax
2Aq0 a
T0
k
Толщина окисла образующегося за импульс:
T
b(t p ) 2
exp a
Ta Tmax T0
2Tmax
2
B1Tmax
tp
Толщина
окисла
резко
зависит
от
максимальной температуры в импульсе и
значительно слабее от его длительности.
Более сильному окислению подвержены термически тонкие металлические пленки,
т.к. в отличие от массивных образцов в толщину окисла будет давать вклад стадия
остывания.
190.
Анализ нагрева окисляющихся металлов в условияхизменения поглощательной способности
Во многих задачах лазерного окисления металлов можно считать пленку растущего
окисла термически тонкой ( c at p c0b , с0 – теплоемкость окисла).
В этом случае одномерная задача лазерного нагрева будет выглядеть следующим
образом:
T
2T
a 2 0
t
x
- уравнение теплопроводности для металла
T
k
A(b)q0
x x 0
в
граничном
условии
учитывается
зависимость
поглощательной способности системы металл окисел от
толщины окисла
T ( x, 0) T0 T ( , t ) T0
T
db B1
exp a b(0) b0
dt b
T (0, t )
- активационный закон приведен для случая n = 0,
m = 1 (Вагнеровский закон окисления)
Функция A(b), например, может рассчитывается стандартными методами анализа
слоисто-неоднородных сред.
Зависимость A(b) (а вместе с ней и характер нагрева поверхности) будет качественно
различаться для случаев прозрачного и поглощающего на длине волны греющего
излучения окисла.
В силу нелинейности задачи её аналитическое решение затруднено, поэтому
оправдано применение численных методов.
191.
Анализ нагрева окисляющихся металлов в условияхизменения поглощательной способности.
Сильнопоглощающий окисел
Качественный
видусловие
зависимости
способности
от времениизлучения
при лазерном
(δ0 – глубина
проникновения
в
Если выполнено
0 поглощательной
4nмощности:
нагреве для различных плотностей
0
окисел,
n0 – вещественный показатель преломления окисла), то при оценке
Сильная
Аррениусовская
зависимость
скорости
поглощательной способности системы
металл-окисел
можно
не учитывать
окисления от температуры будет приводить к
интерференционные явления.
тому,
что
переход
к
режиму,
когда
В данном случае качественно зависимость поглощательной способности от толщины
поглощательная
способность
начинает
пленки окисла будет выглядеть следующим образом:
определяться поглощательной способностью
При
малых
толщинахдовольно
окисла быстро.
(b << δ0)
окисла
осуществляется
поглощательная
способность
определяется
поглощательной способностью металла.
Когда поверхности
толщина окисла
превышает глубину
Соответствующие зависимость температуры
от времени:
проникновения
излучения
в
окисел,
Зависимость T(t)способность
в области системы
неустойчивости
поглощательная
металлпредставляетопределяется
собой переходнуюпоглощательной
кривую между
окисел
двумя
предельными
режимами
нагрева,
способностью
окисла.
соответствующими начальному (неокисленный
металл) и конечному (массивный окисел)
поглощению.
192.
Анализ нагрева окисляющихся металлов в условияхизменения поглощательной способности.
Прозрачный окисел
Рассмотрим качественное
поведение температуры
поверхности
металла,
образующего
Специфический
режим допорогового
нагрева металла
может
реализоваться
при
прозрачный окисел,
в условиях
непрерывного
лазерного нагрева:
образовании
прозрачных
окислов,
когда поглощательная
способность системы металл
окисел изменяется вследствие интерференционных эффектов в окисле.
Т.к. вспособности
процессе роста
окисла
положительная
Схематическая зависимость поглощательной
системы
металл-окисел
от
обратная связь периодически
может
меняться
толщины окисла в случае прозрачного, полупрозрачного
и поглощающего
окисла:
с положительной на отрицательную, то темп
нагрева также будет носить осциллирующий
характер.
Такие
температурные
осцилляции
наблюдались при нагреве медных образцов
непрерывным излучением СО2 лазера.
Временной промежуток между соседними
температурами
максимумами
будет
увеличиваться, т.к. с ростом толщины окисла
уменьшается
скорость
окисления
(за
исключением случая линейного закона
окисления m = 0).
В процессе роста интерференционных окисных пленок положительная обратная
В общем случае также следует учитывать
связь между толщиной окисла и поглощательной способностью периодически
зависимости оптических свойств окисла и
меняется на отрицательную, поэтому должен осциллировать и темп нагрева металла
металла от температуры.
лазерным излучением.
193.
Кинетика роста окисла в условиях, когдалимитирующей стадией является приток кислорода
к поверхности
Предыдущее рассмотрение кинетики окисления относилось к случаю, когда процесс
окисления лимитировался процессами переноса реагентов через слой растущего
окисла. В этом случае кинетика окисления носит активационный характер.
Однако при высоких температурах может оказаться, что наиболее медленной стадией
окажется стадия подвода кислорода к поверхности.
Поток молекул кислорода, падающих на поверхность зависит от концентрации
кислорода у поверхности и их средней тепловой скорости:
jn
nox v
4
nox – концентрация кислорода, <v> - средняя тепловая скорость
Считая, что все молекулы адсорбируются поверхностью скорость роста окисла может
быть записана в виде:
db
jn
dt
Ω – некий удельный объем
Концентрация кислорода в воздухе при нормальных условиях nox0 = 5∙1018 см-3.
Соответственно предельная скорость окисления на воздухе составит ~ 1 см/с.
Однако слои воздуха, прилегающий к поверхности будут быстро обедняться
кислородом и скорость окисления уменьшится.
194.
Кинетика роста окисла в условиях, когдалимитирующей стадией является приток кислорода
к поверхности
В условиях обеднения приповерхностных слоев воздуха кислородом его приток
поверхности будет контролироваться диффузионными процессами.
В приближении одномерной диффузии распределение концентрации кислорода может
быть найдено из решения уравнения диффузии с соответствующими начальными и
граничными условиями.
Границе окисла соответствует координата x =
nox
2 nox
D 2 0
0, ней имеется поверхностны сток частиц.
t
x
На
бесконечности
концентрация
равна
n
v
n
исходной.
D ox
j j ox x 0
x x 0
n
n
4
db
jn
Скорость роста окисла:
dt
nox x nox0 nox t 0 nox0
Решение этой задачи для скорости окисления имеет вид:
b t
4n D 2
v
0
ox
y e y erfc
nox0 v
t
При y << 1 b(t )
4
2 0
b
(
t
)
nox Dt
При y >> 1
y 1
2
v t
y
16 D
- окисел растет линейно
возможной скоростью
с
максимально
- окисление описывается параболическим
законом неактивационного типа
195.
Экзотермическое эффекты при импульсномлазерном воздействии на металлы
Рассмотрим
Реакция
окисления
результаты
металлов
эксперимента
является
по облучению
экзотермической
термически
(т.е. идущей
тонких пластин
с выделением
титана
тепла), однако
импульсами
свободной
обнаружение
генерации
экзотермических
неодимового лазера.
эффектов при импульсном облучении
массивных образцов затруднено.
Слева
зависимости
Действительно даже для окисления в «предельном» режиме с максимальной скоростью
температуры
от
~ 1 см/с дополнительный тепловой поток от реакции будет составлять величину ~ 10
времени
в
ранние
кВт/см2, в то время как типичная плотность мощности излучения (для миллисекундного
моменты времени.
диапазона длительностей) будет ~ 100 кВт/см2.
Черный пунктир слева
Экзотермические эффекты могут быть обнаружены при воздействии на термически
– форма импульса,
тонкие слои металлов с большим тепловым эффектом окисления после окончания
зеленые точки справа –
действия импульса.
зависимость T(t) для
случая
обдува
поверхности.
Видно, что при больших плотностях мощности нагрев образца продолжается и после
окончания воздействия.
Это можно объяснить экзотермичностью окисления, тепловой эффект которого
превышает все виды теплопотерь.
При обдуве образца характер протекающих процессов резко меняется, ввиду
изменения характера притока кислорода к окисляющейся поверхности.
196.
Экзотермическое эффекты при импульсномлазерном воздействии на металлы. Теоретические
оценки
Изучим условия «воспламенения» (т.е. возникновения самоподдерживающейся
реакции окисления) термически тонкой пластины.
В отсутствии теплопроводностных механизмов отвода тепла воспламенение произойдет
при температуре T = Tf , при которой теплопотери (F) образца будут полностью
компенсироваться тепловым эффектом реакции (qr).
F T f qr T f G
db
dt t t p
G – коэффициент, характеризующий тепловой выход реакции
Если окисление происходит по параболическому закону (n = 0, m = 1), то используя
модель эффективного времени, можем записать, что
Ta
Ta
Ta
B1
db
B1
exp
exp
b t p 2 B1te exp
2T
dt
T
b
t
2
t
2
T
p f
t t pp
e
f
f
Термически тонкая пластина остывает в основном за счет радиационных потерь.
F T f 2 SBT
4
f
Ta
B1
exp
Соответственно, 2 SBT G
2T
2te
f
4
f
(Qf
–
пороговая
С учетом, того, что для термически тонкой пластины T f
T0 плотность энергии
ch
(поглощенная)
полученное уравнение позволяет рассчитывать пороговые воспламенения, h –
параметры лазерного импульса приводящие к воспламенению толщина пластины)
термически тонкой пластины.
Qf
197.
Химические механизмы лазерного разрушенияматериалов
Химические реакции, стимулированные действием лазерного излучения, могут
приводить к изменению состава и свойств поверхности, а также к удалению
облучаемого материала (т.е. к абляции).
Далее рассмотрим химические механизмы разрушения твердых тел под действием
лазерного излучения на двух примерах:
1. Разрушение диссоциирующего полупроводника (арсенида галлия (GaAs))
Экспериментально установлено, что в некоторых экспериментах по облучению GaAs
импульсным излучением CO2 лазера в очагах разрушения обнаруживается дефицит
мышьяка.
Для описания разрушения арсенида галлия в этих условиях были предложены 2
модели диффузионная и кинетическая. Мы рассмотрим только диффузионную
модель.
2. «Наноабляция» алмаза
«Наноабляция» алмаза наблюдается при многоимпульсном лазерном воздействии
на алмаз с плотностями мощности импульсов ниже порога графитизации и
обусловлена фотостимулированным окислением.
Скорость «наноабляции» может лежать в диапазоне от 10-7 – 10-2 нм/импульс в
зависимости от условий эксперимента.
198.
Особенности лазерного воздействия надиссоциирующие полупроводники
При
достижении
температуры
разложения Tр = 700 °С, происходит
разложение (диссоциация) GaAs и
испарение летучего компонента
(мышьяка) из поверхностного слоя.
Предполагается, что компонентный
состав среды в зоне реакции
изменяется
во
времени
и
пространстве непрерывно, фронт
реакции оказывается размытым, а
полное
разложение
получается
лишь в асимптотическом пределе.
В модели принято, что изменение состава среды ведет к появлению дополнительного
наведенного поглощения, пропорционального дефициту летучего компонента, то есть:
z, t max 1
n z, t
n0
n – концентрация летучего компонента, n0 – начальная
концентрация
В результате возникновения дополнительного поглощения, наведенного дефицитом
летучего компонента, возникает тепловая неустойчивость (резкое увеличение
скорости роста температуры).
199.
Лазерная наноабляция монокристаллическогоалмаза
Приведем
экспериментальные
результаты
по
лазерной
«наноабляции»
монокристаллического алмаза наносекундными импульсами KrF лазера (λ = 248 нм, tp
= 20 нс, Q0 < 15 Дж/см2, f = 50 Гц) с плотностями энергии ниже порога графитизации
на воздухе.
Изображения сформированных кратеров на
поверхности алмаза при различном числе
импульсов - 3∙105 (сверху) и 3∙106 (снизу).
Скорость абляции всего около 1 нм за
1000 импульсов !!!
Эксперименты по облучению алмаза в
атмосфере
инертных
газов
показали
отсутствие
или
резкой
подавление
«наноабляции».
200.
Лазерная наноабляция монокристаллическогоалмаза
Для объяснения полученных экспериментальных данных был выдвинут следующий
механизм «наноабляции».
Фотовозбуждение электронной подсистемы алмаза приводит к резкому возрастанию
скорости окисления поверхности, т.е. образования CO2 и/или СО, которые являются
летучими компонентами. Таким образом происходит постепенное формирование
отверстия (кратера).
Видно, что по мере повышения
Зависимость скорости «наноабляции» от
давления скорость наноабляции
давления окружающей атмосферы
растет в диапазоне давлений от 10-7
до 10-5 торр.
Это,
очевидно,
объясняется
повышением
концентрации
кислорода и соответственно кол-ва
адсорбируемых молекул кислорода
на поверхности.
Подавление скорости наноабляции
при больших давлениях может быть
объяснено
формированием
на
поверхности слоя адсорбированной
воды
(аква-слоя),
который
ограничивает доступ кислорода к
поверхности.
201.
Лазерная наноабляция монокристаллическогоалмаза
Рассмотрим более детально особенности формирования абляционных кратеров при
различных давлениях.
Двумерные профили поверхности в окрестности
В области низких давлений
зоны лазерного воздействия при различных
наблюдаются специфические
давлениях
искажения
формы
абляционных кратеров.
В
диапазоне
от
атмосферного давления до
10−5 торр наноабляционные
кратеры имеют профиль
близкий к гауссовому, что
является
следствием
гауссового
распределения
интенсивности в лазерном
пучке. Однако, при давлении
10−6 торр дно кратера заметно
уплощается, а при 10−7 торр в
центре кратера появляется
возвышенность.
Данные особенности могут быть объяснены поверхностной диффузией кислорода к
центру пятна из необлученных участков.
202.
Термомеханическое действие лазерногоизлучения
203.
Лазерно-индуцированное разрушение материаловтермоупругими напряжениями
При лазерном воздействии в обрабатываемом материале в результате формирования
локального теплового поля и отсутствия свободного расширения нагретых областей
материала возникают термонапряжения.
Эти напряжения могут превысить предел прочности материала и привести к его
разрушению, что часто происходит при лазерной обработке стекла и других хрупких
материалов.
Величина термонапряжений, возникающих при лазерной
обработке, определяется локальным перегревом и
упругими и реологическими свойствами материала.
Для оценки величины возникающих термоупругих
напряжений справедлива грубая оценка:
E T Tmax
E – модуль упругости, αT –
коэффициент теплового расширения
Устойчивость материала к действию термоупругих напряжений характеризуют
максимальной величиной локального перегрева Tmax, при котором разрушение еще не
происходит.
Локальный перегрев Tmax и, следовательно, величину термоупругих напряжений можно
уменьшить, применив предварительный равномерный подогрев обрабатываемого
материала.
204.
Плоская задача термоупругостиКачественную картину формирования упругих напряжений вызванных лазерным
нагревом можно понять рассмотрев т.н. плоскую задачу термоупругости.
Рассмотрим случай плоского напряженного состояния.
Плоское напряженное состояние возникает
при плоском температурном поле T(x, y, t) в
тонкой пластине, свободной от внешних
сил.
Считаем,
что
пластина
прогрета
равномерно, т.е. H << (at)1/2 , а поле
температур осесимметрично T = T(r) и
известно из решения соответствующей
теплофизической задачи.
В этом случае решение задачи термоупругости может быть получено аналитически:
r
1 R
1
rr r T E 2 T r T0 rdr 2 T r T0 rdr
r 0
R 0
r
1 R
1
r T E 2 T r T0 rdr 2 T r T0 rdr T r T0
r 0
R 0
204
zz 0
z rz r 0
205.
Плоская задача термоупругостиТипичное распределение радиальных и азимутальных напряжений:
rr 0
- радиальные напряжения
сжимающие
0 r r0 (r0 – размер
0 r r0
прогретой области)
азимутальные
напряжения
сжимающие внутри прогретой
области и растягивающие вне её.
Радиальные трещины, сформированные
при лазерной обработке кремния
Формирование
растягивающих
азимутальных
напряжений
может
приводить к формированию радиально
направленных трещин при лазерной
обработке хрупких материалов.
206.
Лазерное термораскалываниеПроцесс разрушения материалов термоупругими напряжениями зачастую является
нежелательным.
Однако процесс формирования трещин при лазерном облучении можно сделать
управляемым и использовать для разделения хрупких материалов (лазерное
термораскалывание).
При нагреве движущимся пучком нагретую
Решение задачи термоупругости в
область можно приближенно представить
это случае будет иметь вид:
прямоугольником:
2 T E
b
b
yy ( x, 0) T max arctg
arctg
(1 p )
x l
x l
Важно, что
yy 0 l x l
yy 0 x l
На
границе
области
происходит
скачкообразное
изменение
знака
напряжений
–
они
становятся
положительными (растягивающими).
Технология лазерного термораскалывания применяется для разделения силикатных
стекол, сапфира, алюмосиликатной керамики, монокристаллического кварца и др.
207.
Разрушение остаточными напряжениямиРассмотрим нагрев и остывание сетклообразного материала:
Если
температура
стекла
меньше
Если
температураразмягчения
превышает температуру
температуры
Тр
(т.е.
На стадии остывания
формируются
размягчения,
топри
происходит
вязкоупругая
температуры
которой
возможны
напряжения имеющие
противоположный
деформация,
приводящаято к происходит
релаксации
вязкие
деформации),
знак.
напряжений.
генерация термоупругих напряжений
Таким образом, основной причиной возникновения остаточных напряжений в стекле
при лазерной обработке является релаксация напряжений во время цикла нагреваниеохлаждение.
Если во время лазерного воздействия происходит полная релаксация напряжений, то
величина остаточных напряжений будет равна величине упругих напряжений при
максимальной температуре, но с обратным знаком – они станут растягивающими.
Величину остаточных напряжений можно оценить как
t
G
ост 1 exp
σ – величина напряжений на термоупругой стадии, η – вязкость,
G – модуль сдвига, t – время вязкой деформации
208.
Лазерное плавление209.
Плавление в квазистационарных условиях приоднородном нагреве
Зависимость температуры от времени при
медленном равномерном нагреве кристалла
с постоянной скоростью:
При T < Tпл температура растет линейно со
временем
(считаем
теплоемкость
постоянной).
При достижении температуры плавления
рост
температуры
прекращается
и
подводимая энергия тратится на разрушение
кристаллической решетки.
Когда к единице объема среды при T = Tпл
будет подведена энергия равная удельной
теплоте плавления кристалл полостью
расплавится.
Далее продолжится линейный рост температуры (но угол наклона прямой может
поменяться т.к. теплоемкость расплава и кристалла различаются).
Процесс плавления происходит только в кристаллических веществах. При
нагревании аморфных тел характерной температуры плавления нет, плотность,
вязкость и другие свойства изменяются непрерывно, а не скачком как при плавлении.
210.
Плавление при неоднородном нагреве. ЗадачаСтефана
Целью решения задачи Стефана является нахождение температурного поля T(x, y, z, t)
в твёрдой и жидкой фазах металла и скорости перемещения границы раздела фаз при
действия на него лазерного излучения.
Поле температур в расплаве и твердой фазе
находится
из
обычных
уравнений
теплопроводности
T1
2T1
a1 2
t
x
- для расплава
T2
2T2
a2 2
t
x
- для твердой фазы
Рассмотрим одномерный случай
На фронте плавления задаются следующие условия:
T1 (h(t ), t ) T2 (h(t ), t ) Tm
- равенство температур
T
T2
dh
Количество
подводимое
к единице
Разность
k1 1 Q1 –теплоты
Qk22 затрачивается
Lm на продвижение
- разница
x
x
dt
площади
фронта
плавления
со
стороны
фронта плавления,
т.е.:
x h (t )
x h (t )
расплава
за время dt: и отводимым к фронту плавления количеством теплоты тратится
между подводимым
на продвижение
фазового
перехода. T T1
границы
T2
dh
T
2
Lm теплоты
Q1 k1 kT11 1 dt dt k2 Tаналогично
dt k2 - количество
dt Lm dh Q2 k2 k12
x h (t )
dt
x x x h (tx) h (t )
x x xh (tx) h (t )
x h (t )
Задачу Стефана
в общемxслучае
можно решить только
численнымиxметодами.
отводимое от единицы площади фронта плавления за время dt
211.
Пример численного решения задачи Стефана прилазерном плавлении
Материал - Al,
Плотность энергии - Q = 5.8 Дж/см2,
Длительность импульса - tp = 30 нс
Скорость плавления ~ 17 м/с
При
быстром
нагреве
практически отсутствует плато
на стадии нагревания.
На стадии остывания такое
плато присутствует.
Tm
Согласно
расчетам
«время
жизни» расплава при указанных
параметрах составляет ~ 100 нс,
а глубина проплавления ~ 800
нм.
Согласно классической задаче Стефана для продвижения фронта плавления в глубину
необходим градиент температуры в расплаве. Т.е. температура поверхности должна
продолжать расти, чтобы фронт плавления продолжал продвигаться вглубь.
212.
Результаты некоторых экспериментов по лазерномуплавлению
Рассмотрим результаты эксперимента по исследованию температурной динамики в
режимах лазерного импульсного плавления ниобия (Nb).
Зависимость температуры поверхности Nb
при действии прямоугольного импульса NdYAG-лазера при различных плотностях
мощности :
В
целом
динамика
температуры
поверхности
совпадает
с
предсказаниями сделанными на основе
решения задачи Стефана.
Однако имеются некоторые особенности.
q1
q2
На стадии нагрева наблюдаются
«короткие»
участки
постоянной
температурой, на стадии охлаждения
эти
участки
гораздо
более
продолжительны.
Температура горизонтального участка
на
стадии
нагрева
превышает
температуру горизонтального участка на
стадии остывания.
Величина этого превышения растёт
с
повышением
плотности
мощности.
212
q1 > q2
213.
Модели плавления1. Колебательная модель плавления
По мере повышения температуры амплитуда колебаний атомов увеличивается.
Согласно Линдеману, когда амплитуда колебаний достигает некоторой критической
(величины) доли расстояния между равновесными положениями атомов, колебания
начинают взаимно интерферировать. В результате чего, кристалл становится
механически неустойчивым.
2
Получено выражение для температуры плавления:
Tm ccTD2VM3 m
где, VМ - молярный объем, m - масса атома, TD - температура Дебая, cc - постоянная,
одинаковая для кристаллов со сходными структурами.
2. Модель гомогенной нуклеации
При нагреве в объеме материала могут возникать (за счет флукутаций) зародыши
жидкой фазы (расплава). По мере приближения к температуре плавления,
количество этих жидких зародышей в кристалле и средние их размеры возрастают
– происходит плавление.
3. Вакансионная модель плавления.
214.
Вакансионная модель плавленияПринимая во внимание отсутствие идеального порядка в кристалле и сохранение
некоторой упорядоченности в жидкости, Я.И. Френкель предложил рассматривать
процесс перехода кристалла в жидкость как процесс проникновения вакансий в
кристалл через его поверхность, при этом вакансии как бы разрыхляют его
структуру.
Процесс аморфизации кристалла можно понимать как процесс образования в
кристалле ''вакансионного раствора'', концентрация которого возрастает с ростом
температуры.
При больших концентрациях вакансий, когда деформированные области
перекрываются, кристаллическая решетка будет деформирована полностью.
В таком, деформированном вакансиями кристалле, атомы, окружающие какой-либо
произвольно выбранный атом, располагаются вокруг него преимущественно на тех
же расстояниях, что и в кристалле, но с некоторым разбросом - сохраняется
ближний порядок.
215.
Вакансионная модель плавленияАнализируется свободная энергия кристалла как функция концентрации вакансий
F(n) при различных температурах.
Равновесным состояниям соответствует
минимум свободной энергии.
При
достижении
температуры
плавления исчезает первый минимум
свободной энергии (с маленькой
концентрацией вакансий), кристалл
переходит в состояние с высокой
концентрацией
–
происходит
плавление.
Переход из состояния с низкой концентрацией вакансий в состояние в высокой
концентрацией не может происходить мгновенно – он ограничен скоростью генерации
вакансий (преимущественно на поверхности) и скоростью диффузии вглубь
кристалла.
Т.о. при быстром нагреве возможны перегревы твердых тел выше температур
плавления без появления текучести.
216.
Роль гидродинамических процессов в расплаве примикроструктурировании поверхности твердых тел
На поверхности расплава при лазерном плавлении всегда есть возмущения
(поверхность расплава не плоская) связанные с различными явлениями:
1. Давление паров
2. Силы связанные с градиентом поверхностного натяжения (эффект Марангони)
3. Конвекция и т.д.
Гидродинамические
возмущения
расплава
при
быстром
остывании
«замораживаются» и формируют микрорельефы различной морфологии.
Примеры такого рода структур на поверхности кремния:
217.
Поляритонный механизм формированияповерхностных периодических структур
при лазерном облучении
218.
Результаты некоторых экспериментов по лазерномумикроструктурированию поверхности металлов и
полупроводников
Титановый сплав (Ti6Al14V), длительность
импульса 30 фс, длина волны 800 нм, частота
следования импульсов 50 кГц, число импульсов 56,
плотность энергии 0.11 Дж/см2.
Германий, длина волны λ = 1.06 мкм, длительность
импульса τ = 200 нс, число воздействующих
импульсов в серии N = 20, плотность мощности
светового потока q0 = 60 МВт/см2.
Кремний, λ =1.06 мкм, τ=1 нс, N = 1, q0=0.7
МВт/см2
Общие особенности: Структуры имеют период
порядка длины волны света и преимущественно
ориентированы своими штрихами перпендикулярно
проекции электрического вектора световой волны на
поверхность (при линейной поляризации излучения).
219.
Поверхностные электромагнитные волныоптического диапазона
Для объяснения упомянутых экспериментов была выдвинута гипотеза о том, что
формирование поверхностных периодических структур (решеток) обусловлено
возбуждением поверхностной периодической электромагнитной волны и её
интерференцией с падающей.
Поверхностными
электромагнитными
волнами,
или
поверхностными
поляритонами называются волны, распространяющиеся вдоль границы раздела двух
разнородных сред и существующие одновременно в них обеих.
Теоретически поверхностные электромагнитные волны (ПЭВ) известны с начала
прошлого века. Их некоторые свойства и структура поля были изучены еще А.
Зоммерфельдом. Однако представления о ПЭВ долгое время были достоянием узкого
круга специалистов и, за исключением радиофизики, практически нигде не
использовались.
В оптику представления о ПЭВ проникли около 50-60-ти лет назад, когда их научились
возбуждать лазерным излучением и детектировать различными методами.
ПЭВ обладают следующими свойствами:
- высокой пространственной локализацией
- возможностью значительного усиления напряженности поля в ПЭВ.
220.
Структура электромагнитного поля ПЭВориентация электрического и магнитного
векторов
в
ПЭВ,
бегущей
вдоль
поверхности в направлении оси х.
x
E1,2
E0x exp k1,2 z exp i t k s x
z
z
E1,2
E01,02
exp k1,2 z exp i t k s x
y
H1,2
H 0y exp k1,2 z exp i t k s x
ПЭВ является частично продольной волной, т.е.
вектор напряженности электрического поля имеет
составляющую
вдоль
направления
распространения.
Амплитуды полей экспоненциально затухают по
мере удаления от границы раздела.
- распределение полей в ПЭВ в плоскости,
перпендикулярной
направлению
распространения
221.
Условия существования ПЭВ, дисперсионныесоотношения
ПЭВ описываются обычными волновыми уравнениями со стандартными граничными
условиями.
Ищем решение в виде:
2
E1,2
B1,2
c
2
c
2
2
1,2 E1,2 0
1,2 B1,2 0
x
E1,2
E0x exp k1,2 z exp ik s x
z
z
E1,2
E01,02
exp k1,2 z exp ik s x
y
B1,2
B0y exp k1,2 z exp ik s x
2
2
2
x k 2 xk
2
0 1,2
k 1,22 E 1,2
E1,2s 2
2
x
2
x
x
x
k
E
k
E
E
0 kчислом
E
0
i
i
00 k1,2 k21,2и волновым
s 1,2 затухания
1,2 001,2
1,2
- 2связь
коэффициентами
1,2 между
1,2
1,2
0 1,2 E1,2
1,2
2
2
c
z rotB
c1,2 i 1,2 0 00 00 1,2
E1,2 E1,2
1 x k1 что
1,2
i
1,2 волне
1,2
1,2 E1,2
Вспомним,
k
в
поверхностной
электромагнитной
s
i2
00
c
2
2
k
k
k
воспользуемся
1,2
0 1,2
s
z k2
z
непрерывности
тангенциальных
компонент
и 22 E1,2
2 условием
2 E1,2
z
2 на
1,2границе:
E1,2 0 E x E x E x .
электрического
поля
2
2
1 z 0
2 z 0
0
z c
x
2
2
2
2
2
2
x E
y
xx
E
Ey
E
E
E
y
y
x
x
x
B1,2
k
E
k0 1,2
x
1,2E1,2
1,2
0
1
0
y
rot2 BB1,2y1,2 2 Bi1,2y c 2 y z k 1,2EB1,2= x2 1 y 2k1 z 2 ex i x 2 c y 2 k1 Bz02y e y
2
2 1,2 B1,2 0
2
2
2
x
Ez 2 Ekz2 2 Ez
z c
x
k
E
x
2y
2 e z i 0 2 0 k B y
k0 1,2 E0
x
2
2 0
rotB1,2 z 0 i c exp iks x k 1,2 Bx 0 exp y iks x z
c
222.
Условия существования ПЭВ, дисперсионныесоотношения
Далее рассмотрим модельный случай, когда диэлектрические проницаемости
контактирующих сред вещественны и поверхностна волна не затухает в направлении
своего распространения (ks - вещественно).
2
2
2
21
k
k
k
k
k1 12 k20 1 1 1 2
1 1 2
k1 k0 1
1
1 2
т.е. ПЭВ могут существовать и
распространяться только вдоль границ
2 0
раздела сред2 с диэлектрическими
2
1 2
1
2
2 2
2разных
2 знаков.
2
ksk 2 k0 2 k 22 k1 2 0проницаемостями
(при
ks k 2 k 0 k 2 k 2
k
k
k
k
0
1
0
2
s
1
0
2
1
0
1
2
0 2 s
1
1
2
более
рассмотрении
с
1 1 2
строгом
вещественными
частями
2
2
k12 k02 1 k1s2
1
2 2
2
2
k 2 k 0 2
112
1 2
2k 2 k диэлектрических
проницаемостей
k
k
k
k
2
0
2
k
1
k
0
0
0
1
s
0
1 2
1
1
1 12 1 2 0 2 разных
1 2знаков)
Среда с отрицательной вещественной
2
k02 1 2 2
частью
диэлектрической
2 1
2
k1 называется
1 k0
2
2
проницаемости
1 2
2 1
поверхностно-активной средой (ПАС).
Кроме того k1 kS k2 означает, что энергия ПЭВ в основном сосредоточена в
поверхностно неактивной среде 1 и переносится вдоль направления распространения
волны.
223.
Поверхностные плазмон-поляритоны на границеметалла с диэлектриком
Для металла описываемого моделью Друде:
p2
p2
( ) 1 2
i
2
2 2
Например, для случая γ < ω < ωp
p ~ 1016 c 1
~ 1013 1014 с 1
Re 0
Re 1
т.е.
металл
является
поверхностно активной средой.
p2
Для границы металла с воздухом ( 1 1 , 2 1 2 ) имеем:
2
p
Дисперсионная зависимость
2
2
1
2
1 22
p
k
для поверхностных плазмонk s k0
k0
0
2
2
2
1 22
2 p
поляритонов
2 p 2
p
2
2
1
p 2 p
k 2 k 0 2
2
2
11 22 c0 p
c0
плазмон-поляритон
k1 k0 1
2
1
22
22
11 22 c00 pp c0 p
c
l2 k 0 2 ~ 30 нм
p
1
2
«свободный» фотон
p
1
l1 k1 2 ~ 3 мкм
2
224.
Способы возбуждения поверхностных плазмонполяритоновИз предыдущего рассмотрения следует, что ks > k0, что затрудняет прямое
преобразование излучения падающего из воздуха в поверхностную электромагнитную
волну (при квантовом описании импульс плазмон-поляритона оказывается больше
импульса фотона).
Рассмотрим 2 возможности возбуждения ПЭВ на границе с металлом.
1. Призменные методы возбуждения ПЭВ (методы нарушенного полного
внутреннего отражения)
Геометрия Отто
Кречмана
Прежде, чем войти в воздух излучение попадает на призму
с диэлектрической
проницаемостью
εp > ε1.
p
В геометрии
Кречмана положение
поверхностно
arcsin
В условиях
полного
внутреннего
активной
среды
(металла)отражения
и диэлектрика
(воздуха)
1
меняются местами относительно призмы.
x – компонента волнового вектора в среде с
диэлектрической
проницаемостью
ε1 будет
равна
ПЭВ возбуждается
на нижней
границе
пленки.
kметаллической
sin
1 .
kx
p sin
x
p
c0
c0
c0
Т.е. возбуждение ПЭВ становится
Из-за поглощения в поверхностно
возможным.
kx
p sin
активной
среде условиях
толщина пленки
должна
При таких
z-компонента
c0
быть
достаточно
мала,
чтобы
волнового
вектора становится
чистодостаточное
количество
мнимой и волна
затухает вэнергии
этом
достигало
границы
направлении на расстояниях
~ λ.раздела
Ясно,
металл/воздух.
металл надо располагать на расстоянии
d < λ.
225.
Способы возбуждения поверхностных плазмонполяритонов2. Метод поверхностной дифракционной решетки
Если
рельеф
поверхности
синусоидально промодулирован с
периодом и амплитуда модуляции
мала по сравнению с длиной волны
света, то в результате взаимодействия
волновой вектор в металле в
направлении
параллельном
к
поверхности распадется в набор
векторов k x k0 x G
2
G
l
d
l = 0, ±1, ±2, …
G – вектор решетки
k0 x
c0
1 sin
В этом случае можно, например, подобрать d при котором выполняется равенство ks = kx.
Эффективность преобразования падающего излучения в ПЭВ при этом будет
пропорциональны высоте модуляции рельефа.
Шероховатые поверхности можно рассматривать как набор периодических решеток с
разными периодами, и, следовательно с их помощью возбуждать поверхностные
плазмон-поляритоны.
226.
Поляритонный механизм микроструктурированияпри лазерном воздействии
Поверхности реальных материалов обладают шероховатостью. В пространственном
спектре шероховатости всегда найдется резонансная решетка на которой происходит
преобразование падающего излучения в ПЭВ.
В процессе своего распространения они интерферируют с падающим лазерным
излучением.
В результате интерференции формируется периодически модулированное
распределение интенсивности, которое в свою очередь вызывает пространственное
промодулированный нагрев материала.
Вследствие активации различного рода тепловых процессов происходит увеличение
высоты резонансного рельефа.
Дальнейшее увеличение высоты рельефа резонансной решетки происходит за счет
наличия положительной обратной связи между коэффициентом преобразования ПЭВ
и высотой решетки.
Для случая нормального падения излучения интерференция происходит за счет
наличия продольной компоненты поля ПЭВ.
i t k x
Пусть E0e i t - поле падающей волны, а E0x e s - продольная компонента
поля ПЭВ
Интерференционное распределение интенсивности
q
x iks x 2
0
E0 E e
E0 E e
x iks x
0
E E e E E 2E E cos k x
0
x iks x
0
2
0
x 2
0
0
x
0
s
- т.е. интерференционное поле имеет период, определяемой длиной волны ПЭВ λs≈ λ.
227.
Тепловые процессы, ответственные заформирование периодического рельефа
Перечислим несколько тепловых процессов формирования поверхностных
периодических структур в условиях периодической модуляции поля температурного
поля.
1. Термокапиллярные силы
Возникновение термокапиллярных сил в
неоднородно нагретом расплаве обусловлено
зависимостью
коэффициента
поверхностного натяжения σS расплава от
температуры.
Обычно
d S
0
dT
Потоки жидкости в расплаве (эффект
Марангони) будут направлены таким
образом, чтобы уменьшить поверхностную
энергию (определяемую коэффициентом
поверхностного натяжения).
Таким образом расплав из нагретых
областей будет перемещаться в холодные.
Сформированный в расплаве рельеф «замораживается» при кристаллизации расплава.
228.
Тепловые процессы, ответственные заформирование периодического рельефа
2. Испарение и действие давления отдачи паров
Скорость испарения сильно зависит от
температуры поверхности.
Наибольшая скорость испарения будет в
местах где температура максимальна.
Помимо чисто испарительного удаления материала из областей с повышенной
температурой, часть материала также может удаляться за счет действия давления
отдачи паров.
3. Неустойчивость Релея-Тейлора
Неустойчивость Релея-Тейлора может наблюдаться на границе расплав-воздух при
ускоренном движении границы вниз на стадии остывания материала (из-за
уменьшения объема нагретого материла).
4. Термодеформации в твердой фазе
5. Термохимические эффекты
6. ….
229.
Цилиндрическое поверхностные электромагнитныеволны
Решения уравнений электродинамики для плоской границы поверхностно-активной
среды с диэлектриком допускают существование цилиндрических поверхностных
волн (ЦПВ), помимо плоских поверхностных электромагнитных волн, рассмотренных
нами ранее.
В отличие от плоской волны ЦПВ исходит из некоторого центра и за счет радиального
разбегания убывает по мере удаления от него вдоль поверхности.
ЦПВ могут возбуждаться на различных радиально-симметричных неоднородностях,
микровыступах и микровпадинах поверхности.
При рассеянии на цилиндрическом выступе линейно поляризованный свет возбуждает
ЦПВ, максимальное значение поля в которой достигается в диэлектрике (воздухе).
пример
радиально-угловой
микрострукутры,
сформированной
на
кремнии при воздействии фемтосекундных
лазерных импульсов, предположительно,
обусловленных возбуждением ЦПВ и её
интерференцией с падающим излучением.
230.
Испарительные механизмы разрушенияпри лазерном нагреве
231.
Испарительные механизмы разрушенияОсновные механизмы поверхностного разрушения материалов связаны с испарением.
Удаление материала может происходить непосредственно при испарении, либо под
действием давления отдачи пара, ударной волны и т.д.
Теоретические модели, описывающие поверхностное разрушение металлов под
действием лазерных потоков в диапазоне плотностей потоков ~ 106 -107 Вт/см2 за
счет испарения, развиты в работах С.И. Анисимова и в последствии Н.М.
Булгаковой, A. Miotello и др.
Механизмы испарительной абляции металлов и металлоподобных материалов:
1. Нормальное
Нормальное испарение
испарение
2. Нормальное кипение
Чему равна скорость испарения поверхности
при температуре T?
Реализуется при длинных (миллисекундных и выше) лазерных воздействиях. Для
более коротких воздействий режим нормального кипения не успевает развиться и
происходит нормальное испарение вещества без кипения.
3. Фазовый взрыв (взрывное вскипание)
В условиях интенсивного нагрева при приближении температуры материала к
критической происходит его распад на паро-капельную смесь.
Наш анализ в основном будет сконцентрирован вокруг процессов нормального
испарения, как одного из наиболее важных испарительных механизмов,
поддающегося сравнительно простым количественным оценкам.
232.
Некоторые сведения из термодинамикиdE TdS
dQ pdV
pdV dN
- первое
начало
термодинамики
первое
начало
термодинамики
переменным числом частиц
для
систем
с
E – внутренняя энергия системы, Q – количество теплоты полученное системой, p –
давление, V – объем системы
S – энтропия, T – температура
N – число частиц, μ – химический потенциал
Для анализа различных термодинамических систем удобно ввести следующие
функции (термодинамические потенциалы):
F E TS
H E pV
- свободная энергия (свободная энергия Гельмгольца)
- энтальпия (тепловая функция)
G E TS pV - термодинамический потенциал (потенциал Гиббса)
dG dE
TdS
SdT
pdV
дифференциала
SdT Vdp
dN G(T, p, N)
dG
dE
SdT
TdS
Vdp
SdT
dN
pdV
Vdp
-Vdp
полный
функции
Выясним характер зависимости G от числа частиц N.
Согласно определению G – экстенсивная величина, т.е. G(T, P, N) ~ N.
G
N T , p
G T , p, N N T , p
Химический
потенциал
есть
термодинамический
потенциал,
отнесенный к одной частице (или
удельный термодинамический потенциал)
233.
Некоторые сведения из термодинамики. Условияравновесия фаз
Общим условием устойчивого
максимальность её энтропии:
S S0 S 0
равновесия
изолированной
системы
является
S – энтропия в неравновесном состоянии, S0 – в равновесном
Рассмотрим изолированную двухфазную систему одного и того же вещества.
S S1 S2
(S1,2 – энтропии первой и второй фазы соответственно)
dS dS1 dS2 0
- условие равновесия
T1dS1 dE1 p1dV1 1dN1
T2 dS2 dE2 p2 dV2 2 dN 2
Тогда
Система
изолирована
E1 E2 const
dE1 dE2
V1 V2 const
dV1 dV2
N1 N 2 const
dN1 dN 2
dE1 p1dV1 1dN1 dE2 p2 dV2 2 dN 2
0
T1
T2
1 1
p1 p2
2 1
dE
dV
1
1 dN1 0
T
T
T
T
1
2
1
2
T2 T1
T1 T2
- условие термического равновесия
p1 p2
- условие механического равновесия
1 2
- условие химического равновесия
234.
Уравнение Клапейрона-КлаузиусаРассмотрим 2 фазы одного и того же вещества (например, жидкость и пар),
находящиеся в равновесии друг с другом.
Условия равновесия:
T1 T2 T
2. Давления в обеих фазах равны p1 p2 p
1. Температуры фаз равны
3. Химические потенциалы фаз равны
1 T , p 2 T , p
Поскольку функции μ1(T, p) и μ2(T, p) различны то давление и температура фаз,
находящихся в равновесии друг с другом могут быть выражены как функции друг
друга, т.е. p = p(T).
1 T , p 2 T , p
d
dT
(при этом считаем, что p есть функция T)
1 1 dp 2 2 dp
G
1
d
SdT Vdp sdT vdp
T p dT T
p dT
N
N
dp
dp
s - энтропия на одну частицу (удельная энтропия)
s1 v1
s2 v2
v – объем на одну частицы (удельный объем)
dT
dT
dp s1 s2
- уравнение Клапейрона-Клаузиуса
dT v1 v2
235.
Кривая насыщения. Фазовая диаграмма.Пример фазовой диаграммы
dp s1 s2
dT v1 v2
Изменению удельной энтропии при переходе от жидкости (1) к
пару (2) соответствует некоторое количество теплоты:
Lev
dp
dT T v2 v1
v2 1
dp Lev p
dT
k T2
dp Lev dT
p
k T2
s2 s1 T Lev
p
kT
v2
ln p
- объем, приходящийся на одну частицу в жидкости
много меньше, чем в газе.
- уравнение Клапейрона-Менделеева
Lev 1
C
k T
p L 1 1
ln ev или
p0 k T0 T
Пусть нам известна точка (p0, T0) на кривой p(T),
тогда ln p0
Lev 1
C
k T0
L 1 1
связь
между
p p0 exp ev k T0 T давлением насыщенного
пара и температурой
В тройной точке три фазы вещества (твердая, жидкая и газообразная)
находятся в
равновесии.
Критическая температура – температура выше которой материал не может быть
Кривая
диаграмме
давление-температура, соответствующая
сконденсирован
ни принакаком
давлении.
этому уравнению
называется
кривойвозможных
насыщения перегревов в область
Спинодаль ограничивает
область
максимально
метастабильных состояний.
236.
Кинетика испарения плоской поверхности в вакуум.Формула Герца-Кнудсена
Сначала рассмотрим пар, находящийся в равновесии с жидкостью, и вычислим число
частиц (молекул, атомов) ударяющихся о поверхность жидкости в единицу времени.
Если бы все налетающие частицы имели
Поэтому и в неравновесной ситуации (например, когда пар над поверхностью ещё
одинаковую скорость то эта величина была бы
практически отсутствует), величина j- будет определяться по формуле:
равна:
Lev 1 1
p0 т.к. скорости
v
dtS
n
n
x
exp
j n vx
jj j vx
частиц
T
2 mkT различны,
22 Sdt
2
k T0 то
n – концентрация
пара
<v
скорость
налетающих
частиц
Далее
несложно вычислить
скорость
движения
границы
жидкости
при испарении:
x> – средняя
m
Вероятность обнаружения
частицы со скоростью vx в паре подчиняется нормальному
vev j v j
v – объем на одну частицу в жидкости
распределению (распределение Максвелла).
L ev 1 1
mvx2 m
2
m
- формула
2
m kT
kT
T
p
exp
окончательно vx vexp
vx
dv
или
exp(
a
)
da
2
ev
0
x
2 m
2 kT 0
2kT 2 mkT2 kT m k0 T0 T Герца-Кнудсена
Lev 1 1
p0
m – масса
p
kTатома (молекулы)
nkT
j
exp
j n
или
ρ – плотность
жидкости
2 mkT
2 m
2 mkT
2 mkT
k T0 T
Lev состоянии
– удельная теплота
парообразования
(напереходящих
один атом!, [Дж/атом])
В
равновесия
число частиц
в жидкость в единицу
времени
равно
(т.е.тогда
переходящих
пар).
В
качестве
p0 числу
удобночастиц
братьпокидающих
атмосферноежидкость
давление,
T0 будетв температурой
кипения приДля
атмосферном
(обычно
в справочниках).
простотыдавлении
полагаем,
что приводится
все частицы
пара падающие на
j j
поверхность жидкости переходят в жидкость (т.е. не отражаются о
поверхности).
237.
Обратная конденсация атомов при лазерномиспарении
Предыдущий анализ не учитывал возможность обратной конденсации атомов
испаряемого вещества.
На
верхней
границе
кнудсеноского
слоя
вследствие столкновений
формируется равновесное
распределение
по
скоростям.
Вблизи
поверхности
функция распределения
максвелловская при vx > 0
(соответствующая температуре поверхности)
В реальности атомы, вылетевшие с поверхности и имеющие первоначально скорость,
направленную от поверхности, в результате столкновений с другими атомами могут
приобрести скорость направленную к поверхности.
Соответственно, формула выведенная ранее требует корректировки.
238.
Полуаналитическая теория кнудсеновского слоя прилазерном испарении
Анализ поведения течения газа в кнудсеновсуом слое возможен в рамках кинетического
Анализ выписанных соотношений показывает, что
уравнения Больцмана:
этом f поток
обратноконденсируемых
атомов
составляет
от в
fПри
T f 0.65T 0 f
– функция
распределения, такая,
что fdvdr
– число 18%
атомов
0 f
vx
потока
испаряемых
элементе атомов.
фазового объема около точки (r,v).
n t 0.31n 0 x
Задача5kT
полагается одномерной (т.е. f зависит только от координаты x), а интеграл
u
столкновений
(правая часть) записывается в приближении времени релаксации.
3m
Далее рассматривается стационарное приближение, пригодное для использования в
случае когда
длительность
лазерного
больше
времени свободного
Таким
образом,
выведенную
ранее импульса
скорость много
испарения
поверхности
в вакуум
3
пробега атома.
необходимо
умножить на поправку связанную с обратной
m конденсацией:
2
mv 2
f x 0 n0
exp
, vx 0
f
f0 f
L условия:
0.82m Граничные
1 1
vx
2 kT0
2kT0
vev Tx
p0 exp ev
k T0 T
2 mkT
3
n0 – концентрация насыщенного пара
m v u 2
m 2
f x n
при температуре T0 (температура
exp
2
kT
2
kT
поверхности)
- концентрация, температура и скорость потока на внешней границе
n , T , u кнудсеновского слоя
Примем, что на поверхности при vx < 0 f f 0
Кроме того выпишем условие равенства потоков массы импульса и энергии:
nu nu p100 n p000 pnlm vxnv ly vzm fdv
p200 p200
p300 p120 p102 p300 p120 p102
239.
Задача о лазерном нагреве с испарениемСделаем следующие основные допущения:
1. Будем рассматривать одномерную задачу.
2. Пренебрежем затратами энергии на плавление и изменением свойств материала
при переходе твердое тело – расплав.
3. Будем считать, что продукты испарения не поглощают падающее излучение.
T
2T Aq0 exp x x0
- уравнение теплопроводности
a 2
t
x
с
T энергии на испарение учтем в граничном условии.
Потери
k
Lev vev T x0
(x0 – текущая координата фронта испарения)
xиспарения
Для
слоя толщиной dx и площадью S необходимо затратить энергию
x0
Скорость vev(T) можно определить по формуле ГерцаdE
,Lt ev
Sdx
T
T x:, 0Sdt
T
0
Кнудсена.
dx
Зависимость
теплоты, температура
затрачиваемое
на фронте
на испарение
испаренияв
qev Levevv(T ) Lev v(T ) - количество
dt
единицу времени с единицы
от времени
площади поверхности
(тепловой поток на границе)
Особенностью решения описанной задачи при
Таким образом, граничное условие
на облучаемой
поверхности
имеет вид:плотностью
воздействии
излучения
с постоянной
мощности
является
выход
температуры
на
T
стационарное
значения, когда
(x0 – текущая координата
фронтаподводимая
испарения) энергия
k
Lev vev T x0
x x0
полностью компенсируется затратами на испарение.
240.
Исследование стационарного режима испаренияУдобно рассматривать задачу в системе координат движущейся с фронтом испарения:
x x v0t
(v0 – скорость испарения в стационарном режиме)
T
T
T
v0
Тогда в уравнении теплопроводности надо сделать замену
t
t
x
T
d
TВ стационарном
x x, t , t Tрежиме
x x, t xкоординатах
v0t
0.
x, t испарения
в подвижных
t
dtx
2
Aq0 x, t
T Далее, опуская штрихи,
Тогда
T x , t
v x TT xTa , tx ,T t x dT
exp( x)
k
v0 Lev что T(x, t) –
считаем,
0
2
x
x
c
x распределение
xt
x x x t
dt
x 0
в движущихся
2
координатах.
Проинтегрируем
T xx ,, tt T Tполученное
x , tx , t Tуравнение
T x ,xt , t по 2глубине.
T x, t
T
v 02T
Aq0
0 Aqv00 Ltxev 2 cT 0 x 2 или
T
x
x
v0
в результате
получим
Aq
t
x
Lev cT 0
0 v0 x a x 2 dx 0 c exp( x)dx
Aq0
v
Обычно
cT << Lev, соответственно 0 L .
Aq0
ev T
Aq0
v0
dx v0 T T 0 v0T (0)
exp(
x
)
dx
Если
x время много меньшее длительности
c
режим cдостигается
стационарный
за
0
0
импульса, то глубина испарения равна:
2
Aq
испарения
v0 Lev
v0 Lev падающей плотности
Tглубина
T
т.е.
пропорциональна
h a v0tTp dx
0at p T -
a
a
0 x 2 Lev x x мощности.
x x 0
x x 0
k
c
(tp – длительность импульса)
241.
Особенность распределения температуры поглубине в условиях стационарного испарения
Особенностью распределения температуры T(x) по глубине при совместном
действии в среде объемного источника тепла и фазового перехода является наличие
максимума на глубине x0.
Действительно, из граничного условия
k
T
v0 Lev следует, что T
0.
x x 0
x x 0
Но на больших расстояниях T(x)
должна убывать, следовательно на
кривой T(x) в некоторой точке x0
должен иметься максимум.
v0
a
1
x0
ln 1
v0 Lev
v0
q
0
a
Оценки показывают, что для металлов:
x0 ~
Tmax T (0) 1000 C
242.
Вынос расплава под действием давления отдачипара
Давление продуктов испарения, оказываемое ими на поверхность расплава приводи к
его вытеснению на края формирующегося отверстия (либо даже к его
разбрызгиванию).
Величину давления отдачи можно приближенно оценить как 0.5 pнас pотд pнас .
pнас – давление насыщенного пара над поверхностью при некоторой температуре
(определяется по формуле Клапейрона-Клазиуса).
pотд – давление отдачи
Примеры кратеров, сформированный при совокупном действии испарения и
выноса расплава под действием давления отдачи при облучении импульсами
различной длительности.
мкс
нс
мс
фс
По мере сокращения длительности импульса снижается кол-во расплава,
соответственно роль этого механизма удаления материала уменьшается.
243.
Поглощение излучения в продуктах испаренияПри импульсном лазерном воздействии поверхность расплава может нагреваться
вплоть до температур порядка 104 K.
При таких температурах пар над поверхностью фактически представляет собой
плазму (ионизированный газ).
Т.к. в плазме возможно дополнительное
поглощение, то плотность мощности на
поверхности будет меньше.
С этим может быть связано насыщение
линейной зависимости глубины кратера от
плотности мощности при её увеличении.
T
I
Коэффициент поглощения в плазме pl ~ 3 exp
1 exp
kT
kT
ω – частота падающего излучения, T – температура плазмы, I – энергия ионизации
?!
фазовый взрыв?
Зависимости
испарённой массы от
плотности энергии
импульса для графита
поглощение в плазме
нормальное испарение
244.
Переход от нормального испарения к фазовомувзрыву
2
Схема
Изображения
установки
полученные
для экспериментального
при различныхисследования
задержках длядинамики
Q = 5.2 Дж/см
разлета
2
Зависимость
Изображения
глубиныполученные
абляции в Al
при
от различных задержках для Q = 4 Дж/см
продуктов лазерной абляции
плотности энергии импульса (tp = 4 нс,
1.06 мкм).
Видно, что при некоторой плотности
энергии (~ 5 Дж/см2) наблюдается
характерное изменение режима абляции.
Излучение лазера на красителях (500 нм), проходящее параллельно поверхности
В продуктах
абляции наблюдается
большое количество
жидкихПолучается
капель – происходит
через
расширяющийся
факел
регистрируется
ПЗС
камерой.
«теневое»
Наблюдается расширение пара в атмосфере
(имеет
место
только
нормальное
испарение).
фазовый
взрыв.
изображение расширяющихся продуктов абляции.
245.
Экспериментальное определение порога абляцииПростая методика определения порогов импульсной лазерной абляции материалов а
также радиуса пучка с гауссовым профилем интенсивности была представлена в работе
J.M. Liu. Simple technique for measurements of pulsed Gaussian-beam spot sizes// Optics
Letters, 1982, V. 7, pp. 196-198
Абляция наблюдается в области, где плотность энергии
превышает пороговую плотность энергии Q*.
Для гауссова пучка Q r
Ep
r
Соответственно, Q*
или
e
2
0
Ep
r2
2
r0
e
2
r0
r2
a2
r0
(Ep – энергия импульса, r0
– радиус пучка по уровню
e-1)
(ra
–
радиус
абляционного кратера)
r 2 Q* r022
r r 0 ln
ln E p r0 ln Q* r02 - т.е. квадрат
r
Ep
2
2 a
a 2
0
радиуса абляционного кратера линейно зависит от
логарифма энергии импульса.
Радиус пучка при этом находится как угловой
коэффициент для данной зависимости, а пороговая
плотность
энергии
определяется
по
точке
пересечения с осью абсцисс.
Пример экспериментальной зависимости
квадратов
диаметров
кратеров
от
логарифма энергии импульса.
246.
Некоторые приложения лазерной абляции1. Прошивка отверстий, перфорация, скрайбирование, резка и т.п.
2. Формирование функциональных рельефов различного назначения.
3. Лазерное напыление тонких пленок (PLD – pulsed laser deposition)
4. Лазерная искровая эмиссионная спектроскопия (LIBS – laser induced breakdown
spectroscopy)
Примеры микрорельефа на стальных валах, применяемых в технологии
Схема
установки для
лазерного
напыления
5. Лазерная очистка (в
т.ч. холодного
реставрация
объектов
культурного
наследия )
и горячего
тиснения.
Схема измерений
Пример полученного
6. Непрямые
методы лазерной модификации прозрачных
материалов спектра
(LIPAA – laser
induced plasma assisted ablation, LIBWE - laser induced backside wet etching и т.д.).
7. Лазерная генерация наночастиц.
8. «Космические приложения» лазерной абляции (лазерная реактивная тяга, защита
от космического мусора, моделирование взрывов на крупные астероиды).
и т.д.
Применяется для определения химического
состава, on-line контроля качества лазерной
очистки и т.д.
247.
Воздействие сверхкоротких лазерныхимпульсов на конденсированные среды
248.
Воздействие сверхкоротких лазерных импульсов наметаллы
В металлах излучение главным образом поглощается на свободных электронах. Это
приводит к увеличению их энергии, которую электроны передают решетке за счет
столкновений (испускания фононов).
Если длительность импульса τ мала или сравнима с характерным временем
перераспределения энергии между электронами и решеткой то нагрев электронной и
решеточной подсистем следует рассматривать раздельно.
Т.е. электронный газ и решетку можно характеризовать в отдельности электронной Te
и решеточной Ti температурами.
Количество энергии, получаемое решеткой от электронного газа в единице объема в
единицу времени равно
ui
Te Ti
t
ui – объемная плотность энергии решетки
β – коэффициент электрон ионного теплообмена [Вт/(см3·K)]
β ~ 1011 Вт/(см3·K), а время выравнивания температур tei ~ 1-10 пс
Для сверхкоротких воздействий время перехода световой энергии в тепловую
оказывается больше длительности импульса, так что нагревание кристаллической
решетки и все остальные тепловые процессы происходят после его окончания.
249.
О возможности введения электронной температурыпри сверхкоротких воздействиях
Эволюция функции распределения
электронов в металле при облучении УКЛИ
Сравнение с экспериментом
для золота:
серебро, Qа = 30 мДж/см2,
tp ~ 150 фс
Электронную температуру нельзя вводить при
воздействии
низкоинтенсивных
фемтосекундных импульсов
Qа = 0.3 мДж/см2,
tp ~ 180 фс
250.
Двухтемпературныя модель при сверхкороткомлазерном воздействии на металлы
ce
Te Te
ke
Aq0 exp( x) (Te Ti )
t x x
ci
Ti Ti
ki
(Te Ti )
t x x
ke
Te
T
0 ki i
0
x x 0
x x 0
Te ( x , t ) Ti ( x , t ) T0
- уравнение теплопроводности
для электронов
- уравнение теплопроводности для решетки
- начальные и граничные условия
Te ( x, t 0) Ti ( x, t 0) T0
В общем случае задача сильно нелинейна
ввиду зависимости коэффициентов модели
от температуры. Точное решение возможно
лишь численными методами.
251.
Модельные зависимости электронной теплоемкостии теплопроводности от электронной температуры
теплоемкость
теплопроводность
Расчеты проведены по однозонной модели металла, коэффициент электрон-ионного
теплообмена для однозонного металла может считаться практически постоянным.
252.
Качественный анализ решения уравненийдвухтемпераутрной модели
При качественном анализе будем полагать, что все теплофизические параметры не
зависят от температуры.
1. Будем полагать, что в течение импульса длительностью τ < tei электроны греются
адиабатически (пренебрегаем электронной теплопроводностью и передачей энергии
в решетку) (0 < t < τ)
ce
Te
Aq0 exp( x)
t
Te (0, )
AQ0
T0
ce
Te ( x, t )
Aq0t
exp x T0
ce
При Q0 ~ 0.1 – 1 Дж/см2 Te > 104 K
2. Считая, что к концу лазерного импульса решетка практически не нагрета, а
процессы теплопроводности еще не срабатывают, нагревание решетки можно
описать уравнениями (τ < t < tei):
ce
Te
Te Ti
t
T
ci i Te Ti
t
После приравнивания левых частей и интегрирования
получаем:
сe Te ( x, t ) Te ( x, ) ci Ti ( x, t ) Ti ( x, )
253.
Качественный анализ решения уравненийдвухтемпераутрной модели
В результате получаем уравнение для изменения температуры решетки
T
сi i tei 1Ti Te ( x, )
t
ci
tei
Ti ( x, ) 0
1 ce ci
ci ce
Решение имеет вид
t t – характерное время выравнивания температур
t
Ti ( x, t ) Te ( x, ) ei 1 exp
ei
ci
tei между электронами и решеткой
Ti ( x, tm ) Ti max
AQ0 exp x
ci
Обычно ci >> ce, тогда tei
tei < tm << tc, tc– время остывания решетки
ce
1 10 пс
Скорость нагрева решетки 1014 – 1015 К/с
3. После выравнивания электронной и
характеризуется одной температурой (t > tm)
Ti
2Ti
a 2 0
t
x
решеточной
T
0
x
T x, t m
AQ0
exp x
c
температур
металл
254.
Качественный анализ решения уравненийдвухтемпераутрной модели
Решение задачи остывания для температуры поверхности имеет вид:
2 a ( t tm )
T (0, t ) T (0, tm )e
ierfc a t tm
Оценки показывают, что время остывания tc в данном случае составляют 0.1 – 1 нс (и
даже выше при более реалистичном рассмотрении).
При обработке фемтосекундными лазерными импульсами тонких пленок на
диэлектрических подложках с малой теплопроводностью остывание пленки
происходит за счет теплоотвода в подложку
k22t k2 t h – толщина пленки, индекс 1 относится к
T (0, t ) T (0) exp
2 2
a
c
h
a
c
h
2 1 2 1 пленке, индекс 2 к подложке
Красная кривая – остывание пленки хрома на стеклянной
подложке после облучения импульсом 10 нс, черная
кривая - остывание пленки хрома на стеклянной
подложке после облучения фемтосекундным импульсом.
Время термического воздействия ультракороткого
лазерного импульса определяется не его длительностью,
а теплофизическими характеристиками среды, а также
размером и формой зоны облучения, что сопоставимо с
временем воздействия наносекундных импульсов.
255.
Методы теоретического исследованиявзаимодействия ультракоротких импульсов с
веществом
Анализ динамики взаимодействия ультракоротких лазерных импульсов
конденсированными средами существенно затруднен по следующим причинам:
с
- результаты экспериментального исследования воздействия ультракоротких
импульсов на конденсированные среды носят косвенный характер (фактически
можно исследовать только изменение коэффициента отражения/пропускания) и
требуют дополнительной интерпретации, приходится судить о динамике процессов
по окончательному результату воздействия.
- воздействие ультракороткого импульса может инициировать совокупность сложных
взаимосвязанных физических процессов (плавление, откольная абляция, фазовый
взрыв, нетермические эффекты, конденсация капель и т.п.) идущих в
сильнонеравновесных условиях, лишь некоторые из них могут быть
проанализированы в рамках термодинамических или кинетических моделей.
Подходы к теоретическому моделированию:
- континуальный (уравнения механики сплошных сред)
- молекулярно-динамический (классические уравнения движения частиц)
256.
Методы молекулярной динамикиМетод МД позволяет изучать эволюцию во времени системы из N частиц посредством
решения системы классических уравнений движения для всех частиц системы.
d 2 ri
mi 2 Fi
dt
i 1, 2,..., N
- 2-ой закон Ньютона
Fi
U (r1 ,...rN )
- потенциал взаимодействия
ri
Потенциал Леннарда-Джонса.
12 6
U (r ) 4
r r
ε – глубина потенциальной ямы
σ – расстояние на котором энергия
взаимодействия становится равной 0 (меняет
знак)
Параметры ε, σ могут быть определены по
экспериментальным значениям модуля упругости,
скорости звука и пр.
Для более точного описания используются более
сложные виды потенциалов.
257.
Методы молекулярной динамикиОсновное достоинство метода МД состоит в том, что для его использования
необходимо определить лишь детали взаимодействий между отдельными атомами
или молекулами в изучаемой системе и не требуется каких-либо предположений о
характере изучаемых процессов или макроскопических феноменологических
законов, имеющих, как правило, сравнительно узкую область применимости.
Область применения метода МД ограничивается необходимостью использования
для вычислений значительных компьютерных ресурсов, прежде всего
процессорного времени.
Схематичное представление характерных масштабов времени и длины, доступных
для моделирования методом квантовой молекулярной динамики (КМД),
классическим методом молекулярной динамики (КММД) и методами механики
сплошной среды при исследовании свойств и структуры материалов
258.
Методы молекулярной динамикиЭлектронная подсистема описывается в рамках классической двухтемпературной
модели.
T
T
ce e ke e Aq0 exp( x) (Te Ti )
t x x
ci
Ti
(Te Ti )
t
N cell
mi vTi
i 1
3k B N cell
Ti cell
2
На боковых границах расчетной МД-области ставятся периодические граничные
условия, на левой границе ставятся особые граничные условия, обеспечивающие
передачу тепла и волн давления.
259.
Анализ процессов плавления металлов привоздействии УКЛИ методами МД
Ni
Учет плавления при континуальном описании
может быть осуществлен следующим
(традиционным) образом. При достижении
температуры плавления её рост прекращается
до тех пор пока решетке не будет передана
энергия определяемая удельной теплотой
плавления.
На
рисунках представлено
сравнение
температурной
динамики
по
двухтемпературной
модели
(ДТМ)
и
комбинированной модели ДТМ+МД.
Имеет место перегрев решетки выше
температуры плавления, важным фактором
влияющим на кинетику плавления является
давление.
260.
Анализ процессов плавления металлов привоздействии УКЛИ методами МД
красные атомы – кристалл, синие - расплав
Ni
Имеет место как гетерогенное (поверхностное) плавление, так и гомогенное
(объемное).
261.
Анализ процессов плавления металлов привоздействии УКЛИ методами МД
При низких интенсивностях относительные вклады гомогенного и гетерогенного
механизмов плавлении определяются скоростью нагрева решетки. Роль
гетерогенного плавления должна возрастать при приближении времени нагрева
решетки к времени прохождения фронта плавления толщины пленки.
Зависимость скорости распространения
фронта плавления в зависимости от
температуры для Ni
При
малых
перегревах
выше
температуры
плавлении,
скорость
продвижения фронта плавления растет
линейно. Выше температуры 1770 K
начинается формирование зародышей
жидкой фазы в объеме.
262.
Анализ процессов абляции металлов привоздействии УКЛИ методами МД
Выделяют 2 механизма абляции:
1. Откольный механизм (спалляция,
фотомехаическая абляция)
2.
Фазовый
взрыв
(взрывное
вскипание, тепловая абляция)
Полное
количество
удаленного
с
поверхности материала (а) и часть
удаленного материала, эжектированная в
виде
индивидуальных
атомов
(мономеров) (б) в зависимости от
плотности энергии излучения.
263.
Схема абляции в откольном режиме при воздействииУКЛИ на металл
Взаимодействие термоупругих напряжений сжатия, вызванных лазерным
нагревом, со свободной поверхностью облучаемого образца может привести
к появлению достаточно больших растягивающих напряжений, которые
могут вызвать механическое разрушение хрупкого материала или
стимулировать кавитацию и фрагментацию в метастабильном расплаве,
сформированном вблизи облучаемой поверхности.
264.
Анализ процессов абляции в откольном режиме привоздействии УКЛИ на металл
Поведение
поверхности
объемного алюминия после
облучения
ультракоротким
импульсом длительностью 100
фс при различных плотностях
энергии. Вставка – зависимость
объема образующихся пустот от
времени.
265.
Анализ процессов абляции в режиме фазовоговзрыва при воздействии УКЛИ на металл
Абляция объемного алюминия в режиме фазового взрыва после воздействия
ультракороткого импульса с длительностью 100 фс.
266.
Анализ процессов абляции при воздействии УКЛИна металл методами МД с учетом неравномерного
распределения плотности мощности
267.
Взаимодействие УКЛИ с полупроводниками идиэлектриками
При поглощении кванта (или квантов) электрон переходит из валентной зоны в
зону проводимости, т.е. происходит фотоионизация. При действии мощных УКЛИ
концентрации неравновесных носителей
могут
достигать
значений
сопоставимых со значением концентрации свободных электронов в металлах.
Наиболее простой теоретический подход к описанию нагрева полупроводников и
диэлектриков в подобных условиях заключается в совместном решении уравнения
для концентрации
неравновесных
носителей,
учитывающего
процессы
ионизации, рекомбинации, диффузии, эмиссии, и системы уравнений
двухтемпературной модели.
Возможно многофотонное поглощение.
Уравнения для плотности мощности и концентрации носителей имеют вид:
q
m q m e (ne )q
x
ne m q m
Re
t
m
m – число квантов излучения
многофотонном процессе
участвующих
Re – описывает рекомбинационные процессы
Явление многофотонного поглощения позволяет проводить объемную обработку
прозрачных широкозонных диэлектриков.
в
268.
Экспериментальные методы исследованиявоздействия УКЛИ на вещество
В эксперименте удается измерять лишь динамику оптических свойств материала с
временным разрешением (100 фс и более).
С помощью линии оптической
задержки формируется задержка
между импульсом накачки и
пробным импульсом.
Отраженный сигнал т пробного
импульса
принимается
фотоприемником.
Повторяя
эксперимент
при
различных
задержках
можно
восстановить динамику изменения
коэффициента отражения.
269.
Экспериментальные методы исследованиявоздействия УКЛИ на вещество
Поверхность кремния после
облучения
импульсом
с
длительностью 120 фс при
плотности энергии 470 мДж/см2
(выше порога абляции).
Начальное увеличение отражение связано с генерацией электрон-дырочной
плазмы, дальнейшее с плавлением кремния, появление темных и светлых колец с
интерференционными явлениями в откольном слое.
270.
Определение динамики концентрациифотовозбужденных носителей в полупроводнике
после облучения УКЛИ
Зависимость коэффициента отражения
кремния от концентрации
фотовозбужденных носителей.
Зависимость коэффициента отражения
пробного импульса (1250 нм) от задержки
при плотности энергии импульса накачки
ниже порога плавления.
выше
При
высоких
уровнях
энергии
порога отражения
плавления)(сспустя
Используя
формулу
Френеля
для (выше
коэффициента
n и kp несколько
по Друде)
пикосекунд
коэффициент
отражения
вновь начинает
возрастать до значения
выше
можно рассчитать
изменение
концентрации
ne фотовозбужденных
носителей
первоначального,
что обусловлено
после окончания действия
импульсапереходом
накачки. кремния жидкое (металлоподобное
состояние).
























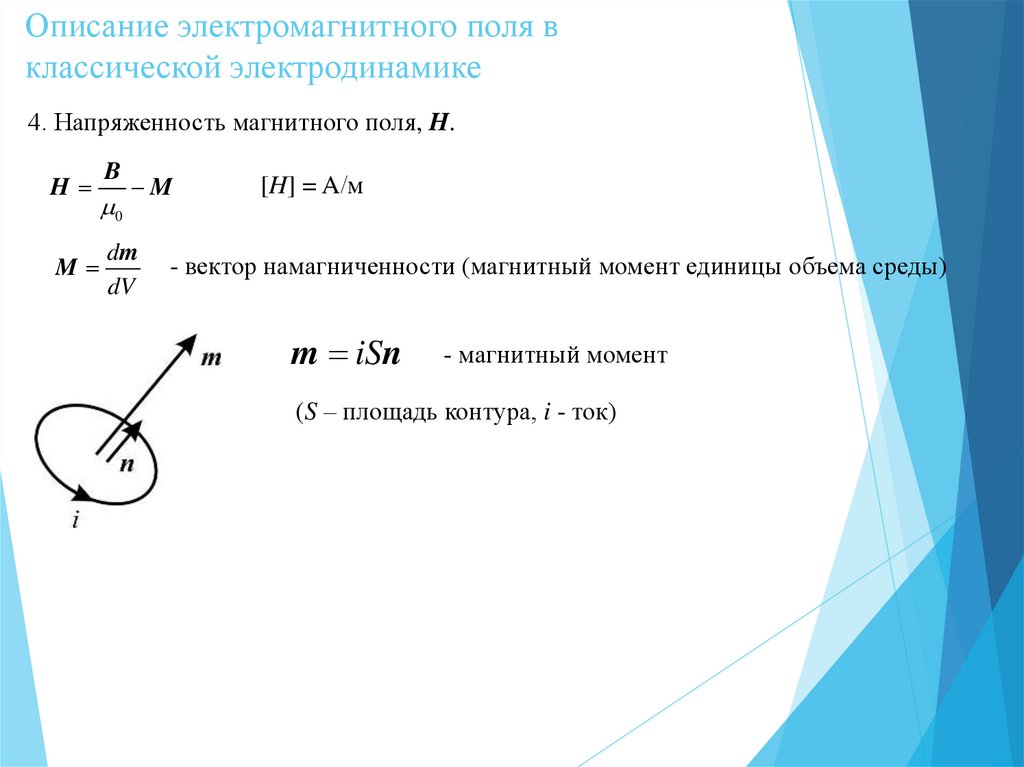
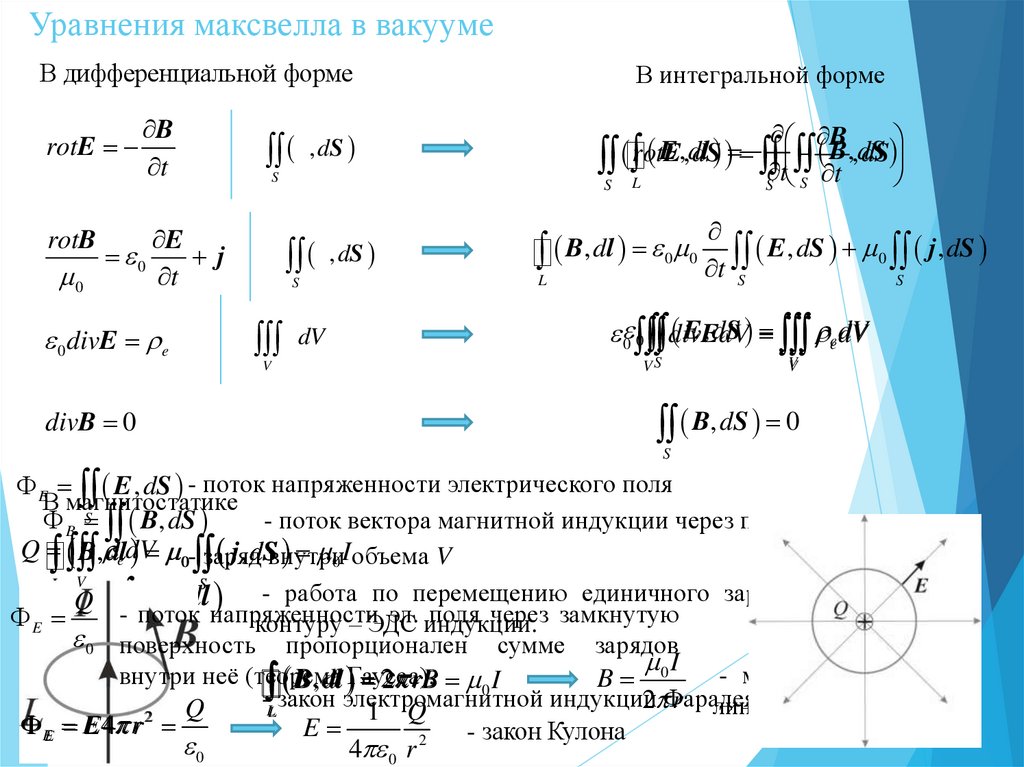




















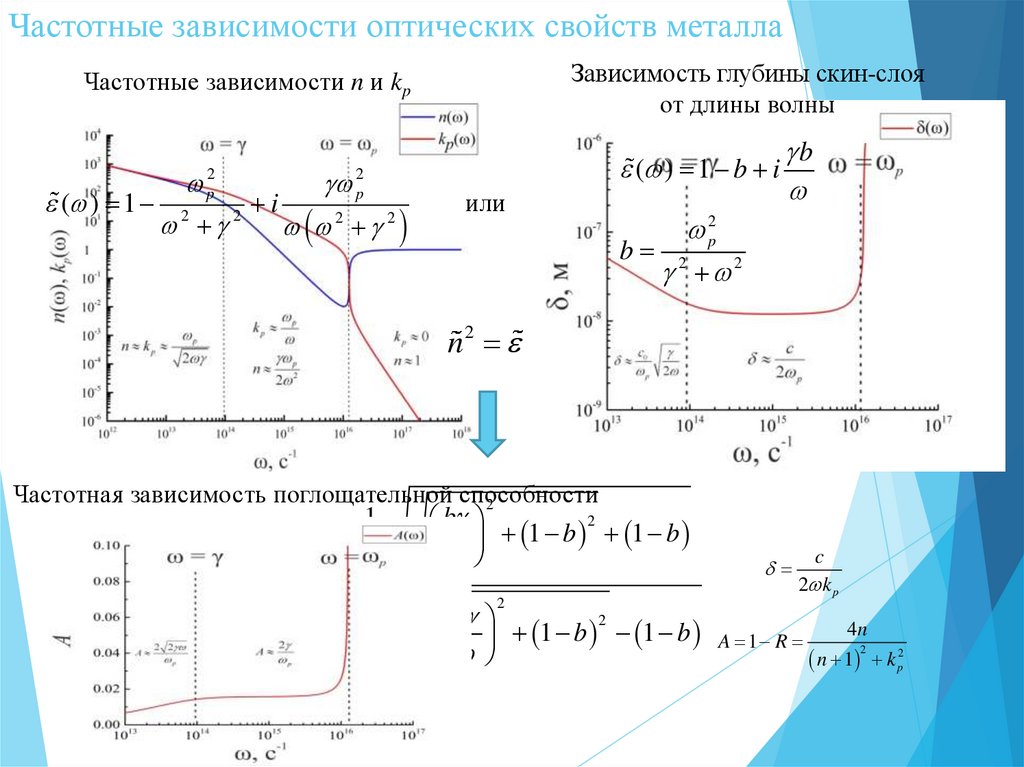

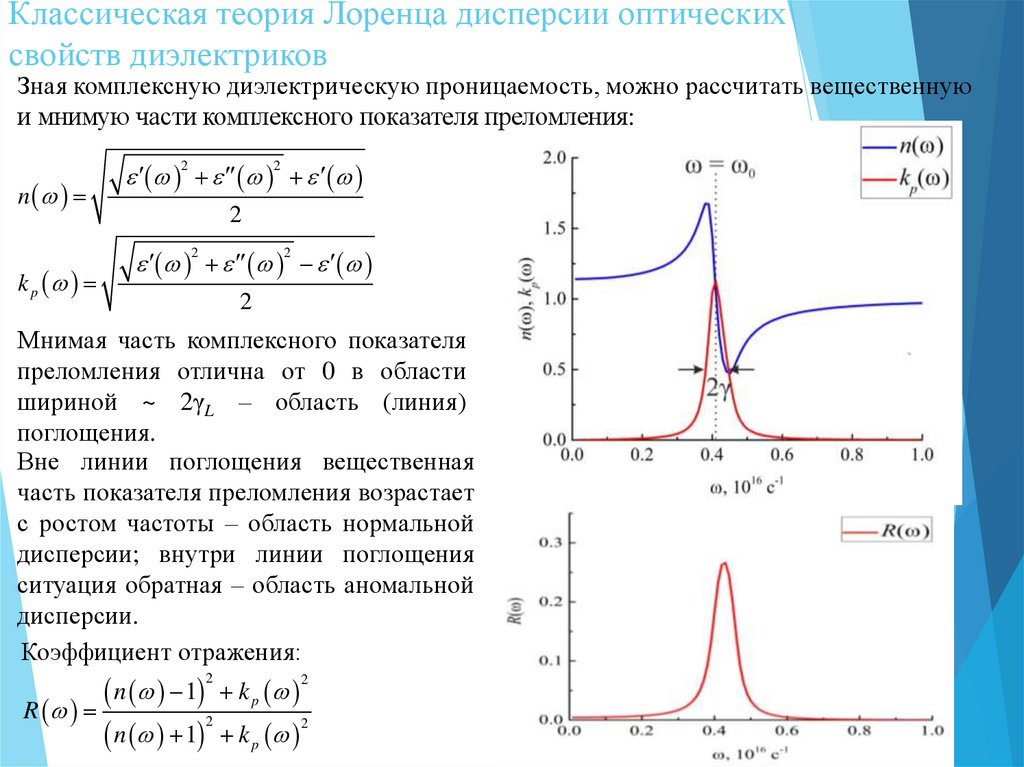

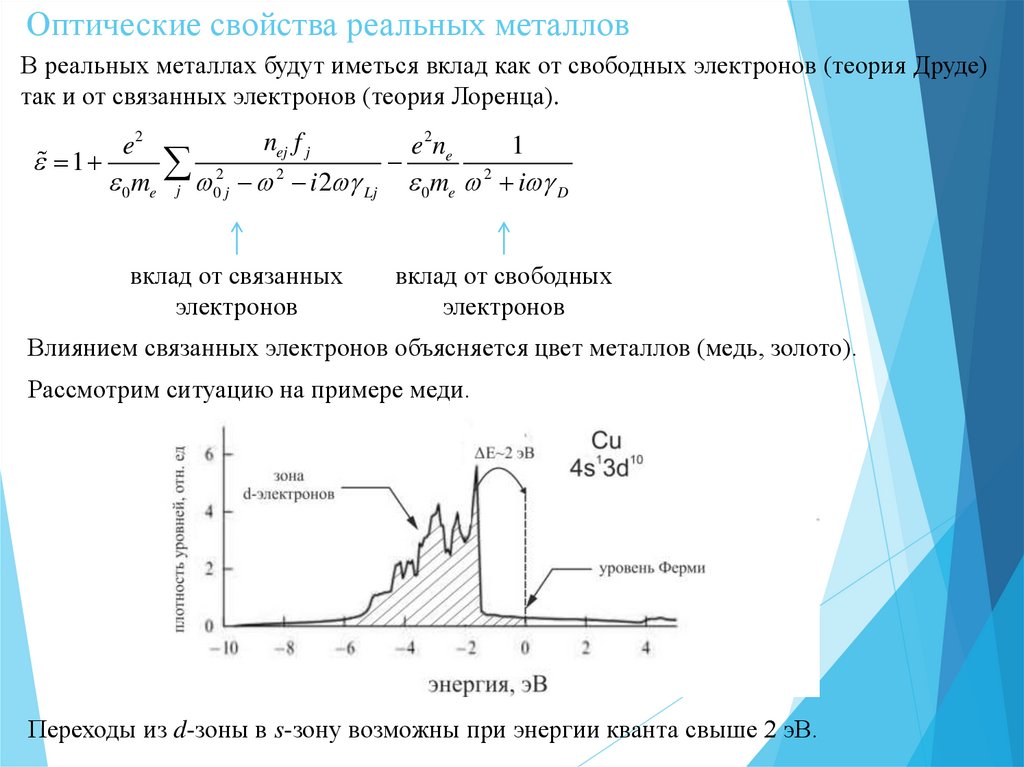







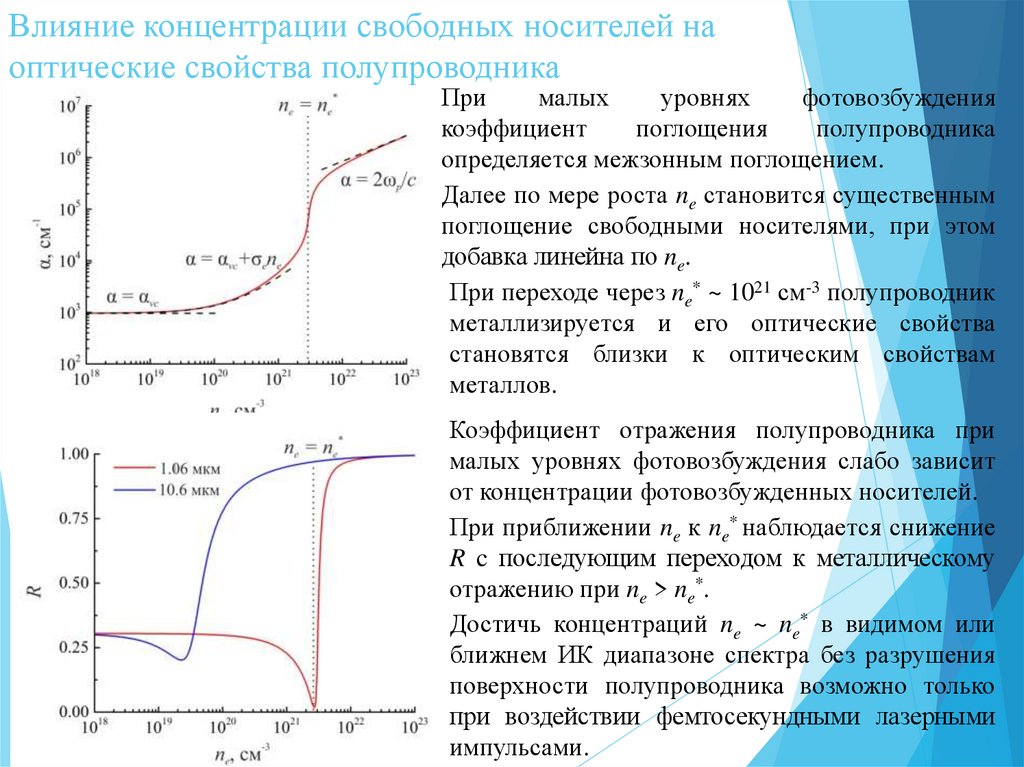









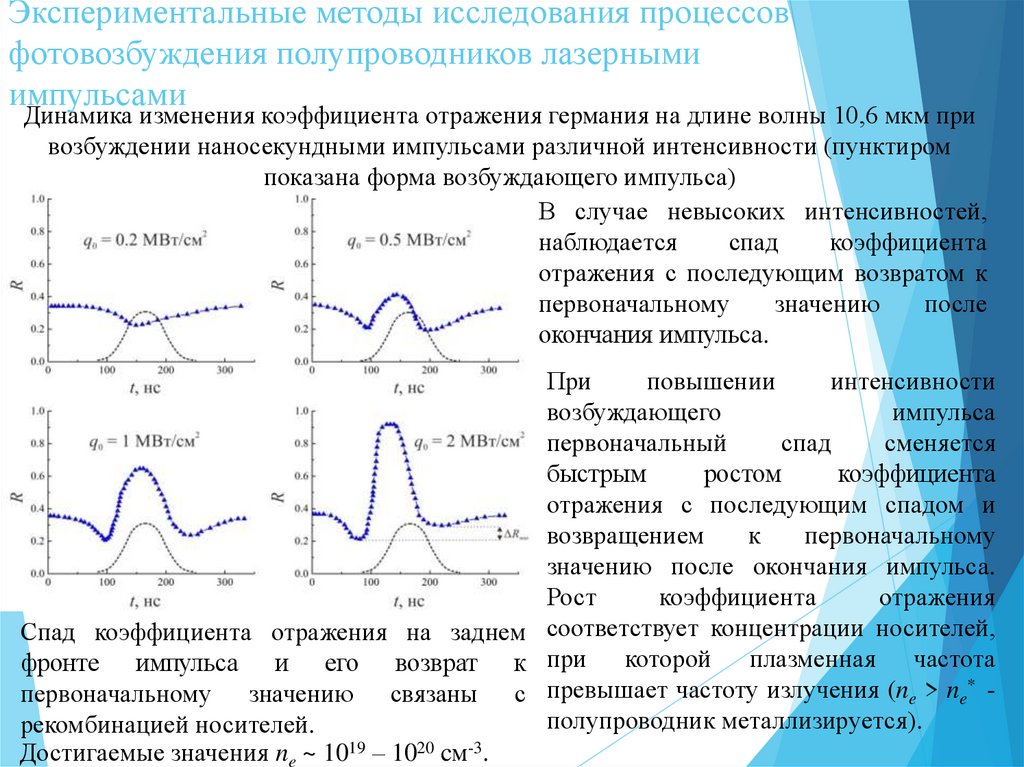

















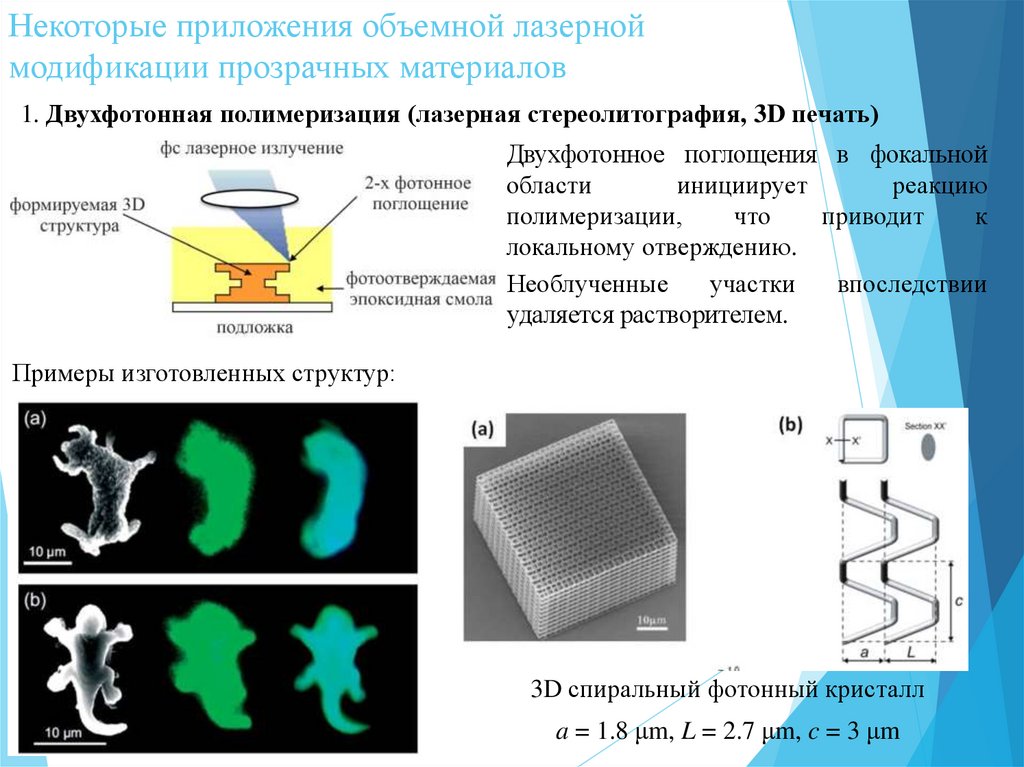








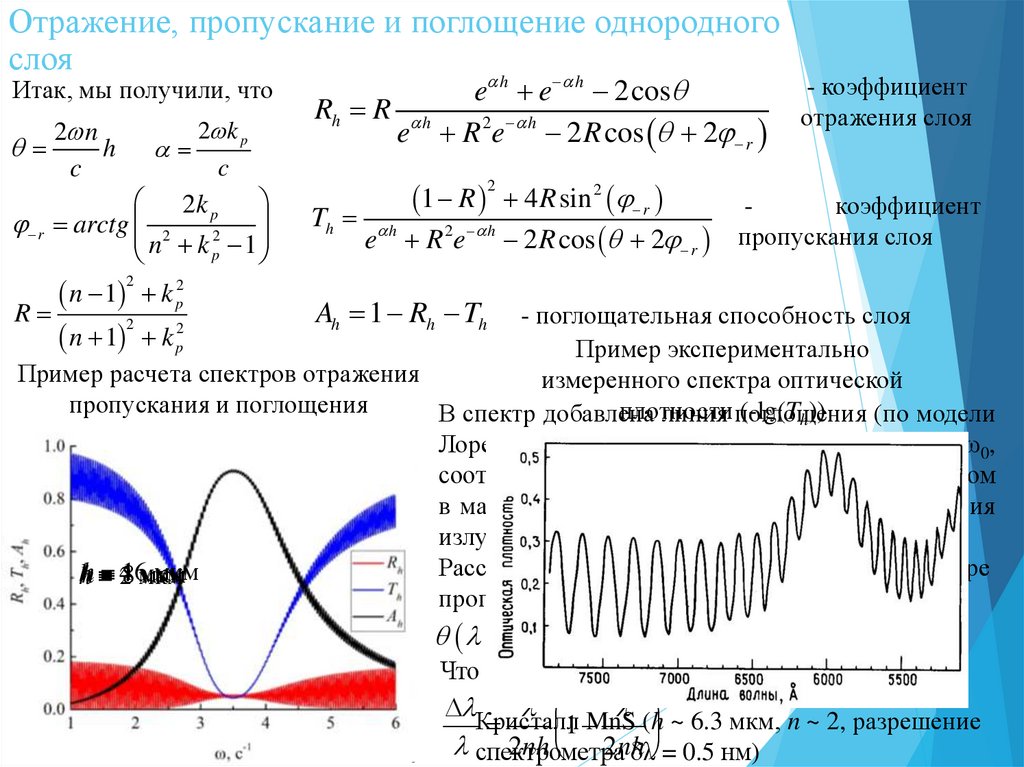






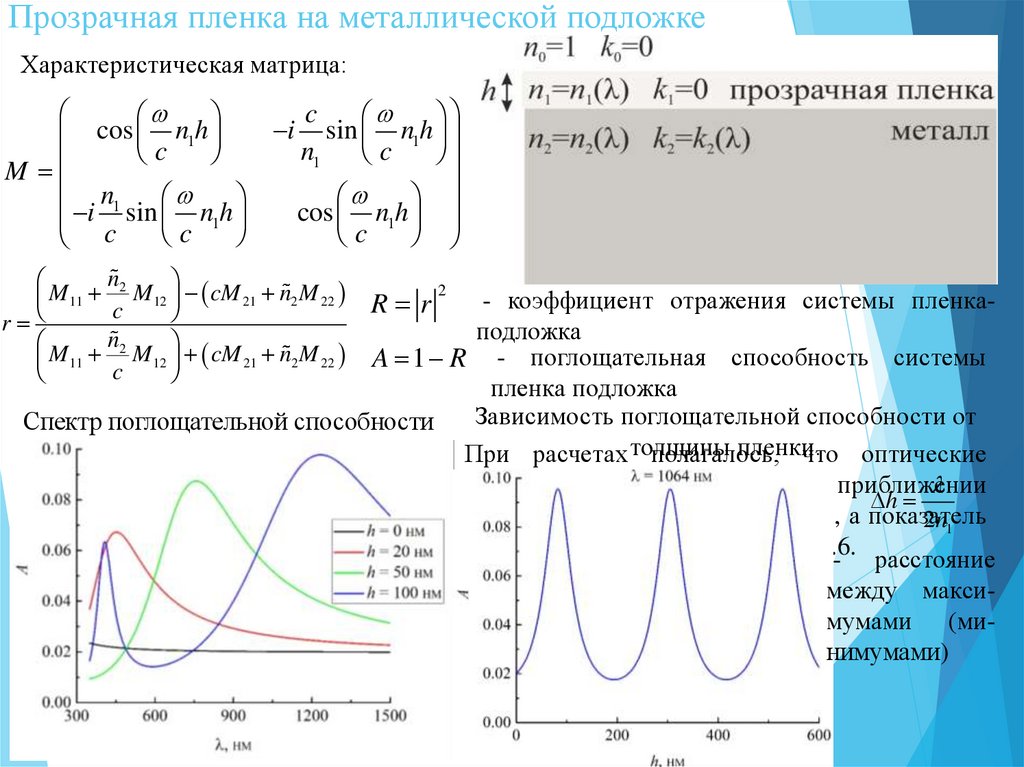




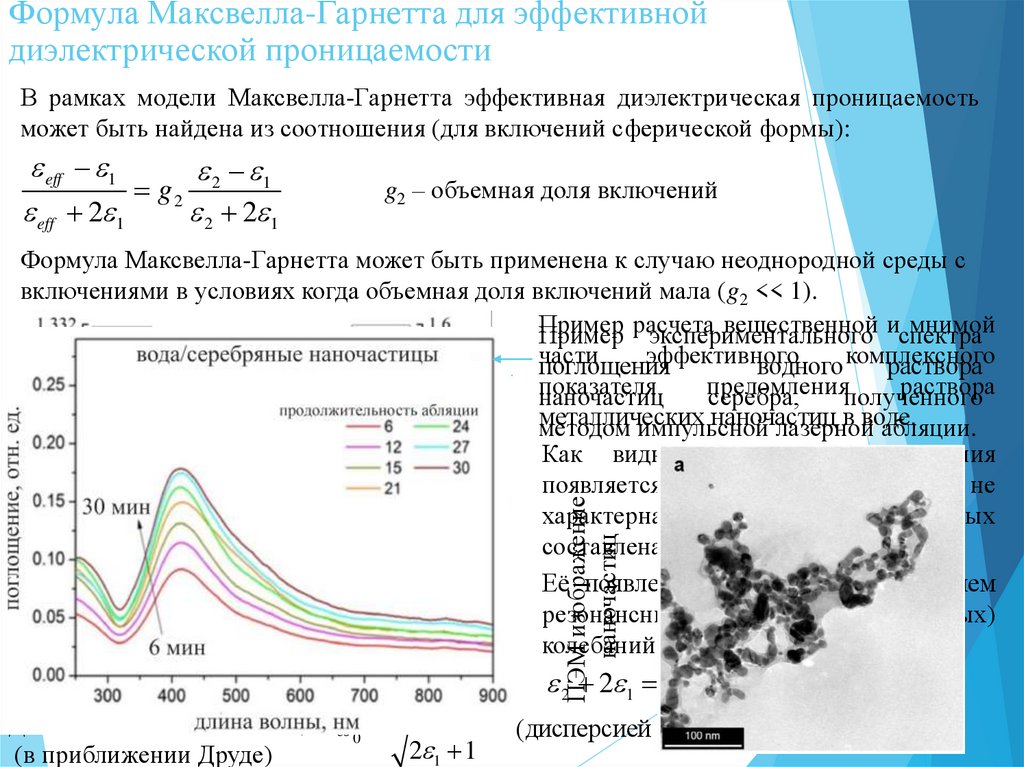
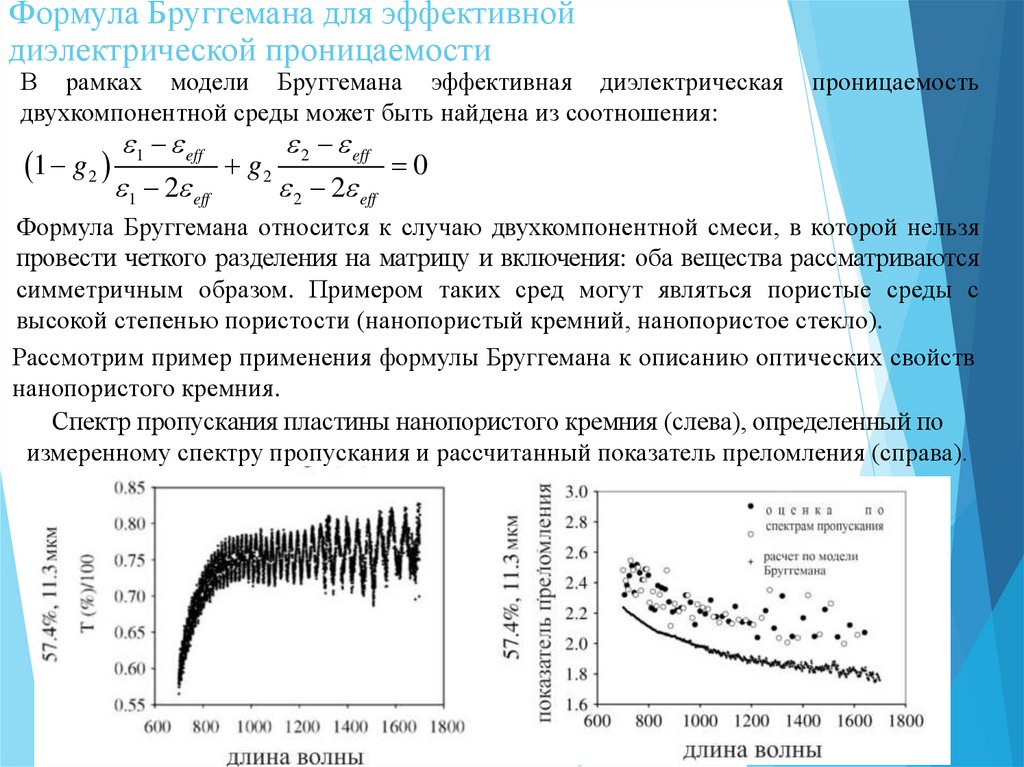























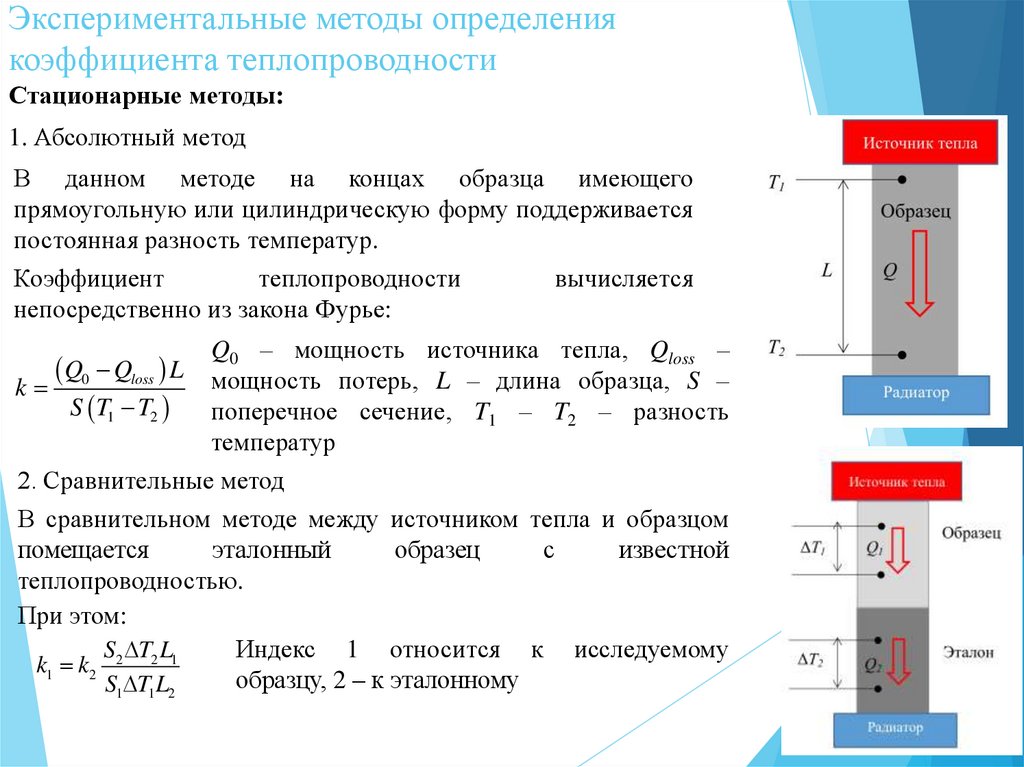
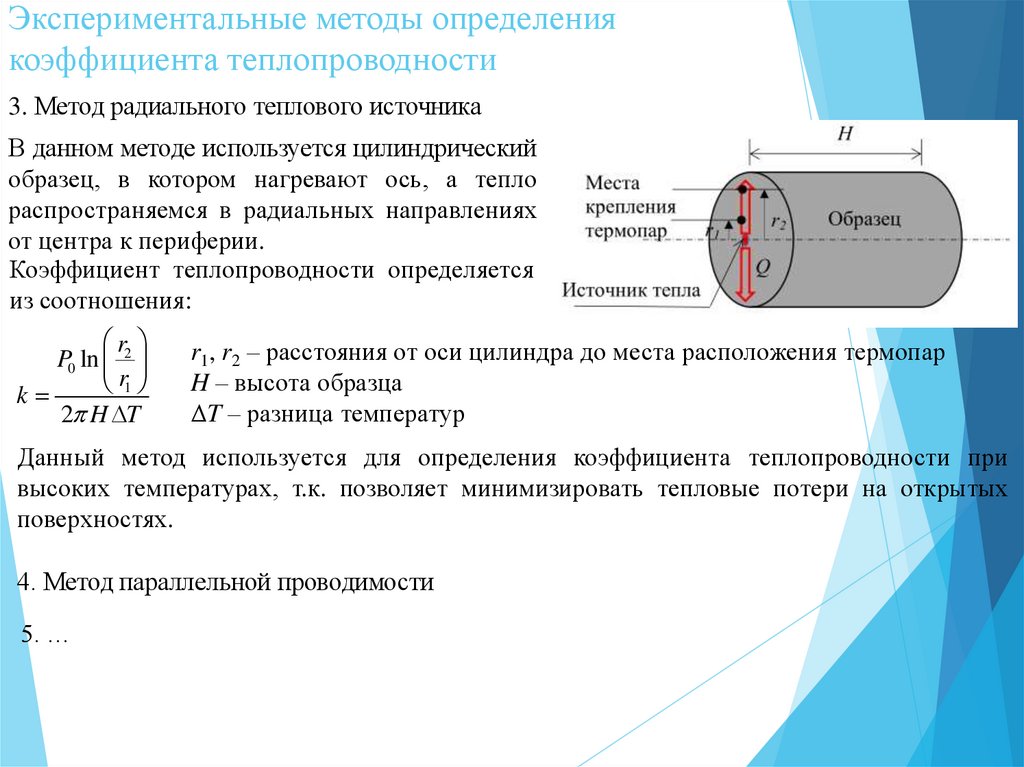

























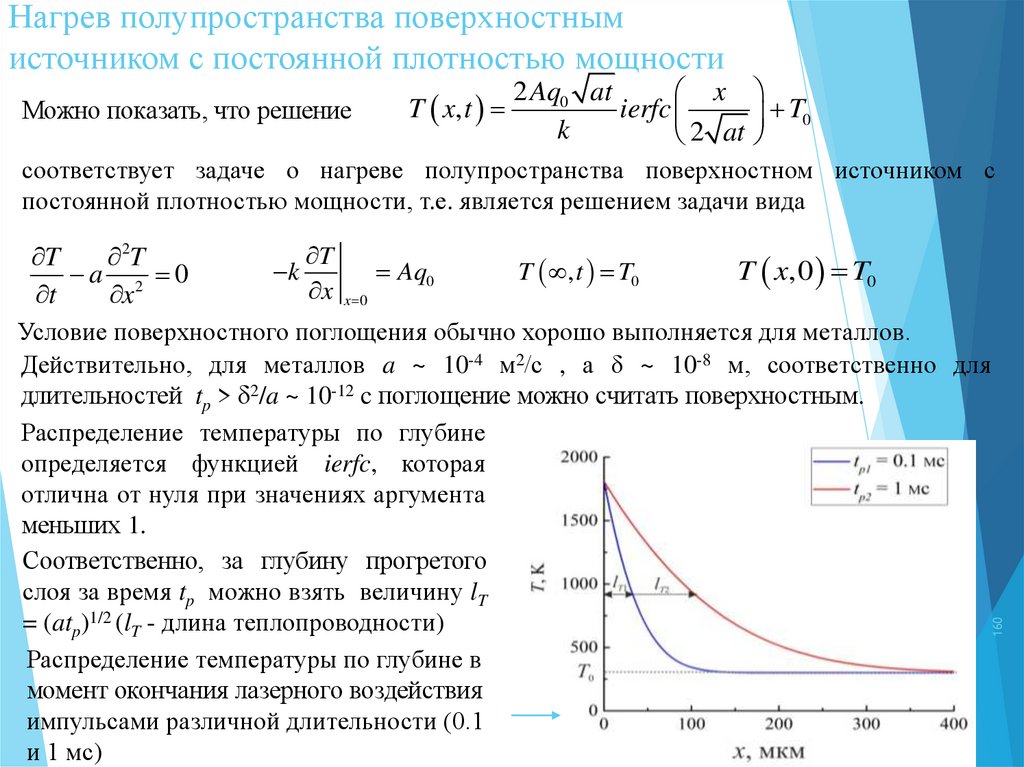

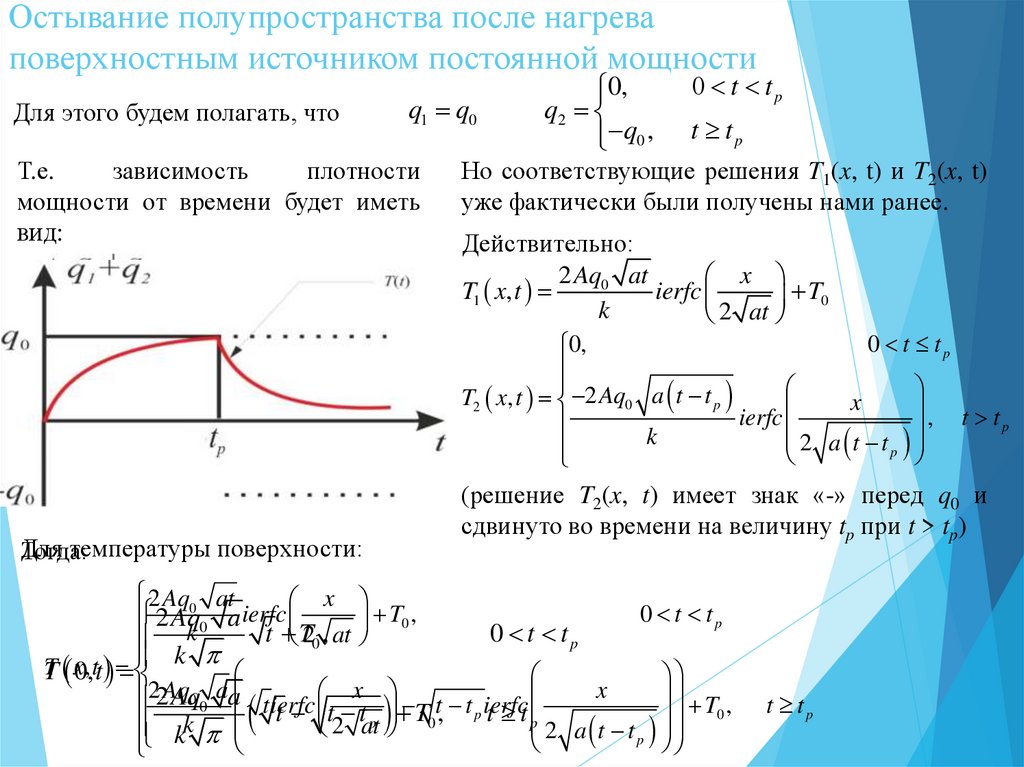






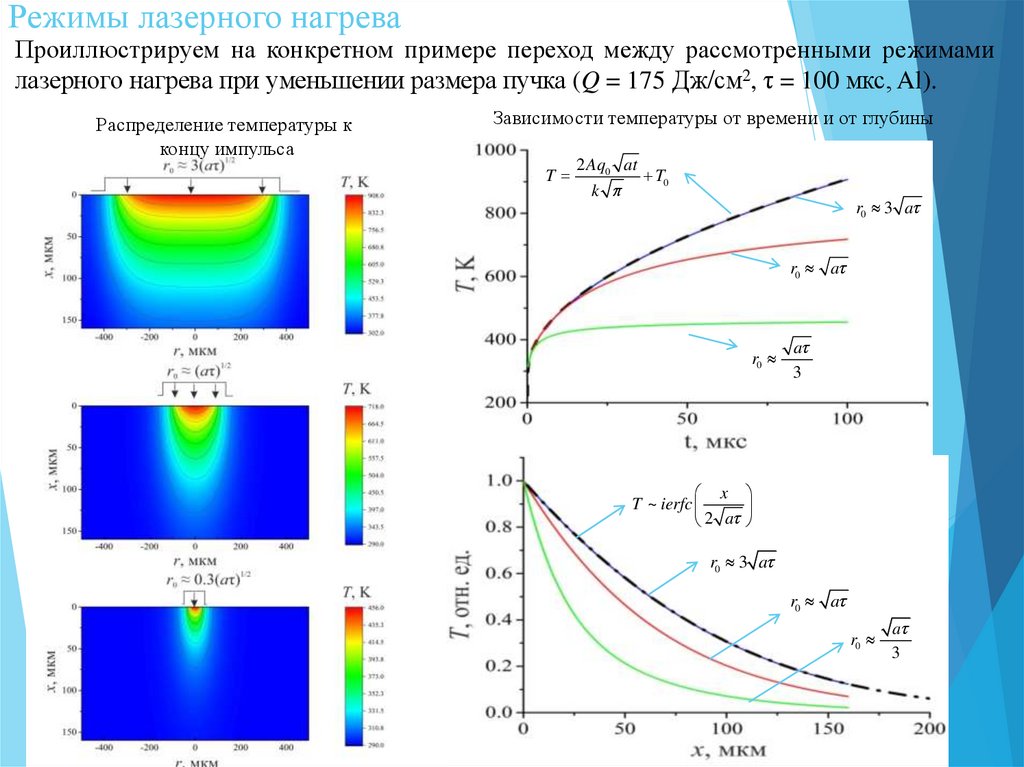

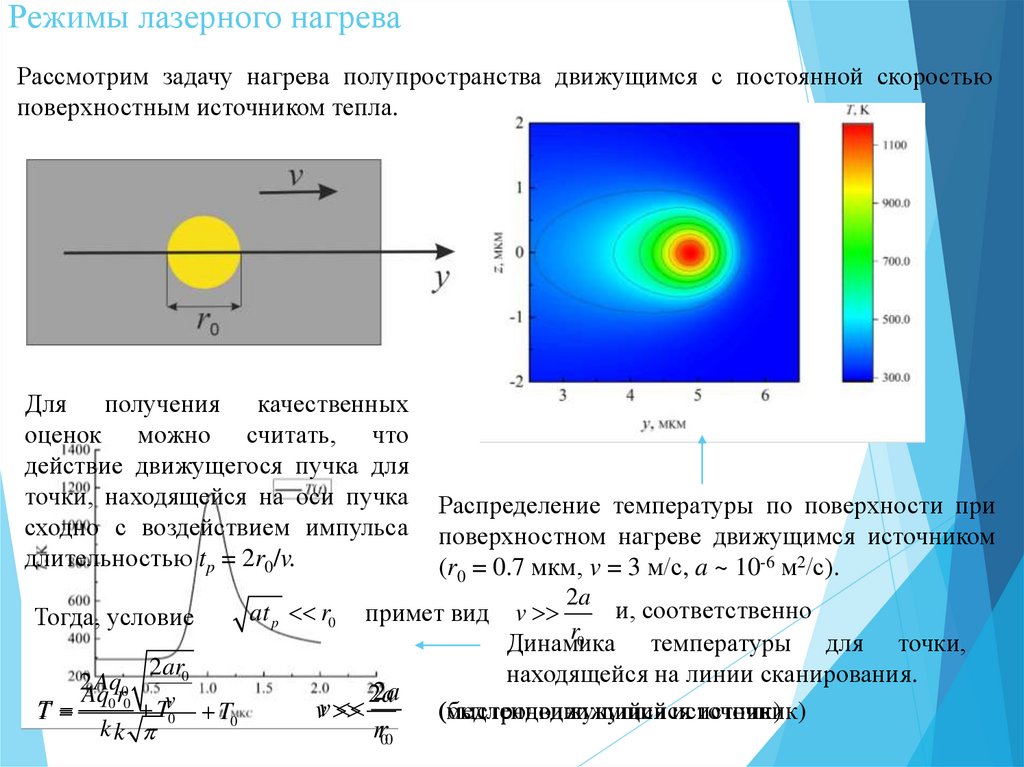



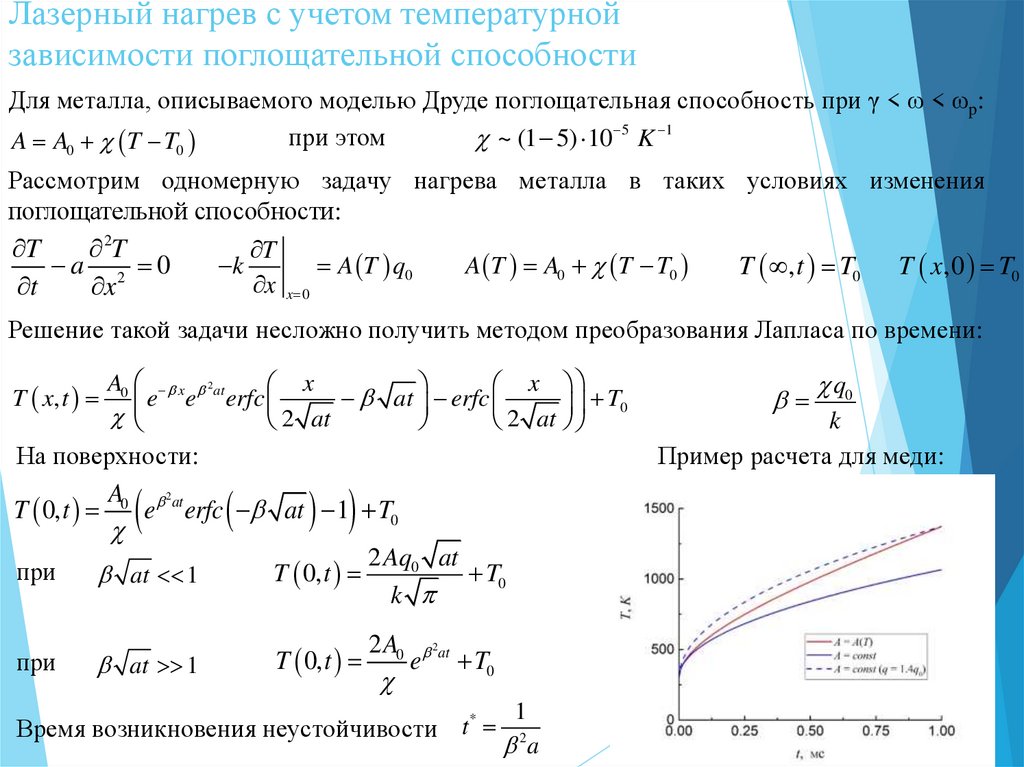


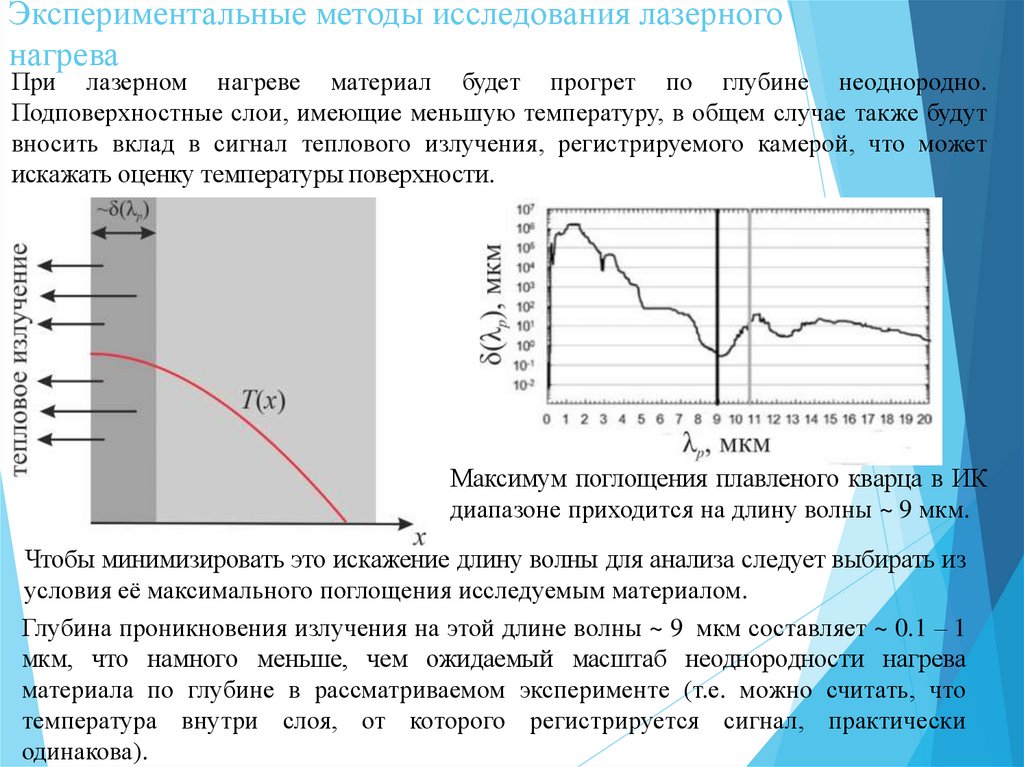






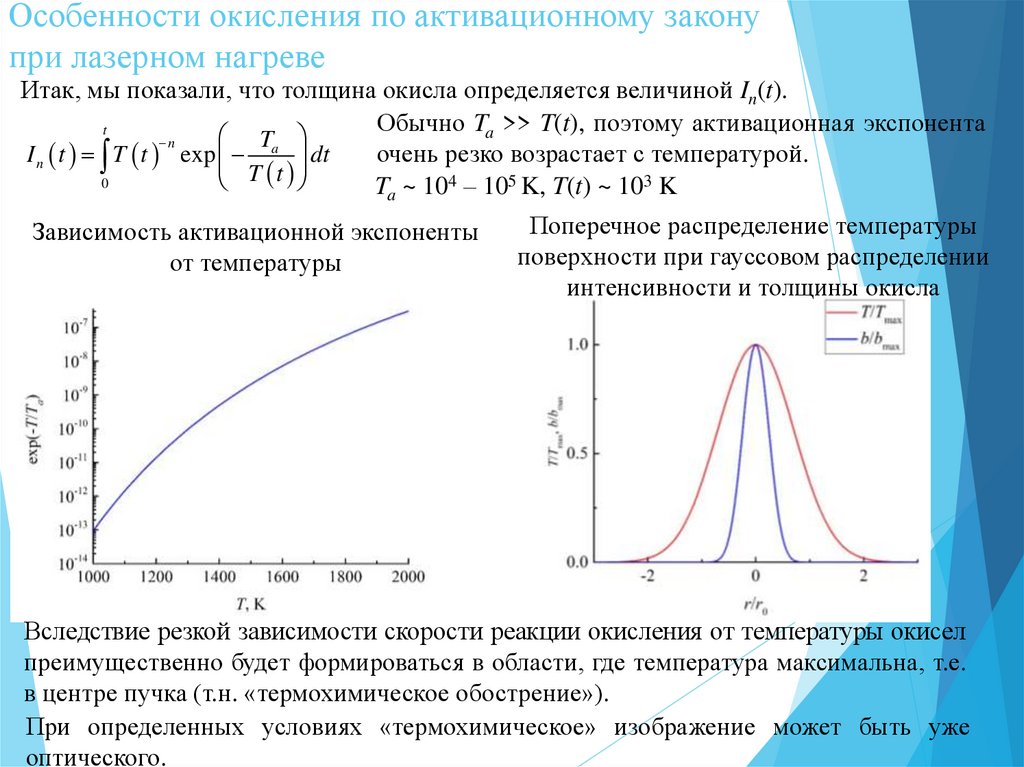
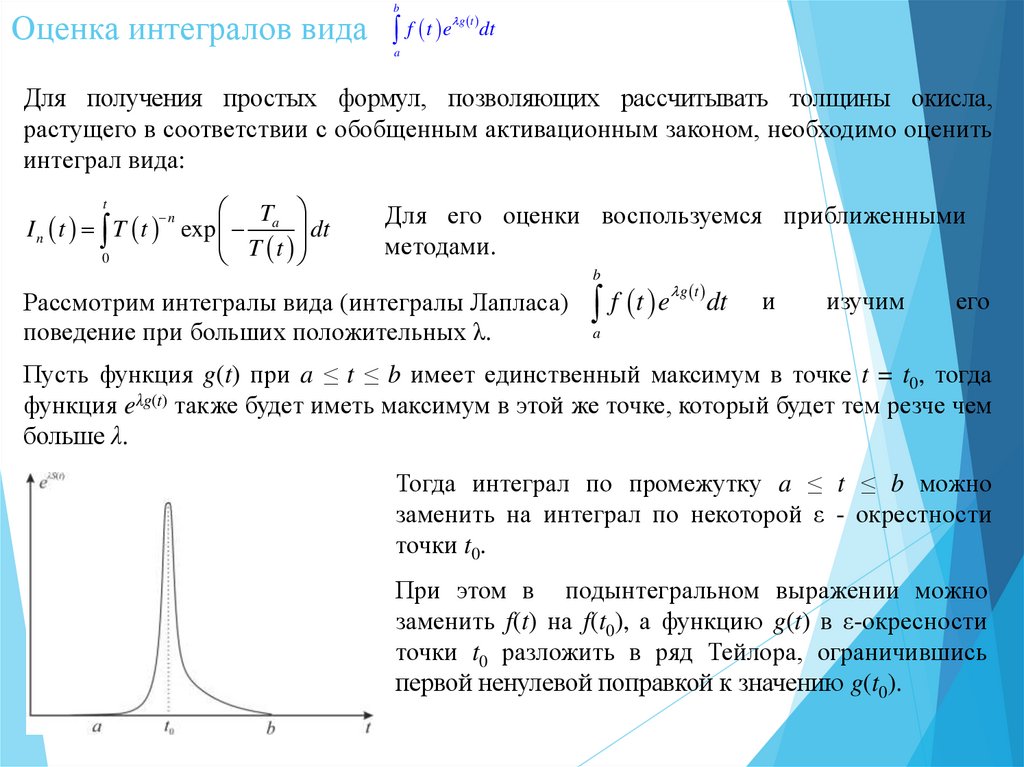




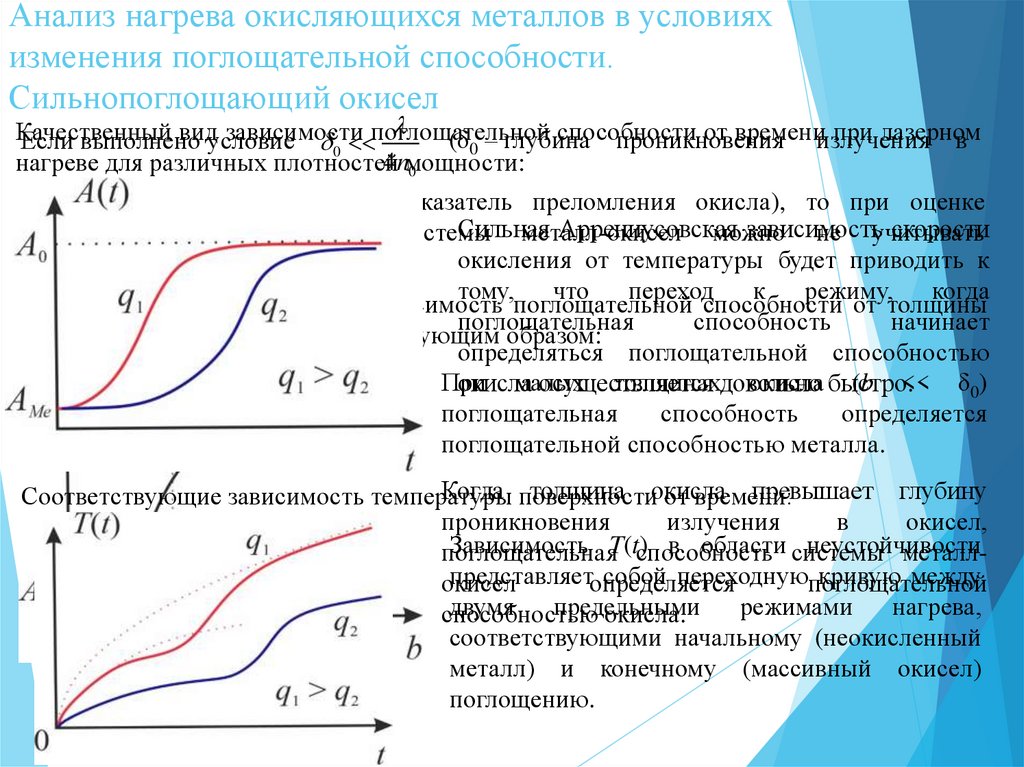



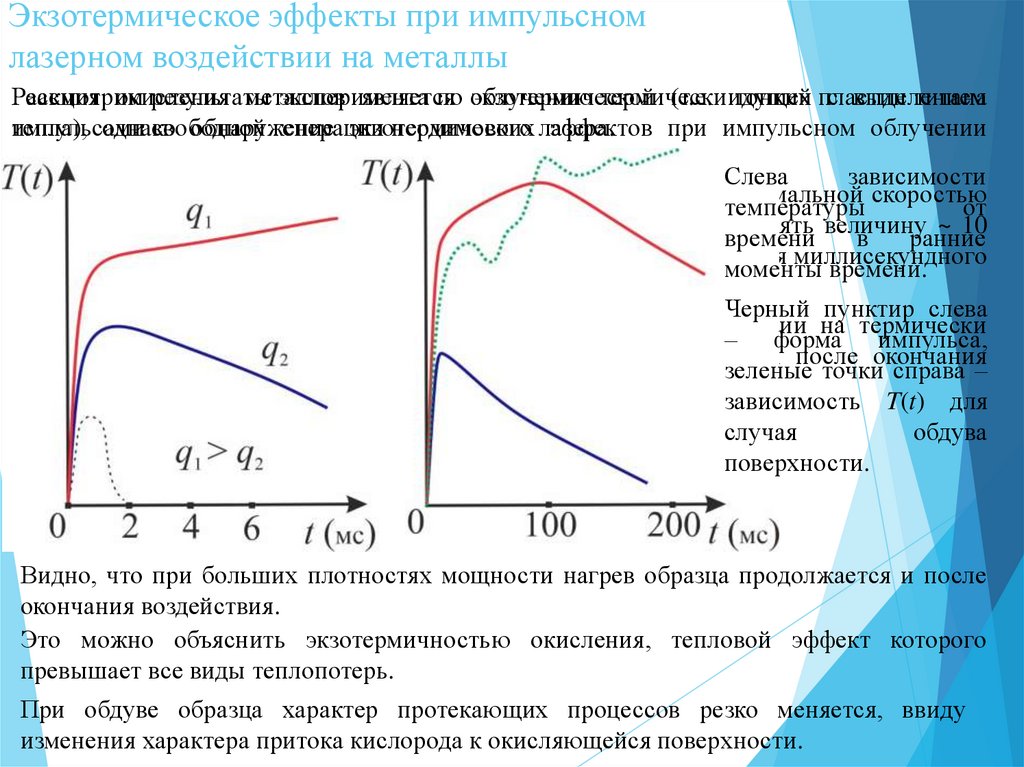



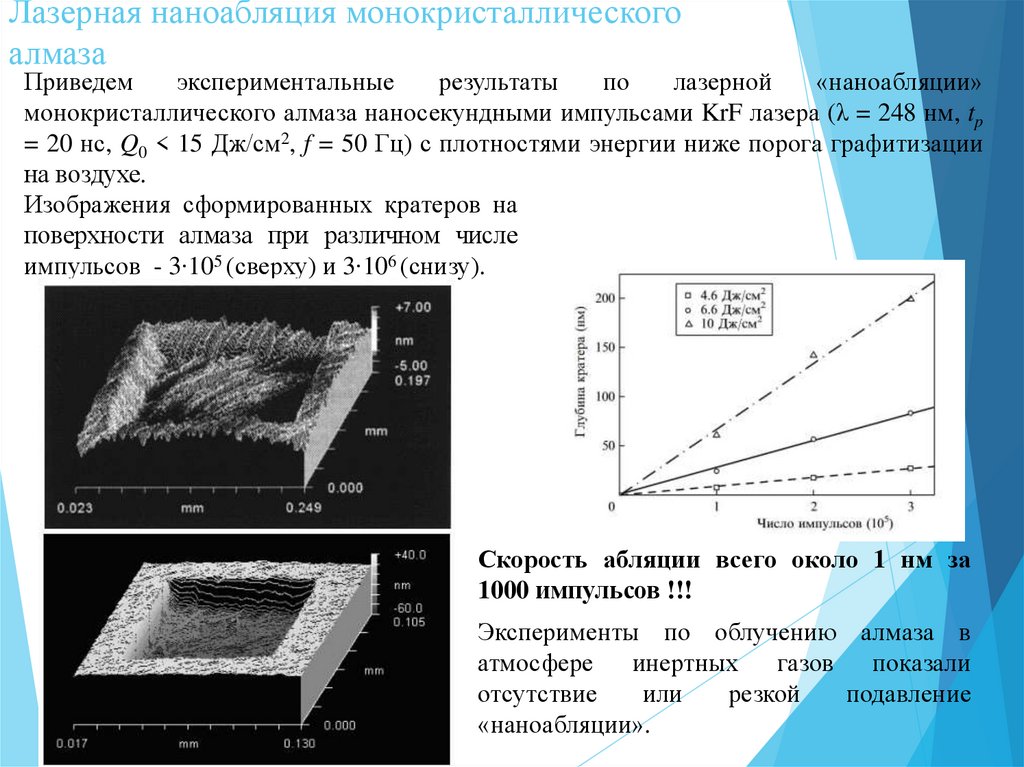
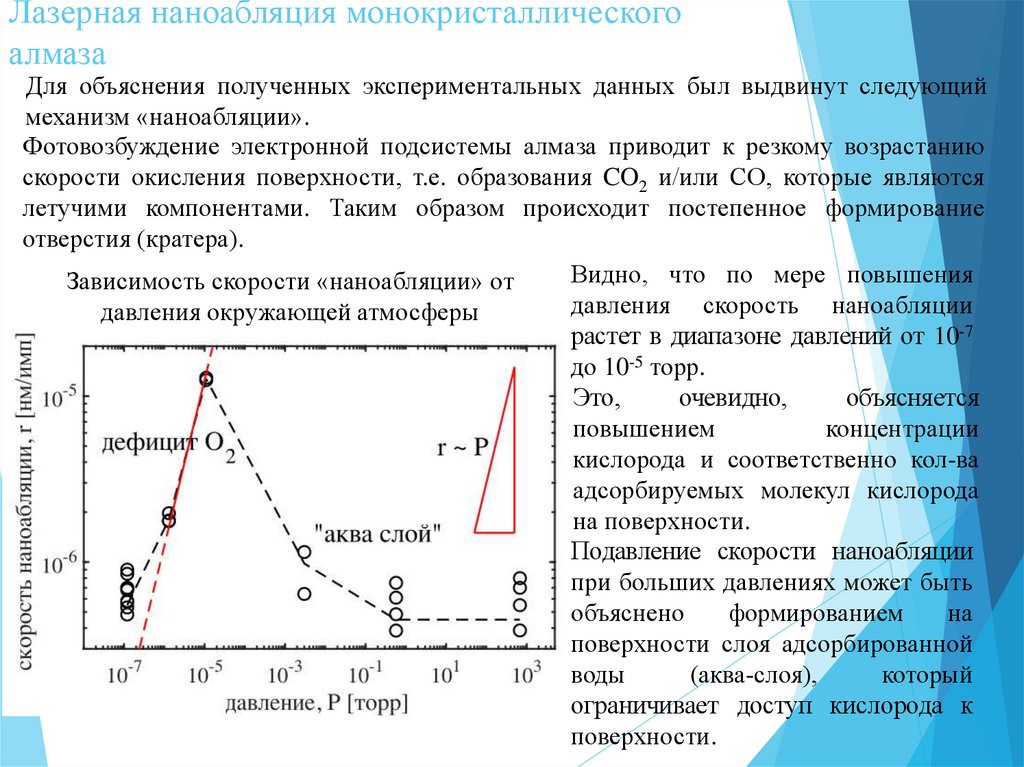


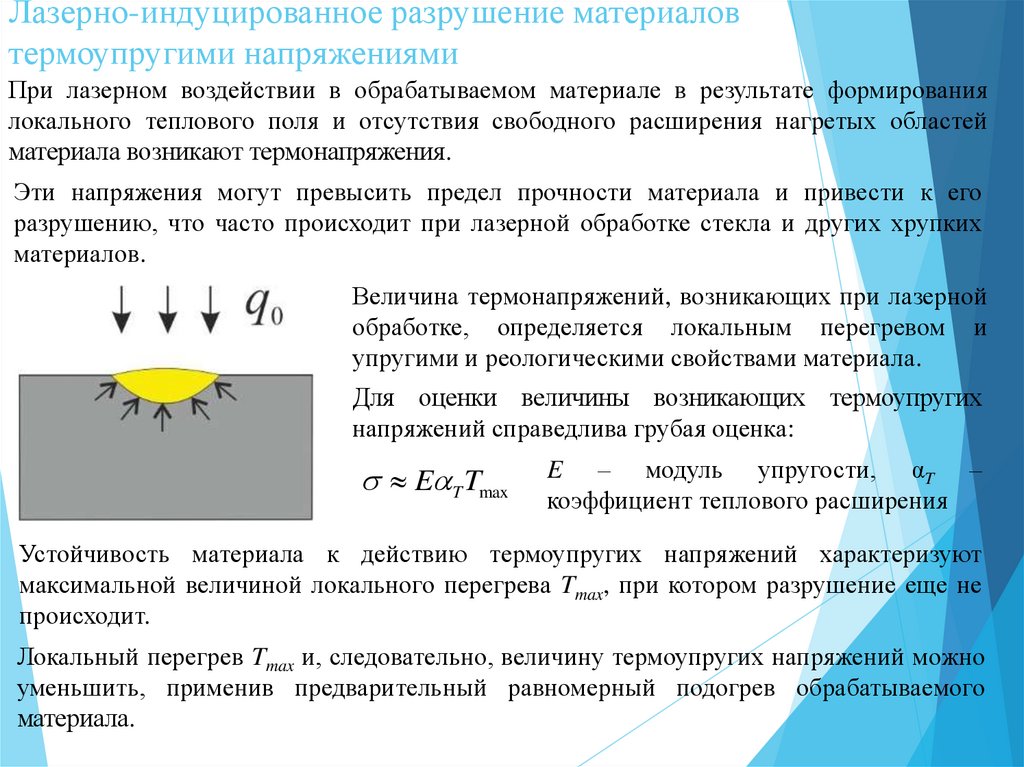





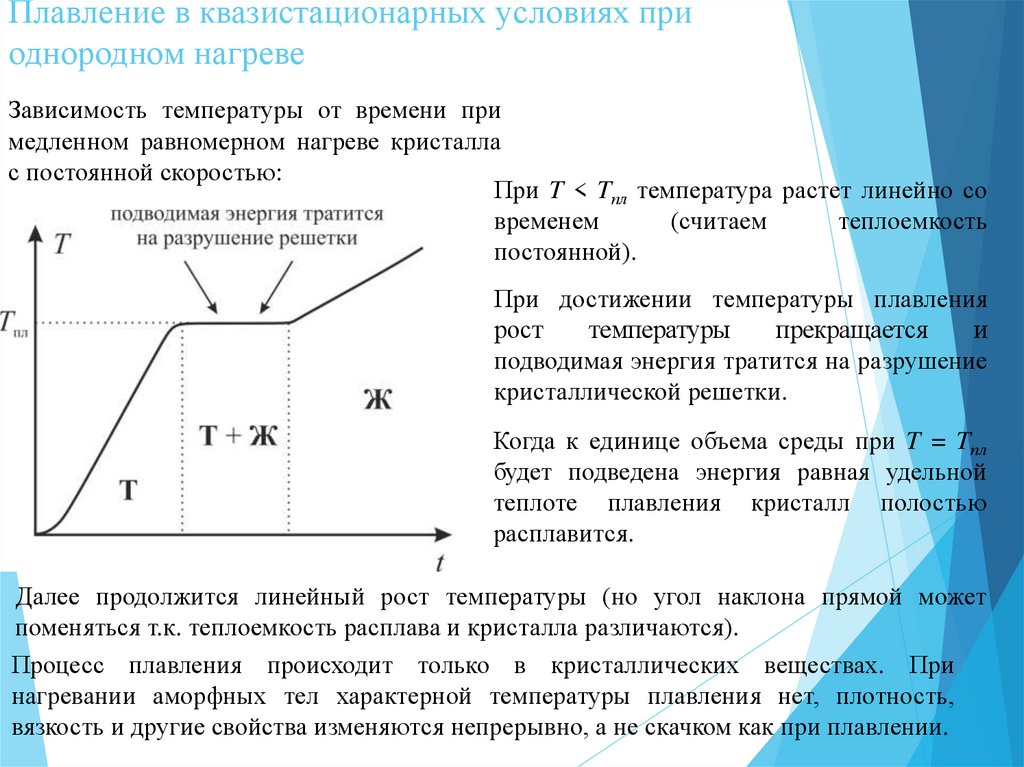

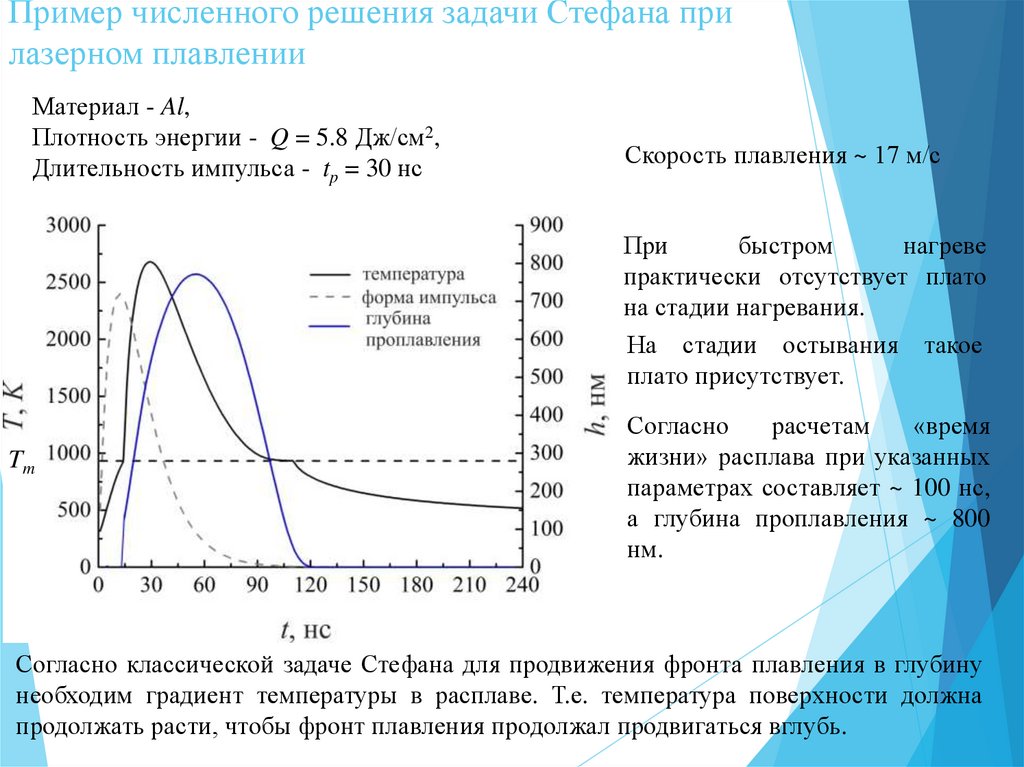
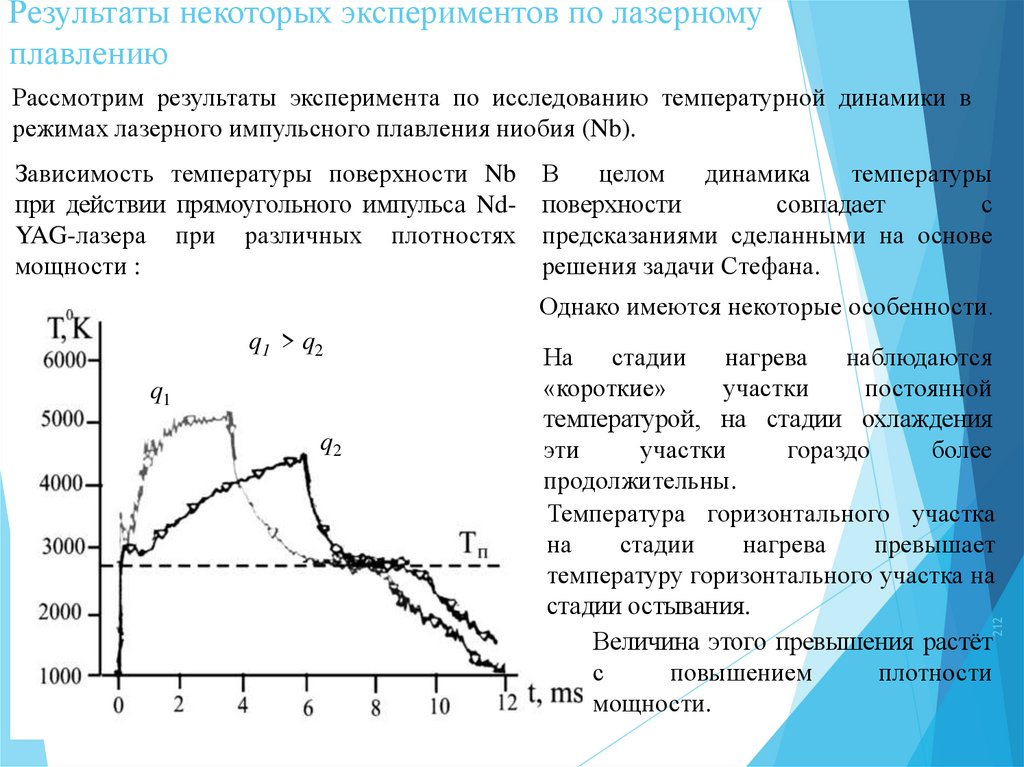


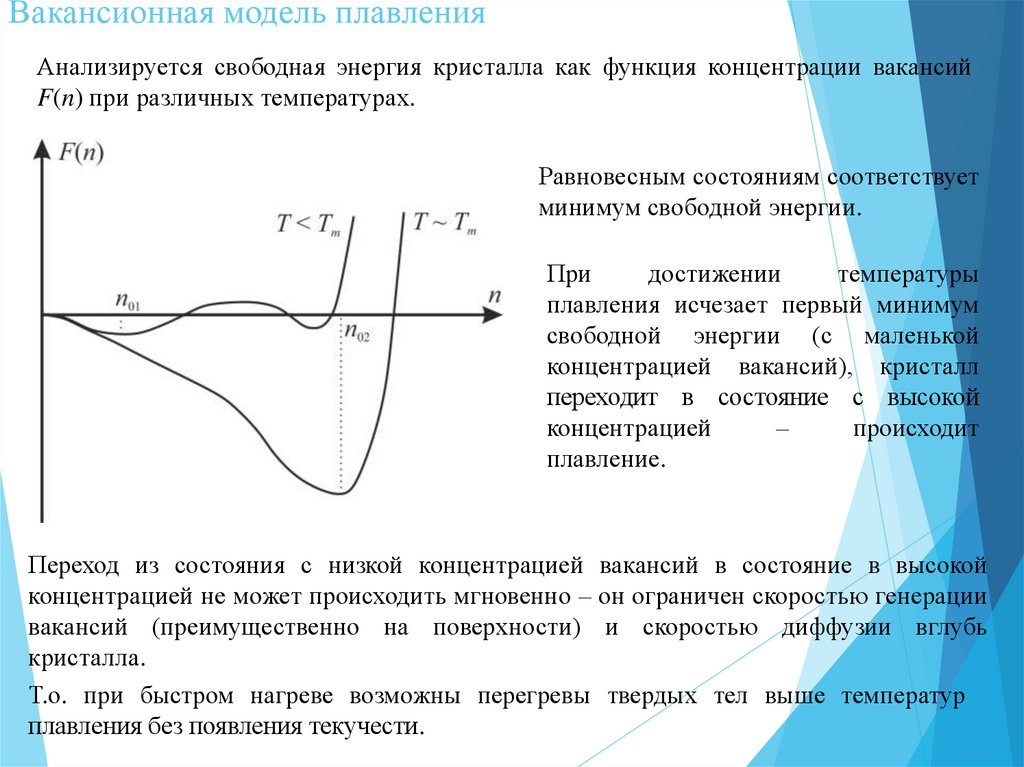







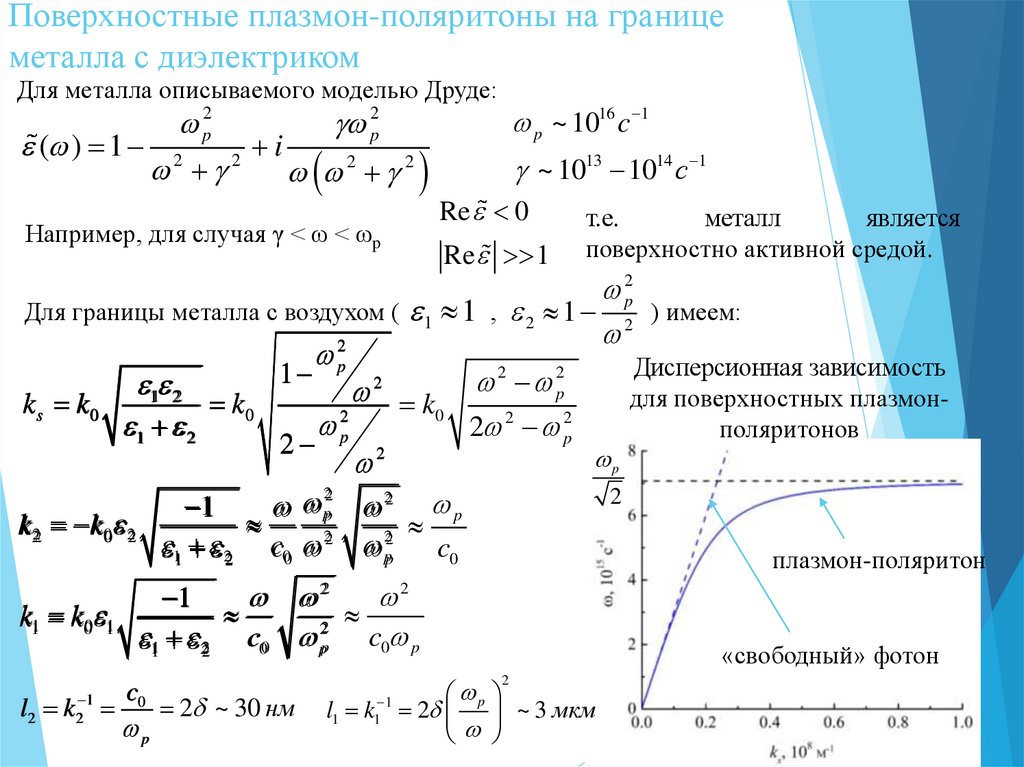



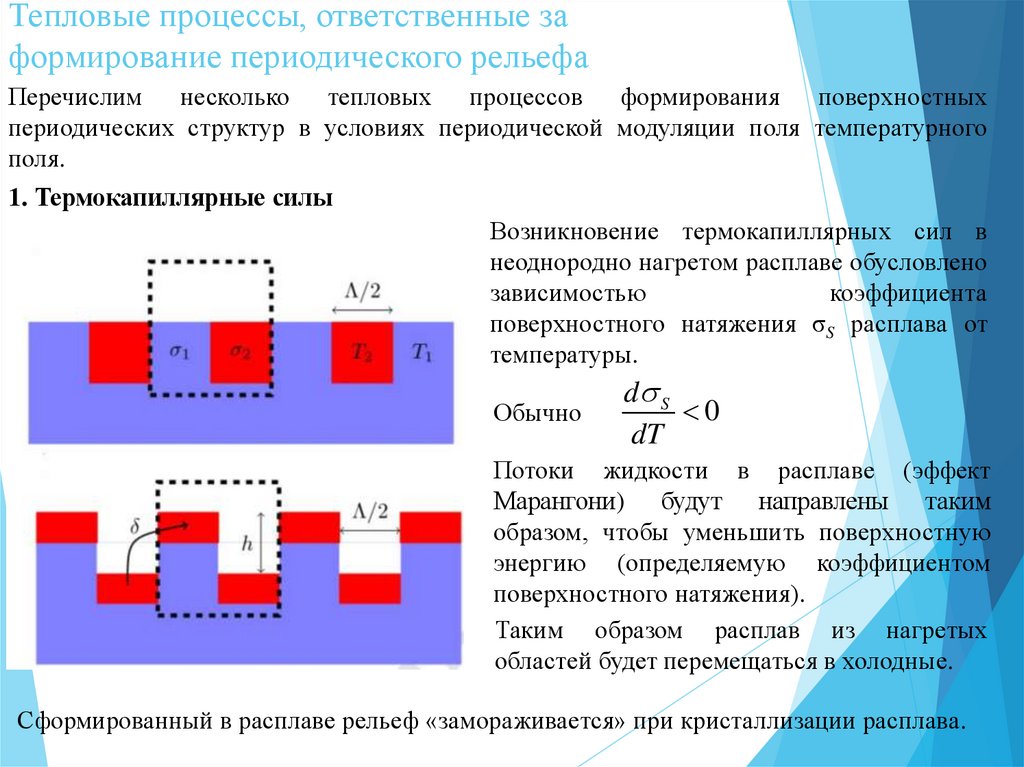







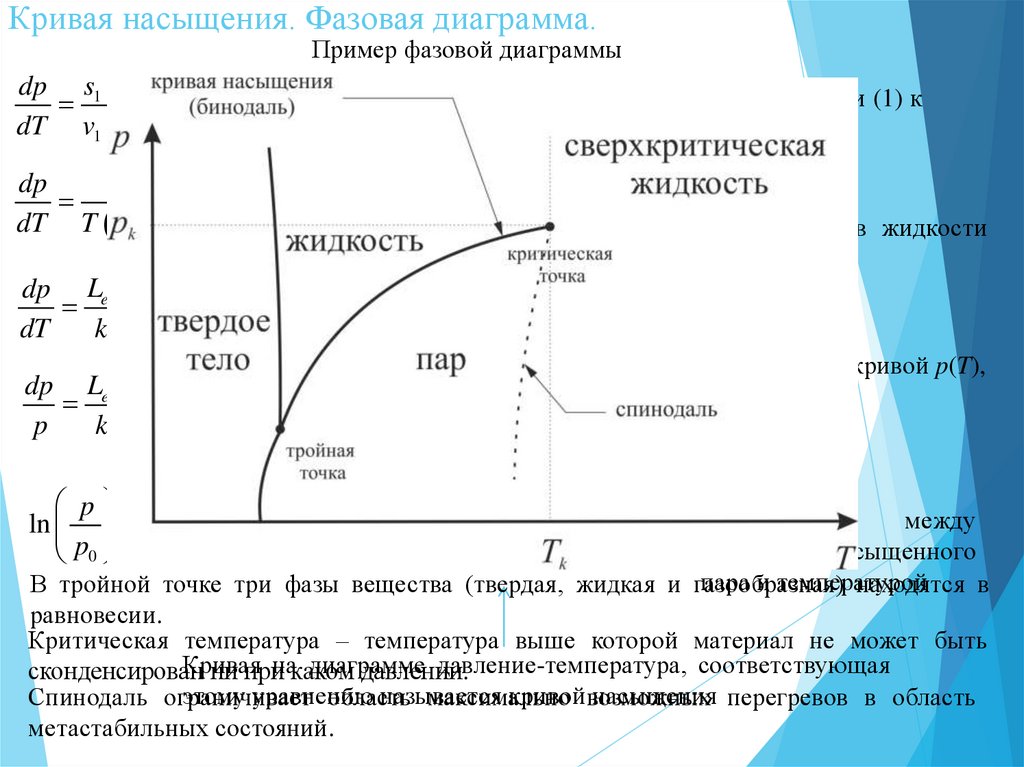

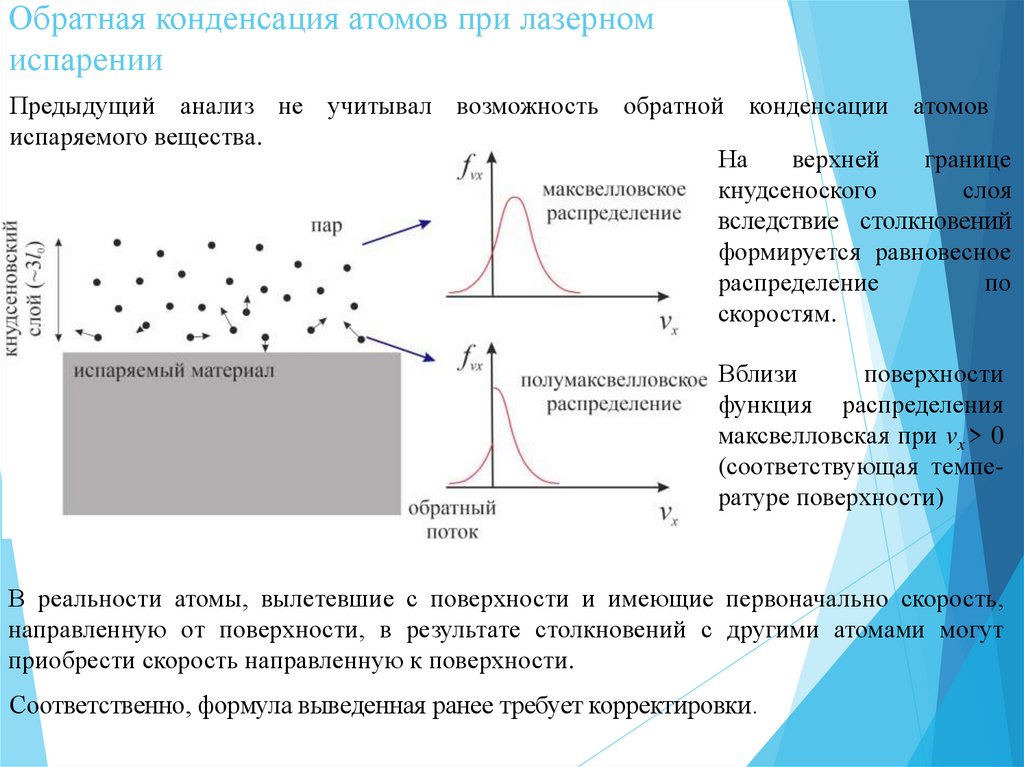



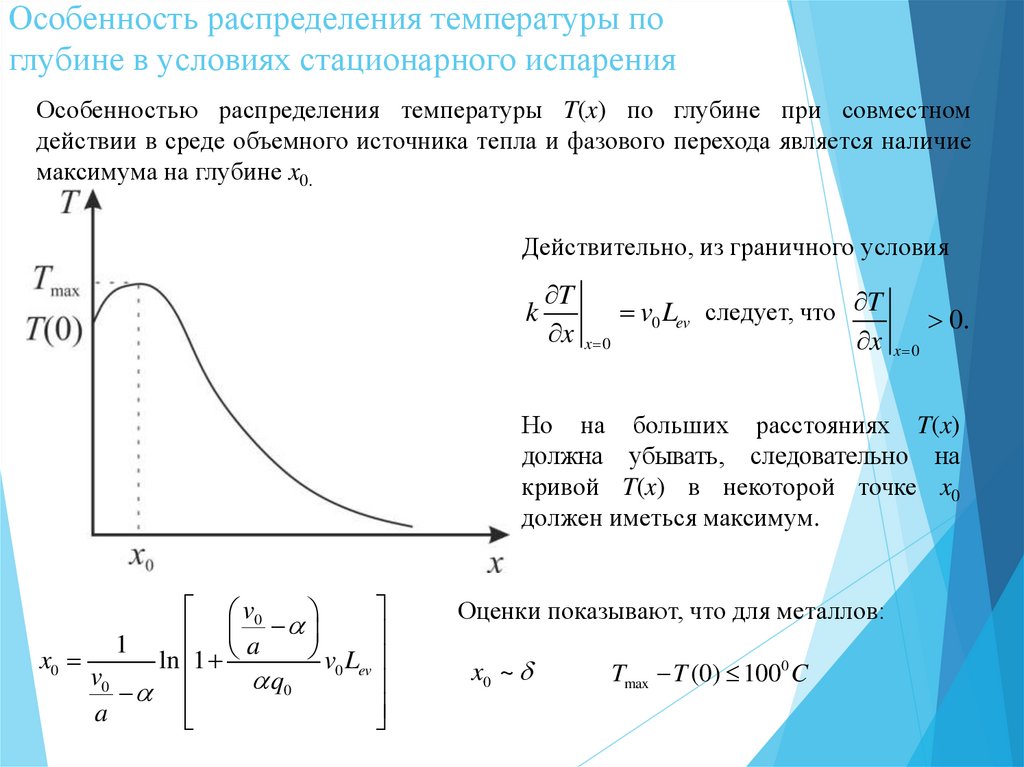
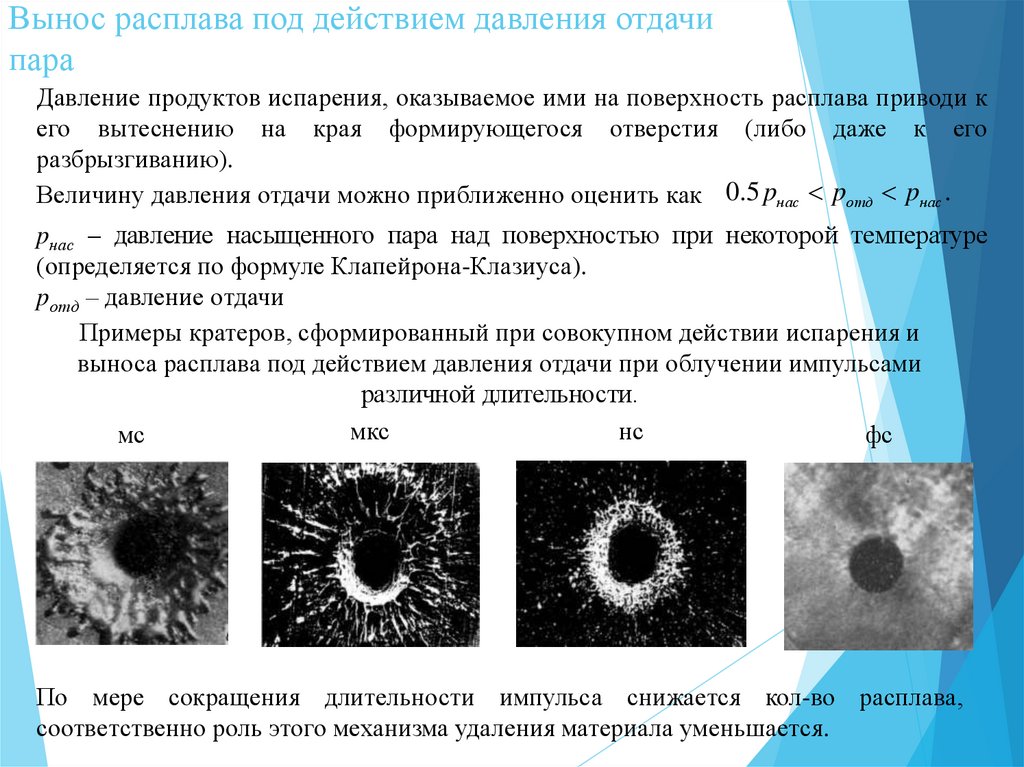
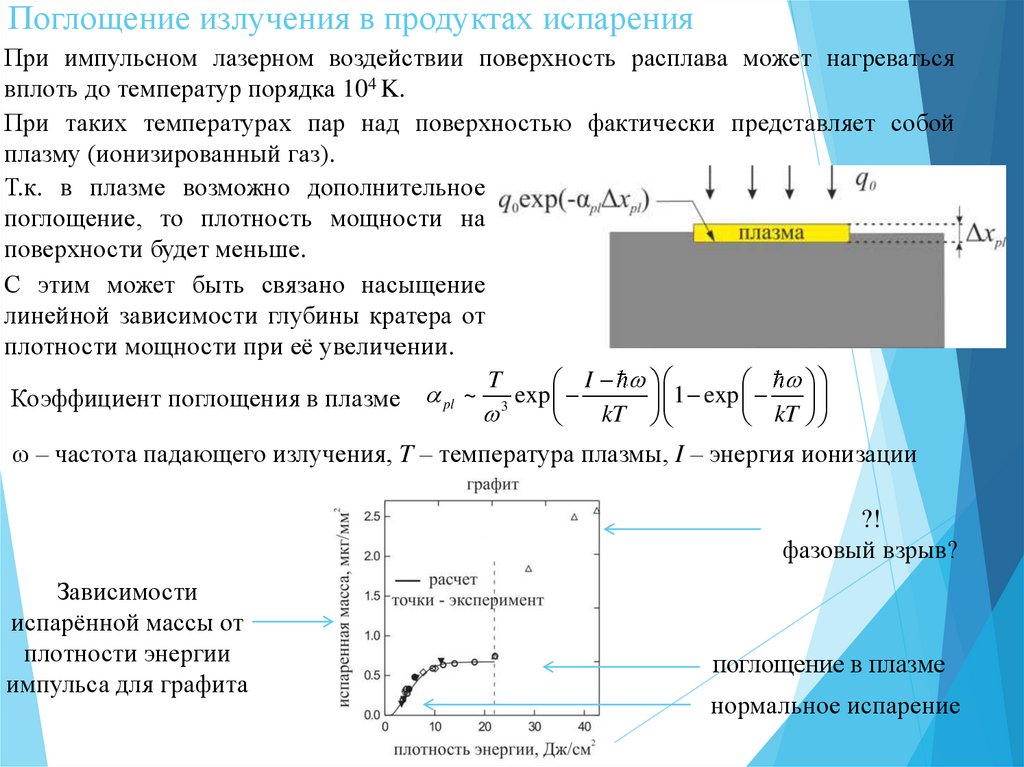
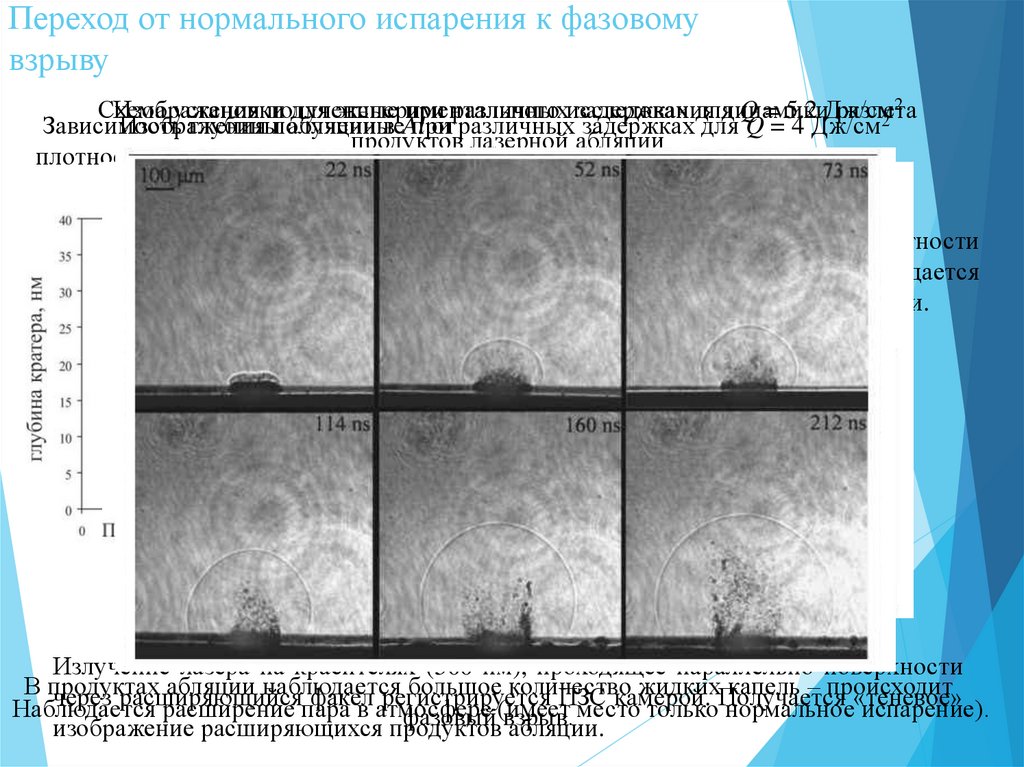
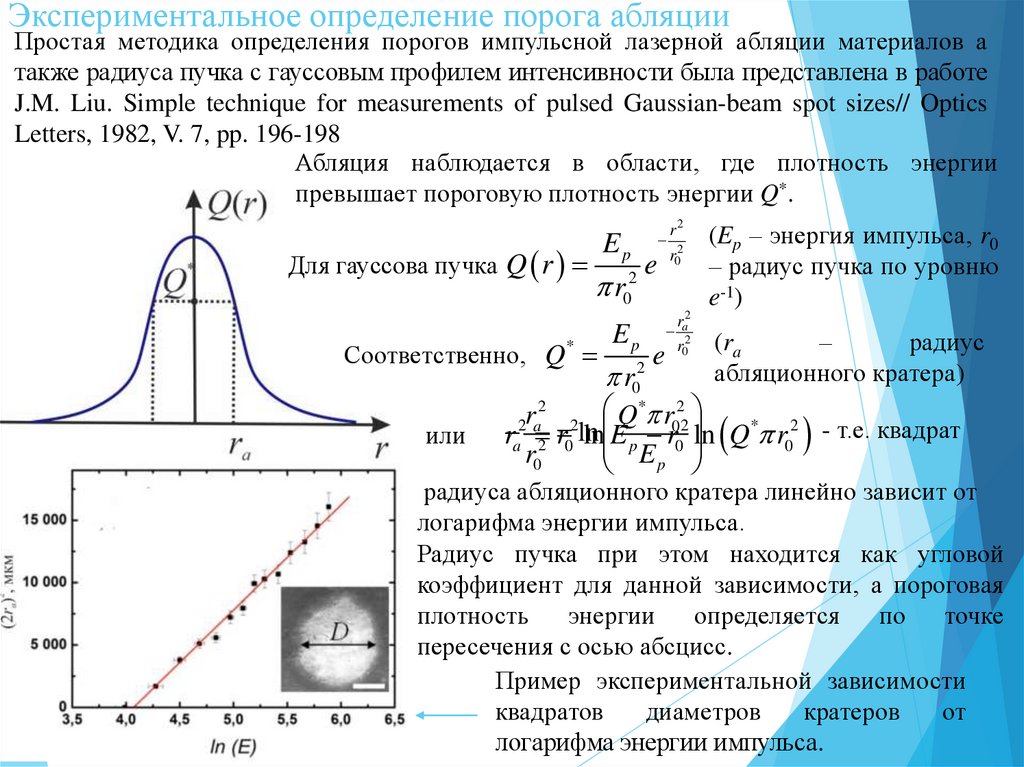




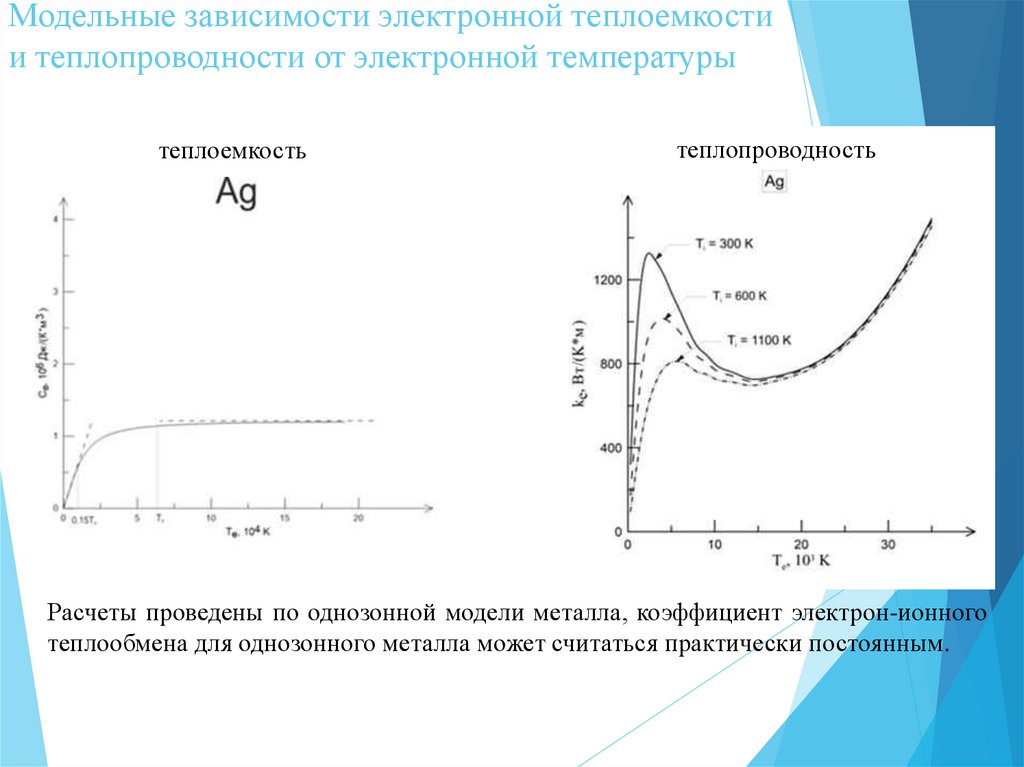






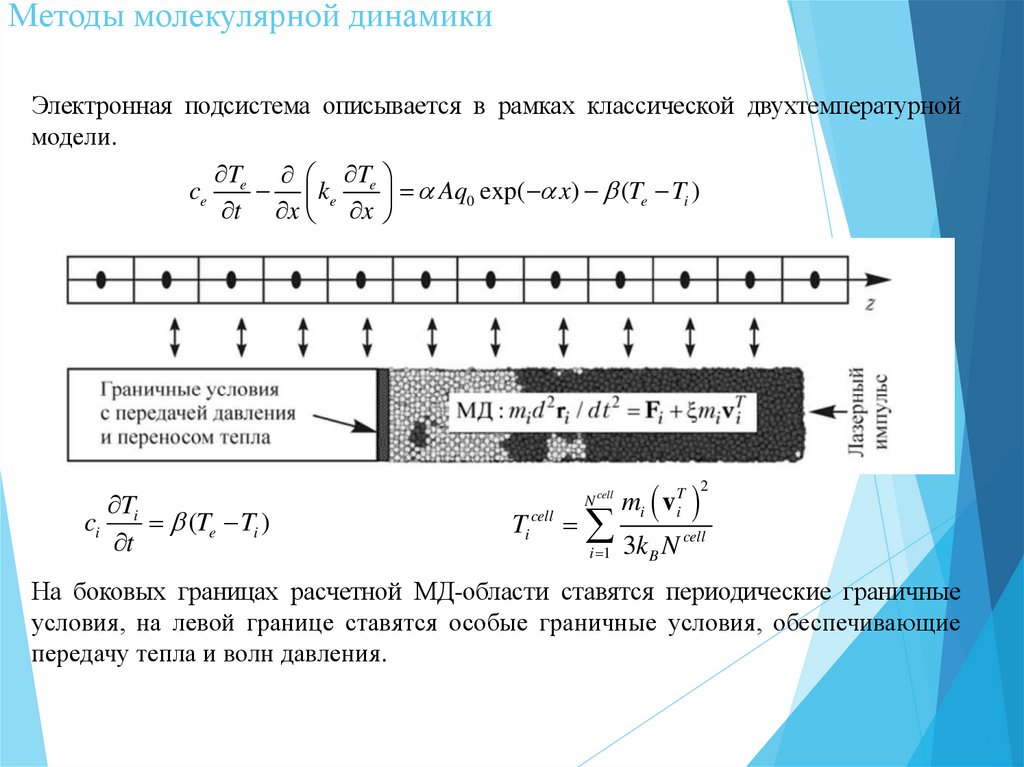
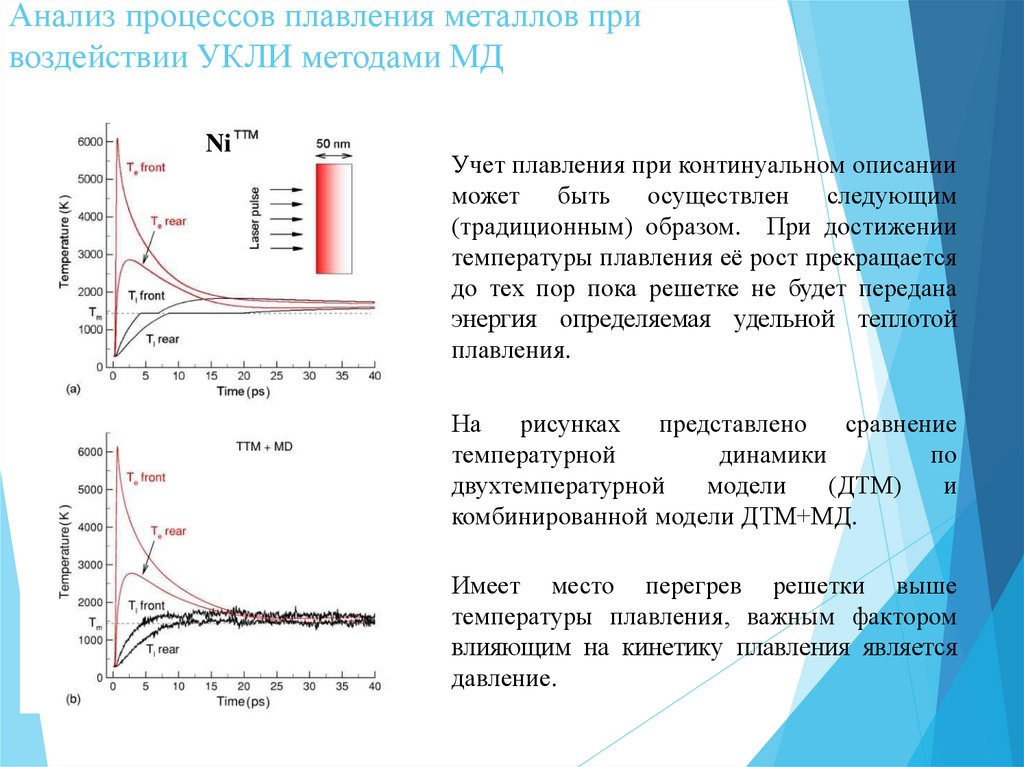
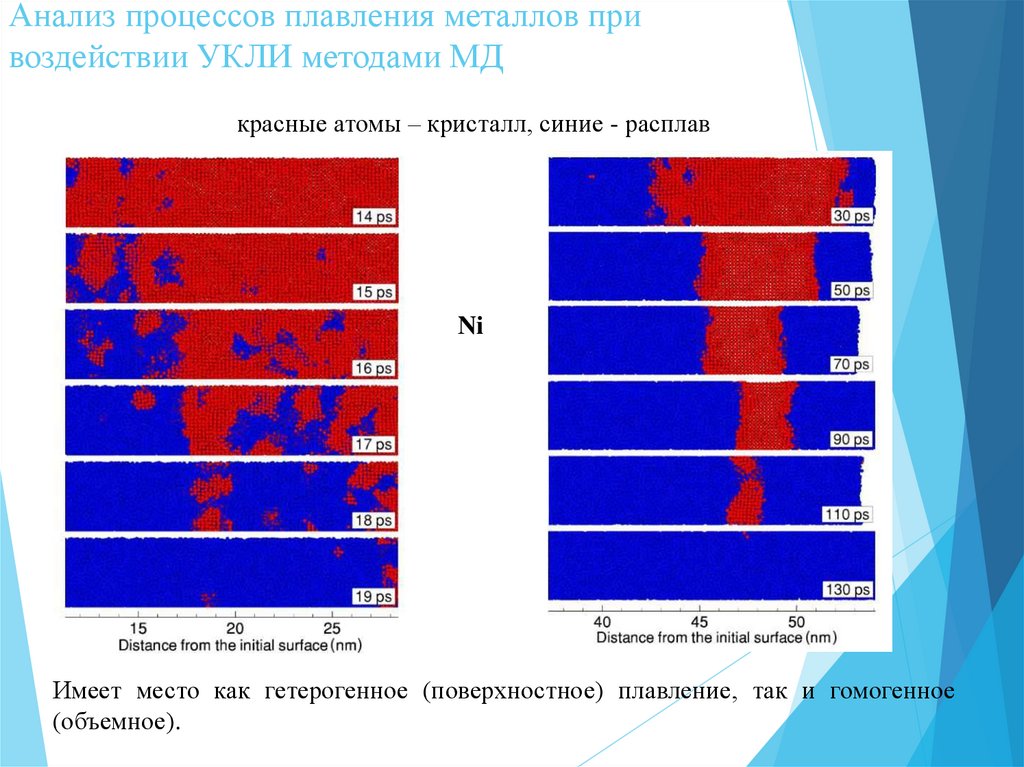

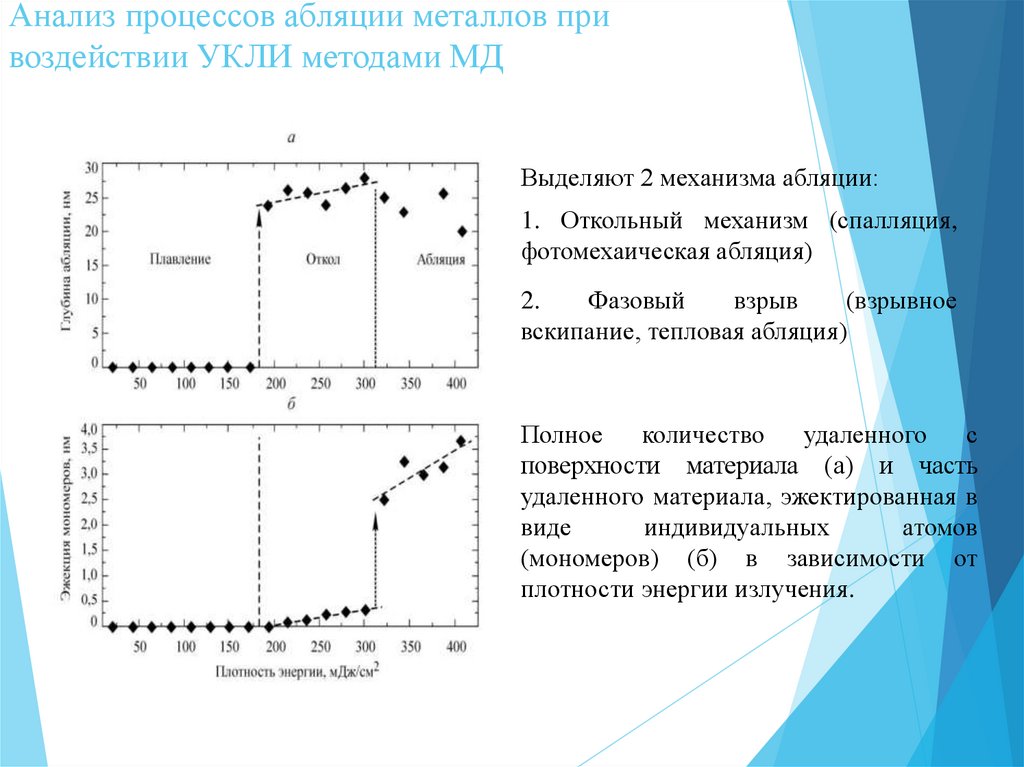
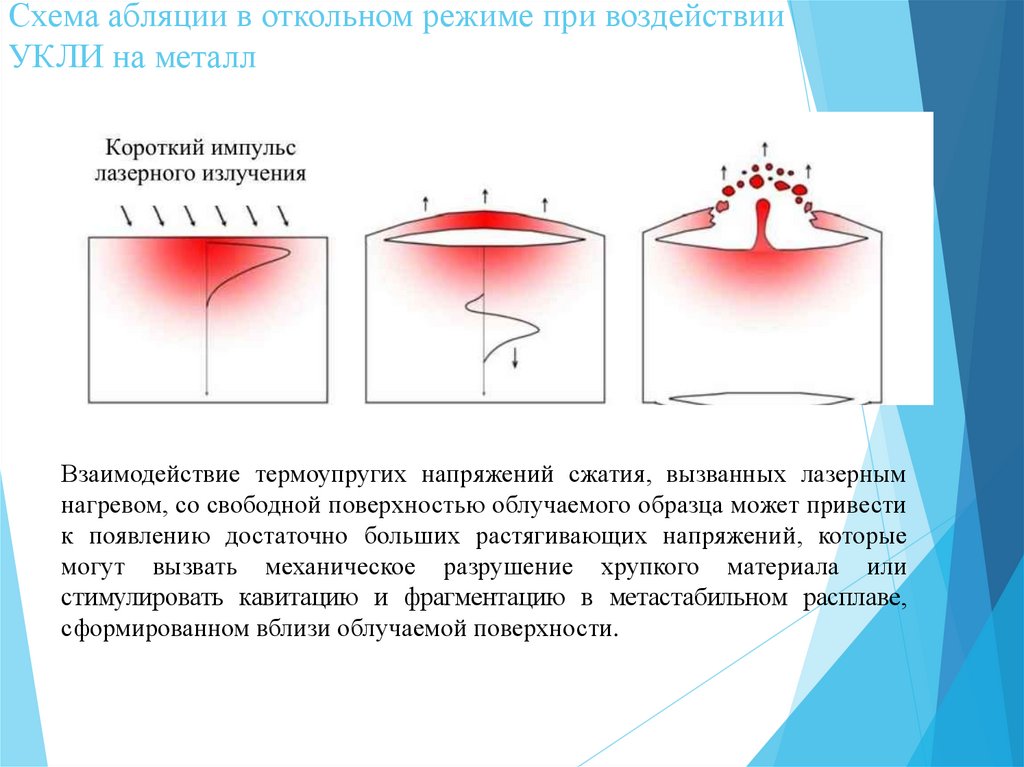


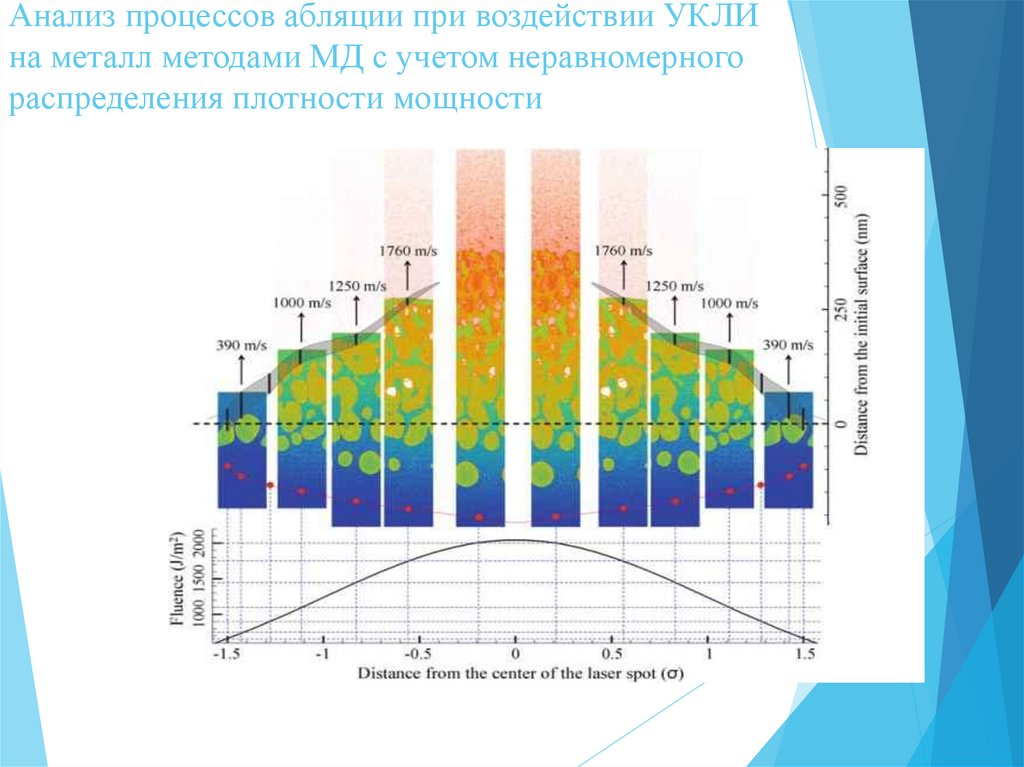




 physics
physics








