Свойства логических операций. Логические элементы

1.

Урок «Свойства логических операций. Логические
элементы»

2.

Алгебра логики
Логические операции
Инверсия
Дизъюнкция
Конъюнкция

3.

Основные свойства логических операций
Законы алгебры логики
1. Переместительный (коммутативный) закон.
При перестановке местами переменных в конъюнкции и дизъюнкции
значение выражения не изменяется.
Конъюнкция – логическое умножение.
Дизъюнкция – логическое сложение.
A&B=B&A
AVB=BVA
A•B=B•A
A+B=B+A

4.

Основные свойства логических операций
Законы алгебры логики
2. Сочетательный (ассоциативный) закон.
При одинаковых знаках операций скобки можно ставить произвольно или
вообще опускать.
Конъюнкция – логическое умножение.
Дизъюнкция – логическое сложение.
(A & B) & C = A & (B & C)
(A V B) V C = A V (B V C)
(A • B) • C = A • (B • C)
(A + B) + C = A + (B + C)
(A • B) • C = A • B • C
(A + B) + C = A + B + C

5.

Основные свойства логических операций
Законы алгебры логики
3. Распределительный (дистрибутивный) закон.
Конъюнкция – логическое умножение.
Дизъюнкция – логическое сложение.
A & (B V C) = (A & B) V (A & C)
A V (B & C) = (A V B) & (A V C)
A • (B + C) = (A • B) + (A • C)
A + (B • C) = (A + B) • (A + C)

6.

Основные свойства логических операций
Законы алгебры логики
4. Закон двойного отрицания.
Двойное отрицание исключает отрицание.
ന=A
A
– (– A) = A

7.

Основные свойства логических операций
Законы алгебры логики
5. Закон исключённого третьего.
Из двух противоречивых высказываний об одном и том же предмете одно
всегда истинно, а второе – ложно, третьего не дано.
Конъюнкция – логическое умножение.
Дизъюнкция – логическое сложение.
A&A=0
AVA=1
A = 0;
A = 1;
0 • 1 = 0.
A = 0;
A = 1;
0 + 1 = 1.
A = 1;
A = 0;
1 • 0 = 0.
A = 1;
A = 0;
1 + 0 = 1.

8.

Основные свойства логических операций
Законы алгебры логики
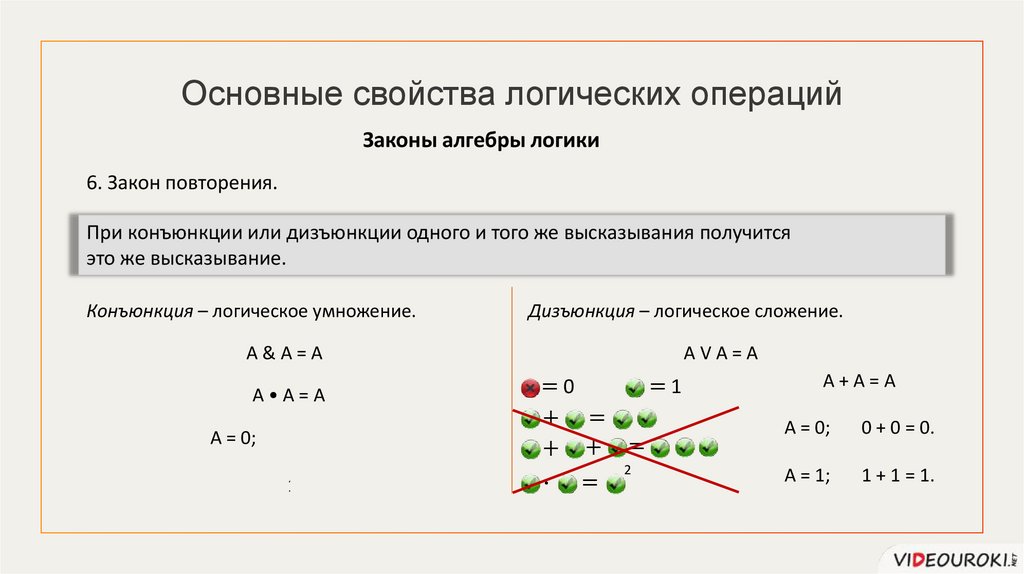
6. Закон повторения.
При конъюнкции или дизъюнкции одного и того же высказывания получится
это же высказывание.
Конъюнкция – логическое умножение.
Дизъюнкция – логическое сложение.
A&A=А
AVA=А
A•A=А
A+A=А
A = 0;
0 • 0 = 0.
A = 0;
0 + 0 = 0.
A = 1;
1 • 1 = 1.
A = 1;
1 + 1 = 1.

9.

Основные свойства логических операций
Законы алгебры логики
6. Закон повторения.
При конъюнкции или дизъюнкции одного и того же высказывания получится
это же высказывание.
Конъюнкция – логическое умножение.
Дизъюнкция – логическое сложение.
A&A=А
A•A=А
A = 0;
A = 1;
0 • 0 = 0.
1 • 1 = 1.
AVA=А
=0
=1
+ =
+ + =
∙
=
2
A+A=А
A = 0;
0 + 0 = 0.
A = 1;
1 + 1 = 1.

10.

Основные свойства логических операций
Законы алгебры логики
7. Законы операций с 0 и 1.
Конъюнкция – логическое умножение.
Дизъюнкция – логическое сложение.
A & 0 = 0;
A • 0 = 0.
A V 0 = А;
A & 1 = A;
A • 1 = А.
A V 1 = 1;A + 1 = 1.
A + 0 = A.

11.

Основные свойства логических операций
Законы алгебры логики
8. Законы общей инверсии.
Для того, чтобы найти инверсию конъюнкции, нужно найти дизъюнкцию
инверсий каждого логического выражения.
Для того, чтобы найти инверсию дизъюнкции, нужно найти конъюнкцию
инверсий каждого логического выражения.
Конъюнкция – логическое умножение.
A&B=АVB
Дизъюнкция – логическое сложение.
AVB=А&B

12.

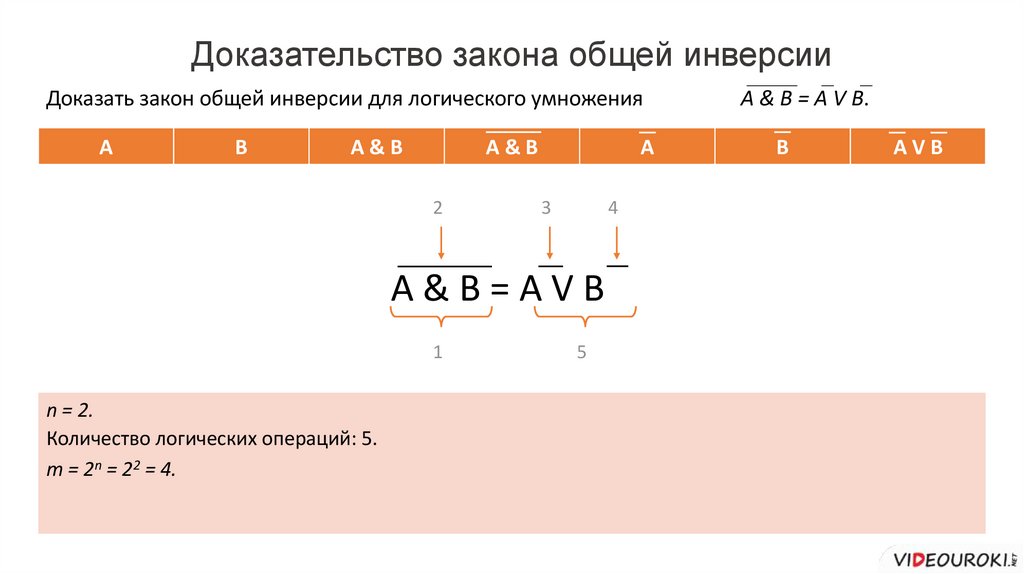
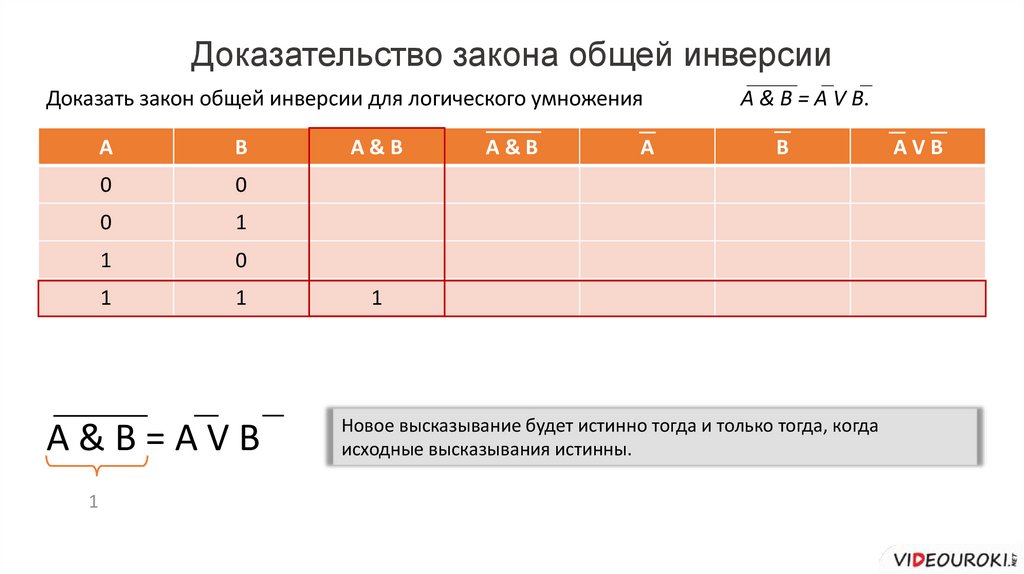
Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A&B=АVB
n = 2.
Количество логических операций: 5.
A & B = А V B.

13.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
2
A&B=АVB
1
n = 2.
Количество логических операций: 5.
A & B = А V B.

14.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
2
3
4
A&B=АVB
1
n = 2.
Количество логических операций: 5.
5
A & B = А V B.

15.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
A&B
A&B
2
A
3
4
A&B=АVB
1
n = 2.
Количество логических операций: 5.
m = 2n = 22 = 4.
5
A & B = А V B.
B
AVB

16.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
A&B
n = 2.
Количество логических операций: 5.
m = 2n = 22 = 4.
2n – 1 = 22 – 1 = 4 – 1 = 3. 0, 1, 2, 3.
A&B
A & B = А V B.
A
B
010 = 002
110 = 012
210 = 102
310 = 112
AVB

17.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
0
0
0
1
1
0
1
1
A&B
n = 2.
Количество логических операций: 5.
m = 2n = 22 = 4.
2n – 1 = 22 – 1 = 4 – 1 = 3. 0, 1, 2, 3.
A&B
A & B = А V B.
A
B
010 = 002
110 = 012
210 = 102
310 = 112
AVB

18.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
0
0
0
1
1
0
1
1
A&B=АVB
1
A&B
A&B
A
A & B = А V B.
B
Новое высказывание будет истинно тогда и только тогда, когда
исходные высказывания истинны.
AVB

19.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
0
0
0
1
1
0
1
1
A&B=АVB
1
A&B
A&B
A
A & B = А V B.
B
1
Новое высказывание будет истинно тогда и только тогда, когда
исходные высказывания истинны.
AVB

20.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
A&B
0
0
0
0
1
0
1
0
0
1
1
1
A&B=АVB
1
A&B
A
A & B = А V B.
B
Новое высказывание будет истинно тогда и только тогда, когда
исходные высказывания истинны.
AVB

21.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
A&B
0
0
0
0
1
0
1
0
0
1
1
1
A&B
A
2
A&B=АVB
А=1
В=0
инверсия
инверсия
А=0
В=1
A & B = А V B.
B
AVB

22.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
A&B
A&B
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
A&B=АVB
A
A & B = А V B.
B
AVB

23.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
A&B
A&B
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
А=1
В=0
инверсия
A
3
A&B=АVB
инверсия
А=0
В=1
A & B = А V B.
B
AVB

24.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A
B
A&B
A&B
A
0
0
0
1
1
0
1
0
1
1
1
0
0
1
0
1
1
1
0
0
А=1
В=0
инверсия
А=0
В=1
4
A&B=АVB
инверсия
A & B = А V B.
B
AVB

25.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A & B = А V B.
A
B
A&B
A&B
A
B
0
0
0
1
1
1
0
1
0
1
1
0
1
0
0
1
0
1
1
1
1
0
0
0
A&B=АVB
5
Новое высказывание будет ложно тогда и только тогда, когда
ложны исходные высказывания.
AVB

26.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A & B = А V B.
A
B
A&B
A&B
A
B
0
0
0
1
1
1
0
1
0
1
1
0
1
0
0
1
0
1
1
1
1
0
0
0
A&B=АVB
5
Новое высказывание будет ложно тогда и только тогда, когда
ложны исходные высказывания.
AVB
0

27.

Доказательство закона общей инверсии
Доказать закон общей инверсии для логического умножения
A & B = А V B.
A
B
A&B
A&B
A
B
AVB
0
0
0
1
1
1
1
0
1
0
1
1
0
1
1
0
0
1
0
1
1
1
1
1
0
0
0
0
A&B=АVB

28.

Пример
Найти значение логического выражения
(D > 1) V (D < 2). D = 1.
Решение:
D = 1.
(D > 1) V (D < 2) = (1 > 1) V (1 < 2) = 0 V 1 = 0 V 0 = 0.
(1 > 1) – ложно.
(1 > 1) = 0.
(1 < 2) – истинно.
6. Закон повторения: при конъюнкции или дизъюнкции
одного и того же высказывания, получится это же
высказывание.
Дизъюнкция: A V A = А.
(1 < 2) = 1.
Ответ: (D > 1) V (D < 2) = 0, при D = 1.

29.

Построение таблиц истинности для логических
выражений. Свойства логических операций

30.

Построение таблиц истинности для логических
выражений. Свойства логических операций
1.
Переместительный (коммутативный) закон: A & B = B & A; A V B = B V A.
2. Сочетательный (ассоциативный) закон: (A & B) & C = A & (B & C);
= A V (B V C).
(A V B) V C
3. Распределительный (дистрибутивный) закон:
C) = (A & B) V (A & C); A V (B & C) = (A V B) & (A V C).
4. Закон двойного отрицания: A = A.ന
A & (B V
5. Закон исключённого третьего: A & A = 0; A V A = 1.
6. Закон повторения: A & A = А; A V A = А.
7. Законы операций с 0 и 1: A & 0 = 0, A & 1 = A; A V 0 = А, A V 1 = 1.
8. Законы общей инверсии: A & B = А V B; A V B = А & B.

31.

Алгебра логики
Дискретная форма —
это форма представления, при которой информация преподнесена в виде
фиксированного набора отдельных значений.
Дискретные устройства —
это устройства, которые обрабатывают дискретные значения (сигналы).
Логический элемент —
это дискретный преобразователь, который выдаёт после обработки двоичных
сигналов значение одной из логических операций.

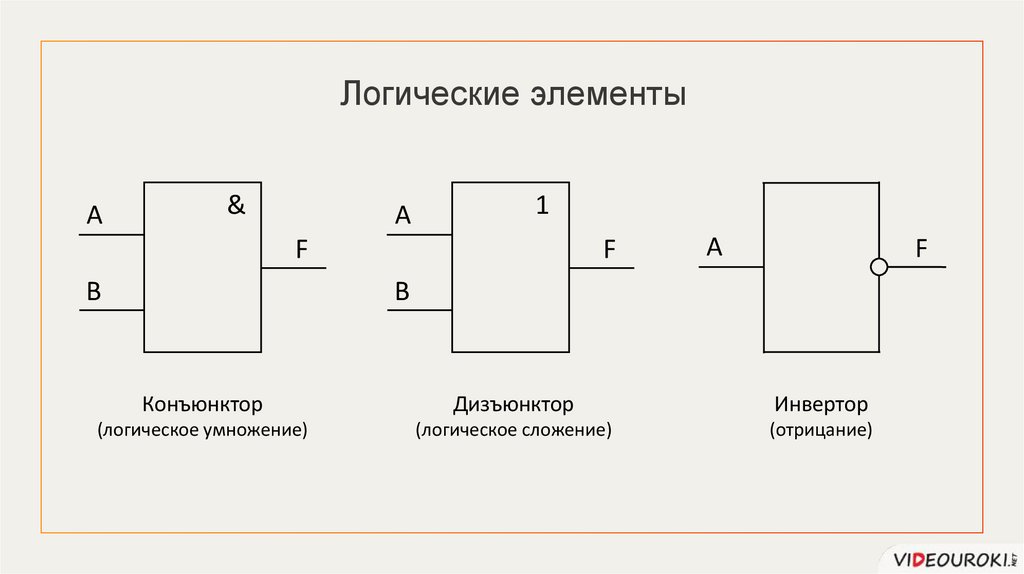
32.

Логические элементы
A
&
A
1
F
B
F
A
F
B
Конъюнктор
Дизъюнктор
Инвертор
(логическое умножение)
(логическое сложение)
(отрицание)

33.

Конъюнктор (И)
Реализуется операция логического умножения.
А – входные данные первого элемента.
В – входные данные второго элемента.
F – выходные данные.
&
A
F
B
Таблица истинности для конъюнкции
A
B
F
0
0
0
0
1
0
1
0
0
1
1
1
Единица на выходе получится тогда и только тогда, когда на всех входах будут единицы.

34.

Дизъюнктор (ИЛИ)
Реализуется операция логического сложения.
А – входные данные первого элемента.
В – входные данные второго элемента.
F – выходные данные.
1
A
F
B
Таблица истинности для дизъюнкции
A
B
F
0
0
0
0
1
1
1
0
1
1
1
1
Единица на выходе получится тогда, когда хотя бы на одном входе будет единица.

35.

Инвертор (НЕ)
Реализуется операция отрицания.
А – входные данные элемента.
F – выходные данные.
Таблица истинности для инверсии
A
F
A
F
0
1
1
0
Если на входе ноль, то на выходе будет единица. Если на входе единица, то на выходе будет
ноль.

36.

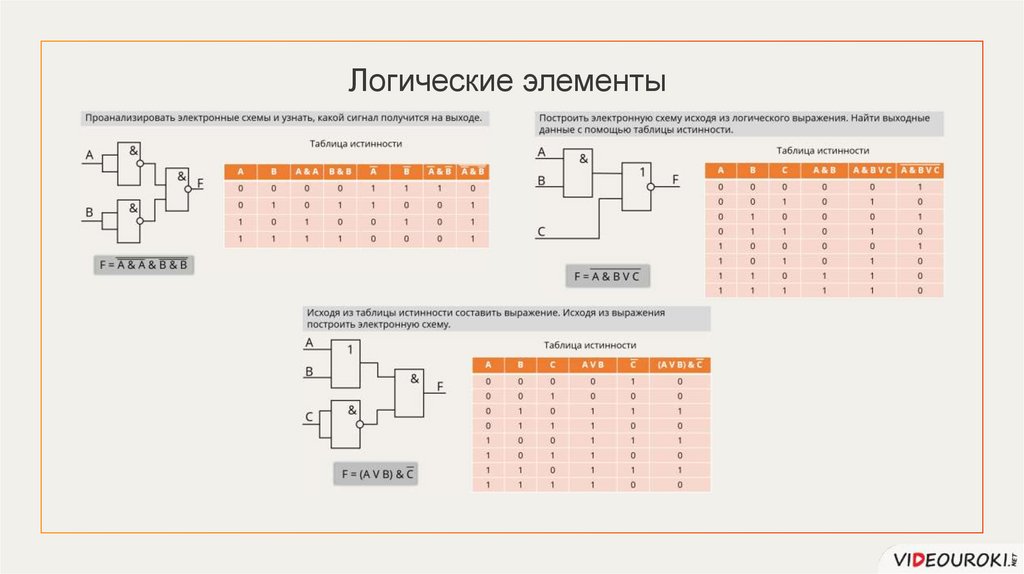
Задание
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
&
A
&
F
A
&
A
F
F
В
В
&
1

37.

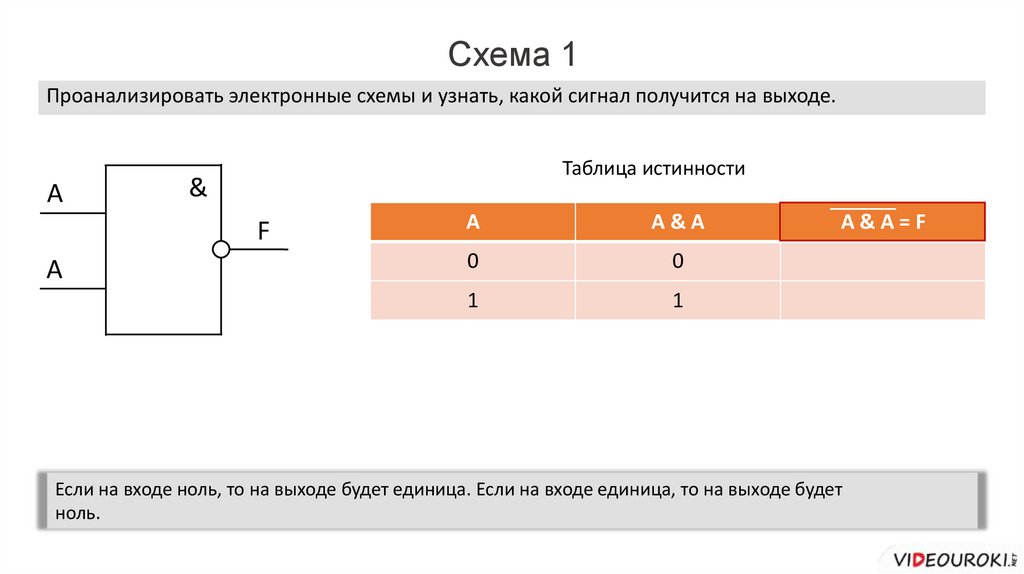
Схема 1
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
F
A
A

38.

Схема 1
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
F
A
A
0
1

39.

Схема 1
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
F
A
A
0
1
A&A

40.

Схема 1
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
F
A
A
0
1
A&A
A&A

41.

Схема 1
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
F
A
A
0
1
A&A
A&A=F

42.

Схема 1
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
F
A
A
A&A
0
0
1
1
A&A=F
Если на входе ноль, то на выходе будет единица. Если на входе единица, то на выходе будет
ноль.

43.

Схема 1
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
F
A
A
A&A
A&A=F
0
0
1
1
1
0

44.

Схема 1
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
Таблица истинности
&
A
F
A
F=Ā
A
A&A
A=F
0
0
1
1
1
0

45.

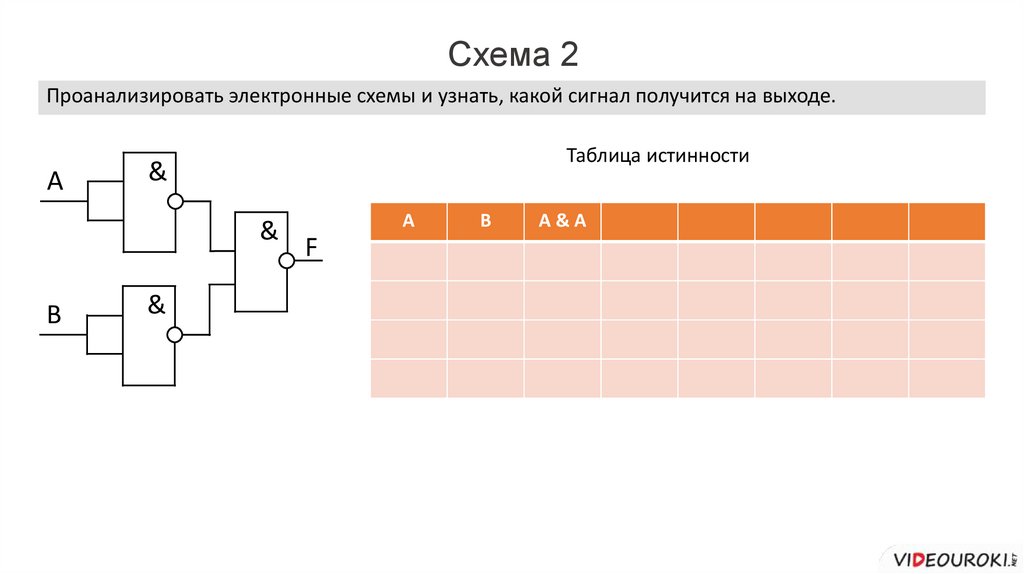
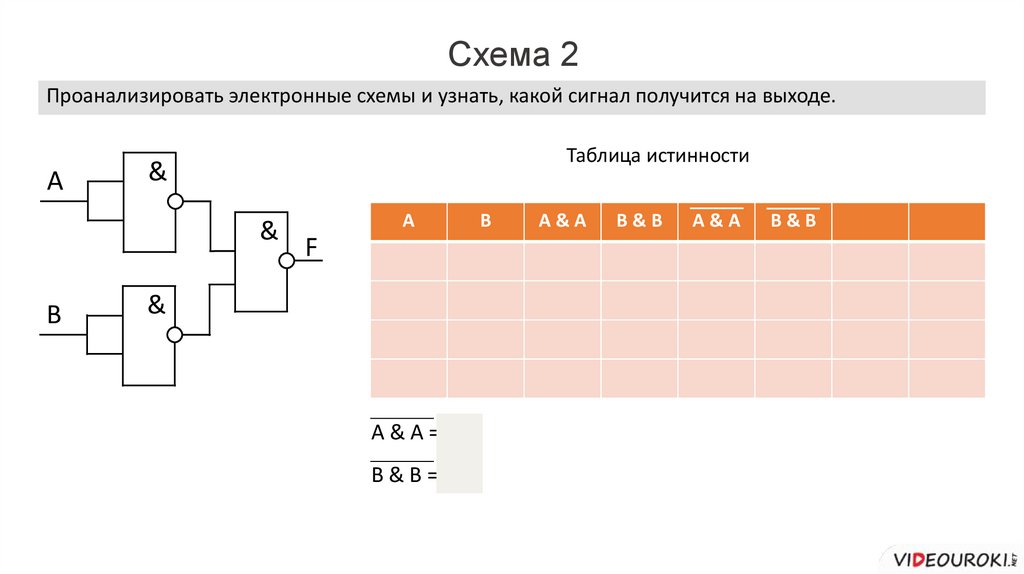
Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
F

46.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
A
F
B

47.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
A
F
B
A&A

48.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
A
F
B
A&A
B&B

49.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
A
F
&
A&A=A
B&B=B
B
A&A
B&B
A&A
B&B

50.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
A
F
B
A&A
B&B
A
B

51.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
A
F
B
A&A
B&B
A
B
A&B

52.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
A
F
B
A&A
B&B
A
B
A&B
A&B

53.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
F
A
B
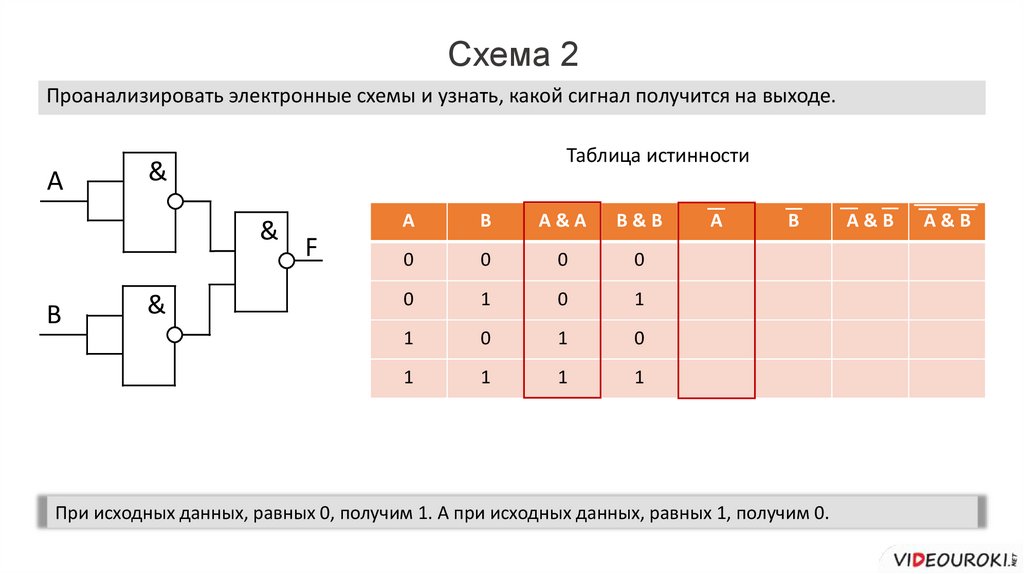
0
0
0
1
1
0
1
1
A&A
B&B
A
B
A&B
A&B

54.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
F
A
B
A&A
0
0
0
0
1
0
1
0
1
1
1
1
B&B
A
B
A&B
A&B

55.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
F
A
B
A&A
B&B
0
0
0
0
0
1
0
1
1
0
1
0
1
1
1
1
A
B
При исходных данных, равных 0, получим 1. А при исходных данных, равных 1, получим 0.
A&B
A&B

56.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
F
A
B
A&A
B&B
A
0
0
0
0
1
0
1
0
1
1
1
0
1
0
0
1
1
1
1
0
B
При исходных данных, равных 0, получим 1. А при исходных данных, равных 1, получим 0.
A&B
A&B

57.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
F
A
B
A&A
B&B
A
B
0
0
0
0
1
1
0
1
0
1
1
0
1
0
1
0
0
1
1
1
1
1
0
0
Единица на выходе получится тогда и только тогда, когда на всех входах будут единицы.
A&B
A&B

58.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
F
A
B
A&A
B&B
A
B
A&B
0
0
0
0
1
1
1
0
1
0
1
1
0
0
1
0
1
0
0
1
0
1
1
1
1
0
0
0
При исходных данных, равных 0, получим 1. А при исходных данных, равных 1, получим 0.
A&B

59.

Схема 2
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
&
&
В
&
F=A&A&B&B
F
A
B
A&A
B&B
A
B
A&B
A&B
0
0
0
0
1
1
1
0
0
1
0
1
1
0
0
1
1
0
1
0
0
1
0
1
1
1
1
1
0
0
0
1

60.

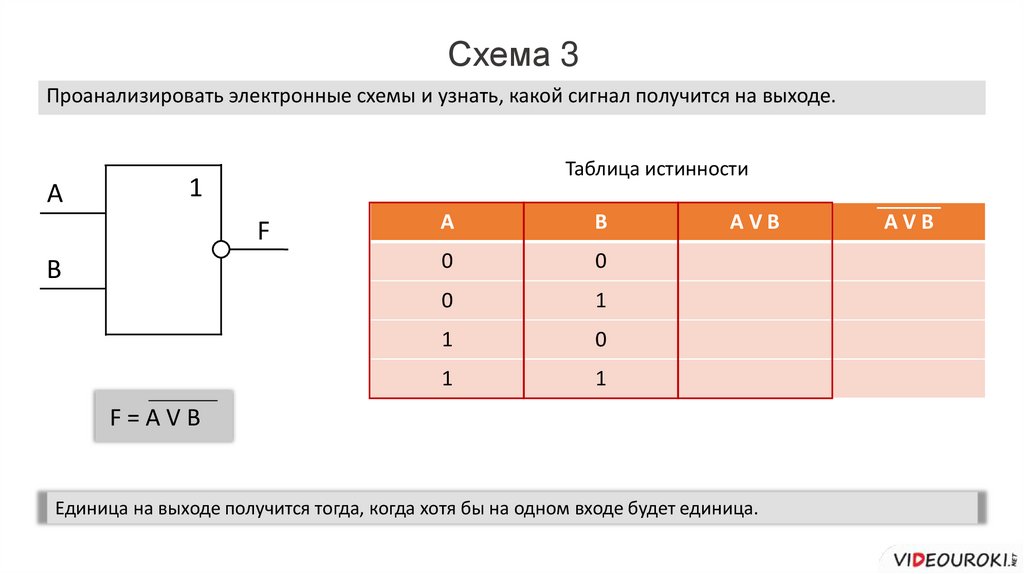
Схема 3
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
1
F
B
F=AVB

61.

Схема 3
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
1
F
B
F=AVB

62.

Схема 3
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
1
F
B
F=AVB
A
B
0
0
0
1
1
0
1
1

63.

Схема 3
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
1
F
B
F=AVB
A
B
0
0
0
1
1
0
1
1
AVB

64.

Схема 3
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
1
F
B
A
B
0
0
0
1
1
0
1
1
AVB
F=AVB
Единица на выходе получится тогда, когда хотя бы на одном входе будет единица.
AVB

65.

Схема 3
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
1
F
B
A
B
AVB
0
0
0
0
1
1
1
0
1
1
1
1
F=AVB
При исходных данных, равных 0, получим 1. А при исходных данных, равных 1, получим 0.
AVB

66.

Схема 3
Проанализировать электронные схемы и узнать, какой сигнал получится на выходе.
A
Таблица истинности
1
F
B
F=AVB
A
B
AVB
AVB
0
0
0
1
0
1
1
0
1
0
1
0
1
1
1
0

67.

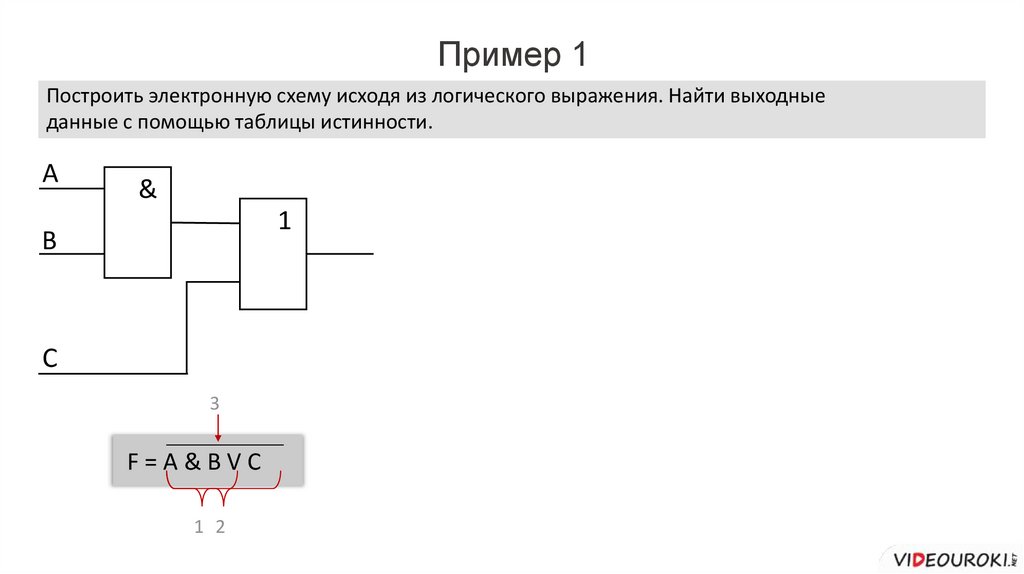
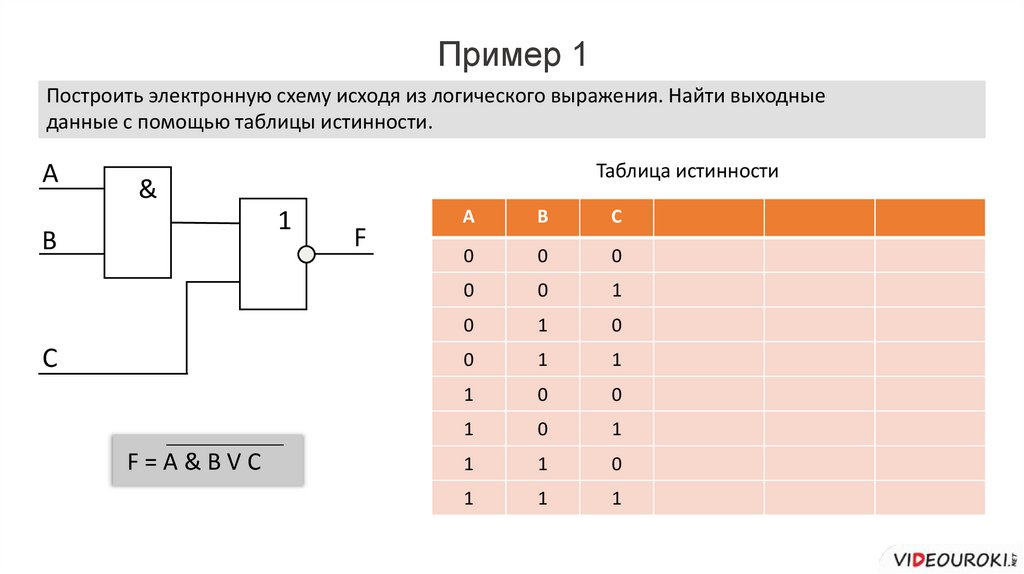
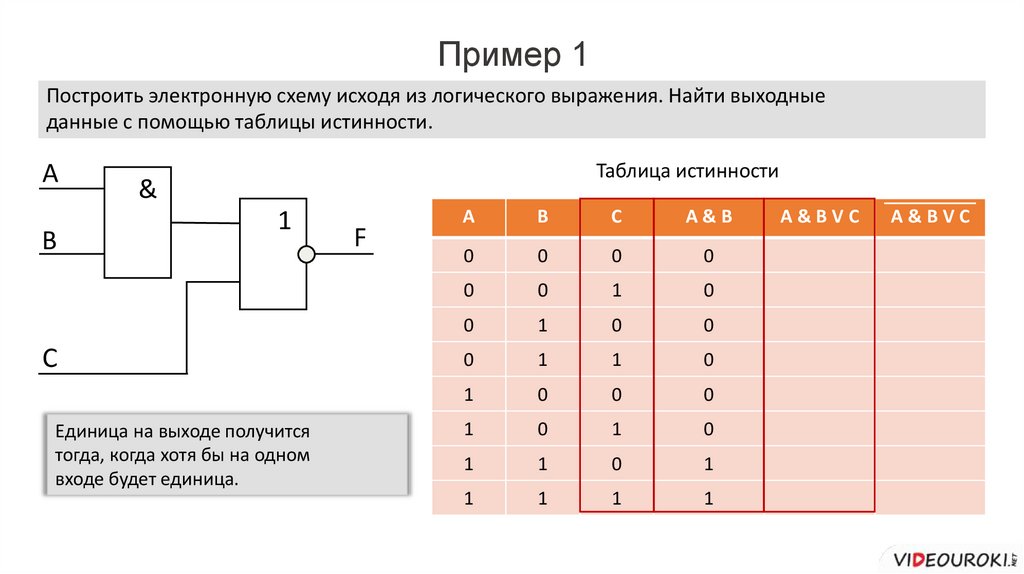
Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
&
1
B
C
3
F=A&BVC
1 2

68.

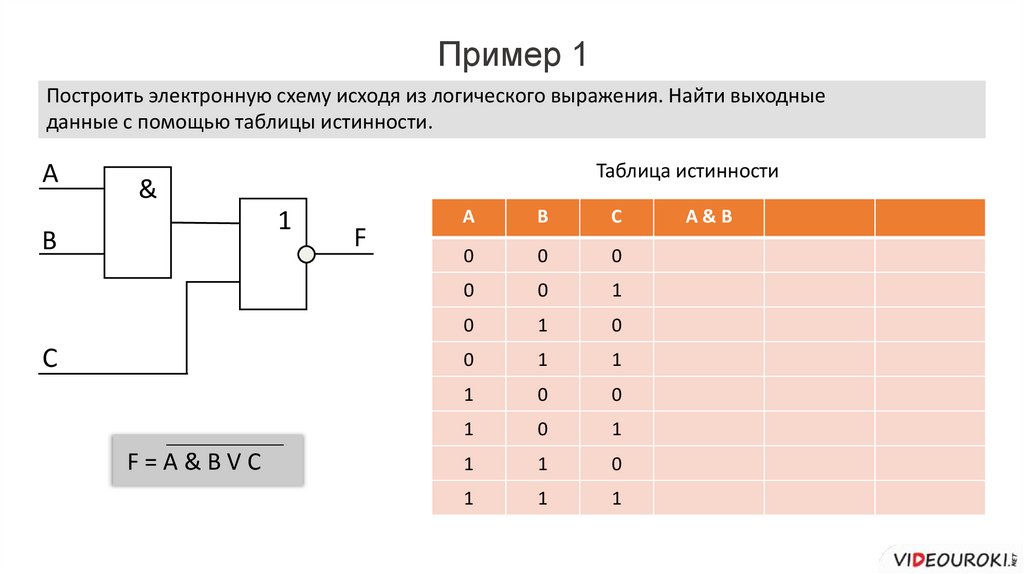
Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
Таблица истинности
&
1
B
C
3
F=A&BVC
F

69.

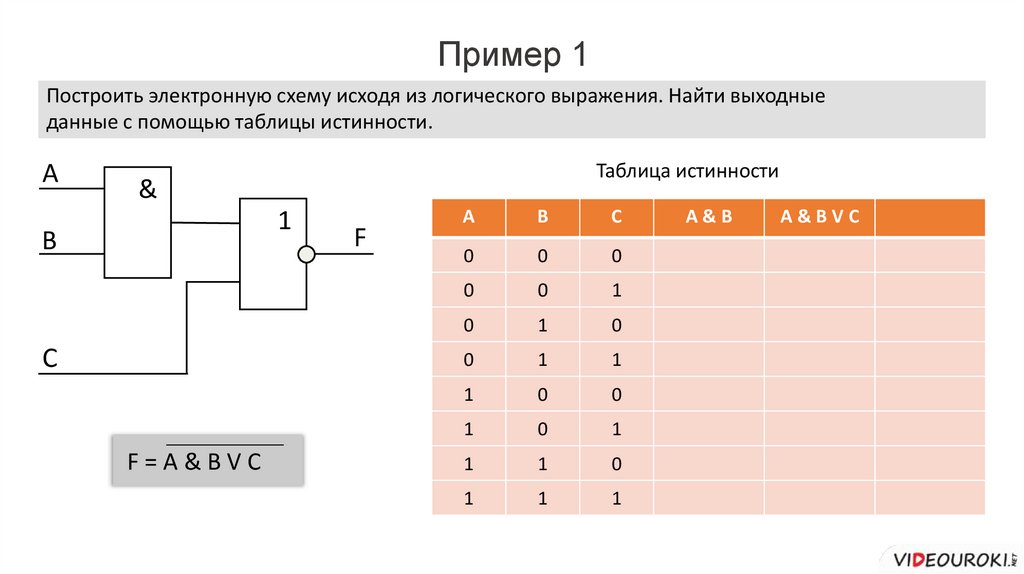
Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
Таблица истинности
&
1
B
C
F=A&BVC
F
A
B
C
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1

70.

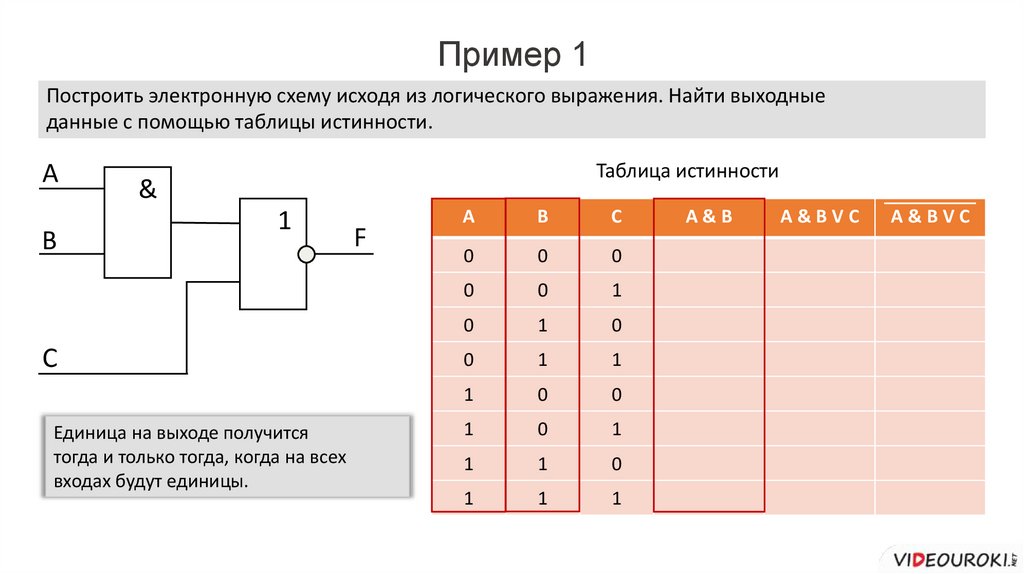
Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
Таблица истинности
&
1
B
C
F=A&BVC
F
A
B
C
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
A&B

71.

Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
Таблица истинности
&
1
B
C
F=A&BVC
F
A
B
C
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
A&B
A&BVC

72.

Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
B
Таблица истинности
&
1
C
Единица на выходе получится
тогда и только
F = A тогда,
& B Vкогда
C на всех
входах будут единицы.
F
A
B
C
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
A&B
A&BVC
A&BVC

73.

Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
B
Таблица истинности
&
1
C
Единица на выходе получится
тогда, когда
F = хотя
A &бы
B VнаCодном
входе будет единица.
F
A
B
C
A&B
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
A&BVC
A&BVC

74.

Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
B
Таблица истинности
&
1
C
Если на входе элемент ноль, то на
выходе будет единица.
F=A&BVC
Если на входе единица, то на
выходе будет ноль.
F
A
B
C
A&B
A&BVC
0
0
0
0
0
0
0
1
0
1
0
1
0
0
0
0
1
1
0
1
1
0
0
0
0
1
0
1
0
1
1
1
0
1
1
1
1
1
1
1
A&BVC

75.

Пример 1
Построить электронную схему исходя из логического выражения. Найти выходные
данные с помощью таблицы истинности.
A
Таблица истинности
&
1
B
C
F=A&BVC
F
A
B
C
A&B
A&BVC
A&BVC
0
0
0
0
0
1
0
0
1
0
1
0
0
1
0
0
0
1
0
1
1
0
1
0
1
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
1
0
1
1
1
1
1
0

76.

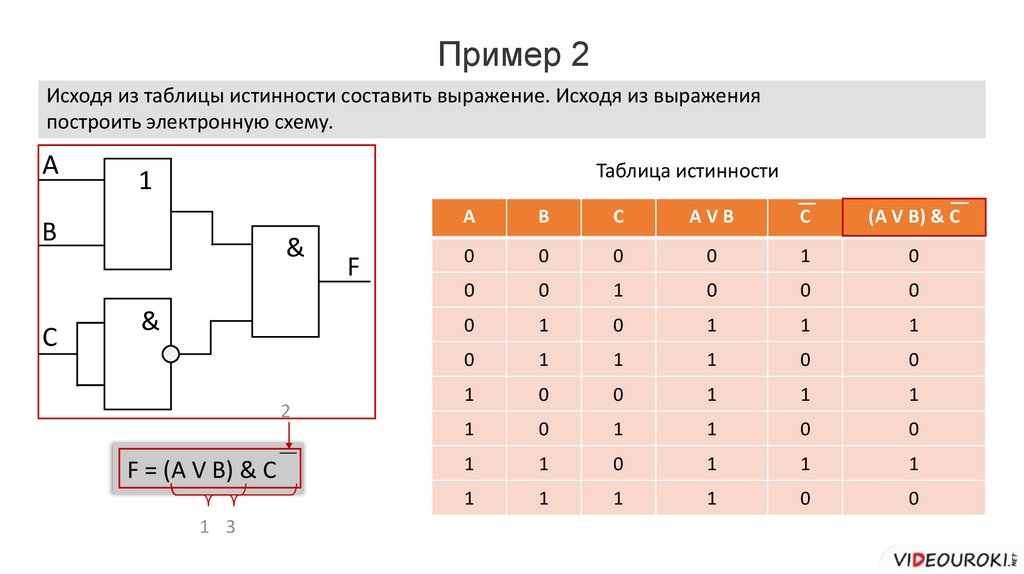
Пример 2
Исходя из таблицы истинности составить выражение. Исходя из выражения
построить электронную схему.
Таблица истинности
Единица на выходе получится
тогда, когда хотя бы на одном
входе будет единица.
A
B
C
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
AVB
C
(A V B) & C

77.

Пример 2
Исходя из таблицы истинности составить выражение. Исходя из выражения
построить электронную схему.
Таблица истинности
При исходных данных, равных 0,
получим 1. А при исходных
данных, равных 1, получим 0.
A
B
C
AVB
0
0
0
0
0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
1
C
(A V B) & C

78.

Пример 2
Исходя из таблицы истинности составить выражение. Исходя из выражения
построить электронную схему.
Таблица истинности
Единица на выходе получится
тогда и только тогда, когда на всех
входах будут единицы.
A
B
C
AVB
C
0
0
0
0
1
0
0
1
0
0
0
1
0
1
1
0
1
1
1
0
1
0
0
1
1
1
0
1
1
0
1
1
0
1
1
1
1
1
1
0
(A V B) & C

79.

Пример 2
Исходя из таблицы истинности составить выражение. Исходя из выражения
построить электронную схему.
A
Таблица истинности
1
B
C
&
&
2
F = (A V B) & C
1 3
F
A
B
C
AVB
C
(A V B) & C
0
0
0
0
1
0
0
0
1
0
0
0
0
1
0
1
1
1
0
1
1
1
0
0
1
0
0
1
1
1
1
0
1
1
0
0
1
1
0
1
1
1
1
1
1
1
0
0

80.

Логические элементы

81.

Логические элементы