Свойства логических операций

1. Свойства логических операций

2.

1в
2в
1. Запишите название
логического сложения и его
обозначение.
1. Запишите название
логического умножения и
его обозначение.
2. Подсчитать количество переменных и количество
операций (записать!)
Построить таблицу истинности для выражения
A & (В v ¬A) & В
(А v В) & ¬Av В

3. Для любых логических формул A, B, C истинны следующие неравенства

1. Закон двойного отрицания
¬¬A=A
Двойное отрицание исключает отрицание.

4. Для любых логических формул A, B, C истинны следующие неравенства

2. Закон повторения
- для логического умножения
A&A=A
- для логического сложения
AvA=A

5. Для любых логических формул A, B, C истинны следующие неравенства

3. Коммутативный (переместительный) закон
- для логического умножения
A&B=B&A
- для логического сложения
AvB=B vA

6. Для любых логических формул A, B, C истинны следующие неравенства

4. Ассоциативный (сочетательный) закон
- для логического умножения
(A & B) & C = A & (B & C)
- для логического сложения
(A v B) v C = A v (B v C)

7. Для любых логических формул A, B, C истинны следующие неравенства

5. Дистрибутивный (распределительный) закон
- для логического умножения
A & (B v C) = (A & B) v (A & C)
- для логического сложения
A v (B & C) = (A v B) & (A v C)

8. Для любых логических формул A, B, C истинны следующие неравенства

6. Законы поглощения
- для логического умножения
A & (A v C) = A
- для логического сложения
A v (A & C) = A

9. Для любых логических формул A, B, C истинны следующие неравенства

7. Законы общей инверсии (законы де Моргана)
- для логического умножения
¬(A & B) = ¬A v ¬B
- для логического сложения
¬(A v C) = ¬A & ¬B

10. Для любых логических формул A, B, C истинны следующие неравенства

8. Законы исключения третьего
- для логического умножения
A & ¬A = 0
- для логического сложения
A v ¬A = 1

11. Для любых логических формул A, B, C истинны следующие неравенства

9. Законы операций с 0 и 1
- для логического умножения
A & 0 = 0; A & 1 = A
- для логического сложения
A v 0 = A; A v 1 = 1

12.

Д/з
Проведите доказательство распределительного
закона
1 В - для логического сложения
A v (B & C) = (A v B) & (A v C)
2 В - для логического умножения:
A & (B v C) = (A & B) v (A & C)

13.

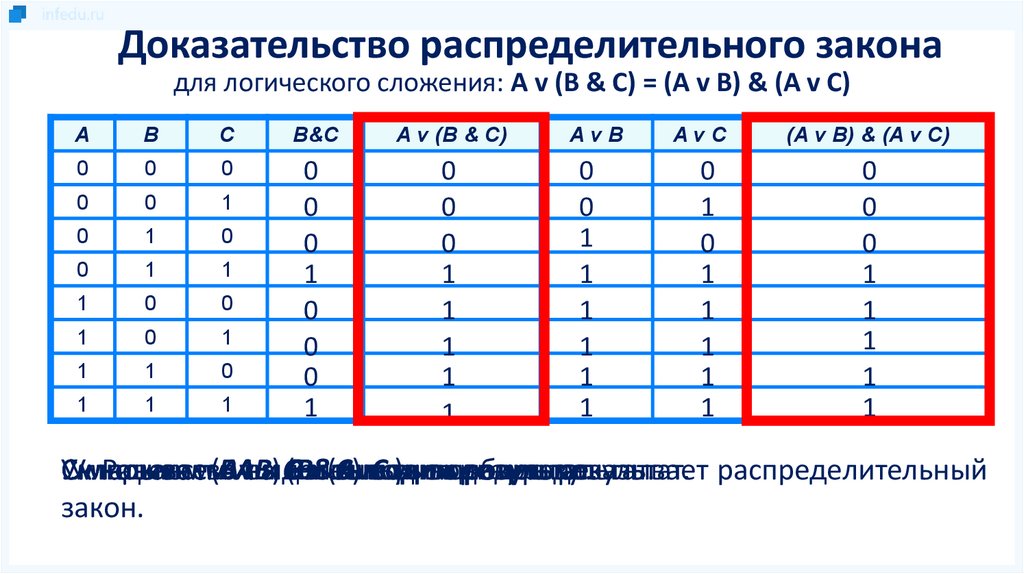
Доказательство распределительного закона
для логического сложения: A v (B & C) = (A v B) & (A v C)
A
B
C
B&C
A v (B & C)
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
0
0
0
1
0
0
0
1
0
0
0
1
1
1
1
1
AvB
0
0
1
1
1
1
1
1
AvC
0
1
0
1
1
1
1
1
(A v B) & (A v C)
0
0
0
1
1
1
1
1
Умножаем
Складываем
Умножаем
Равенство
(АvB)
ВАна
выделенных
и С(В&С)
Внаии(AvC
C
выводим
выводим
и выводим
)и столбцов
выводим
результат.
результат.
результат.
доказывает
результат. распределительный
закон.

14.

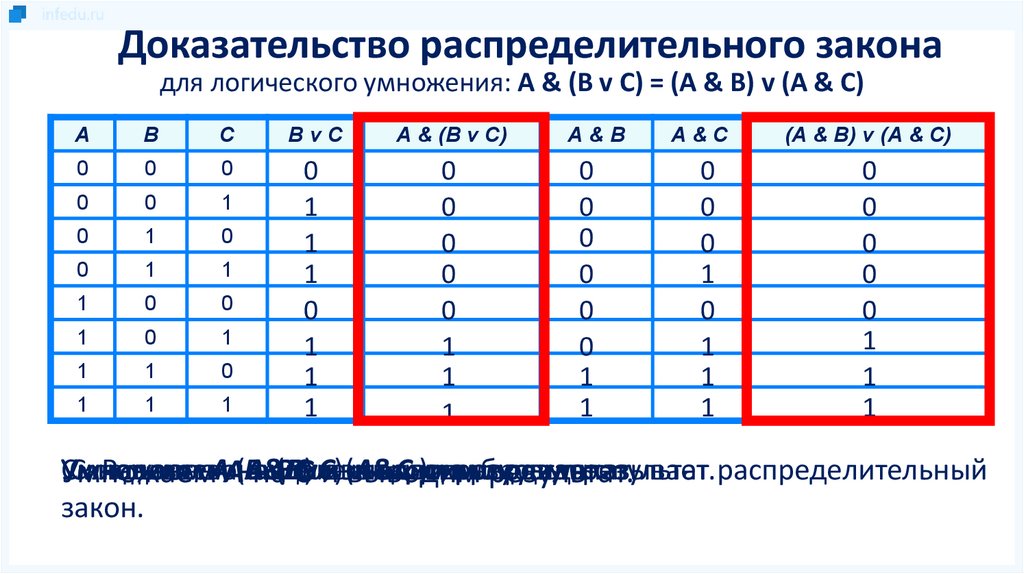
Доказательство распределительного закона
для логического умножения: A & (B v C) = (A & B) v (A & C)
A
B
C
BvC
A & (B v C)
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
0
0
0
0
0
1
1
1
A&B
0
0
0
0
0
0
1
1
A&C
0
0
0
1
0
1
1
1
(A & B) v (A & C)
0
0
0
0
0
1
1
1
Умножаем
Складываем
Складываем
Равенство
АА(А&B)
на
Ввыделенных
и(ВvС)
ВСCииивыводим
выводим
(A&C
и выводим
)и
столбцов
выводим
результат.
результат
результат.
доказывает
результат. распределительный
Умножаем
на
выводим
результат.
закон.