Свойства логических операций

1.

СВОЙСТВА ЛОГИЧЕСКИХ
ОПЕРАЦИЙ

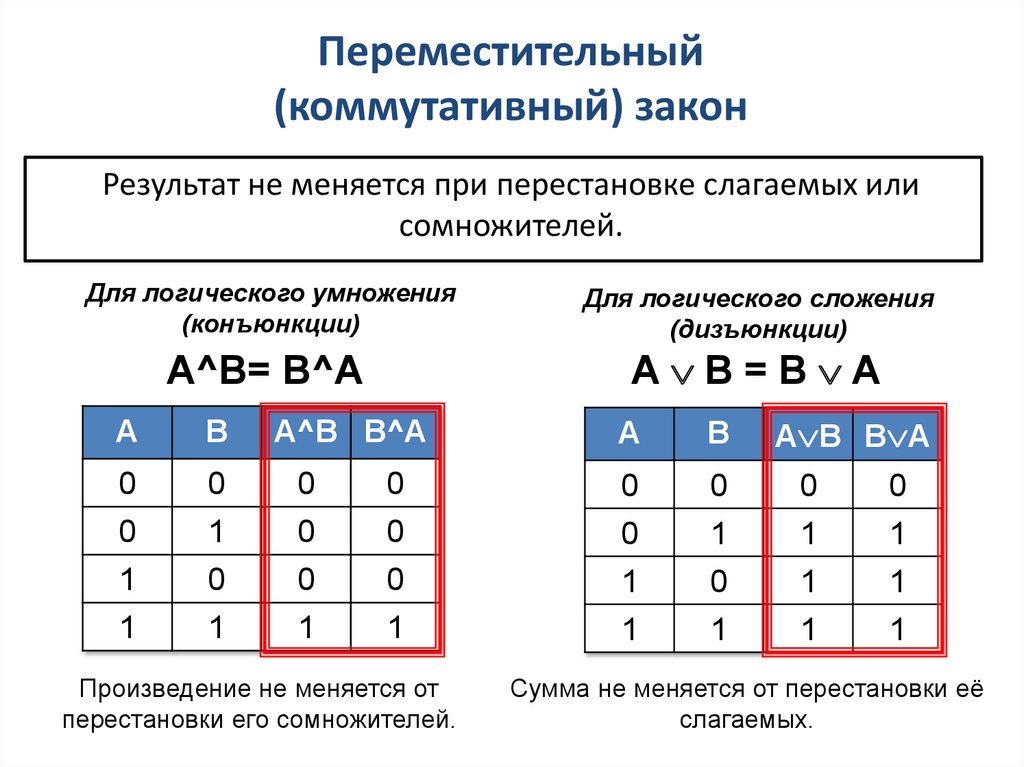
2. Переместительный (коммутативный) закон

Результат не меняется при перестановке слагаемых или
сомножителей.
Для логического умножения
(конъюнкции)
Для логического сложения
(дизъюнкции)
A^B= B^A
A B=B A
А
В
0
0
0
0
1
1
1
A B B A
А
В
0
0
0
0
0
0
0
0
1
1
1
0
0
0
1
0
1
1
1
1
1
1
1
1
1
A^B B^A
Произведение не меняется от
перестановки его сомножителей.
Сумма не меняется от перестановки её
слагаемых.

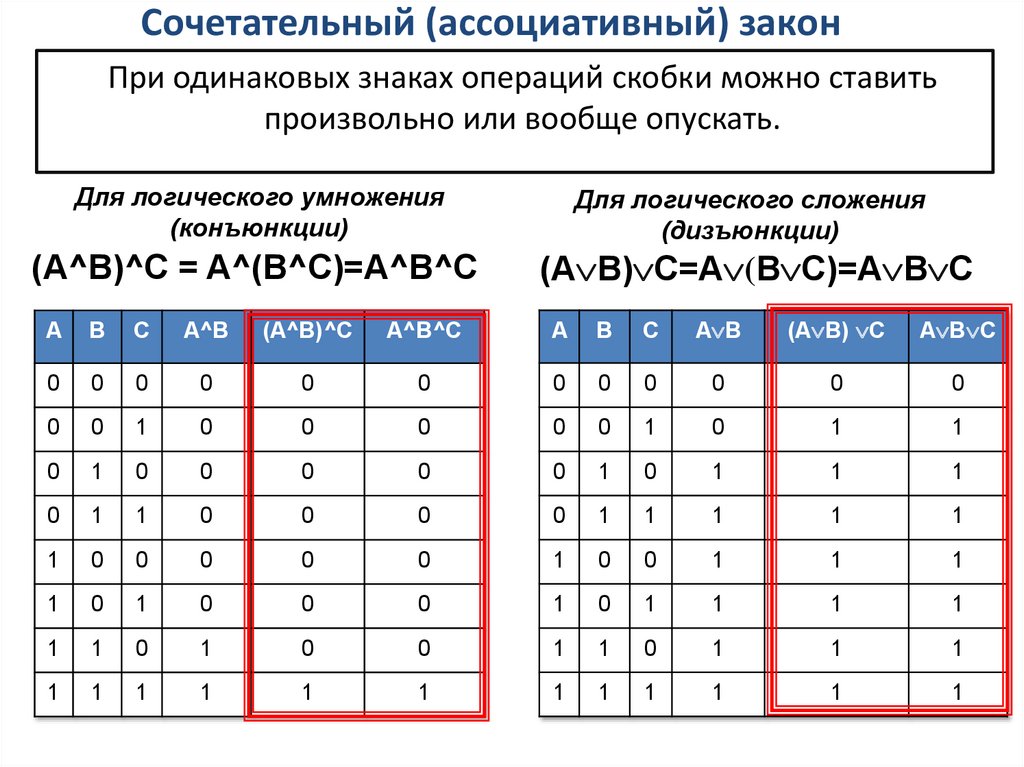
3. Сочетательный (ассоциативный) закон

При одинаковых знаках операций скобки можно ставить
произвольно или вообще опускать.
Для логического умножения
(конъюнкции)
Для логического сложения
(дизъюнкции)
(A^B)^C = A^(B^C)=A^B^C
(A B) C=A (B C)=A B C
А
В
C
A^B
(A^B)^C
A^B^C
А
В
C
A B
(A B) C
A B C
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
1
1
0
1
0
0
0
0
0
1
0
1
1
1
0
1
1
0
0
0
0
1
1
1
1
1
1
0
0
0
0
0
1
0
0
1
1
1
1
0
1
0
0
0
1
0
1
1
1
1
1
1
0
1
0
0
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

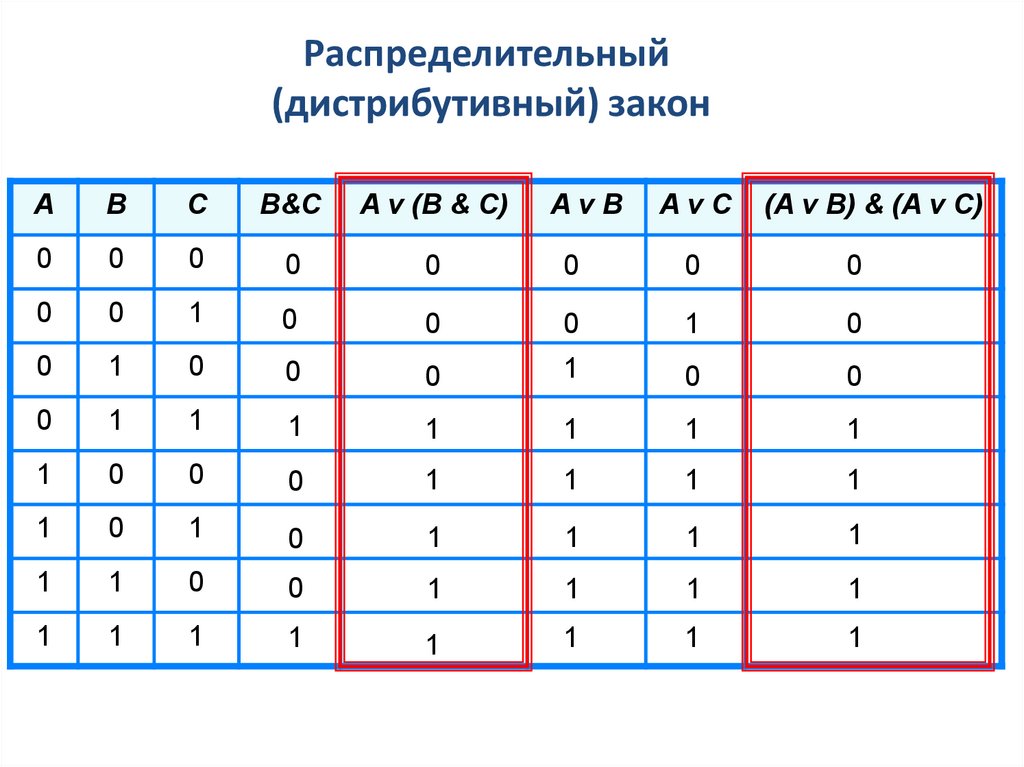
4. Распределительный (дистрибутивный) закон

Операцию можно выполнить по частям – для каждого
слагаемого, входящего во второй сомножитель.
Для логического умножения
(конъюнкции)
A ^ (B C)
=
(A ^ B) (A ^ C)
Для логического сложения
(дизъюнкции)
A (B ^ C)
=
(A B) ^ (A C)

5. Распределительный (дистрибутивный) закон

A
B
C
B&C
A v (B & C)
AvB
AvC
(A v B) & (A v C)
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
0
0
0
1
1
1
1
1
0
1
0
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1

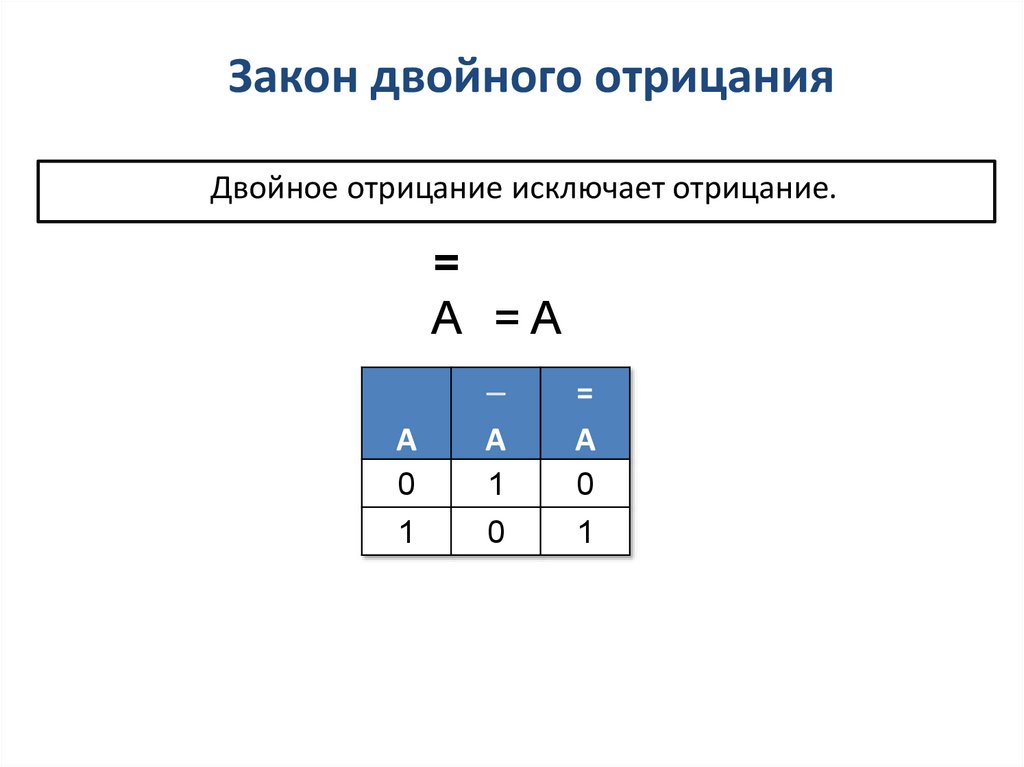
6. Закон двойного отрицания

Двойное отрицание исключает отрицание.
=
A =A
A
A
=
A
0
1
0
1
0
1

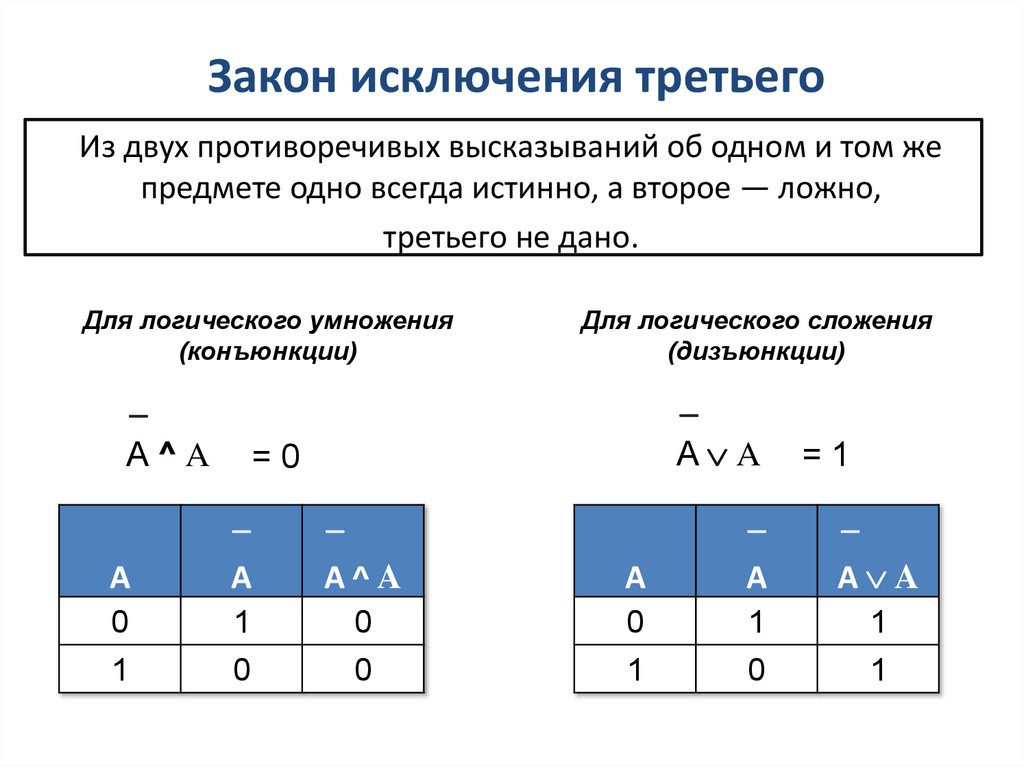
7. Закон исключения третьего

Из двух противоречивых высказываний об одном и том же
предмете одно всегда истинно, а второе — ложно,
третьего не дано.
Для логического умножения
(конъюнкции)
A^A
Для логического сложения
(дизъюнкции)
A A
=0
A
A
A^A
0
1
1
0
=1
A
A
A A
0
0
1
1
0
1
0
1

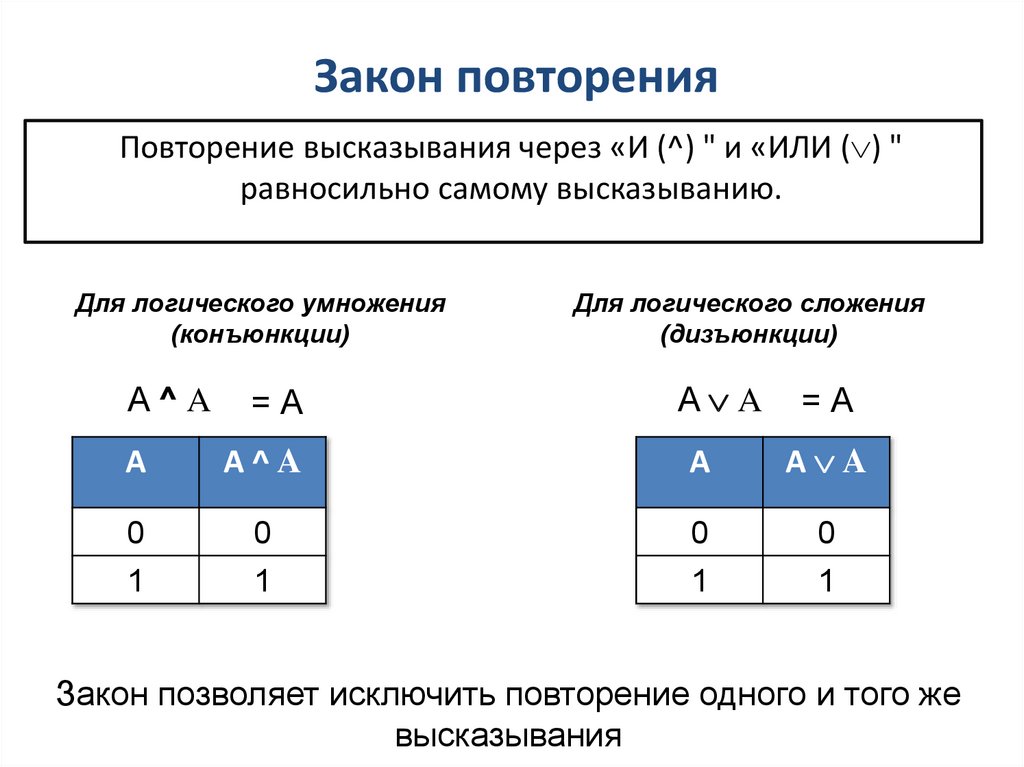
8. Закон повторения

Повторение высказывания через «И (^) " и «ИЛИ ( ) "
равносильно самому высказыванию.
Для логического умножения
(конъюнкции)
A^A
=А
Для логического сложения
(дизъюнкции)
A A
=А
A
A^A
A
A A
0
0
0
0
1
1
1
1
Закон позволяет исключить повторение одного и того же
высказывания

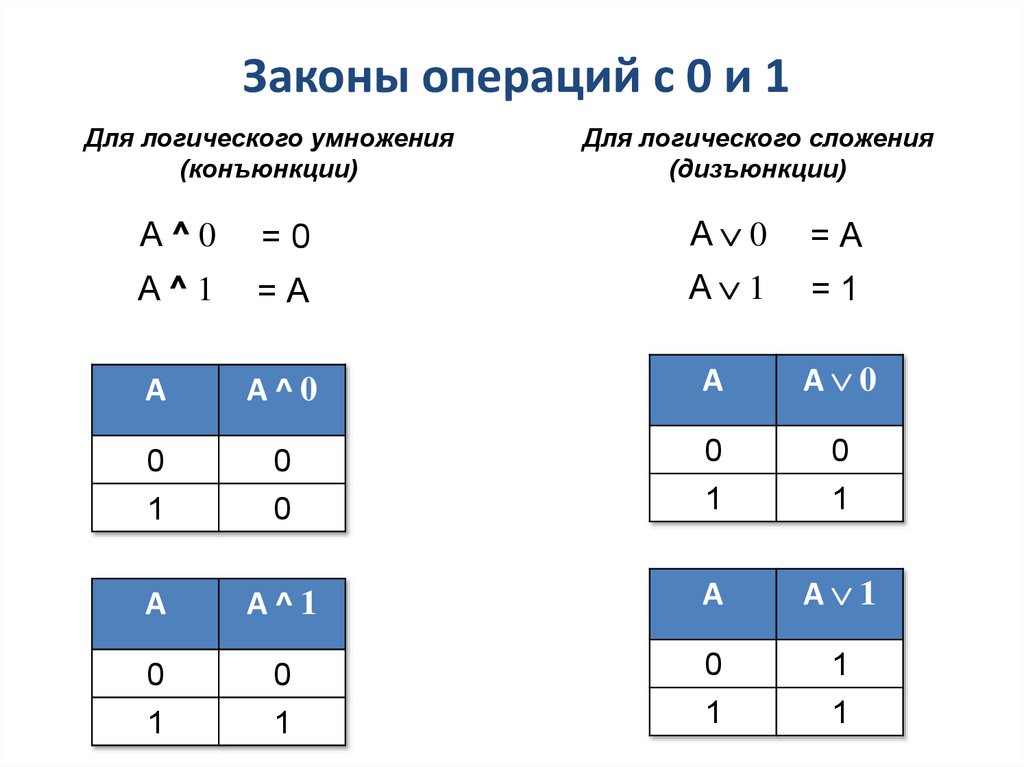
9. Законы операций с 0 и 1

Для логического умножения
(конъюнкции)
Для логического сложения
(дизъюнкции)
A^0
=0
A 0
=А
A^1
=А
A 1
=1
A
A^0
A
A 0
0
0
0
0
1
0
1
1
A
A^1
A
A 1
0
0
0
1
1
1
1
1

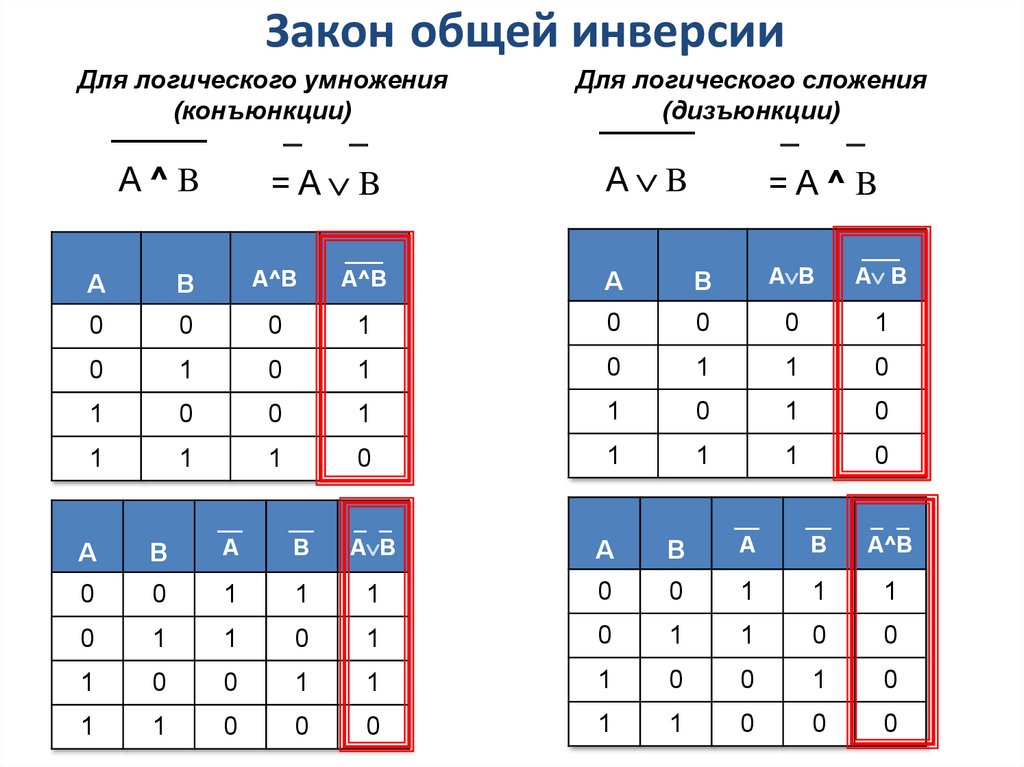
10. Закон общей инверсии

Для логического умножения
(конъюнкции)
_____
Для логического сложения
(дизъюнкции)
_____
A^B
=A B
=A^B
А
В
A^B
___
A^B
А
В
A B
___
A B
0
0
0
1
0
0
0
1
0
1
0
1
0
1
1
0
1
0
0
1
1
0
1
0
1
1
1
0
1
1
1
0
A B
__
B
_ _
A B
А
В
__
A
__
B
_ _
A^B
А
В
__
A
0
0
1
1
1
0
0
1
1
1
0
1
1
0
1
0
1
1
0
0
1
0
0
1
1
1
0
0
1
0
1
1
0
0
0
1
1
0
0
0

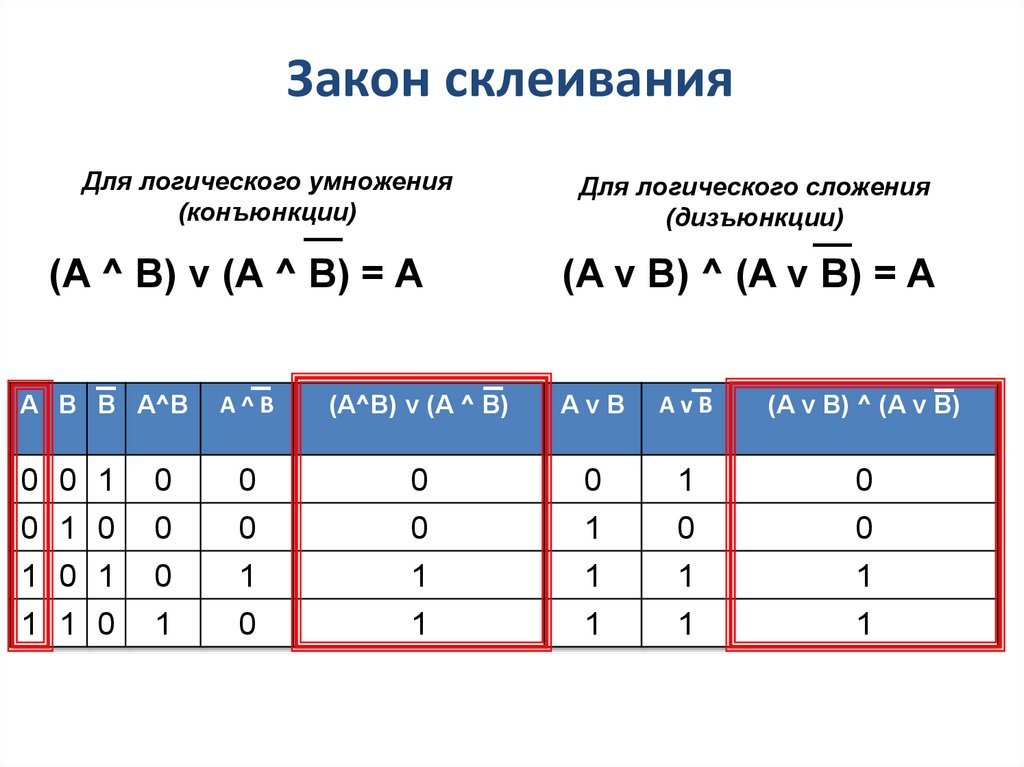
11. Закон склеивания

Для логического умножения
(конъюнкции)
Для логического сложения
(дизъюнкции)
__
__
(A ^ B) v (A ^ B) = A
_
А В B A^B
(A v B) ^ (A v B) = A
_
_
A^B
(A^B) v (A ^ B)
_
_
AvB
AvB
(A v B) ^ (A v B)
0 0 1
0
0
0
0
1
0
0 1 0
0
0
0
1
0
0
1 0 1
0
1
1
1
1
1
1 1 0
1
0
1
1
1
1

12.

13.

14. Домашняя работа

Упростите следующие выражения:
1.
2.
3.
A A B