Экономические индексы

1. Экономические индексы

1.
2.
3.
4.
Сущность и виды индексов
Индивидуальные и общие
индексы
Индексы средних величин
Территориальные индексы

2. 1. Сущность и виды индексов

Индекс - относительная величина,
характеризующая изменение уровней
сложных социально-экономических
показателей:
во времени,
в пространстве или
по сравнению с планом.
Индексы, по аналогии с относительными
величинами, могут быть построены как
индексы динамики, выполнения плана,
планового задания, сравнения.

3. Задачи:

характеристика общего изменения
сложного экономического показателя
и отдельных его элементов;
измерение влияния факторов на
общую динамику сложного
показателя

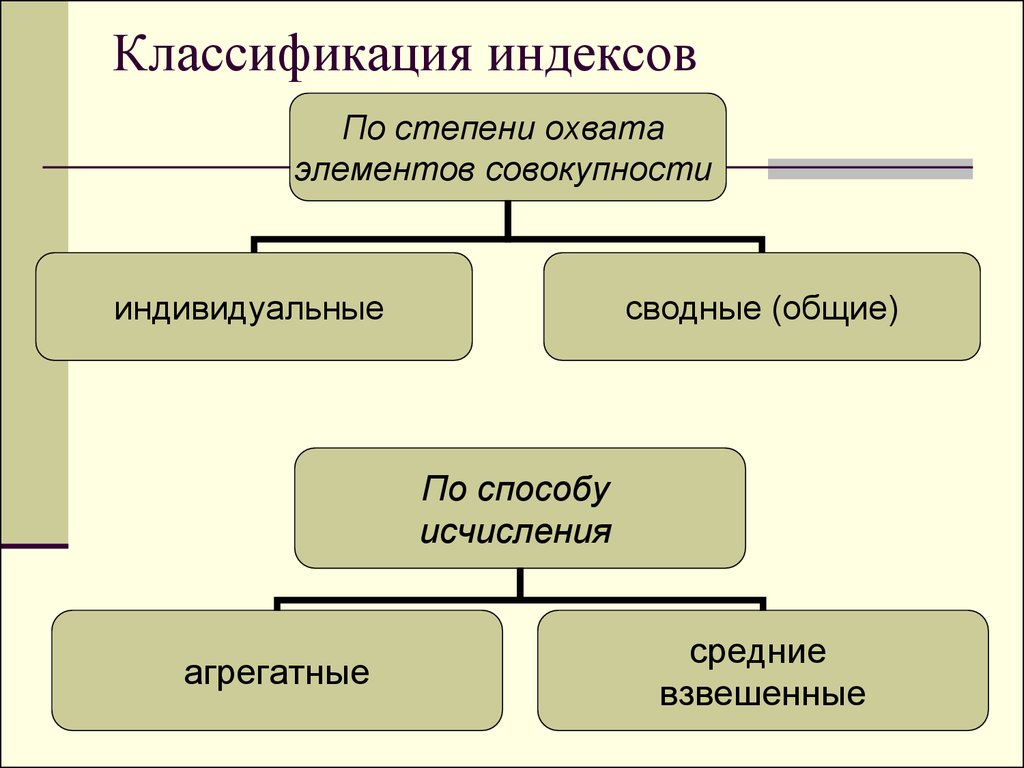
4. Классификация индексов

По степени охвата
элементов совокупности
индивидуальные
сводные (общие)
По способу
исчисления
агрегатные
средние
взвешенные

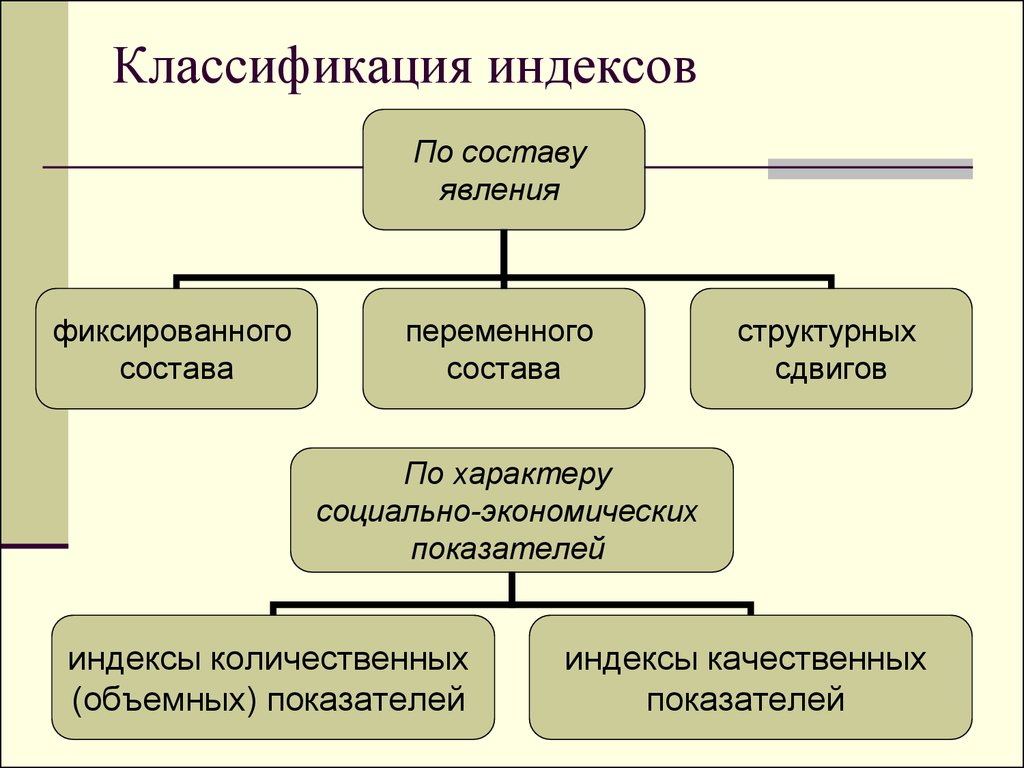
5. Классификация индексов

По составу
явления
фиксированного
состава
переменного
состава
структурных
сдвигов
По характеру
социально-экономических
показателей
индексы количественных
(объемных) показателей
индексы качественных
показателей

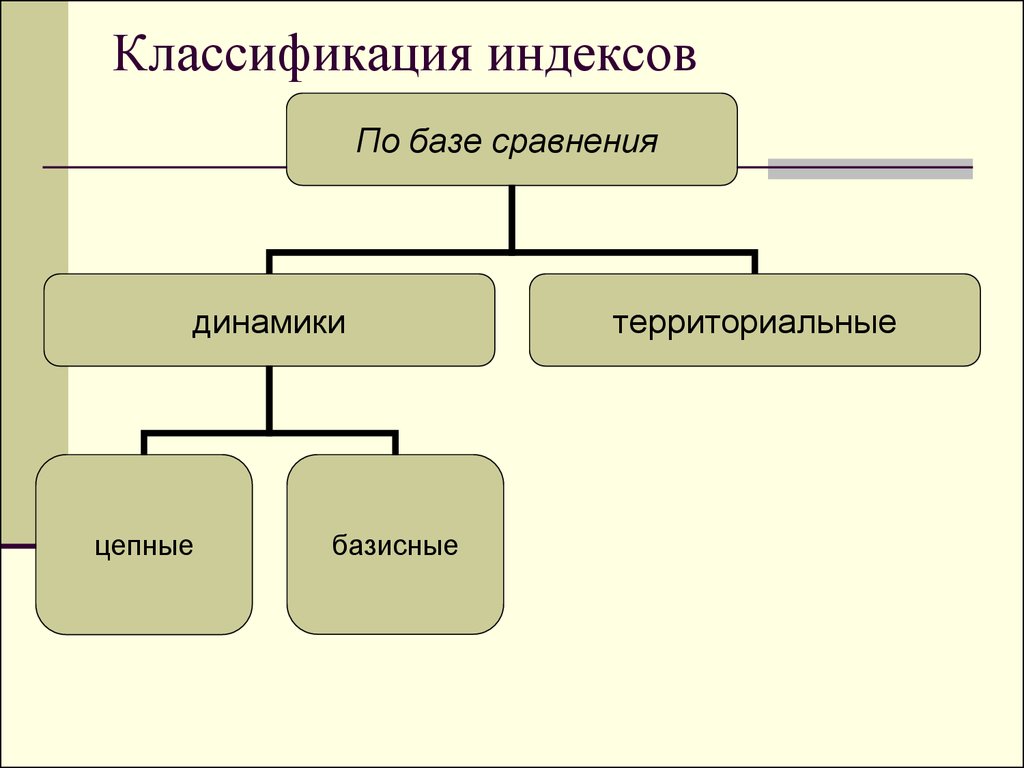
6. Классификация индексов

По базе сравнения
динамики
цепные
базисные
территориальные

7. Символические обозначения:

i
I
q
индивидуальный индекс
t
затраты труда (рабочего времени) на единицу продукции.
р
z
цена за единицу продукции
общий (сводный) индекс
количество продукции одного вида в натуральном выражении
себестоимость единицы продукции
Например,
ip — индивидуальный индекс цен на
отдельный вид продукции (товара)
Iq - общий индекс физического объема
продукции

8. 2. Индивидуальные и общие индексы

Индивидуальные - характеризуют
изменение только одного элемента
совокупности
Сводный (общий) - характеризует
изменение по всей совокупности
элементов сложного явления

9. Индивидуальные индексы 1. динамические

цены
p1
ip ,
p0
q1
,
физического объема iq
q0
p
q
1
1
товарооборота i
i
i
.
pq
p q
p0 q0

10.

Товар
I период
II период
Цена за Кол-во Цена
единиза едицу, руб.
ницу,
руб.
Колво
i p iq i pq
p0 q0 p1 q1
А
Б
В
20
30
15
7500
2000
1000
25
30
10
9500 1,25 1,27 1,59
2500 1,0 1,25 1,25
1500 0,67 1,5 1,00

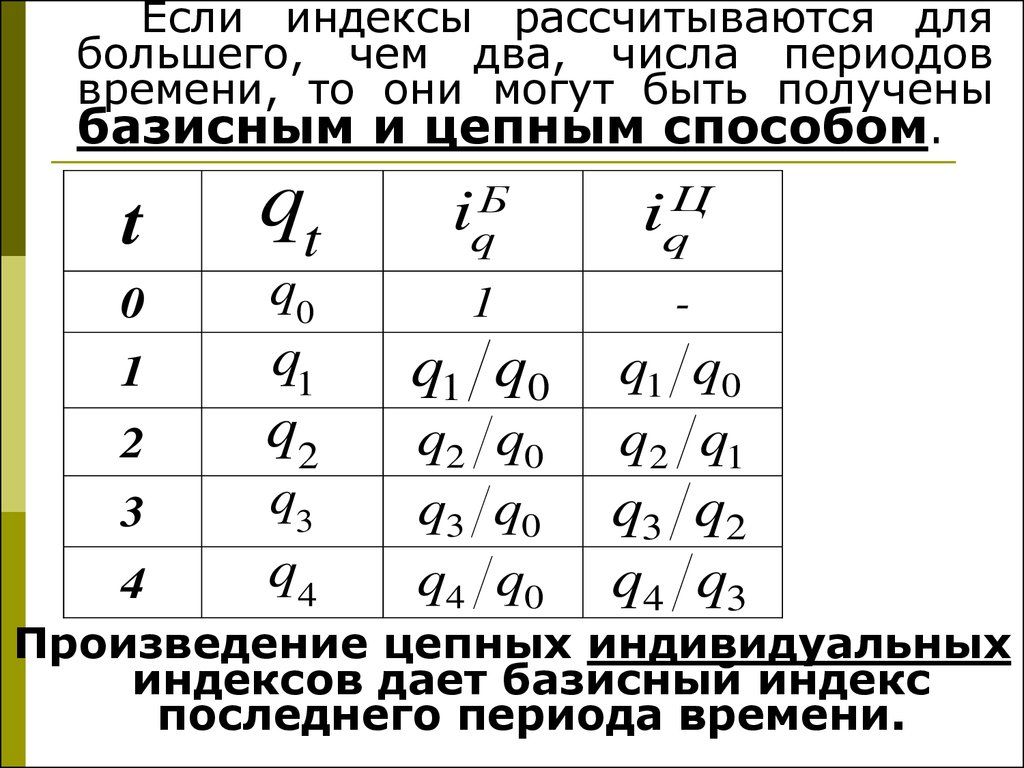
11.

Если индексы рассчитываются для
большего, чем два, числа периодов
времени, то они могут быть получены
базисным и цепным способом.
t
qt
iqБ
iqЦ
0
q0
1
-
1
q1
2
q2
q1 q0
q1 q0
q2 q1
3
q3
q2 q0
q3 q0
q4 q0
q3 q2
q4 q3
q4
4
Произведение цепных индивидуальных
индексов дает базисный индекс
последнего периода времени.

12. Индивидуальные индексы 2. выполнения плана

себестоимости
z1
iz ,
zпл
q1
,
физического объема iq
qпл
z
q
1 1 i i .
общих затрат i
zq
z q
zпл qпл

13. Сводные (общие) индексы:

Агрегатные
Средние взвешенные
Идея состоит в том, чтобы привести
отдельные несуммируемые
элементы совокупности разного
качества к такому виду, который
позволит их просуммировать

14. Основные агрегатные индексы (относительное изменение)

Агрегатный индекс цены:
Ip
pq
p q
1 1
0 1
Агрегатный
объема:
Iq
q p
q p
1
0
0
0
индекс
физического
Агрегатный
индекс
общей
стоимости (товарооборота):
I pq
pq
p q
1 1
0
0
I pq I p I q

15.

Произведение
цепных
общих
индексов дает базисный индекс
последнего периода времени только
тогда, когда общие цепные индексы
рассчитаны с постоянными
весами.
p1 q 2 p1 q3 p1 q4
p1 q1 p1 q 2 p1 q3
p1 q4
p1 q1

16. Основные агрегатные индексы (абсолютное изменение) – разность числителя и знаменателя соответствующего индекса

•Товарооборота
всего, в том
числе за счет:
•изменения
цен
pq p1 q1 p0 q0
p
pq p1 q1
p0 q1
q
pq p0 q1 p0 q0
•изменения
количества
проданных товаров
p
q
pq pq pq

17. Принципы построения агрегатных индексов

1.
2.
3.
4.
5.
Обозначается буквой I со знаком индексируемого
показателя.
Относительный показатель (представлен дробью)
В числителе дроби записывается значение
индексируемого показателя в отчетном периоде, в
знаменателе значение базы сравнения
(предшествующий период, плановое значение,
значение того же показателя на других
территориях)
измеряется в коэффициентах или в процентах.
Отражает, во сколько раз, на сколько процентов
или на сколько единиц изменилось значение
индексируемого показателя в отчетном периоде по
сравнению с базой

18. Принципы построения агрегатных индексов

6.
в числителе и знаменателе производится
суммирование произведений двух величин:
индексируемый показатель
вес индексируемого показателя конкретной
единицы (соизмеритель). Он одинаков для
числителя и знаменателя и определяется
видом индексируемого показателя
если индексируется количественный
(первичный)признак, то признак-вес
закрепляется на базисном уровне
если качественный (вторичный)– на отчетном.

19.

Например.
цены:
Построим
Ip
агрегатный
индекс
p1
p0
Так как цены, относящиеся к различным
товарам,
непосредственно
суммировать
нельзя, то нужно выбрать показатель (вес
индекса), чтобы действие суммирования
имело смысл. Таким показателем является
товарооборот или выручка. Нас интересует
только изменение цен, влияние второго
фактора
необходимо
устранить,
зафиксировав
количество
продаж
на
1
постоянном уровне.
p
I
p q
p0 q

20. Возможны два варианта:

1.
Количество
проданных
товаров
фиксируется
на
уровне отчетного периода:
П
Ip
где
I pП -
p1 q1
,
p0 q1
индекс Пааше.

21. 2. Количество проданных товаров фиксируется на уровне базисного периода:

Л
Ip
где
Л
Ip
-
p1 q0
p0 q0
индекс Ласпейреса.
,

22. Для получения единого результата используется индекс Фишера:

Ф
Ip
П Л
I p I p .

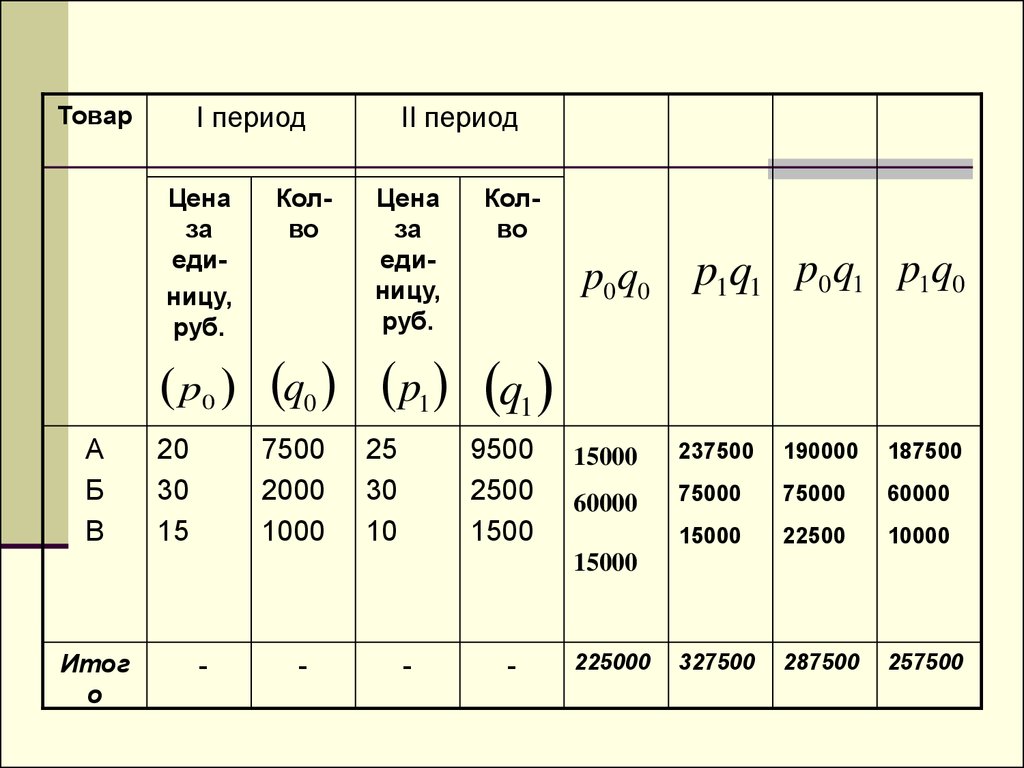
23.

Товар
I период
Цена
за
единицу,
руб.
Колво
II период
Цена
за
единицу,
руб.
p0 q0 p1
А
Б
В
20
30
15
7500
2000
1000
25
30
10
Колво
p0 q0
p1q1 p0 q1 p1q0
q1
9500
2500
1500
15000
237500
190000
187500
60000
75000
75000
60000
15000
22500
10000
327500
287500
257500
15000
Итог
о
-
-
-
-
225000

24. Средние взвешенные индексы

Являются производными от агрегатного
индекса
При их построении веса для
индивидуальных индексов должны быть
подобраны так, чтобы было обеспечено
тождество средневзвешенного индекса
агрегатному.

25.

p1 q1 p1 q1
Ip
Ip
p0 q1
p1 q1
ip
p1
p1
ip
p0
p0
ip

26.

p0 q1 iq p0 q0
Iq
Iq
p 0 q 0
p 0 q 0
q1
iq
q1 iq q0
q0

27. Средние взвешенные индексы

Средний взвешенный арифметический индекс
физического объема продукции:
iq 0 p0
Iq
q0 p0
Средний взвешенный гармонический индекс
цены:
Ip
pq
pq
i
1 1
1 1

28.

Ip
pq
1
i p q
1 1
73000
1,016, или 101,6%.
71877
1 1
p
Товар
Реализация в
текущем
периоде, руб.
Изменение
цен
%
ip
p1q1
ip
p1q1
А
Б
В
23000
21000
29000
+4,0
+2,3
-0,8
Итого
73000
-
1,040 22115
1,023 20528
0,992 29234
-
71877

29. 3. Индексы средних величин

Применяются для анализа совокупности
однородных единиц (одноименная
продукция, товар, материалы),
распределенных на группы с разными
значениями индексируемого показателя.
Цель расчета— выявить влияние отдельных
факторов на динамику среднего значения
индексируемого показателя.
Рассматривается производство товара А
несколькими предприятиями. У каждого
предприятия определенный объем
производства и своя себестоимость товара А.
Требуется проанализировать, как изменяется
средняя цена товара.

30. Индексы переменного, постоянного состава и структурных сдвигов

Индекс переменного состава отражает
изменение средней себестоимости товара А
по группе предприятий
z1 z1q1 z0 q0
Iz
z0
q1 q0
Средняя себестоимость изменяется в
результате:
1. изменения себестоимости на
отдельных предприятиях;
2. изменения удельного веса
предприятий в общем объеме

31. Индексы переменного, постоянного состава и структурных сдвигов

Индекс фиксированного состава
показывает, как изменяется средняя
себестоимость в результате изменения
себестоимости товара по отдельным
предприятиям
I
z
z
z
q
11
q
1
z
q
01
q
1

32. Индексы переменного, постоянного состава и структурных сдвигов

Индекс структурных сдвигов показывает,
как изменяется средняя себестоимость в
результате изменения удельного веса
предприятий в общем объеме производства
товаров (в результате структурных сдвигов)
I
q
z
z q z q
q q
0 1
0 0
1
0

33. Индексы переменного, постоянного состава и структурных сдвигов

Индексы взаимосвязаны между собой:
Iz I I
z
z
q
z
Абсолютное изменение средней
себестоимости определяется как разность
между первой и второй составляющей
соответствующего индекса
p1 q1 p0 q0
p
q1
q0

34. 4. Территориальные индексы

Позволяют сравнивать один и тот же
индексируемый показатель по двум
разным объектам или территориям
(объекты А и Б, например).
При их построении в качестве веса могут
использоваться показатели как для
региона А, так и для региона Б,
суммарные или средние показатели.

35. Территориальные индексы цен

p А q А
Ip
pБ q А
pБ qБ
Ip
p А qБ
p А q q q q
Ip
А
Б
p Б q

36. Территориальный индекс физического объема продаж

p q А
Iq
,
p qБ
где
p - средняя цена для двух регионов.
p А q А p Б q Б
p
q А qБ

37.

Территориальный индекс
товарооборота по двум регионам
p А q А
I pq
p Б q Б