Similar presentations:
Экономические индексы
1. Экономические индексы
2.
Индексамив статистике называются
обобщающие
показатели
сравнения во времени или
пространстве
величин
какого-либо общественного
явления.
3.
Индексный метод применяетсядля решения следующих задач:
для изучения изменения явлений во
времени;
для проведения пространственных
сравнений;
для характеристики степени
выполнения плана;
для характеристики степени
влияния структурных изменений.
4. Индексы подразделяются на индивидуальные и общие (сводные).
5. Индивидуальным называется индекс, который применяется для определения степени изменения отдельного элемента сложного общественного явл
Индивидуальнымназывается индекс, который
применяется для
определения степени
изменения отдельного
элемента сложного
общественного явления.
6. Индивидуальный индекс цены
p1ip ,
p0
где
p1 – цена отчетного периода;
p0 – цена базисного периода.
7. Индивидуальный индекс физического объема товарооборота
q1iq ,
q0
где q1 – количество проданного товара
в отчетном периоде;
q0 – количество проданного товара
в базисном периоде.
8. Индивидуальный индекс товарооборота
p1 q1i pq
i p iq.
p0 q0
9.
ТоварI период
II период
Цена за Кол-во Цена
единиза едицу, руб.
ницу,
руб.
Колво
i p iq i pq
p0 q0 p1 q1
А
Б
В
20
30
15
7500
2000
1000
25
30
10
9500 1,25 1,27 1,59
2500 1,0 1,25 1,25
1500 0,67 1,5 1,00
10. Общим индексом называется относительный показатель, характеризующий изменение сложного явления, состоящего из элементов, не поддающихся
Общим индексомназывается относительный
показатель, характеризующий
изменение сложного явления,
состоящего из элементов, не
поддающихся
непосредственному
суммированию.
11. Идея построения общего индекса цен
Общий индекс цен показывает, как всреднем
меняются
цены
по
всем
рассматриваемым товарным группам.
Так как цены, относящиеся к различным
товарам, непосредственно суммировать
нельзя, то нужно выбрать некий показатель,
чтобы действие суммирования имело смысл.
Таким
показателем
является
товарооборот или выручка
12. На величину товарооборота влияют два фактора:
уровеньцен;
количество проданных товаров.
Так как нас интересует только изменение
цен, то влияние второго фактора необходимо
устранить. Для этого количество проданных
товаров фиксируется на постоянном уровне.
Ip
p1 q
p0 q
13. Возможны два варианта:
1.Количество проданных товаров
фиксируется на уровне отчетного
периода:
p
q
П
1
1
Ip
,
p0 q1
где
I pП -
индекс Пааше
14. 2. Количество проданных товаров фиксируется на уровне базисного периода:
pq
Л
1
0
Ip
,
p0 q0
где
Л
Ip
-
индекс цен Ласпейреса
15. Для получения единого результата используется индекс Фишера, который рассчитывается как средняя геометрическая величина из индексов Паа
Для получения единогорезультата используется
индекс Фишера,
который рассчитывается как
средняя геометрическая величина
из индексов Пааше и Ласпейреса:
Ф
Ip
П Л
I p I p
16. Общий индекс физического объема товарооборота
Iqq1 p0
q0 p0
Данный индекс показывает, как
изменяется общая выручка в связи с
изменением
количества
проданных
товаров
17. Общий индекс стоимости товарооборота
p1 q1I pq
p0 q0
18. Эти индексы представляют собой систему:
I pq I p IqП
ЛП
19. или:
I pq I p IqЛП
П
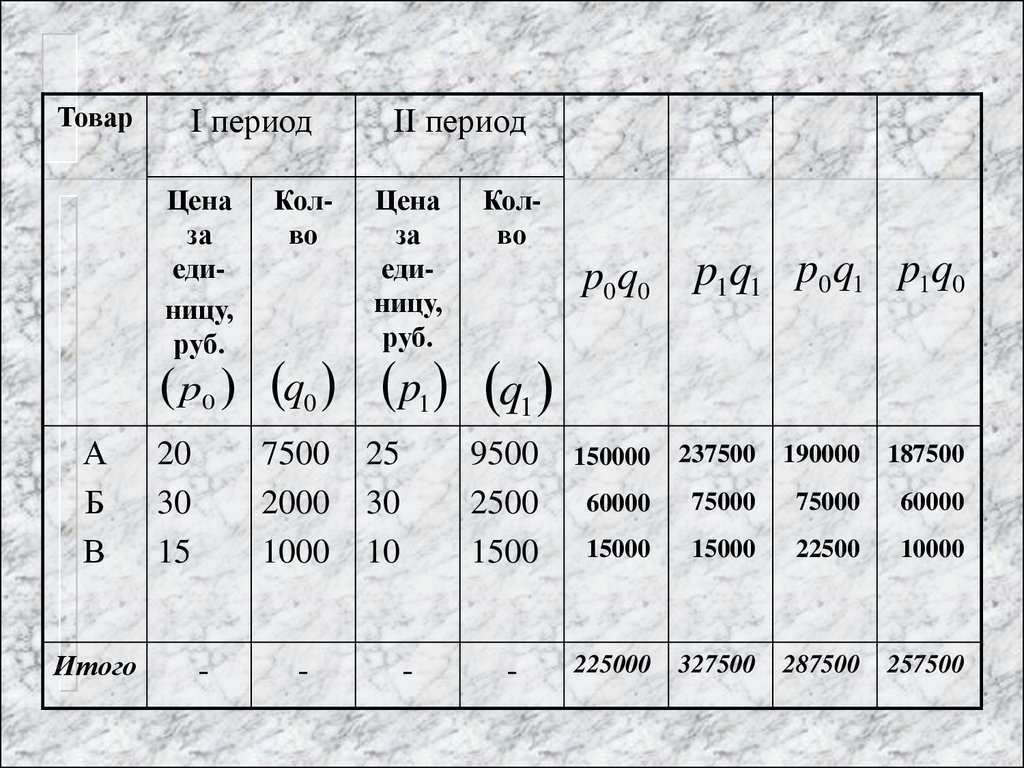
20.
ТоварI период
Цена
за
единицу,
руб.
Колво
II период
Цена
за
единицу,
руб.
p0 q0 p1
А
Б
В
Итого
20
30
15
7500
2000
1000
-
-
25
30
10
-
Колво
p0 q0
p1q1 p0 q1 p1q0
q1
9500
2500
1500
150000
237500
190000
187500
60000
75000
75000
60000
15000
15000
22500
10000
-
225000
327500
287500
257500
21. Факторный анализ
Для анализа влияния отдельныхфакторов на прирост товарооборота
берут разность между числителем и
знаменателем соответствующего общего
индекса
22. 1. Абсолютное изменение товарооборота (числитель минус знаменатель индекса стоимости товарооборота):
.1 Абсолютное изменение
товарооборота (числитель минус
знаменатель индекса стоимости
товарооборота):
pq p1 q1 p0 q0
23. Факторный анализ
Прирост стоимости товарооборотапроисходит под влиянием двух
факторов: изменения количества
проданных товаров и изменения цены за
единицу товара. Сумма приростов под
влиянием этих факторов должна
равняться общему приросту стоимости
товарооборота
24. Факторный анализ
Для получения сопоставимыхрезультатов рекомендуется соблюдать
такую последовательность включения
факторов в анализ: вначале идут
количественные факторы (в нашем
случае q), затем качественные (Р)
25. 2. Абсолютное изменение товарооборота за счет изменения количества проданных товаров (числитель минус знаменатель общего индекса физичес
.2 Абсолютное изменение
товарооборота за счет изменения
количества проданных товаров
(числитель минус знаменатель
общего индекса физического объема
товарооборота по Ласпейресу):
q pq p0 q1 p0 q0
26. 3. Абсолютное изменение товарооборота за счет изменения цен (числитель минус знаменатель индекса цен по Пааше):
.3 Абсолютное изменение
товарооборота за счет изменения
цен (числитель минус знаменатель
индекса цен по Пааше):
p pq p1 q1 p0 q1
Здесь возможны два случая:
экономия
или
перерасход
покупателей
изменения цен
за
счет
27. Взаимосвязь абсолютных величин
pq q pq p pq28. Средний гармонический индекс
29.
p1 q1p1 q1 I
Ip
; p
p
q
1
1
p0 q1
ip
p1
p1
ip
p0
p0
ip
30. В данном случае общий индекс цен рассчитывается как средняя гармоническая величина из индивидуальных индексов, где в качестве весов высту
В данном случаеобщий индекс цен
рассчитывается как средняя
гармоническая величина из
индивидуальных индексов, где в
качестве весов выступают величины
товарооборота отчетного периода.
xh
w
w
x
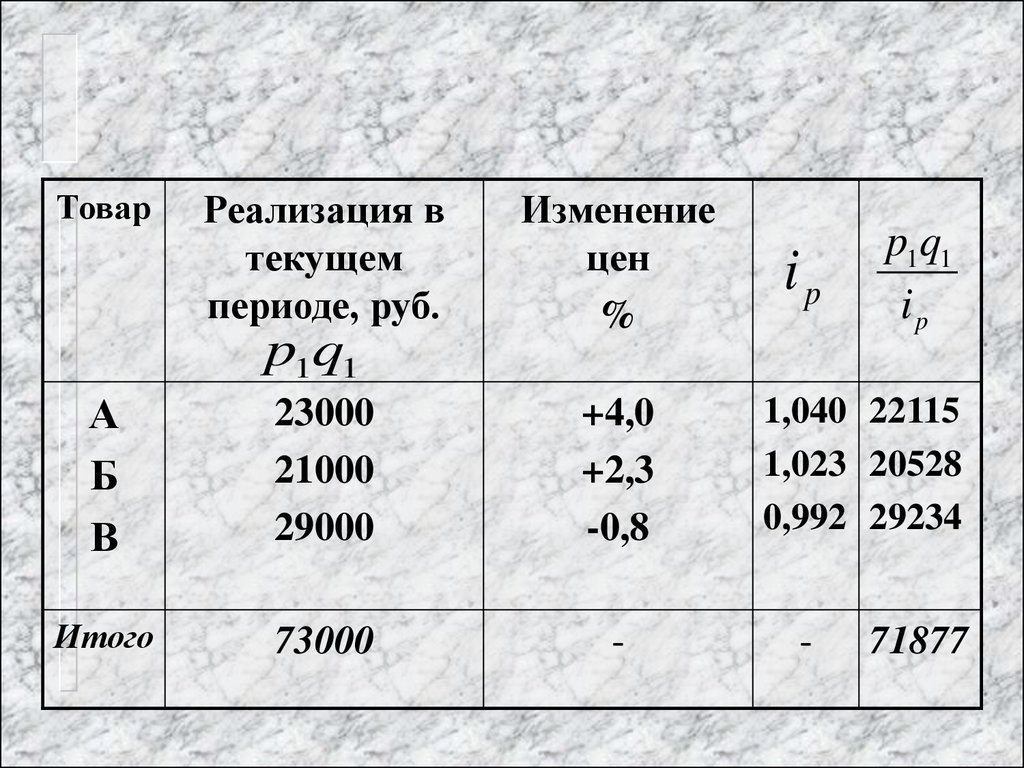
31.
ТоварРеализация в
текущем
периоде, руб.
p1q1
Изменение
цен
%
А
Б
В
23000
21000
29000
+4,0
+2,3
-0,8
Итого
73000
-
ip
p1q1
ip
1,040 22115
1,023 20528
0,992 29234
-
71877
32.
Ippq
1
i p q
1 1
73000
1,016( 1,6%)
71877
1 1
p
Цены по данной товарной группе в
текущем периоде по сравнению с
базисным в среднем возросли на 1,6%
33. Средний арифметический индекс
34.
Iqp0 q1
;
p0 q0
Iq
iq p0 q0
p0 q0
q1
iq
q1 iq q0
q0
35. В данном случае общий индекс физического объёма товарооборота рассчитывается как средняя арифметическая величина из индивидуальных инде
В данном случаеобщий индекс физического
объёма товарооборота
рассчитывается как средняя
арифметическая величина из
индивидуальных индексов физического
объема товарооборота , где в качестве
весов выступают величины
товарооборота базисного периода:
x f
x
f
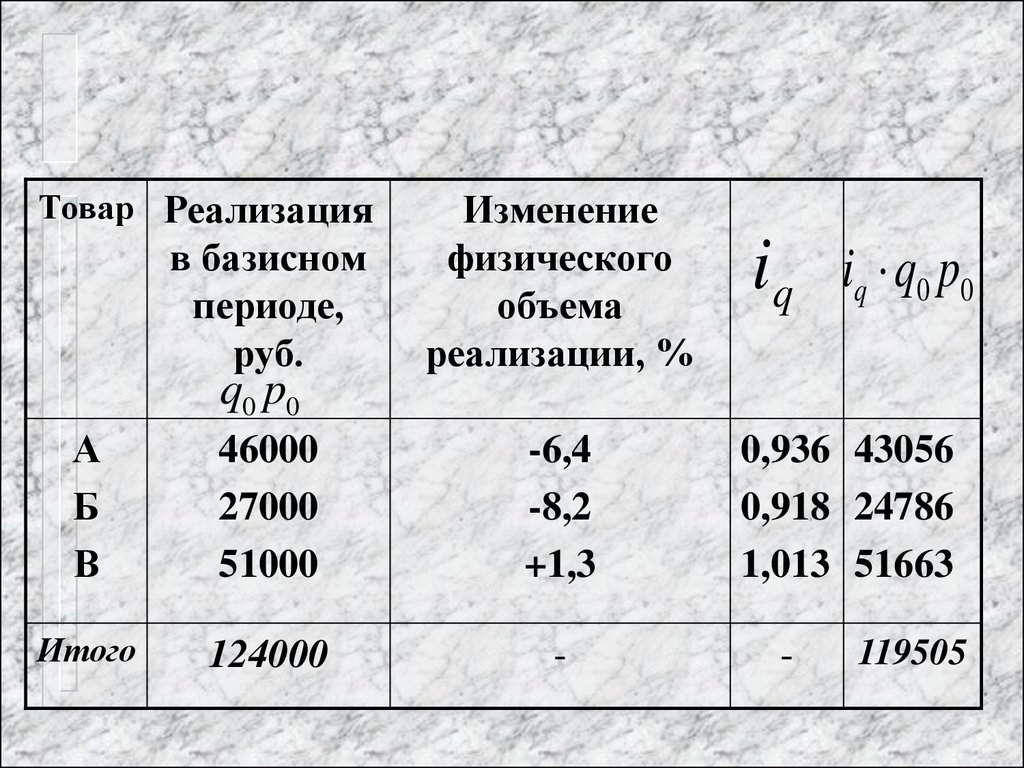
36.
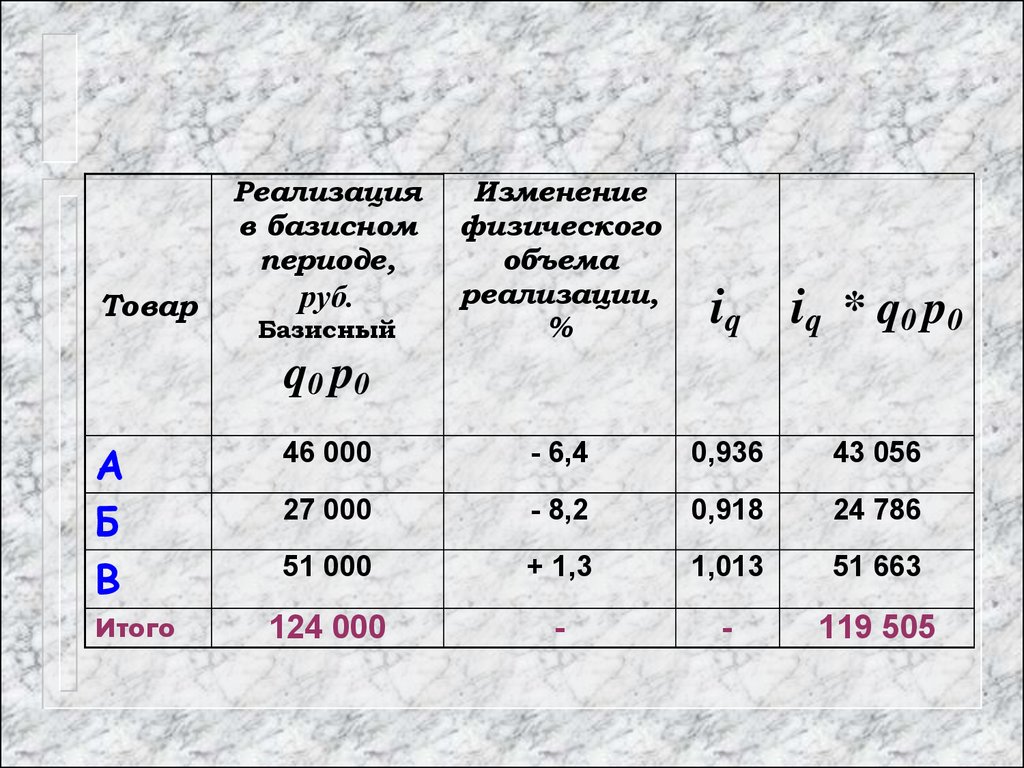
Товар Реализацияв базисном
периоде,
руб.
Изменение
физического
объема
реализации, %
А
Б
В
46000
27000
51000
-6,4
-8,2
+1,3
Итого
124000
-
q0 p0
iq
iq q0 p0
0,936 43056
0,918 24786
1,013 51663
-
119505
37.
Iqiq p
q p
q 0 0
0 0
119505
0,964( 3,6%)
124000
Физический объем реализации данных
товаров в среднем снизился на 3,6%
38. Индексы средних уровней (индексы переменного состава, постоянного состава и структурных сдвигов)
39. Рассматривается реализация товара А несколькими фирмами. У каждой фирмы определенный объем реализации и своя цена. Требуется проанализир
Рассматривается реализациятовара А несколькими фирмами. У
каждой фирмы определенный
объем реализации и своя цена.
Требуется проанализировать,
как изменяется средняя цена
товара
40. .Индекс средней цены (Индекс переменного состава)
Индекс средней цены.
(Индекс переменного состава)
p1 p1 q1 p0 q0
Ip
q1
q0
p0
41. Из формулы индекса переменного состава видно, что средняя цена изменяется в результате действия двух факторов:
изменениецен в отдельных фирмах;
изменение удельного веса фирм в
общем объеме реализации товаров.
Следовательно, индекс переменного
состава может быть разложен на два
субиндекса, каждый из которых
характеризует действия одного из этих
факторов
42. 1. Субиндекс - индекс постоянного состава. Он показывает, как изменяется средняя цена в результате изменения цен в отдельных фирмах.
1. Субиндекс индекс постоянного состава.Он показывает, как изменяется средняя
цена в результате изменения цен в
отдельных фирмах.
Ip
p
p1 d1
p0 d1
p1 q1
q1
p0 q1
q1
43. 2. Субиндекс - индекс структурных сдвигов. Он показывает, как изменяется средняя цена в результате изменения удельного веса фирм в общем объ
2. Субиндекс индекс структурных сдвигов.Он показывает, как изменяется средняя
цена в результате изменения удельного
веса фирм в общем объеме реализации
товаров (в результате структурных
сдвигов):
Ip
d
p0 q1 p0 q0
q1
q0
44. Перечисленные индексы образуют систему:
I p I p I pp
d
45. 1. Абсолютное изменение средней цены исчисляется как разность делимого и делителя индекса переменного состава
p1 q1 p0 q0p
q1
q0
46. 2. Изменение средней цены за счет изменения цен в отдельных фирмах исчисляется как разность делимого и делителя индекса фиксированного сос
2. Изменение средней ценыза счет изменения цен в
отдельных фирмах
исчисляется как разность делимого и делителя
индекса фиксированного состава:
p1 q1 p0 q1
p p
q1
q1
47. 3. Изменение средней цены за счет структурных сдвигов исчисляется как разность делимого и делителя индекса структурных сдвигов:
p0 q1 p0 q0pd
q1
q0
48. Перечисленные абсолютные величины образуют систему:
p p p pd49. Трехфакторные индексы
50. Cтоимость материальных затрат на производство продукции зависит от:
q - количества выпускаемойпродукции ;
m - удельных расходов сырья и
материалов ;
p - цен на сырье и материалы.
51.
z p m qz
где – материальные затраты
на производство.
52. Индекс материальных затрат на производство
p1 m1 q1I pmq
p0 m0 q 0
53. Индекс объема производства
p0 m0 q1Iq
p 0 m0 q 0
54. Индекс удельных расходов
p0 m1 q1Im
p 0 m0 q1
55. Индекс цен сырья
p1 m1 q1Ip
p0 m1 q1
56. Эти индексы образуют систему
I pmq I p I m I q57. Территориальные индексы
58.
При построении территориальныхиндексов возникают вопросы о базе
сравнения и объекте, на уровне которого
следует зафиксировать веса индекса.
Эти вопросы решаются, исходя из
конкретных задач исследования.
Например, необходимо сравнить
уровни цен двух регионов
(регионов А и Б).
59.
pq
А
А
I p
p Б q А
В качестве весов берем
количество
товаров,
проданных в регионе А.
60.
pq
Б
Б
I p
p А q Б
В качестве весов берем
количество
товаров,
проданных в регионе Б.
61. Данные индексы не взаимосвязаны между собой:
неДанные индексы
взаимосвязаны между собой:
1
I p
I p
62. Для получения единого результата в качестве весов используется суммарный объем продаж двух регионов.
q q А qБp А q
Ip
p Б q
63. Возможно построение индекса цен на основе метода косвенной стандартизации.
pq
p
q
А
А
Б
Б
I p
,
p q А
p q Б
64. где - средняя цена для двух регионов.
где p - средняя цена длядвух регионов.
p А q А p Б q Б
p
q А qБ
65. Индекс физического объема товарооборота
p q АIq
,
p qБ
где
p
- веса.
66. Индекс товарооборота по двум регионам
p А q АI pq
p Б q Б
I pq I q I p
67. Цепные и базисные индексы
68.
Если индексы рассчитываются длябольшего, чем два, числа периодов
времени, то они могут быть получены
базисным и цепным способом.
Рассмотрим построение базисных и
цепных индексов на примере индекса
физического
товарооборота.
объема
69. Индивидуальные индексы
70.
Рассмотримреализацию какоголибо товара в разные
периоды времени.
71.
tqt
iqБ
iqЦ
0
q0
1
-
1
q1
q1 q0
q1 q0
2
q2
q2 q1
3
q3
q2 q0
q3 q0
4
q4
q4 q0
q3 q2
q4 q3
72.
q0 - количествопроданного
товара в базисном периоде;
q1-
количество проданного
товара в первом периоде и
так далее.
73. Произведение цепных индексов дает базисный индекс последнего периода времени.
q1 q2 q3 q4 q 4q0 q1 q2 q3 q0
74. Общие индексы
75.
Отмеченная выше взаимосвязьбезусловна
только
для
индивидуальных индексов.
Для общих же индексов эта
взаимосвязь будет справедлива лишь
тогда, когда общие индексы будут
рассчитываться с так называемыми
постоянными весами.
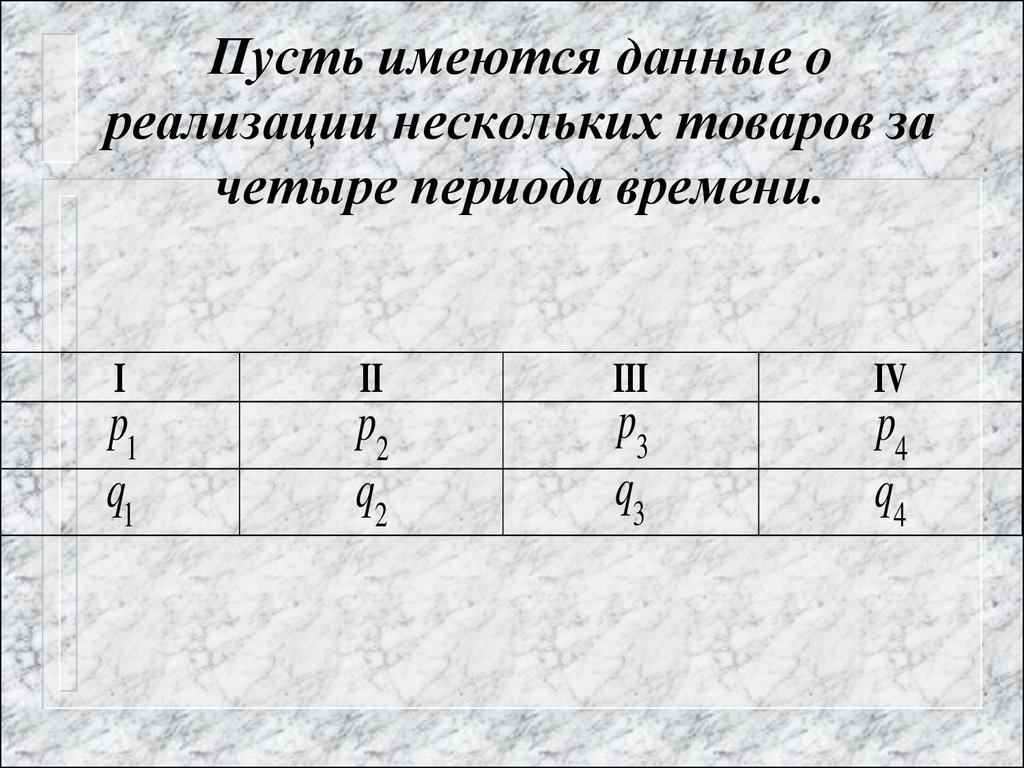
76. Пусть имеются данные о реализации нескольких товаров за четыре периода времени.
III
III
IV
p1
q1
p2
q2
p3
q3
p4
q4
77. Система базисных индексов
За базисный принимается первыйпо порядку период времени.
p1 q3
Iq3 1
p1 q1
p1 q2
Iq
21
p1 q1
p1 q4
Iq 4 1
p1 q1
78. Система цепных индексов с постоянными весами
p1 q2Iq 2 1
p1 q1
p1 q3
Iq3 2
p1 q4
p1 q2
Iq 4 3
p1 q3
79.
p1 q 2 p1 q3 p1 q4p1 q1 p1 q 2 p1 q3
p1 q4
p1 q1
80. Система цепных индексов с переменными весами
p1 q2Iq 2 1
p1 q1
p 2 q 3
Iq3 2
p 2 q2
p3 q 4
Iq4 3
p 3 q 3
81.
Реализацияв базисном
периоде,
Товар
руб.
Базисный
Изменение
физического
объема
реализации,
%
iq iq * q0 p0
q0 p0
A
Б
В
Итого
46 000
- 6,4
0,936
43 056
27 000
- 8,2
0,918
24 786
51 000
+ 1,3
1,013
51 663
124 000
-
-
119 505
82.
Iq = iq q0 p0 / q0 p0 ==119 505 / 124 000 =
0, 964 или 96,4 %
Физический объем реализации данных
товаров в среднем снизился на 3,6 %



























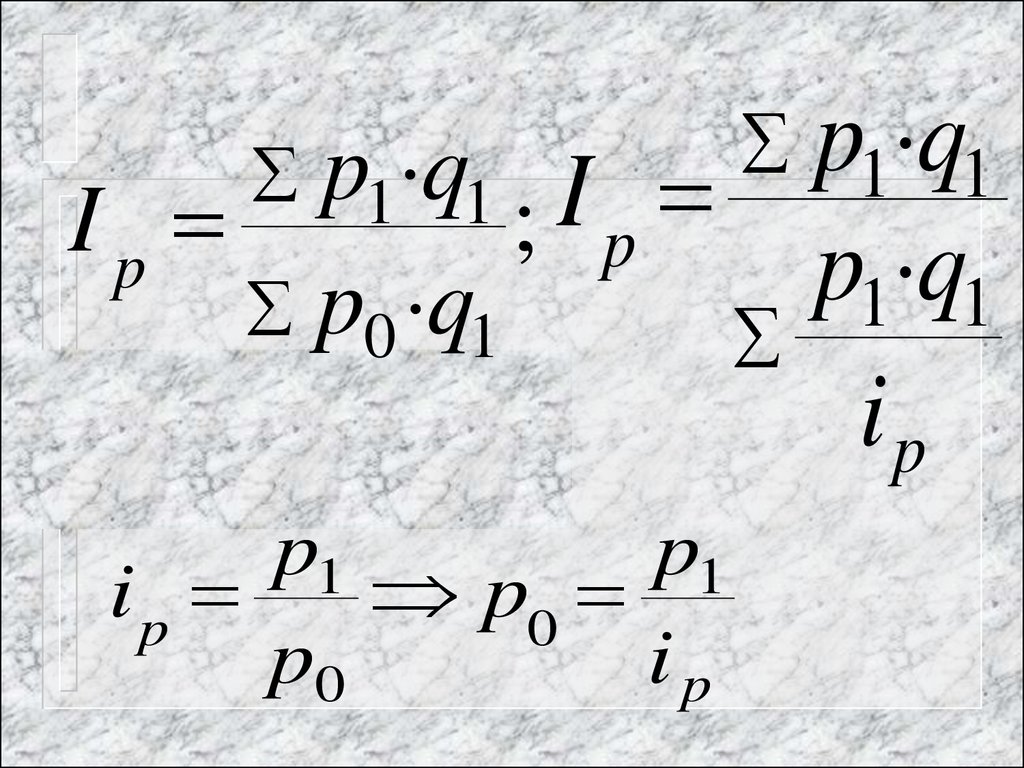



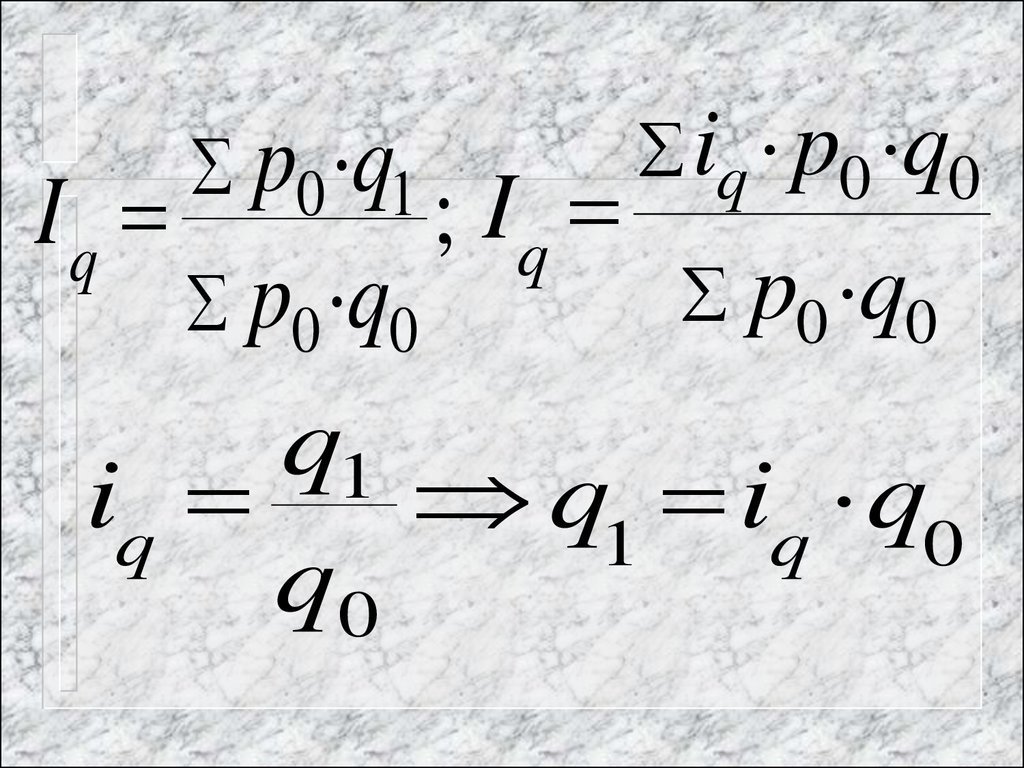



















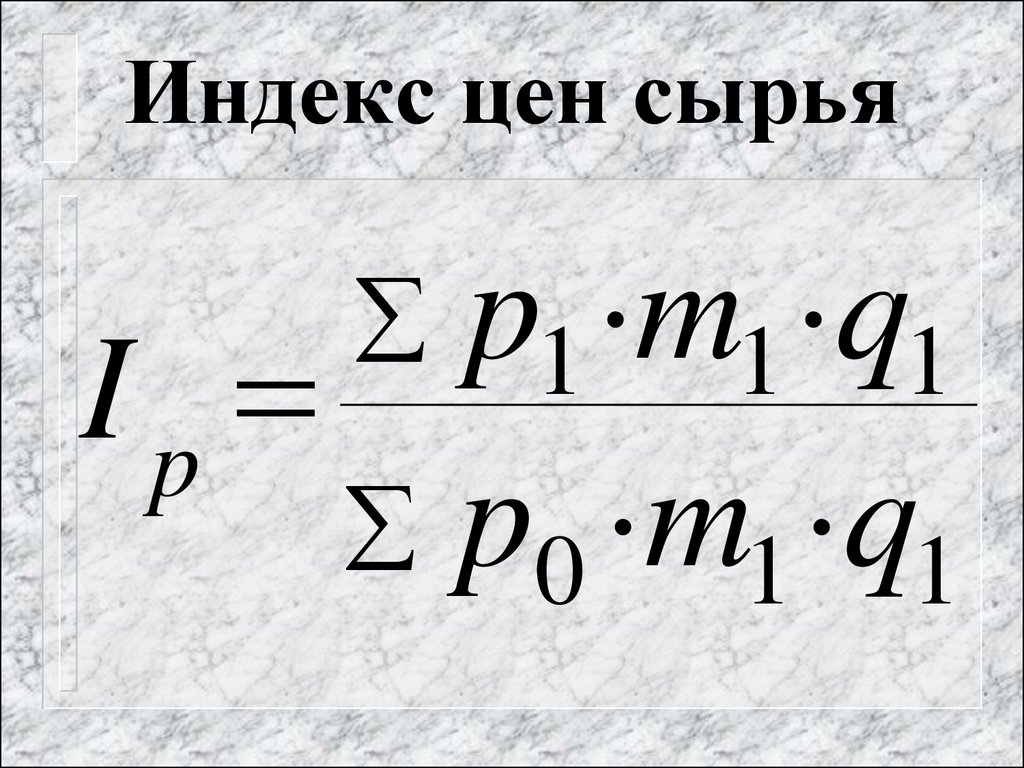









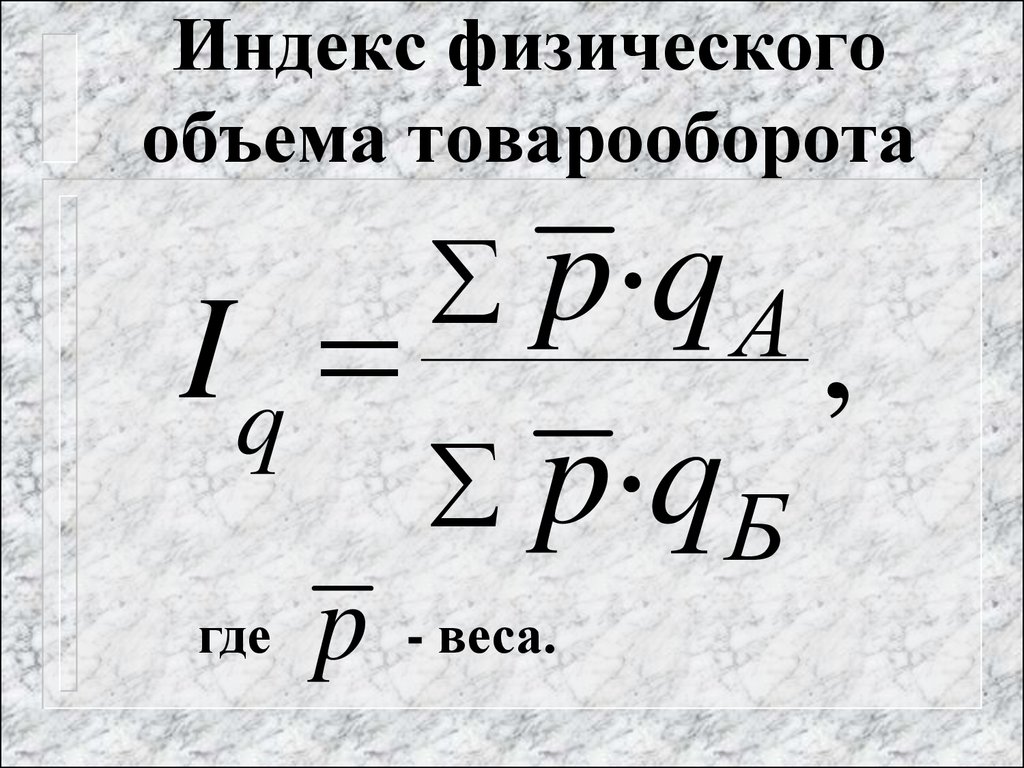












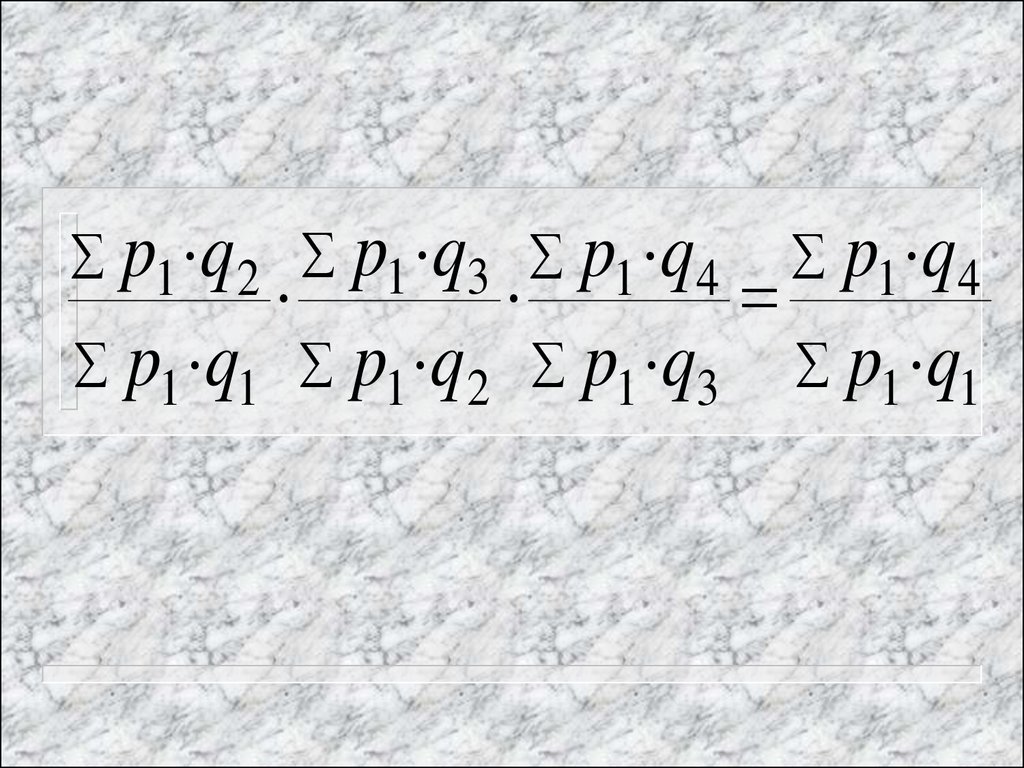


 economics
economics








