Similar presentations:
Индексы
1. ИНДЕКСЫ
Индекс - это относительный показательдинамики общественных явлений, который
характеризует изменение объёма или
уровня явлений в отчётном периоде по
сравнению с базисным.
2.
условные обозначения:i - индивидуальный индекс;
I - общий индекс;
р - цена единицы продукции;
q - объём выпуска продукции.
3. индивидуальные индексы
p1ip
p0
q1
iq
q0
q1 p1
iqp
q0 p0
индивидуальный индекс цен
индивидуальный индекс физического объёма
индивидуальный индекс стоимости
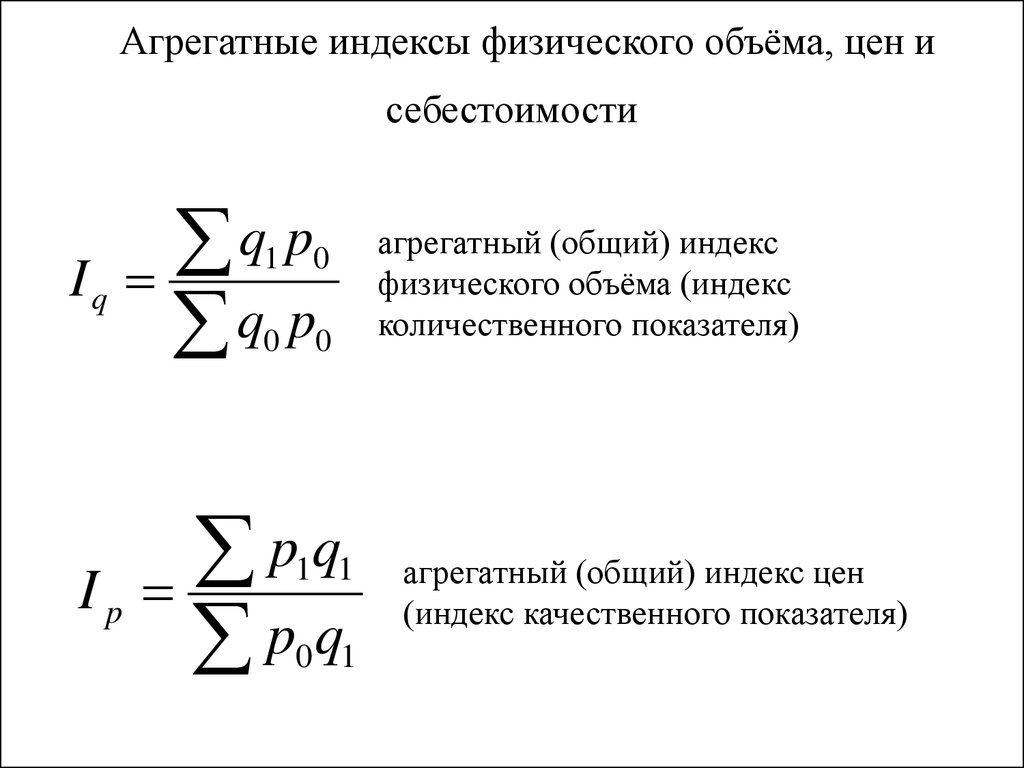
4. Агрегатные индексы физического объёма, цен и себестоимости
IqIp
qp
q p
1
0
0
0
pq
p q
1 1
0 1
агрегатный (общий) индекс
физического объёма (индекс
количественного показателя)
агрегатный (общий) индекс цен
(индекс качественного показателя)
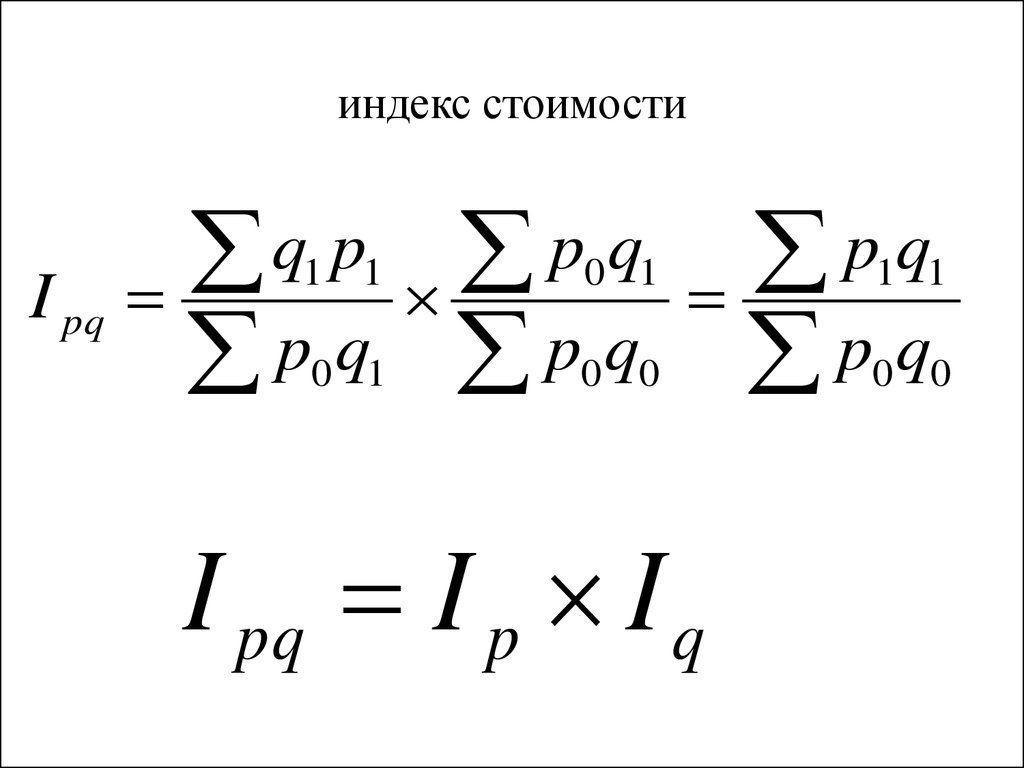
5. индекс стоимости
I pqq p p q
p q p q
1
1
0 1
0 1
0 0
pq
p q
I pq I p I q
1 1
0 0
6. Формулы агрегатных индексов позволяют разложить общий абсолютный прирост стоимости по факторам
pq pq q pq p ,pq p1q1 p0 q0
pq q p0 q1 p0 q0
pq p p1q1 p0 q1
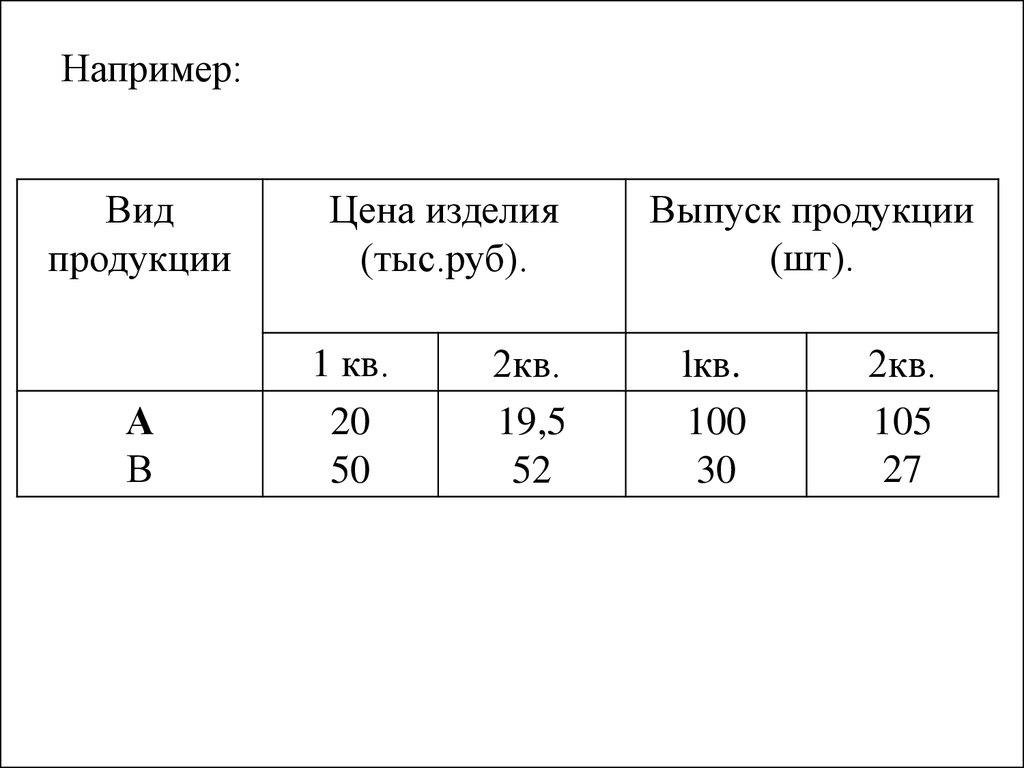
7. Например:
Видпродукции
А
В
Цена изделия
(тыс.руб).
1 кв.
20
50
2кв.
19,5
52
Выпуск продукции
(шт).
lкв.
100
30
2кв.
105
27
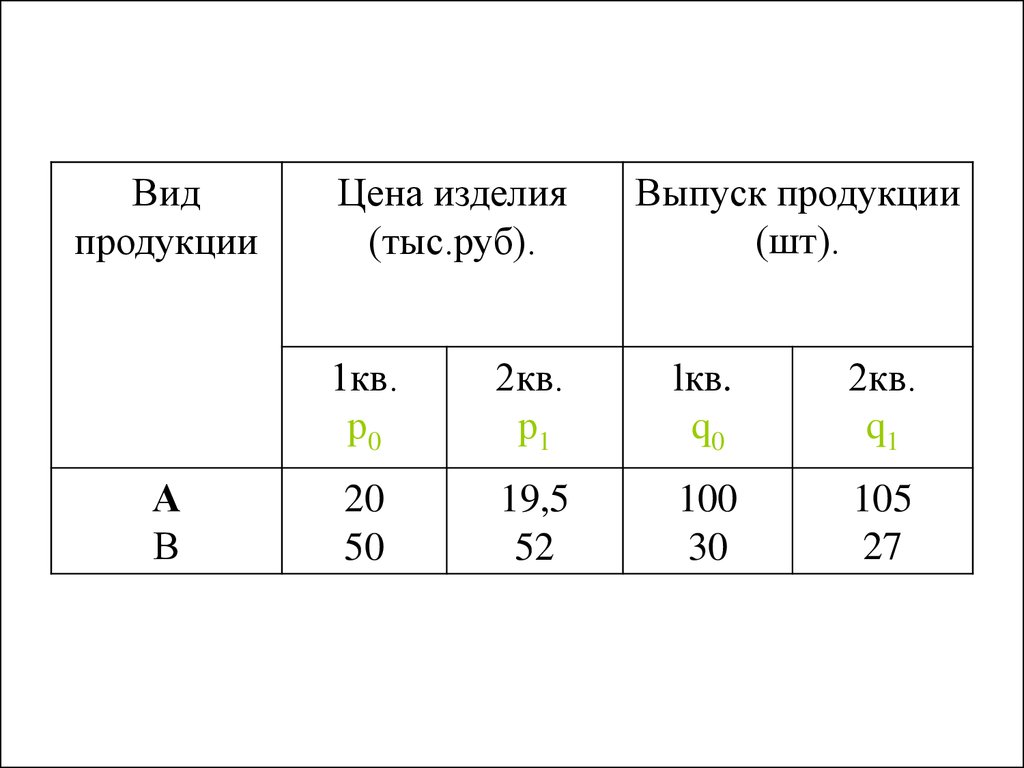
8.
Видпродукции
А
В
Цена изделия
(тыс.руб).
Выпуск продукции
(шт).
1кв.
р0
2кв.
р1
lкв.
q0
2кв.
q1
20
50
19,5
52
100
30
105
27
9. Решение
1. Определим общий индекс стоимости:I pq
p q
p q
1
1
0
0
105 19.5 52 27
20 100 50 30
3451.5
0
100
3500
pq
0
98.61
0
0
p1q1 p0 q0 3451.5 3500 48.5тыс. руб.
Таким
образом
стоимость
продукции
уменьшилась на 1,39%, а экономический
эффект составил 48,5 тыс.руб.
10. 2. Определим общий индекс цены:
2. Определим общий индекс цены:Ip
pq
p q
1 1
0 1
19,5 105 52 27 3451,5
0
100
50 27 20 105
3450
0
100,04
0
0
pq p
p1q1 p0 q1 3451.5 3450 1.5тыс. руб.
Таким образом, общий индекс цены возрос на 0,04%, а
абсолютный прирост стоимости, вызванный увеличением цен
равен 1,5 тыс. руб.
11. 3. Определим общий индекс физического объёма:
3. Определим общий индекс физического объёма:Iq
pq
p q
0 1
0 0
20 105 50 27 3450
0
100
50 30 20 100 3500
0
98.57
0
0
pq q p0q1 p0q0 3450 3500 50тыс. руб.
Таким образом, на 1,43% стоимость снизилась из-за
уменьшения выпуска продукции, что в абсолютном
выражении равно 50 тыс. руб.
12. индексы себестоимости
z1iz
z0
Индивидуальный индекс себестоимости
характеризует изменение себестоимости отдельных
видов продукции
13.
Сводный индекс себестоимости рассчитываетсядля определения себестоимости нескольких видов
продукции, выпускаемых предприятием.
При этом себестоимость взвешивается по
объему производства отдельных видов продукции
текущего периода.
Iz
zq
z q
1 1
0 1
14.
z z1q1 z 0 q1показывает сумму экономии предприятия от
снижения себестоимости.
15.
Iqqz
q z
1 0
0 0
Сводный индекс физического объема, взвешенный по
себестоимости
16. Сводный индекс затрат на производство
I zqzq
z q
1 1
0
I zq I z I q
0
z q q z
z q q z
1 1
1 0
0 1
0 0
17. Средние арифметические и средние гармонические индексы
На практике очень часто не известныабсолютные значения индексируемых величин, а
имеются данные об их относительном изменении.
В таких случаях вместо агрегатных индексов
вычисляются
средние
из
индивидуальных
индексов, которые в свою очередь делятся на:
- средние арифметические
- средние гармонические
Применение той или иной формулы индекса
зависит от имеющейся в нашем распоряжении
информации
18. Средний арифметический индекс физического объема
Iqi p q
p q
q
0 0
0 0
iq d 0
19. Рассмотрим вывод:
Iqqp
q p
1
0
0
т.к.
0
q1
iq
q0
Iq
q1 i q0
i p q
p q
q
0
0
0
0
iq d 0
20. средний гармонический индекс физического объёма
Iqp q
p q
i
0
1
0
1
q
I q1 p0 ,
q
q0 p0
q1
q1
iq
q0
q0
iq
q 1 p0
Iq
q1 p0
i
q
21. Для индексов цены вывод аналогичен
Ipi p q
p q
p
0 1
средний арифметический индекс
цены
0 1
Ip
pq
pq
i
1
1
p
1
1
средний гармонический
индекс цены
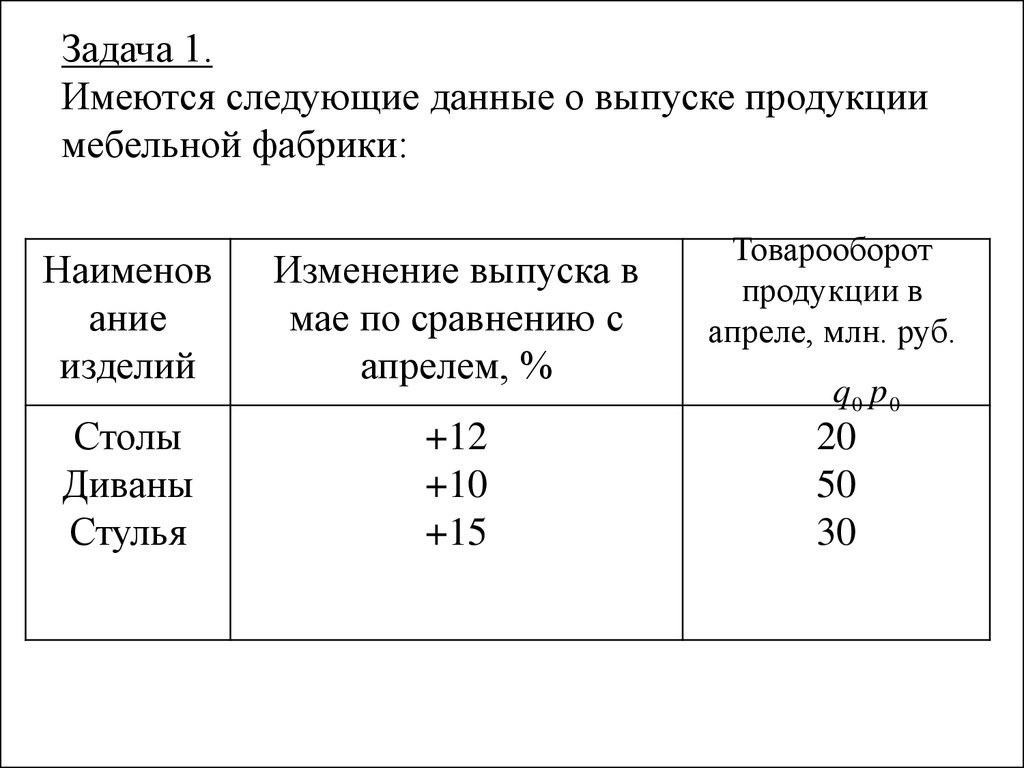
22. Задача 1. Имеются следующие данные о выпуске продукции мебельной фабрики:
Наименование
изделий
Изменение выпуска в
мае по сравнению с
апрелем, %
Столы
Диваны
Стулья
+12
+10
+15
Товарооборот
продукции в
апреле, млн. руб.
q0 p0
20
50
30
23. Определить увеличение выпуска всей продукции в мае по сравнению с апрелем (в %), т.е. рассчитать общий индекс физического объема. Решение.
Общий индекс физического объема может бытьрассчитан как средний арифметический:
Iq
iq p
q p
0
0
0
0
или 111,9%
1,12 20 1,10 50 1,15 30
1,119
20 50 30
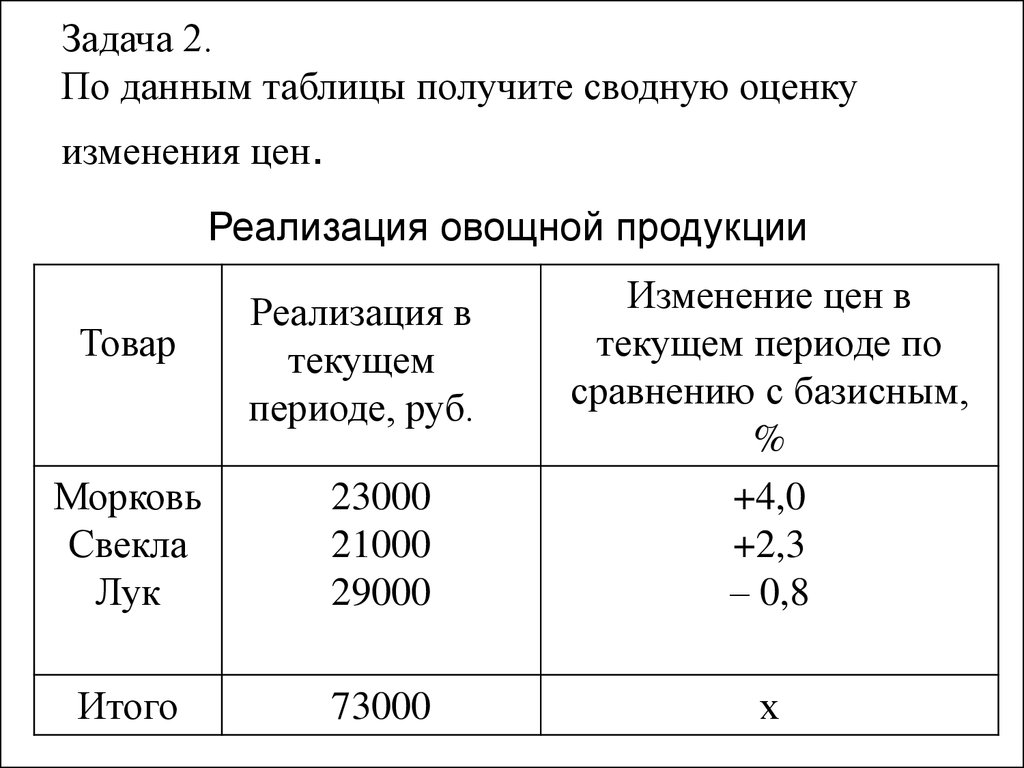
24. Задача 2. По данным таблицы получите сводную оценку изменения цен.
Реализация овощной продукцииМорковь
Свекла
Лук
23000
21000
29000
Изменение цен в
текущем периоде по
сравнению с базисным,
%
+4,0
+2,3
– 0,8
Итого
73000
х
Товар
Реализация в
текущем
периоде, руб.
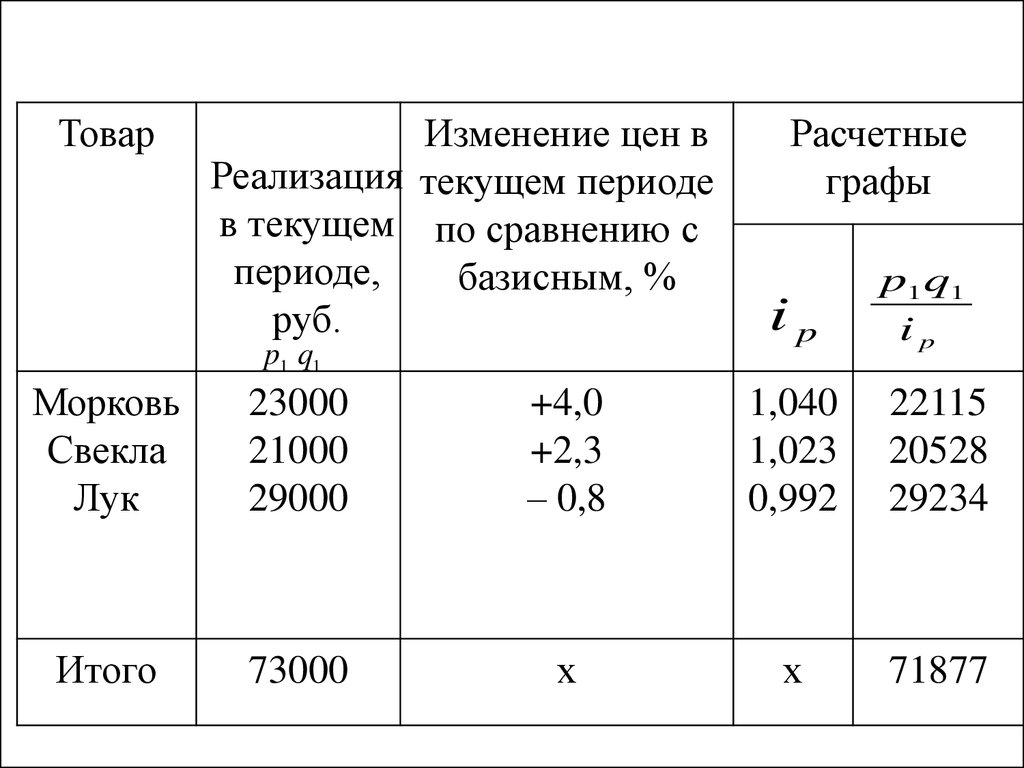
25.
ТоварИзменение цен в
Реализация текущем периоде
в текущем по сравнению с
периоде,
базисным, %
руб.
p1 q1
Расчетные
графы
ip
p1 q1
ip
Морковь
Свекла
Лук
23000
21000
29000
+4,0
+2,3
– 0,8
1,040
1,023
0,992
22115
20528
29234
Итого
73000
х
х
71877
26. Решение
Вычислим средний гармонический индекс цен:Ip
pq
pq
i
1 1
1 1
p
23000 21000 29000
73000
1,016
23000 21000 29000 71877
1,040
1,023
0,992
или 101,6%.
Таким образом, цены по данной товарной группе в
текущем периоде по сравнению с базисным
периодом, в среднем выросли на 1,6%.
27. Базисные и цепные индексы, их взаимосвязь
Так как индексы являются относительной величинойдинамики, то они также могут быть базисными и
цепными:
– базисные индексы получают сопоставлением с
уровнем периода, принятого за базу сравнения, т.е.
база сравнения, остаётся постоянной;
– цепные индексы получают сопоставлением
текущих уровней с предшествующим, т.е. база
сравнения непрерывно меняется.
28. Для индивидуальных индексов цен, физического объёма и стоимости продукции справедливо следующие правила:
1. Последовательное произведение цепных индексовдаёт базисный индекс последнего периода:
I бП i Ц1 i Ц 2 i Ц П
или
I 4 i 1 i2 i 3 i4
0
0
0
0
0
29. 2. Отношение базисного индекса отчётного периода к базисному индексу предшествующего периода даёт цепной индекс отчётного периода
2. Отношение базисного индекса отчётного периодак базисному индексу предшествующего периода
даёт цепной индекс отчётного периода
IЦП
I бП
I бП 1
или
I4
3
I4
I3
0
0
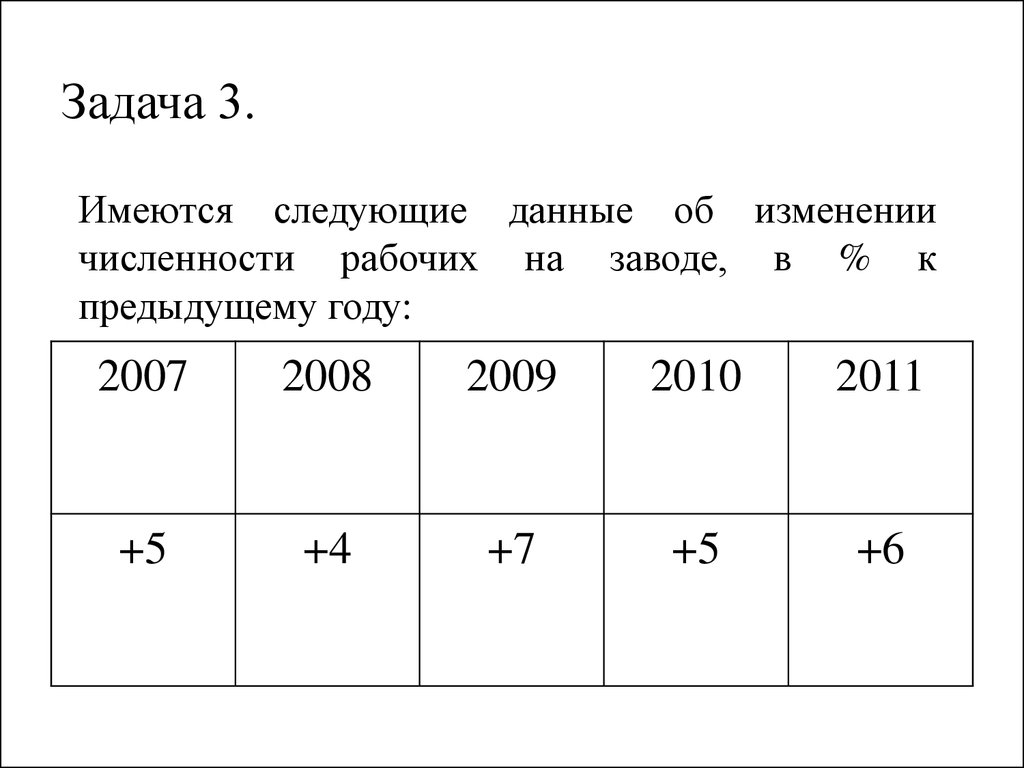
30. Задача 3.
Имеются следующие данные об изменениичисленности рабочих на заводе, в % к
предыдущему году:
2007
2008
2009
2010
2011
+5
+4
+7
+5
+6
31. Определить на сколько процентов увеличилось число рабочих на заводе за 5 лет, т.е. в 2011 году по сравнению с 2006 годом.
Решение.Зная, что базисный индекс можно получить путем
перемножения цепных индексов, находим:
I ч. р. 2011
1,05 1,04 1,07 1,05 1,06 1,30
2006
(или 130%), т.е. за 5 лет число рабочих на заводе
возросло на 30%.
32. Индексы средних величин
Индекс переменного состава -I n.c.
- отношение 2-х средних величин – учитывает
одновременно и структурные изменения в
составе совокупности
и изменение уровня
I
качественного признака
у отдельных объектов.
Если индексируемую величину обозначить
через х, а веса через f , то в общем виде
индекс переменного состава можно записать в
виде:
n .c .
33.
I n .c .x f x f
f f
1
1
1
0
0
0
34.
2. Индекс постоянного составаI пост.
- вычисляется по типу индекса цены.
Если при расчете средних величин за два
периода зафиксировать веса одного и
того же периода, то при сравнении таких
средних величин индекс постоянного
(или фиксированного) состава:
35.
I пост.x f x f
f f
1
1
1
0
1
1
36.
3. Индекс рассчитанных по типуIq
индекс структурных изменений (сдвигов) -
I стр.
- показывает, во сколько раз изменился общий
средний уровень за счёт изменения удельного веса
каждого объекта в общем объёме признака. При
сравнении средних показателей принимают
неизменными значения х, тогда на динамику
изменения средних будет оказывать влияние
только изменение весов.
37.
I стр.х f x f
f f
0
1
1
0
0
0
38. Взаимосвязь:
I пер. I стр. I пост.39. Задача
Провести анализ изменения цен реализациитовара А в двух регионах
Регион
1
2
июнь
июль
Цена, Продано, Цена, Продано,
руб
шт
руб
шт
12
10000
13
18000
17
20000
19
9000
40.
1. Вычислить индексы переменного,постоянного
состава и структурных сдвигов.
2. Проверить взаимосвязь вычисленных
индексов
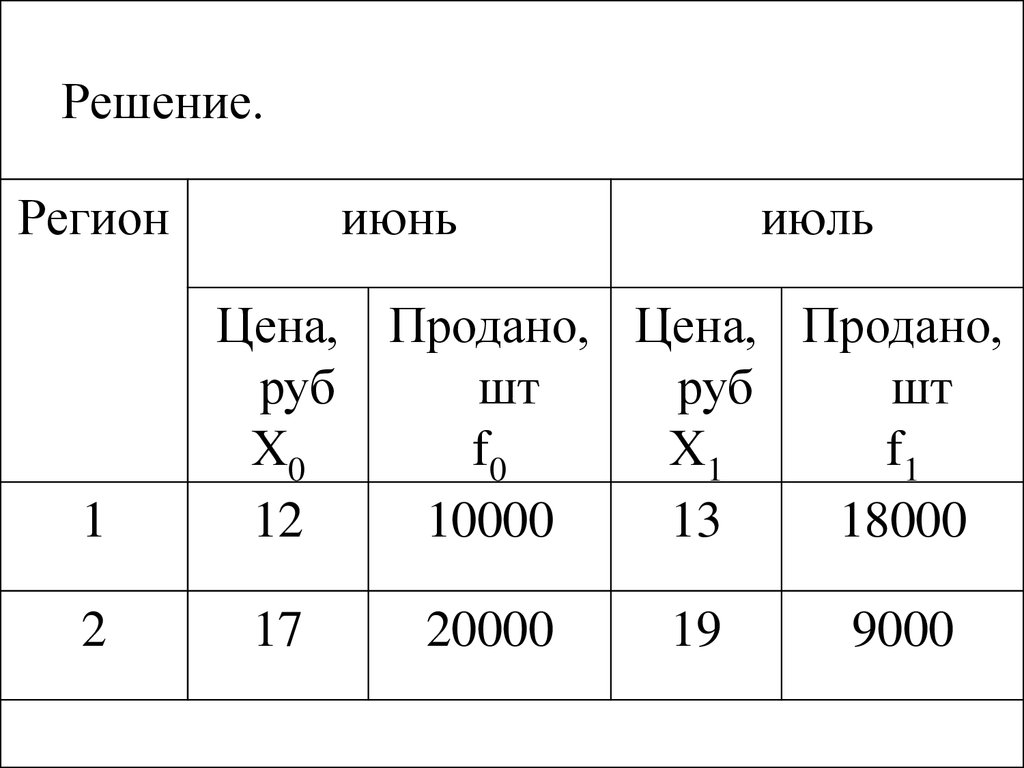
41. Решение.
Регион1
2
июнь
июль
Цена, Продано, Цена, Продано,
руб
шт
руб
шт
Х0
f0
Х1
f1
12
10000
13
18000
17
20000
19
9000
42. 1. Вычислим индекс переменного состава
I n .c .x f x f
f f
1 1
0 0
1
0
13 18000 19 9000 12 10000 17 20000
18000 9000
10000 20000
15
0,978
15,33
или 97,8%
43. 2. Вычислим индекс постоянного состава
I пост.x f x f
f f
1 1
0 1
1
1
13 18000 19 9000 12 18000 17 9000
18000 9000
18000 9000
15
1,097
13,67
или 109,7%
44. 3. Вычислим индекс структурных сдвигов
I стр.х f x f
f f
0 1
1
0
0
0
12 18000 17 9000 12 10000 17 20000
18000 9000
10000 20000
13,67
0,8917
15,33
или 89,17%
45. Проверим взаимосвязь вычисленных индексов:
I пер. I стр. I пост.0,978=1,097 х 0,8917 (верно)
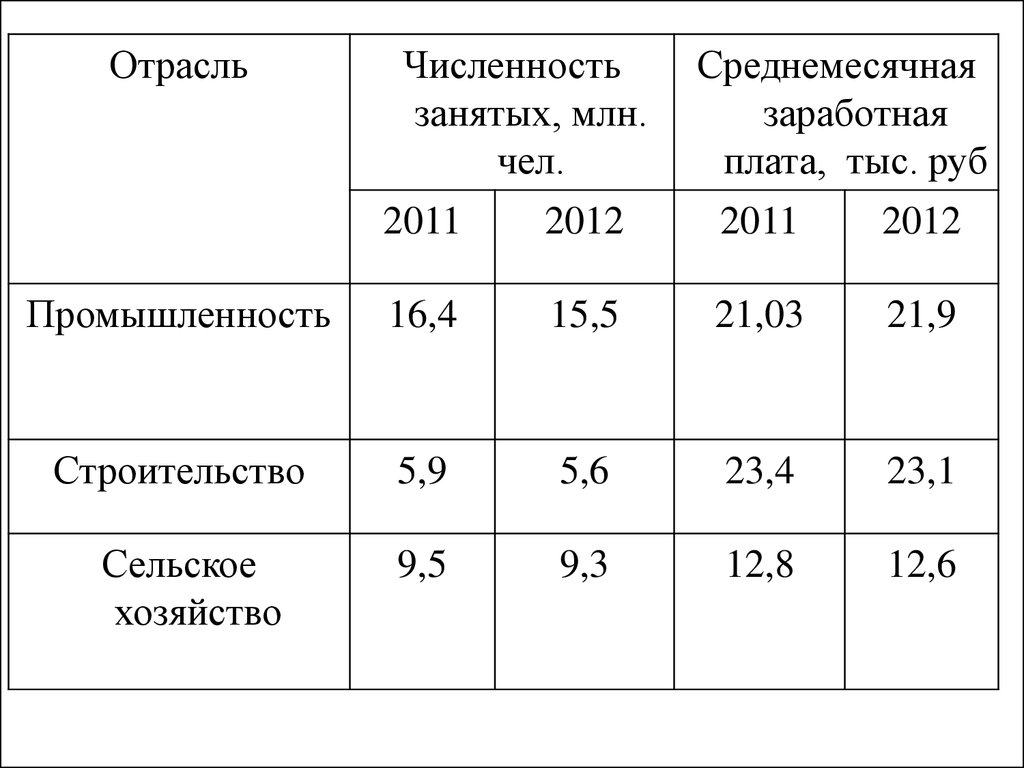
46. Задача 2:
Имеются следующие данные за 2011 и2012 гг. о средней заработной плате
и численности занятых в трех отраслях
экономики РФ:
47.
ОтрасльЧисленность
занятых, млн.
чел.
Среднемесячная
заработная
плата, тыс. руб
2011
2012
2011
2012
Промышленность
16,4
15,5
21,03
21,9
Строительство
5,9
5,6
23,4
23,1
9,5
9,3
12,8
12,6
Сельское
хозяйство
48.
Вычислитьиндексы
переменного,
постоянного
состава и структурных сдвигов средней
заработной
платы.
Проверить
взаимосвязь
вычисленных индексов
Решение.
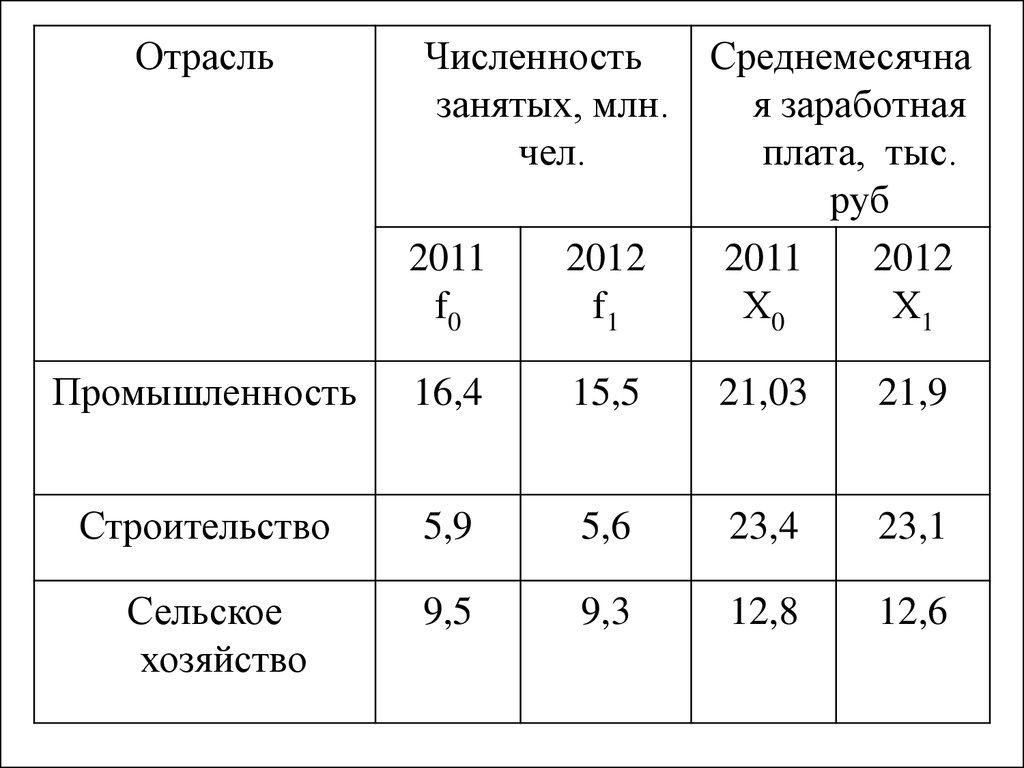
49.
Отрасль2011
f0
2012
f1
Среднемесячна
я заработная
плата, тыс.
руб
2011
2012
Х0
Х1
Промышленность
16,4
15,5
21,03
21,9
Строительство
5,9
5,6
23,4
23,1
9,5
9,3
12,8
12,6
Сельское
хозяйство
Численность
занятых, млн.
чел.
50. 1. Вычислим индекс переменного состава
I n .c .x f x f
f f
1
1
1
0
0
0
21,9 15,5 23,1 5,6 12,6 9,3
15,5 5,6 9,3
21,03 16,4 23,4 5,9 12,8 9,5
16,4 5,9 9,5
19,28
Или 101,42%
1,0142
19,01
51. 2. Вычислим индекс постоянного состава
I пост.x f x f
f f
1
1
1
0
1
1
21,9 15,5 23,1 5,6 12,6 9,3
15,5 5,6 9,3
21,03 15,5 23,4 5,6 12,8 9,3
15,5 5,6 9,3
19,28
Или 101,7%
1,017
18,95
52. 3. Вычислим индекс структурных сдвигов
I стр.х f x f
f f
0
1
1
0
0
0
21,03 15,5 23,4 5,6 12,8 9,3
15,5 5,6 9,3
21,03 16,4 23,4 5,9 12,8 9,5
16,4 5,9 9,5
18,95
0,9968
Или 99,68%
19,01
53. Проверим взаимосвязь вычисленных индексов:
I пер. I стр. I пост.1,0142=1,017 х 0,9968 (верно)
























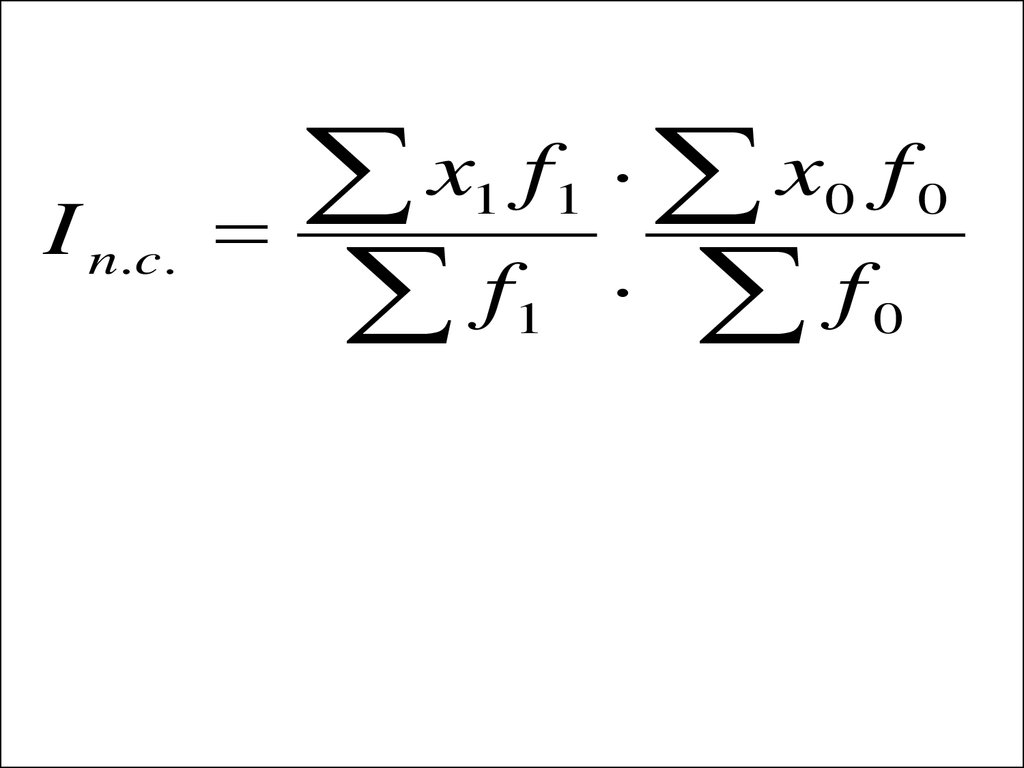

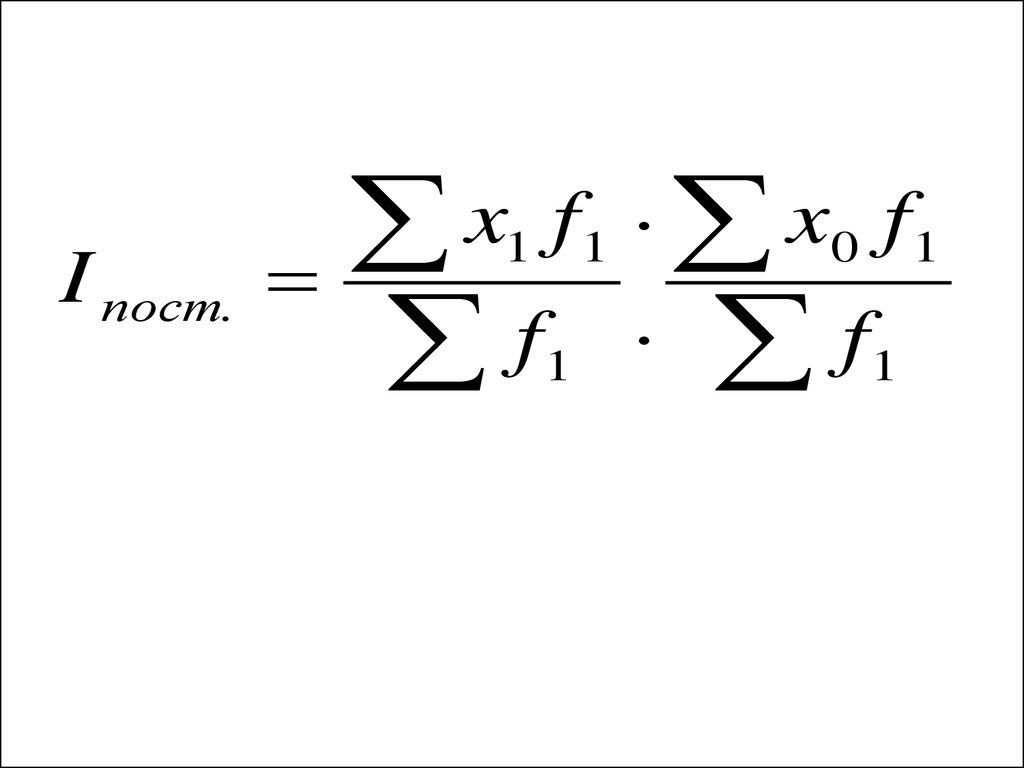

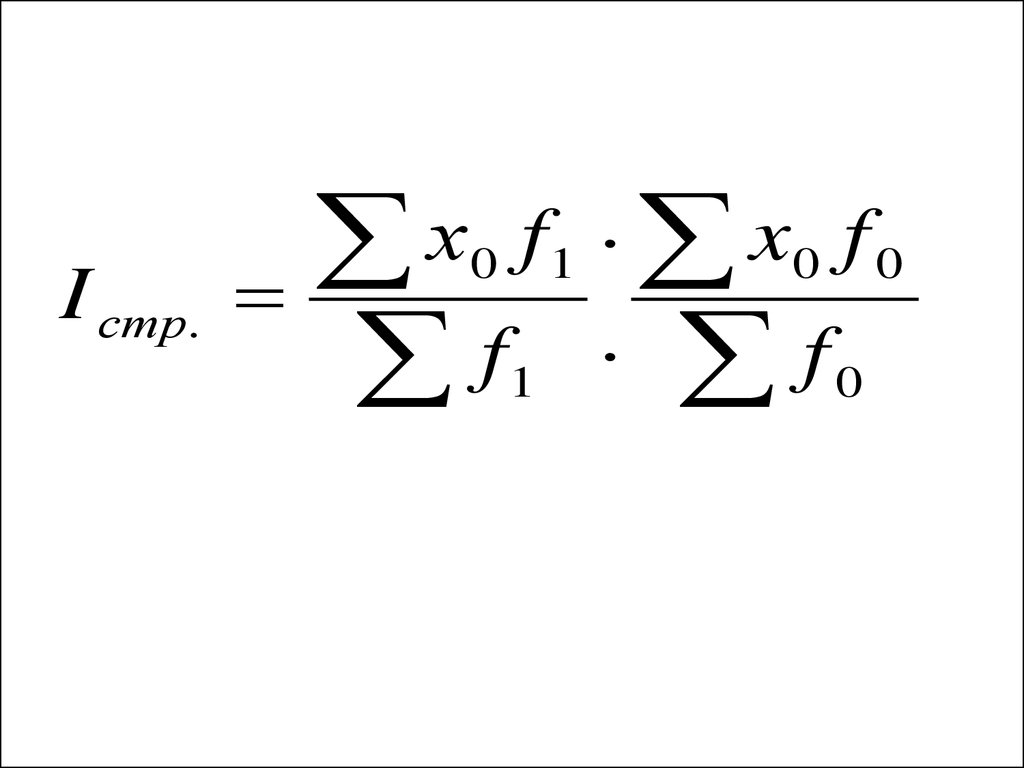
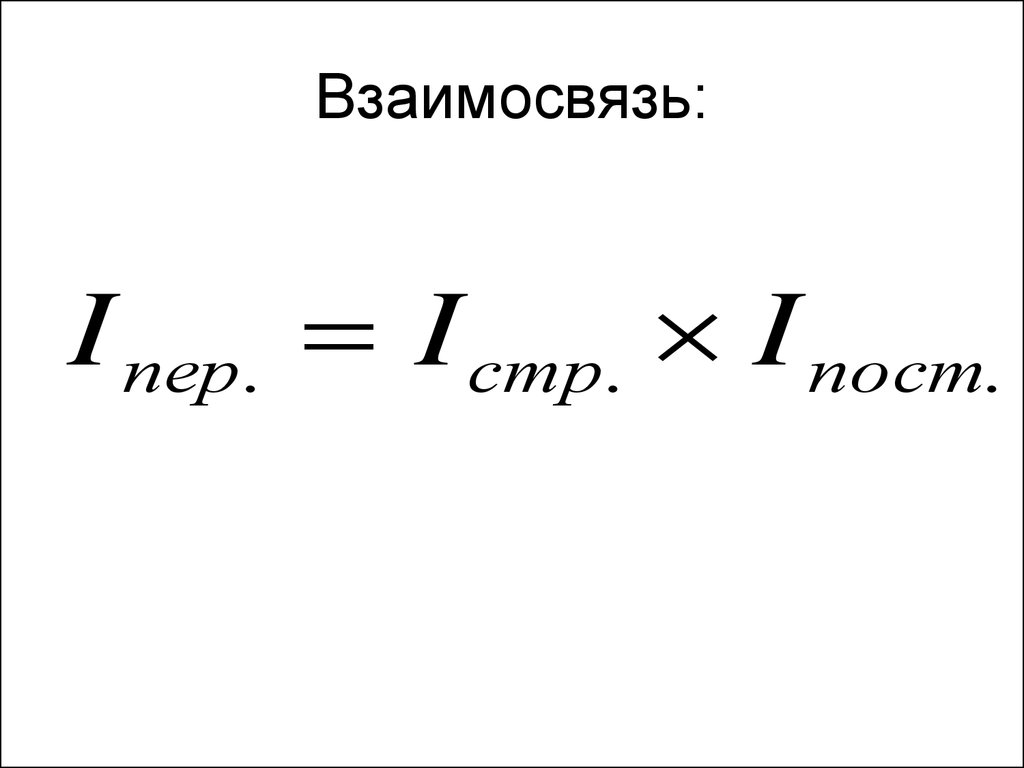












 economics
economics








