Биомехатронные системы. Лекция 1. Двойной маятник

1. БИОМЕХАТРОННЫЕ СИСТЕМЫ

2.

Лекция 1
Двойной маятник:
оптимальное управление раскачиванием и торможением
Гимнаст раскачивается на перекладине, управляя, в основном, углом в тазобедренном
суставе; момент в запястном суставе при этом весьма мал.
Человек управляет колебаниями качелей вокруг точки подвеса, перемещаясь на них
подходящим образом, в то время как в точке подвеса качелей отсутствует какой-либо
«внешний» управляющий момент. В обоих последних случаях человек надлежащим
образом использует силу тяжести.
Животные, человек могут перемещать “звенья” своего тела только одно относительно
другого.
Однако делают они это так, чтобы внешние силы, возникающие при
относительном движении, – силы взаимодействия с окружающей средой, гравитационные
силы – осуществляли движение тела как целого желаемым образом.
Например, ходьба, бег животных, ползание пресмыкающихся происходит благодаря
силам трения с опорной поверхностью. Животные “организуют” надлежащие воздействия
этих внешних сил при относительном движении звеньев тела.

3.

Другой пример

4.

Уравнения движения двойного маятника
T1
1 2
I1
2
1
1
2
vC vD r
m2vC2 I C
2
2
1
1
2
I C I 2 m2 r22 T2 m2vC2 I 2 m2 r22
2
2
T2
I 2 m2 r22 I C
xC l sin r2sin
yC l cos r2cos
xC l cos r2cos
yC l sin r2sin
vC2 xC2 yC2 l cos r2cos l sin r2sin
2
2
l 2 2 r22 2lr2 cos cos sin sin
2
l 2 2 r22 2lr2 cos
2
T T1 T2
1
2
2
I1 2 m2 l 2 2 r22 2lr2 cos I 2 m2 r22
2
1
2
I1 2 m2 l 2 2 2lr2 cos I 2
2
1
2
a11 2 2a12 cos a22
2
a11 I1 m2l 2
a12 m2lr2
a22 I 2

5.

1
2
a11 2 2a12 cos a22
2
Кинетическая энергия:
T
Потенциальная энергия:
b1 cos b2 cos
b1 m1r1 m2l g b2 m2 r2 g
Обобщенная работа:
Уравнения Лагранжа:
W L
d d T d T
0
dt d
d
d d T d T
L
dt d
d
T
a11 2a12 cos a12 cos a22 j1 ( ) j2 ( )
T
a12 cos a22 j2 ( ) a22
j1 ( ) a11 a22 2a12 cos j2 ( ) a22 a12 cos
j1 ( ) j2 ( ) 2a12 sin a12 2 sin b1 sin b2 sin
j2 ( ) a22 a12 2 sin b2 sin L
j1 ( ) a11 a22 2a12 cos - момент инерции жесткого двухзвенника

6.

K b1 sin b2 sin
j2 ( )
K
j1 ( )
j1 ( )
F ( )
0
2
T
j1 ( ) j2 ( )
d j2 ( ) d d
F
dt
j1 ( ) dt dt
j2 ( )
a22 a12 cos
d
d Aarctg Btg
j1 ( )
a a22 2a12 cos
2
2
0 11
A
a11 a22
K
a11 a22
a11 a22
2
a11 a22 2a12
a11 a22 2a12
B
4a122
4a122 a11 a22 2a12 a11 a22 2a12
a11 I1 m2l 2 a12 m2lr2 a22 I 2
?
a11 a22 2a12 I1 m2l I 2 2m2lr2 I1 m2l m 2m2lr2 0
2
I 2 m2 22
I 2 m2 r22 IC2
2
- теорема Штейнера
2
2 2
m2 22 m2r22 IC2
I1 m2l 2 m2 22 2m2lr2 I1 m2l 2 m2 r22 2m2lr2
I1 m2 l 2 r22 2lr2 I1 m2 l r2 0
2
2 r2

7.

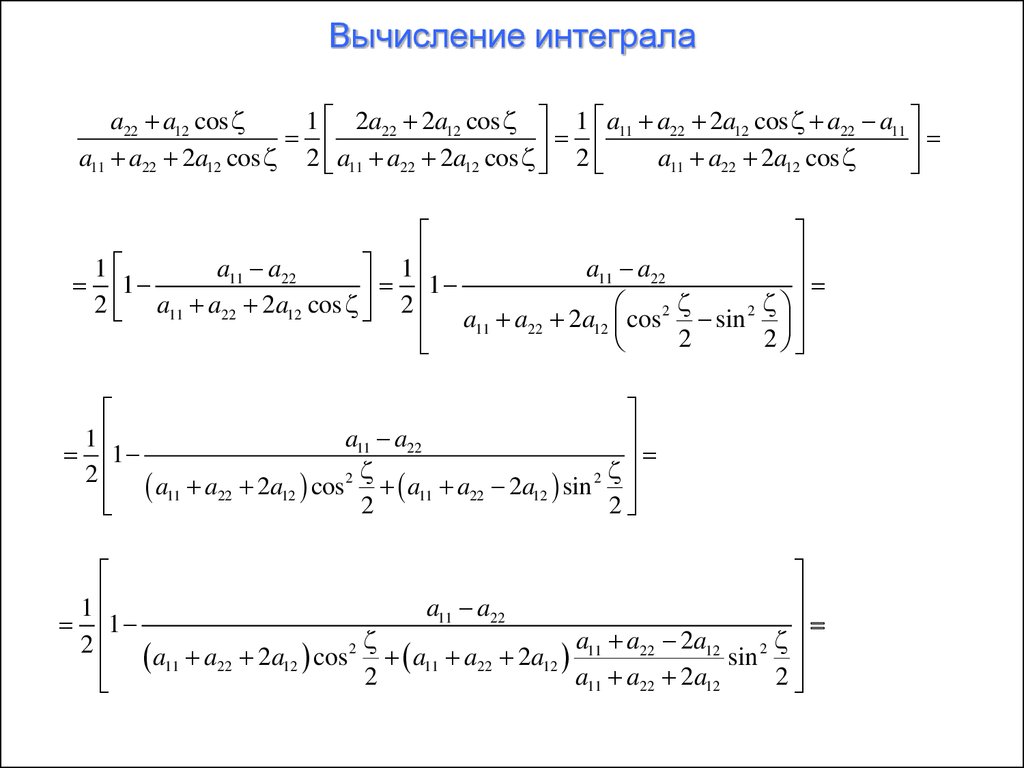
Вычисление интеграла
a22 a12 cos
1 2a22 2a12 cos 1 a11 a22 2a12 cos a22 a11
a11 a22 2a12 cos 2 a11 a22 2a12 cos 2
a11 a22 2a12 cos
1
a11 a22
a11 a22
1
1
1
2 a11 a22 2a12 cos 2
a11 a22 2a12 cos 2 sin 2
2
2
a11 a22
1
1
2
2
2
a11 a22 2a12 cos a11 a22 2a12 sin
2
2
a11 a22
1
1
a11 a22 2a12
2
2
2
sin
a11 a22 2a12 cos a11 a22 2a12
2
a11 a22 2a12
2

8.

1 AB
a11 a22
1
1
1
1
2 a11 a22 2a12 cos 2 B 2sin 2 2 2 cos 2 B 2sin 2
2
2
2
2
A
0
a11 a22 2a12
a11 a22
, B
, AB
2
a11 a22 2a12
a11 a22 2a12
a11 a22 4a122
a11 a22
1
1
1
1
1
1
AB
A
B
2
2
1 B 2 tg 2 2 cos 2
1 B 2 tg 2
2 cos 2
2
2
2
2
d
A
arctg
B
tg
d 2
2
j2 ( )
a22 a12 cos
d
d Aarctg Btg F
j1 ( )
a a22 2a12 cos
2
2
0 11
F 0 0

9.

Приведённый угол
K b1 sin b2 sin
j2 ( )
K
j1 ( )
j1 ( )
K
T
j1 ( ) j2 ( )
d j2 ( ) d d
F
dt
j1 ( ) dt dt
Вместо угла введем новую переменную p:
p F
p F
Если 0, то p, поскольку F 0 0
p
K
j1 ( )
K f p,
f p, b1 sin p F b2 sin p F
dK f ( p, ) j1 ( )
dp
K
min max
min , max const
min , max ( , )

10.

Оптимальное управление, раскачивающее маятник
Начальное состояние: p(0) 0,
Если (0) 0, то
K (0) 0
(0) p(0)
Постановка задачи:
max[ p(t1 )]
min max
K (t1 ) 0
t1 0
Если 0, то p(t ) (t ) и p(t1 ) p(0) (0)

11.

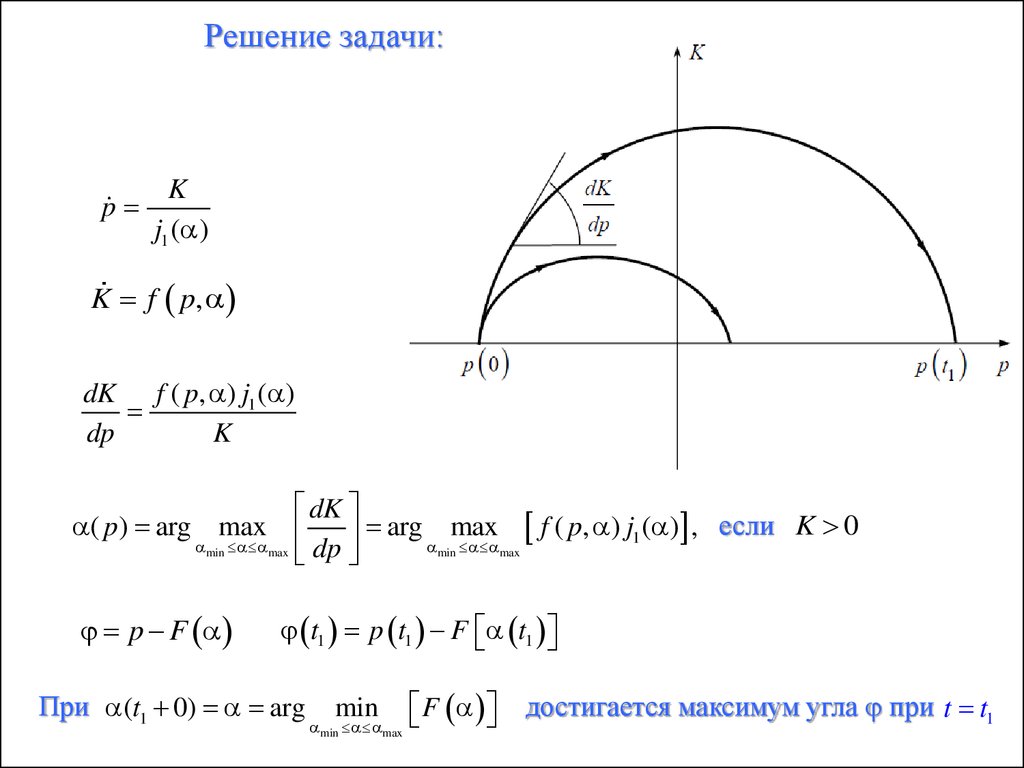
Решение задачи:
p
K
j1 ( )
K f p,
dK f ( p, ) j1 ( )
dp
K
dK
( p) arg max
arg max f ( p, ) j1 ( ) , если K 0
min max
min max
dp
p F
t1 p t1 F t1
При (t1 0) arg
min
min max
F
достигается максимум угла при t t1

12.

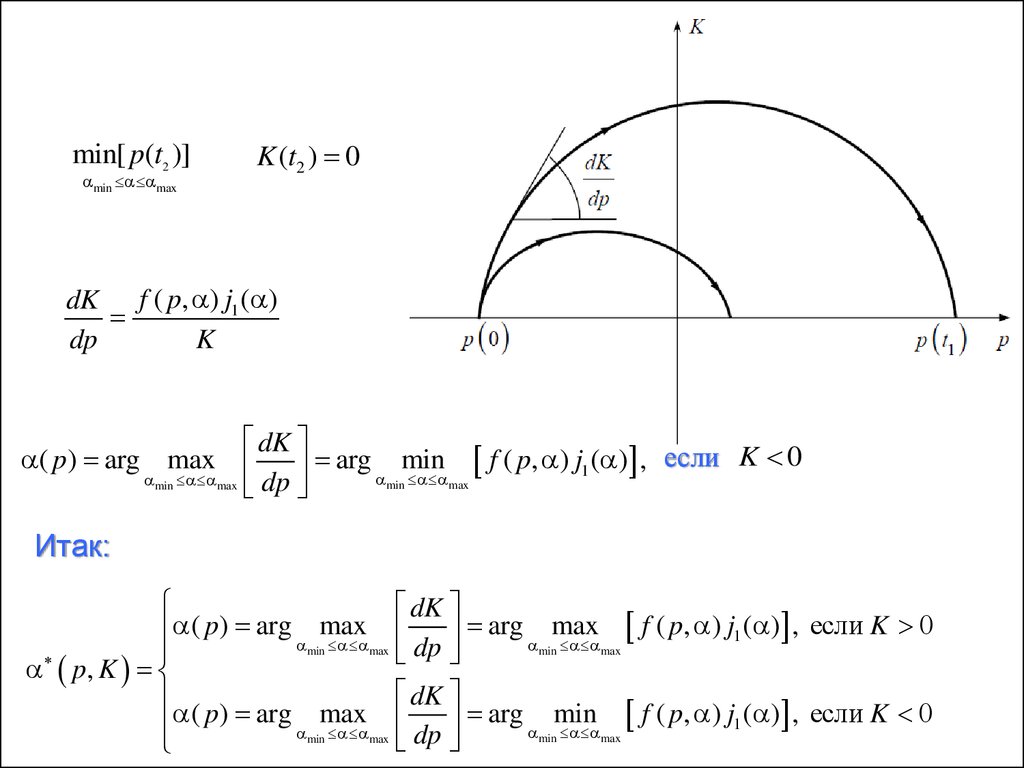
min[ p(t2 )]
min max
K (t2 ) 0
t2 0
dK f ( p, ) j1 ( )
dp
K
dK
arg min f ( p, ) j1 ( ) , если K 0
min max
min max
dp
( p) arg max
Итак:
dK
(
p
)
arg
max
f ( p, ) j1 ( ) , если K 0
dp arg minmax
min max
max
p, K
( p) arg max dK arg min
f ( p, ) j1 ( ) , если K 0
dp
min max
min max