Цветовые системы

1. Цветовые системы

Хроматический (окрашенный) свет характеризуется следующими
параметрами:
- электромагнитным спектром, охватывающим диапазон длин волн
примерно от 380 до 780 нм;
- потоком лучистой энергии, излучаемой в единицу времени и измеряемой
в ваттах;
- световым потоком, оцениваемым по зрительному ощущению и
измеряемым в люменах;
- светлотой, цветовым тоном и насыщенностью, отражающими уровень
производимого световым потоком зрительного ощущения и определяющей
цветовое восприятие.

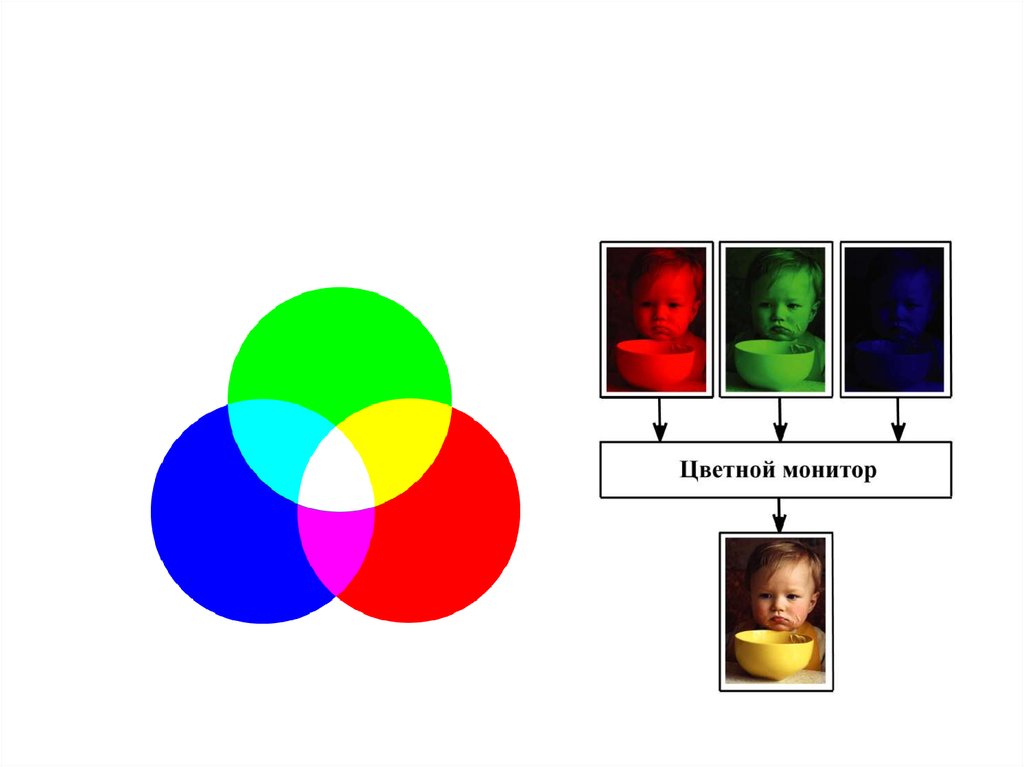
2. Цветовая система RGB

Субъективные измерения цветовых координат смешения трех чистых
спектральных цветов (при одинаковой мощности монохроматических
излучений с равной энергией) привели к разработке принятого
Международной комиссией по освещению (МКО) стандартного набора
монохроматических первичных основных цветов: красного (R) с длиной
волны 700 нм, зеленого (G) – 546,1 нм и синего (B) – 435,8 нм.
В соответствии с теорией цветового зрения предполагается наличие в
сетчатке глаза светочувствительных приемников (колбочек) трех видов: 65%
из них воспринимают красный свет, 33% - зеленый свет и 2% - синий свет.
R
max
( ) R ( ) d ,
min
G
max
( )G ( ) d ,
min
B
max
( ) B ( ) d ,
min

3. Цветовая система RGB

Трехцветное выражение цвета
опирается на установленный
опытным путем факт, что для
большинства встречающихся в
природе цветов можно
выполнить зрительное
уравнивание со смесями взятых
в различных пропорциях только
трех основных цветов. Эта
связь взаимно однозначна
независимо от спектрального
распределения излучения
данного цвета.
X
x
;
X Y Z
Y
y
;
x y z 1.
X Y Z
Z
z
.
X Y Z

4. Полноцветное и палитровое представление

Система
Значения RGB компонент
счисления
Шестнадцате-
0
33
66
99
СС
FF
0
51
102
153
204
255
ричная
Десятичная

5.

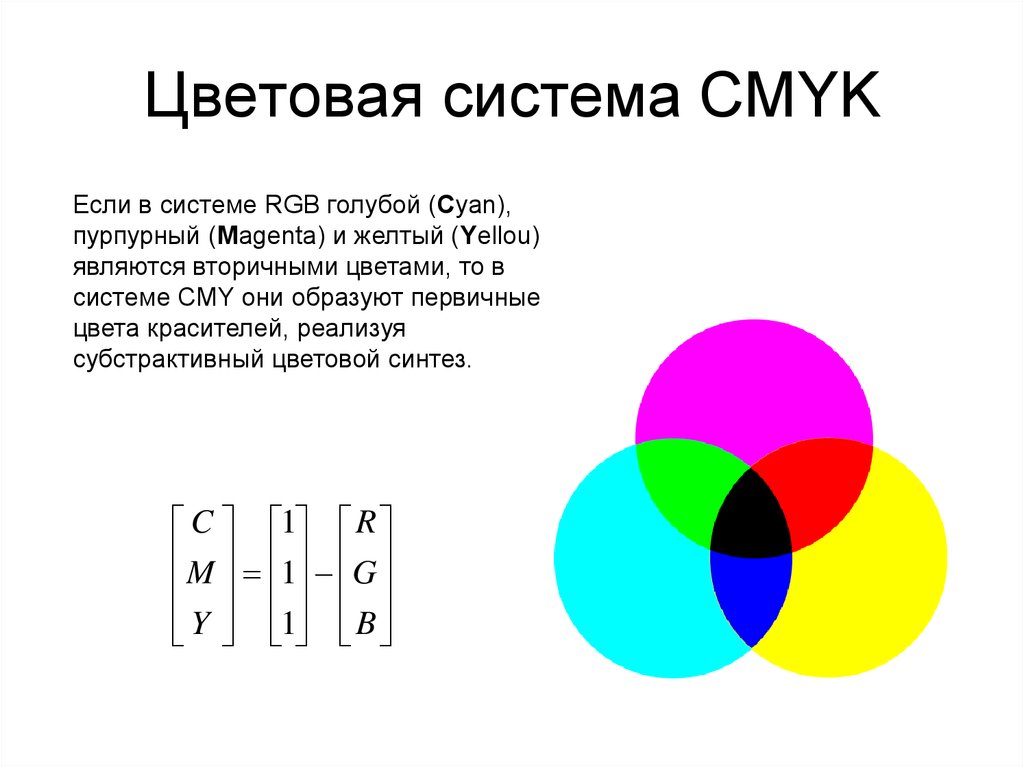
6. Цветовая система CMYK

Если в системе RGB голубой (Cyan),
пурпурный (Magenta) и желтый (Yellou)
являются вторичными цветами, то в
системе CMY они образуют первичные
цвета красителей, реализуя
субстрактивный цветовой синтез.
C 1 R
M 1 G
Y 1 B

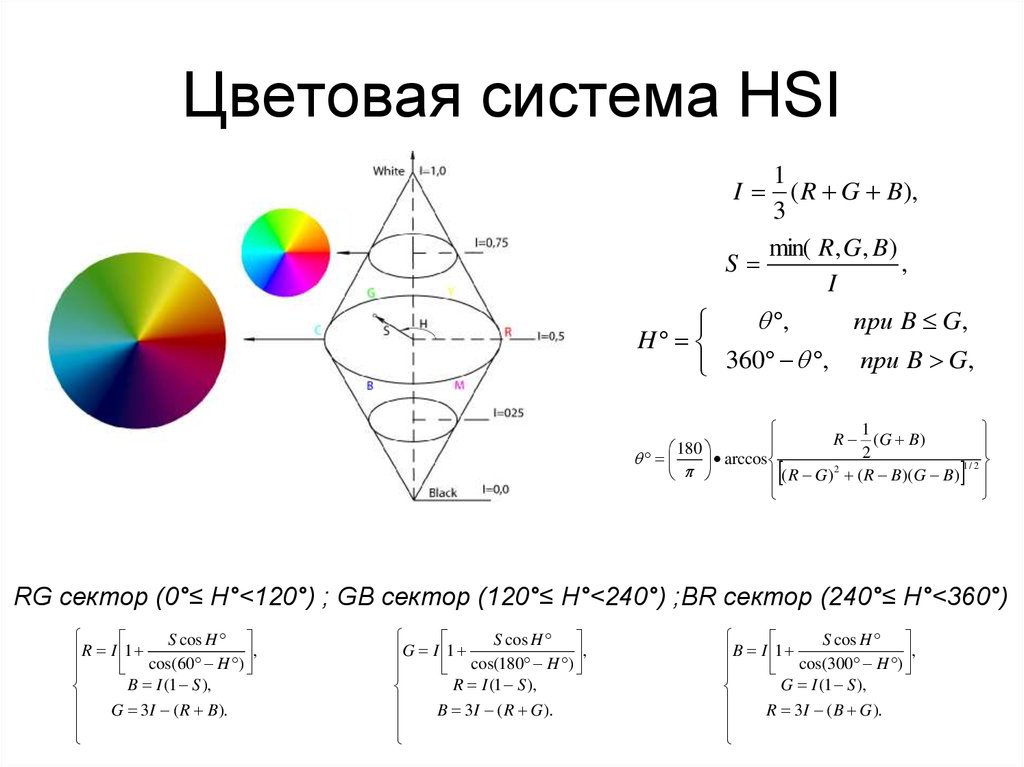
7. Цветовая система HSI

1
I ( R G B ),
3
min( R, G , B)
S
,
I
,
при B G,
H
360 , при B G,
1
R (G B )
180
2
arccos
1
/
2
2
( R G ) ( R B)(G B)
RG сектор (0°≤ H°<120°) ; GB сектор (120°≤ H°<240°) ;BR сектор (240°≤ H°<360°)
S cos H
R I 1
,
cos(60 H )
B I (1 S ),
G 3I ( R B).
S cos H
G I 1
,
cos(180 H )
R I (1 S ),
B 3I ( R G ).
S cos H
B I 1
,
cos(300 H )
G I (1 S ),
R 3I ( B G ).

8. Цветовые системы YUV, YIQ, YDRDB, YCRCB

E Y = 0,299 E R + 0,587 E G + 0,114 E B;
E R-Y = E R - E Y;
E B-Y = E B - E Y.
E I = -0,27 E B-Y + 0,74 E R-Y;
E Q = 0,41 E B-Y + 0,48 E R-Y;
E U = 0,493 E B-Y;
E V = 0,877 E R-Y.
D B = 1,5 E B-Y;
D R = -1,9 E R-Y.
CR = round(112 E R-Y/0,701 + 128);
CB = round(112 E B-Y/0,886 + 128),

9. Статические эталонные изображения

10. Статические эталонные изображения

11. Цифровое представление видеоинформации

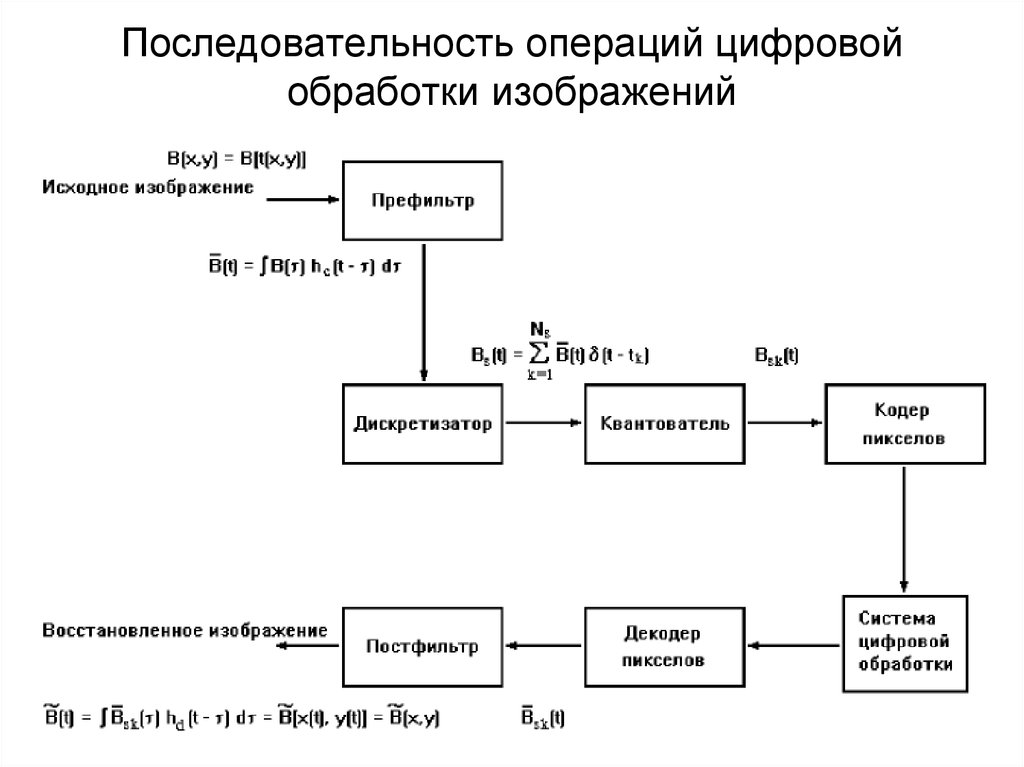
B(x, y) – плотность излучаемой световой энергии в точке (x, y)

12. Последовательность операций цифровой обработки изображений

13. Фурье-преобразование, теорема о дискретизации

B(x, y)
B(x, y) в координатах 0 x X; 0 y Y:
c
mn
mn (x, y),
m n
Y X
1
nx my
exp 2 i (
),
X
Y
XY
mn (x, y)
cmn =
( x,y) dx
mn ( x,y) kl
mn ( x,y) dx
dy,
0 0
Y X
B(x,y)
dy = mk nl.
0 0
f x
n
≤FX - периодов на единицу длины по оси х
X
f y
m
≤F - периодов на единицу длины по оси у
Y Y
f s f 2x f 2y . - пространственная частота двумерного изображения
M
B (x, y)
N
cmn mn (x, y)
m M n N
B (xk , y k )
M
fx
2N 1
Fx ;
2X
fy
2M 1
Fy ,
2Y
N
cmn mn (xk , yk ).
m M n N
Количество ненулевых коэффициентов cmn равно NS= (2M+1)(2N+1)=NX•NY

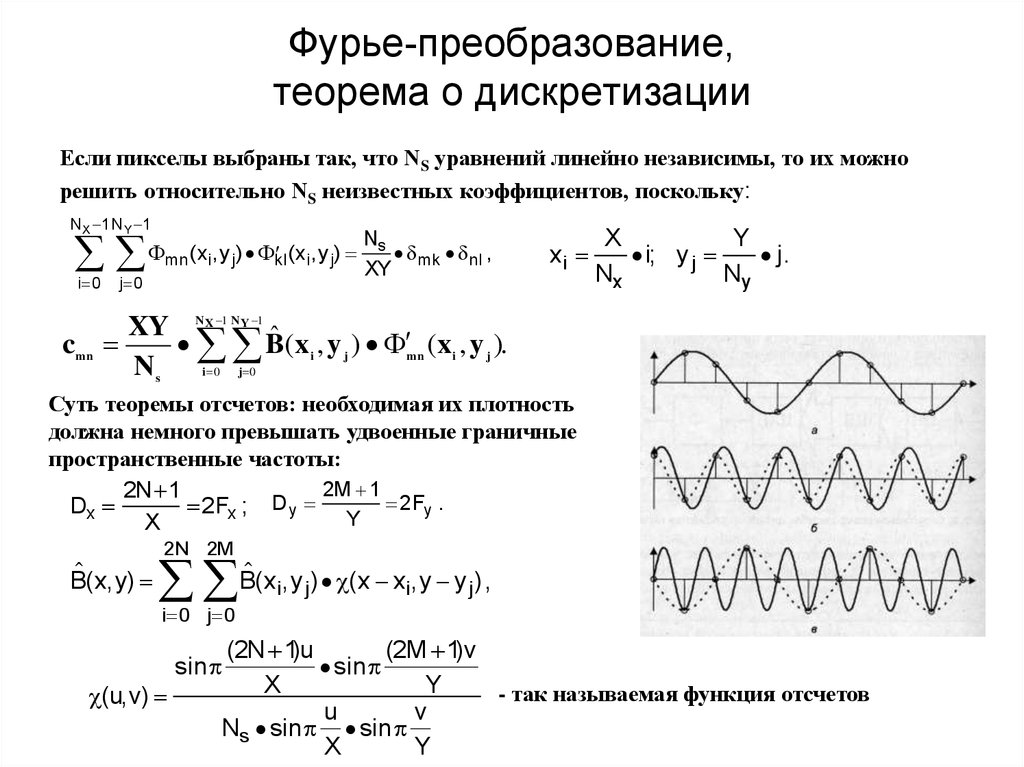
14. Фурье-преобразование, теорема о дискретизации

Если пикселы выбраны так, что NS уравнений линейно независимы, то их можно
решить относительно NS неизвестных коэффициентов, поскольку:
NX 1 N Y 1
i 0
mn (xi, y j) kl
(xi, y j)
j 0
Ns
,
XY mk nl
xi
X
Y
i; y j
j.
Nx
Ny
XY N X 1 NY 1 ˆ
cmn
B(x i , y j ) mn (x i , y j ).
N s i 0 j 0
Суть теоремы отсчетов: необходимая их плотность
должна немного превышать удвоенные граничные
пространственные частоты:
2M 1
2N 1
2 Fy .
Dx
2 Fx ; D y
Y
X
2N 2M
B (x, y)
B (x , y ) (x x , y y ),
i
j
i
j
i 0 j 0
(u, v)
(2N 1)u
(2M 1)v
sin
X
Y
- так называемая функция отсчетов
u
v
Ns sin sin
X
Y
sin

15. Функция отсчетов, эффект Гиббса

16. Изображение, изменяющееся во времени

Теорема отсчетов
B(x, y)
c
mnp mnp (x, y, t),
m,n,p
mnp (x, y, t)
1
XYT
exp 2 i (
nx my pt
),
X
Y
T
T Y X
cmnp =
B(x,y,t)
mnp ( x,y,t) dx
0 0 0
p
- временная частота.
T
dy dt,

17. Квантование Импульсно-кодовая модуляция (ИКМ)

Задача квантования аналоговой величины uн≤u≤uк необходимо выбрать
такой набор пороговых уровней dj и уровней rj, что при dj u < dj+1 "u"
заменяется на число rj
Мера ошибки:
uk
d j 1
e (u uˆ ) p(u)du (u rj ) 2 p(u)du,
J
2
j 0
uн
dj
Если число уровней квантования велико
uj
dj
(uk uн )
uн
uk
uн
3
3
du
p(u )
du
p (u )
u’н ,
uj
d dj
j (uk uн )
uн , j 0,1,.....,J ; r j j 1
, j 0,1,.....,J 1.
J
2

18. Квантование Импульсно-кодовая модуляция (ИКМ)

Квантование Ллойда-Макса
rj 2d j rj 1;
d j 1
d u p(u )du .
r j
d j 1
j
p (u )du
dj
d j 1
d j 1
2
emin u p(u )du rj p(u )du .
j 0 d j
dj
J 1
Распределения
Гаусса и
Лапласа
u2
1
p(u)
exp 2
2
2
u 2
p(u )
exp
2
1

19.

20.

21.

22.

23.

24.

25.

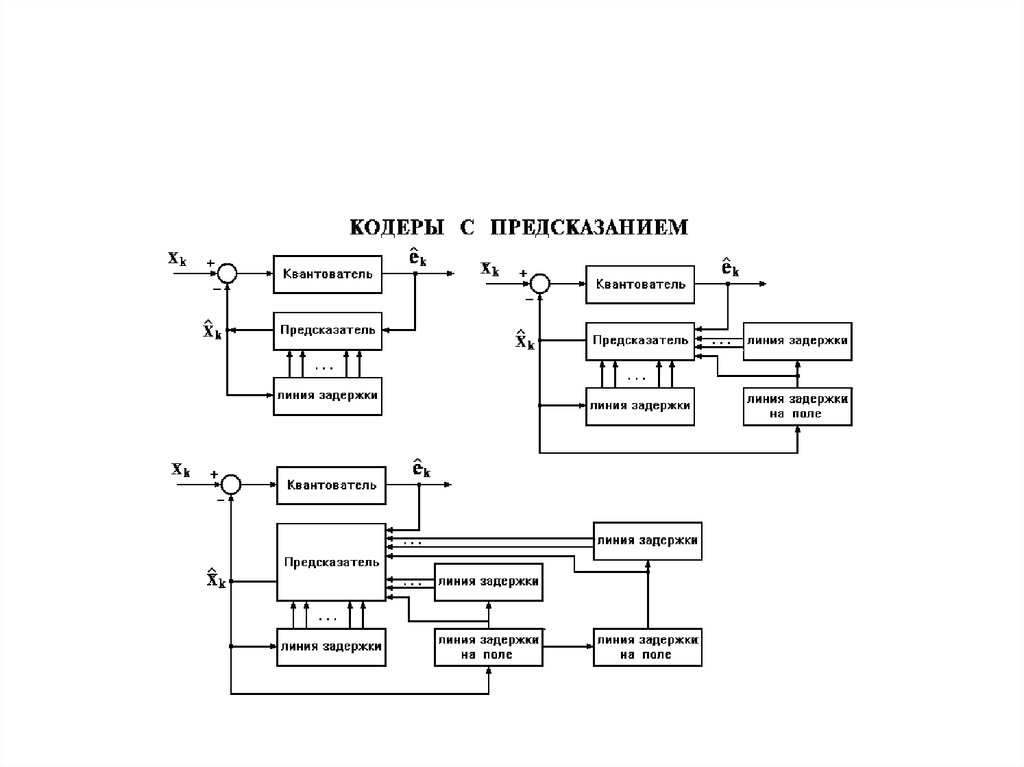
26. Групповое кодирование изображений

Дискретные линейные
ортогональные преобразования

27. Кодирование с дискретным преобразованием

N
c j t mj bm , 1 j N
m 1
T t mj
c T b,
b T 1 c

28. Дискретные линейные ортогональные преобразования

• Дискретное преобразование Фурье (ДПФ)
• Действительное дискретное преобразование
Фурье (ДДПФ)
• Преобразование Хаара
• Преобразование Уолша-Адамара
• Дискретное синусное преобразование
• Дискретное косинусное преобразование (четное и
нечетное)
• Преобразование Кахунена-Лоэва (Хоттелинга)
• Наклонное преобразование
• Полиномиальные преобразования (Лежандра,
Чебышева)

29. Дискретные линейные ортогональные преобразования

N1
N2
F (m1 , m2 ) X (n1 , n2 ) A(n1 , n2 ; m1 , m2 )
n1 1 n2 1
N1
N2
X (n1 , n2 ) F (m1 , m2 ) B(n1 , n2 ; m1 , m2 )
m1 1 m2 1
N1
N2
A(n , n ; m , m ) A ( j , j ; m , m )
B(n , n ; m , m ) B ( j , j ; m , m ) (n
m1 1 m2 1
1
2
1
2
1
2
1
2
N1
N2
1
m1 1 m2 1
N1
N2
2
1
2
1
2
1
2
1
j1 , n2 j2 )
A(n , n ; m , m ) A (n , n ; k , k )
B(n , n ; m , m ) B (n , n ; k , k ) (m k , m
m1 1 m2 1
1
2
1
2
1
2
1
N1
2
N2
m1 1 m2 1
1
2
1
2
1
2
1
A(n1 , n2 ; m1 , m2 ) AC (n1 , m1 ) AR (n2 , m2 )
B(n1 , n2 ; m1 , m2 ) BC (n1 , m1 ) BR (n2 , m2 )
2
1
1
2
k2 )

30. Требования к преобразованиям для использования в видеокодировании

• Обратимость преобразования
• Концентрация энергии преобразования
в меньшем числе коэффициентов
• Декорреляция коэффициентов
преобразования
• Относительная простота вычислений
прямого и обратного преобразований

31. Дискретное преобразование Фурье

1
2 i
1 N 1 N 1
2 i
F (u, v) X ( j, k ) exp [
(u j vk )] X (i, j )
N
N j 0 k 0
N
N 1 N 1
F (u, v) exp[ N
(u j vk )]
u 0 v 0
AR (n, m) AC (n, m) tn
1
2 i
1
2
i
2
exp(
nm)
cos
nm
sin
nm
N
N
N
N
N
N
BR (n, m) BC (n, m) tn*
1
2 i
1
2
i
2
exp(
nm)
cos
nm
sin
nm
N
N
N
N
N
N
t0R t0 ;
P (u )
1
2 i
X n exp(
nu )
N
N n 0
N 1
1 N 1
2
i N 1
2 i
X n cos
nu
X n sin
nu
N
N
N n 0
N n 0
P(1 m) P* ( N m 1), 0 m N 2
.......................
t 2Rn 1 2 Re t n ;
t 2Rn 2 Im t n ;
.......................
2 Im t N 1 , N 2 M 1,
2
t NR
t N , N 2M .
2

32. Дискретное преобразование Фурье

33. Преобразование Хаара

H4
1
1 1
1
1
1
1
4 2 2
0
0
1
1
2
0
2
0
0
1 0
H16
2 2
16
0
0
0
0
0
0
0
1
H8
8
1
1
0
0
2 2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
0
0
0
0
2
2
0
0
0
0
2
2
0
0
0
0
2
2
0
0
0
0
0
0
0
0
2
2 2 2
0
0
0
0
0
0
0
0
2 2
0
0
0
0
2
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
2
2
2
2
0
0
0
0
0
0
0
2
2
2
0
0
0
0
0
0
0
0
0
2
2
2
2
0
0
0
0
0
0
0
0
0
2
2
0
0
0
0
0
0
0
0
0
2
2
2
2
2
0
0
2
2
0
0
0
0
0
0
0
0
0
2
2
0
0
0
0
0
2
2
2
2
0
2
0
0
2
0
0
0
2
0
0
0
0
0
0
0
2 2
1
2
2 2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2 2
2 2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2 2
2 2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2 2
2 2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2 2
2 2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2 2
2 2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2 2
2 2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2 2
1

34. Преобразование Хаара

35. Преобразование Уолша-Адамара

Преобразование УолшаАдамара
H2
H4
1 1 1
2 1 1
1 H2
2 H2
H2
H2
H2N
1 HN
2 HN
1
1
1
1
1 1 1 1 1
2 1 1 1 1
1 1 1 1
HN
HN
0
3
2
1
1 N 1 N 1
F (u , v) X ( j, k ) ( 1) q ( j ,k ,u ,v ) ,
N j 0 k 0
n 1
q ( j , k , u , v) [ g i (u ) ji g i (v) ki ],
1
H4y
1
1
1
1 1 1 1 1
2 1 1 1 1
1 1 1 1
0
1
2
3
i 0
g 0 (u ) u n 1 ;
g1 (u ) u n 1 un 2 ;
g 2 (u ) u n 2 u n 3 ;
.............................
g n 1 (u ) u1 u0 ;
N 2 n , ui , vi , ji , ki биты

36. Преобразование Уолша-Адамара

Преобразование УолшаАдамара

37. Преобразование Уолша-Адамара

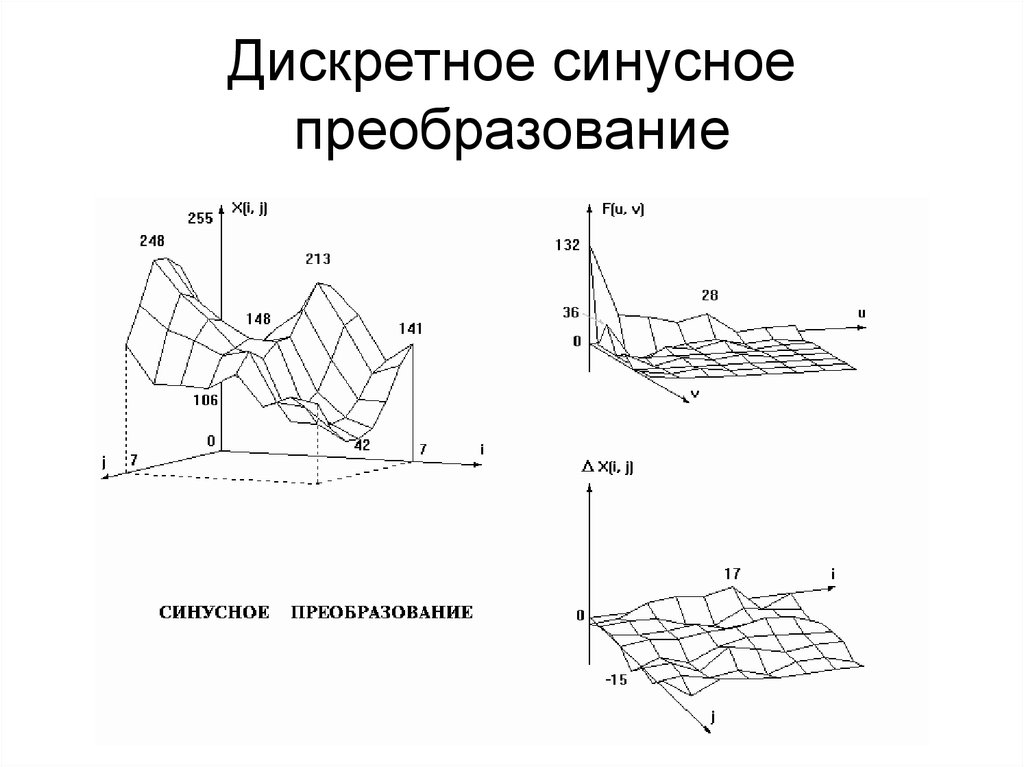
Преобразование УолшаАдамара

38. Дискретное синусное преобразование

2 N 1 N 1
( j 1)(u 1)
(k 1)(v 1)
F (u, v)
X ( j, k ) sin
sin
N 1 j 0 k 0
N 1
N 1

39. Дискретное синусное преобразование

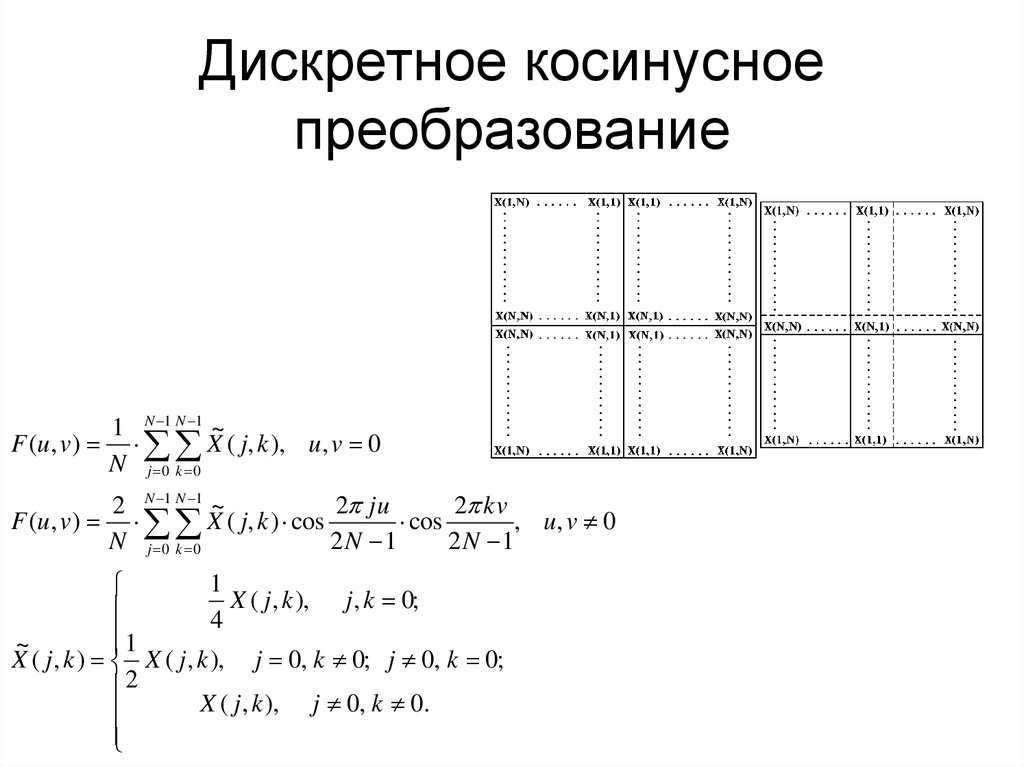
40. Дискретное косинусное преобразование

1 N 1 N 1 ~
F (u , v) X ( j, k ), u , v 0
N j 0 k 0
2 N 1 N 1 ~
2 ju
2 kv
F (u , v) X ( j, k ) cos
cos
, u, v 0
N j 0 k 0
2N 1
2N 1
1
X ( j , k ), j , k 0;
4
~
1
X ( j , k ) X ( j , k ), j 0, k 0; j 0, k 0;
2
X ( j , k ), j 0, k 0.

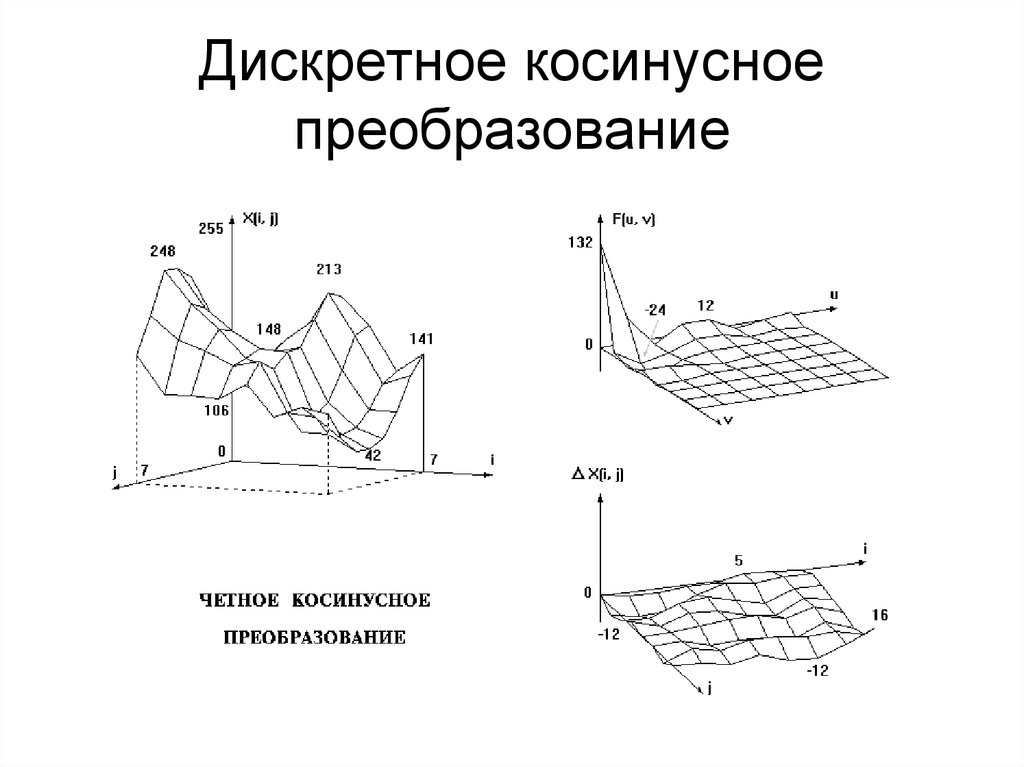
41. Дискретное косинусное преобразование

N 1 N 1
2
u (2 j 1)
v(2k 1)
F (u, v) C (u ) C (v) X ( j, k ) cos
cos
,
N
2N 1
2N 1
j 0 k 0
1
, n 0,
C ( n) 2
1, n 0.
2 N 1 N 1
u (2 j 1)
v(2k 1)
X ( j , k ) C (u ) C (v) F (u, v) cos
cos
N u 0 v 0
2N 1
2N 1
Степень
сжатия
Хаара
4.0
4.5
5.0
2.38(7)
2.56(7)
2.72(7)
Среднеквадратичные (максимальные)
ошибки преобразований
УолшаСинусное
Косинусное
Адамара
2.42(7)
2.04(5)
1.61(4)
2.82(8)
2.22(7)
1.61(5)
2.77(9)
2.34(6)
1.61(6)

42. Дискретное косинусное преобразование

43. Преобразование Кархунена-Лоэва

Преобразование КархуненаЛоэва

44. Преобразование Кархунена-Лоэва

Преобразование КархуненаЛоэва

45. Визуальная избыточность изображений

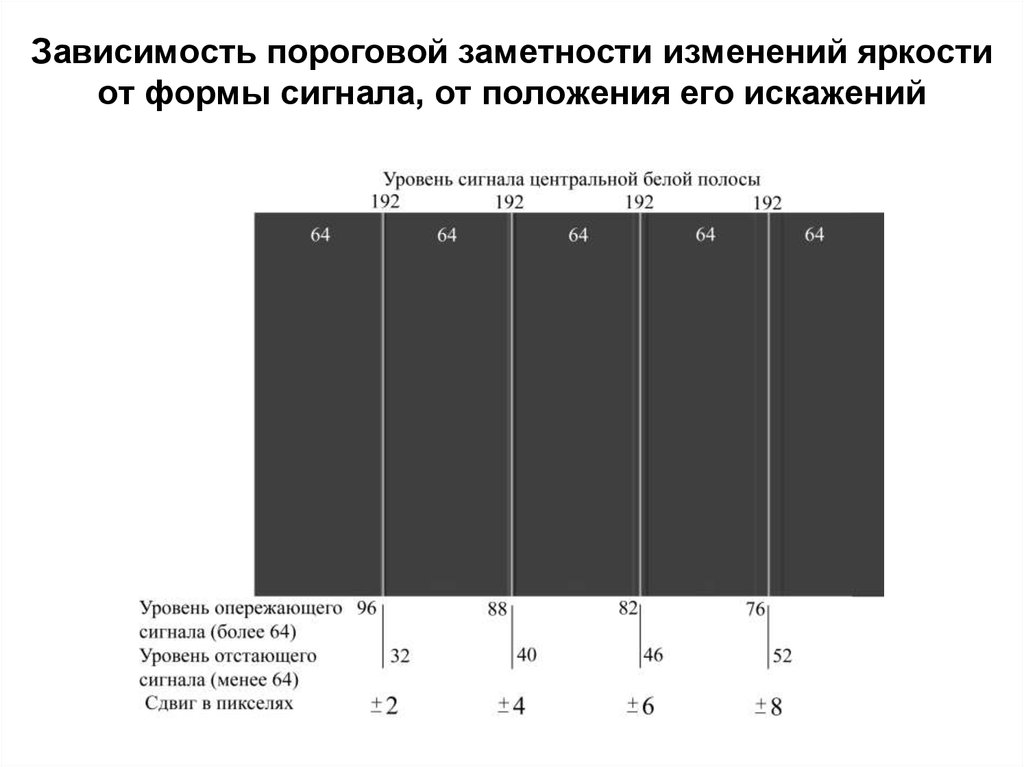
Устранение визуальной избыточности изображений является
основным резервом сокращения передаваемой информации.
Ошибки в изображении заметны глазом, если они превышают
«порог заметности». Существуют различные подходы к
определению «порога заметности» в различных условиях
наблюдения изображений.
Заметность искажений изображений зависит от ряда факторов
объективного и субъективного характера:
- оптической неидеальности зрения,
- непроизвольных движений глаза (смещение точки внимания
каждые 0,3-0,7 сек и даже чаще) при восприятии неподвижных
изображений;
- средней яркости фона;
- временных и пространственных вариаций яркости в
окрестности рассматриваемого элемента;
- пространственной и временной формы сигнала изображения и
др.

46. Заметность изменений яркости далеко расположенных деталей

47. Заметность изменений яркости близко расположенных деталей

Детали на равномерном фоне
Детали на измененном фоне

48. Изображение вертикальных белых линий, расположенных на различных расстояниях от белых широких полос (эффект пространственного

маскирования)

49. Зависимость пороговой заметности изменений яркости от формы сигнала, от положения его искажений

50. Специфические особенности восприятия цветов

На визуально воспринимаемый цвет влияют следующие факторы:
- спектральный состав света, который излучается источником;
- спектральное распределение излучения, попадающего в глаз
наблюдателя от всех объектов, находящихся в поле зрения;
- пространственное распределение и форма объектов;
- наличие цветовой памяти глаза (хроматическая адаптация) и др.
Восприятие цвета для источников света характеризуются тремя
факторами - светимостью, цветовым тоном и насыщенностью, для
объектов - освещенностью, цветовым тоном и насыщенностью.
Светимость характеризуется интенсивностью излучаемого источником
светового потока, а освещенность определяет долю отраженного или
пропущенного объектом падающего света.
Цветовой тон - субъективно воспринимаемый признак цвета.
Насыщенность - признак цвета, выражающий степень его отличия от
белого цвета той же яркости.
Человек способен различить примерно 12 тысяч цветностей. В
стандартном телевидении может быть воспроизведено лишь около
четырех тысяч цветностей. По этой причине можно использовать два
шестиразрядных кода, определяющих цветоразностные сигналы.
Важно знать пороги цветоразличения, т.е. минимальные изменения
цветности, различаемые глазом человека.

51. Пороги цветоразличения Мак-Адама и Райта

В 1960 г. МКО приняла диаграмму uv, переход от координат (x,y) к
координатам (u,v) осуществляется линейным преобразованием:
4x
6y
u
;v
2x 12 y 3
2x 12 y 3
Усредненный порог цветоразличения установлен равным 0,0038 единиц
шкал u, v.
Вдоль линии спектральных
цветов укладывается около 300
порогов Мак-Адама, а вдоль
линии пурпурных цветов - 130.
Вдоль периметра цветового
треугольника размещается
лишь 256 цветовых тонов.

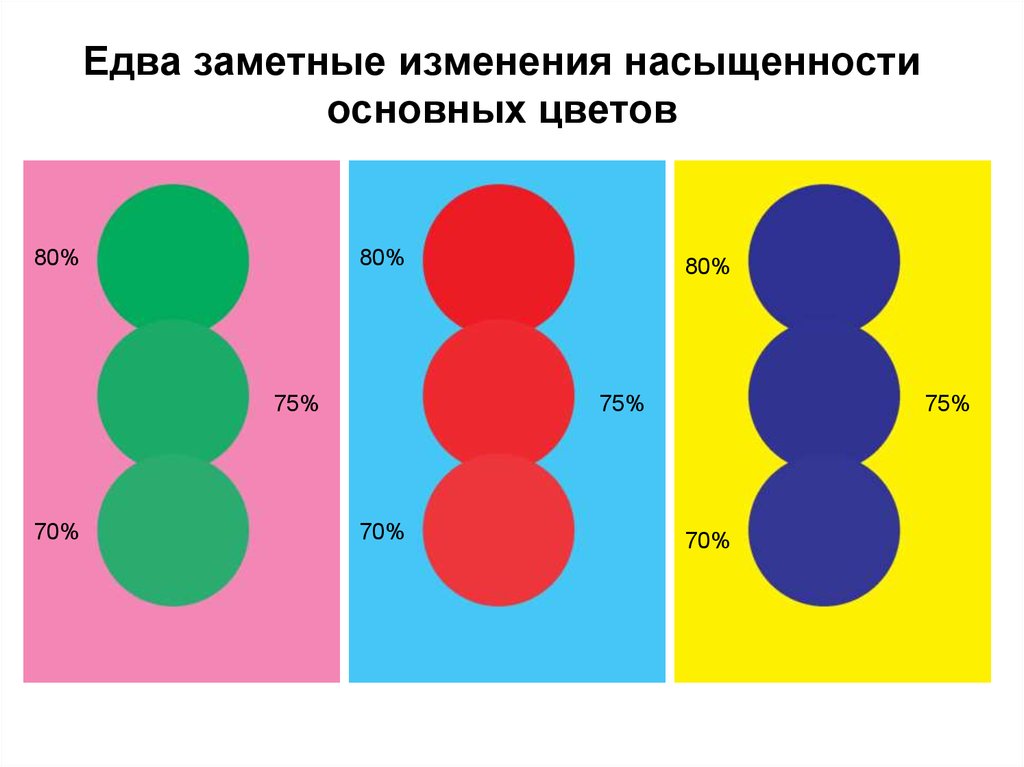
52. Едва заметные изменения насыщенности основных цветов

80%
80%
75%
70%
80%
75%
70%
75%
70%

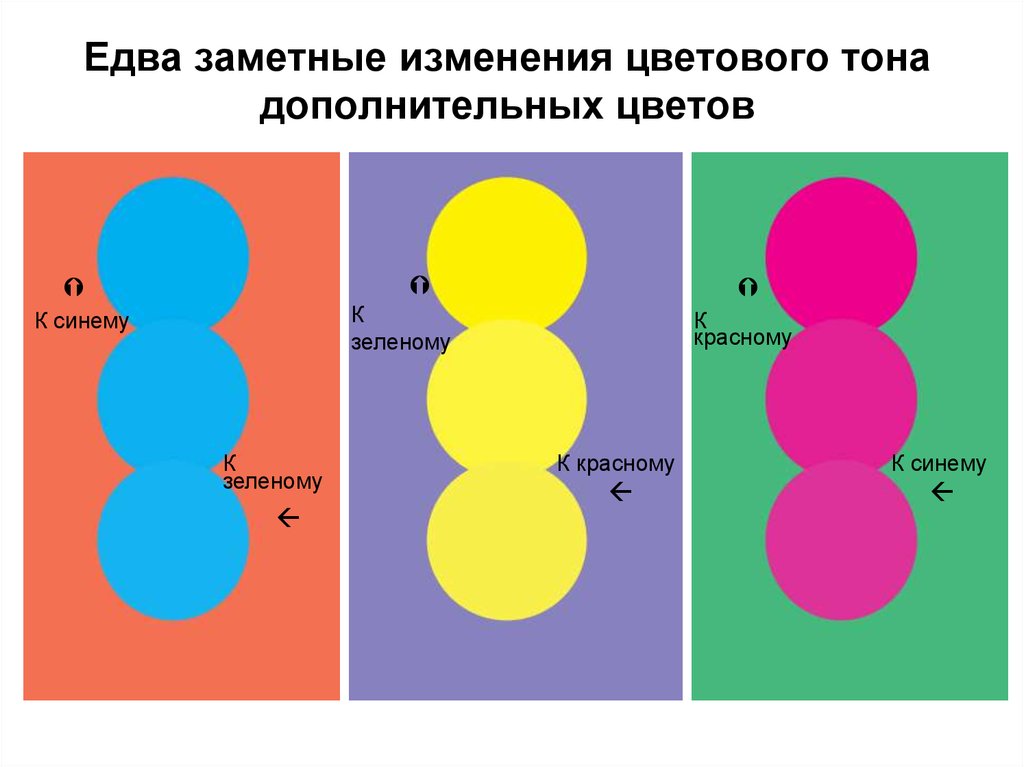
53. Едва заметные изменения цветового тона дополнительных цветов

К
зеленому
К синему
К
зеленому
К
красному
К красному
К синему

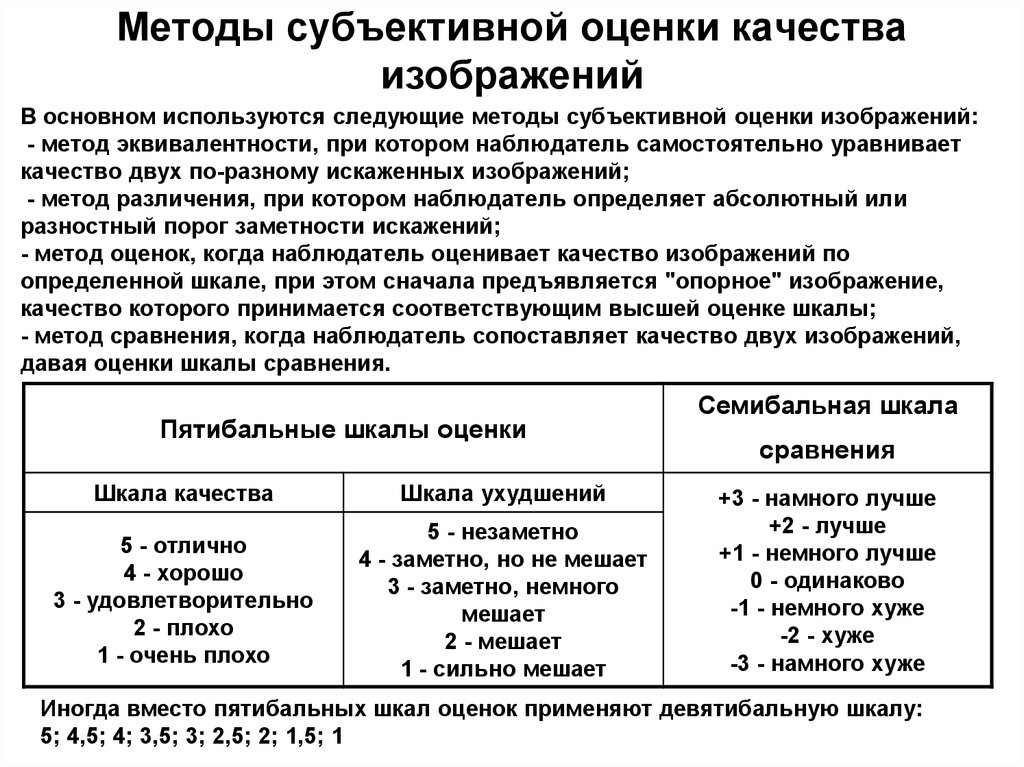
54. Методы субъективной оценки качества изображений

В основном используются следующие методы субъективной оценки изображений:
- метод эквивалентности, при котором наблюдатель самостоятельно уравнивает
качество двух по-разному искаженных изображений;
- метод различения, при котором наблюдатель определяет абсолютный или
разностный порог заметности искажений;
- метод оценок, когда наблюдатель оценивает качество изображений по
определенной шкале, при этом сначала предъявляется "опорное" изображение,
качество которого принимается соответствующим высшей оценке шкалы;
- метод сравнения, когда наблюдатель сопоставляет качество двух изображений,
давая оценки шкалы сравнения.
Пятибальные шкалы оценки
Шкала качества
Шкала ухудшений
5 - отлично
4 - хорошо
3 - удовлетворительно
2 - плохо
1 - очень плохо
5 - незаметно
4 - заметно, но не мешает
3 - заметно, немного
мешает
2 - мешает
1 - сильно мешает
Семибальная шкала
сравнения
+3 - намного лучше
+2 - лучше
+1 - немного лучше
0 - одинаково
-1 - немного хуже
-2 - хуже
-3 - намного хуже
Иногда вместо пятибальных шкал оценок применяют девятибальную шкалу:
5; 4,5; 4; 3,5; 3; 2,5; 2; 1,5; 1