Similar presentations:
Задачи по квантовой механике
1.
2.
3.
• Решением данного уравнения является функция:ce
ik r
ce
ipr
(координатная часть плоской волны).
Домножим на временную часть:
( x, y, z , t ) ce
p r Et
i
- уравнение плоской волны (волны де Бройля).
4.
Этот факт является исходным для квантовоймеханики. Свободной частице, обладающей
энергией E и импульсом p, сопоставлялась волна
де Бройля.
Коэффициент С находится из условия нормировки
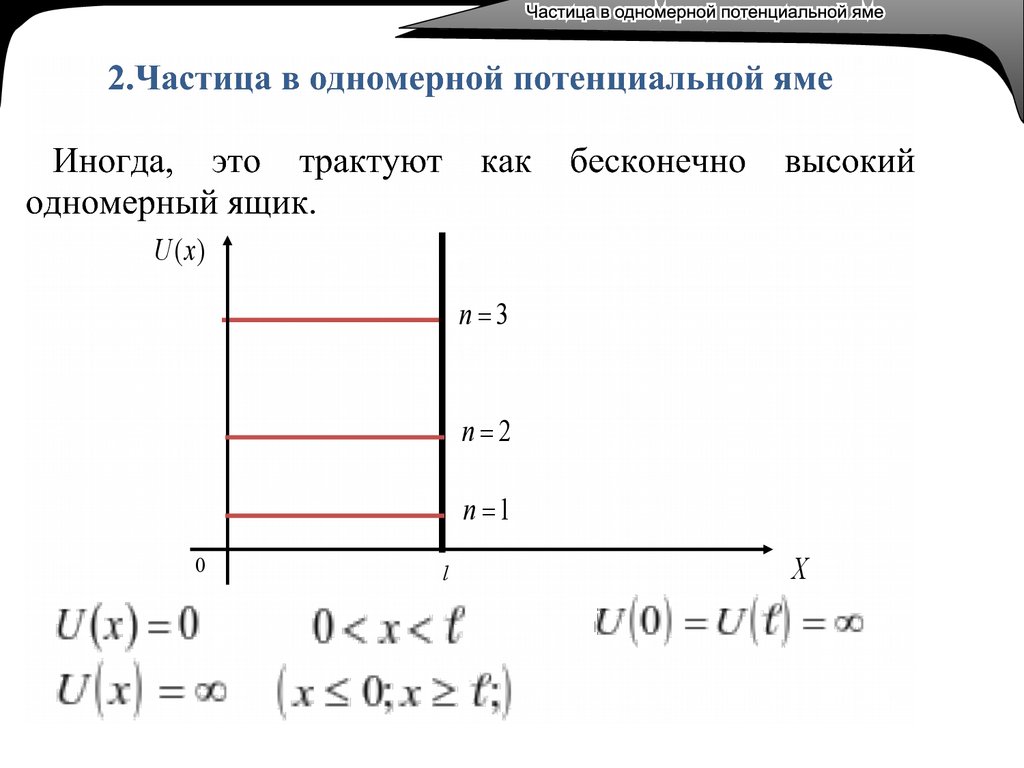
5.
U (x)n 3
n 2
n 1
0
l
X
6.
• Вероятность обнаружить частицу за пределамиямы равна нулю.
x 0; x l;
x 0
• Граничные условия:
0 0; l 0
7.
8.
• Решение ищем в видеx a sin(kx );
• Используем граничные условия
0 a sin( ) 0
(l ) a sin kl 0
• Волновое число квантуется
k n
,
n 1; 2; 3......
( 0);
n
kn
l
9.
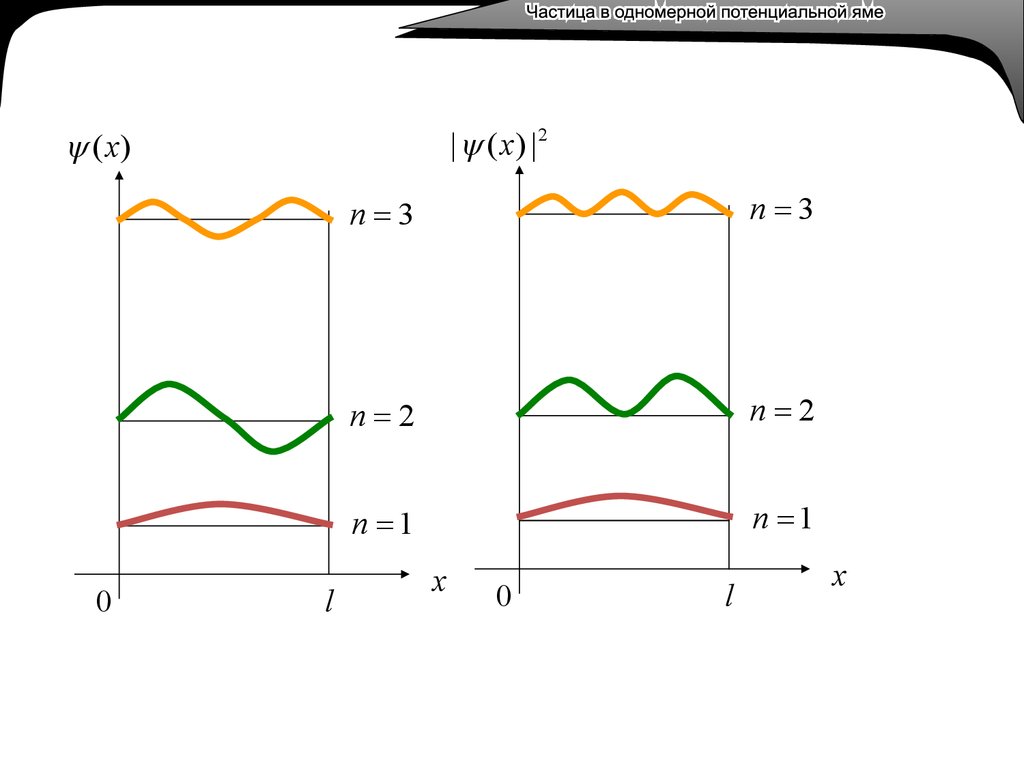
10.
• Получаем собственные волновые функции2
n
x
sin( x);
• И собственные значения энергии частицы в
потенциальной яме, исходя из того, что
kn
2
2 2 2
2mEn E n ; n 1;2;3;.....
n
2
;
2
2
m
11.
| ( x ) |2(x)
0
l
n 3
n 3
n 2
n 2
n 1
n 1
x
0
l
x
12.
13.
• Уравнение Шредингера имеет видm x
2
x 0
x E
2m
2
2
2
• Данное дифференциальное уравнение имеет
решение только для определенных значений
энергии
1
E , 0,1,2,3,.....
2
- колебательное квантовое число, на
которое накладывается правило отбора 1.
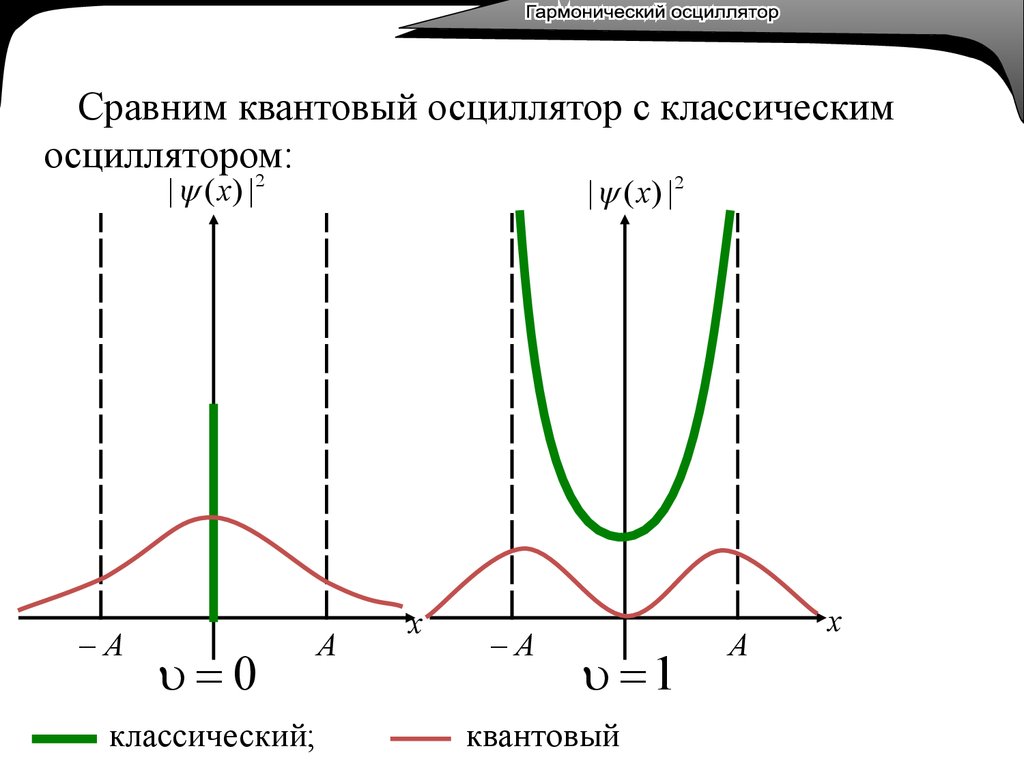
14.
Сравним квантовый осциллятор с классическимосциллятором:
2
| ( x) |
A
0
классический;
| ( x ) |2
A
x
A
1
квантовый
A
x
15.
16.
UE
U0
I
II
x
0
2 2
ψ 2 ( E U 0 )ψ 2 0
2m
2ψ 2
2m
( E U 0 )ψ 2 0
2
2m
( E U 0 ) 2
2
17.
18.
19.
UU0
I
E
II
0
x
20.
21.
• Воспользуемся достигнутыми результатами для того,чтобы рассчитать вероятность, с которой частица
может быть обнаружена под барьером в точках с
координатами от x до x dx, а также эффективную
глубину проникновения частицы x > 0.
Для упрощения расчетов положим A1 1,
принципиально ничего не меняет. Тогда
1 e kx
ik kx
2k x
e ; 2
e
ik
k i
что
22.
• Вероятность обнаружения частицы подпотенциальным барьером в точке с координатой
2
2 . Вероятность нахождения
определяется
частицы в интервале dx определяется
dP 2
dP
2
x
4k 2
2 x
dx 2
e
dx.
2
k
g ( x) называется плотностью
Отношение
dx
вероятности. Эффективной глубиной проникновения
частицы называют такую глубину, на которой
плотность вероятности уменьшается в e раз.
23.
• Эффективная глубина проникновения частицызависит от ее массы, энергии и высоты
потенциального барьера
2
4k 2
4
k
2 x
g ( x) 2
e
; g (0) 2
;
2
2
k
k
4k 2
2 xэф
g ( xэф ) 2
e
;
2
k
g (0)
1
h
2 xэф
e; e
e; 2 xэф 1; xэф
.
g ( x)
2 2 2m(U 0 E )
24.
UU0
I
E
II
0
III
l
x
25.
26.
A3A1
A1 B1 A2 B2
l
l
ikl
A
e
B
e
A
e
2
2
3
ikA1 ikB1 A2 B2
A e l B e l ikA e ikl
2
2
3
2
~e
2 l
e
2 l
e
2 (U 0 E ) 2 m
• Коэффициент пропускания зависит от массы частицы,
ширины и высоты потенциального барьера, а также от
энергии, налетающей на барьер частицы.
l






















 physics
physics








