Similar presentations:
Лекция 8. Общая физика. Элементы квантовой механики
1.
ЛЕКЦИЯ 8ПЛАН ЛЕКЦИИ
1. Гармонический квантовый осциллятор.
2. Прохождение частицы через потенциальный барьер.
. Туннельный эффект.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
1
2.
ГАРМОНИЧЕСКИЙ КВАНТОВЫЙ ОСЦИЛЛЯТОР.Сведения о гармоническом осцилляторе
из курса классической физики:
Любую колебательную систему называют осциллятором. Если
поведение осциллятора подчиняется гармоническому закону, то это
гармонический осциллятор.
Дифференциальное
уравнение
гармонических
колебаний
записывается в виде
d2x
2
0 x 0 , его решение 2
dt
x A cos 0 t .
Часто для простоты рассматривают одномерный гармонический
осциллятор.
Одномерным гармоническим осциллятором называют частицу
массой m, совершающую одномерное движение под действием
упругой силы F kx.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
2
3.
ГАРМОНИЧЕСКИЙ КВАНТОВЫЙ ОСЦИЛЛЯТОР.Упругая сила удерживает частицу в окрестности положения
равновесия, всегда направлена в сторону положения равновесия и
пропорциональна отклонению частицы от положения равновесия.
Все это означает наличие потенциальной ямы для частицы, причем
дно этой ямы находится как раз в точке равновесия.
Выражение для потенциальной
kx 2
U
энергии такой частицы имеет вид:
2
Собственная частота классического гармонического осциллятора
равна k m . Выразив отсюда k, получим
m 2 x 2
U
2
Это уравнение параболы.
Следовательно,
классический
одномерный
гармонический
осциллятор – это частица, совершающая колебания в
параболической бесконечно глубокой потенциальной яме между
точками с координатами x0 и –x0 - точками поворота.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
3
4.
ГАРМОНИЧЕСКИЙ КВАНТОВЫЙ ОСЦИЛЛЯТОР.Рассмотрим поведение микрочастицы в такой потенциальной яме –
гармонический квантовый осциллятор.
Поведение
микрочастицы
U(x)
описывается волновой функцией.
Будем считать, что упругая среда
стационарна.
E
Это значит, что коэффициент
упругости среды k есть константа,
не зависящая от времени.
Тогда возможны стационарные
частицы,
которые
- x0
x0
x состояния
0
интересно рассмотреть.
С учетом уравнения для потенциальной энергии запишем
одномерное стационарное уравнение Шредингера в виде:
2 2 m
m 2 x 2
0 . E – полная энергия осциллятора.
2 E
2
2
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
4
5.
ГАРМОНИЧЕСКИЙ КВАНТОВЫЙ ОСЦИЛЛЯТОР.2 2 m
m 2 x 2
0
2 E
2
x
2
В теории дифференциальных уравнений доказывается, что это
уравнение имеет конечные, однозначные и непрерывные решения
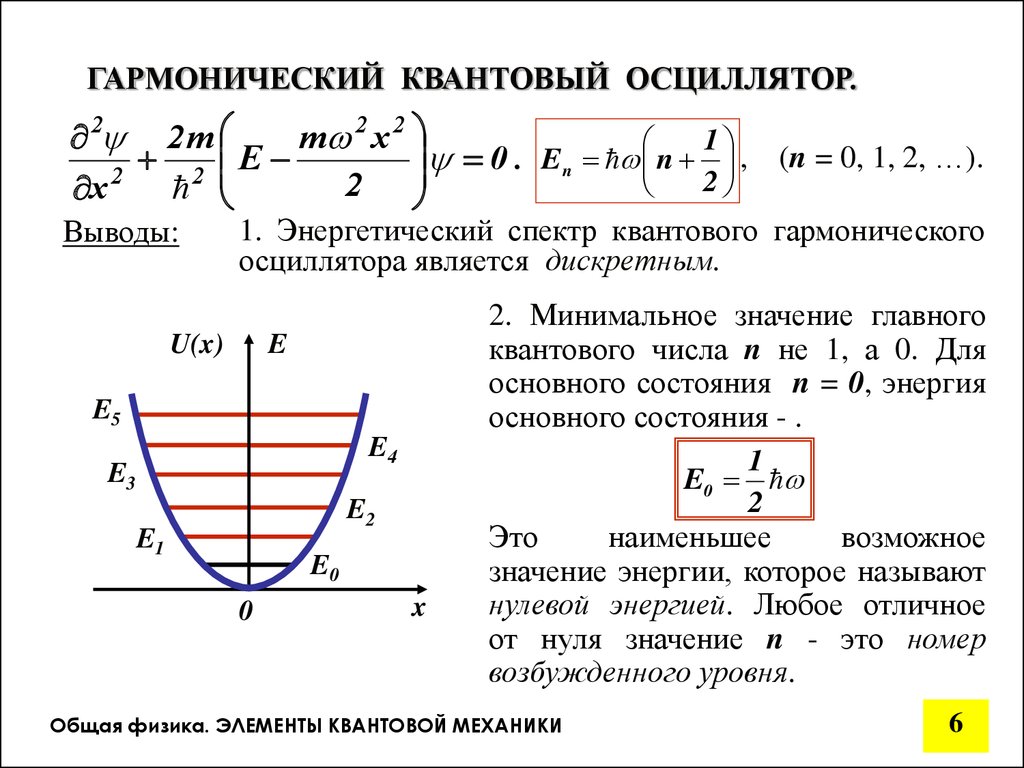
при значениях параметра E, равных
1
En n ,
2
E
U(x)
E5
Изобразим
условную
схему
энергетических уровней квантового
осциллятора,
вписанных
для
наглядности
в
кривую
потенциальной энергии.
E4
E3
E2
E1
E0
0
(n = 0, 1, 2, …).
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
5
6.
ГАРМОНИЧЕСКИЙ КВАНТОВЫЙ ОСЦИЛЛЯТОР.2 2 m
m 2 x 2
E
0 . En n 1 , (n = 0, 1, 2, …).
2
2
x 2 2
Выводы:
1. Энергетический спектр квантового гармонического
осциллятора является дискретным.
E
U(x)
E5
E4
E3
E2
E1
E0
0
x
2. Минимальное значение главного
квантового числа n не 1, а 0. Для
основного состояния n = 0, энергия
основного состояния - .
1
E0
2
Это
наименьшее
возможное
значение энергии, которое называют
нулевой энергией. Любое отличное
от нуля значение n - это номер
возбужденного уровня.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
6
7.
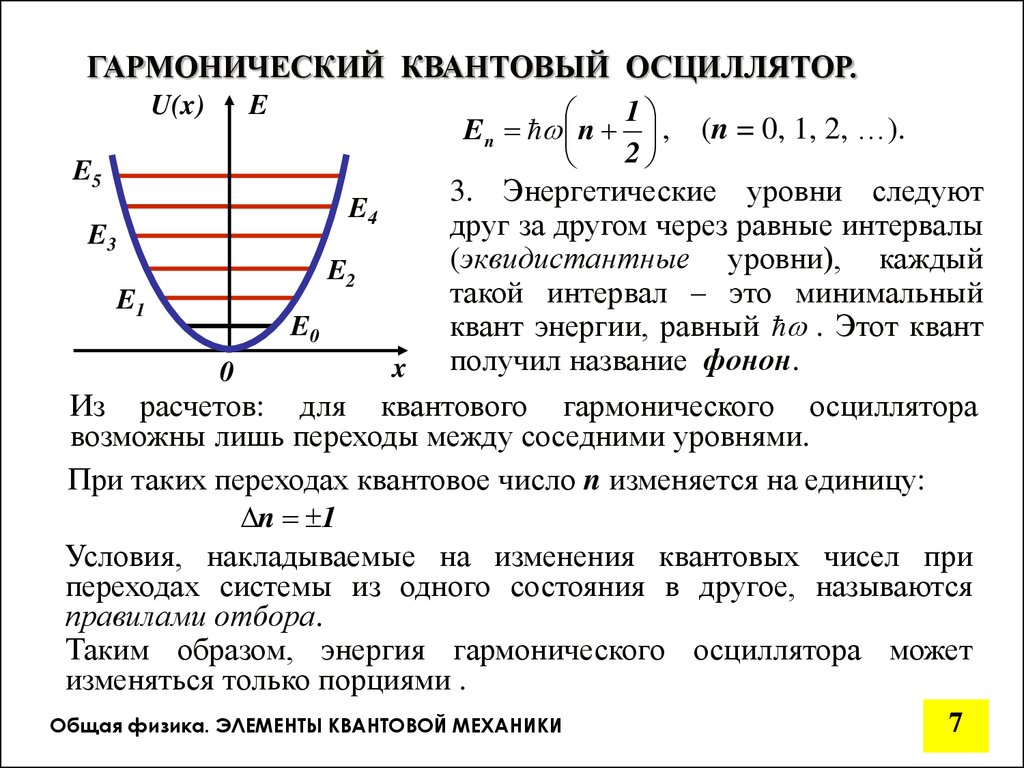
ГАРМОНИЧЕСКИЙ КВАНТОВЫЙ ОСЦИЛЛЯТОР.E
U(x)
1
En n , (n = 0, 1, 2, …).
2
E5
3. Энергетические уровни следуют
E4
друг за другом через равные интервалы
E3
(эквидистантные уровни), каждый
E2
такой интервал – это минимальный
E1
E0
квант энергии, равный . Этот квант
получил название фонон.
x
0
Из расчетов: для квантового гармонического осциллятора
возможны лишь переходы между соседними уровнями.
При таких переходах квантовое число n изменяется на единицу:
n 1
Условия, накладываемые на изменения квантовых чисел при
переходах системы из одного состояния в другое, называются
правилами отбора.
Таким образом, энергия гармонического осциллятора может
изменяться только порциями .
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
7
8.
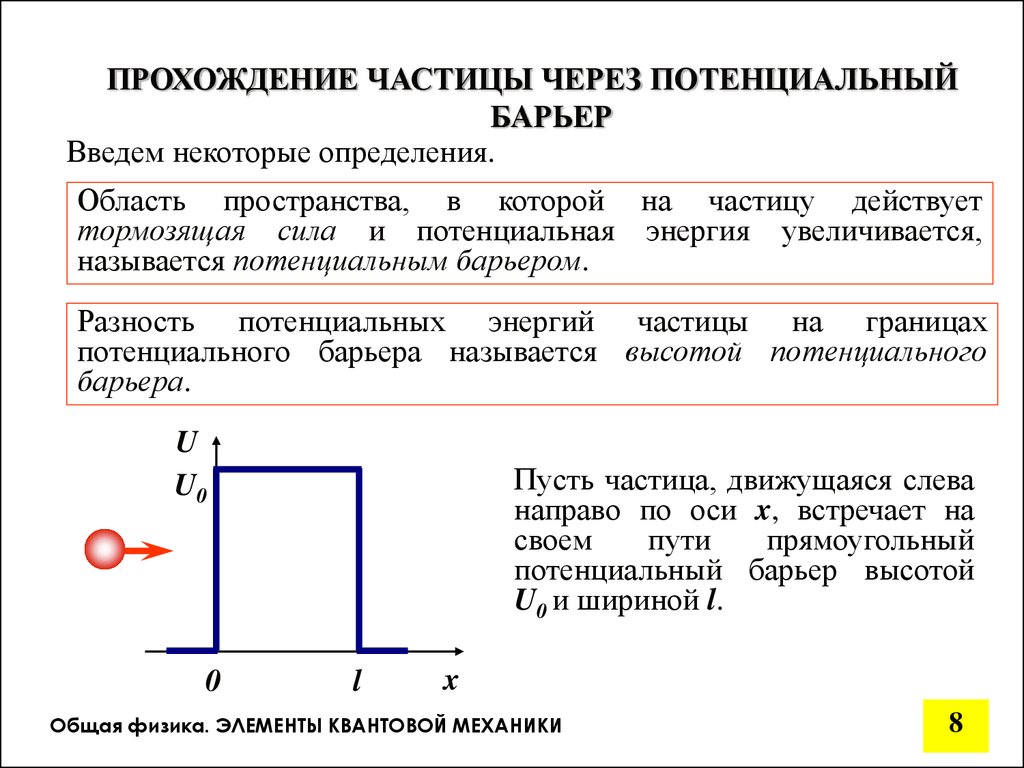
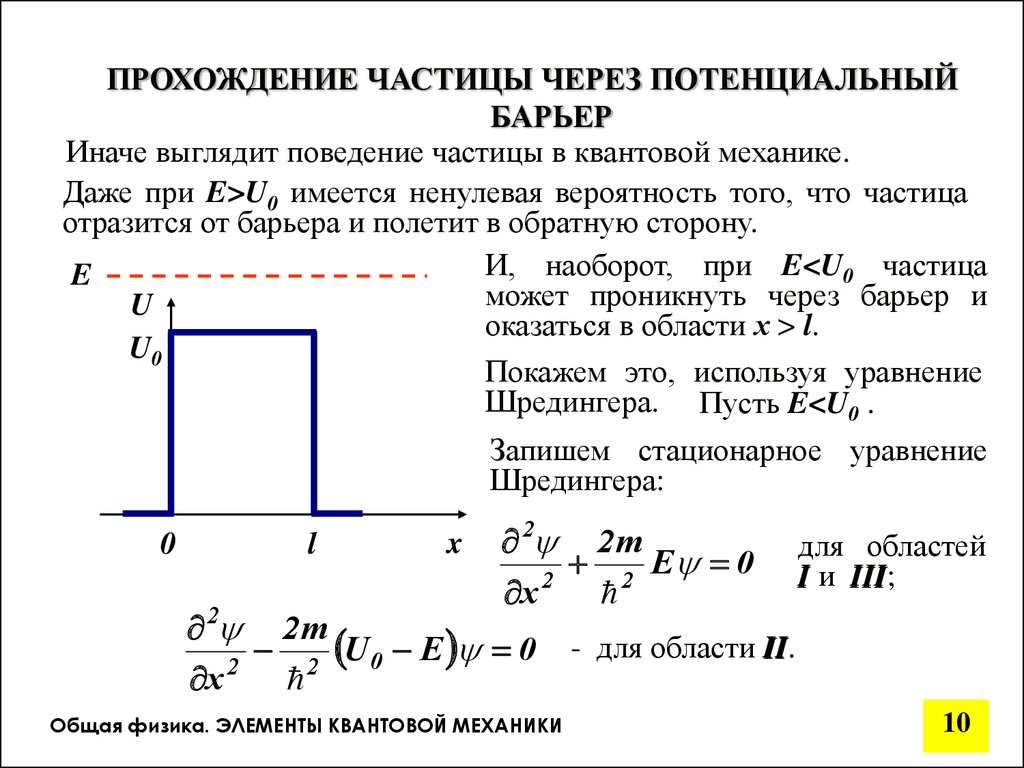
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
Введем некоторые определения.
Область пространства, в которой на частицу действует
тормозящая сила и потенциальная энергия увеличивается,
называется потенциальным барьером.
Разность потенциальных энергий частицы на границах
потенциального барьера называется высотой потенциального
барьера.
U
U0
0
Пусть частица, движущаяся слева
направо по оси x, встречает на
своем
пути
прямоугольный
потенциальный барьер высотой
U0 и шириной l.
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
8
9.
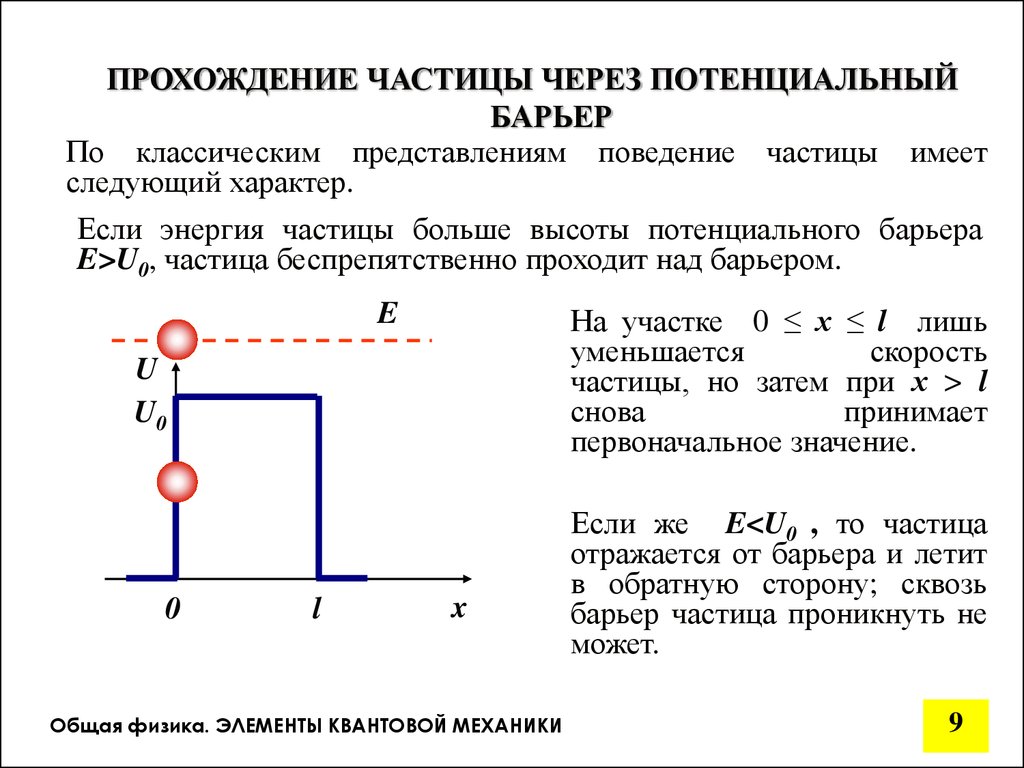
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
По классическим представлениям поведение частицы имеет
следующий характер.
Если энергия частицы больше высоты потенциального барьера
E>U0, частица беспрепятственно проходит над барьером.
E
На участке 0 ≤ х ≤ l лишь
уменьшается
скорость
частицы, но затем при х > l
снова
принимает
первоначальное значение.
U
U0
0
l
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Если же E<U0 , то частица
отражается от барьера и летит
в обратную сторону; сквозь
барьер частица проникнуть не
может.
9
10.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
Иначе выглядит поведение частицы в квантовой механике.
Даже при E>U0 имеется ненулевая вероятность того, что частица
отразится от барьера и полетит в обратную сторону.
И, наоборот, при E<U0 частица
E
может проникнуть через барьер и
U
оказаться в области х > l.
U0
Покажем это, используя уравнение
Шредингера. Пусть E<U0 .
Запишем стационарное уравнение
Шредингера:
0
l
x
2 2 m
2 E 0
2
x
2 2 m
2 U 0 E 0
2
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
для областей
I и III;
III
- для области II.
II
10
11.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙU
БАРЬЕР
U0
2
2m
2 E 0 - для областей I и III
2
x
2 2 m
2 U 0 E 0 - для области II
2
x
E
I
II
III
0
l
Введем обозначения:
x
k2
2m
E,
2
2m
2 U 0 E
2
С учетом этих обозначений перепишем уравнения:
2 1 , 3
2
k
1 ,3 0
2
x
2 2
2
2 0
2
x
Нижними индексами у пси-функций обозначили области, которым
соответствует уравнение Шредингера.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
11
12.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙU
БАРЬЕР
U0
2
x
E
I
0
l
k 2 1 ,3 0
2 2
2
2 0
2
x
III
II
1 ,3
2
x
Данные уравнения – это линейные дифференциальные однородные
уравнения второго порядка с постоянными коэффициентами
Такие уравнения обычно решают методом подстановки.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
12
13.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙU
БАРЬЕР
U0
2
x
E
I
II
III
1 ,3
2
k 2 1 ,3 0
2 2
2
2 0
2
x
x
0
l
Решение уравнений будем искать в виде
постоянная величина.
exp x , где
-
Подставим это решение в первое уравнение:
exp x ,
x
2
2
exp x . В итоге получим:
2
x
2 exp x k 2 exp x 2 k 2 0
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
13
14.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙU
БАРЬЕР
U0
2
x
E
I
II
III
1 ,3
2
k 2 1 ,3 0
2 2
2
2 0
2
x
2 k 2 0
Отсюда ik (два мнимых корня).
x
0
l
Для второго уравнения получим 2 2 0 , (два
действительных корня).
Общие решения уравнений для каждой из областей:
1 A1 exp ikx B1 exp ikx - для области I.
2 A2 exp x B2 exp x - для области II.
3 A3 exp ikx B3 exp ikx
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
- для области III .
14
15.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
1 A1 exp ikx B1 exp ikx
2 A2 exp x B2 exp x
3 A3 exp ikx B3 exp ikx
Для того, чтобы знать вид
волновых функций в каждой из
областей,
нужно
найти
значения констант А1 , А2 , А3 ,
В1 , В2 , В3 .
Константы определяются путем «сшивания» уравнений на
границах областей с помощью граничных условий.
Однако предварительно проведем общий анализ уравнений.
В уравнении для области II с ростом x первое слагаемое
неограниченно нарастает.
Поэтому для того, чтобы пси-функция удовлетворяла условию
ограниченности, постоянная А2 должна быть равна нулю.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
15
16.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
1 A1 exp ikx B1 exp ikx
2 A2 exp x B2 exp x
В результате уравнение для
области II будет иметь вид:
3 A3 exp ikx B3 exp ikx
2 B2 exp x
В областях I и III общие решения представляют собой
суперпозицию волн, распространяющихся в положительном
(решение вида exp ikx ) и отрицательном (решение вида exp ikx )
направлениях оси х.
В области III - за барьером – есть только проходящая волна,
поэтому константу В3 следует положить равной нулю.
Вспомним, что волны, которые ассоциируются со свободно
движущимися частицами, получили название волн де Бройля.
Следует отметить, что в области II функция уже не соответствует
плоской волне, поскольку показатель степени не мнимый, а
действительный.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
16
17.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
В итоге решения уравнений
для трех выделенных областей
можно записать в виде:
1 A1 exp ikx B1 exp ikx
2 B2 exp x
3 A3 exp ikx
Для определения оставшихся неизвестных коэффициентов
используются условия непрерывности волновой функции на
границах барьера – в точках х = 0 и х = l:
1 0 2 0 ,
2 l 3 l
Для того чтобы волновая функция была гладкой, т.е. не имела
изломов, в точках х = 0 и х = l должны быть равны нулю и ее
первые производные:
1 0 2 0
,
x
x
2 l 3 l
x
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
17
18.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
1 A1 exp ikx B1 exp ikx Используя граничные условия,
нетрудно получить систему
2 B2 exp x
уравнений, из которой и
определяются
неизвестные
3 A3 exp ikx
константы.
Естественно, эта задача решена. Ограничимся лишь более
подробным рассмотрением интересующей нас ситуации –
прохождение частицы через барьер.
При условии Е<U0 (полная энергия частицы меньше высоты
потенциального барьера), законы классической физики однозначно
не разрешают частице проникнуть сквозь барьер.
Проведенный анализ движения частицы с позиций квантовой
механики уже позволяет сделать вывод о том, что частица имеет
отличную от нуля вероятность прохождения через потенциальный
барьер конечной ширины.
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
18
19.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
1 A1 exp ikx B1 exp ikx
2 B2 exp x
3 A3 exp ikx
U
U0
E
I
1
II
0
III
l
2
Уравнения для функций 1 , .2
и 3 можно
качественно
проиллюстрировать рисунком.
x
3
x
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
Из уравнений следует, что
волновая функция не равна
нулю и внутри барьера, а в
области III, если барьер не
очень
широк,
волновая
функция будет опять иметь вид
волн де Бройля с той же
частотой, что и в области I, но
с меньшей амплитудой.
19
20.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
Таким образом, квантовая механика приводит к принципиально
новому специфическому квантовому явлению.
При преодолении потенциального барьера частица как бы
пробивает «туннель» в этом барьере, в связи с чем это явление
получило название туннельного эффекта.
Введем некоторые характеристики, позволяющие описать
туннельный эффект.
Вероятность прохождения частицы через барьер определяется
отношением квадратов модулей амплитуд прошедшей и
падающей волн:
D
A3
2
A1
2
и называется коэффициентом прохождения (или коэффициентом
прозрачности).
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
20
21.
ПРОХОЖДЕНИЕ ЧАСТИЦЫ ЧЕРЕЗ ПОТЕНЦИАЛЬНЫЙБАРЬЕР
По аналогии можно ввести и коэффициент отражения частицы от
2
барьера:
B1
Очевидно, что D R 1
R
2
A1
Связь коэффициента D с параметрами барьера выражается
приближенным соотношением вида:
2
D exp 2 l exp
2 m U 0 E l
С классической точки зрения туннельный эффект абсурден, так
как частица в «туннеле» должна была бы обладать отрицательной
кинетической энергией, поскольку в туннеле Е<U0.
Туннельный эффект явление чисто квантовое, не имеющее
аналога в классической физике.
В квантовой механике деление полной энергии на потенциальную и
кинетическую не имеет смысла
Общая физика. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ
21
















 physics
physics








