Простейшие задачи квантовой механики. Прохождение частицы через потенциальный барьер. Туннельный эффект

1. Кислицын А.А. Физика атома, атомного ядра и элементарных частиц

11 (1). Простейшие задачи квантовой
механики.
Прохождение частицы через
потенциальный барьер. Туннельный
эффект.

2. Рассмотрим одномерное движение частицы в об-ласти, где существует потенциальный барьер: "ступенька" прямоугольной формы.

Рассмотрим одномерное движение частицы в области, где существует потенциальный барьер:
"ступенька" прямоугольной формы. Направим ось
x по направлению движения частицы. На границе
областей 1 и 2 частица либо пройдет через барьер в область 2, либо отразится и будет двигаться
в область 1 в противоположном направлении. Если слева направо движется поток частиц, то часть
из них пройдет через барьер, а часть отразится.
Задача заключается в определении вероятностей
прохождения и отражения
частицы при прохождении
через барьер.

3.

В классической механике если кинетическая энергия частицы больше высоты барьера: T = E > U0,
то частица преодолевает барьер с достоверностью. В квантовой механике это не так: частица может отразиться от барьера с некоторой вероятностью R≠0.
В классической механике при E < U0 переход частицы из области 1 в область 2 невозможен: отражение с достоверностью происходит на границе областей. В квантовой механике имеется вероятность найти частицу в области 2.
Доказательства этих отличий основаны на решении
уравнения Шредингера.

4.

Запишем уравнение Шредингера:
2m
2 E U 0, где
2
x
2
0, x 0
U
U 0 , x 0
Найдем решения отдельно в области 1 и 2, а затем, используя условие непрерывности, согласуем
эти решения (“сошьем”) между собой.
В области 1:
d 2 1 2m
2 E 1 0
2
dx
2
d
2
m
2
В области 2:
2 ( E U 0 ) 2 0
2
dx
(11.1)
(11.2)

5.

Обозначим: k1
1
2mE ;
k2
1
2m( E U 0 ) (11.3)
Тогда записанные уравнения принимают вид:
d 2 1
2
k
1 1 0 ;
2
dx
d 2 2
2
k
2 2 0
2
dx
а их общие решения:
1 a1e
ik1 x
2 a2 e
b1e
ik2 x
(11.4)
ik1 x
b2 e
(11.5)
ik2 x
a1 – амплитуда падающей волны, в области 1,
b1 – амплитуда отраженной волны, в области 1,
a2 – амплитуда прошедшей волны, в области 2,
b2 – амплитуда отраженной волны, в области 2.

6.

В рассматриваемой задаче частицы, прошедшие в
область 2, при движении в этой области никаких
препятствий не встречают, поэтому отраженного
потока в этой области быть не должно, значит
амплитуда отраженной волны в области 2
должна равняться нулю: b2 = 0.
Амплитуды b1 и a2 найдем из условий непрерывности при x = 0:
1 x 0 2
d 1
dx
x 0
d 2
dx
x 0
a1 b1 a2
a1ik1 b1ik1 a2ik2
x 0
k2
a1 b1 a2
k1
(11.6)

7.

Это два уравнения относительно двух неизвестных коэффициентов b1 и a2. Решая эту
систему находим:
2k1
k1 k2
a2
a1 ; b1
a1 .
k1 k2
k1 k2
(11.7)
Отсюда коэффициент отражения:
U0
2
1
1
b1 k1 k2
E
R 2
a1 k1 k2
U
1 1 0
E
2
2
(11.8)
Более подробно задача рассмотрена в приложении (в следующей презентации).

8.

Рассмотрим теперь прохождение частиц через прямоугольный потенциальный
барьер конечной ширины d:
0,
U U 0 ,
0,
x 0
0 x d
x d
Отличие от предыдущей задачи состоит в том, что
отражение происходит на двух границах: 1-2 и 2-3.
Поэтому:
ik x
ik x
1 a 1 e
1
2 a 2 e
3 a 3 e
b1e
ik2 x
ik1 x
b2 e
1
ik2 x

9.

Очевидно, что амплитуды прошедших и отраженных
волн будут пропорциональны амплитуде падающей волны a1, поэтому для упрощения вычислений
положим a1 = 1. Как и в предыдущей задаче, амплитуды b1, a2, b2, a3 найдем из условий непрерывности и d /dx на границах x = 0 и x = d. Условия
непрерывности на границах x = 0 и x = d дают:
(11.11)
1 b1 a2 b2
ik2d
ik2d
ik1d
(11.12)
a2e b2e
a3e
Из условий непрерывности d /dx на границах x = 0 и
x = d получаем:
ik1a1 ik1b1 ik2a2 ik2b2
(11.13)
ik2d
ik2 d
ik1d
(11.14)
ik a e ik b e
ik a e
2 2
2 2
1 3

10.

Мы получили систему из 4-х уравнений относительно 4-х неизвестных b1, a2, b2, a3. Наибольший интерес представляет квадрат модуля отношения a3
(амплитуда прошедшей волны) к амплитуде падающей волны a1 в случае, когда высота барьера
больше, чем энергия частиц. Это отношение называется коэффициентом прозрачности барьера D :
D = a3/a1 2.
Т.к. a1 = 1, достаточно найти a3. Решение дает следующий результат:
2
16 E
E
D
1 e
U0 U0
2 m (U 0 E )d
Вывод этой формулы приведен в приложении (следующая презентация).

11.

Итак, частица с энергией E < U0 может пройти сквозь
барьер. Вероятность этого (невозможного с точки
зрения классической физики) события (прозрачность барьера D) сильно зависит от ширины барьера d, массы частицы m и разности (U0 - E) между
высотой барьера и энергией частицы (все эти величины находятся в показателе экспоненты).
Явление прохождения частицы сквозь потенциальный барьер называется туннельным эффектом.
В этом названии образно подчеркивается тот факт,
что частица не "взбирается" на вершину барьера,
а проходит сквозь барьер как бы через туннель.
При этом частица не теряет энергию, она выходит
из барьера с той же энергией, с какой в него попадает.

12.

Туннельный эффект может быть обнаружен в эксперименте в том случае, если проницаемость барьера не слишком мала, т.е. если показатель экспоненты по модулю ненамного больше единицы:
2
(11.15)
2m U E d 1
0
Прохождение частицы сквозь барьер кажется парадоксом, т.к. в области 2 (в области барьера) частица имеет отрицательную кинетическую энергию:
p2
T
U0 E 0
2m
или мнимый импульс, что не имеет физического
смысла.

13.

На самом деле никакого парадокса здесь нет, если
учесть, что потенциальная энергия - это функция
координат, а кинетическая энергия - функция импульса. Формула
p2
E
U ( x)
2m
предполагает, что мы одновременно знаем величину и кинетической энергии, и потенциальной. Но
соотношения неопределенностей для координаты
и импульса утверждают, что одновременное точное измерение этих величин невозможно. Это
значит, что невозможно одновременно точно измерить кинетическую и потенциальную энергию.

14.

Если мы в эксперименте в результате какого-то измерения обнаружили частицу в области 2, то мы
зафиксировали ее координату с неопределенностью, меньшей, чем ширина барьера d. Значит, частица при этом измерении получила дополнительный импульс Δp, больший, чем / d , и дополнительную энергию, большую, чем
2
(11.16)
2
2
p / 2m / 2md
С другой стороны, из формулы (11.15), возведя ее в
квадрат, находим
2
4 U 0 E
2
2md
Мы видим, что добавка (11.16) как раз такая, какая
нужна, чтобы полная энергия частицы достигла (и
даже несколько превысила) значение U0.

15.

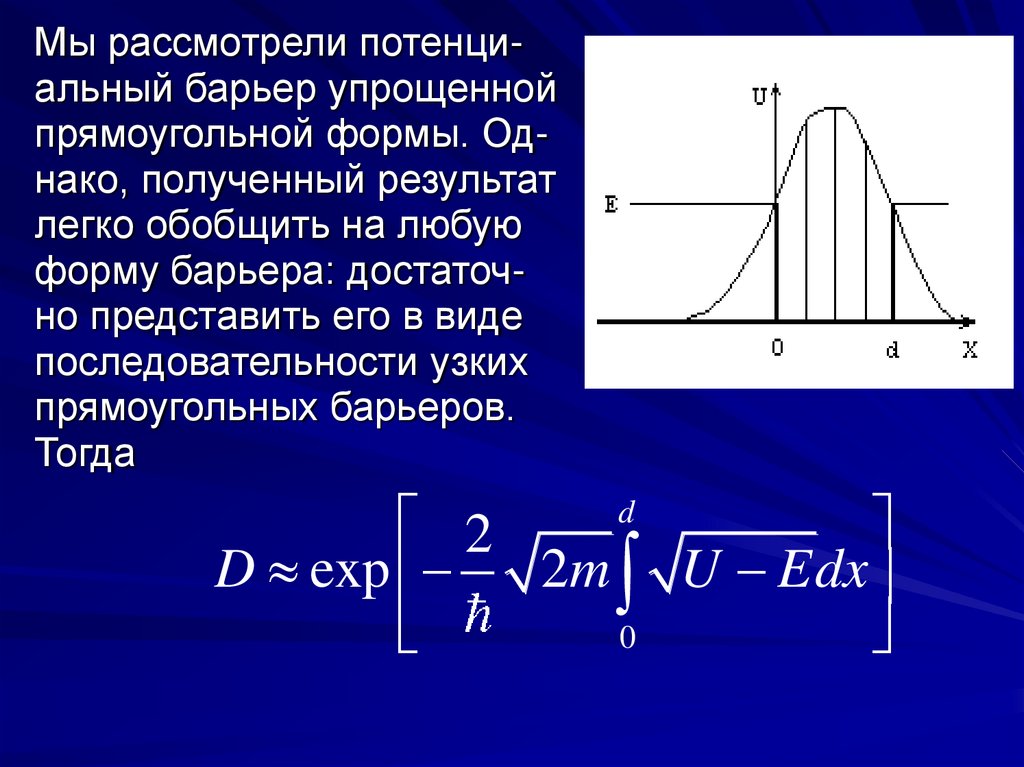
Мы рассмотрели потенциальный барьер упрощенной
прямоугольной формы. Однако, полученный результат
легко обобщить на любую
форму барьера: достаточно представить его в виде
последовательности узких
прямоугольных барьеров.
Тогда
2
D exp
2m U Edx
0
d

16.

Туннельный эффект объясняет
многие явления, невозможные с
точки зрения классической механики
(например, альфа-распад), а также
используется в электронных
приборах (туннельные диоды,
полевые транзисторы, зондовые
микроскопы и др.).