Similar presentations:
Математический аппарат квантовой механики (теория линейных, эрмитовых операторов)
1.
Математический аппаратквантовой механики
(теория линейных,
эрмитовых операторов)
2.
При сравнении уравнения Шредингера2 2
i
,
t
2m
(1)
с записью закона сохранения энергии
2
p
E
,
2m
(2)
было замечено, что (1) и (2) совпадают,
если сопоставить физическим величинам E и p
математические операторы:
E
i
,
t
p i
3. Операторы
Понятие оператора.Оператор - математическое понятие, означающее
соответствие между элементами двух множеств Х и Y,
относящее каждому элементу х из Х некоторый элемент у
из Y.
В конце XIX века Георг Кантор определил множество как «единое имя
для совокупности всех объектов, обладающих данным свойством».
Эти объекты называются элементами множества. Множество объектов,
обладающих свойством A(x), обозначается {x|A(x)}.
Если некое множество Y={x|A(x)}, то A(x) называется
характеристическим свойством множества Y.
4. Операторы
Понятие оператора.Оператор есть символическая запись тех действий,
которые необходимо проделать над произвольной
функцией и для получения некоторой другой
функции v.
Иными словами, оператор – это рецепт, по которому
одной функции сопоставляется другая функция.
Понятие оператора является обобщением понятия
функции.
В тех случаях, когда Х и Y — числовые множества,
пользуются обычно термином «функция».
5. Операторы
Примеры операторов:1. Оператор дифференцирования:
du
v( x) Lu( x )
dx
2. Оператор интегрирования:
v( x) Lu( x) u( x)dx
3. Оператор возведения в степень:
n
v Lu u u n
4. Единичный оператор
(оставляет функцию неизменной):
d
L
dx
L ...dx
L ... n
Lu u 1u Eu
6. Свойства операторов и действия с ними
Понятие линейного оператора.Оператор называется линейным, если он удовлетворяет
следующему условию:
L au( x) bv( x) L au( x) L(bv( x))
aLu( x) bLv( x) где a и b постоянные
Примеры НЕЛИНЕЙНЫХ операторов – степень, корень.
Сложение операторов.
Суммой операторов называется такой оператор, результат действия
которого равен сумме результатов действия слагаемых:
C A B, если Cu Au Bu
7. Свойства операторов и действия с ними
Умножение операторов.Оператор С называется произведением операторов A на B слева
- если: Cu A( Bu)
C AB
Вообще говоря, произведение операторов зависит от порядка
сомножителей:
C AB C BA
C AB C BA
Если
то операторы называются
коммутирующими, или перестановочными. Для них
AB BA 0
Если
AB BA 0 , то операторы некоммутирующие.
8.
Пример некоммутирующих операторов.Рассмотрим операторы координаты,
d
d
x x
dx dx
d
x и
dx
и покажем, что
d
d
d
dx
du
du
du
x u
xu xu u x
u x
1u x
dx
dx
dx
dx
dx
dx
dx
Отсюда
d d
x x
1
dx
dx
Но
d d
x x
0 !!
dy
dy
9.
Оператор независимой переменной определяется какумножение на эту переменную:
x
Обратный оператор.
1
Данному оператору F можно сопоставить обратный оператор F
определяемый соотношением:
1
1
F F ,
FF
или
1 1
FF F F 1
Например, если F - дифференциальный оператор, то
обратным ему будет интегральный.
10. Математическая схема квантовой механики (К.м.)
Первым основным понятием К. м. является квантовое состояние.Выбор математического аппарата К. м. диктуется физическим
принципом суперпозиции квантовых состояний, вытекающим из
волновых свойств частиц.
Согласно этому принципу, суперпозиция любых возможных
состояний системы, взятых с произвольными (комплексными)
коэффициентами, является также возможным состоянием
системы.
Объекты, для которых определены понятия сложения и
умножения на комплексное число, называется векторами.
Т. о., принцип суперпозиции требует, чтобы состояние системы
описывалось некоторым вектором — вектором состояния (с которым
тесно связано понятие амплитуды вероятности, или волновой
функции), являющимся элементом линейного «пространства
состояний». Это позволяет использовать математический аппарат,
развитый для линейных (векторных) пространств. Вектор состояния
обозначается (по Дираку)
11.
Кроме сложения и умножения на комплексное число, векторможет подвергаться ещё двум операциям.
Во-первых, его можно проектировать на другой вектор, т. е.
составить скалярное произведение с любым другим вектором
состояния ; оно обозначается как , * dV
и является, в общем случае, комплексным числом. Простейший случай:
Скалярное произведение вектора с самим собой, , — положительное
число; оно определяет длину (норму) вектора. Длину вектора состояния
удобно выбрать равной единице; его общий фазовый множитель
произволен. Различные состояния отличаются друг от друга направлением
вектора состояния в пространстве состояний.
Во-вторых, можно рассмотреть операцию перехода от вектора к
вектору (или произвести преобразование )
Символически эту операцию можно записать
как результат действия на
вектор некоторого линейного оператора L :
L
12.
Линейные операторы, в силу принципа суперпозиции состояний, имеютв К. м. особое значение; в результате воздействия линейного оператора на
суперпозицию произвольных векторов
и получается
суперпозиция
преобразованных векторов:
'
'
L c1 1 c2 2 c1L 1 c2 L 2 c1 1 c2 2
Важную роль для оператора L играют такие векторы ,
для которых
совпадает по направлению с , т. е.
L
Такие векторы называют собственными векторами оператора , а числа
— его собственными значениями. Собственные векторы принято
обозначать просто . Собственные значения образуют либо
дискретный ряд чисел (тогда говорят, что оператор имеет дискретный
спектр), либо непрерывный набор (непрерывный спектр), либо
частично дискретный, частично непрерывный.
13.
Очень важный для К. м. класс операторов составляютлинейные эрмитовы операторы. Собственные значения
эрмитового оператора вещественны.
Линейный оператор А называется эрмитовым, если для любых
двух векторов х и у выполняется равенство
(Ax, у) = (х, Ау), где (х, у) — скалярное произведение.
*
*
Т.е. A d A d
Это определение эквивалентно условию:
Ax A x где A сопряженный оператор. Т.о. : A A
т.е. эрмитовы операторы самосопряженные.
Примечание: сопряженный оператор определяется условием
(A+ g,x) = (g,Ax), или
*
g AxdV x A g dV
*
14.
Линейный оператор А называется эрмитовым, еслиA d
*
*
A d
d
p x i
dx
Проверим, является ли эрмитовым оператор
d
i dx i *d i *
dx
*
i d *
d *
d *
d
d
dx i
i
dx i
dx i
dx
dx
dx
dx
dx
*
Проверили – является!
Кстати, очень похожий оператор
d
- не эрмитов!
dx
*
15. Свойства с.ф. и с.з.
1.Собственные векторы (функции), эрмитового оператора,принадлежащие различным собственным значениям,
ортогональны друг к другу, т. е.
0
*
dV
0
16. Свойства с.ф. и с.з.
2. Собственные значения эрмитового оператора являютсявещественными числами
3. Система собственных функций эрмитового оператора
является полной, т.е. не существует такой функции, которая
была бы ортогональна им, не являясь собственной
функцией
17.
Поскольку собственные векторы эрмитового оператора,принадлежащие различным собственным значениям, ортогональны друг
к другу, из них можно построить ортогональный базис («декартовы оси
координат») в пространстве состояний. Удобно нормировать эти
базисные векторы на 1, 1 .
Произвольный вектор можно разложить по этому базису
c ; c
При этом:
c
2
что эквивалентно теореме Пифагора;
если
нормирован на 1, то
c
2
1
18.
Любой линейный оператор M в выбранном базисе может бытьпредставлен матрицей: M
i M k
,
i
k
*
Если M - эрмитов оператор, то M ,
M
k , i . (Для j , являющихся
i k
собственными векторами оператора M , матрица M , диагональна.)
i k
Если сопоставить с произвольным вектором c
столбец из его
c
1
c2
коэффициентов .
в выбранном базисе, то действие оператора M на ,
.
M ' , сводится к матричному умножению:
. . c c'
. . c c '
. . . . . . . .
. . . . . . . .
M 11 M 12
M 21 M 22
1
1
2
2
c'1
где столбец c'2 отвечает координатам вектора
'
i
ik k
k
.
.
c M c
' в том же базисе:
19. Связь математического описания с физикой
Принципиальное значение для построения математическогоаппарата К. м. имеет тот факт, что
для каждой физической величины существуют некоторые
выделенные состояния системы, в которых эта величина
принимает вполне определённое (единственное) значение.
По существу это свойство является определением физической
(измеримой) величины,
а состояния, в которых физическая величина имеет определённое
значение, называются собственными состояниями этой величины.
Согласно принципу суперпозиции, любое состояние системы
может быть представлено в виде суперпозиции собственных
состояний какой-либо физической величины. Возможность такого
представления математически эквивалентна возможности
разложения произвольного вектора по собственным векторам
линейного эрмитового оператора.
20.
В соответствии с этим в К. м. каждой физической величине L ,(координате, импульсу, моменту количества движения, энергии и
т.д.) ставится в соответствие линейный эрмитов оператор
.
Собственные значения оператора интерпретируются, как
возможные значения физической величины L, проявляющиеся при
измерениях.
Если вектор состояния — собственный вектор оператора , то
физическая величина L имеет определённое значение.
В противном случае L принимает различные значения с
вероятностью |c |2, где c — коэффициент разложения > по >:
c
21. Основные постулаты квантовой механики Постулат 1
Состояние системы полностью описывается вектором(функцией) состояния, который должен быть однозначным (с
точностью до произвольной фазы) и иметь конечную норму.
Полнота описания подразумевает, что задание вектора состояния
в определенный момент времени позволяет найти вектор
состояния в любой другой момент времени и указать вероятности
результатов измерения всех физических величин в заданном
состоянии системы.
Полное в указанном смысле описание квантовомеханической системы (с
помощью вектора состояния) оказывается невозможным в случае, когда
рассматриваемая система является подсистемой некоторой большей системы и
существенно взаимодействует с её остальными частями. В этом случае
система не обладает определенным вектором состояния, и её описание
производится с помощью матрицы плотности.
Состояния, описываемые вектором состояния, называются чистыми
состояниями, в отличие от смешанных состояний, описываемых матрицей
плотности. Описание с помощью матрицы плотности является наиболее общей
формой квантовомеханического описания. Оно лежит в основе квантовой
22. Основные постулаты квантовой механики Постулат 2
Каждой физической величине соответствует линейный эрмитовоператор.
Конкретный вид линейных эрмитовых операторов, соответствующих
таким физическим величинам, как импульс, угловой (орбитальный)
момент, энергия, постулируется исходя из принципа соответствия,
требующего, чтобы в пределе h 0 рассматриваемые физические
величины принимали "классическое" значения, и согласуется с общими
принципами определения этих величин на основе законов сохранения.
Вместе с тем в К. м. существуют такие линейные эрмитовы операторы
[например, отвечающие преобразованию векторов состояния при
отражении осей координат (пространственной инверсии), перестановке
одинаковых частиц и др.], которым соответствуют измеримые
физические величины, не имеющие классических аналогов,
например, чётность.
23.
Постулат 3При измерении физической величины получается одно из
собственных значений оператора, изображающего эту
величину
24. Основные постулаты квантовой механики Постулат 4
В разложении произвольного вектора состояния системы поортонормированной системе собственных векторов f i , c f i
i
физической величины f , значения c fi
2
2
i
равны вероятностям
обнаружить систему в состояниях | fi >, т. е. вероятностям того, что
при измерении f её значение окажется равным fi.
В случае, когда величина f имеет непрерывный спектр, а
собственные состояния нормированы условием:
< f | f ' > = (f - f '), где - дельта-функция Дирака,
2
выражение c f f y
2
представляет собой плотность
вероятности, т. е. вероятность dwf, f+df обнаружить величину f в
интервале (f, f+df) равна:
dwf, f+df = |cf |2df.
25. Пояснение к постулату 4
Условиеdwf, f+df = |cf|2df
формально противоречит постулату 1, т. к. вектор состояния | f >,
принадлежащий непрерывному спектру, имеет бесконечную норму.
Дело в том, что "монохроматическое" состояние | f >, выделенное из
непрерывного спектра, является идеализацией, как например,
монохроматическая плоская э.-м. волна, которая должна была бы
заполнять всё пространство и иметь поэтому бесконечную энергию.
В действительности, любая физическая величина, принимающая
непрерывные значения, может быть определена лишь в некотором
интервале f, зависящем от точности прибора. Вектор состояния,
отвечающий такому определению, представляет собой волновой
пакет, составленный из монохроматических состояний f в интервале
f и имеющий конечную норму. Т. о., для физических векторов
состояния противоречия с постулатом 1 нет.
26.
Физические постулаты и собственные функцииосновных операторов физических величин
1. Каждая динамическая переменная, характеризующая
движение частицы, может быть представлена линейным
оператором.
Это может быть просто оператор умножения, например, r, если речь идет
о координате частицы, дифференциальный оператор, например, оператор
импульса p i , или иной.
Каждому оператору соответствует линейное уравнение для нахождения
собственных значений.
Так, например, оператору соответствует уравнение
u u ,
где u - собственная функция оператора
собственному значению .
, соответствующая
27.
2. В результате точного измерения динамической переменной,характеризуемой оператором , может получиться лишь
какое-либо из собственных значений .
Следствием этого является вещественность собственных
значений всех операторов, характеризующих физические
переменные.
Предположим, что все собственные функции любой
динамической переменной образуют полную систему, т.е. по
ним можно разложить произвольную непрерывную функцию.
Приведенная ниже волновая функция разложена по
собственным функциям u оператора
A u .
28.
3. Число измерений, при которых получается собственноезначение , пропорционально квадрату абсолютной
величины |С |2 коэффициента при u в разложении
функции :
С u .
Из этого следует, что некоторое собственное значение
можно измерить с достоверностью лишь в том случае,
когда волновая функция, описывающая частицу, совпадает с
собственной функцией u .
29. Операторы и собственные функции координаты и импульса
30. Вид операторов в координатном представлении
Установим вид операторов в координатном представлении, когдаволновая функция частицы зависит от ее координат, = (x,y,z).
Координаты x,y,z являются независимыми переменными, поэтому
отвечающие им операторы сводятся к умножению на эти координаты:
x x;
y y ; z z или xi xi
(i 1, 2, 3)
Вид операторов импульса определяется тем, что законы движения
должны переходить в классические при ћ 0. В координатном
представлении операторы проекций импульса записываются так:
px
; py
; pz
i x
i y
i z
или в векторной форме :
p , где , ,
i
x y z
Справедливы следующие перестановочные соотношения:
p x x p , (i, k 1, 2, 3)
i k
k i i ik
1 при i k
ik 0 при i k
31. Вид операторов в импульсном представлении
Рассмотрим вид этих же операторов в импульсномпредставлении, когда волновая функция частицы зависит от
трех проекций импульса:
= ( px, py, pz ).
Здесь независимыми переменными являются проекции
импульса, поэтому отвечающие им операторы сводятся к
умножению на величины px, py, pz, а оператор координаты
определяется из перестановочных соотношений, и равен:
x i
;
p x
или :
y i
; z i
p y
pz
i
r i i
j
k
p
p
p
p
x
y
z
32. Собственные функции и собственные значения оператора импульса
Уравнения для собственных функций и собственных значений оператораимпульса имеют вид:
i
(p r )
p x
Его
решения
есть
i x p x p x
p
i
i
Ae
p y
y
pz
z
p y p y Они описывают состояния с заданным импульсом p.
pz pz
В таком состоянии может находиться свободно
двигающаяся частица, обладающая непрерывным
спектром собственных значений.
2
1 не годится, так как
В этом случае условие нормировки dp
отлична от нуля при любых значениях p, и интеграл расходится.
Для таких спектров удобно пользоваться нормировкой на - функцию:
p dx ( px px ) , это дает: p
*
px
x
1
2 π
3/ 2
e
i
(p r )
33. Дельта – функция Дирака
Дельта-функция — это не функция в общепринятом смыслеОна определяется не заданием ее величины для всех значений
аргумента, а заданием правил интегрирования ее произведений с
непрерывными функциями!
Обозначается, как (x).
Эта функция сингулярная, она равна нулю всюду, кроме точки x = 0
В точке x = 0 она столь велика, что интеграл от этой функции,
содержащий точку x = 0 , равен 1, т.е.:
( x)dx 1
Наиболее важное свойство -функции выражается равенством:
b
a
для любой непрерывной F(x) , если интервал
F ( x ) ( x )dx F (0) (a,b) содержит точку x = 0. Смещение начала
координат преобразует это выражение к виду:
F ( x) ( x a)dx F (a)
Эта формула верна для любой непрерывной функции — скалярной,
векторной, тензорной и т.д.
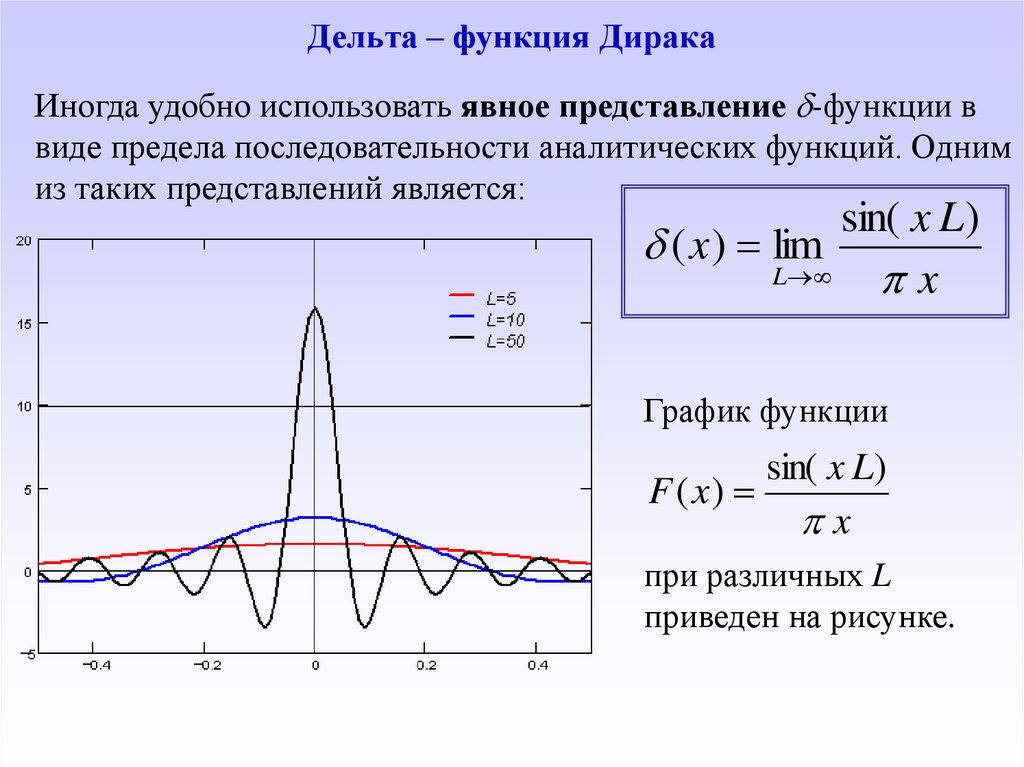
34. Дельта – функция Дирака
Иногда удобно использовать явное представление -функции ввиде предела последовательности аналитических функций. Одним
из таких представлений является:
sin( x L)
( x ) lim
L
x
График функции
sin( x L)
F ( x)
x
при различных L
приведен на рисунке.
35.
Оператор полной энергии (гамильтониан)Рассмотрим теперь следствия из постулатов, перечисленных на прошлой
лекции, на примере оператора полной энергии частицы.
Опыт показывает, что кинетическая энергия T микрочастиц связана с
импульсом p так же, как и для макроскопических тел, то есть
кинетическая энергия частиц с массой m и импульсом p равна
p2
1
T
px2 p y2 pz2
2m 2m
Тогда оператор кинетической энергии естественно записать в виде
p2
1
T
px2 p y2 pz2
2m 2m
px i ;
x
p y i ;
y
где
pz i
z
36.
Оператор кинетической энергииТ.о.
2 2
T
где 2 оператор Лапласа :
2m
2
2
2
2 2 2 2
x y z
Уравнение
T T
имеет решение в виде волны де Бройля:
i
1
T ( x, y , z )
e
3/ 2
2
px x p y y pz z
Эта же функция является собственной функцией операторов
импульса, так что кинетическая энергия T измерима
одновременно с импульсами px, py, pz (операторы T, px, py, pz
коммутируют между собой).
37.
Оператор полной энергииОператор потенциальной энергии есть просто функция координат x,y,z
частицы V(x,y,z).
Оператор полной энергии есть сумма операторов
кинетической
и потенциальной энергии:
H T V ( x, y, z ) Он называется также оператор
Гамильтона, или просто гамильтониан.
Вид потенциальной энергии заимствуется из опыта, и характеризует
силовое поле, действующее на частицу.
Операторы T и V не коммутируют, поэтому нельзя измерить отдельно
кинетическую и потенциальную энергию – только полную.
Для того, чтобы полная энергия имела определенное значение,
существенно, чтобы потенциальная энергия V(r) не зависела от времени.
Тогда собственные функции u(r) оператора энергии
2 2
H
V (r )
2m
не должны зависеть от времени.
2 2
V (r ) uE (r ) EuE (r )
2m
38.
39.
Важные операторы квантовой механикиФизическая величина
r
x, y, z
Координата
p
px , p y , p z
Импульс
L r p
Момент
количества
движения, или
угловой
(вращательный)
момент
Lx ypz zp y
Lx zpx xpz
L xp yp
y
x
x
Энергия в
нерелятивистском
приближении
p2
E
U (r )
2m
Оператор
r
x, y , z
i
i
,
i
,
i
x
y
z
L i r
L
i
y
z
x
z
y
x
L y i z
x
z
x
y
Lz i
y
x
2 2
H
U (r )
2m
40.
Принцип неопределенностиВ общем виде принцип неопределенности был сформулирован
Гейзенбергом в 1927 г. Согласно этому принципу, невозможно
одновременно точно определить значения некоторых пар физических
величин, описывающих атомную систему. Величины, входящие в пары,
представляют собой канонически сопряженные переменные в смысле
Гамильтона.
Примерами таких пар являются:
- координата частицы x и соответствующая компонента импульса px ;
- z-компонента Jz момента импульса и угол поворота в плоскости xy;
- энергия частицы E и момент времени t ее измерения.
В количественной формулировке принцип неопределенности утверждает,
что произведение неопределенностей двух сопряженных переменных по
порядку величины не меньше постоянной Планка
x p x , J z , t E .
Другими словами, невозможно точно определить значение одной из
величин пары, не потеряв при этом всех сведений о второй величине.
41.
Принцип дополнительности.Чтобы выразить смысл и значение принципа неопределенности в более
«физических» терминах, Бор в 1928 г. ввел новый принцип
дополнительности.
Согласно этому принципу, атомные явления невозможно описывать с той
полнотой, какая требуется классической динамикой. Ряд величин,
дополняющих друг друга и дающих полное классическое описание,
фактически являются «взаимоисключающими».
Формулировки принципа дополнительности:
Ни в каком эксперименте невозможно одновременно наблюдать
корпускулярные и волновые свойства микрочастиц.
В дальнейшем была предложена более общая формулировка, содержащая
предыдущую как частный случай:
получение экспериментальной информации об одних физических
величинах, описывающих микрообъект, неизбежно связано с потерей
информации о некоторых других величинах.
42.
Принцип дополнительности.С точки зрения экспериментатора, принцип
дополнительности означает, что, в силу свойств физических
приборов, измерения, точность которых превышает
требования принципа неопределенности, вообще
невозможны.
Если исходить из принципа дополнительности, то
корпускулярно-волновой дуализм квантовых объектов перестает
быть парадоксальным: волновой и корпускулярный аспекты
оказываются дополнительными и проявляются во
взаимоисключающих экспериментальных условиях.
Всякая попытка выявить один из аспектов, требует
соответствующего экспериментального устройства, которое
лишает нас возможности наблюдать другой аспект поведения
объекта.
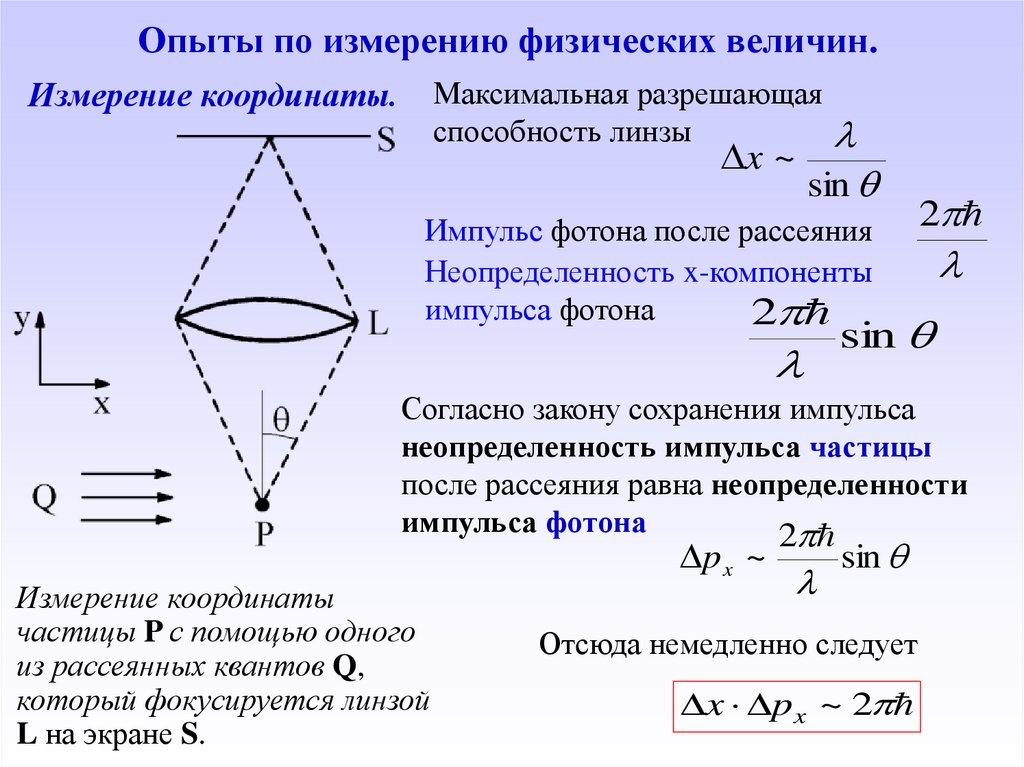
43.
Опыты по измерению физических величин.Максимальная разрешающая
способность линзы
Измерение координаты.
x ~
sin
Импульс фотона после рассеяния
Неопределенность x-компоненты
импульса фотона
2
2
sin
Согласно закону сохранения импульса
неопределенность импульса частицы
после рассеяния равна неопределенности
импульса фотона
2
Измерение координаты
частицы P с помощью одного
из рассеянных квантов Q,
который фокусируется линзой
L на экране S.
p x ~
sin
Отсюда немедленно следует
x px ~ 2
44.
Измерение импульса.Пусть частица - это атом в возбужденном состоянии. Когда он
неподвижен, то испускает фотон с частотой 0. Из-за эффекта
Доплера при движении атома к наблюдателю со скоростью v
наблюдаемая частота будет приближенно определяться формулой
0 1 v / c ,
так что
v c / 0 1 .
Достаточно точное измерение импульса mv путем измерения
частоты требует относительно большого времени .
Минимальная ошибка
~
2
.
45.
Таким образом, момент испускания фотона определяется толькос точностью до .
В этот момент импульс атома уменьшается на / c, а его
скорость – на / mc.
Соответственно из-за конечности в координату атома вносится
неопределенность
x
.
mc
Неопределенность импульса составляет
p x m v
а произведение x∙ p :
mc
0
~
2 mc
0
2 mc
x p x ~
~ 2 .
mc
.
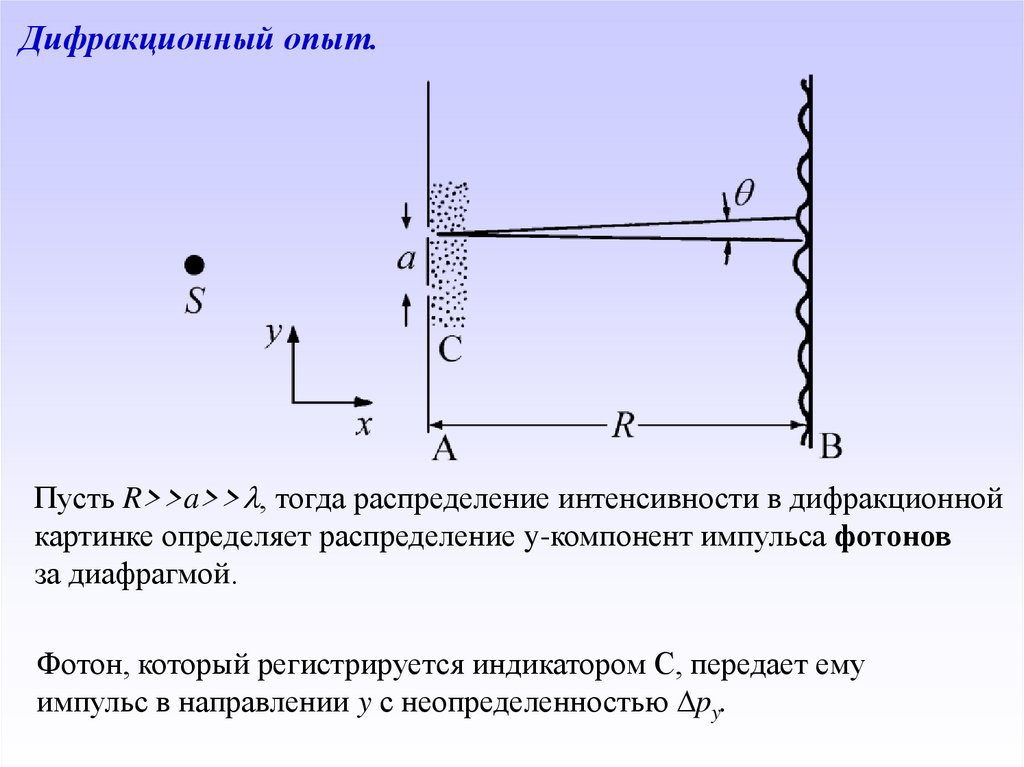
46.
Дифракционный опыт.Пусть R>>a>> , тогда распределение интенсивности в дифракционной
картинке определяет распределение y-компонент импульса фотонов
за диафрагмой.
Фотон, который регистрируется индикатором С, передает ему
импульс в направлении y с неопределенностью py.
47.
Чтобы дифракционная картинка сохранилась, неопределенностьpy должна быть много меньше импульса, необходимого для
попадания фотона в соседний минимум
p y p y
Из теории дифракции известно, что
2a
Чтобы знать через какую щель прошел фотон, неопределенность
y-координаты индикатора должна быть
a
y
2
Таким образом
p y y
2
48.
Аналогично можно исследовать зависимость от времениСоотношение между интервалом времени и разбросом
коэффициентов Фурье по частотам дается выражением
Используя
t 1
E , получаем
t E
Замечание:
Из-за дисперсии скорости волновые пакеты, вообще говоря, расплываются со
временем. Поэтому, строго говоря, нельзя отождествлять частицу с некой
локализованной в пространстве совокупностью волн.
49.
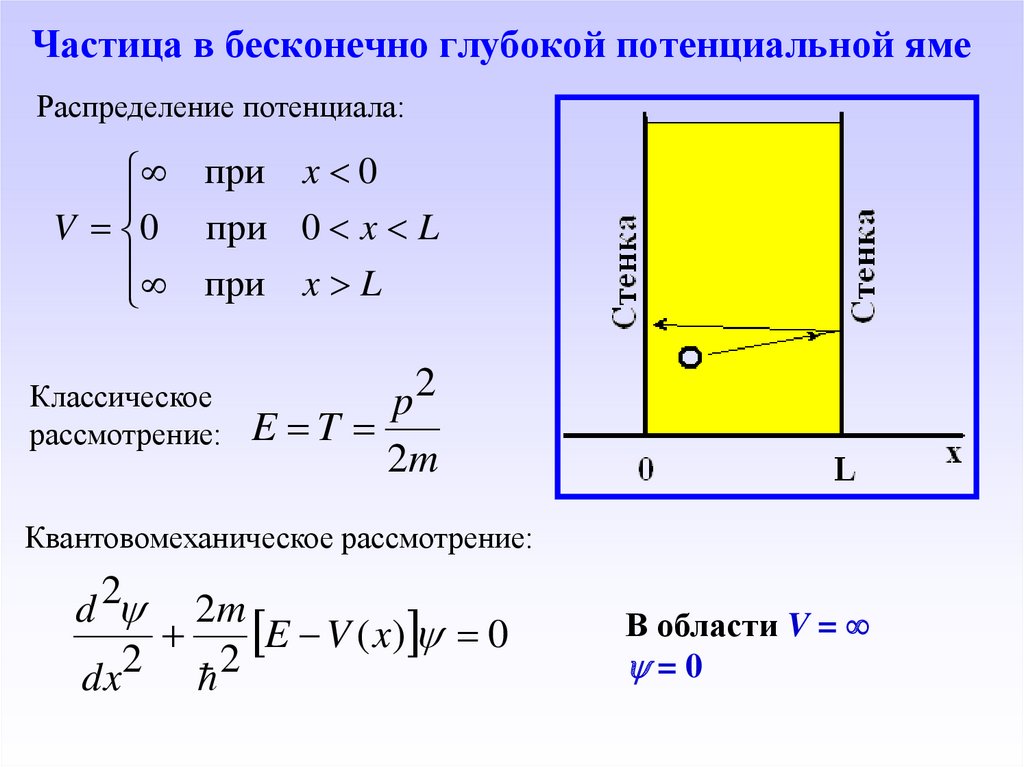
50. Частица в бесконечно глубокой потенциальной яме
Распределение потенциала:при x 0
V 0 при 0 x L
при x L
Классическое
рассмотрение:
p2
E T
2m
Квантовомеханическое рассмотрение:
2
d
2m
E V ( x) 0
dx2 2
В области V =
=0
51.
Внутри ямы уравнение имеет вид:d 2
2
k
0 где
2
dx
2mE
k 2
2
Его решение:
( x) Asin( kx) B cos(kx)
Из гран. условий следует:
Из (0) 0 B 0
Из ( L) 0 kL n , где n 1, 2,...
Отсюда:
2k 2 2 2 2
E
n En ;
2
2m 2mL
2
n
n ( x)
sin
x
L
L
то есть
энергия квантована!















































 physics
physics








