Similar presentations:
Векторная алгебра
1.
Федеральное государственное бюджетное образовательное учреждениевысшего образования
«Оренбургский государственный университет»
Кафедра прикладной математики
И.Г. Руцкова
Электронный курс лекций «Линейная алгебра»,
часть 10
Оренбург 2016
2.
Скалярная проекция вектора на осьa cos a ,l .
прl a a cos a ,l .
(1)
(2)
3.
Геометрический смысл координат вектораa x , y , z ,
a x i y j z k,
,
x a cos , y a cos , z a cos ,
x прOX a a cos ,
y прOY a a cos ,
(5)
z прOZ a a cos .
cos 2 cos 2 cos 2 1
(6)
(4)
4.
Скалярное произведение векторовa b cos a , b .
Обозначения: a b a b cos a , b , (8)
Пример 1.
a 6, b 7 , a , b ;
3
(7)
a ,b a b cos a , b
(9)
1
a ,b a b cos a , b 6 7 21.
2
(10)
(11)
a ,b a b cos a , b a прa b ,
a ,b a b cos a , b b прb a
5.
Свойства скалярного произведенияa ,b a ,b ,
a , b a ,b
(12)
a ,b b пр a b пр
b
b
(14)
a b пр a a ,b
a , b b,a b,a a ,b
a b ,c a ,c b ,c ,
(13)
b
a ,b c a ,b a ,c
(15)
6.
Пример 2.Решение.
(5 a 2 b ,6 b 3 c ) (5 a ,6 b 3 c ) ( 2 b ,6 b 3 c )
(5 a , 6 b ) (5 a , 3 c )
( 2 b , 6b) ( 2 b , 3 c )
5 6 ( a , b ) 5 3 ( a , c ) 2 6 ( b , b ) 2 3 ( b , c )
30 ( a , b ) 15 ( a , c ) 12 ( b , b ) 6( b , c )
30 | a | | b | cos a , b 15 | a | | c | cos ( a , c ) 12 | b |2 6 | b | | c | cos ( b , c )
1
1
30 4 5 0 15 4 8 12 25 6 5 8 0 240 300 120 420
2
2
7.
Формула для определения скалярного произведения векторов,заданных своими координатами
Теорема 8.
8
a ,b x x
1
2
y1 y2 z1 z2 .
(16)
a ,b x i y j z k , x
Доказательство.
1
1
1
2
i y2 j z 2 k
x1 i , x2 i x1 i , y2 j x1 i , z2 k y1 j , x2 i y1 j , y2 j y1 j , z2 k
z1 k , x2 i z1 k , y2 j z1 k , z2 k x1 x2 i , i x1 y2 i , j x1 z2 i ,k
x1 i , x2 i y2 j z2 k y1 j , x2 i y2 j z2 k z1 k , x2 i y2 j z2 k
y1 x2 j , i y1 y2 j , j y1 z2 j ,k z1 x2 k , i z1 y2 k , j z1 z2 k ,k
i , i i 2 1, j , j
2
j 1,
k , k k 2 1
x1 x2 y1 y2 z1 z2
i , j j , i 0, i , k k , i 0, j , k k , j 0,
Пример 3.
a 3;1;4 ,
b 2;3; 5 ;
a ,b 3 2 1 3 4 5 6 3 20 26 3 23
8.
Приложения скалярного произведения9.
10.
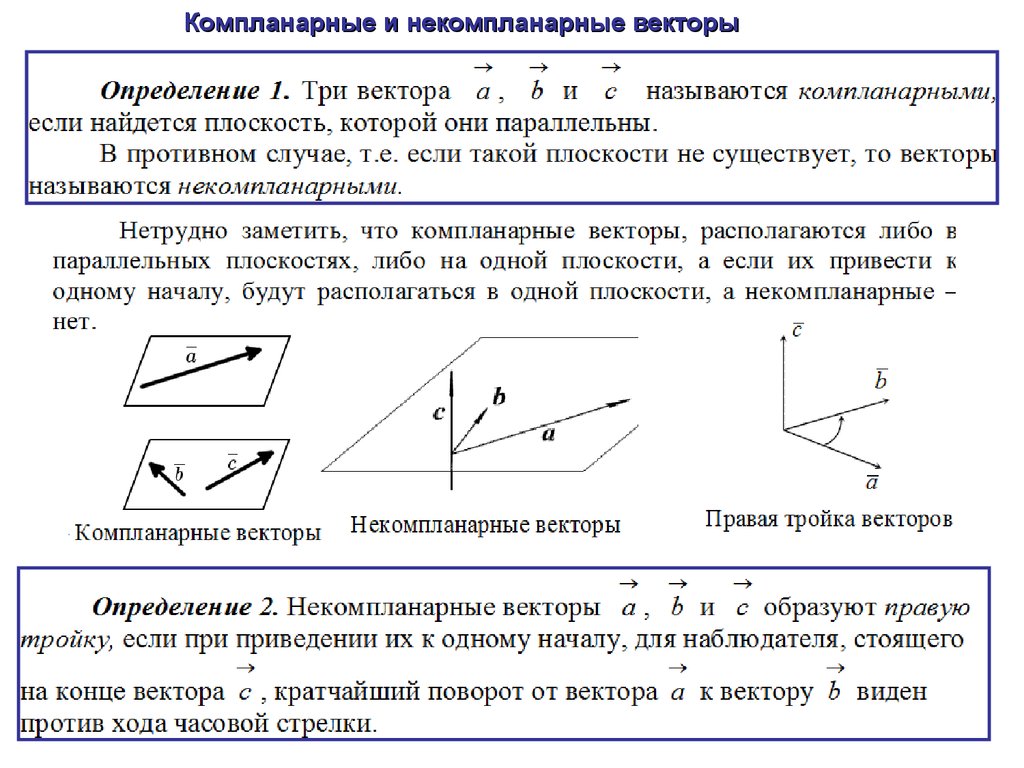
Компланарные и некомпланарные векторы11.
Векторное произведение векторов: определение1)
с a b ,
Пример 1.
1
с b;
3) | c | | a | | b | sin a , b .
с a ,b
5
| a | 8, | b | 4 , a , b
;
6
с a,
1
a
,
b
|
a
|
|
b
|
sin
a
,
b
8
4
16
2
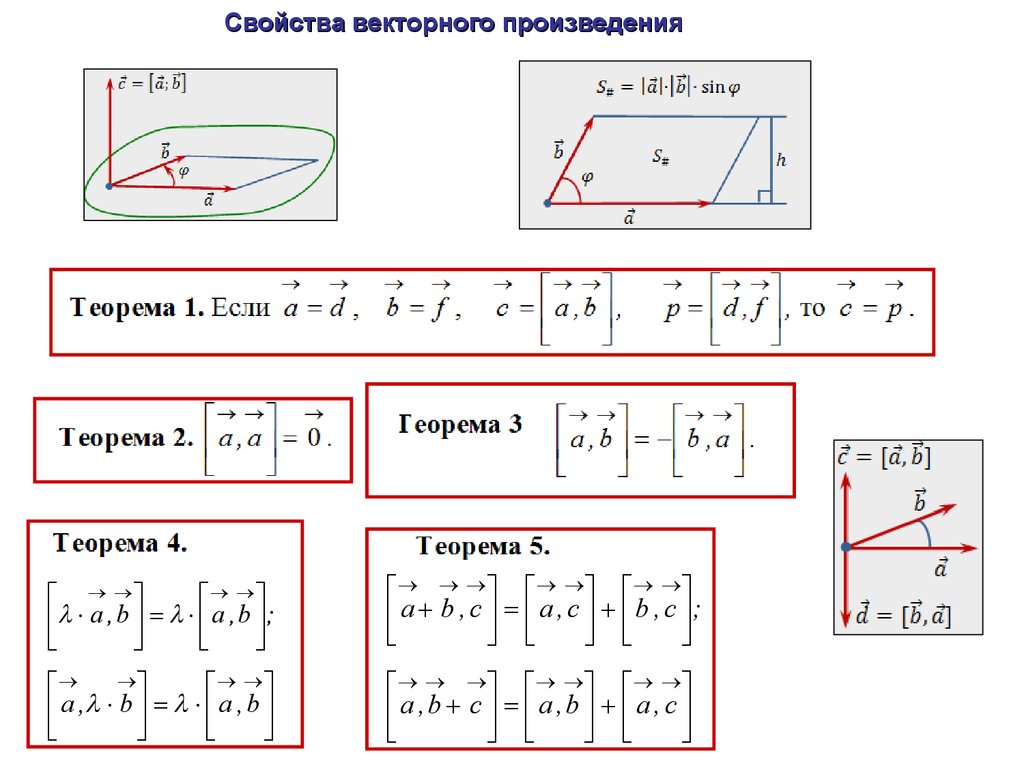
12.
Свойства векторного произведенияa , b a , b ;
a b , c a , c b , c ;
a , b a , b
a ,b c a ,b a , c
13.
Пример 2. | a | 3, | b | 4 , a , b .6
Найдите
Решение.
5 a 2 b , b
5 a 2 b , b 5 a , b 2 b , b 5 a , b 2 b , b 5 a , b 2 0
1
5 a , b 5 | a | | b | sin a , b 5 3 4 30
2
j, j 0,
i , i 0,
k i,
k j,
| i | | j | sin i , j 1 1 sin 1;
2
i , j k;
k ,k 0 .
j , i i , j k
| k | | i | | j | sin i , j ;
j ,k i
k , j i
k , i j
i ,k j
14.
Определение векторного произведения векторов, заданных координатамиa , b y1 z 2 y 2 z1 ; x1 z 2 x2 z1 ; x1 y 2 x2 y1
a , b x1 i y1 j z1 k , x2 i y 2 j z 2 k
Доказательство.
x1 i , x2 i y 2 j z 2 k y1 j , x2 i y 2 j z 2 k z1 k , x2 i y 2 j z 2 k
x1 i , x2 i x1 i , y 2 j x1 i , z 2 k y1 j , x2 i y1 j , y 2 j y1 j , z 2 k
z1 k , x2 i z1 k , y2 j z1 k , z2 k x1x2 i , i x1 y2 i , j x1z2 i , k
y1x2 j , i y1 y2 j , j y1z2 j , k z1x2 k , i z1 y2 k , j z1z2 k , k
0 x1 y2 k x1z2 j y1x2 k 0 y1z2 i z1x2 j z1 y2 i 0
y1 z 2 z1 y 2 i z1 x2 x1 z 2 j x1 y 2 y1 x2 k
15.
Практический алгоритмa , b y1 z 2 y 2 z1 ; x1 z 2 x2 z1 ; x1 y 2 x2 y1
y1
z1
y2
z2
y1z2 y2 z1 ,
y1
a ,b y
2
x1
y1
z1 1
x2
y2
z2
i
j
k
1 1
i
y1
z1
y2
z2
x1
z1
x2
z2
z1
z2
1
1 2
i
j
x1z2 x2 z1 ,
x1
z1
x2
z2
x1
z1
x2
z2
1
i
a , b x1
x2
Пример 3.
a 0 ,1,4 ,
b 2 ,3,7
i
a ,b 0
2
j
1
3
j
1 3
j
y1
y2
k
x1
y1
x2
y2
x1
x2
y1
x1
y1
x2
y2
x1 y 2 x2 y1
k
y1
i
y2
y2
z1 x1
j
z2
x2
z1 x1
k
z2
x2
k
z1
z2
k
4
7
1 4 0 4 0 1
i
j
k
3 7
2 7
2 3
5 i 8 j 2 k
y1
y2
16.
Приложения векторного произведенияa ,b
sin a , b
| a | | b |
Пример 4.
Решение.
2 a 5 b ,3 a 4 b 2 a ,3 a 4 b 5 b ,3 a 4 b
2 a ,3 a 2 a ,4 b 5 b ,3 a 5 b ,4 b
6 a , a 8 a , b 15 b , a 20 b , b 6 0 8 a , b 15 a ,b 20 0 23 a , b
17.
Приложения векторного произведенияS ABCD
S ABC
AB , AD
1
2
AB , AC .
Пример 5.
AB 3,2 ,4 ;
Решение.
i
j
AB
,
AC
3 2
1 7
AC 1,7 ,5
k
2 4 3
4 3 2
4 i
j
k
18 i 19 j 23 k ;
7 5
1 5
1 7
5
S ABC
1
2
1
AB , AC 2
18 2 19 2 23 2 1
2
1214 .
18.
Смешанное произведение векторовa b c a , b , c
19.
Свойства смешанного произведенияТеорема 1.
1) a b c b a c b c a c b a c a b a c b , a , b , c .
2)
a , b , c ; R
a b c a b c ;
3)
a b c a b c ;
a1 a2 b c a1 b c a2 b c ,
a b1 b2 c a b1 c a b2 c ,
a b c1 c2 a b c1 a b c2 .
Замечание.
a b c a b c .
a1 ,a2 , b , c ;
a ,b1 ,b2 , c ;
a , b ,c1 ,c2 .
a b c a , b , c a , b , c
20.
Свойства смешанного произведенияПример 1.
Доказательство.
a b b c c a a b c c a b b c c a
a b c a a c c a b b c a b c c a
a b c a b a a c c a c a 0 b c c b c a a b c 0 0 0 0 b c a
a b c b a c a b c a b c 2a b c
21.
Определение смешанного произведения векторов, заданных координатамиТеорема 2.
a x1 , y1 , z1 , b x2 , y2 , z2 , c x3 , y3 , z3 ,
Доказательство.
a b c a , b , c ,
x1
a b c x2
y1
y2
z1
z2
x3
y3
z3
a , b y1z2 y2 z1 ; x1z2 x2 z1 ; x1 y2 x2 y1 ,
a b c a , b , c y1z2 y2 z1 x3 x1z2 x2 z1 y3 x1 y2 x2 y1 z3 .
x1
x2
x3
y1
y2
y3
Пример 2.
z1
y
z2 x3 1 3 1 1
y2
z3
z1
x
y3 1 3 2 1
z2
x2
z1
x
z3 1 3 3 1
z2
x2
y1
y2
x3 y1z2 y2 z1 y3 x1z2 x2 z1 z3 x1 y2 x2 y1
a 1; 2; 3 , b 1; 0; 6 , c 3; 2; 4 ;
1 2 3
a b c 1 0 6 0 6 36 0 12 8 62
3
2 4
22.
Приложения смешанного произведения векторовДоказательство.
a ,b S e .
a b c a , b , c S e ,c S e , c S | e | | c | cos S | c | cos ,
| c | cos пр с h
e
| c | cos пр с h ,
e
cos 0 ,
a b c S h
a b c S h
23.
Приложения смешанного произведенияПример 3.
AB 3; 6; 4 ,
AC 1; 1; 0 ,
AD 2; 6; 7 ;
3 6 4
1
37
V
|
37
|
.
ABCD
AB AC AD 1 1 0 21 24 0 8 0 42 37 ,
6
6
2 6 7
24.
Приложения смешанного произведенияДоказательство.
Доказательство.
А, B , C , D AB , AC , AD AB , AC , AD - компланарн ы
AB AC AD 0






















 mathematics
mathematics








