Предмет математического анализа

1. ПРЕДМЕТ МАТЕМАТИЧЕСКОГО АНАЛИЗА

2. Основные понятия

Математический
анализ – это раздел
высшей математики, в рамках которого
изучаются переменные величины и
исследуются их зависимости.
Все, что может быть измерено,
называют величиной.

3.

Основные группы величин
Переменные величины:
скорость;
время;
давление;
и т.п.
Постоянные величины:
количество дней в
неделе;
ускорение свободного
падения;
и т. п.

4. Переменные величины:

Непрерывные
величины –
это величины,
значения которых
заполняют
некоторый
промежуток
Дискретные
величины –
это величины,
значения которых
изолированы

5. Обозначения:

= f (x) – функция одной
переменной;
y
D
(y) – область определения функции;
E
(y) – множество значений функции.

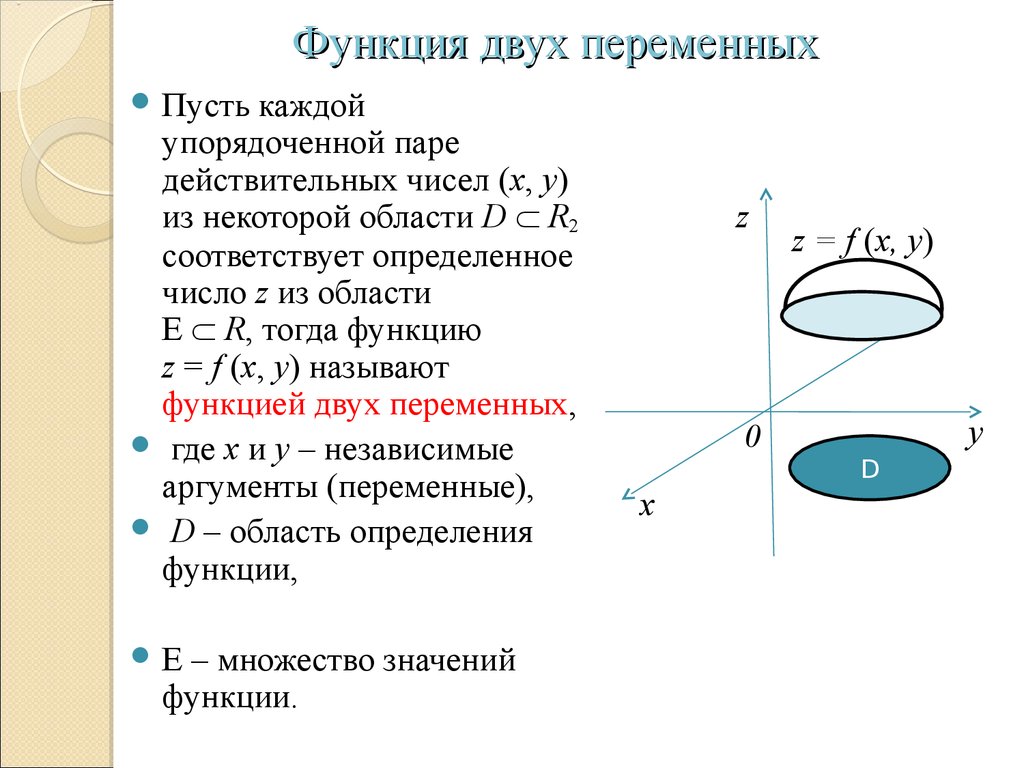
6. Функция двух переменных

Пусть
каждой
упорядоченной паре
действительных чисел (x, y)
из некоторой области D R2
соответствует определенное
число z из области
E R, тогда функцию
z = f (x, y) называют
функцией двух переменных,
где x и y – независимые
аргументы (переменные),
D – область определения
функции,
E
– множество значений
функции.
z
0
x
z = f (x, y)
y
D

7. Основные элементарные функции:

степенная
функция;
показательная функция;
логарифмическая функция;
тригонометрическая функция;
обратная тригонометрическая функция.

8.

9. Область определения функций

10. Область определения функций

11. Определение:

Функция, составленная из основных
элементарных функций называется
элементарной, если:
1)в своей области определения она
задается одним аналитическим
выражением;
2)она получена с помощью конечного
числа арифметических операций.

12.

Примеры
элементарных функций
x - sin 5 x + ln(3x + 2)
y=
tg 7 x - 45 x - 6
6
y = ln(4 x + 2) - e
6 x -1
Примеры
неэлементарных функций
2
3
y = 1 + 5 x + 6 x - 7 x + .....
ì2 x, x < 0;
y=í
î 5, x ³ 0.

13. Способы задания функции одной переменной

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ
одной переменной
графический;
2. табличный;
3. аналитический:
а) явный вид:
у = f (x),
б) неявный вид: F (x, y) = 0,
в) параметрический вид: ì x
1.
= x (t ),
í
î y = y (t ).
t1 £ t £ t2

14. Спасибо за внимание!!! =)