Similar presentations:
Введение в математический анализ
1. Тема: ВВЕДЕНИЕ В Математический анализ
Тема: ВВЕДЕНИЕВ МАТЕМАТИЧЕСКИЙ АНАЛИЗ
2. §1. МНОЖЕСТВА И ФУНКЦИИ
ОПР. Под множеством понимаетсясовокупность
объектов
произвольной
природы.
Эти
объекты
называются
элементами множества.
Множества
обозначаются
обычно
заглавными латинскими буквами: A, B, C и
так далее, а их элементы – строчными: a, b,
c,...
3. Основные числовые множества:
1,2,..., n,... - множество натуральных чисел;Z 0, 1, 2,..., n,...
- множество целых чисел;
m
m Z, n
n
-
множество рациональных
чисел
(множество
конечных
и
периодических десятичных дробей);
4.
R -множество
действительных
(вещественных) чисел − это множество
периодических
и
непериодических
десятичных дробей - числовая ось (прямая):
x0 1 0 1
x0
x
важнейшее свойство действительных
чисел
свойство
непрерывности:
действительные числа сплошь заполняют
числовую
ось,
т.е.
между
двумя
различными действительными числами
всегда
можно
вставить
новое
действительное число.
5. § 2. Функции, их свойства. График функции
Пусть даны два непустых множества X , Y .Соответствие f , которое каждому
элементу x множества X сопоставляет
единственный элемент y множества Y,
называется функцией и обозначается
y f ( x) или f : X Y .
Множество X D f – область определения
функции,
E f { y y f ( x), x X } – множество значений.
6.
Пусть задана функция y f ( x).Если элементами множеств Х и У являются
действительные числа, т. е. x , y , то
функцию f называют числовой функцией.
Переменная
x называется при этом
аргументом или независимой переменной,
а y – функцией или зависимой переменной.
Относительно величин x и y говорят,
что они находятся в функциональной
зависимости.
f (c) – частное значение функции f при x c.
7. График функции
ОПР. Графиком функции y y( x), x X R.является множество всех точек x, y
плоскости Oxy ,
для каждой из которых значение аргумента
x является абсциссой,
а значение функции y - ординатой.
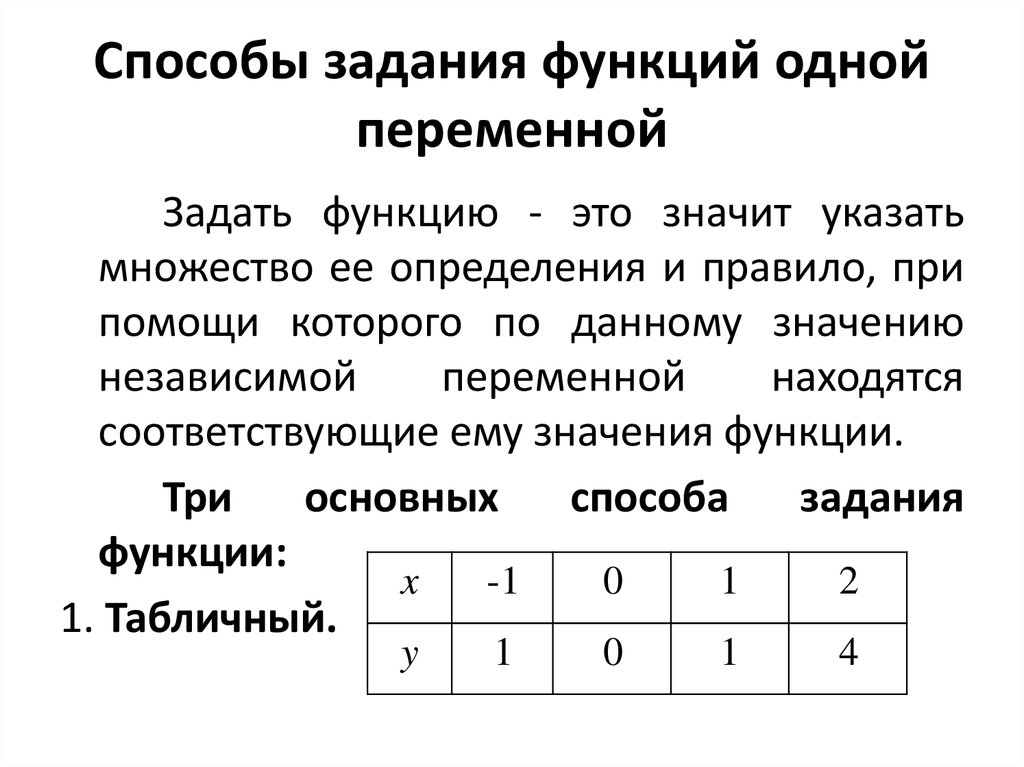
8. Способы задания функций одной переменной
Задать функцию - это значит указатьмножество ее определения и правило, при
помощи которого по данному значению
независимой
переменной
находятся
соответствующие ему значения функции.
Три
основных
способа
задания
функции:
x
-1
0
1
2
1. Табличный.
y
1
0
1
4
9.
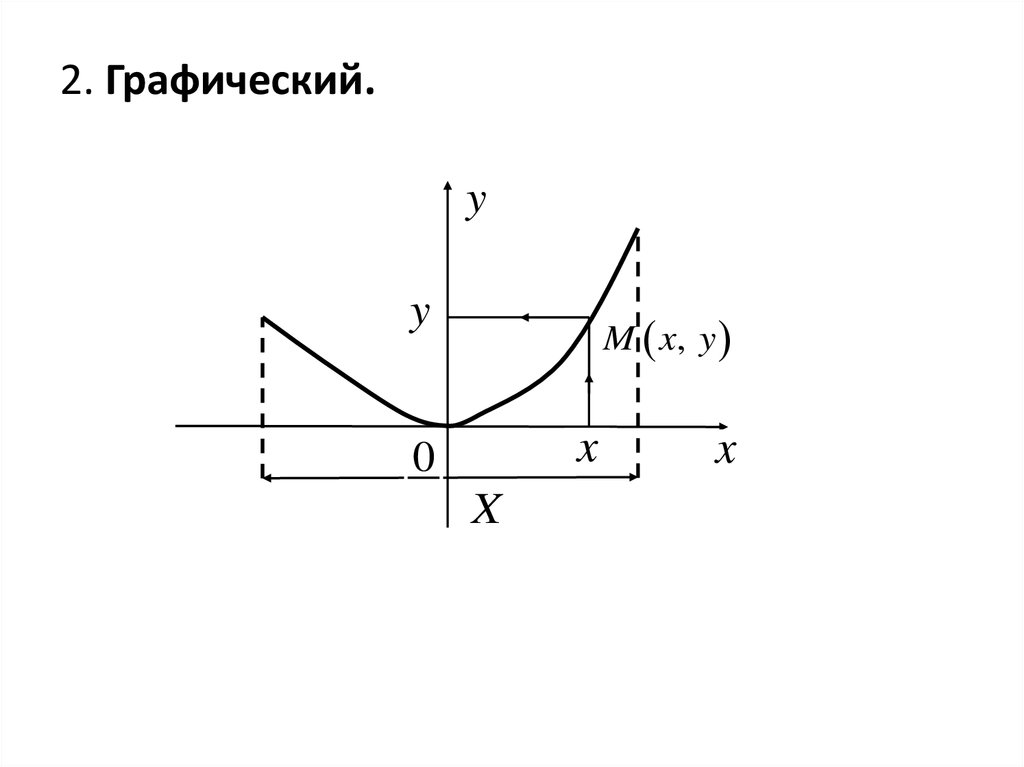
2. Графический.y
y
M x, y
x
0
X
x
10.
3. Аналитический.Например, y 1 x2
11. сложная функция
СЛОЖНАЯ ФУНКЦИЯПусть функция y x
отображает
числовое множество X D в множество
Y E , а функция z f y
отображает
множество E D fв множество E f.
Тогда функция z f x
называется сложной функцией, или
суперпозицией функций и f
.
Она определена на множестве X D и
отображает его в множество E f .
12.
Функция y x считается промежуточным аргументом для функции z f x .Например, функцию z sin 2 x можно
рассматривать как сложную, образованную
суперпозицией функций
y 2 x и z sin y.
13. Свойства функций одной переменной
1. Четность и нечетность функции.2. Периодичность функции.
3. Монотонность функции.
4. Ограниченность функции.
14. §2. Предел функции
15. Окрестность точки
Окрестностью B a точки a R( конечной точки) называется любой интервал,
содержащий эту точку: B a , a
(
)
a
x
-окрестностью B a точки а называется
интервал вида a , a
(
a
a
)
a
x
16.
Если из окрестности B a саму точкуa R удалить, то получим проколотую
Bˆ a окрестность этой точки.
(
a
)
x
17.
Число A называется пределом функцииy f ( x) при x a , если для любого, как
угодно малого 0, найдется такое число
0 , что для всех х, удовлетворяющих
условию x a , будет выполнятся
неравенство f x A
C помощью логической символики:
A lim f x 0 0
x a
0 x a
f x A
18. Геометрический смысл предела функции
yy f x
A
A
A
0
a a a
x
19.
A lim f x .x a
это значит, что для любой -окрестности
точки A найдется такая проколотая окрестность точки ɑ , что для всех x из этой
-окрестности соответствующие значения
функции f ( x )
лежат в -окрестности
точки A.
Т. Е. точки графика функции y f ( x ) лежат
внутри полосы шириной 2 ,
ограниченной прямыми y A и
y A
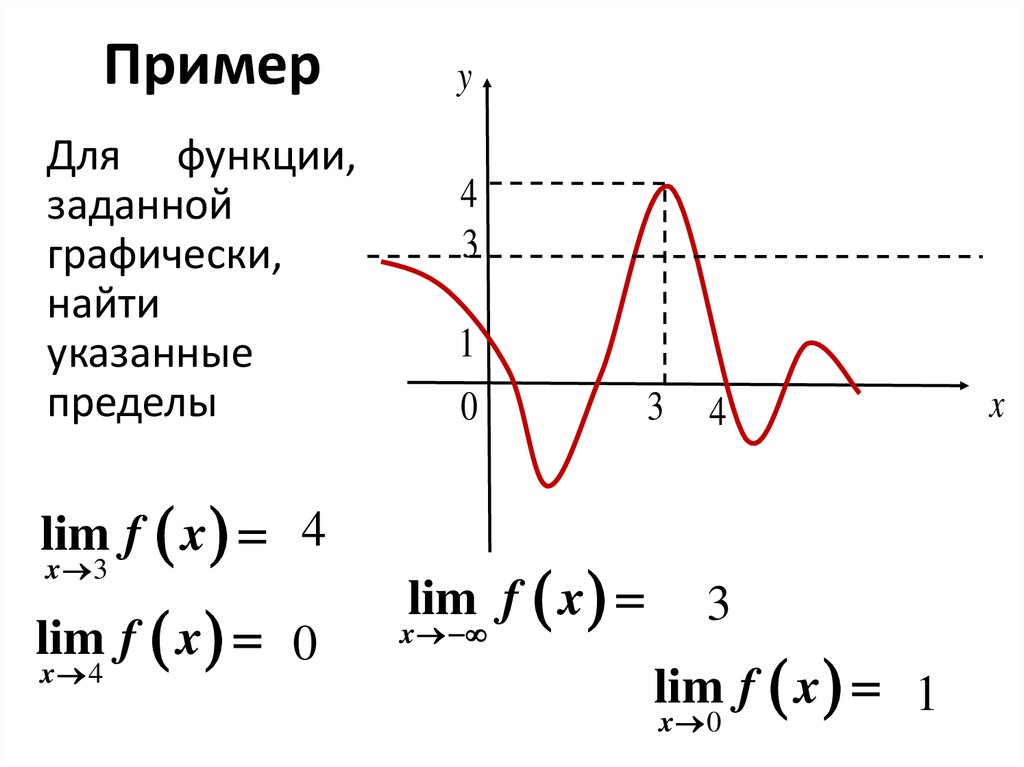
20. Пример
Для функции,заданной
графически,
найти
указанные
пределы
lim f x 4
x 3
lim f x 0
x 4
y
4
3
1
0
lim f x
x
3
4
3
lim f x 1
x 0
x
21. 4.2. Односторонние пределы
ОПР. Если значения функции y f ( x)стремятся к пределу A1 при x a причем,
х принимает только значения меньше a , то
записывают A1 lim f x
x a 0
и A1 называют пределом слева в точке a .
A1 lim f x B A1 Bˆ a
x a 0
x Bˆ a , x a f x B A1
22.
Если х принимает толькобольшие чем a , то записывают
значения
lim f x A2
x a 0
и A2 называют пределом справа в точке a
23.
Значения односторонних пределовобычно записывают следующим образом:
для предела слева A1 lim f x f a 0
x a 0
и предела справа A2 lim f x f a 0
x a 0
24.
Если существует lim f x A , тоx a
существуют и оба односторонних предела,
причем A A1 A2
Справедливо и обратное утверждение:
если существуют оба предела lim f x
x a 0
и lim f x и они равны, то существует
x a 0
предел lim f x и A A A
x a
1
2
Если же A1 A2 , то lim f x не
x a
существует.
25. Пример
yДля функции,
заданной
графически,
найти
указанные
пределы
lim f x
x 0
lim f x 4
x 0
3
4
3
0
1
3
lim f x
x 3 0
x
4
lim f x 4
x 3 0
26. 4.3. Основные теоремы о пределах
Предположим,что
существуют
конечные пределы функций f x и g x
при x a :
lim f x A, lim g x B.
x a
x a
Тогда
имеют
место
следующие
основные свойства конечных пределов.
27.
Поскольку для основных элементарныхфункций во всех точках их области
определения имеет место свойство
lim f x f a ,
x a
то при вычислении пределов, прежде всего
вместо х подставляем предельное значение
и, если значение определено, то используя
арифметические операции над пределами,
вычисляем предел.
28. Арифметические операции над пределами:
1) lim c f x c lim f x , где c constx a
x a
Пример. 1)
2)
lim 3 x 3 lim x 3 2,
x 2
x 2
lim (4 x ) 4 lim x 4 ( 3) 36.
2
x 3
2
x 3
2
29.
2)lim f x g x
x a
lim f x lim g x A B;
x a
x a
Пример. 1)
lim(4 x 5 x 3)
2
x 1
4 lim x 5 lim x lim3 4 1 5 1 3
2
x 1
6.
2
x 1
x 1
30.
3) lim f x g x lim f x lim g x ;x a
x a
x a
Пример.
1) lim( x e ) lim x lim e 1 e e.
2 x
x 1
2
x 1
x
x 1
2
1
31.
4)lim f x
f x x a
lim
,
x a
g
x
lim g x
lim g x 0
x a
x a
x 3) 22 3 7
x 3 lim(
1) lim
x 2
7
x 2 x 1
lim( x 1)
2 1 1
2
2
x 2
32.
При вычислении пределов используютследующие равенства:
C
0,
C
0 ,
0
C 0,
C ,
0
C , , 0,
0 ,
C const .
33. Пример
1. Вычислить lim x 7 x 4x 2
Решение.
2
lim x 7 x 4 lim x lim 7 x lim 4
2
2
x 2
x 2
x 2
2 7 * 2 4 6
2
x 2
34.
2. Вычислитьx 3x 2
lim 2
x 1 x x 4
2
Решение.
x 3 x 2
x 3 x 2 lim
x 1
lim 2
2
x 1 x x 4
lim x x 4
2
2
x 1
1 3 2 0
0
1 1 4 6
35.
Однако, часто при подстановке в f xвместо x предельного значения а
получаются выражения вида:
0
;
;
0
;
1
;
0
и
другие,
которые
называются
неопределенностями и которые нужно
«раскрывать» специальными методами.
36. Замечательные пределы
При вычислении пределов выражений,содержащих тригонометрические функции,
часто используют предел
sin x
lim
1,
x 0
x
который
называется
замечательным пределом.
первым
37.
Справедливы также равенстваsin ( x )
lim
1,
( x ) 0 ( x )
tg ( x )
lim
1,
( x ) 0 ( x )
arcsin ( x )
lim
1,
( x ) 0
( x )
arctg ( x )
lim
1,
( x ) 0
( x )
38.
Равенстваx
1
1
1 t t e,
lim 1 e , lim
t 0
x
x
называются вторым замечательным
пределом.
Здесь число е - предел числовой
n
последовательности
1
1 , n 1,2,3,...
n
n
1
lim 1 e .
n
n
39.
e является числом иррациональным,е= 2,718281828459045….
При практических вычислениях обычно
ограничиваются первыми двумя знаками
после запятой.
Число е играет очень важную роль в
математическом анализе.
Показательная функция с основанием е,
называется экспонентой: y e x
40.
Логарифм по основанию е называетсянатуральным
логарифмом
и
обозначается ln x. Таким образом:
ln x log e x .
41. Раскрытие некоторых видов неопределенностей
Неопределенность вида0
0
А) При вычислении предела дроби,
содержащей
тригонометрические
функции, в случае, когда предел и
числителя, и знаменателя равен нулю,
можно
использовать
первый
замечательный предел.
42. Пример
sin7 xНайти предел функции lim
x 0 sin5 x
Решение.
1
sin 7 x
7x
sin 7 x
7x
7
0
7
x
lim
lim
lim
x 0 sin 5 x
x 0 sin 5 x
x 0 5 x
5
0
5x
5x
1
43.
Б) При нахожденииP x
lim
x a Q x отношения двух
многочленов P x и Q x , если P a Q a 0
то следует числитель и знаменатель дроби
разделить на разность x a один или
несколько
раз,
пока
не
исчезнет
неопределенность.
44. Пример
23
x
x 2
Вычислить lim
x 1
x2 1
Решение. При x 1 числитель и знаменатель
дроби стремятся к нулю. Используем
2
ax
bx c a x x1 x x2
формулу
3 x x 2 3 x
2
2
x 1 3 x 2 x 1
3
3 x 2 x 1
3 x2 x 2
3x 2 5
lim
lim
lim
2
x 1
x 1 x 1 x 1
x 1 x 1
2
x 1
45.
0В) При раскрытии неопределенности 0 в
случае иррациональных выражений в
числителе и (или) знаменателе следует
избавится от иррациональности путем
умножения
на
соответствующее
сопряженное выражение или производя
замену переменных.
46. Пример
Вычислить2x 1 3
lim
x 4
x 4
x 3
Решение. При
числитель и
знаменатель
дроби
равны
нулю.
Домножим числитель и знаменатель на
выражение, сопряженное числителю
2 x 1 3 , получим
47.
2x 1 3 0lim
lim
x 4
x 4
0 x 4
2x 1 3
2x 1 3
x 4 2 x 1 3
2 x 1 9
2 x 8
lim
lim
x 4
x 4 2 x 1 3 x 4 x 4 2 x 1 3
2 x 4
2
2 1
lim
lim
.
x 4
x 4 2 x 1 3 x 4 2 x 1 3 3 3 3
В преобразованиях использовали формулу
a b
a b
a b
2
2
a b.
48.
2.2. Неопределенность видаP x
А). При нахождении предела lim
x Q x
отношения двух многочленов P x и Q x
при x числитель и знаменатель дроби
целесообразно разделить на x n, где n –
высшая степень этих многочленов.
49. Пример
4 x4 3 x2 5Найти предел функции lim
x 2 x 7 x 3 3 x 4
Решение. Имеем неопределенность
Разделим числитель и знаменатель
дроби на 4 тогда
x ,
0
0
3
5
4
4
2
2
4
4x 3x 5
4 0 0 4
x
x
lim
lim
3
4
x 2 x 7 x 3 x
x 2 7 3 0 0 3 3
x3 x
0
0





























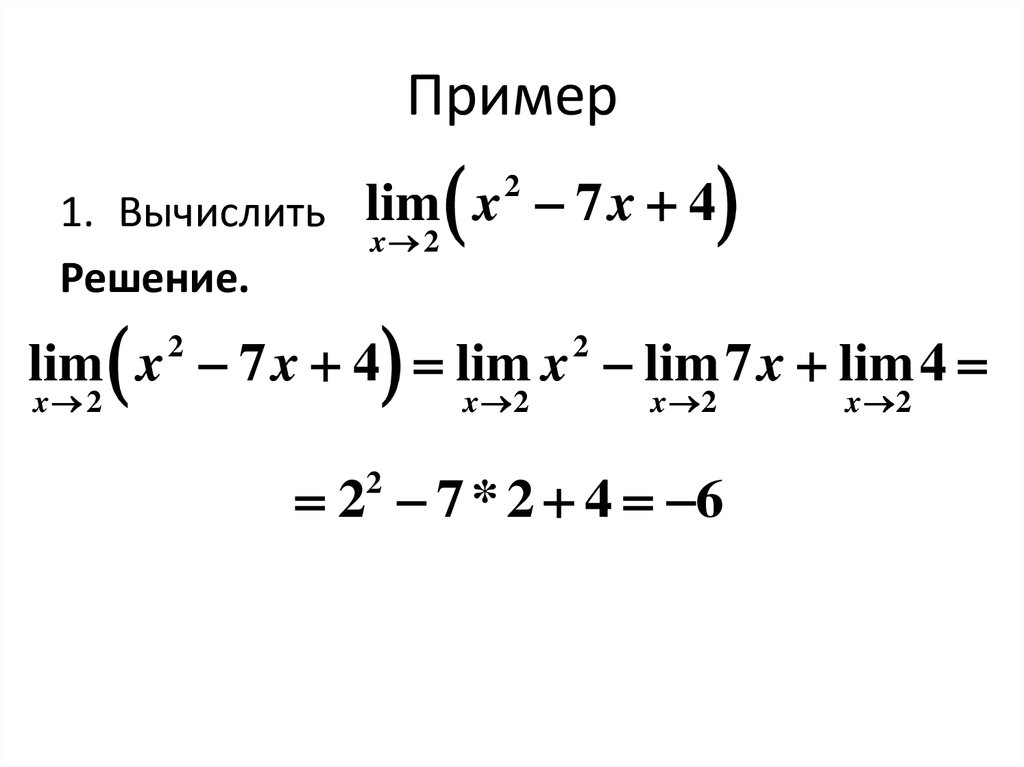
















 mathematics
mathematics








