Similar presentations:
Математический анализ. Дифференциальное исчисление функции одной переменной
1. Математический анализ
2.
1. Н.С.Пискунов, Дифференциальное иинтегральное исчисления
2. Л.Д.Кудрявцев, Краткий курс
математического анализа.
3. И.В.Пивоварова, Л.Я.Дубинина,
Л.С.Никулина, Сборник задач по
высшей математике 2003.
3.
1. Высшая математика. Практикум ч.2.Шуман Г.И., Волгина О.А., Голодная Н.Ю.,
Одияко Н.Н.
2. Высшая математика. Практикум ч.3.
Шуман Г.И., Волгина О.А.
3. Высшая математика. Практикум ч.4.
Шуман Г.И., Волгина О.А.
4.
Дифференциальное исчисление функцииодной переменной (производная).
1. Задача, приводящая к понятию
производной.
2. Определение производной.
3. Геометрический смысл производной.
4. Основные правила дифференцирования.
5. Производные основных элементарных
функций.
5. Введение в анализ
6.
• Функцией называется правило, покоторому каждому элементу x некоторого
М соответствует единственный
элемент y другого множества N.
множества
y f x
x
y
- независимая переменная (аргумент);
- зависимая переменная;
М - область определения функции;
N - множество значений функции.
7.
• Графиком функции y f (x) наз.множество точек плоскости XOY , для
каждой из которых абсцисса x
является значением аргумента, а
ордината y - соответствующее значение
данной функции.
8.
Способы задания функции:1) аналитический;
2) табличный;
3) графический.
9. Основные элементарные функции
10.
Постояннаяy conct .
Степенная
y x , n действительное число, n 0.
n
Показательная
y a a 0, a 1 .
x
11.
Логарифмическая y log a x a 0, a 1 .Тригонометрические
y sin x, y cos x, y tgx, y ctgx.
Обратные тригонометрические
y arcsin x, y arccos x,
y arctgx, y arcctgx.
12.
• Окрестностью точки x 0 числовойпрямой называется любой ( ) интервал
a; b содержащий эту точку (U x ).
0
a
Если x U x0 , то
x0
b
a x b.
13.
окрестностью точки x 0
числовой прямой называется
x
;
x
x
U
интервал 0
,т.е. если
x ,
0
то x0 x x0 или x x0 .
0
x0
x0
x0
14.
x0a; b
15.
X x -произвольное множество.Ограниченное сверху:
действител ьное число M : x X x M .
Ограниченное снизу:
действител ьное число M : x X x M .
Ограниченное:
M 0 : x X x M M x M
16. Предел функции
17.
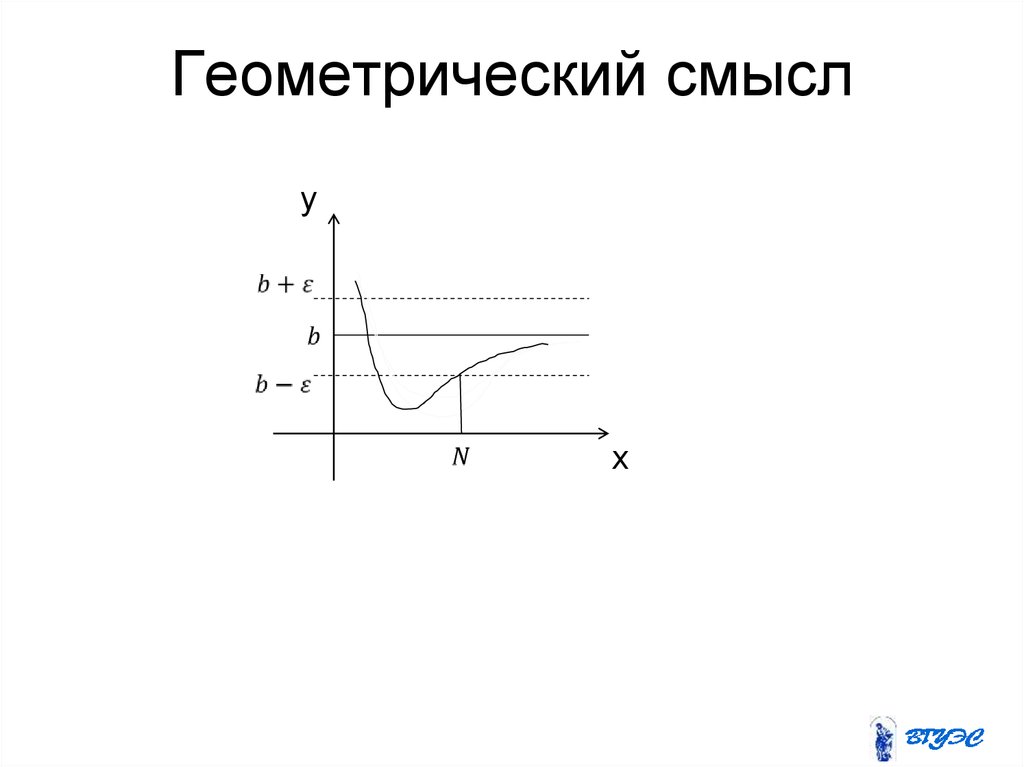
"b"18. Геометрический смысл
yx
19.
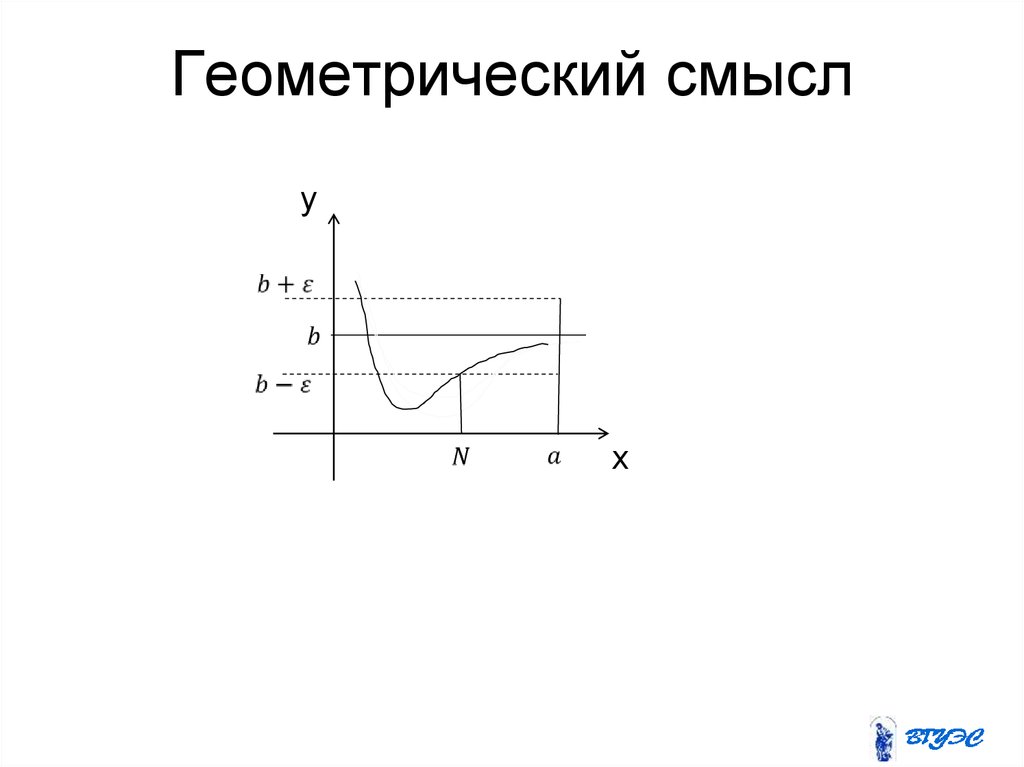
"b"20. Геометрический смысл
yM
x
21.
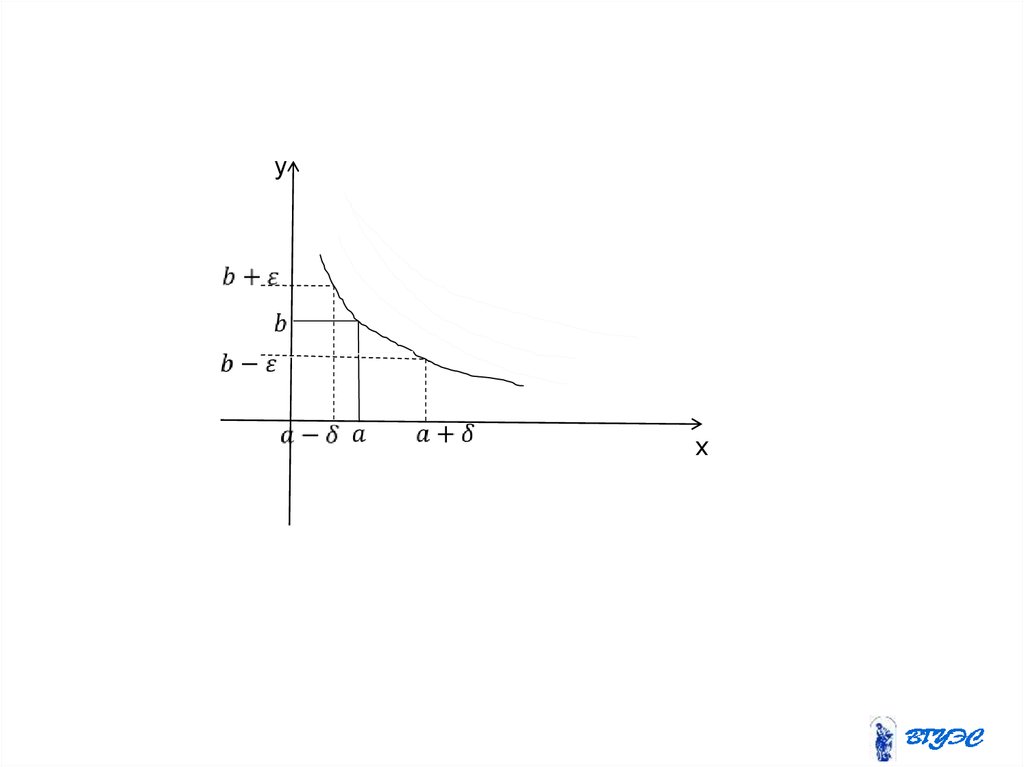
"b"22. Геометрический смысл
yx
23.
"b"24. Геометрический смысл
yM
x
25.
lim f ( x)x a 0
lim f ( x)
x a 0
26.
U a ,U a ,
27.
yx
28.
• Рассмотрим функциюy 2x
x 3 0
x
2
2,5
2,9
2,99 2,999 2,9999
y
4
5
5,8
5,98 5,998 5,9998
x 3 0
x
y
4
3,5
3,1
3,01
3,001
8
7
6,2
6,02
6,002
29.
2 x 6lim
x 3 0
lim 2 x 6
x 3
2
x
6
lim
x 3 0
30. Бесконечно малые функции
y f xa
lim f x 0
x a
x a
31.
32. Свойства бесконечно малых функций
33.
34. Бесконечно большие функции
y f xx a
lim f x .
x a
35.
• Теорема. Еслиx бесконечно малая
1
при x a и x 0 , то
x
бесконечно большая при
x a.
• Теорема. Если f x бесконечно
1
большая функция при x a , то f x
бесконечно малая при x a.
36.
37. Свойства пределов
38.
1) lim C C ;x a
2) lim C f x C lim f x ;
x a
x a
3) lim f x g x lim f x lim g x ;
x a
x a
x a
4) lim f x g x lim f x lim g x ;
x a
x a
x a
f x
lim
f x
5) lim
, lim g x 0.
g x lim g x
x a
x a
x a
x a
39.
6) Еслиlim f ( x) A и lim g ( x) B , то
x a
x a
lim f ( x)
g ( x)
x a
A
B
40. Теорема о зажатой переменной
41. Первый замечательный предел
42.
sin x1
lim
x
x
a
x 0
43.
Доказательство проведем для частногослучая ( x) x , т.е. докажем, что
sin x.
lim
x 0
0
0 ,
x
1
Неопределенность
свойство о пределе
частного не применимо.
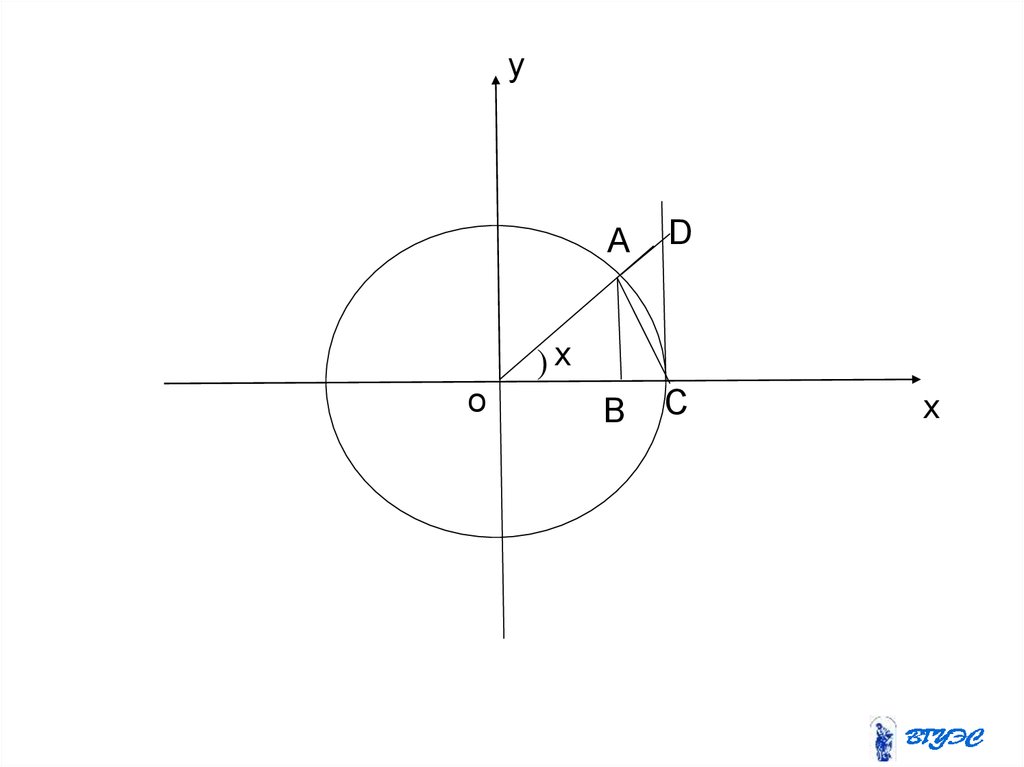
44.
yA
D
B
C
)x
o
x
45.
• Докажем, чтоlim sin x 0
x 0
АС x
и
cos x 1.
lim
x 0
АВ sin x
CD tgx
0 AB AC
0 sin x x
46.
lim0
0
x 0
sin x 0
lim
x 0
lim
x
0
x 0
lim
cos
x
lim
1
sin
x
1
x 0
x 0
2
47.
S OAC S сект .OAC S ODC1
1
1
OC AB OC AC OC CD
2
2
2
AB AC CD
sin x x tgx
x
1
1
sin x cos x
sin x
cos x
1
x
48.
limcos
x
1
sin x
x 0
1
lim
x 0
lim
1
1
x
x 0
x
lim
1
x 0
sin x
49.
tgxlim
1
;
x 0
x
sin x
sin x 1
lim
lim
1
1
1
.
x 0
x cos x x 0 x cos x
x
lim
1;
x 0
tgx
50.
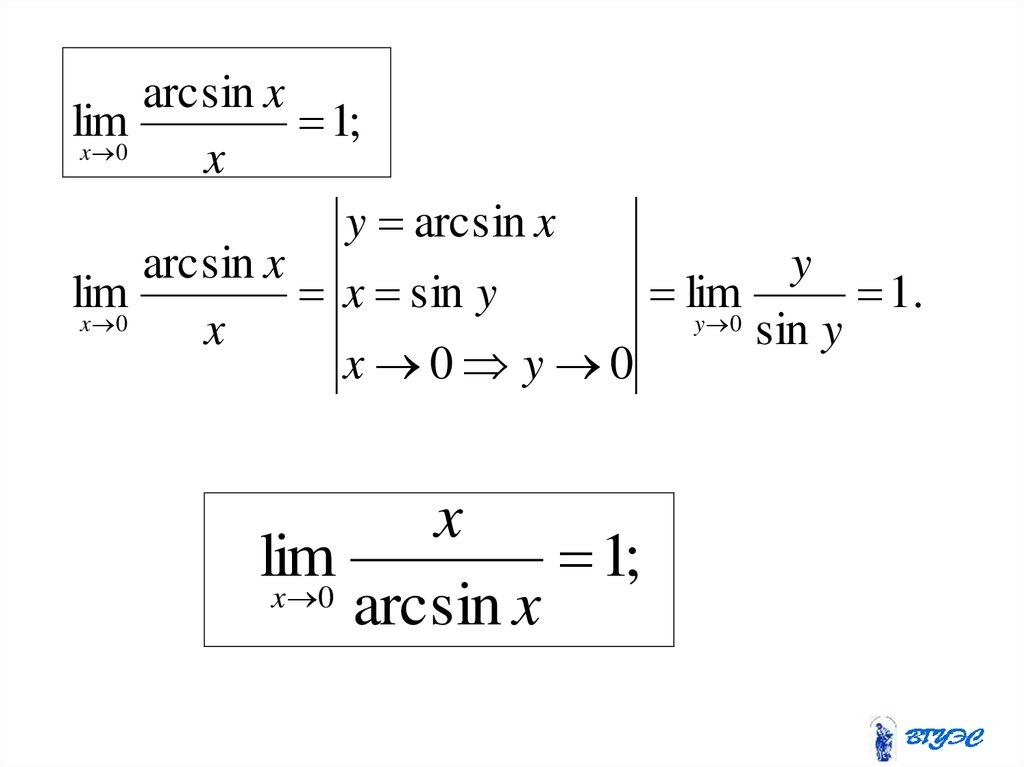
arcsin xlim
1;
x 0
x
y arcsin x
arcsin x
y
lim
x
sin
y
lim
1
.
x 0
y 0
x
sin y
x 0 y 0
x
lim
1
;
x 0
arcsin x
51.
arctgxlim
1
;
x 0
x
x
lim
1
x 0
arctgx
52. Второй замечательный предел
1x
lim
1
x
x
a
x 0
e
x
1
1 e
lim
x
x
1 x e
lim
x 0
1
x
53.
log a x 11
lim
lim log a x 1
x 0
x 0
x
x
1
1
x
x
lim log a x 1 log a lim x 1 log a e.
x 0
x 0
log a x 1
lim
log
e
.
a
x 0
x
ln x 1
lim
ln
e
1
x 0
x
54.
y ax 1a 1 a y 1
y
1
lim
lim
x 0
y 0
x
log a y 1 log a e
x log a y 1
x
x
x 0 y 0
a 1
1
lim
x 0
x
log a e
x
e 1
1
lim
1
x 0
x
log e e
x
55. Сравнение бесконечно малых
56.
• Пусть x и x бесконечно малыефункции при x a :
1) x и x называются б.м. одного
порядка малости при x a , если
существует конечный
x
0
lim
x a x
57.
2) бесконечно малые x и x одногопорядка малости при x a называются
эквивалентными бесконечно малыми,
если
x
1.
lim
x
x a
58.
• Приx 0
sin x
tgx
arcsin x
arctgx
ln x 1
e 1
x
~
~
x
x
~
~
~
~
x
x
x
x
59.
3) бесконечно малая x называетсябесконечно малой более высокого
порядка чем бесконечно малая x при
x a , если
x
0.
lim
x a x
60.
4) если не существует конечногоx
,
lim
x a x
то x и x называются
несравнимыми бесконечно малыми при
x a.
61.
• Теорема. Пусть ( x) ~ 1 ( x) и ( x) ~ 1 ( x)бесконечно малые функции при x a (а
конечно и бесконечно) и существует
( x)
lim
x a
( x)
, тогда существует
1 ( x )
( x)
lim
lim
.
x a
1 ( x) x a ( x)
62.
1 ( x)1 ( x) ( x) ( x)
lim
lim
x a
1 ( x) x a ( x) 1 ( x) ( x)
1 ( x)
( x)
( x)
( x)
lim
lim
lim
lim
x a
( x) x a 1 ( x) x a ( x) x a ( x)
1 ( x)
( x)
( x)
lim
lim
lim
x a
( x ) x a ( x ) x a 1 ( x )
63.
64.
65. Непрерывность функции
66. Непрерывность в точке
67.
• Функция y f x наз. непрерывной вточке , если:
1) функция определена в точке a и
некоторой её окрестности;
a
f x
2) существует lim
x a
;
f
x
f
x
lim
lim
x a 0
x a 0
3) lim f x lim f x f a
x a 0
x a 0
f a
f
x
f
lim
x
lim
x a
x a
68. Классификация точек разрыва
69.
• Точка, в которой нарушаетсянепрерывность функции, называется
точкой разрыва этой функции.
• Точка разрыва a функции y f x
называется точкой разрыва первого рода,
если существуют конечные пределы
f x lim f x
lim
x a 0
x a 0
70.
• Если хотя бы один из одностороннихпределов не существует или равен
бесконечности, то точка a называется
точкой разрыва второго рода.
• Точка разрыва называется точкой
устранимого разрыва функции y f x ,
если
f x lim f x f a .
lim
x a 0
x a 0
71.
a• Пусть
- точка разрыва первого рода
функции y f x . Скачком функции в
точке a
называется
h lim f x lim f x .
x a 0
x a 0
72. Свойства функций непрерывных в точке
73. Непрерывность на отрезке
74.
• Функция y f x называетсянепрерывной на отрезке a; b , если она
определена на этом отрезке, непрерывна
в каждой точке интервала a; b , а на
концах отрезка непрерывна соответственно
слева и справа, т.е.
f x f a
lim
x a 0
f x f b
lim
x b 0
75. Свойства функций непрерывных на отрезке
76.
1.Если функция y f x непрерывнана отрезке a; b , то она достигает на
этом отрезке своего наибольшего и
наименьшего значений.
Следствие. Если функция y f x
непрерывна на отрезке a; b , то она
ограничена на этом отрезке.
77.
2.Если функция y f x непрерывнана отрезке a; b и на его концах
принимает значения разных знаков, то
внутри отрезка a; b существует по
крайне мере одна точка, в которой
значение функции равно нулю.
78.
3. Пусть функция y f x непрерывнана a; b и f a A, f b B, A B.
Тогда для любого числа C ,заключенного
между A и B , найдется точка c a; b ,
такая, что
f c C.
79.
• Пусть дана функция y f x .Рассмотрим два значения её аргумента:
Исходное x 0 и новое x .
Разность x x0 наз.приращением
аргумента в точке x 0 и обозначим x:
x x x0
80.
• Разность y y0 f x f x0 наз.приращением функции в точке x 0 :
y f x f x0 .
x x0 x
y f x0 x f x0
81.
f x f x0lim
x x
0
f x f x0 0
lim
x x
0
f x f x0 y
x x0 x
lim y 0
x 0
82.
• Функция наз. непрерывной в точке.если бесконечно малому приращению
аргумента соответствует бесконечно
малое приращение функции.


































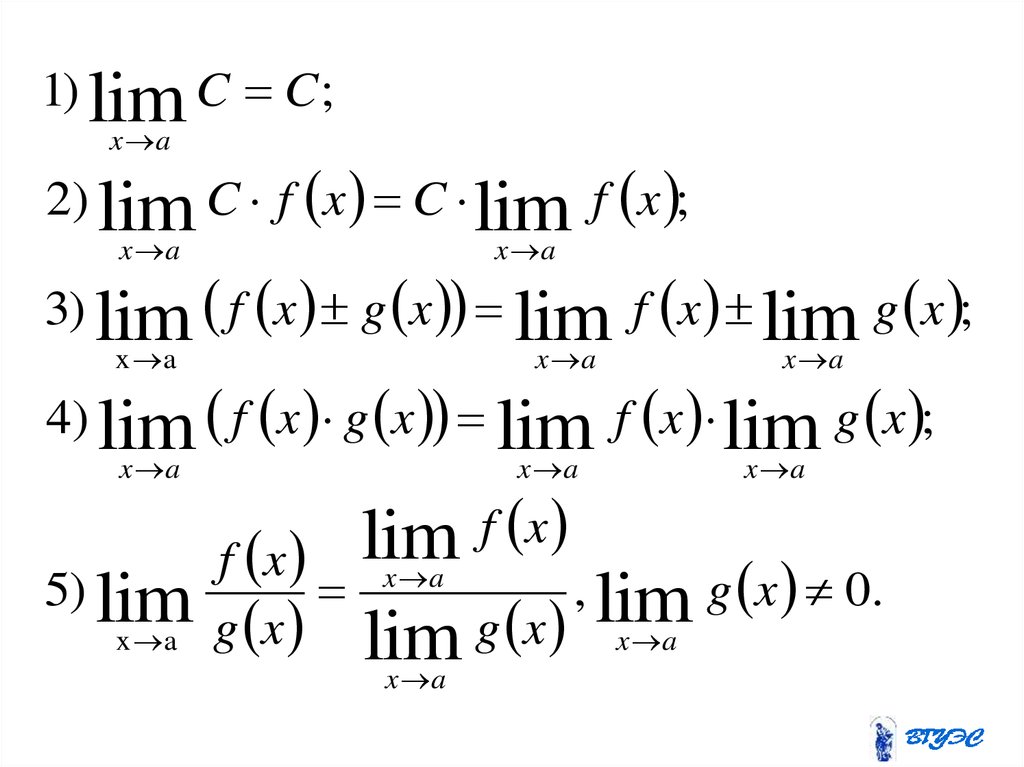



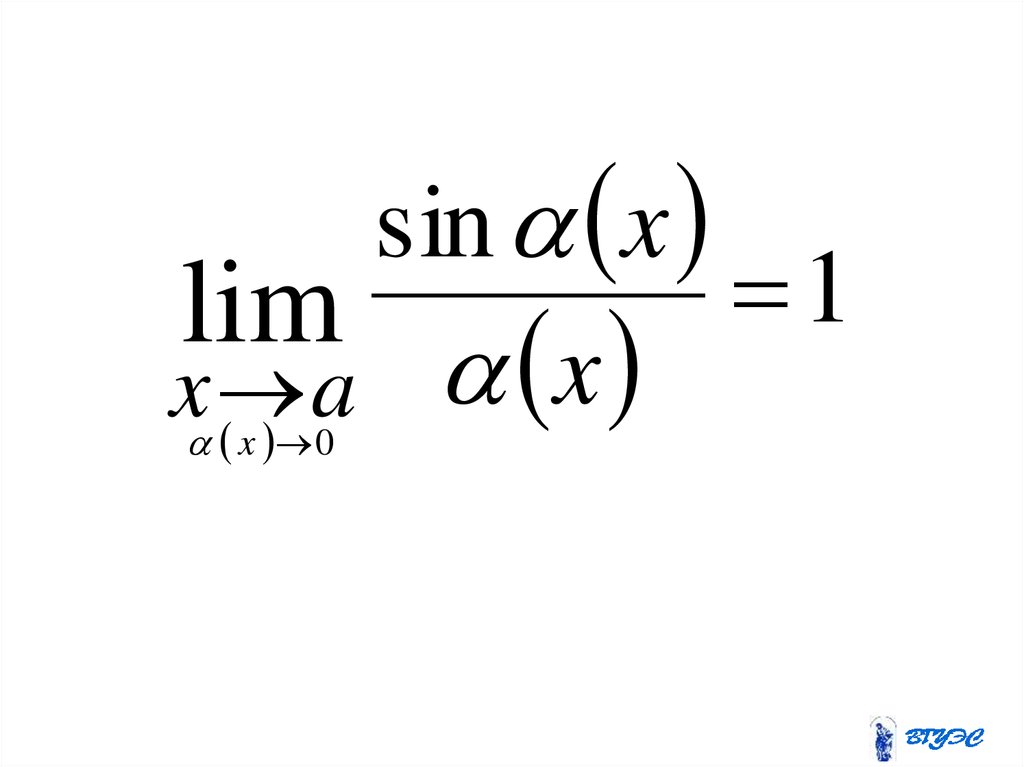

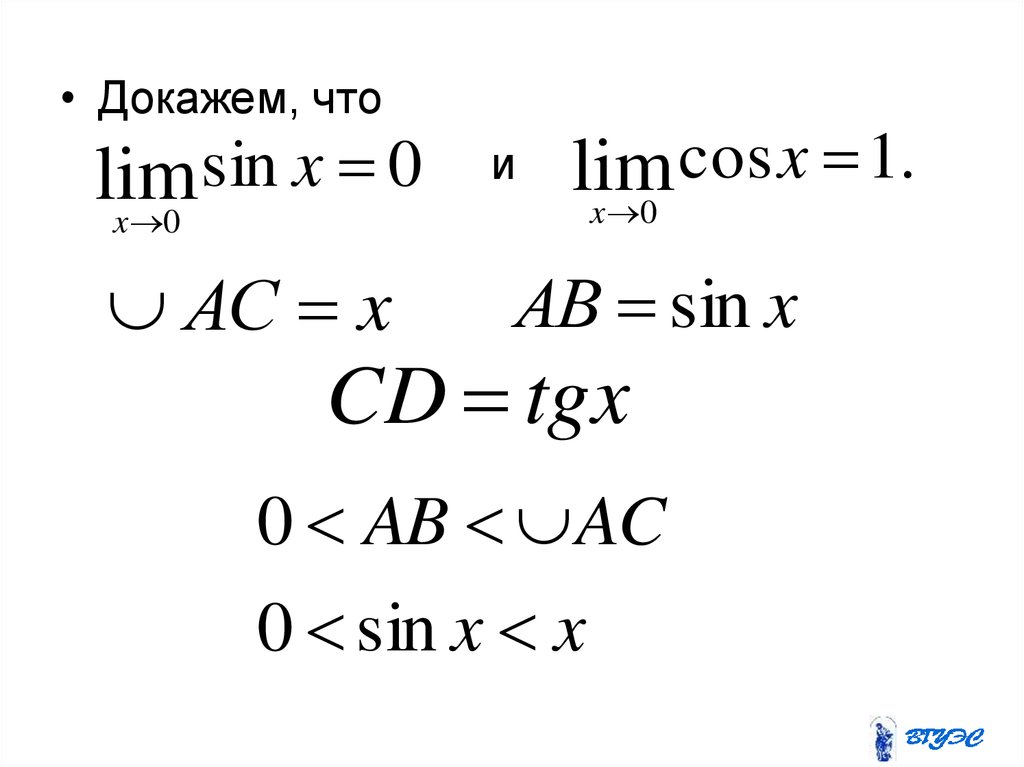
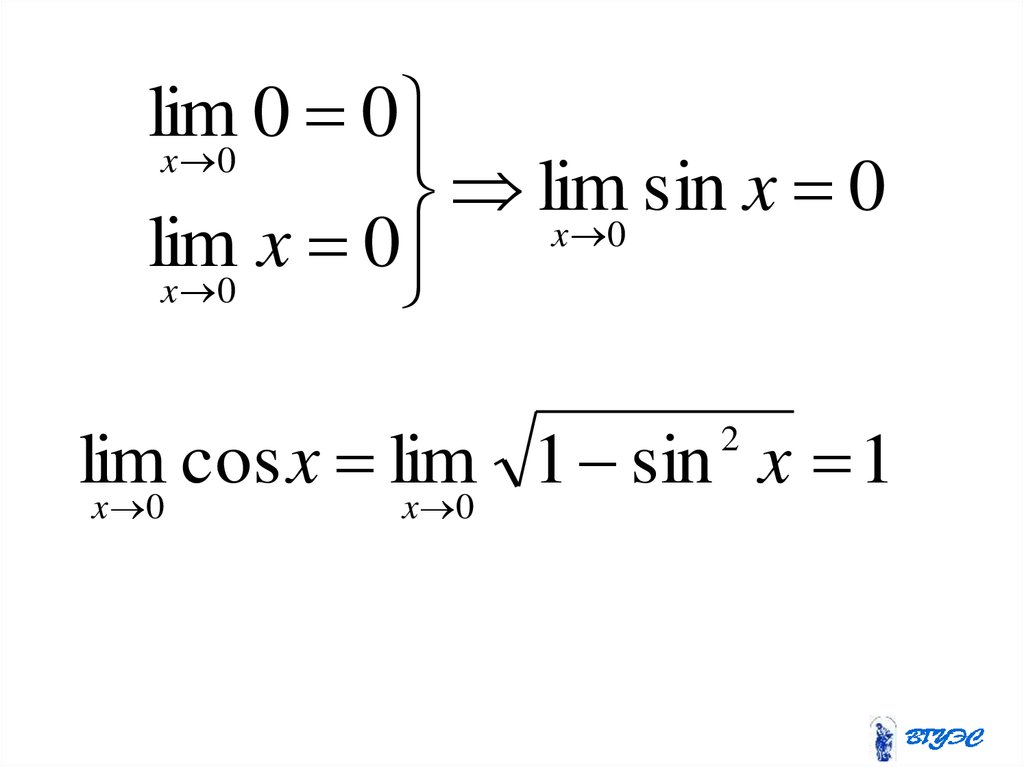


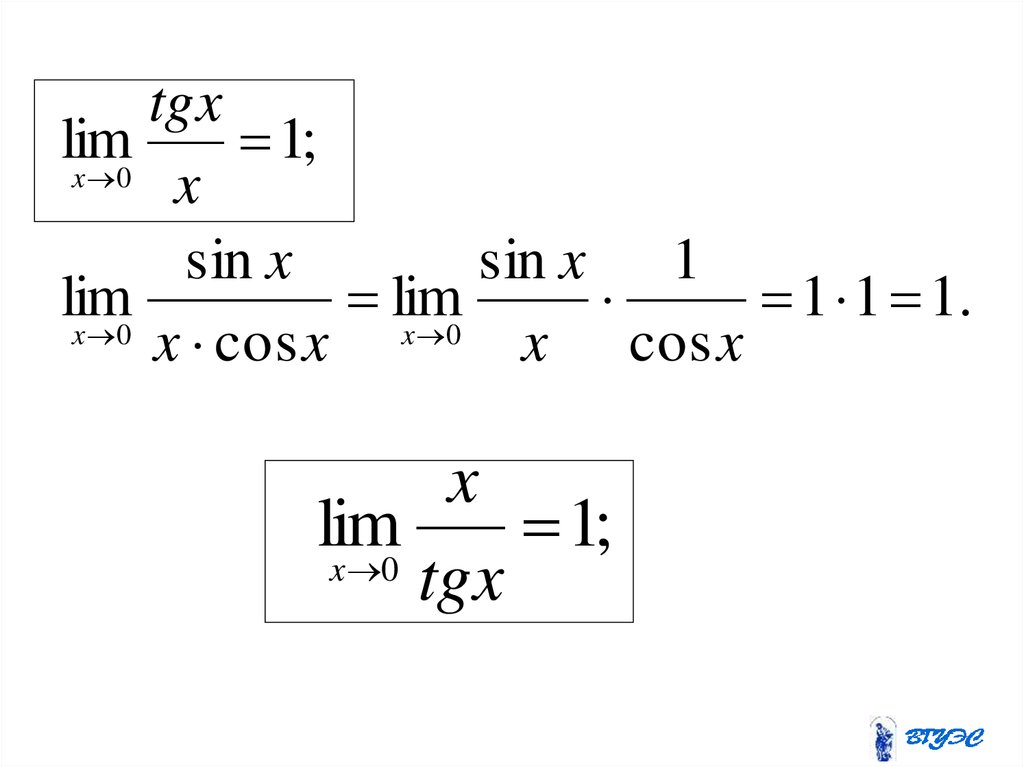
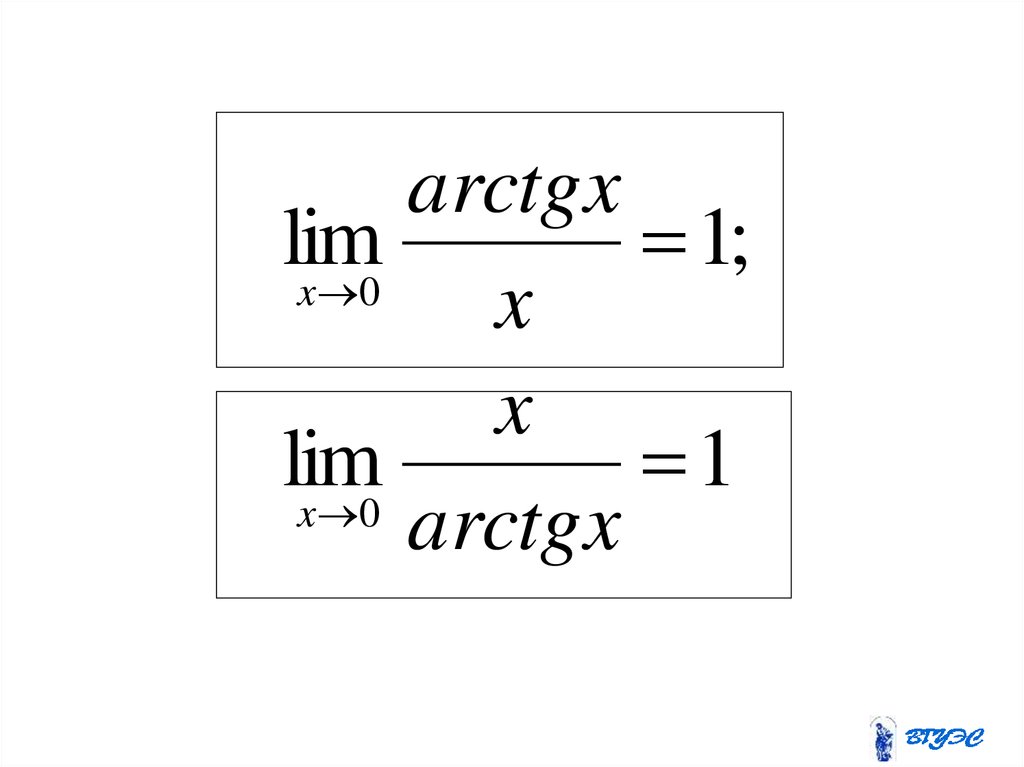
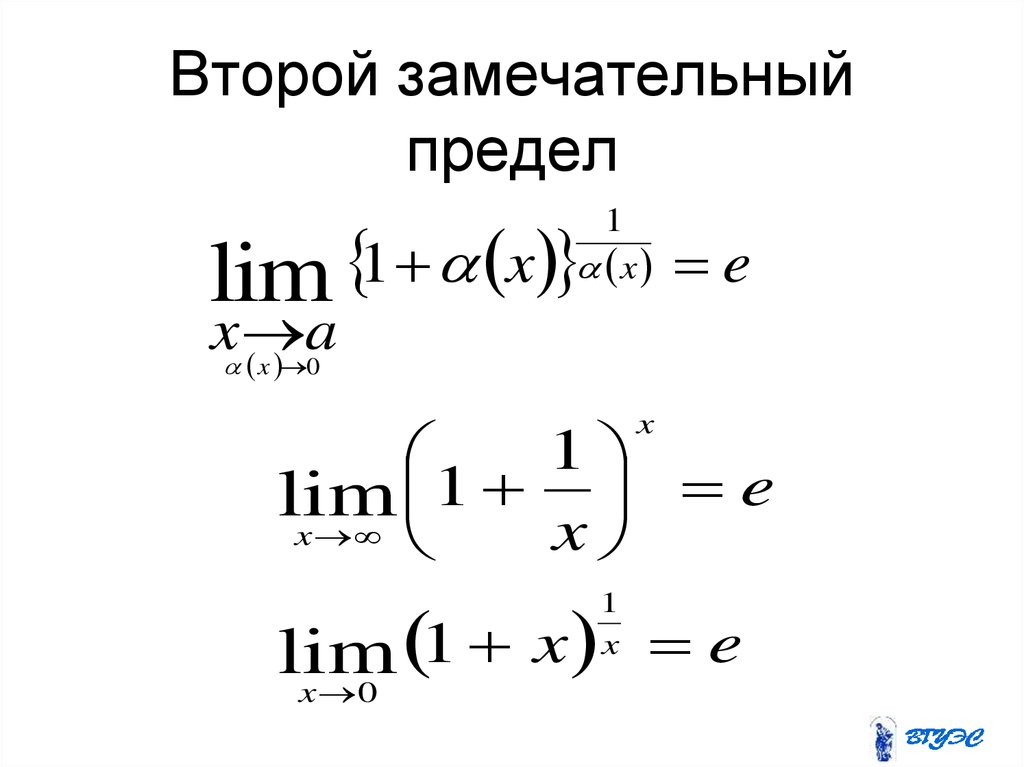









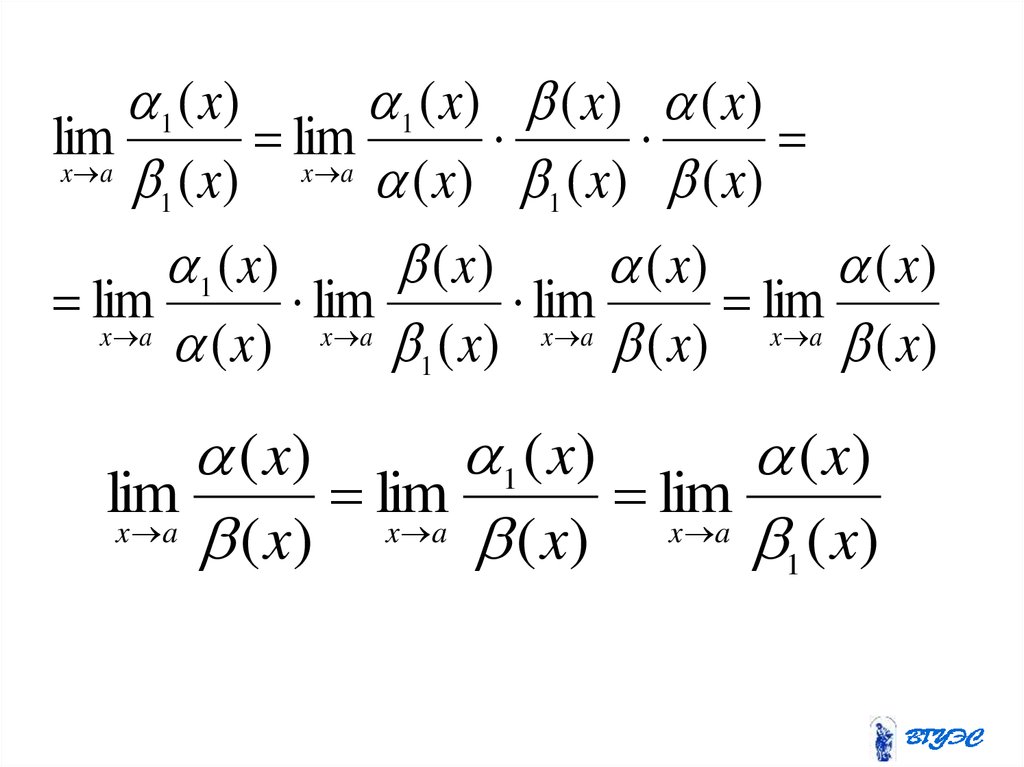

















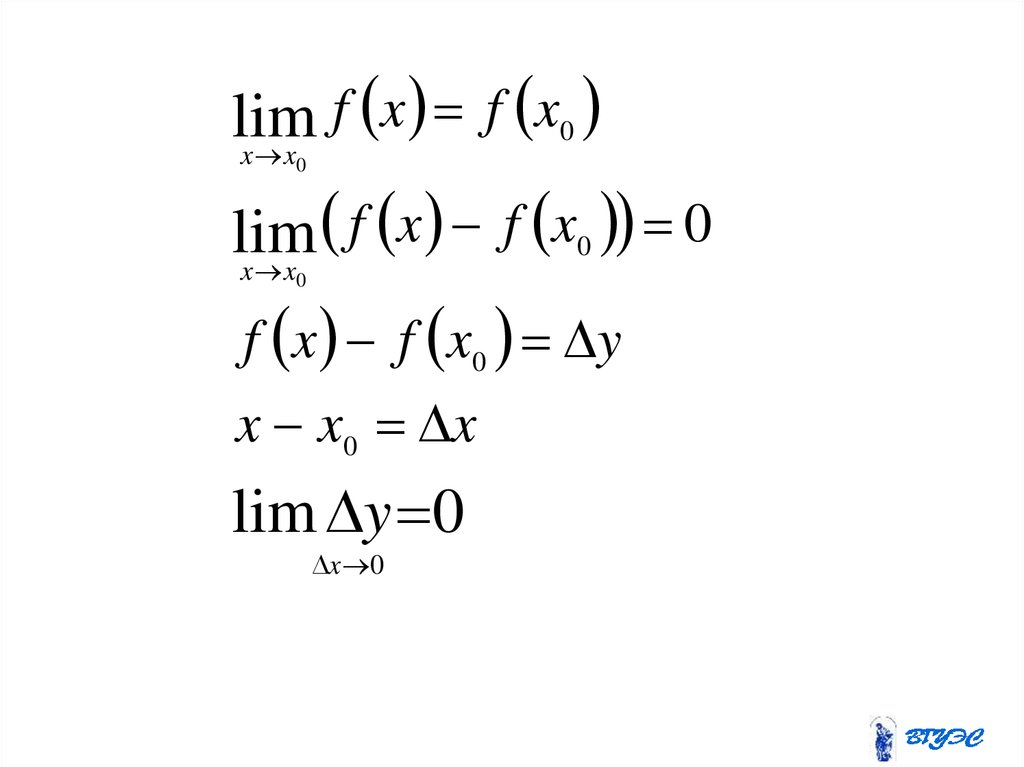

 mathematics
mathematics








