Similar presentations:
Пределы. Числовая последовательность. Предел числовой последовательности
1. Пределы
Числовая последовательность. Предел числовойпоследовательности.
Функция действительного аргумента. Предел функции.
Односторонние пределы.
Бесконечно большие и бесконечно малые функции
Теорема о связи бесконечно малых и бесконечно больших
функций.
Теорема о связи между функцией, ее пределом и
бесконечно малой функцией.
Основные теоремы о пределах.
Признаки существования пределов.
Первый и второй замечательные пределы.
Эквивалентные бесконечно малые и их применение.
Непрерывные функции. Точки разрыва функции и их
классификация.
2. Числовая последовательность
Числовой последовательностью {xn } {x1 , x2 , x3 ,..., xn ,...}называется функция xn f (n), заданная на
множестве натуральных чисел n N
xn -общий или n-ый член числовой
последовательности
( 1)
1 1 1
( 1)
{ 2 } { 1, , , ,..., 2 ,...}
n
4 9 16
n
n
n
3. Предел числовой последовательности
Число a называется пределом последовательности{xn } , если ( 0)( n0 N ) : ( n n0 ) xn a
В этом случае записывают, что lim xn a или
n
xn a при n
Последовательность, имеющая предел называется
сходящейся, в противном случае расходящейся
a
xn
xn 2
xn 1
a
a
(a , a ) - окрестность точки a; n xn a
4. Примеры
( 1)( 1)
( 1)
lim
0 ( 2 0, 2 0)
2
n n
n
n
n
n
1.
n
0
1
1
9
1
16
1
4
1
2
2n 1
2 0 2 1
n
lim
2. lim
n 4n 1
n 4 1 4 0 4 2
n
5. Функции действительного аргумента
Пусть X и Y – некоторые непустые множестваЕсли каждому элементу x множества X ставится в
соответствие один и только один элемент y множества
Y, то говорят, что на множестве X задана функция
y=f(x), то есть f : X Y
Множество X – область определения функции
Y – множество значений функции
Если элементы множеств X и Y являются
действительными числами, то функция f называется
числовой или функцией действительного аргумента
6. Функции действительного аргумента
Основными элементарными функциями являются:степенная функция
y x , R
показательная функция
y а , a 0, a 1
x
логарифмическая функция
y log a x, a 0, a 1
тригонометрические функции
y sin x, y cos x, y tgx, y ctgx
обратные тригонометрические функции
y arcsin x, y arccos x, y arctgx, y arcctgx
Способы задания функции:
аналитический, табличный, графический, словесный
7. Предел функции
Пусть функция y=f(x) определена в некоторойокрестности точки x0 , кроме, быть может, самой
точки x0
Число А называется пределом функции в точке x0 или
при x x0 , если
( 0)( ( ) 0)( x x0 : x x0 )
будет выполнено f ( x) A
В этом случае записывают, что
lim f ( x) A .
x x0
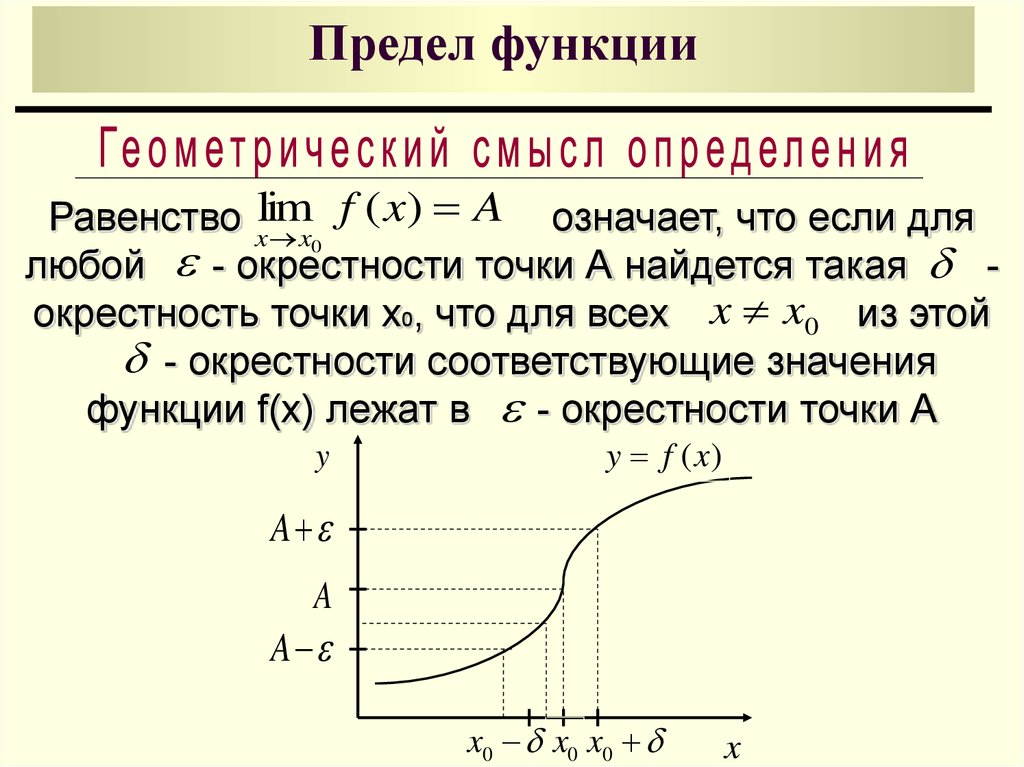
8. Предел функции
f ( x) A означает, что если дляРавенство xlim
x0
любой - окрестности точки А найдется такая окрестность точки x0, что для всех x x0 из этой
- окрестности соответствующие значения
функции f(x) лежат в - окрестности точки А
y
y f (x)
A
A
A
x0 x0 x0
x
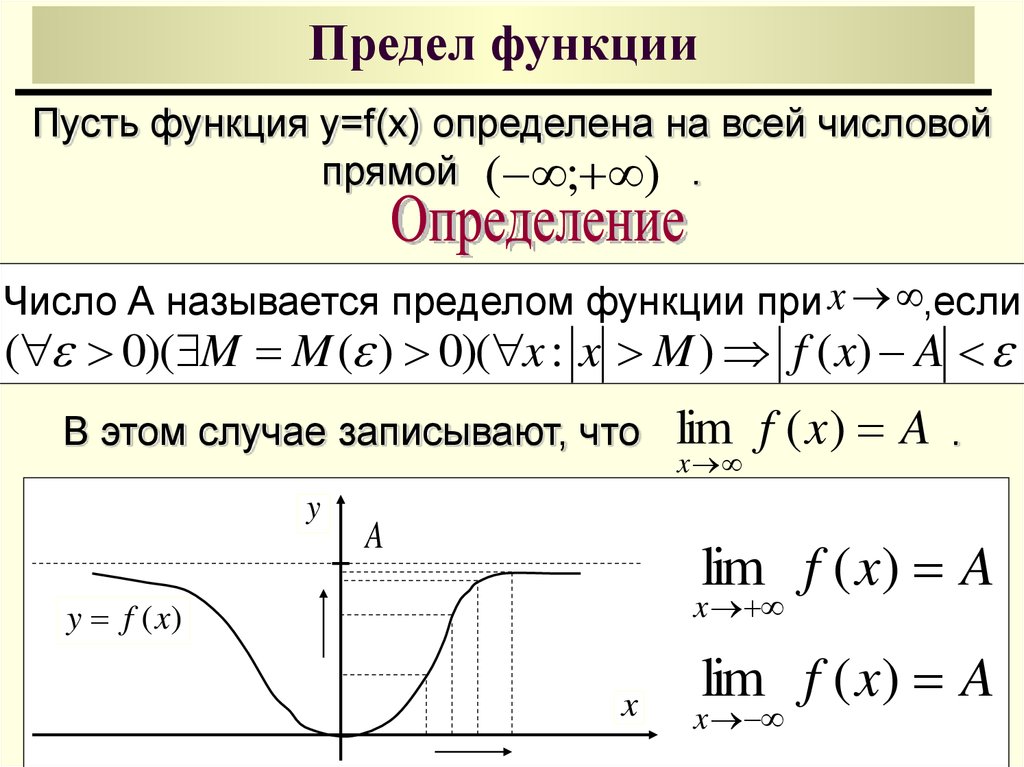
9. Предел функции
Пусть функция y=f(x) определена на всей числовойпрямой ( ; ) .
Число А называется пределом функции при x ,если
( 0)( M M ( ) 0)( x : x M ) f ( x) A
В этом случае записывают, что
y
A
lim f ( x) A .
x
lim f ( x) A
x
y f (x)
x
lim f ( x) A
x
10. Односторонние пределы
Односторонние пределы вводят в рассмотрение,когда важен способ приближения x к x0
Число А1 называется пределом функции y=f(x) в точке
x0 слева lim f ( x) A1 , если
x x0 0
( 0)( ( ) 0) : ( x ( x0 , x0 )) f ( x) A1
Число А2 называется пределом функции y=f(x) в точке
lim f ( x) A1 , если
x0 справа x
x 0
0
( 0)( ( ) 0) : ( x ( x0 , x0 )) f ( x) A2
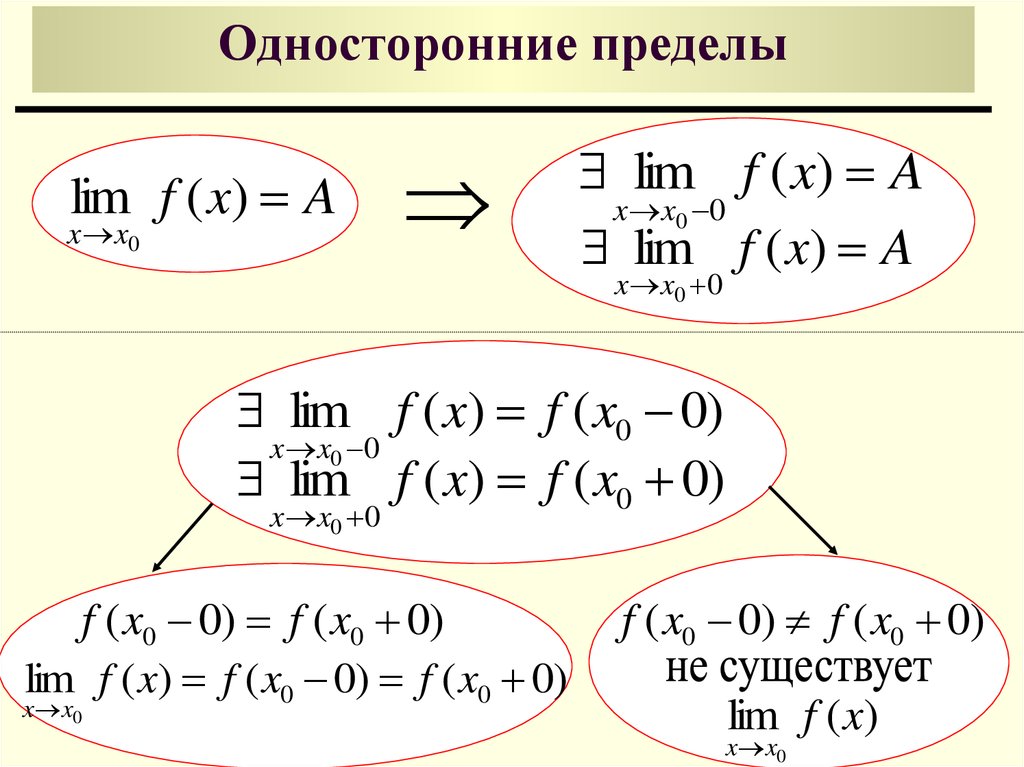
11. Односторонние пределы
lim f ( x) Ax x0
lim f ( x) A
x x0 0
lim f ( x) A
x x0 0
lim f ( x) f ( x0 0)
x x0 0
lim f ( x) f ( x0 0)
x x0 0
f ( x0 0) f ( x0 0)
lim f ( x) f ( x0 0) f ( x0 0)
x x0
f ( x0 0) f ( x0 0)
lim f ( x)
x x0
12. Бесконечно большие функции
Функция y=f(x) называется бесконечно большойпри x x0 , если
( M 0)( (M ) 0)( x : 0 x x0 ) f ( x) M
lim f ( x) .
x x0
1
lim
x 2 0 x 2
В этом случае записывают, что
y
1
y
x 2
2
x
1
lim
x 2 0 x 2
1
lim
x 2 x 2
13. Бесконечно малые функции
Функция y=f(x) называется бесконечно малойпри x x0 , если
( 0)( ( ) 0)( x : 0 x x0 ) f ( x)
В этом случае записывают, что
y
y x2
lim f ( x) 0
x x0
lim x 0
2
x 0 0
lim x 0
2
x 0 0
lim x 0
2
0
x
x 0
.
14. Свойства бесконечно малых функций
( x), ( x), ( x),.. - бесконечно малые функцииlim ( x) 0
x x0
lim ( x) 0
lim ( ( x) ( x)) 0
x x0
x x0
lim ( x) 0
x x0
lim ( ( x) ( x)) 0
x x0
(x) - ограниченная функция
lim ( x) 0
x x0
lim f ( x) A 0
x x0
lim
x x0
( x)
f ( x)
0
15. Теорема о связи б.б.ф. и б.м.ф.
Если функция (x ) является бесконечно малой при( x) 0 ) и ( x) 0 , то функция 1 / ( x)
x x0 ( xlim
x0
1 / ( x) )
является бесконечно большой при x x0( xlim
x
0
Если функция y=f(x) является бесконечно большой
f ( x) ), то функция 1 / f ( x )
при x x0 ( xlim
x0
1 / f ( x) 0 )
является бесконечно малой при x x0( xlim
x
0
16. Связь между функцией, ее пределом и бесконечно малой функцией
Если число А является пределом функции y=f(x) приx x0 ( lim f ( x) А ) и (x ) - бесконечно малая функция
x x0
при x x0 ( lim ( x) 0), то функцию f(x) в окрестности
x x0
точки x0 можно представить в виде суммы числа А и
бесконечно малой функции (x ) ( f ( x) А ( x) )
Если функцию y=f(x) в окрестности точки x0 можно
представить в виде суммы числа А и бесконечно
( x) 0 ), то число А
малой функции (x ) при x x0 (xlim
x0
является пределом функции f(x) при x x0 ( lim f ( x) А )
x x0
17. Основные теоремы о пределах
Пусть f(x) и g(x) – функции, для которых существуютпределы lim f ( x) A
lim g ( x) B
x x0
Аналогично при
x
x x0
Предел суммы (разности) двух функций равен сумме
(разности) их пределов
lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0
Функция может иметь только один предел при
x x0
18. Основные теоремы о пределах
lim ( f ( x) g ( x)) lim f ( x) lim g ( x)x x0
x x0
x x0
lim g ( x) 0
x x0
lim ( f ( x) / g ( x)) lim f ( x) / lim g ( x)
x x0
1.
x x0
lim c f ( x) c lim f ( x)
x x0
x x0
2. lim ( f ( x)) ( lim f ( x)) , n N
x x0
n
x x0
n
x x0
19. Основные теоремы о пределах
x 14 x 320
( x 2)( x 16)
( ) lim
1) lim
2
x 2
x 2 ( x 2)( x 4)
x 6x 8
0
x 16 18
lim
9
x 2 x 4
2
2
3
2
2
2 x 3x 1
x
2) lim
(
)
lim
x 4 x 2 2 x 5
x
2
4
x
2 0 0 2 1
4 0 0 4 2
1
x2
5
2
x
20. Признаки существования пределов
о пределе промежуточнойфункции
Если функция f(x) заключена между двумя функциями
(x ) и g(x), стремящимися к одному и тому же пределу,
то она также стремится к этому пределу
( x) f ( x) g ( x)
lim ( x) a
x x0
lim g ( x) a
x x0
lim f ( x) a
x x0
21. Признаки существования пределов
о пределе монотоннойфункции
Всякая монотонно возрастающая
или монотонно убывающая
и ограниченная функция
имеет предел при x
lim arctgx
x
2
, lim arctgx
x
2
Эта теорема справедлива и для последовательности
22. Замечательные пределы
sin xlim
1
x 0
x
sin 3 x
0
3 sin 3 x
lim
( ) lim
x 0
3 x 0
x
0
3x
sin 3 x
3 lim
3 1 3
3 x 0
3x
23. Замечательные пределы
1x
lim (1 x) e
x 0
1 x
lim (1 ) e
x
x
x
2
2 x
1
2
lim (1 ) (1 ) lim ((1 ) )
x
x
x
x
x
2
1 2 2
2
2
( lim (1 ) ) e
x
x
2
2
24. Эквивалентные бесконечно малые
(x ), (x) - бесконечно малые функцииd ef ( x)
одинакового порядка
lim
k 0
x x0 ( x)
( x)
lim
1
(x ) ~ (x) при x x0
x x ( x)
d ef
0
( x)
(x ) О ( ( x)) при x x0
lim
0
x x ( x)
d ef
0
25. Основные теоремы о пределах
10x
0
8
1) lim 2 ( ) lim x 0
x 0 x
x 0
0
10
x -бесконечно малая более высокого порядка малости,
2
чем x
sin x
0
( ) 1 sin x ~ x при x 0
2) lim
x 0
x
0
tgx
0
tgx
sin x
( ) lim
lim
3) lim
x 0 x
x 0 x
x 0 cos x x
0
1
sin x
lim
lim
1 1 1 tgx~ x при x 0
x 0 cos x x 0
x
26. Эквивалентные бесконечно малые
о замене бесконечномалой на эквивалентную
Предел отношения двух бесконечно малых функций
не изменится, если каждую или одну из них заменить
эквивалентной ей бесконечно малой
( x)
(x ) ~ (x ), при x x0
lim
lim
x x ( x)
x x
(x) ~ (x ), при x x0
0
0
( x)
( x)
27. Эквивалентные бесконечно малые
tg 6 x0
6x
6
lim
( ) lim
lim 2
x 0 sin 3 x
x 0 3 x
x 0 3
0
sin x ~ x, при x 0 sin 3x ~3 x, при 3x 0
tg x ~ x, при x 0 tg 6x ~ 6x, при 6x 0
28. Таблица эквивалентности
1) sin x x, x 03) arcsin x x, x 0
x2
5)1 cos x , x 0
2
x
7)а 1 x ln a, x 0
9) log a (1 x) x log a e, x 0
2)tgx x, x 0
4)arctgx x, x 0
6)е x 1 x, x 0
8) ln( 1 x) x, x 0
10)(1 x) k 1 kx, k 0, x 0
x
11) 1 x 1 , x 0
2
29. Определение непрерывности функции y=f(x) в точке x0
Функция y=f(x) называется непрерывной в точке x0 , если:1. эта функция определена в точке x0 и ее окрестности ;
2. существует lim f ( x)
x x0 def
3. lim f ( x) f ( x ) ( 0)( ( ) 0)( x x : x x )
0
0
0
x x0
f ( x) f ( x0 )
x x0 x
f ( x) f ( x0 ) y
Функция y=f(x) называется непрерывной в точке x0 , если:
1. эта функция определена в точке x0 и ее окрестности ;
2. lim y 0
x 0
30. Определение непрерывности функции y=f(x)на интервале (а,b)
Функция y=f(x) называется непрерывной на интервале(a,b) , если она непрерывна в каждой точке этого
интервала
С – постоянная
x - степенная
x
a - показательная
log a x - логарифмическая
тригонометрические
sin x
arcsin x
cos x
arccos x
tgx
arctgx
ctgx
arcctgx
31. Точки разрыва функции
Точка x=x0 называется точкой разрыва функции y=f(x),если в ней не выполняется по крайней мере одно из
условий непрерывности функции
32. Точки разрыва
Точка x=x0 называется точкой разрыва функции y=f(x) I рода,если существуют конечные пределы
f ( x0 0) lim f ( x) ,
x x0 0
f ( x0 0) lim f ( x)
x x0 0
причем не все 3 числа f ( x0 ), f ( x0 0), f ( x0 0) равны между собой
Точка x=x0 называется точкой разрыва функции y=f(x) II рода,
если по крайней мере один из односторонних пределов в этой
точке
f ( x 0) lim f ( x) , f ( x 0) lim f ( x)
0
x x0 0
не существует или равен
0
x x0 0
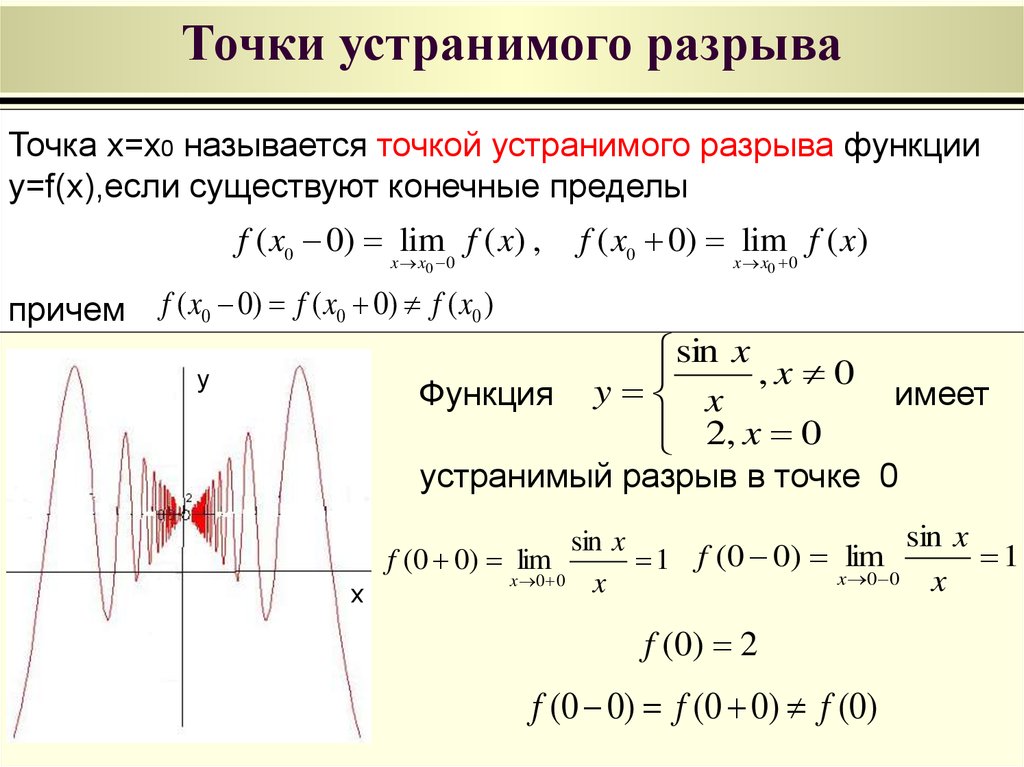
33. Точки устранимого разрыва
Точка x=x0 называется точкой устранимого разрыва функцииy=f(x),если существуют конечные пределы
f ( x0 0) lim f ( x) ,
x x0 0
причем
f ( x0 0) lim f ( x)
x x0 0
f ( x0 0) f ( x0 0) f ( x0 )
y
sin x
,x 0
y
Функция
имеет
x
2, x 0
устранимый разрыв в точке 0
sin x
sin x
1
f (0 0) lim
1 f (0 0) lim
x
0
0
x 0 0
x
x
x
f ( 0) 2
f (0 0) f (0 0) f (0)
34. Точки скачка
Точка x=x0 называется точкой скачка функции y=f(x),еслисуществуют конечные пределы
f ( x0 0) lim f ( x) , f ( x0 0) lim f ( x)
x x0 0
x x0 0
причем y f ( x0 0) f ( x0 0) , где f ( x0 0) f ( x0 0) - скачок функции
y=f(x) в точке x0
x 1, 1 x 2
Функция y
имеет
2 x, 2 x 5
скачок в точке 2
y
x
-1
2
5
f (2 0) lim f ( x) 0
x 2 0
f (2 0) lim f ( x) 1
x 2 0
f ( 2) 0
f (2 0) f (2 0)
f (2 0) f (2 0) 1 - скачок
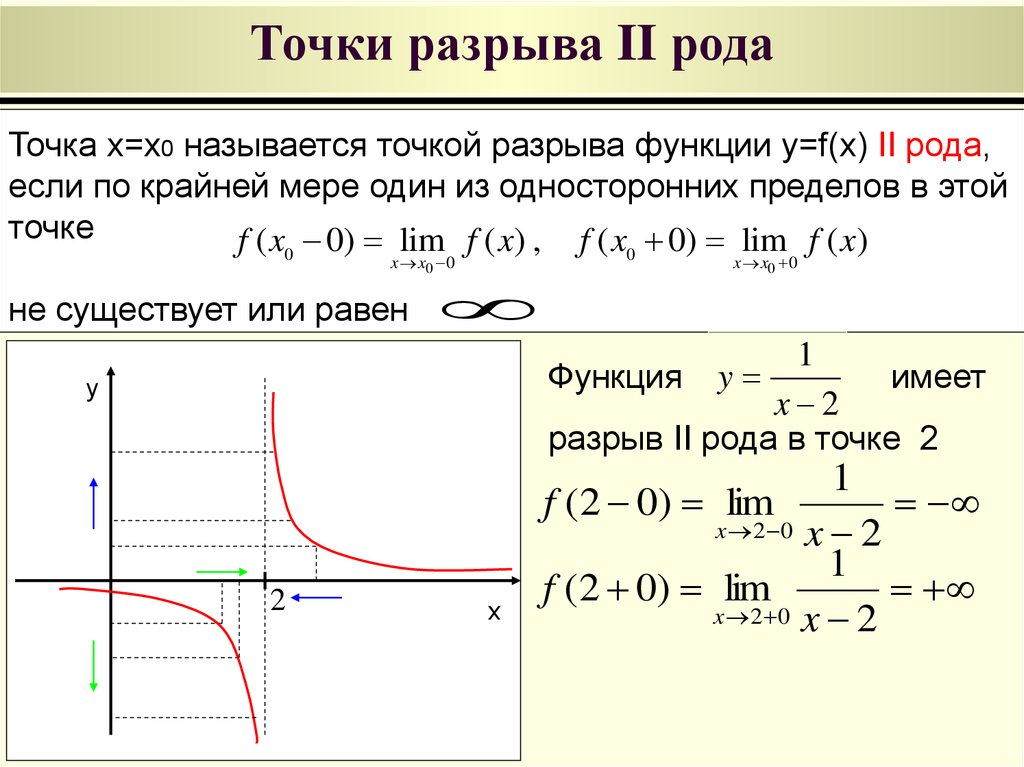
35. Точки разрыва II рода
Точка x=x0 называется точкой разрыва функции y=f(x) II рода,если по крайней мере один из односторонних пределов в этой
точке
f ( x 0) lim f ( x) , f ( x 0) lim f ( x)
0
0
x x0 0
не существует или равен
x x0 0
1
Функция y
имеет
x 2
разрыв II рода в точке 2
y
2
x
1
f (2 0) lim
x 2 0 x 2
1
f (2 0) lim
x 2 0 x 2
36. Свойства непрерывных функций
y f ( x) g ( x),непрерывная
функция в точке x0
y=f(x); y=g(x)
непрерывные
функции в точке x0
y f ( x) g ( x)
непрерывная
функция в точке x0
f ( x)
y
, g ( x0 ) 0
g ( x)
непрерывная
функция в точке x0
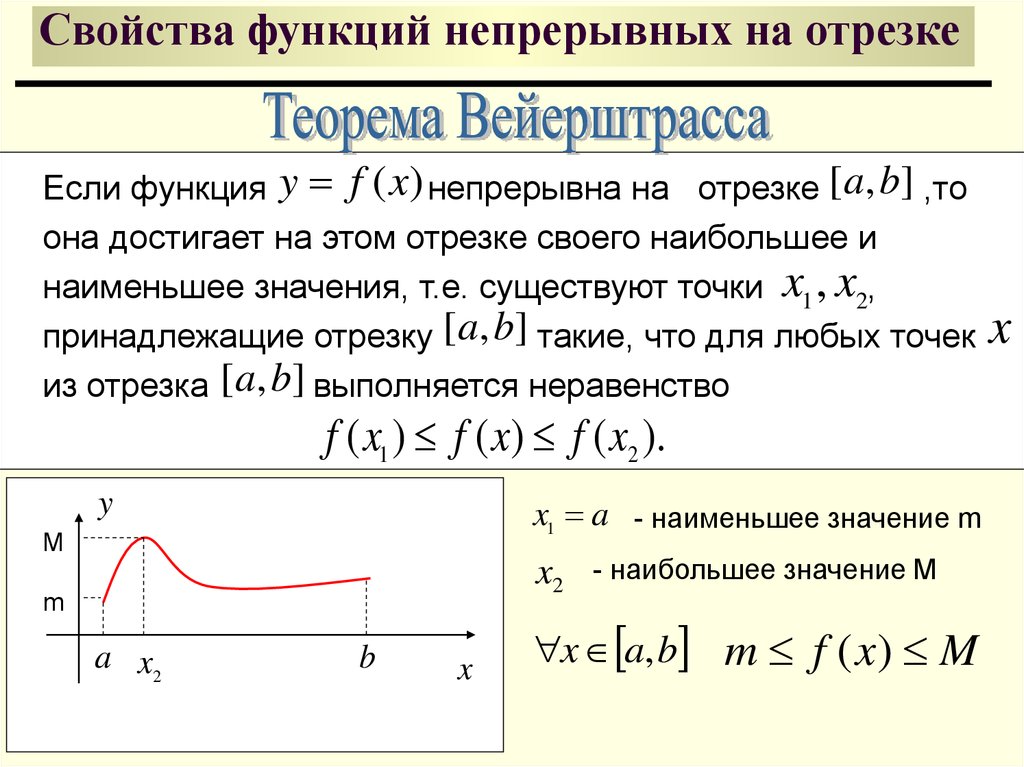
37. Свойства функций непрерывных на отрезке
Если функция y f ( x) непрерывна на отрезке [ a, b] ,тоона достигает на этом отрезке своего наибольшее и
наименьшее значения, т.е. существуют точки x1 , x2,
принадлежащие отрезку [ a, b] такие, что для любых точек
из отрезка [ a, b] выполняется неравенство
f ( x1 ) f ( x) f ( x2 ).
y
x1 a - наименьшее значение m
M
x2
m
a x2
b
x
- наибольшее значение M
x a, b m f ( x ) M
x
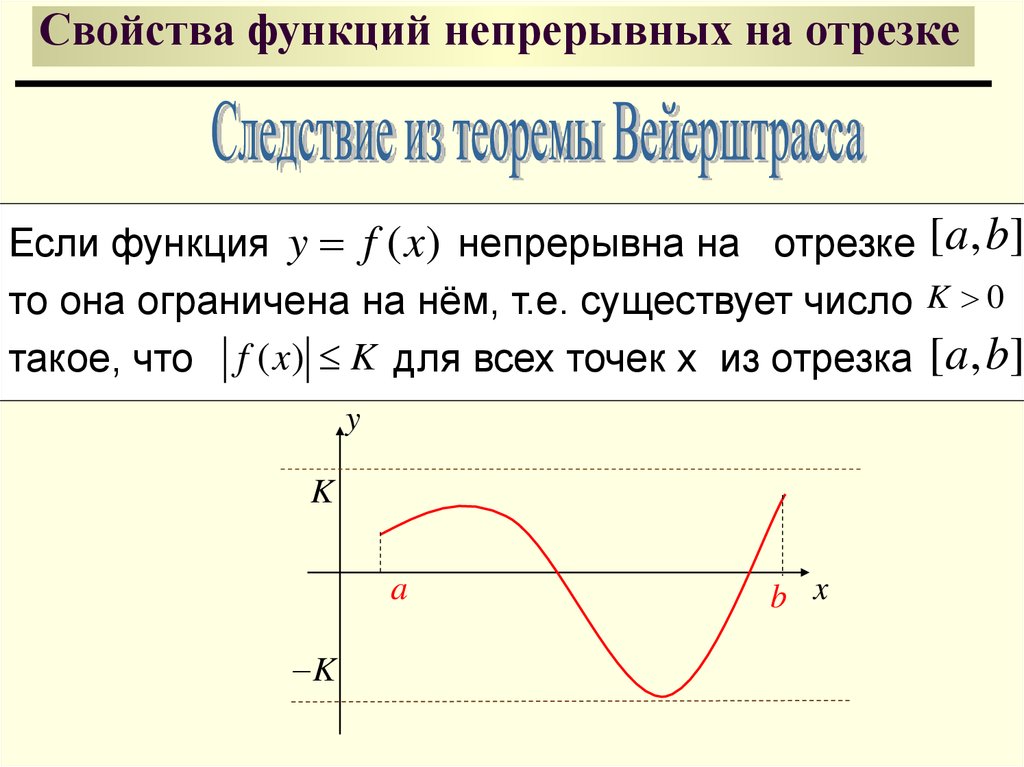
38. Свойства функций непрерывных на отрезке
Если функция y f ( x) непрерывна на отрезке [ a, b]то она ограничена на нём, т.е. существует число K 0
такое, что f ( x) K для всех точек x из отрезка [ a, b]
y
K
a
K
b x
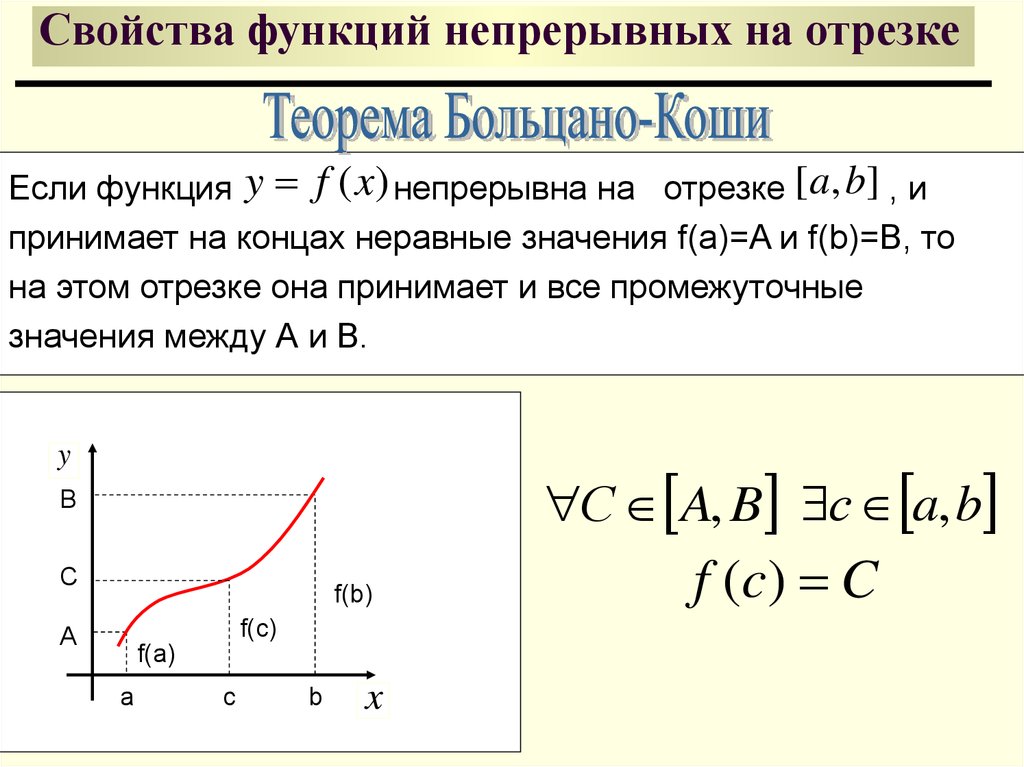
39. Свойства функций непрерывных на отрезке
Если функция y f ( x) непрерывна на отрезке [ a, b] , ипринимает на концах неравные значения f(a)=A и f(b)=B, то
на этом отрезке она принимает и все промежуточные
значения между А и В.
y
С A, B с a, b
B
C
f(b)
f(c)
A
f(a)
a
c
b
x
f (c ) C
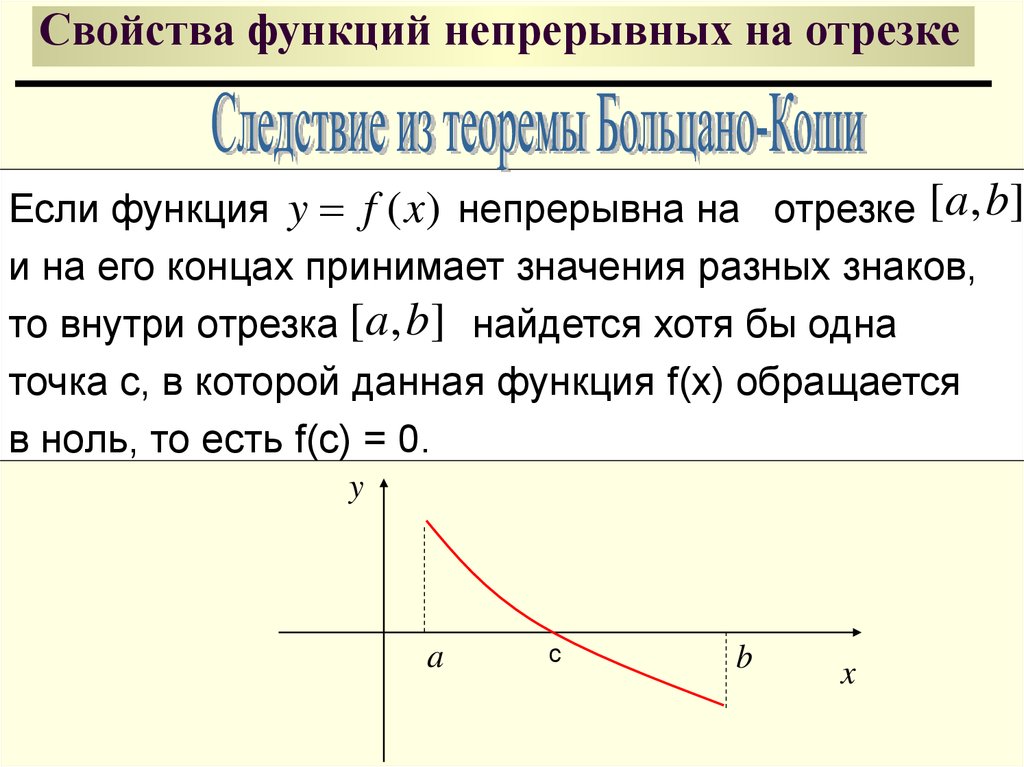
40. Свойства функций непрерывных на отрезке
Если функция y f ( x) непрерывна на отрезке [ a, b]и на его концах принимает значения разных знаков,
то внутри отрезка [ a, b] найдется хотя бы одна
точка с, в которой данная функция f(x) обращается
в ноль, то есть f(c) = 0.
y
a
c
b
x































 mathematics
mathematics








