Длина окружности. Площадь круга

1.

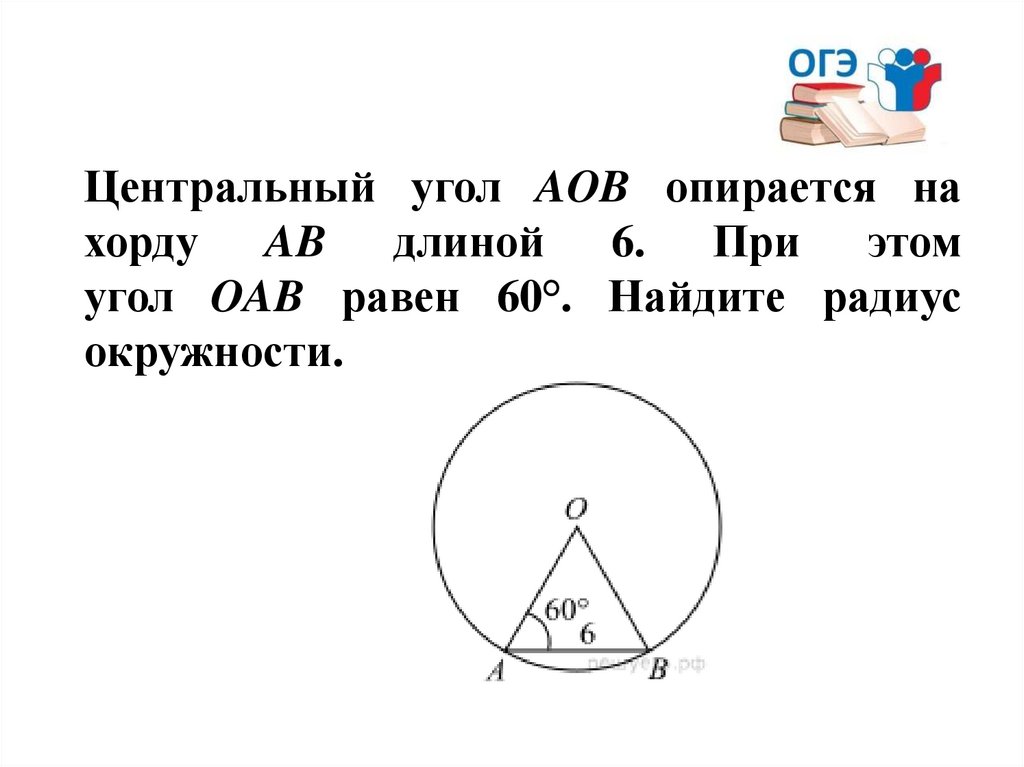
Центральный угол AOB опирается на
хорду AB длиной 6. При этом
угол OAB равен 60°. Найдите радиус
окружности.

2. № 1

№1
Сформулируйте
определение
правильного
многоугольника.

3. № 2

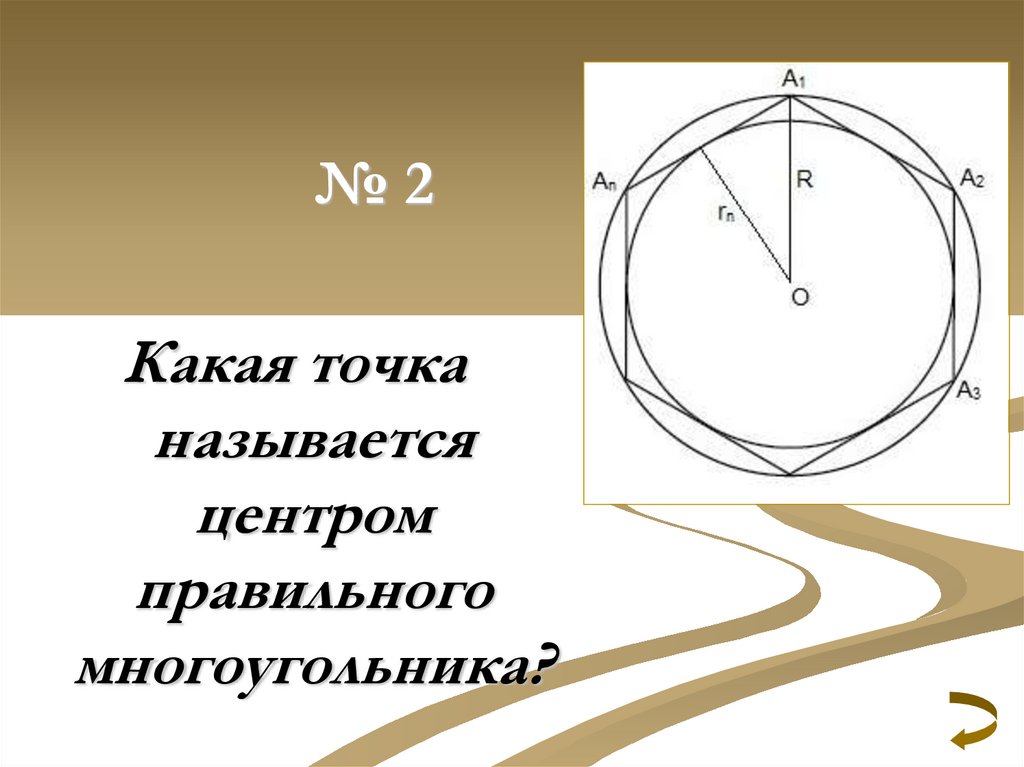
№2
Какая точка
называется
центром
правильного
многоугольника?

4. № 3

№3
Запишите формулу для
нахождения угла
правильного
многоугольника.

5. Окружность описанная около правильного многоугольника

Окружность называется описанной около
многоугольника если все вершины этого
многоугольника лежат на окружности

6. Окружность, вписанная в правильный многоугольник

Окружность называется вписанной в многоугольник,
если все стороны многоугольника касаются этой
окружности

7.

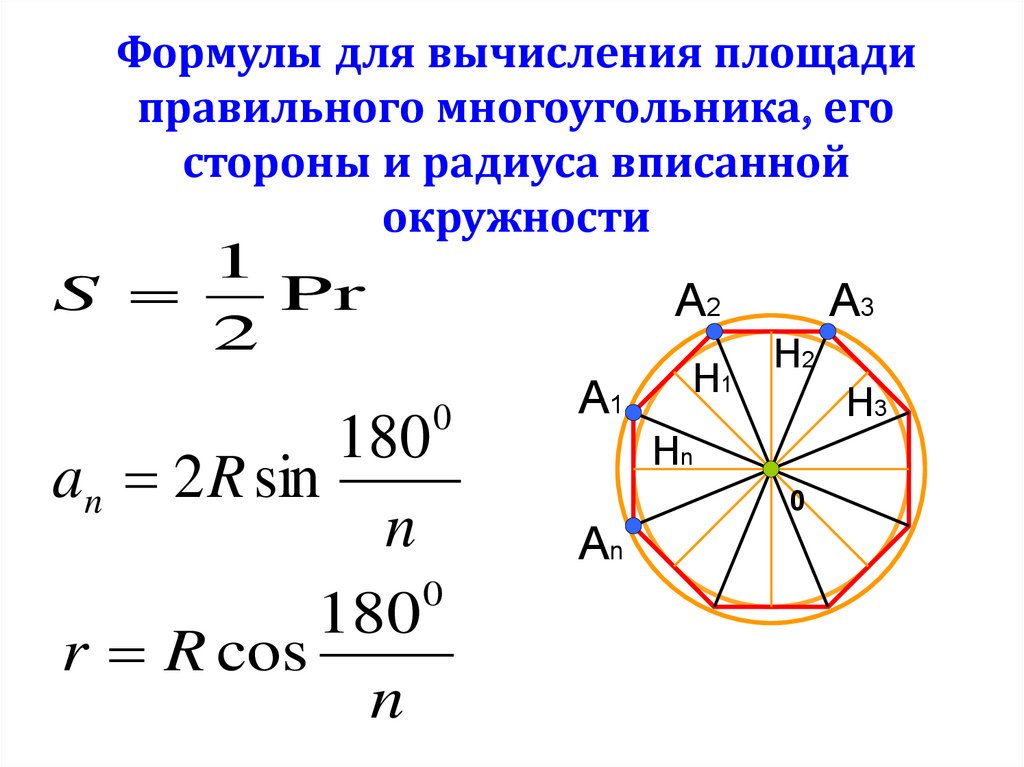
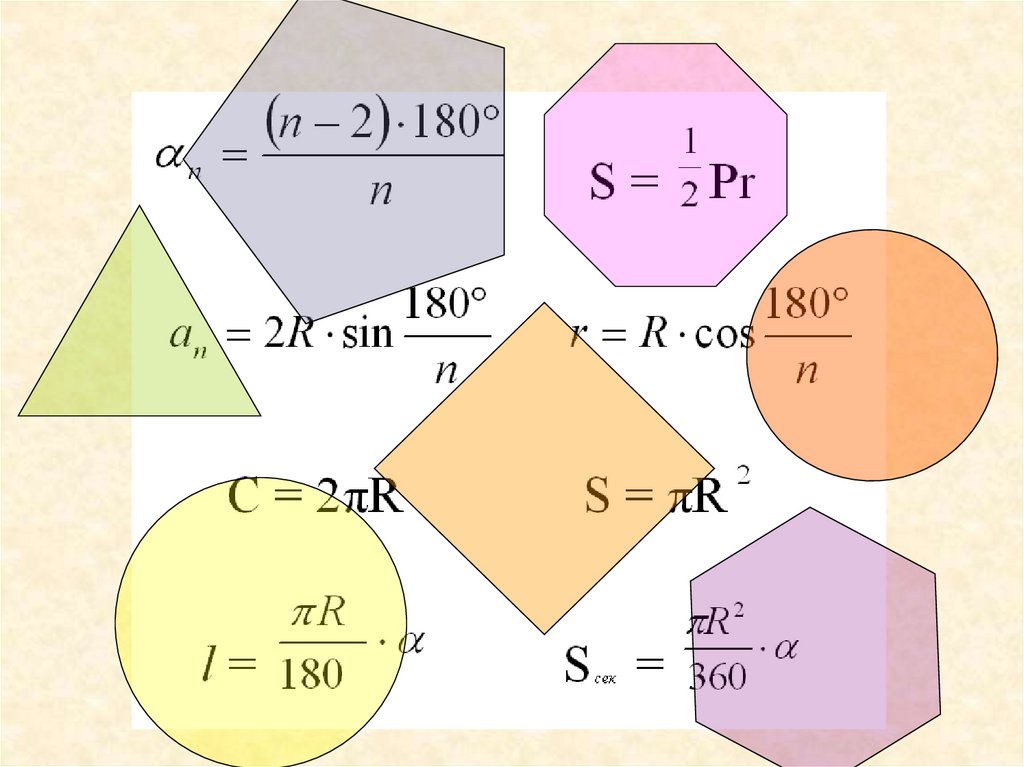
Формулы для вычисления площади
правильного многоугольника, его
стороны и радиуса вписанной
окружности
1
S
Pr
2
A2
0
180
an 2 R sin
n
0
180
r R cos
n
A1
H1
A3
H2
H3
Hn
0
An

8.

9.

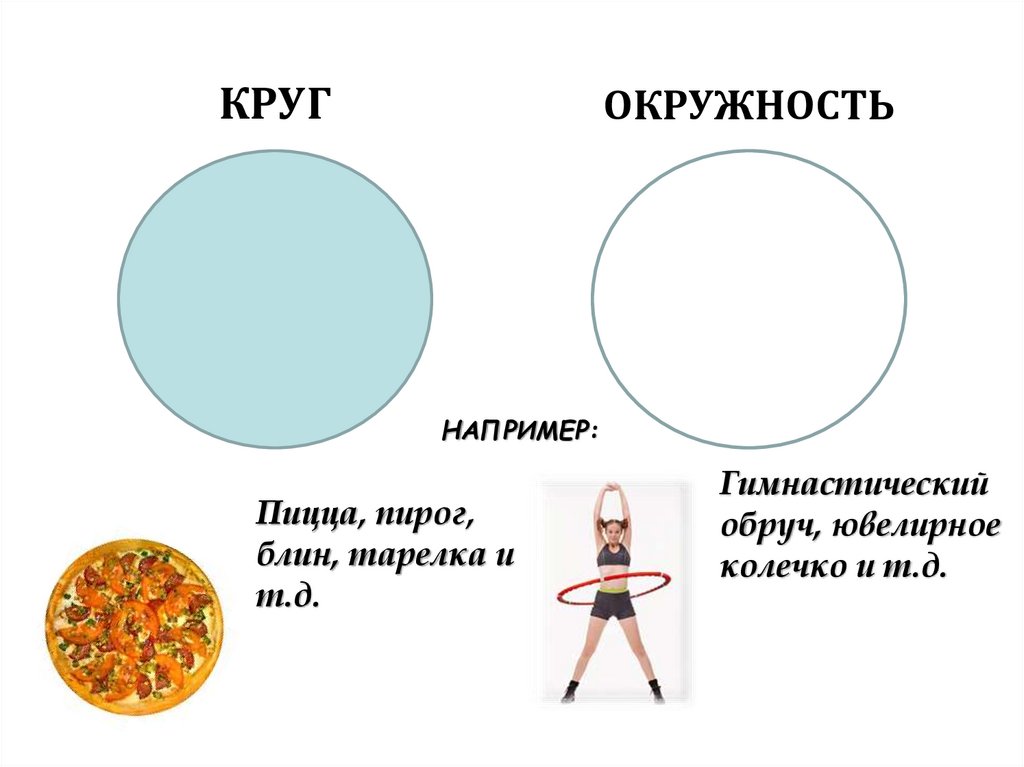
КРУГ
ОКРУЖНОСТЬ
НАПРИМЕР:
Пицца, пирог,
блин, тарелка и
т.д.
Гимнастический
обруч, ювелирное
колечко и т.д.

10.

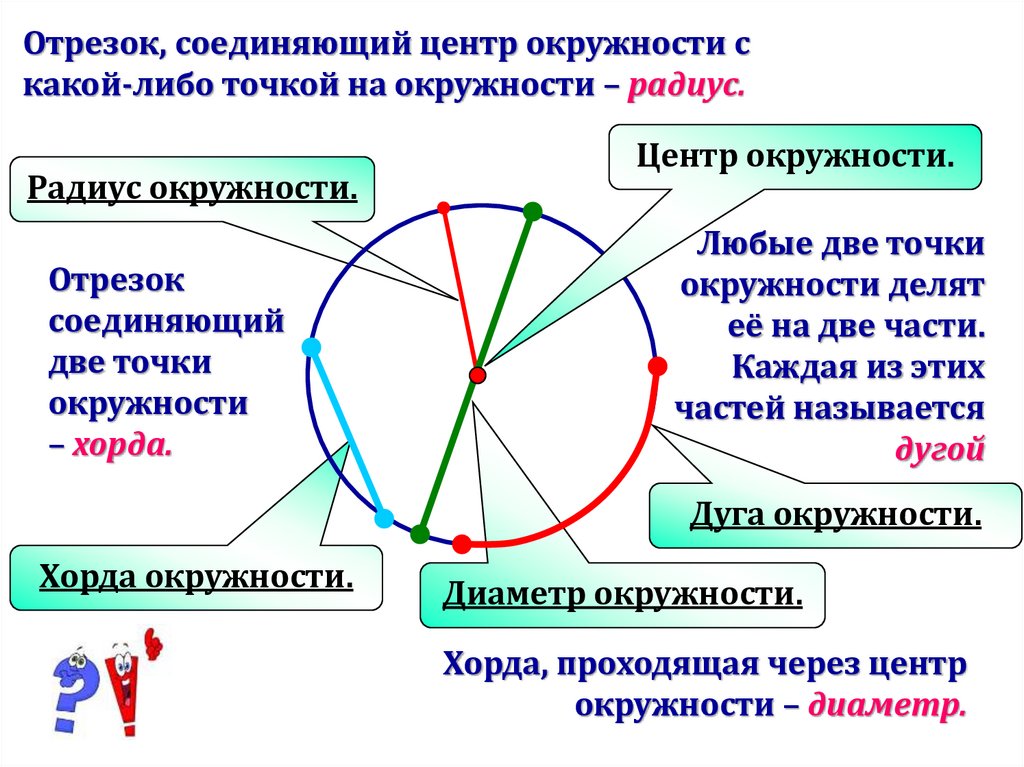
Отрезок, соединяющий центр окружности с
какой-либо точкой на окружности – радиус.
Радиус окружности.
Отрезок
соединяющий
две точки
окружности
– хорда.
Центр окружности.
Любые две точки
окружности делят
её на две части.
Каждая из этих
частей называется
дугой
Дуга окружности.
Хорда окружности.
Диаметр окружности.
Хорда, проходящая через центр
окружности – диаметр.

11.

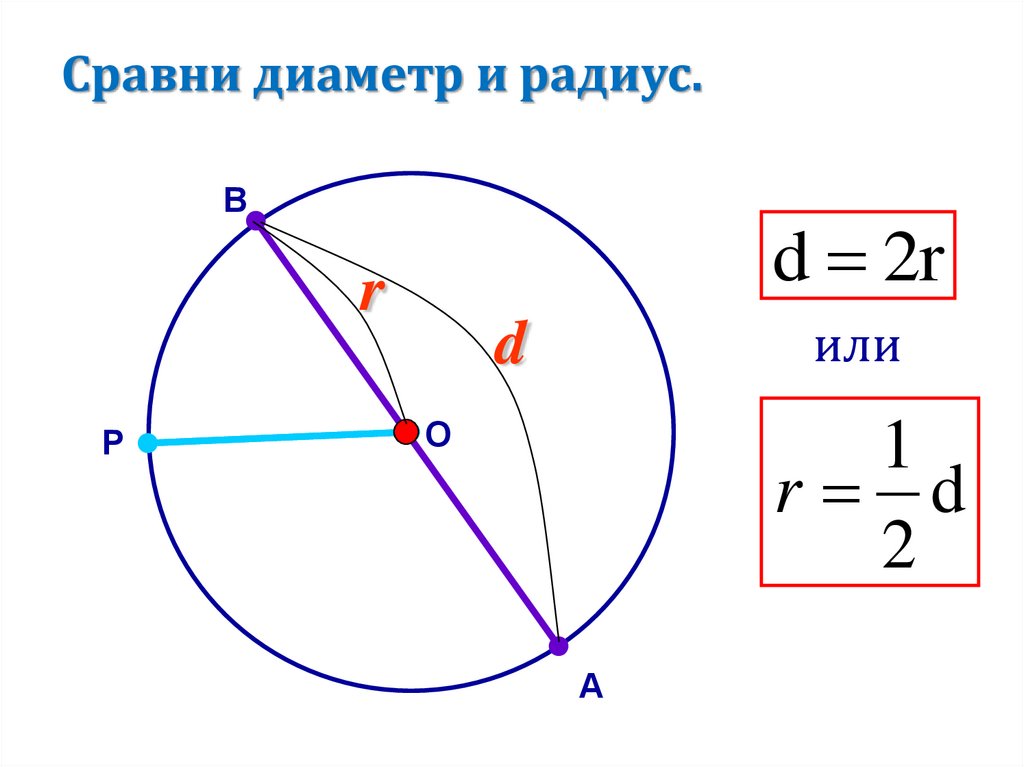
Сравни диаметр и радиус.
В
d 2r
r
P
или
d
1
r d
2
O
А

12.

Назвать все радиусы и
диаметры окружности

13. Длина окружности и длина дуги окружности

.
.
А
.
А1
Длина отрезка АА1 – длина окружности.(С)
Доказано, что отношение длины окружности к ее диаметру
есть одно и то же число для всех окружностей.
С
2R
22
7
3,14159...

14.

С – длина окружности
.R
С D
С 2 R
3,14
- длина дуги окружности
.
C
2 R
R
360
360
180
R
180

15. Решите задачи

1) Заполните пустые клетки таблицы.
С
R
18
82
3
С 2 R
2) Найдите длину дуги окружности радиуса 6
см, если его градусная мера равна:
а) 300, б) 900.
R
180

16. Устно!!! Реши задачи из учебника

№ 1102
№ 1103

17. Задача 1. Вообразите, что вы обошли землю по экватору. На сколько при этом верхушка вашей головы прошла более длинный путь, чем

кончик вашей ноги?
• Решение.
1) Ноги прошли путь 2 R , где R радиус земного шара.
2) Верхушка головы - 2 R 1,7 , где 1,7м рост
человека.
3) Разность путей равна 2 R 1,7 - 2 R 2 1,7 10,7м.
Итак голова прошла путь на 10,7 м больше, чем ноги.
Ответ:10,7 м.

18. Задача 2. Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1м, то сможет ли между проволокой и

землёй проскочить мышь.
Обычно отвечают, что промежуток будет тоньше волоса.
• Решение. Пусть длина промежутка х см.
Если R радиус земли, то длина проволоки была 2 Rсм,
а станет 2 (R + x)см.
А по условию задачи их разность равна 100 см.
Уравнение.
2 R x - 2 R 100,
2 x 100,
100
x
,
2
x 16 см.
Ответ:16 см.

19.

Радиус круга равен 3, а длина
ограничивающей его окружности
равна 6π. Найдите площадь
круга.
В
ответ
запишите
площадь, деленную на π.

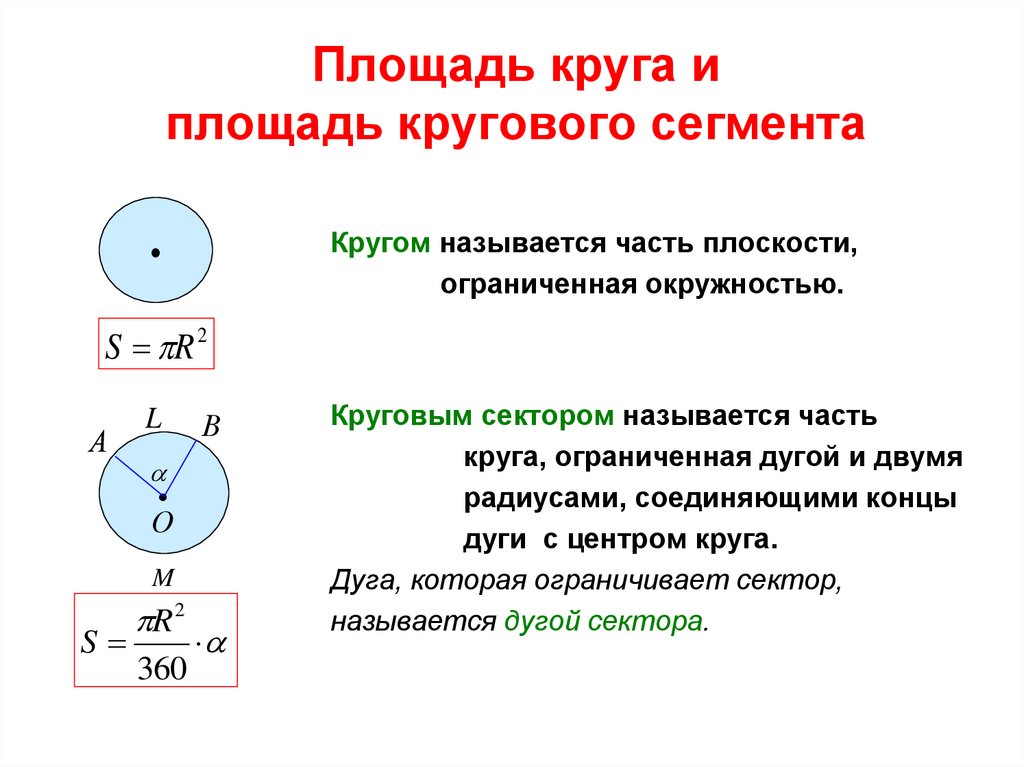
20. Площадь круга и площадь кругового сегмента

Кругом называется часть плоскости,
ограниченная окружностью.
S R 2
А
L
В
О
M
S
R 2
360
Круговым сектором называется часть
круга, ограниченная дугой и двумя
радиусами, соединяющими концы
дуги с центром круга.
Дуга, которая ограничивает сектор,
называется дугой сектора.

21. Решите задачи

1)
Заполните пустые клетки таблицы,
где S - площадь круга радиуса R .
S
R
49
9
3
S R 2
2) Из круга, радиус которого 10 см, вырезан сектор
с дугой в 600. Найдите площадь оставшейся
части круга.
S
R 2
360

22. Задача

Веер имеет форму
кругового сектора.
Найдите площадь этого
сектора и длину дуги,
которую образует
развернутый веер, если
радиус равен 30 см, а
градусная мера угла
160°.

23.

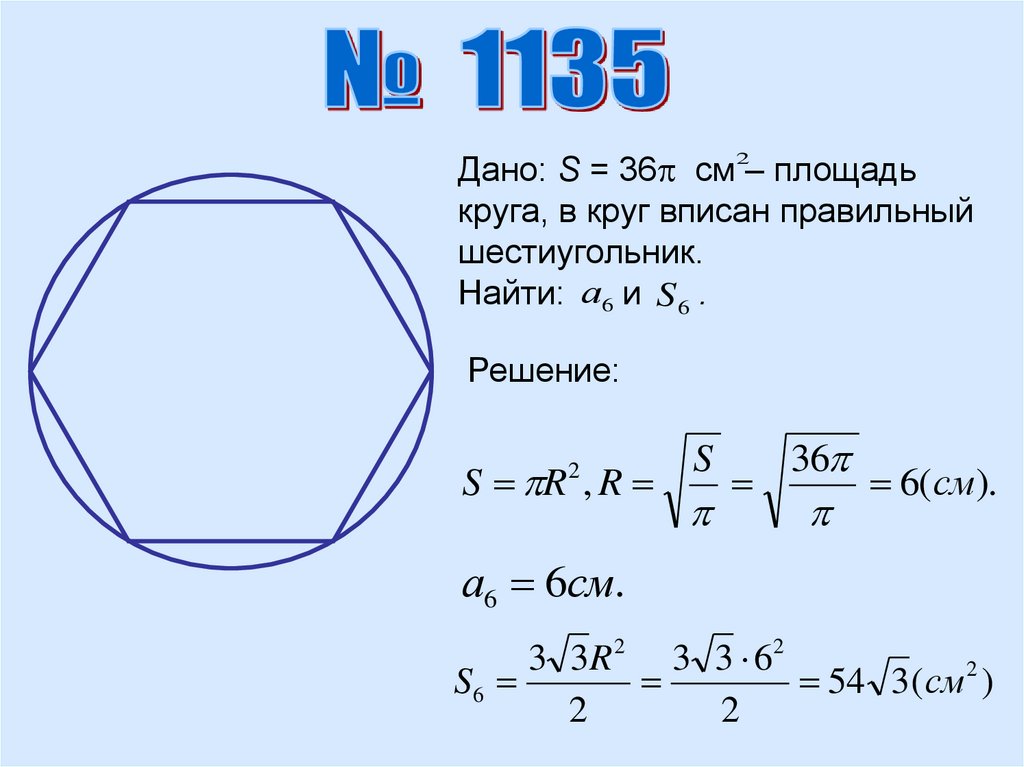
Дано: S = 36 см – площадь
круга, в круг вписан правильный
шестиугольник.
Найти: а6 и S 6 .
2
Решение:
S R , R
2
S
36
6(см).
а6 6см.
3 3R 2 3 3 6 2
S6
54 3 ( см 2 )
2
2

24. Проверочный тест

1. Найдите угол правильного
десятиугольника
1) 288°
2) 144°
3) 164°
2. Найдите сторону правильного
треугольника, если радиус описанной
около него окружности равен 2 м.
1) 2√3 м
2) 2 м
3) 6 м
3. Найдите площадь кругового сектора
радиуса 4 см, если его центральный угол
равен 90°.
1) π см 2
2) 4π см 2 3) 8π см 2

25.

4. Найдите радиус описанной около квадрата
окружности, если сторона квадрата равна 6 м.
1) 6√2 м
2) 12 м
3) 3√2 м
5. Найдите радиус окружности, вписанной в
правильный треугольник, если радиус
описанной около него окружности равен 2 м.
1) 1 м
2) 2 м
3) 4 м
6. Найдите длину дуги окружности радиуса 6 дм,
если её градусная мера равна 120°.
1) 2 π
2) 3 π
3) 4π

26. Ответы

№1
№2
№3
№4
№5
№6
2
1
2
3
1
3

27.

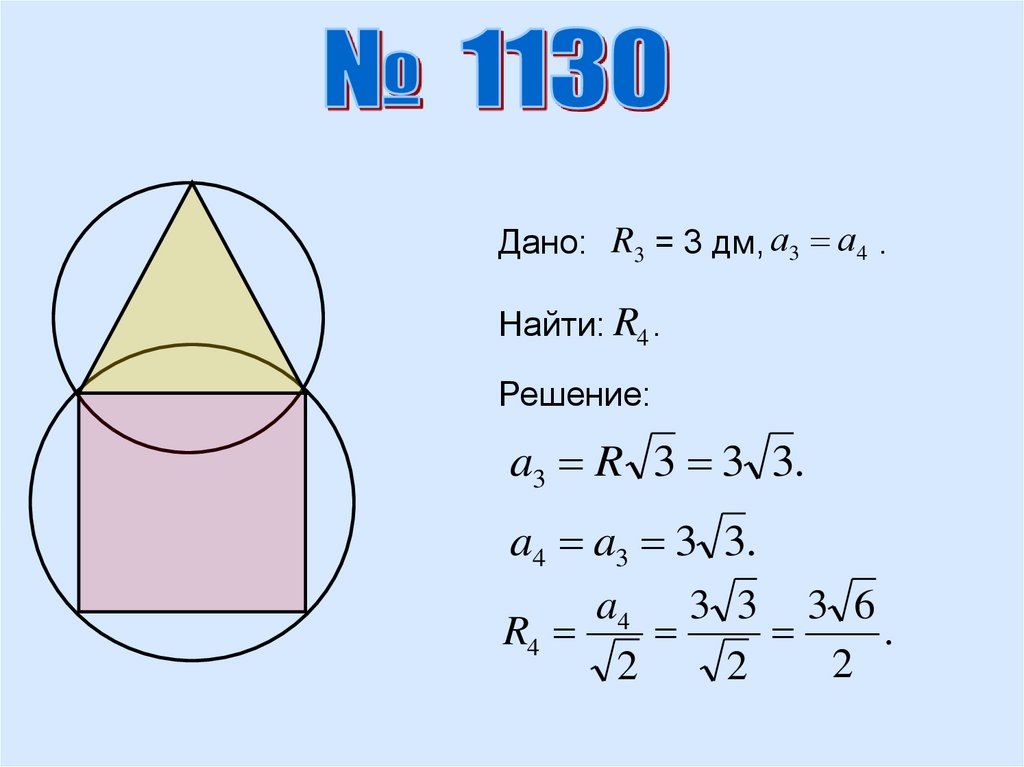
Дано: R3 = 3 дм, а3 а4 .
Найти: R4 .
Решение:
a3 R 3 3 3.
a4 a3 3 3.
a4 3 3 3 6
R4
.
2
2
2

28.

29. Задача № 3

Найдите площадь кольца,
ограниченного двумя
окружностями с общим центром и
радиусами 3 см и 7 см.

30. Задача № 4

Периметр квадрата, вписанного в
окружность, равен 48 см. Найдите
сторону правильного пятиугольника,
вписанного в ту же окружность.