Similar presentations:
Длина окружности. Площадь круга
1. Длина окружности. Площадь круга.
C 2 R,S R ,
C 2 r
S r
2
2
2. Длина окружности и площадь круга
ГеометрияДлина окружности
и
площадь круга
3. Оглавление :
§1. Правильные многоугольникиПравильный многоугольник
Окружность, описанная
около правильного
многоугольника
Окружность вписанная в
правильный многоугольник
Формулы для вычисления
площади правильного
многоугольника, его
стороны и радиуса
вписанной окружности
Построение правильных
многоугольников
§2. Длина окружности и площадь
круга
Длина окружности
Площадь круга
Площадь кругового сектора
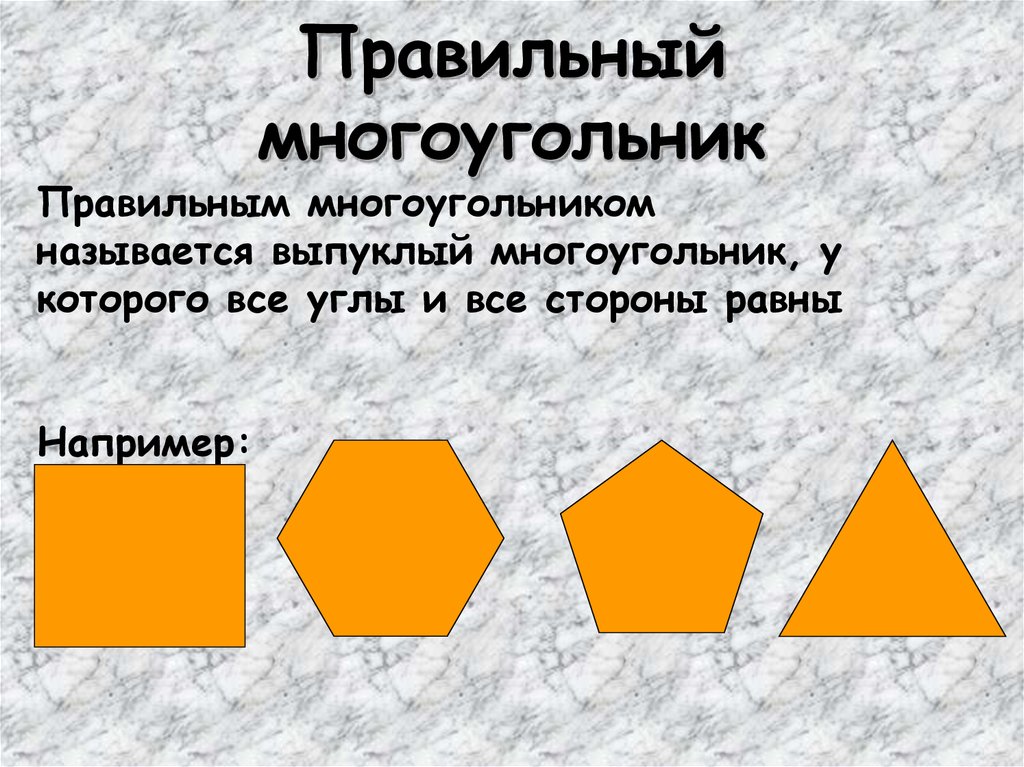
4. Правильный многоугольник
Правильным многоугольникомназывается выпуклый многоугольник, у
которого все углы и все стороны равны
Например:
5.
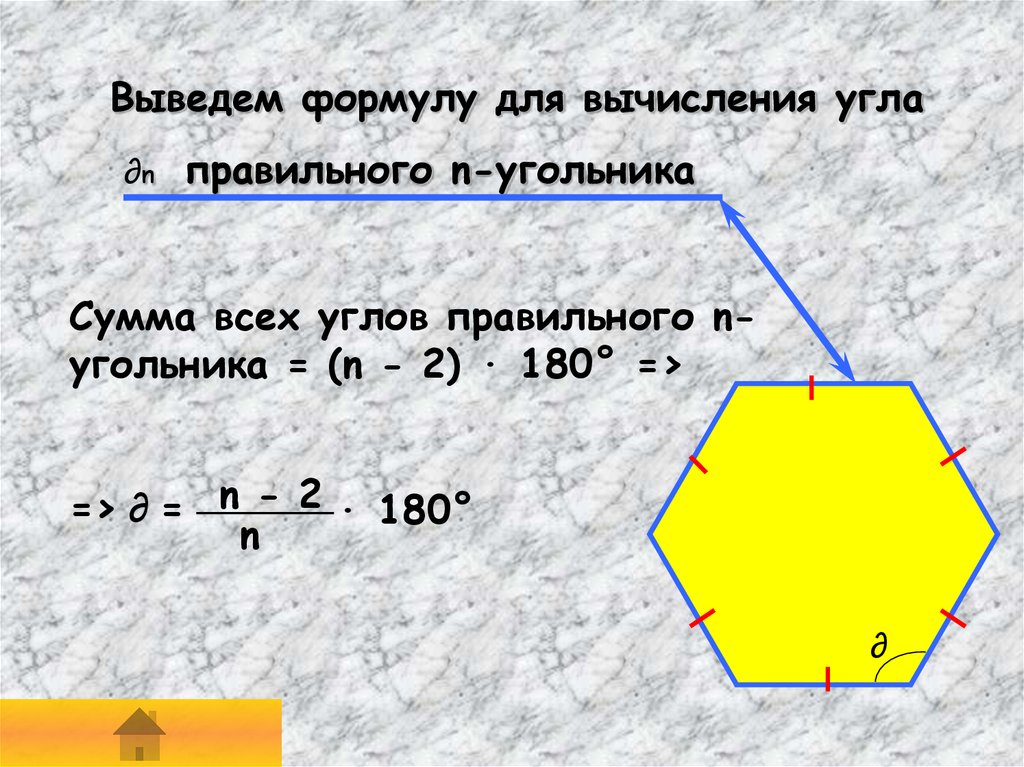
Выведем формулу для вычисления угла∂n правильного n-угольника
Сумма всех углов правильного nугольника = (n - 2) · 180° =>
=> ∂ = n - 2 · 180°
n
∂
6. Окружность описанная около правильного многоугольника
Окружность называется описанной околомногоугольника если все вершины этого
многоугольника лежат на окружности
ТЕОРЕМА:
Возле любого правильного
многоугольника можно описать
окружность, и притом только
одну
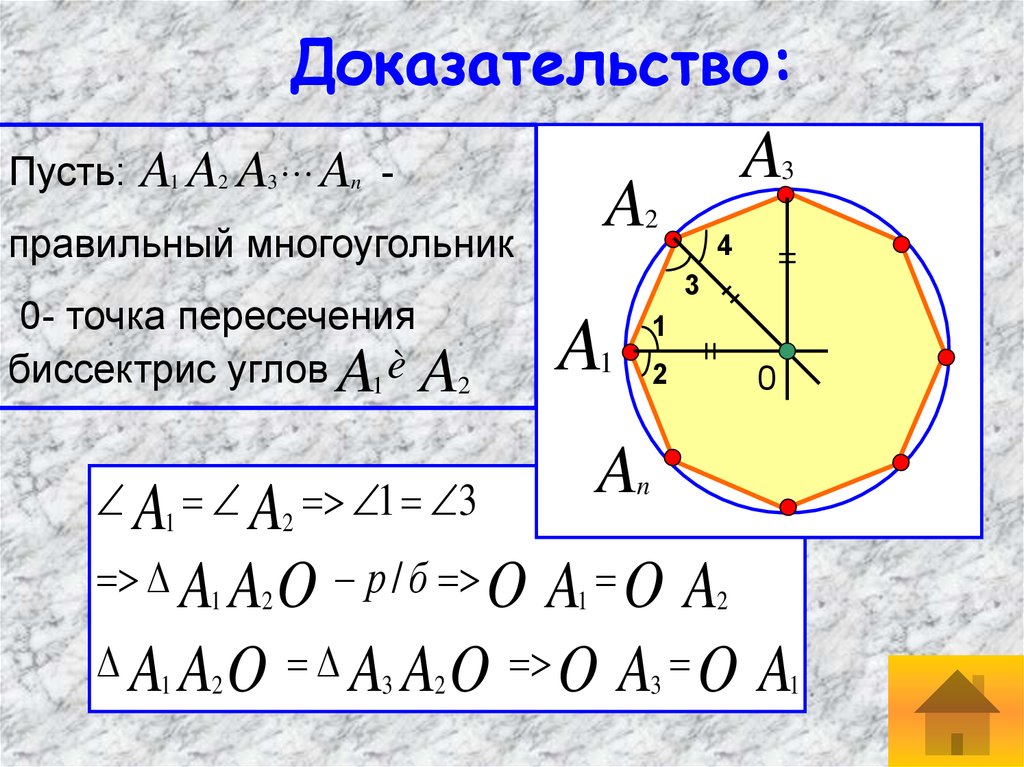
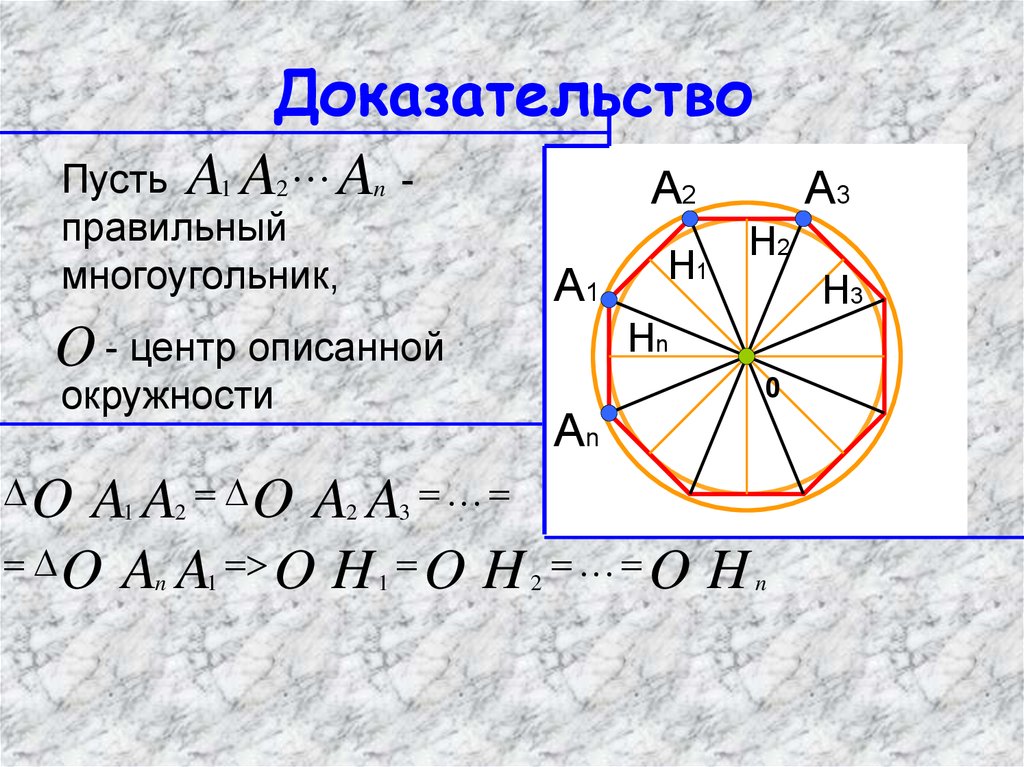
7. Доказательство:
Пусть:A A A A
1
2
3
n
-
2
4
3
1
A
1
2
0
A
A1 A2 1 3
A1 A2 O р / б O
3
A
правильный многоугольник
0- точка пересечения
биссектрис углов A1 è A2
A
n
A O A
A A O A A O O A O A
1
2
3
2
1
2
3
1
8.
9. Окружность, вписанная в правильный многоугольник
Окружность называется вписанной в многоугольник,если все стороны многоугольника касаются этой
окружности
ТЕОРЕМА:
В любой правильный
многоугольник можно вписать
окружность, и притом только
одну
10. Доказательство
Пусть A A A A21
2
правильный
многоугольник,
A1
окружности
2
n
2
1
H1
H3
A A A O
1
2
n
0
An
A A O A A
O A A O H O H
1
H2
Hn
O - центр описанной
O
A3
n
3
1
2
O
H
n
11.
Центр окружности,описанной около
правильного
многоугольника,
совпадает с центром
окружности,
вписанной в тот же
многоугольник, ЭТА
ТОЧКА НАЗЫВАЕТСЯ ЦЕНРОМ
ПРАВИЛЬНОГО
МНОГОУГОЛЬНИКА
Окружность, вписанная в
правильный многоугольник,
касается сторон
многоугольника в их
серединах
12.
Допустим:Формулы
для вычисления
A2
A3
S- площадь правильного n-угольника
H
площади правильного
H
A1
H
an- его сторона
многоугольника, его стороны
и
H
P- периметр
0
радиуса
вписанной
окружности
R- радиус описанной окружности
An
2
1
3
n
r- радиус вписанной окружности
1
S 2 an r
1
1
1
S n a n r ( n a n )r Pr
2
2
2
13.
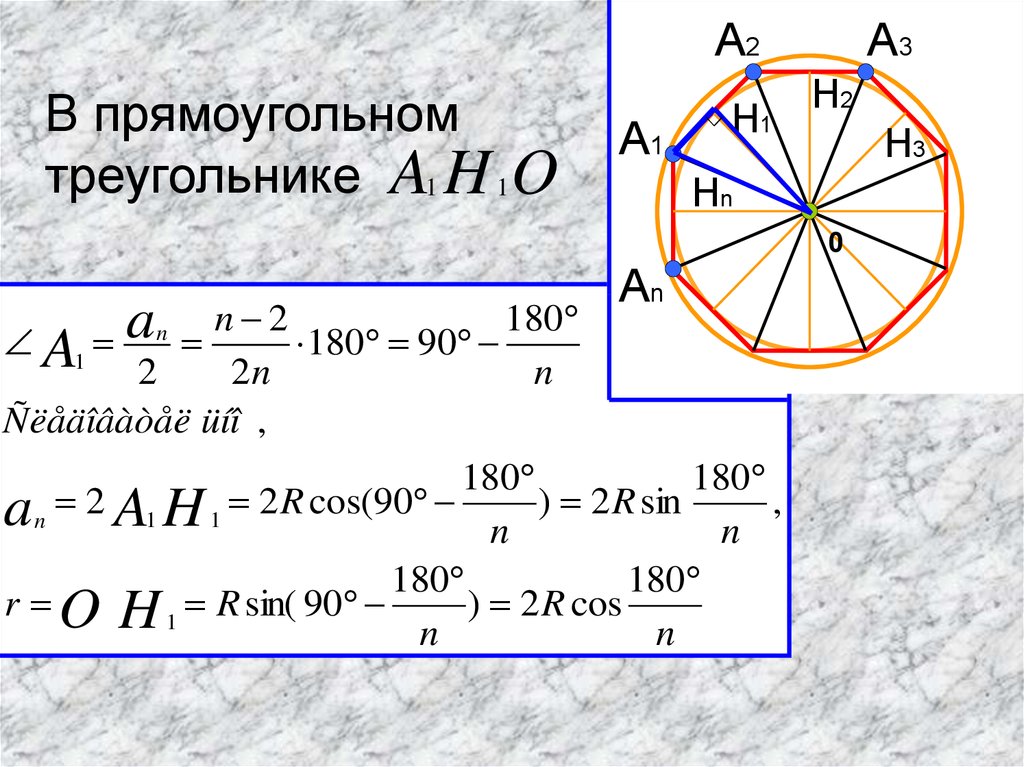
A2В прямоугольном
треугольнике A1 H 1 O
A1
H1
A3
H2
H3
Hn
0
n 2
180
A1
180 90
2
2n
n
Ñëåäîâàòåë üíî ,
a
An
n
180
180
an 2 A1 H 1 2 R cos(90 n ) 2 R sin n ,
180
180
r O H 1 R sin( 90
) 2 R cos
n
n
14.
Если в формуле180
an 2 R sin n
вместо «n»
подставить числа: 3, 4 и 6, то получим
выражения для сторон правильного
треугольника, квадрата и шестиугольника:
180
3
a3 2 R sin 3 2 R sin 60 2 R 2 R 3
180
2
a4 2 R sin 4 2 R sin 45 2 R 2 R 2
180
1
a6 2 R sin 6 2 R sin 30 2 R 2 R
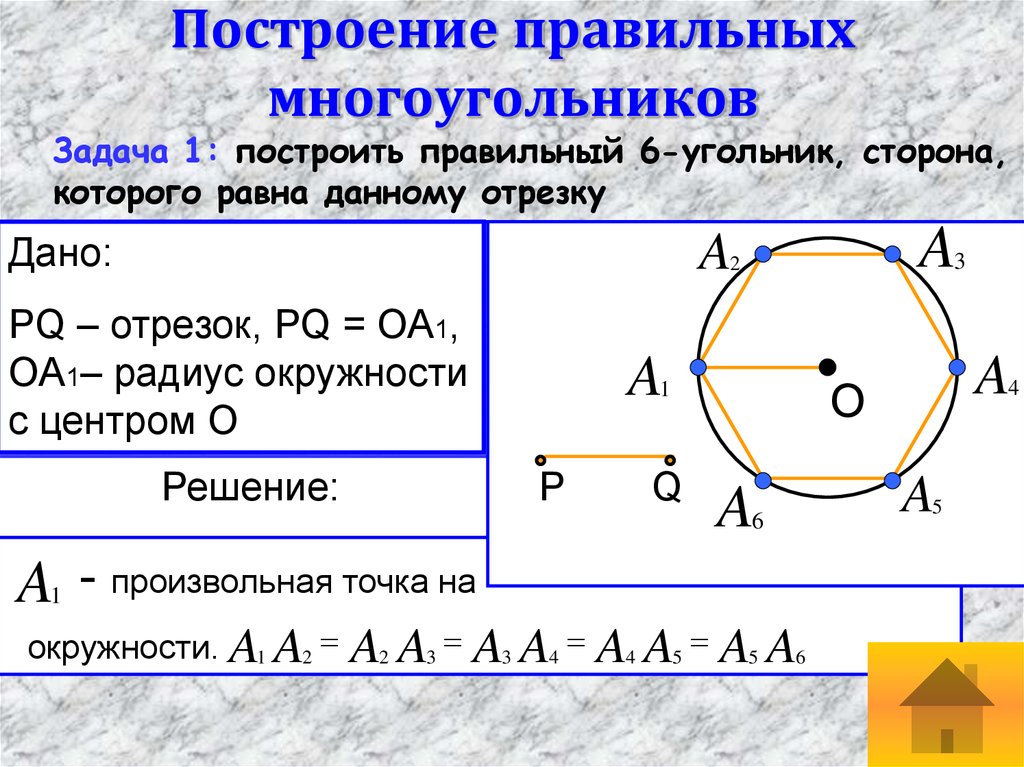
15. Построение правильных многоугольников
Задача 1: построить правильный 6-угольник, сторона,которого равна данному отрезку
Дано:
A
A
3
2
PQ – отрезок, PQ = OA1,
OA1– радиус окружности
с центром O
A
1
Решение:
P
Q
A
A
5
AA1- произвольная точка на
1
A A A A A A A A
2
3
3
4
4
4
O
6
окружности. A1 A2
A
5
5
6
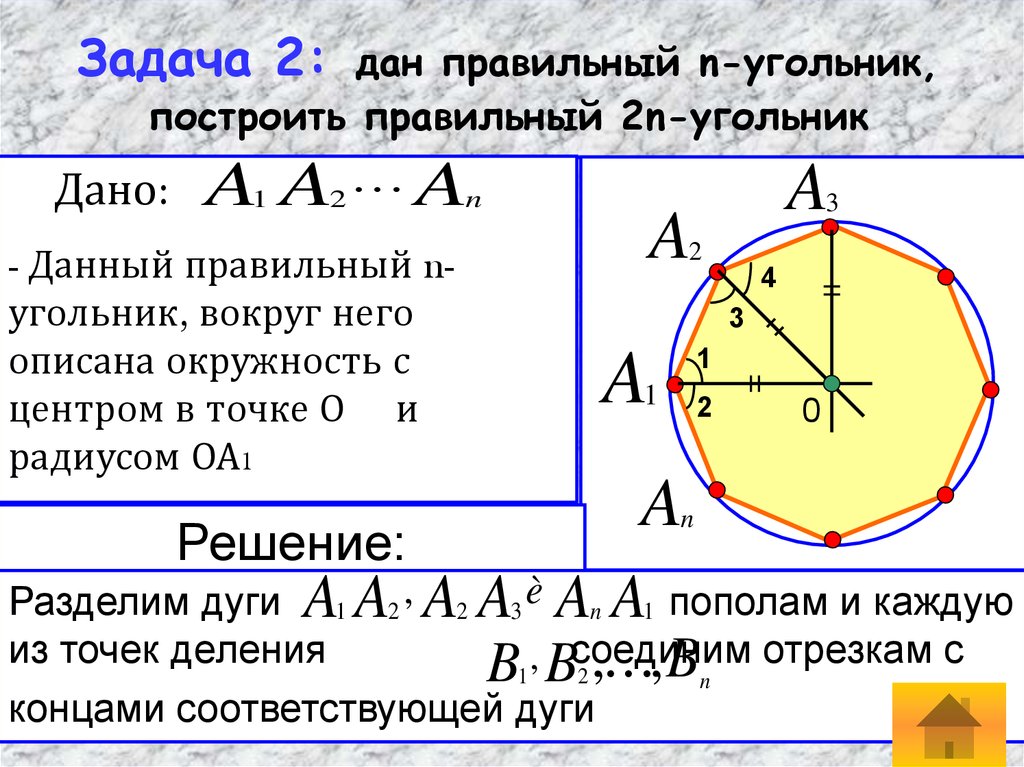
16. Задача 2: дан правильный n-угольник, построить правильный 2n-угольник
Дано:A A A
1
2
- Данный правильный nугольник, вокруг него
описана окружность с
центром в точке О и
радиусом ОА1
Решение:
n
A
3
A
2
4
3
1
A
1
2
0
A
n
Разделим дуги A1 A2 , A2 A3 è An A1 пополам и каждую
из точек деления
отрезкам с
B1 , Bсоединим
2 , , Bn
концами соответствующей дуги
17. Длина окружности
AA1
С
2R
C 2 R
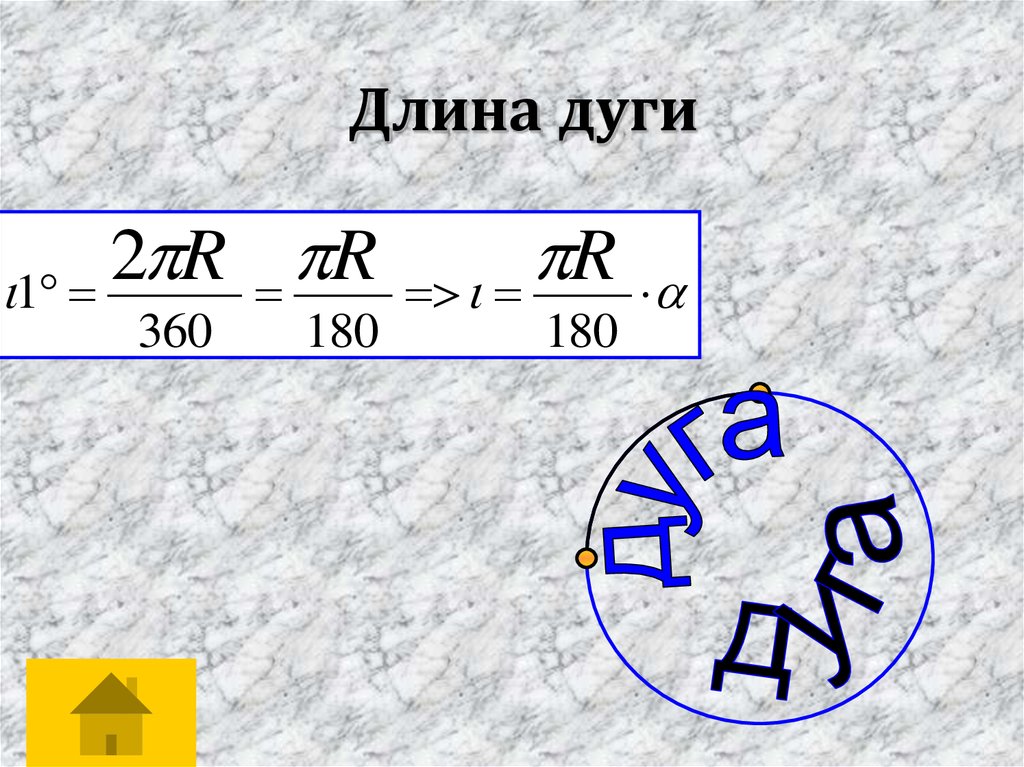
18. Длина дуги
2R
R
1
360
180
R
180
19.
Площадь кругаКруг- часть плоскости, ограниченная окружностью
2
S R
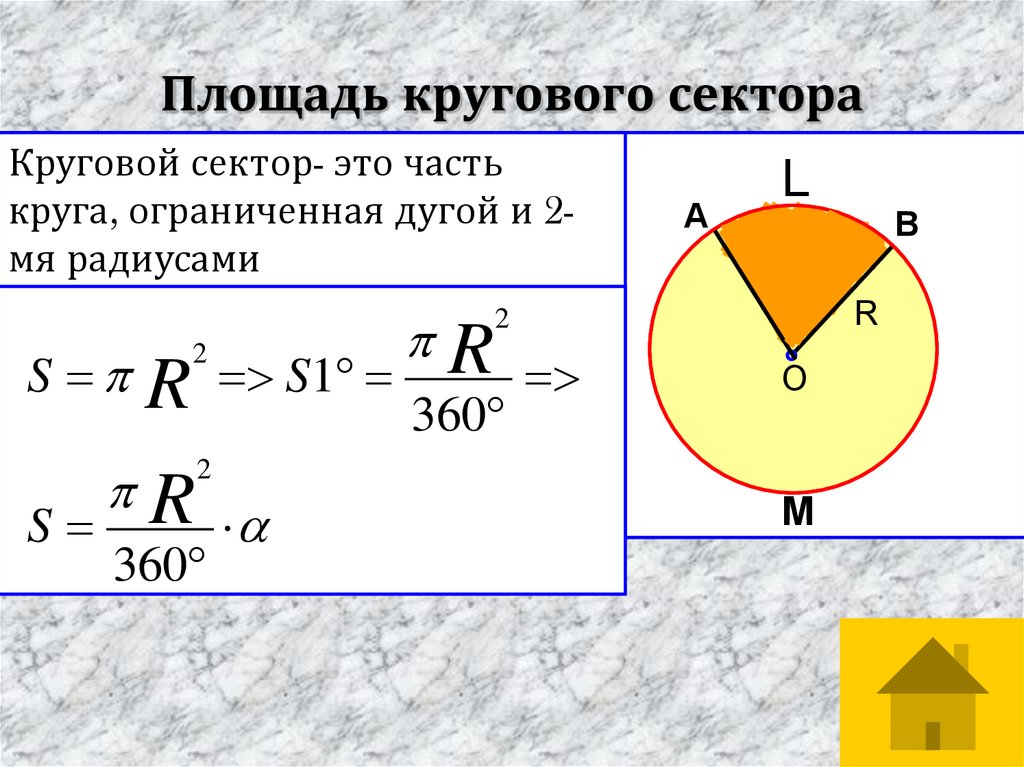
20. Площадь кругового сектора
Круговой сектор- это частькруга, ограниченная дугой и 2мя радиусами
S
S
R
2
R
S1
R
A
L
B
R
2
360
О
2
360
M











 mathematics
mathematics








