Полуправильные многоугольники. Длина и площадь

1.

МОУ « Теньгушевская средняя обшеобразовательная школа»
Геометрия
9 класс
Дополнительные главы к
школьному учебнику
« Учитель-методист» А.П.Родина.
2007-2008 учебный год.

2. Полуправильные многоугольники. Длина и площадь.

Цели: 1) Углубить знания учащихся по теме
«Многоугольники».
2) Ввести понятие равноугольнополуправильного и равностороннеполуправильного многоугольника.
3) Познакомить с теоремой Барбье о
длине кривой постоянной ширины
и площадью фигуры.

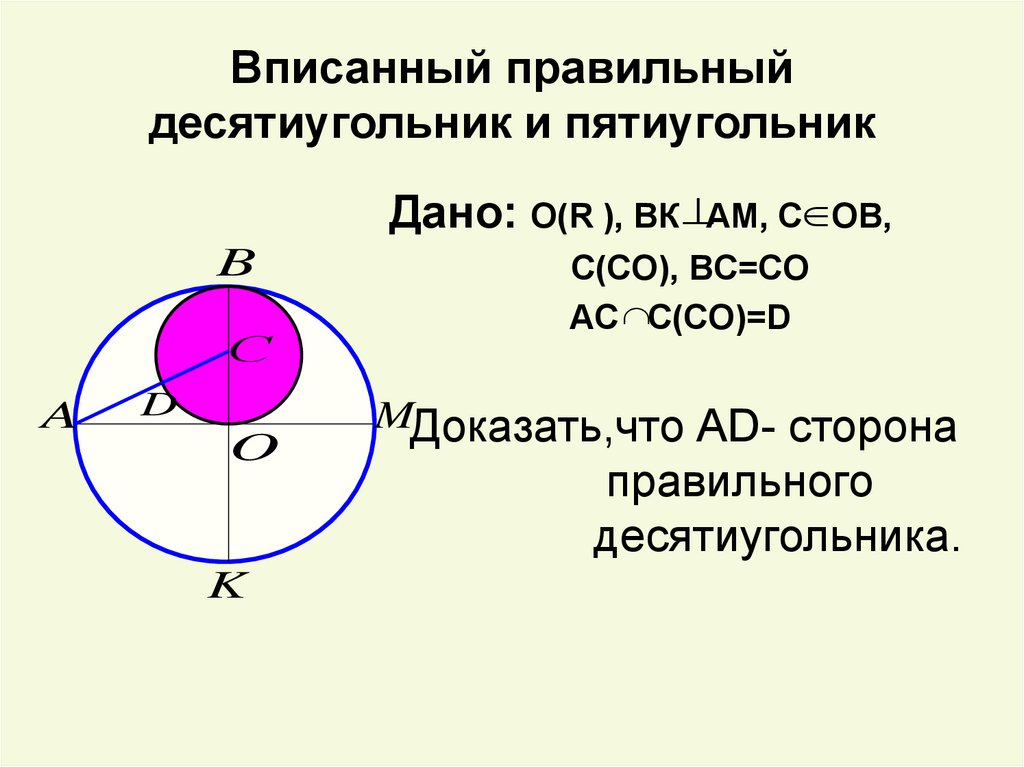
3. Вписанный правильный десятиугольник и пятиугольник

Дано: О(R ), BК AM, C OB,
B
С
A
D
O
K
C(CO), BC=CO
AC C(CO)=D
MДоказать,что АD- сторона
правильного
десятиугольника.

4. Доказательство

B
A
Доказательство
1) МАВ=144-угол
десятиугольника,
360
M
O R
АОВ=
=36,то ОАВ= ОВА=72
10
ВАС=36-т.к.АС-биссектриса.
AB
BC
АОВ ~ САВ-по двум углам, OB =
ОА=R,
AB
BC=OB-OC=R-AB,значит
C
AB R AB
5 1
=
,то
АВ=
R.
R
AB
2
2) АВ=2RSin18, тогда
5 1
Sin18 =
4
5 1
2RSin18=
R,
2

5.

B
C
D
A
M
O
А3
A2
A1
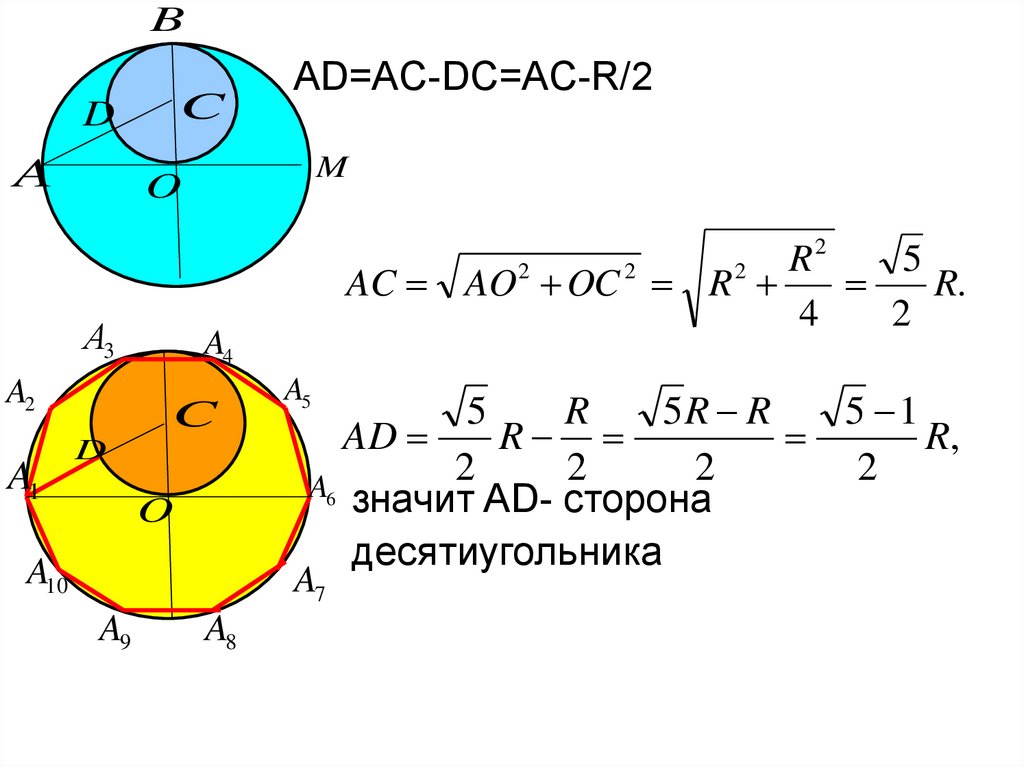
AD=AC-DC=AC-R/2
2
R
5
2
2
2
AC AO OC R
R.
4
2
A4
C
D
O
A10
A5
5
R
5R R
5 1
AD
R
R,
2
2
2
2
A6 значит AD- сторона
десятиугольника
A7
A9
A8

6. Построение правильного десятиугольника

При помощи одного циркуля

7. Построение

S
E
H
F
Q
N
P
M
K
L
• 1. O(R)
• 2. A1A2=A2A3=A3A4=
=A4A5=A5A6=R
• 3. A1(A1A3) A4(A1A3)=B
• 4. A3C=A5C=OB
• 5. OC-сторона
десятиугольника
• 6. EF, FN, NM, MK, KL,
LP, PQ, QH, HS
• EFNMKLPQHSИСКОМЫЙ

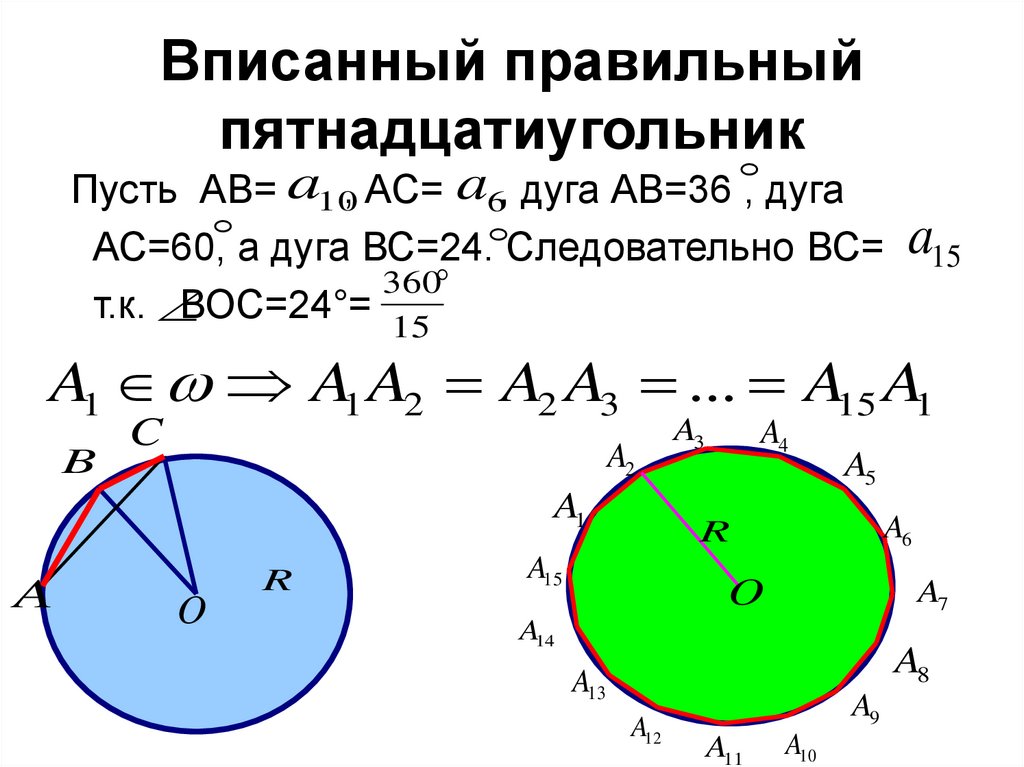
8. Вписанный правильный пятнадцатиугольник

Пусть АВ= a10, АС= a6, дуга АВ=36 , дуга
АС=60, а дуга ВС=24. Следовательно ВС=
360
т.к.
ВОС=24°=
a15
15
A1 A1 A2 A2 A3 ... A15 A1
B
C
A2
A1
A
O
R
A3
A4
A5
A6
R
A15
O
A7
A14
A8
A13
A12
A9
A11
A10

9. Теорема Гаусса (1777-1855гг)

Теорема Гаусса (17771855гг)
Построение правильного n-угольника
с помощью линейки и циркуля
возможно тогда и только тогда, когда
число n имеет следующее разложение
m
на множители n 2 p1 p2 ... ps
где mцелое неотрицательное число , а
- p1, p2,... ps
различные между собой простые числа
k
2
вида
2 1

10. Примеры

2
• При m =0, s=1, n= 2 1 для к=0;1;2;3;4 получаем
n=3, n=5, n=17, n=257, n=65537.
• При m=0, s=2 имеем n p1 p2 , если p 3
1
p2 5 , то n=15.
• Число
7
простое
,
но
оно
не
является
числом
2k
2 1 , поэтому с помощью циркуля и линейки
нельзя точно построить правильный семиугольник
k
2
• 9 ≠ 2 1 ,поэтому построить правильный
девятиугольник нельзя.
• 360 ≠ 23 32 5 не удовлетворяет т.Гаусса,т.к.
3 входит дважды. Следовательно нельзя
разделить окружность на 360 равных частей,т.е.
нельзя построить угол в один градус.
k

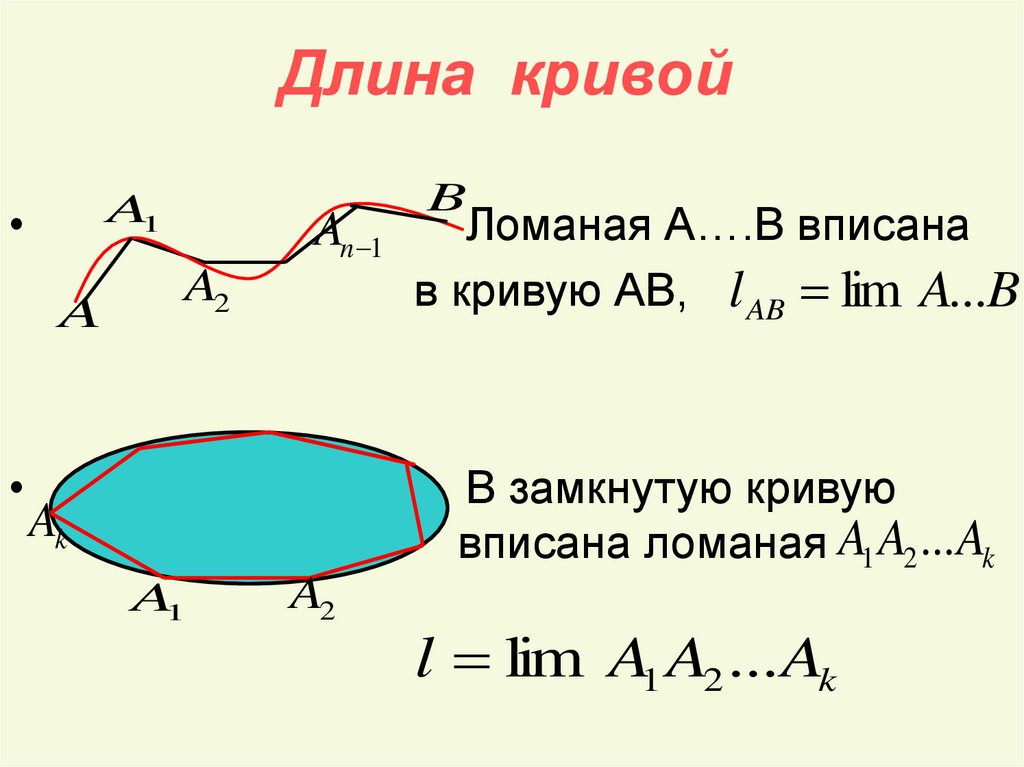
11. Длина кривой

A1
A
An 1
A2
B
Ломаная А….В вписана
в кривую АВ, l AB lim A...B
B замкнутую кривую
вписана ломаная A1 A2 ... Ak
Ak
A1
A2
l lim A1 A2 ... Ak

12.

• Теорема Барбье Длина любой кривой
постоянной ширины d равна πd.
• Доказательство. Представим себе каток постоянной
ширины d, который катится без проскальзывания между
параллельными прямыми а и b.
• Пусть а неподвижна, а прямая b движущаяся с постоянной
скоростью v. Cделав один оборот каток переместится на
расстояние l, где l-длина кривой, ограничивающей каток.
Прямая b переместится тоже на lпо отношению к катку, тогда по
отношению к неподвижной прямой- на 2 , l 2l Каток
vt
вращается вокруг точки (А(а);С(b)) с угловой скоростью
вращения катка
то скорость движения прямой b будет
.
Итак 2l dt,но
, тогда 2l 2 d ,
t 2
l d
v d

13. Площадь фигуры

14. Полуправильные многоугольники

Определение. Выпуклый многоугольник с
четным числом вершин называется
равноугольно-полуправильным, если его
стороны, взятые через одну, равны и все его
углы равны.(пример-прямоугольник)
Теорема1. Около любого равноугольнополуправильного многоугольника можно
описать окружность, и притом только одну.

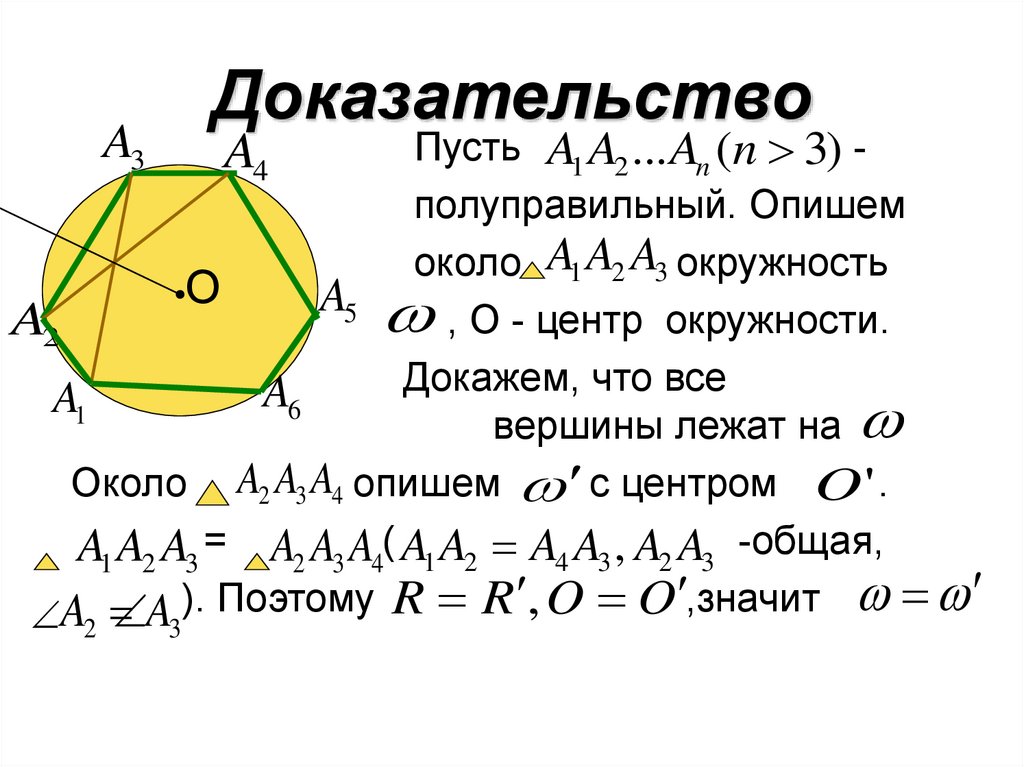
15. Доказательство

Пусть A1 A2 ... An (n 3) полуправильный. Опишем
около A1 A2 A3 окружность
O
A5 , О - центр окружности.
A2
Докажем, что все
A
A1
6
вершины лежат на
Около A2 A3 A4 опишем с центром O ' .
A1 A2 A3 = A2 A3 A4( A1 A2 A4 A3 , A2 A3 -общая,
).
Поэтому
,значит
R
R
,
O
O
A
A
A3
2
A4
3

16.

► Определение
Выпуклый многоугольник с
четным числом вершин называется
равносторонне-полуправильным, если
его углы, взятые через один, равны и
все его стороны равны.
► Теорема
В любой равностороннеполуправильный многоугольник можно
вписать окружность, и притом только
одну.

17.

C
H
P
B
D
O
A
M
АО, ВО, …КО - биссектрисы
углов А, В,…К.
AO BO ... KO, O-центр
вписанной окружности.
ОН ВС,ОР СD, OH=OP=r
K
• Действительно, НСО= РСО,т.к. ОНС= ОРС= 90,
ОСН= ОСР, ОС- общая.
• Следствие1. Не в любой равноугольно- полуправильный
многоугольник можно вписать окружность(примерпрямоугольник)
• Следствие2. Не для любого равностороннеполуправильного многоугольника существует описанная
окружность.

18. Домашнее задание

Подготовиться к контрольной работе, повторив
материал пунктов 105-112 и решив задачи:
1)Периметр правильного пятиугольника,
вписанного в окружность, равен 6 дм. Найдите
сторону правильного треугольника, вписанного в ту
же окружность.
2) Найдите площадь круга, если площадь
вписанного в ограничивающую его окружность
треугольника равна 12 3cm2.
3)Найдите длину окружности, если площадь
вписанного в нее правильного четырехугольника
2
равна 32 m

19.

Молодцы!