Similar presentations:
Теория и алгоритмы. Решения типовых задач на взаимное пересечение геометрических объектов
1.
Лекция 7ТЕОРИЯ И АЛГОРИТМЫ
РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ НА
ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ
ГЕОМЕТРИЧЕСКИХ
ОБЪЕКТОВ
Красовская Н.И.
2.
Качественная сторона очерчивает круг задач, вкоторых определяется расположение
объектов относительно друг друга
Такие задачи называют
позиционными
Красовская Н.И.
3.
Задачу построения точек пересечения какой-нибудьзаданной линии с поверхностью называют
первой основной позиционной задачей
Задачу построения линий пересечения
двух заданных поверхностей называют
второй основной позиционной задачей
Красовская Н.И.
4.
Решение задач на пересечениегеометрических
объектов, занимающих
проецирующее положение
Красовская Н.И.
5.
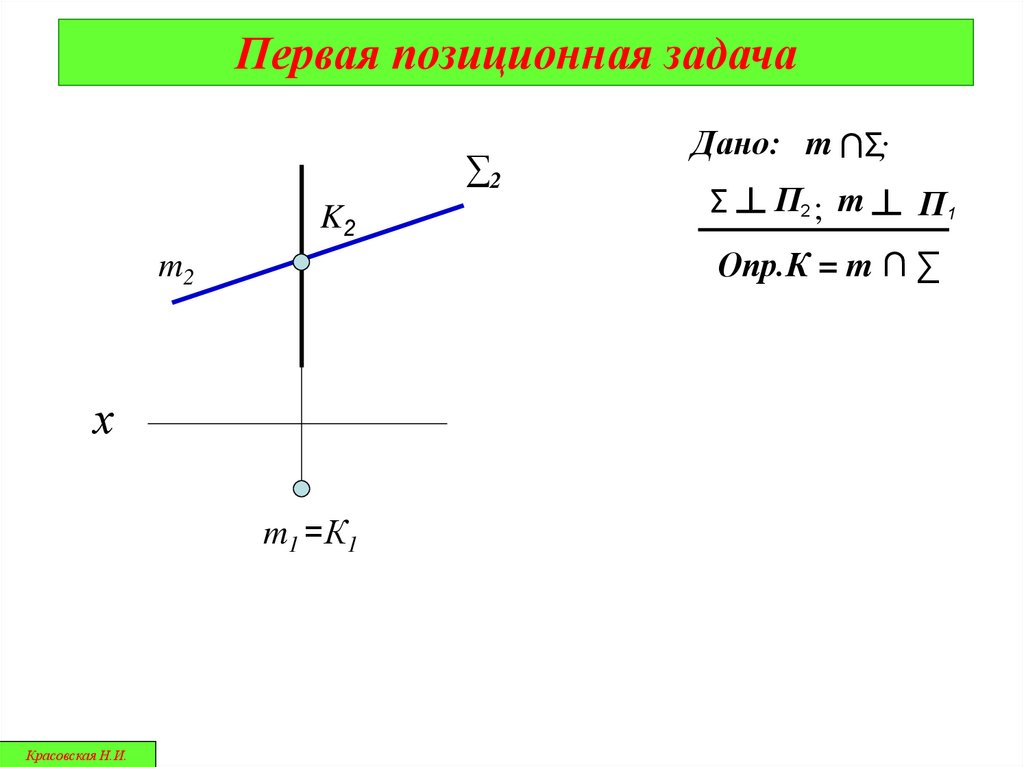
Первая позиционная задача∑2
K2
∑
┴ П2 ; m ┴ П1
Опр.К = m ∩ ∑
m2
х
m1 =К1
Красовская Н.И.
Дано: m ∩∑;
6.
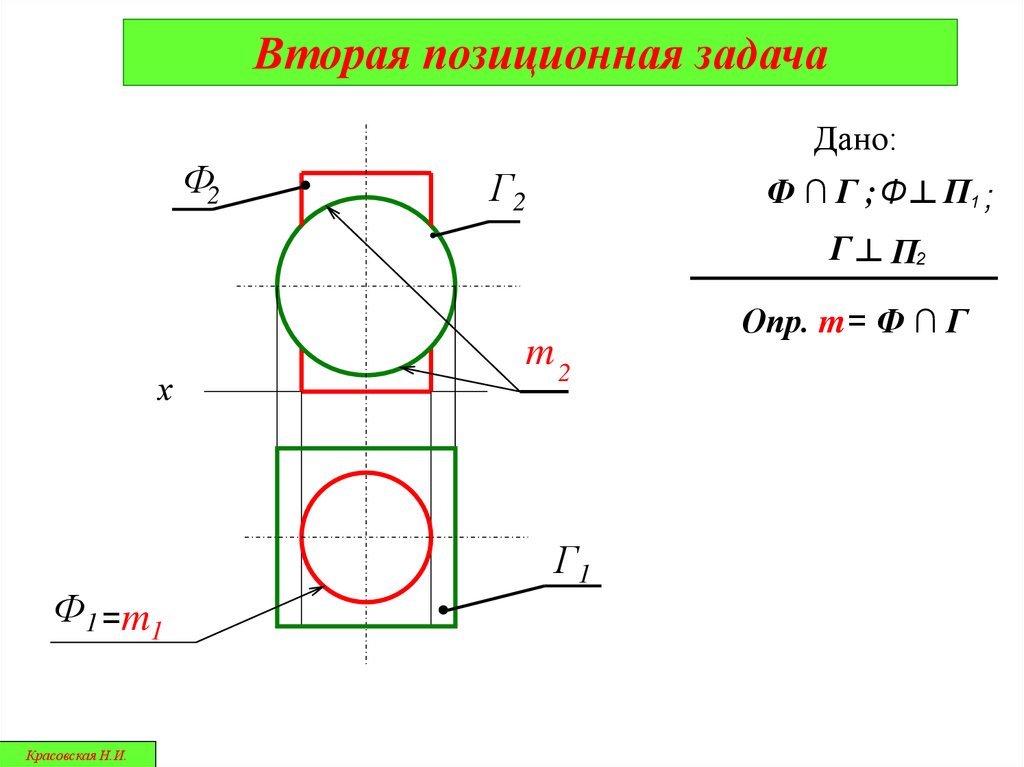
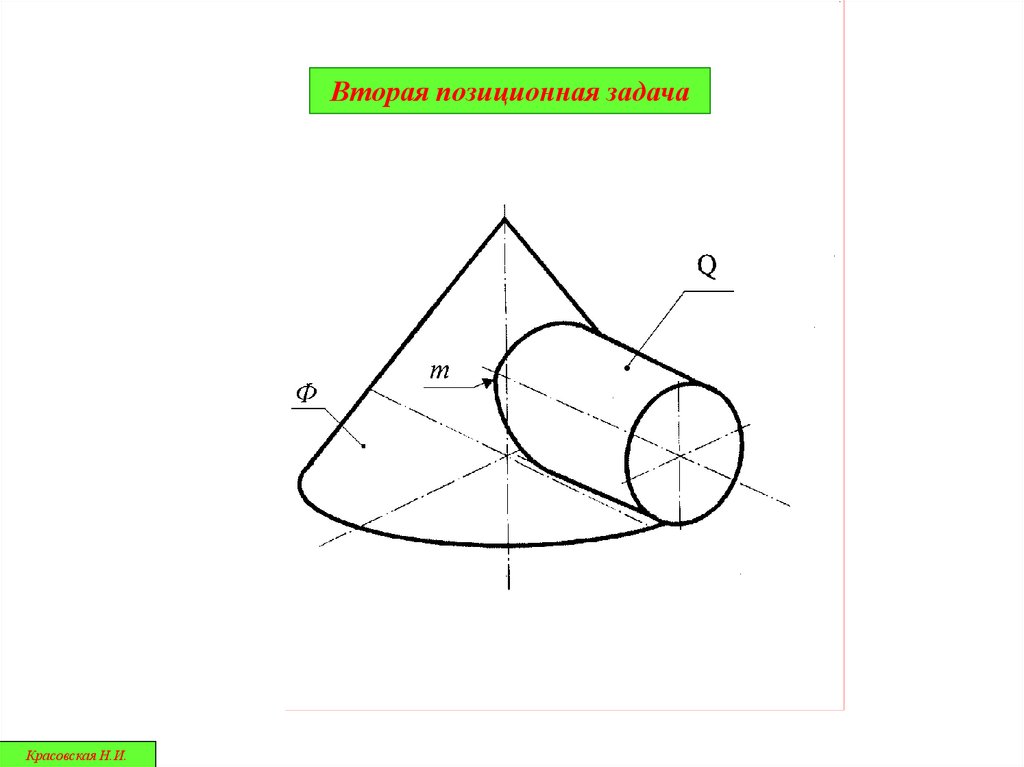
Вторая позиционная задачаДано:
Ф2
Г2
Ф ∩ Г ;Ф ┴ П1 ;
Г ┴ П2
х
Ф1 =m1
Красовская Н.И.
m2
Г1
Опр. m= Ф ∩ Г
7.
Aлгоритм1. Искомый общий элемент
уже задан
на чертеже
2. Его проекции частично или полностью
совпадают с заданными проекциями-носителями
пересекающихся проецирующих геометрических объектов
3. Решение задачи
сводится к обозначению
проекций искомого общего элемента
4. Третья проекция элемента пересечения находится
по законам проекционной связи
Красовская Н.И.
8.
Решение задачна пересечение проецирующего
геометрического объекта с
геометрическим объектом
общего положения
Красовская Н.И.
9.
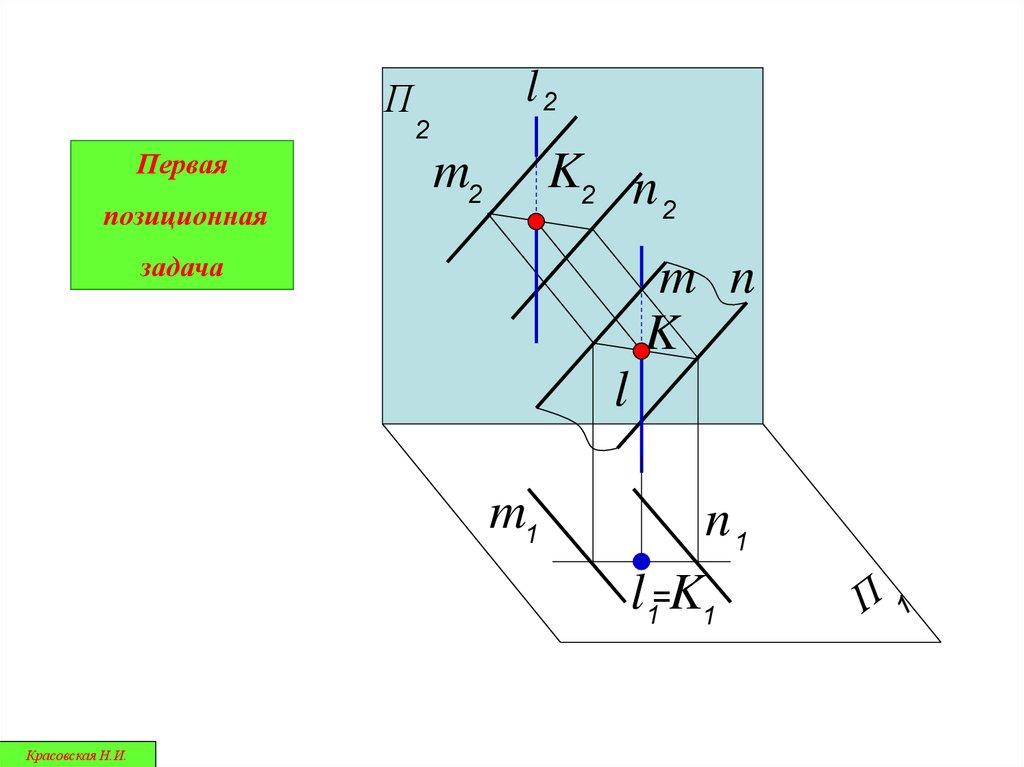
ППервая
позиционная
l2
2
m2
K2 n
2
задача
m n
K
l
m1
n1
l1=K1
Красовская Н.И.
10.
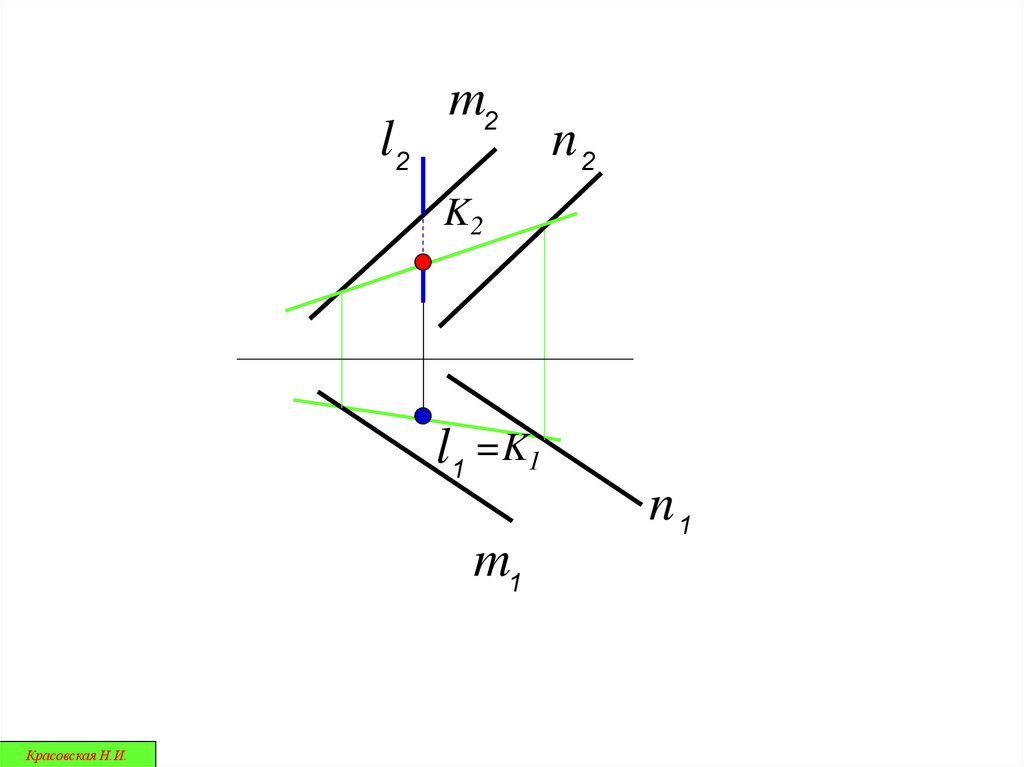
l2m2
n2
K2
l1 =K1
n1
m1
Красовская Н.И.
11.
Красовская Н.И.12.
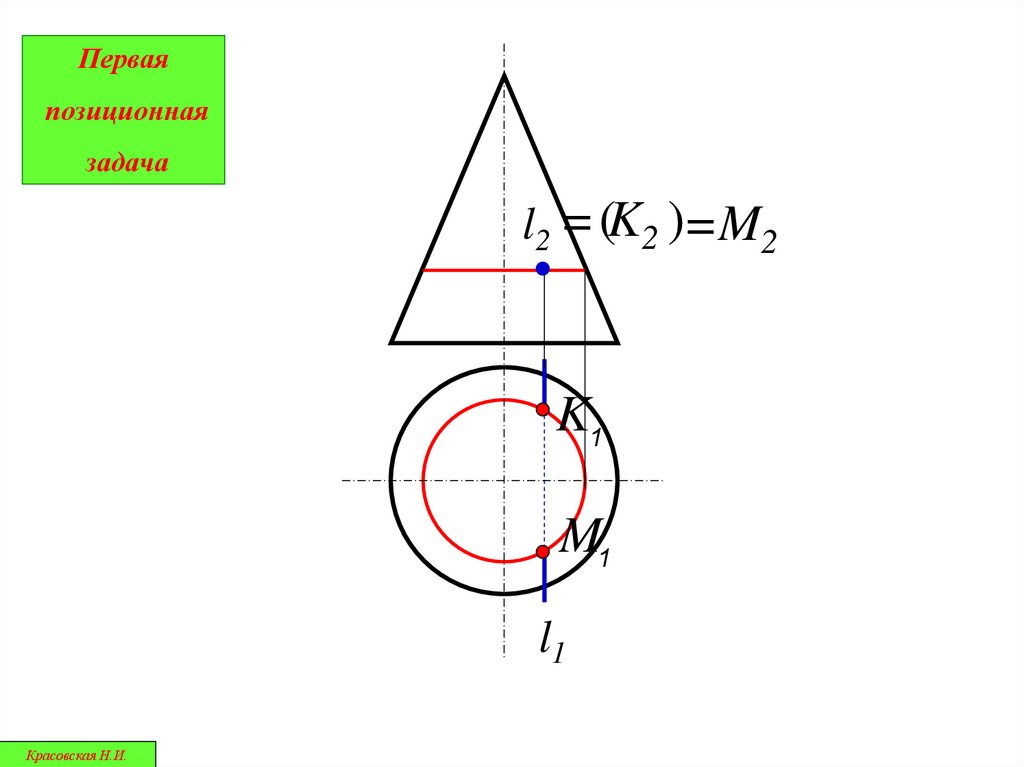
Перваяпозиционная
задача
l2 = (K2 )=M2
K1
M1
l1
Красовская Н.И.
13.
Красовская Н.И.14.
Красовская Н.И.15.
Вторая позиционная задачаКрасовская Н.И.
16.
Красовская Н.И.17.
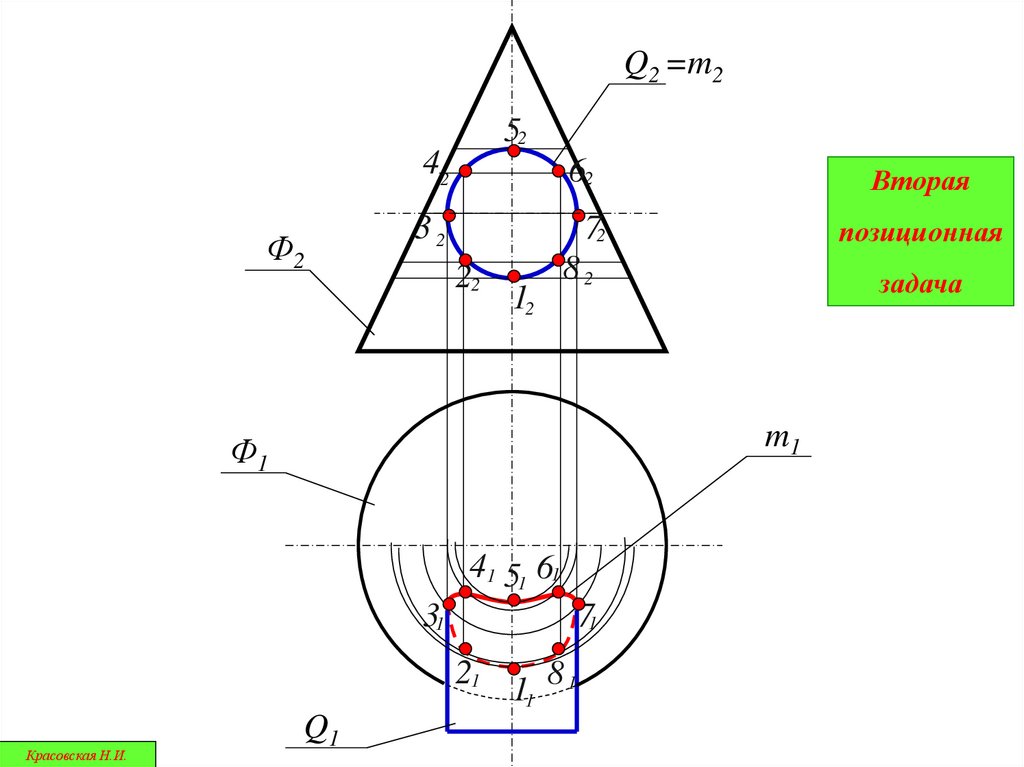
Q2 =m252
42
Ф2
62
32
72
22
12
позиционная
82
задача
m1
Ф1
41 51 61
31
71
21 1 8 1
1
Красовская Н.И.
Вторая
Q1
18.
Алгоритм1.Одна проекция искомого общего элемента уже задана на
чертеже
2. Она частично или полностью
совпадает с заданной проекцией — носителем
проецирующего геометрического объекта
3. Вторая проекция искомого общего элемента находится
из условия принадлежности геометрическому объекту
общего положения
4. Третья проекция элемента пересечения строится
по законам проекционной связи
Красовская Н.И.
19.
Сечение поверхностейпроецирующей плоскостью
Красовская Н.И.
20.
Коническиесечения
Красовская Н.И.
21.
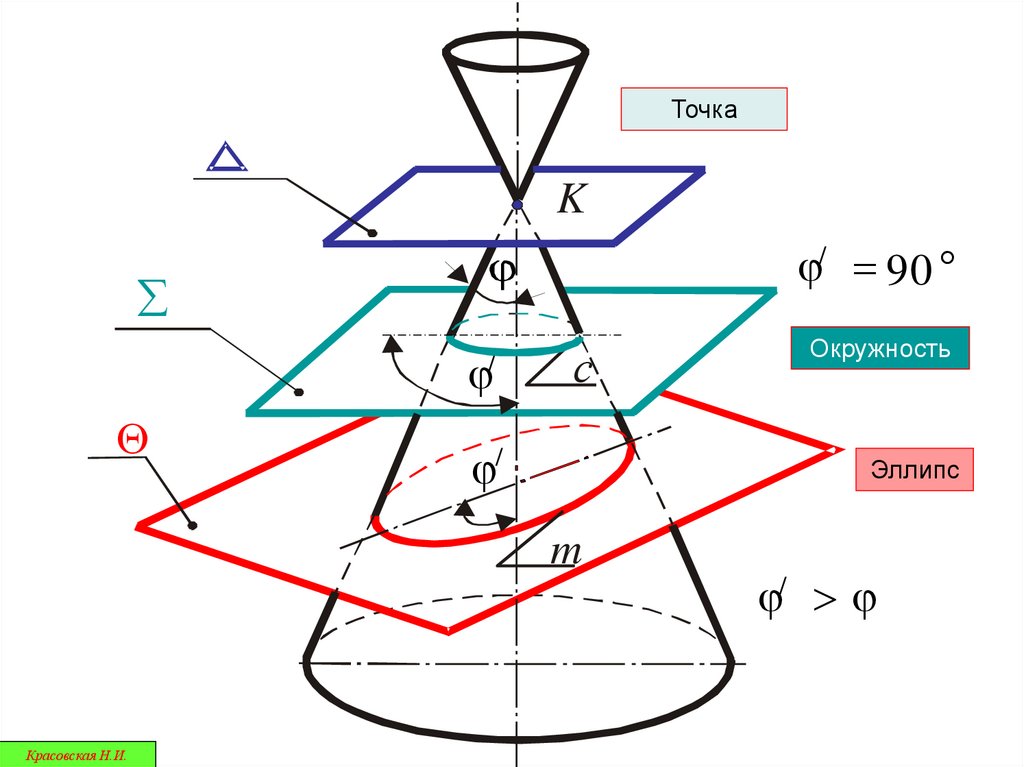
В результате сечения конической поверхностиплоскостью получаются кривые второго
порядка:
окружности, эллипсы, параболы и гиперболы
Эти кривые называют
кониками
Красовская Н.И.
22.
ТочкаK
j/ = 90
с
j
/
Q
j
/
Эллипс
m
Красовская Н.И.
Окружность
j/ > j
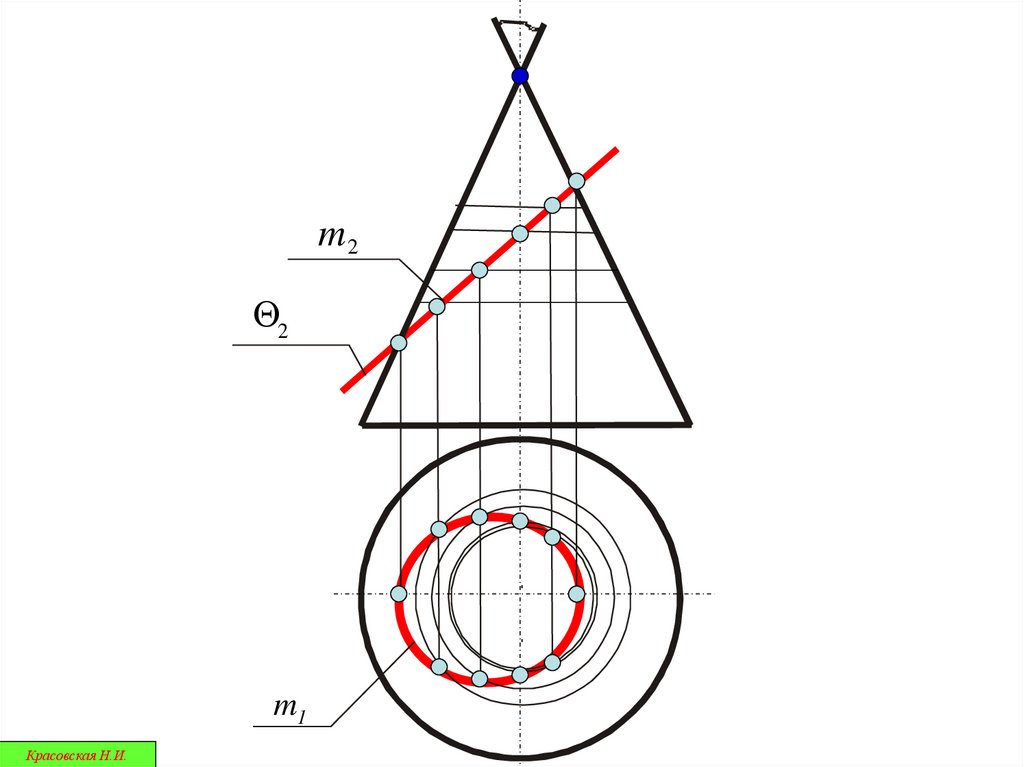
23.
Красовская Н.И.24.
m2Q2
m1
Красовская Н.И.
25.
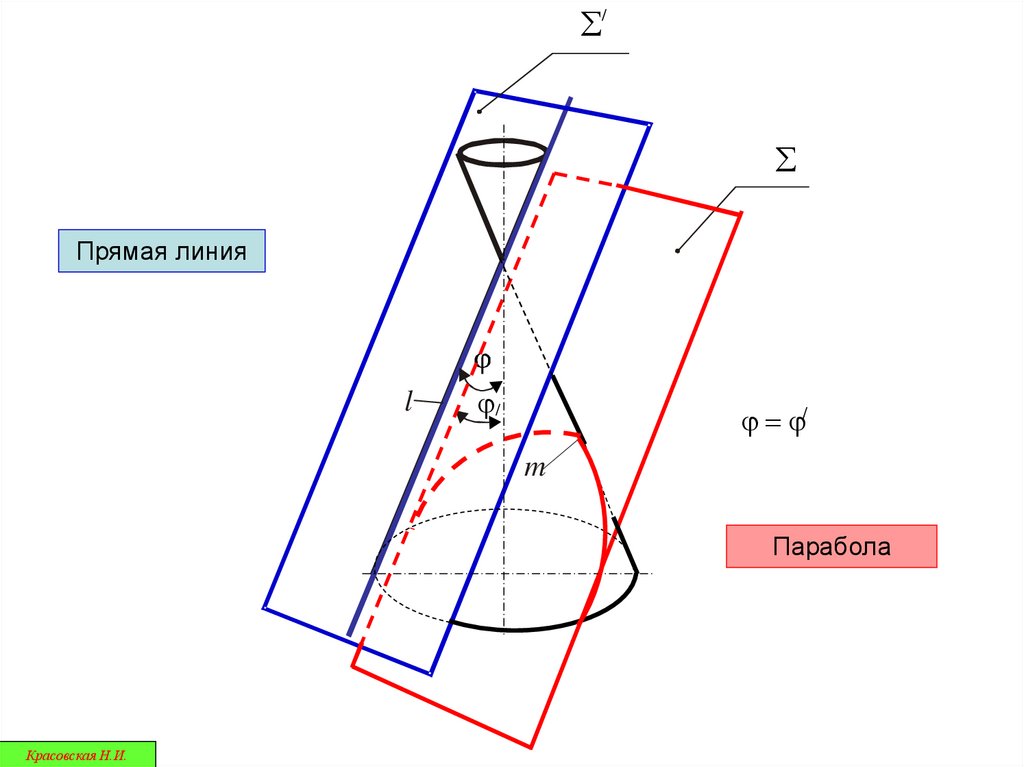
/Прямая линия
l
j/
j = j/
m
Парабола
Красовская Н.И.
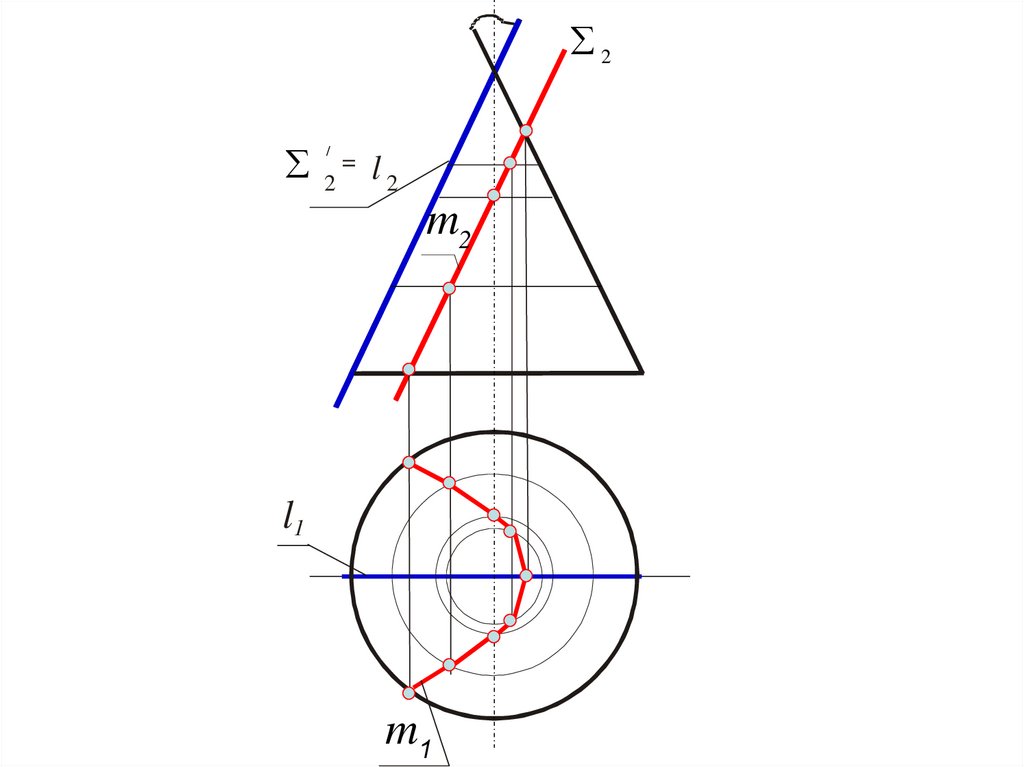
26.
2/
2
=
l2
m2
l1
m1
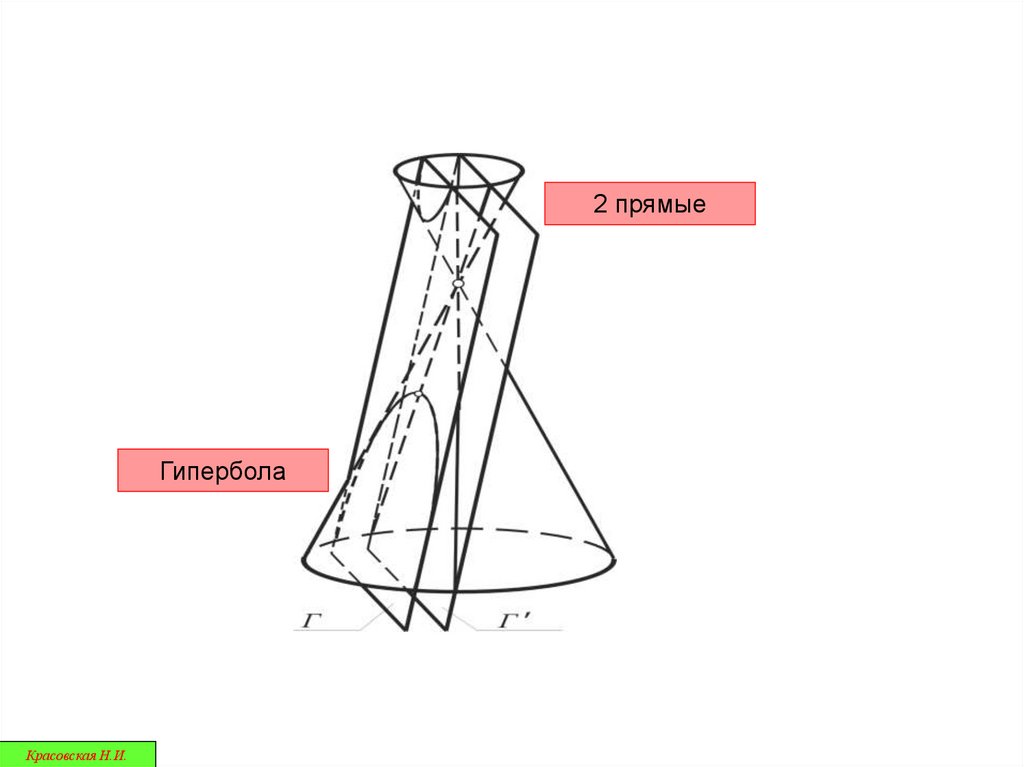
27.
2 прямыеГипербола
Красовская Н.И.
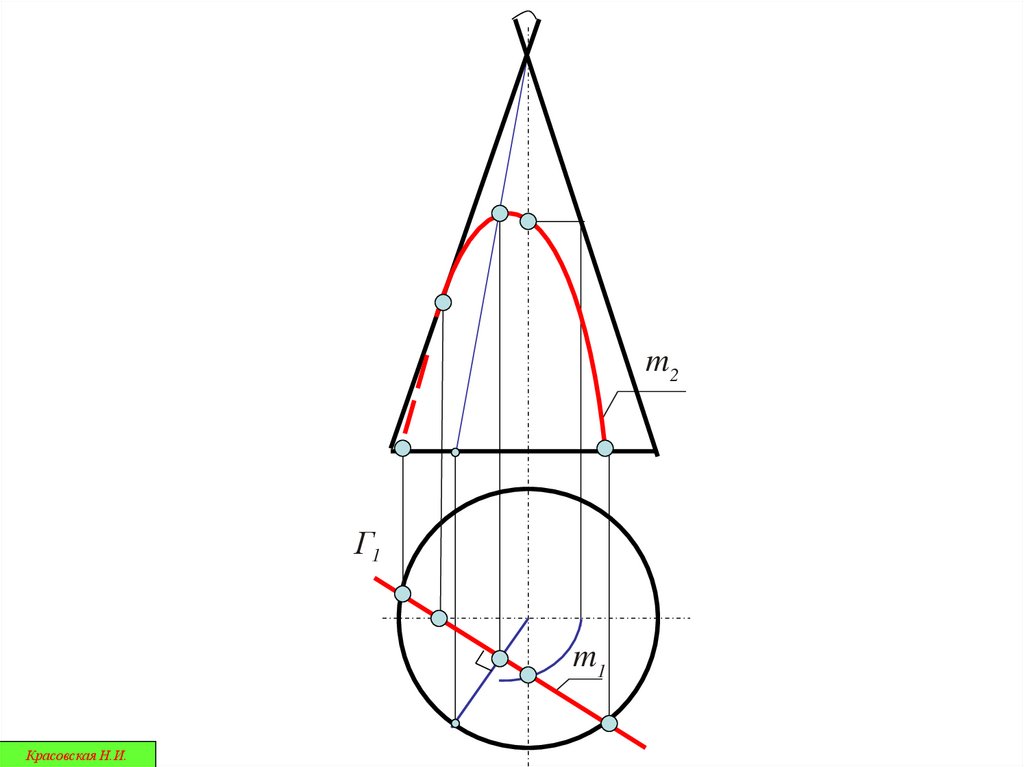
28.
m2Г1
m1
Красовская Н.И.
29.
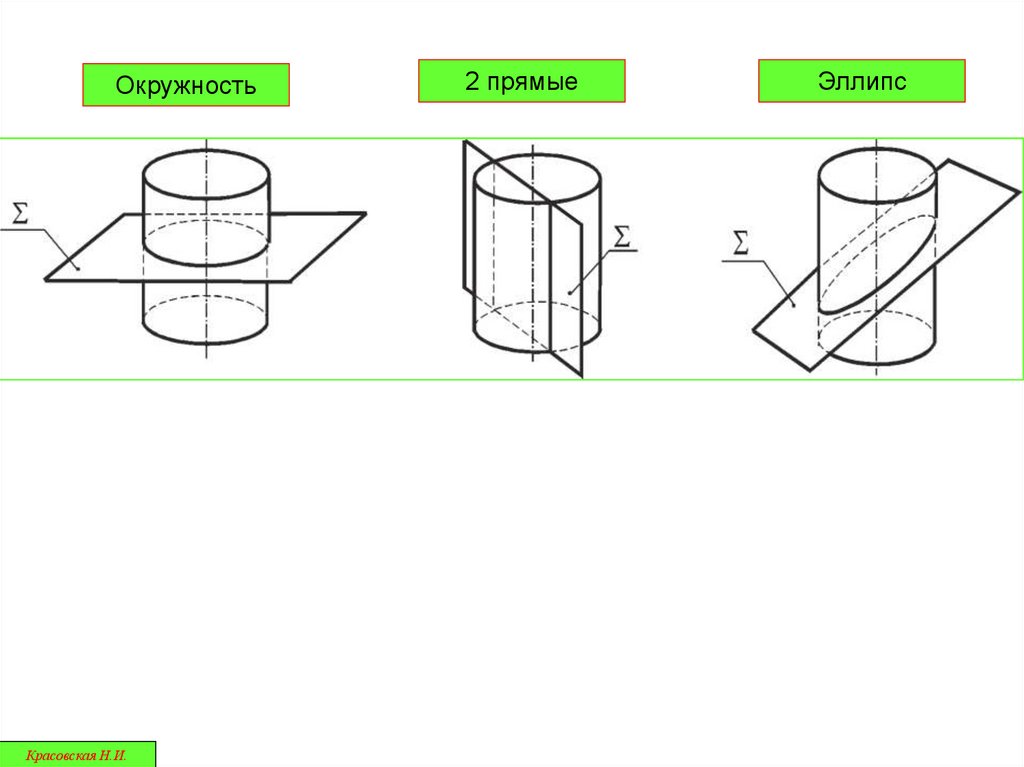
Цилиндрические сеченияКрасовская Н.И.
30.
ОкружностьКрасовская Н.И.
2 прямые
Эллипс
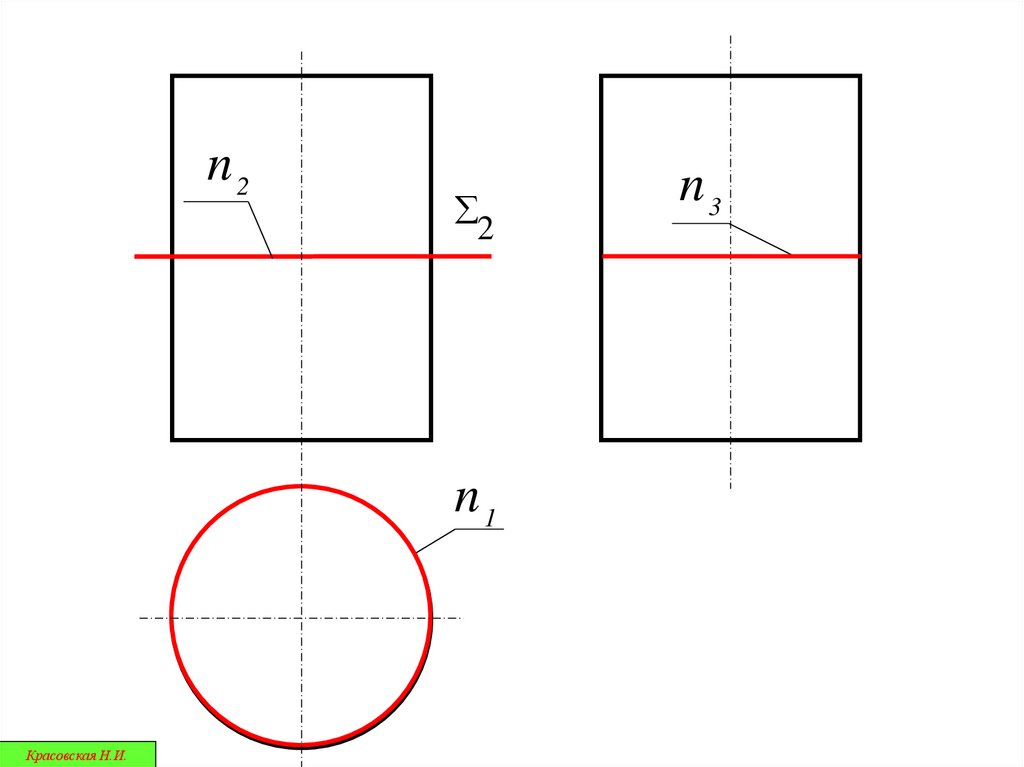
31.
n22
n1
Красовская Н.И.
n3
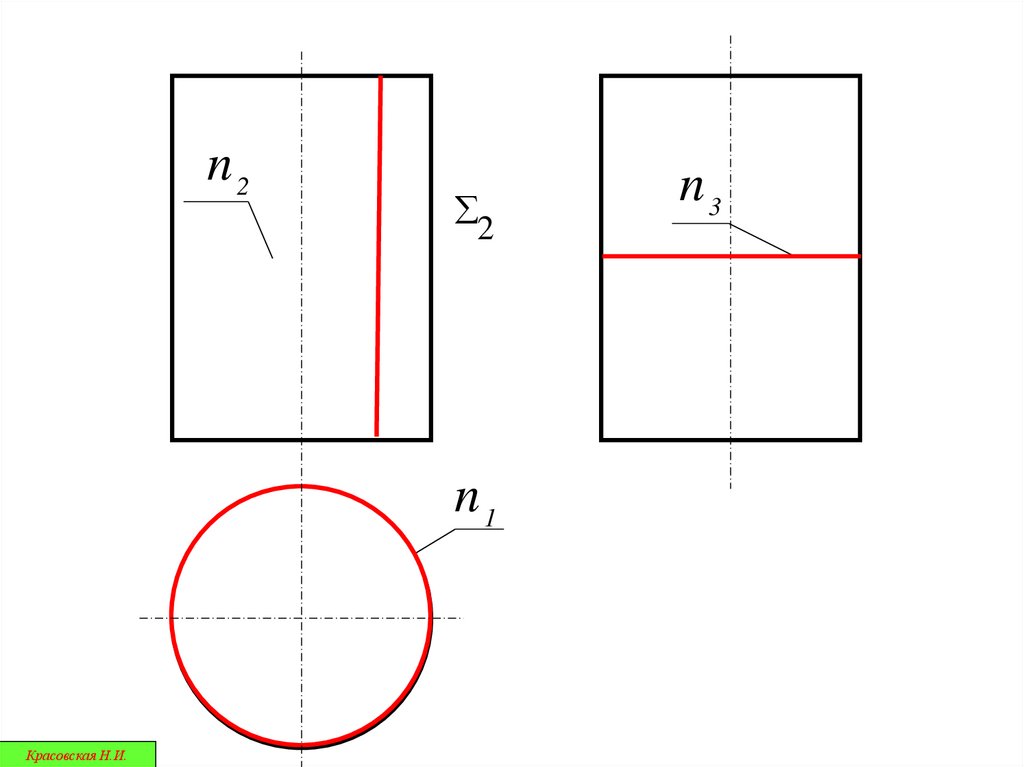
32.
n22
n1
Красовская Н.И.
n3
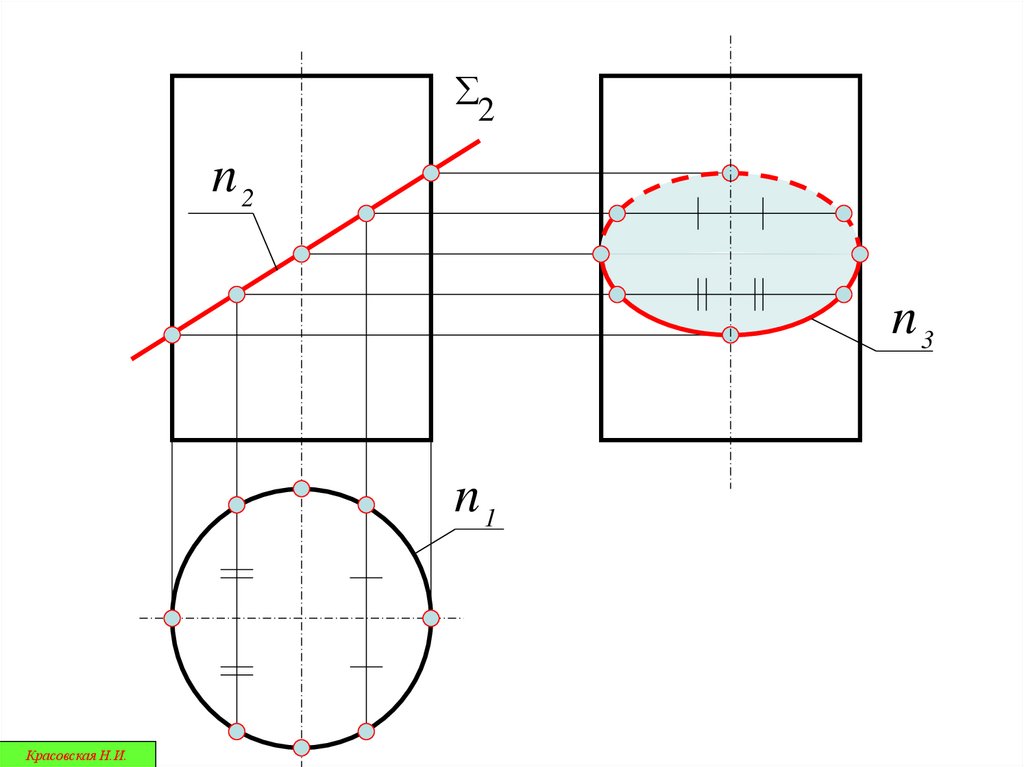
33.
2n2
n3
n1
Красовская Н.И.
34.
Сферическиесечения
Красовская Н.И.
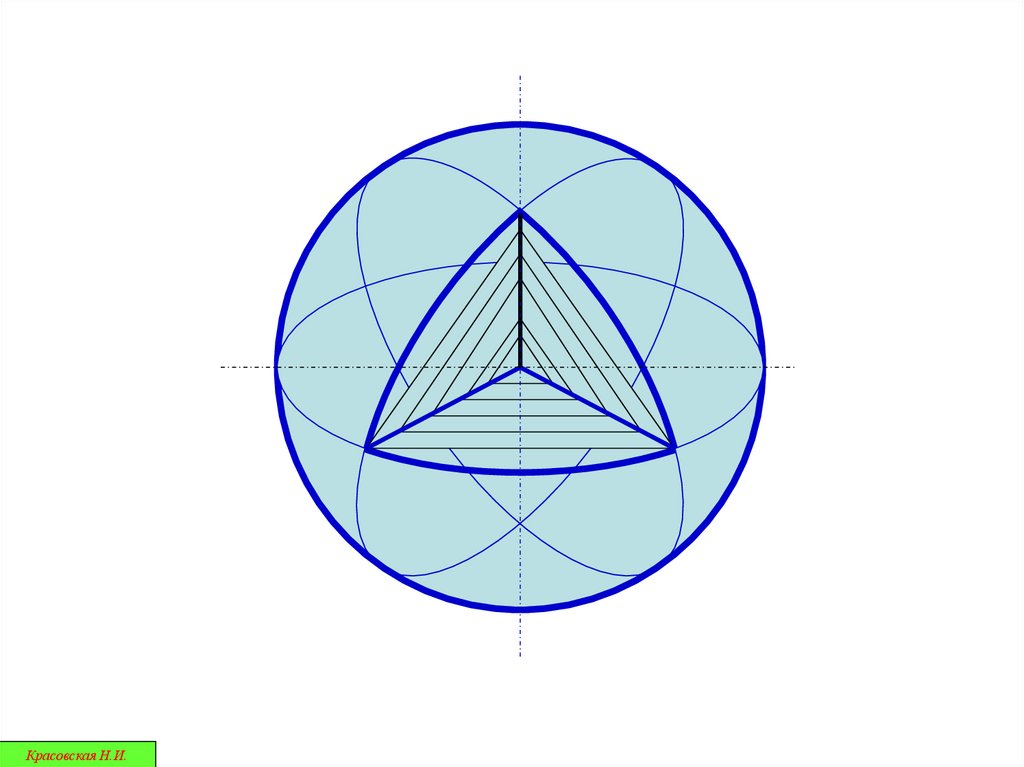
35.
При пересечении поверхности сферыплоскостью всегда получается
окружность
Красовская Н.И.
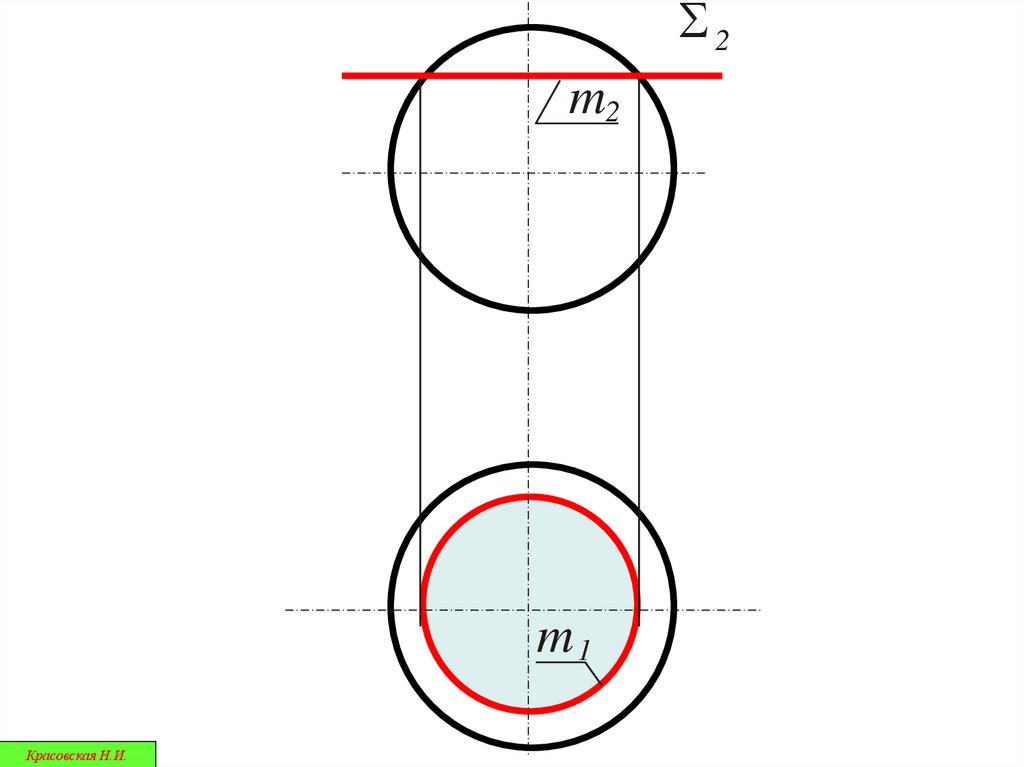
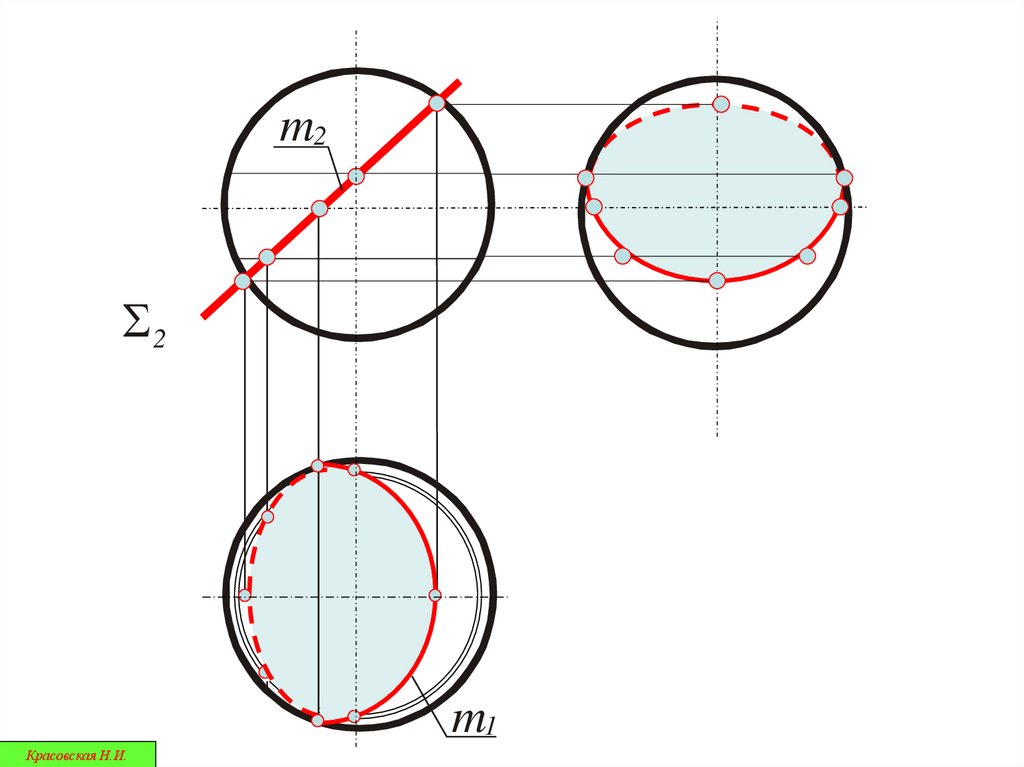
36.
Красовская Н.И.37.
S2m2
m1
Красовская Н.И.
38.
m2S2
m1
Красовская Н.И.
39.
Сечения многогранникапроецирующей плоскостью
Красовская Н.И.
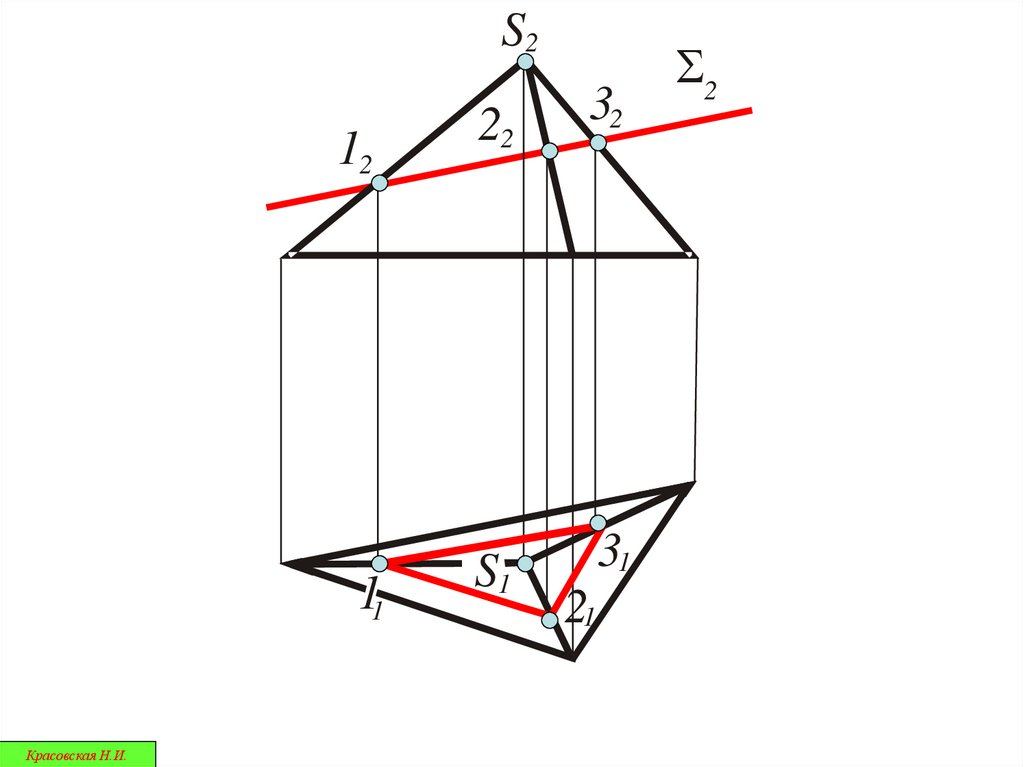
40.
В сечении многогранной поверхностивсегда получается плоский
многоугольник
Красовская Н.И.
41.
S2Красовская Н.И.
12
22
32
11
S1
31
21
S2
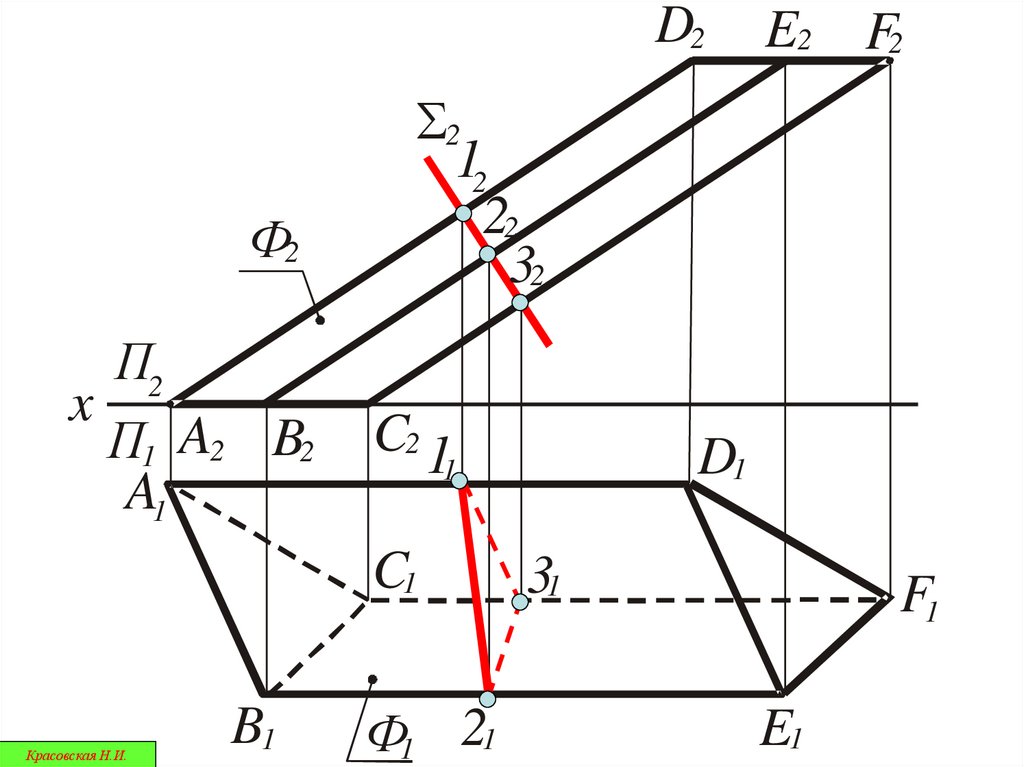
42.
D2Ф2
П2
x
П1 A2 B2
A1
S2
12
22
32
C2 1
B1
D1
1
C1
Красовская Н.И.
E2 F2
Ф1 21
31
F1
E1
43.
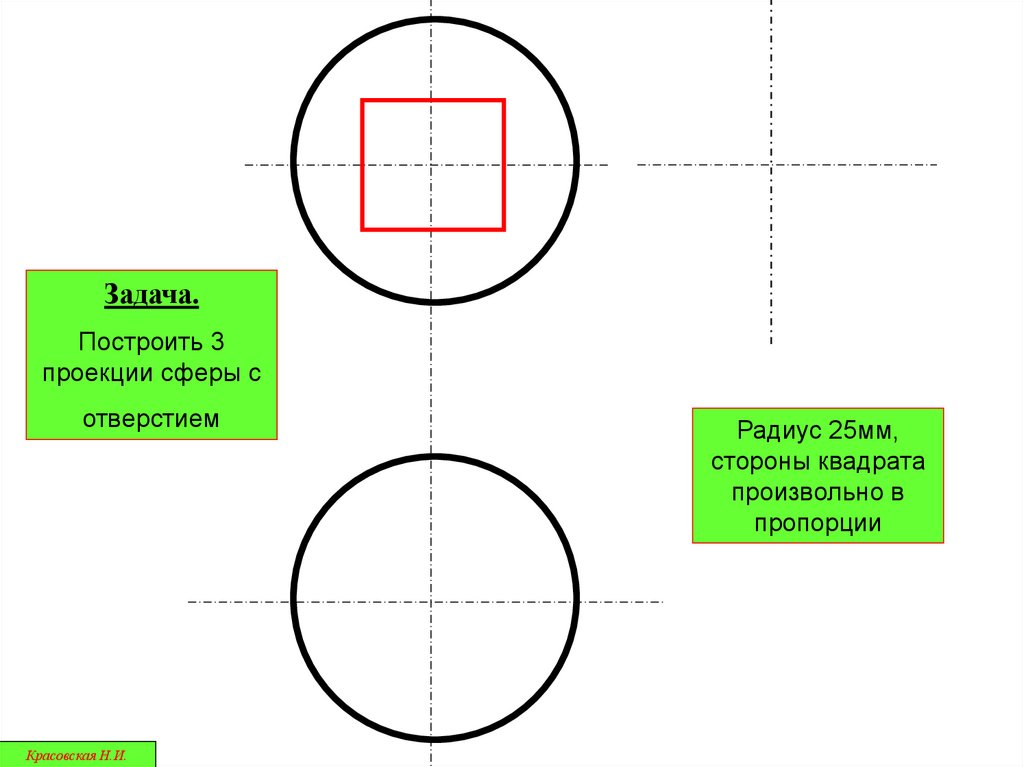
Задача.Построить 3
проекции сферы с
отверстием
Красовская Н.И.
Радиус 25мм,
стороны квадрата
произвольно в
пропорции















 drafting
drafting








