Similar presentations:
Позиционные задачи. Метод конкурирующих точек (Лекция 3)
1.
Лекция 3Проф. Пиралова О.Ф.
1
2.
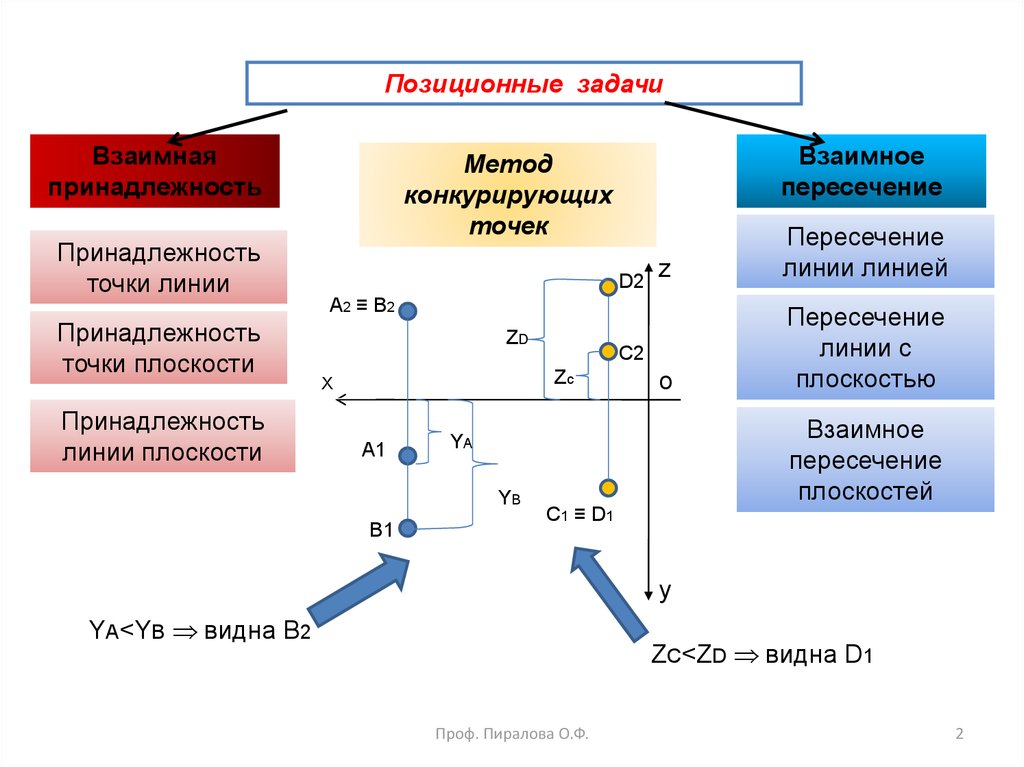
Позиционные задачиВзаимная
принадлежность
Принадлежность
точки линии
Принадлежность
точки плоскости
Принадлежность
линии плоскости
Взаимное
пересечение
Метод
конкурирующих
точек
D2
z
Пересечение
линии линией
o
Пересечение
линии с
плоскостью
A2 ≡ B2
ZD
C2
Zc
Х
A1
YB
B1
Взаимное
пересечение
плоскостей
YA
С1 ≡ D1
y
YA<YB видна В2
ZC<ZD видна D1
Проф. Пиралова О.Ф.
2
3. Основные графические задачи
Все графические задачи условноделятся на 2 класса.
1-й класс – задачи позиционные;
2-й класс – задачи метрические.
Позиционными называются такие
задачи, в которых определяется взаимное
расположение различных геометрических
фигур относительно друг друга.
Проф. Пиралова О.Ф.
3
4. Позиционные задачи
• Позиционныезадачи условно
делятся на две
группы:
Позиционные
задачи
Задачи на
принадлежность
Проф. Пиралова О.Ф.
Задачи на
пересечение
4
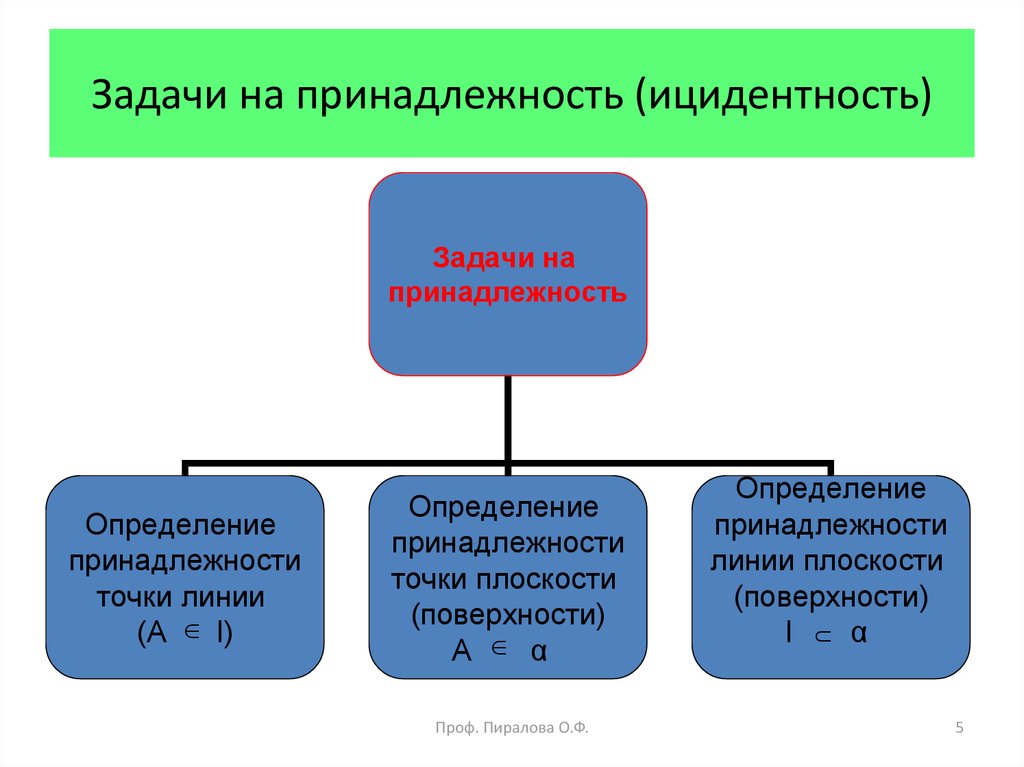
5. Задачи на принадлежность (ицидентность)
Задачи напринадлежность
Определение
принадлежности
точки линии
(А l)
Определение
принадлежности
точки плоскости
(поверхности)
A α
Проф. Пиралова О.Ф.
Определение
принадлежности
линии плоскости
(поверхности)
l α
5
6. Принадлежность точки линии
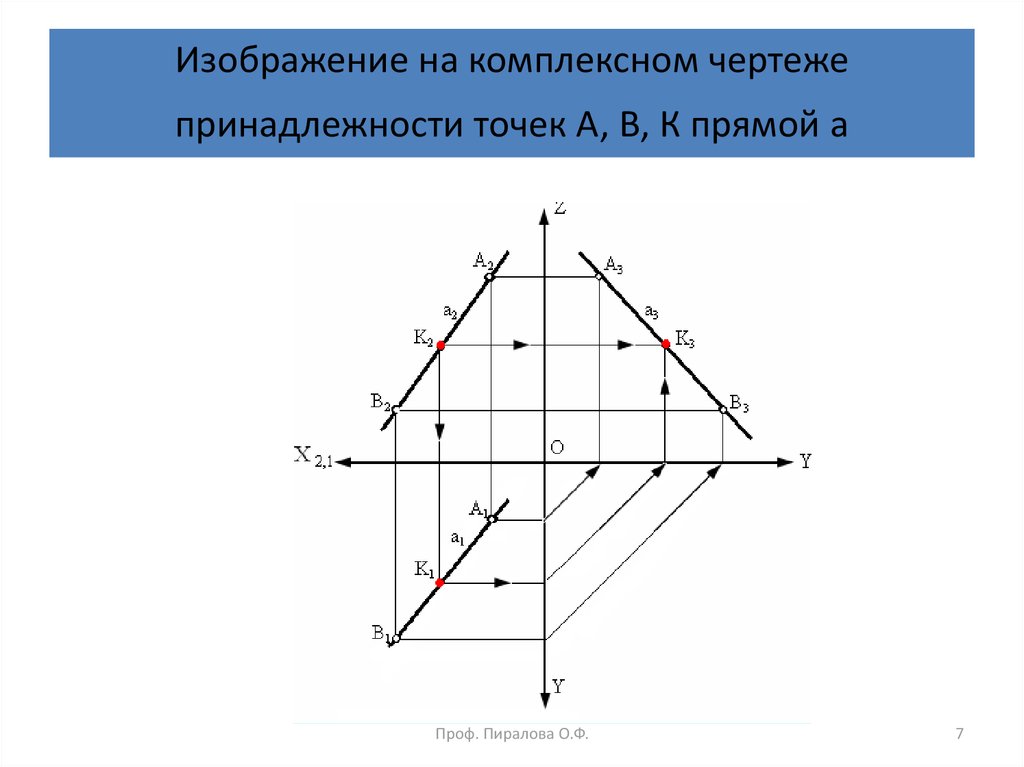
Из инвариантного свойства 3 параллельного
проецирования следует, что проекции точки К (К1, К2 и К3)
принадлежащие прямой а, должны принадлежать
соответствующим проекциям этой прямой т. е. Если хотя бы
одна проекция точки не принадлежит соответствующей
проекции прямой, то эта точка не принадлежит прямой.
Из инвариантного свойства 4 следует, что проекции точки
К (К1, К2 и К3), принадлежащие прямой АВ, делят
соответствующие проекции отрезка в том же отношении, в
каком точка К делит отрезок АВ.
Проф. Пиралова О.Ф.
6
7. Изображение на комплексном чертеже принадлежности точек А, В, К прямой а
Проф. Пиралова О.Ф.7
8. МЕТОД КОНКУРИРУЮЩИХ ТОЧЕК
Метод конкурирующих точек используется вначертательной геометрии для определения
взаимной видимости двух геометрических фигур.
Конкурирующими называются точки
пространства, у которых совпадают какие-либо
две одноименные проекции.
Проф. Пиралова О.Ф.
8
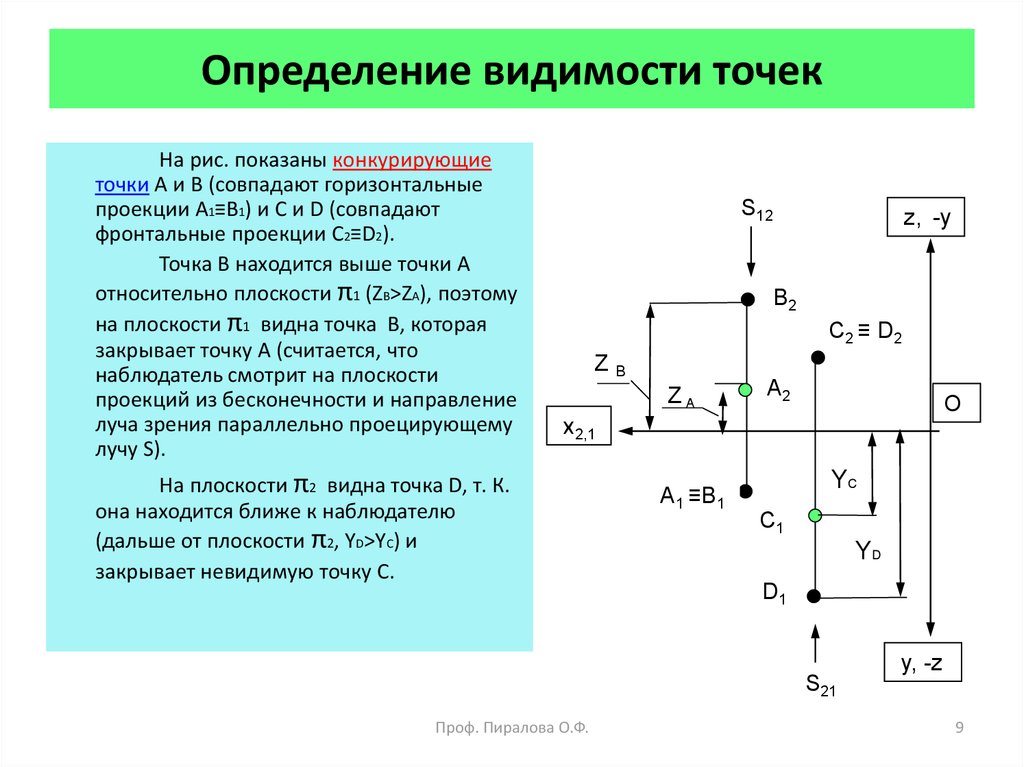
9. Определение видимости точек
На рис. показаны конкурирующиеточки А и В (совпадают горизонтальные
проекции А1≡В1) и C и D (совпадают
фронтальные проекции С2≡D2).
Точка В находится выше точки А
относительно плоскости π1 (ZB>ZA), поэтому
на плоскости π1 видна точка В, которая
закрывает точку А (считается, что
наблюдатель смотрит на плоскости
проекций из бесконечности и направление
луча зрения параллельно проецирующему
лучу S).
S12
z, -y
B2
C2 ≡ D2
ZB
ZА
A2
О
x2,1
На плоскости π2 видна точка D, т. К.
она находится ближе к наблюдателю
(дальше от плоскости π2, YD>YC) и
закрывает невидимую точку С.
YC
A1 ≡B1
C1
YD
D1
S21
Проф. Пиралова О.Ф.
y, -z
9
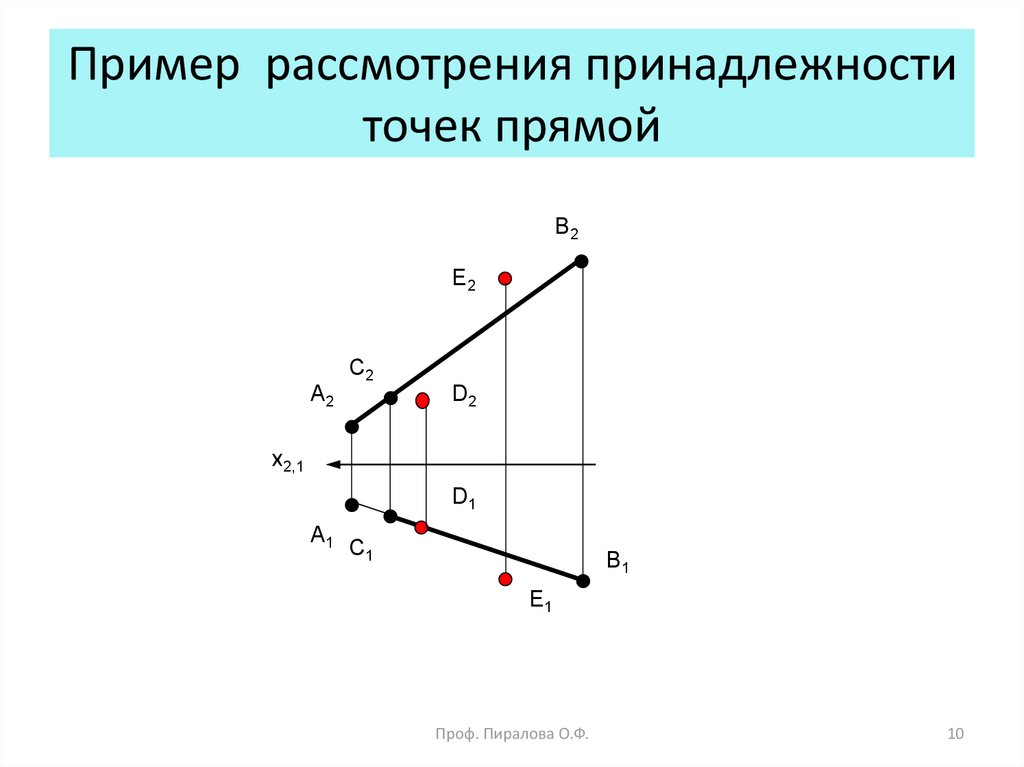
10. Пример рассмотрения принадлежности точек прямой
B2E2
C2
A2
D2
x2,1
D1
A1
C1
B1
E1
Проф. Пиралова О.Ф.
10
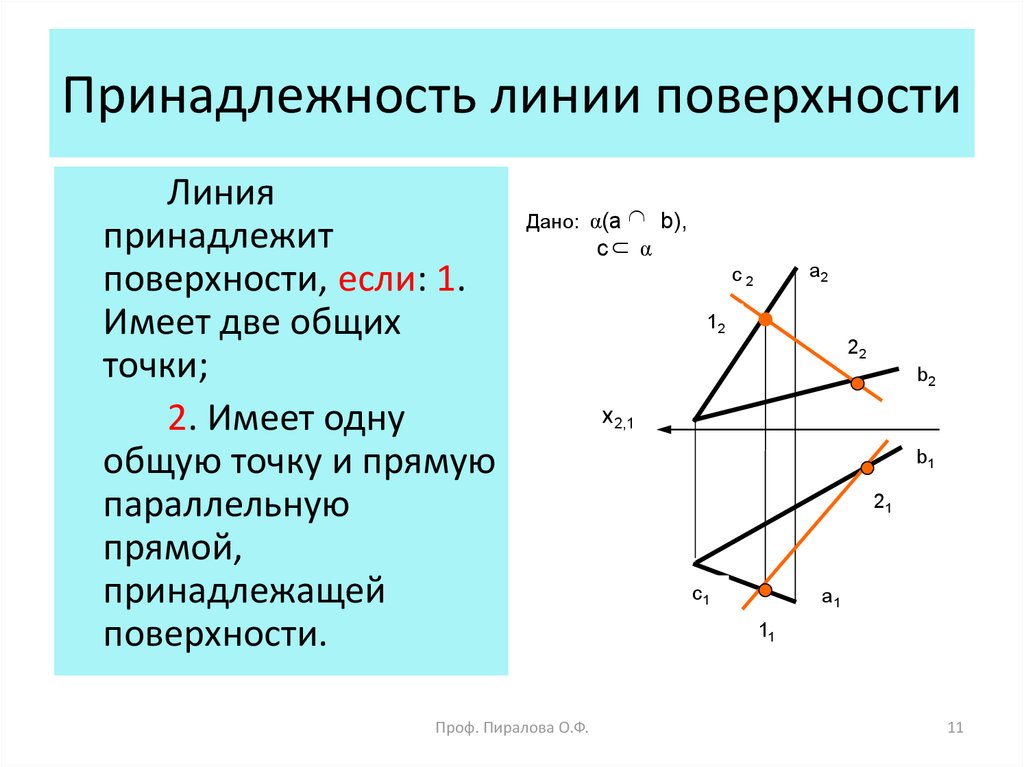
11. Принадлежность линии поверхности
Линияпринадлежит
поверхности, если: 1.
Имеет две общих
точки;
2. Имеет одну
общую точку и прямую
параллельную
прямой,
принадлежащей
поверхности.
Дано: α(a b),
Проф. Пиралова О.Ф.
с α
a2
с2
12
22
b2
x2,1
b1
21
с1
a1
11
11
12. Условие принадлежности точки поверхности
Точка принадлежитповерхности, если она
принадлежит прямой
принадлежащей
поверхности
Проф. Пиралова О.Ф.
12
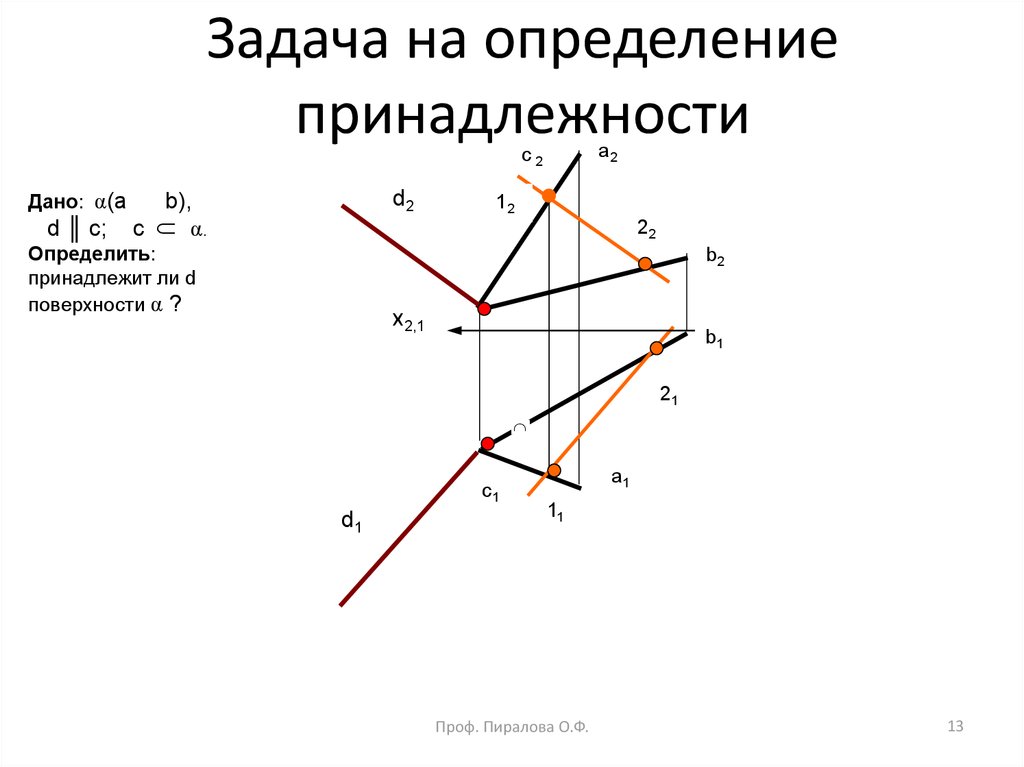
13. Задача на определение принадлежности
a2с2
Дано: α(a
d ║ с;
d2
b),
с α.
12
22
Определить:
принадлежит ли d
поверхности α ?
b2
x2,1
b1
21
с1
d1
a1
11
Проф. Пиралова О.Ф.
13
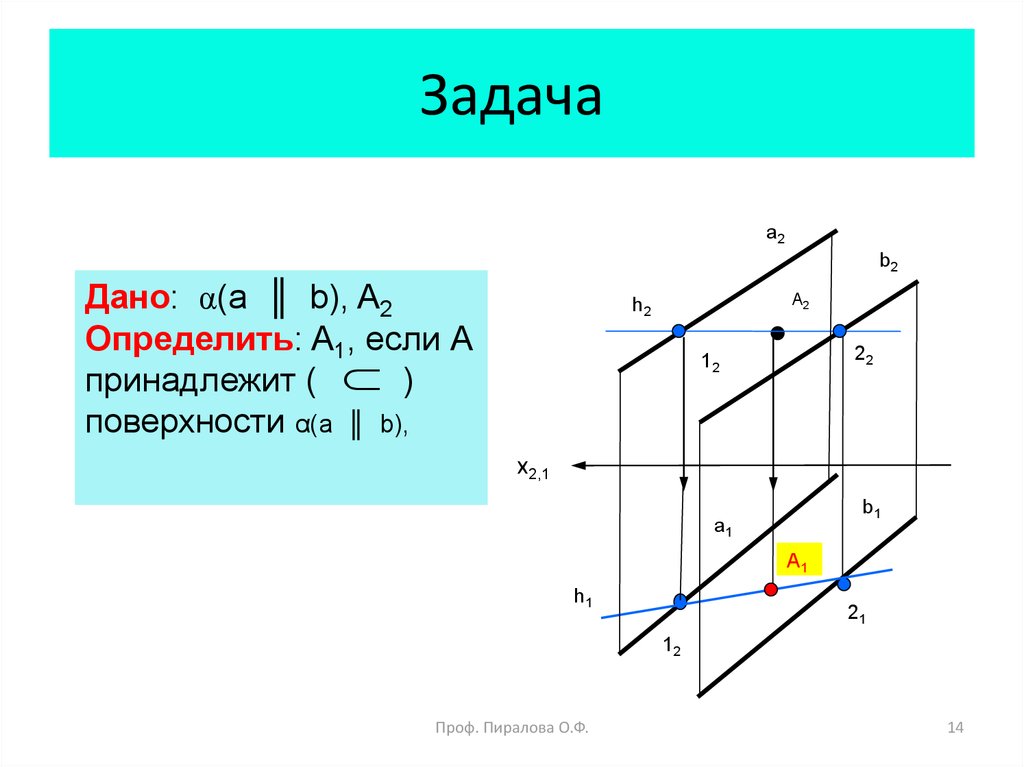
14. Задача
а2b2
Дано: α(a ║ b), A2
Определить: A1, если А
принадлежит ( )
поверхности α(a ║ b),
A2
h2
22
12
x2,1
b1
a1
A1
h1
21
12
Проф. Пиралова О.Ф.
14
15.
Задачи напересечение
Пересечение
линии с линией
l m
Пересечение
линии с
поверхностью
l α
Проф. Пиралова О.Ф.
Пересечение
поверхности
с поверхностью
α β
15
16. Взаимное положение прямых. Пересечение прямых
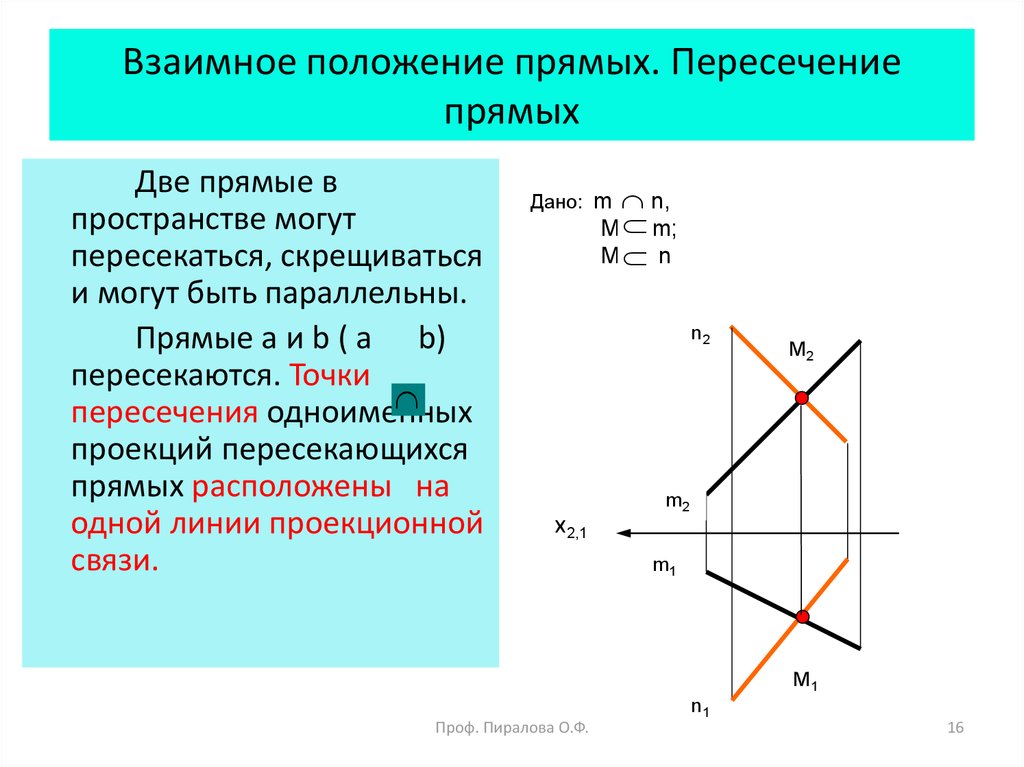
Две прямые впространстве могут
пересекаться, скрещиваться
и могут быть параллельны.
Прямые a и b ( a b)
пересекаются. Точки
пересечения одноименных
проекций пересекающихся
прямых расположены на
одной линии проекционной
связи.
Дано: m
n,
M m;
M n
n2
M2
m2
x2,1
m1
M1
n1
Проф. Пиралова О.Ф.
16
17. Параллельные прямые
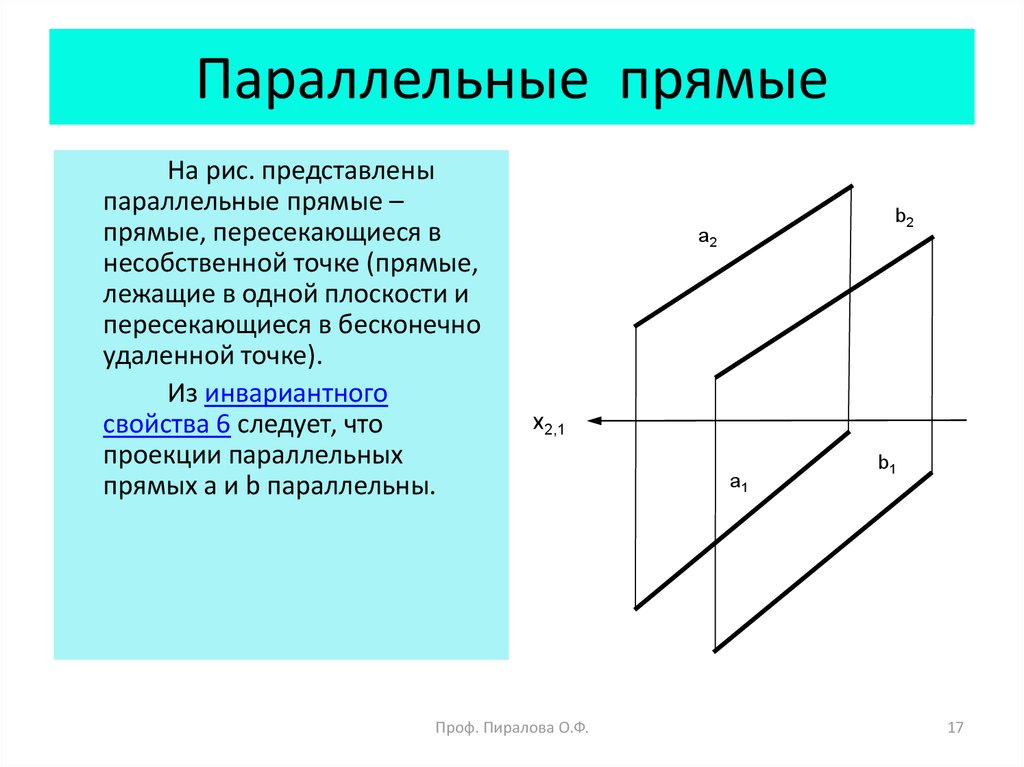
На рис. представленыпараллельные прямые –
прямые, пересекающиеся в
несобственной точке (прямые,
лежащие в одной плоскости и
пересекающиеся в бесконечно
удаленной точке).
Из инвариантного
свойства 6 следует, что
проекции параллельных
прямых а и b параллельны.
b2
а2
x2,1
Проф. Пиралова О.Ф.
a1
b1
17
18. Скрещивающиеся прямые
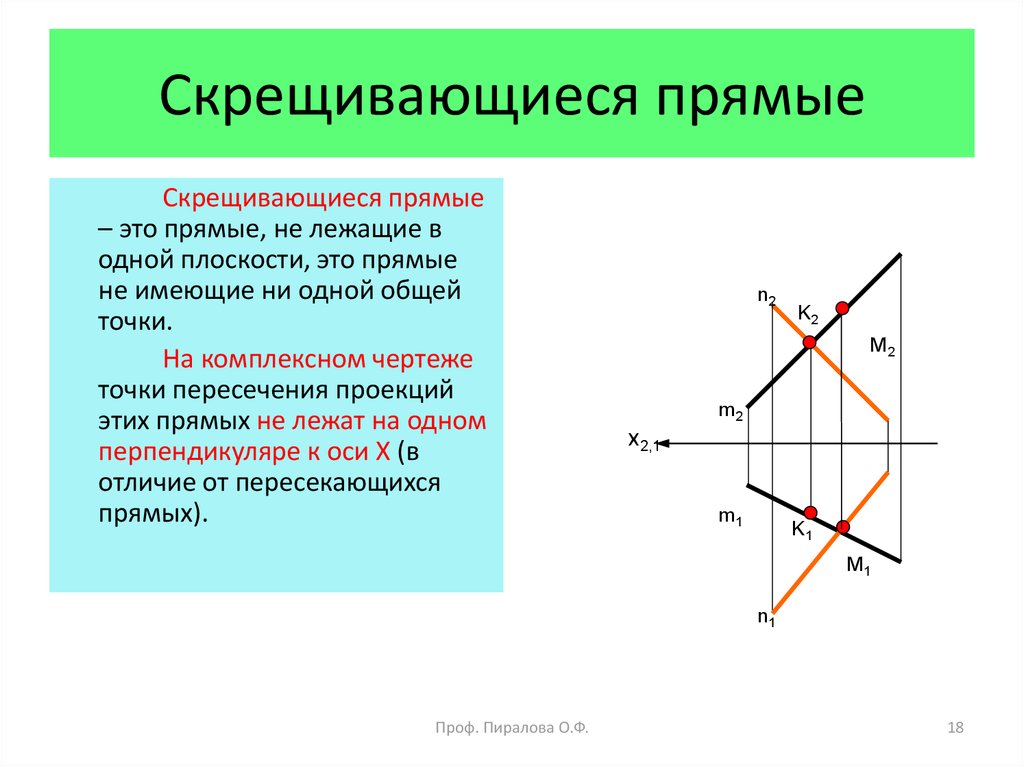
Скрещивающиеся прямые– это прямые, не лежащие в
одной плоскости, это прямые
не имеющие ни одной общей
точки.
На комплексном чертеже
точки пересечения проекций
этих прямых не лежат на одном
перпендикуляре к оси Х (в
отличие от пересекающихся
прямых).
n2
K2
M2
m2
x2,1
m1
K1
M1
n1
Проф. Пиралова О.Ф.
18
19. Условие перпендикулярности двух прямых
Две прямые перпендикулярны, если уголмежду ними составляет 90°.
Кроме того, в начертательной геометрии
существует еще одно утверждение на эту
тему:
Две прямые перпендикулярны, если одна
из них линия уровня.
Для подтверждения этого заключения
рассмотрим примеры.
Проф. Пиралова О.Ф.
19
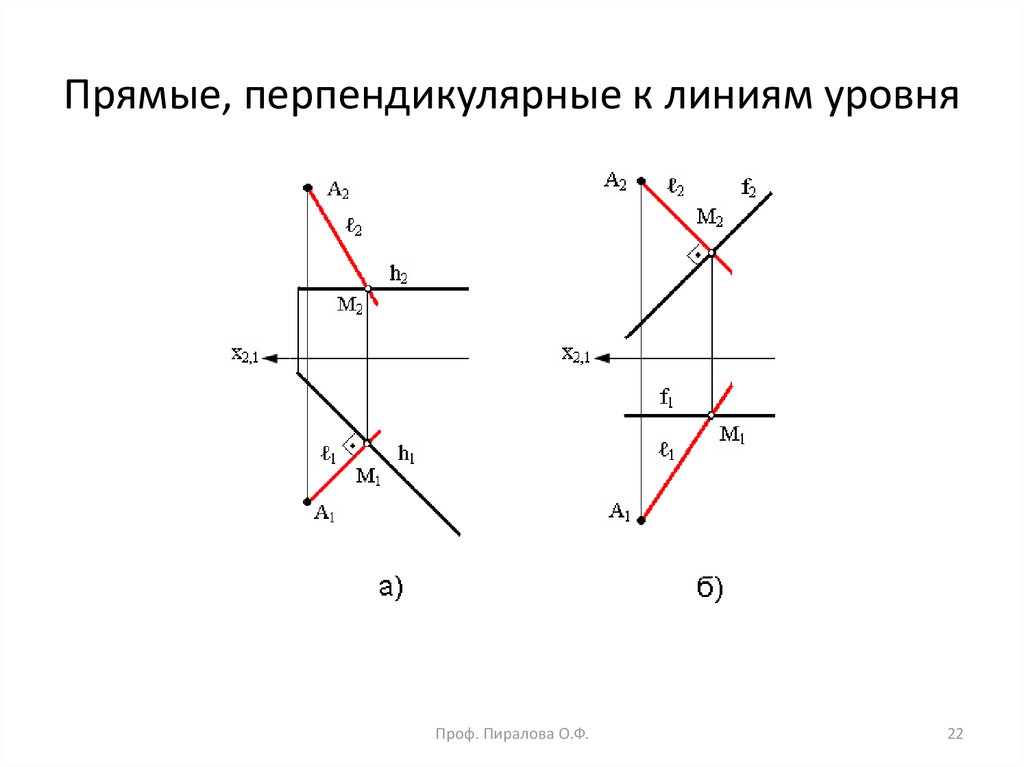
20. Пример: через точку А провести прямую ℓ, пересекающую горизонталь h под прямым углом ℓ h
┴Так как одна из сторон h прямого угла параллельна
плоскости π1, то на эту плоскость прямой угол
спроецируется без искажения. Поэтому через
горизонтальную проекцию А1 проведем горизонтальную
проекцию искомой прямой ℓ 1 h 1. Отметим
┴
горизонтальную проекцию точки пересечения прямой и
горизонтали М1= ℓ1 ∩ h1. Отметим горизонтальную
проекцию точки пересечения прямой и горизонтали М1=
ℓ1 ∩ h1. Найдем по принадлежности фронтальную
проекцию точки пересечения М2. Точки А2 и М2
определяют фронтальную проекцию искомой прямой ℓ.
Две проекции прямой определяют ее положение в
пространстве.
Проф. Пиралова О.Ф.
20
21.
Если вместо горизонтали будет заданафронталь f, то геометрические построения
по проведению прямой ℓ f аналогичны ┴
рассмотренным с той лишь разницей, что
построения неискаженной проекции
прямого угла следует начинать с
фронтальной проекции (рис. б).
Проф. Пиралова О.Ф.
21
22. Прямые, перпендикулярные к линиям уровня
Проф. Пиралова О.Ф.22
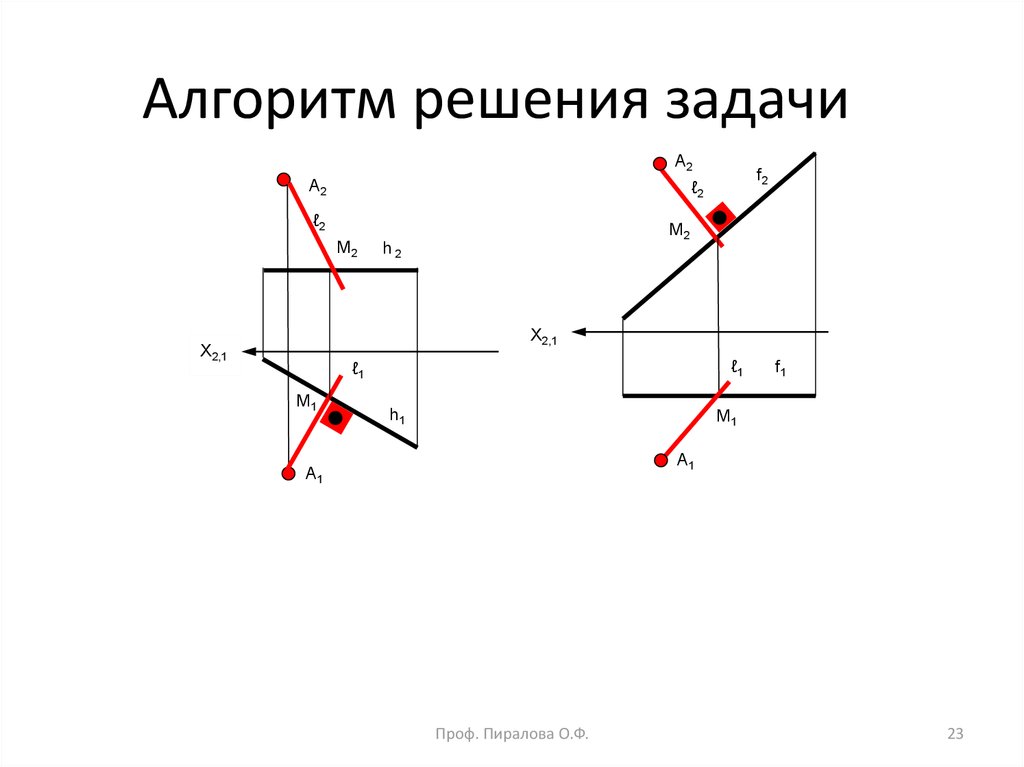
23. Алгоритм решения задачи
А2А2
f2
ℓ2
ℓ2
М2
М2
h2
X2,1
X2,1
ℓ1
ℓ1
М1
f1
М1
h1
А1
А1
Проф. Пиралова О.Ф.
23
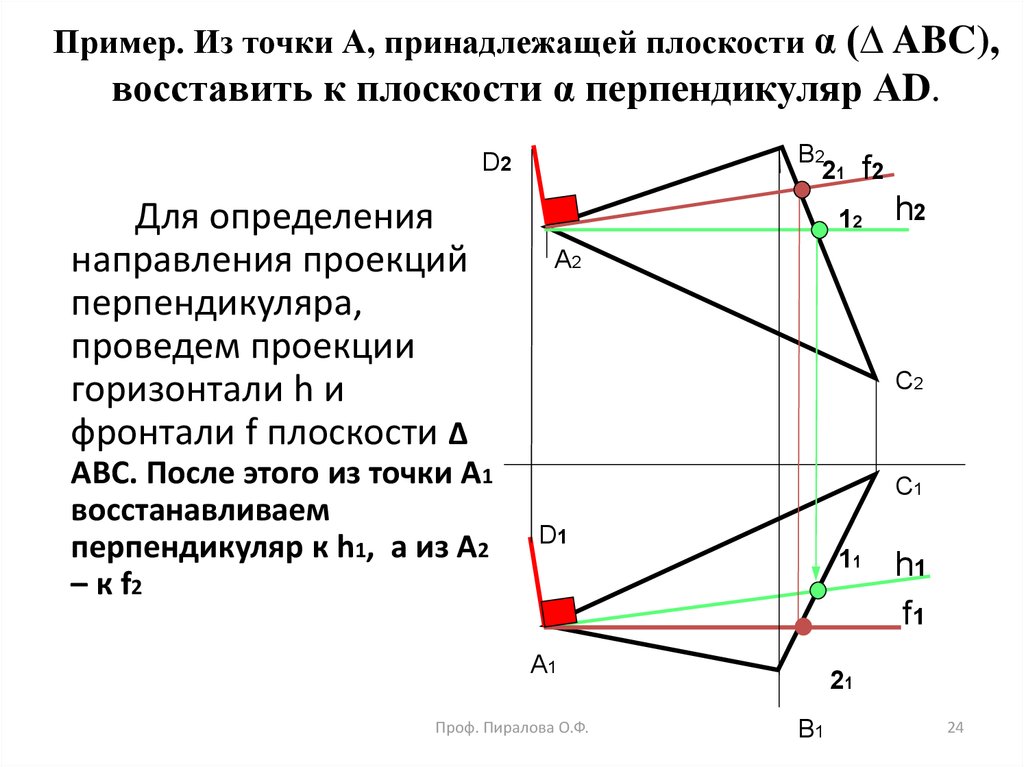
24. Пример. Из точки А, принадлежащей плоскости α (∆ ABC), восставить к плоскости α перпендикуляр АD.
В221
D2
Для определения
направления проекций
перпендикуляра,
проведем проекции
горизонтали h и
фронтали f плоскости ∆
ABC. После этого из точки А1
восстанавливаем
перпендикуляр к h1, а из А2
– к f2
12
f2
h2
А2
С2
С1
D1
11
А1
Проф. Пиралова О.Ф.
h1
f1
21
В1
24
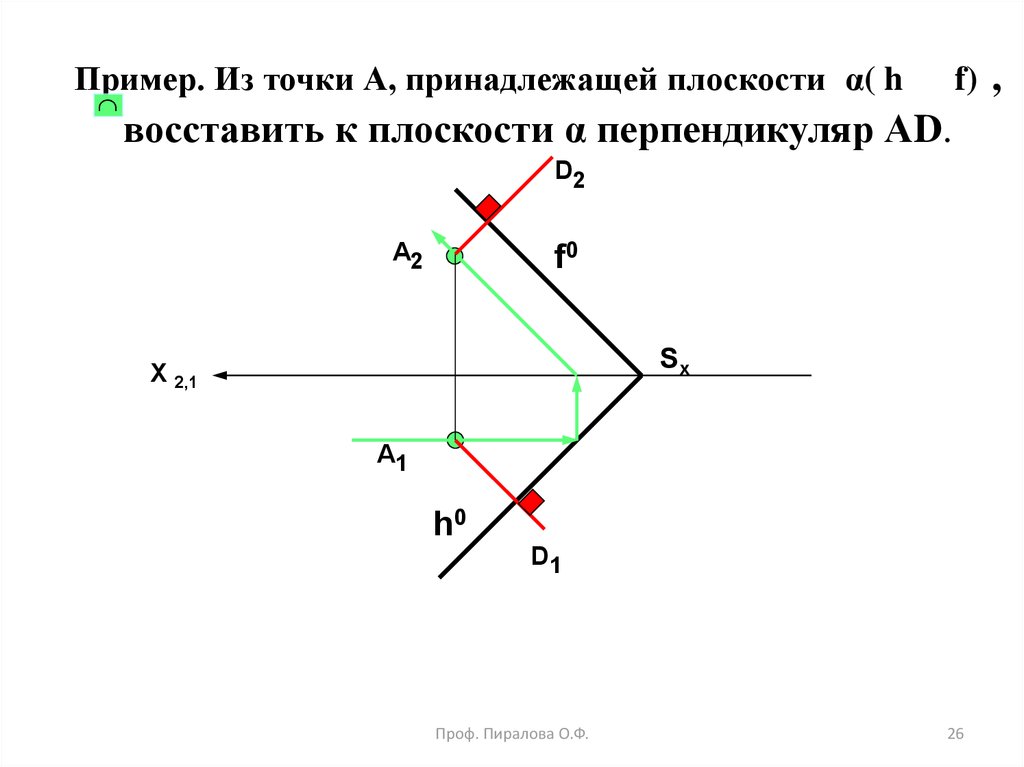
25.
Если плоскость задана следами, длятого, чтобы прямая в пространстве была
перпендикулярна плоскости, необходимо и
достаточно, чтобы проекции этой прямой
были перпендикулярны к одноименным
следам
Проф. Пиралова О.Ф.
25
26. Пример. Из точки А, принадлежащей плоскости α( h f) , восставить к плоскости α перпендикуляр АD.
D2f0
A2
Sx
X 2,1
A1
h0
D1
Проф. Пиралова О.Ф.
26
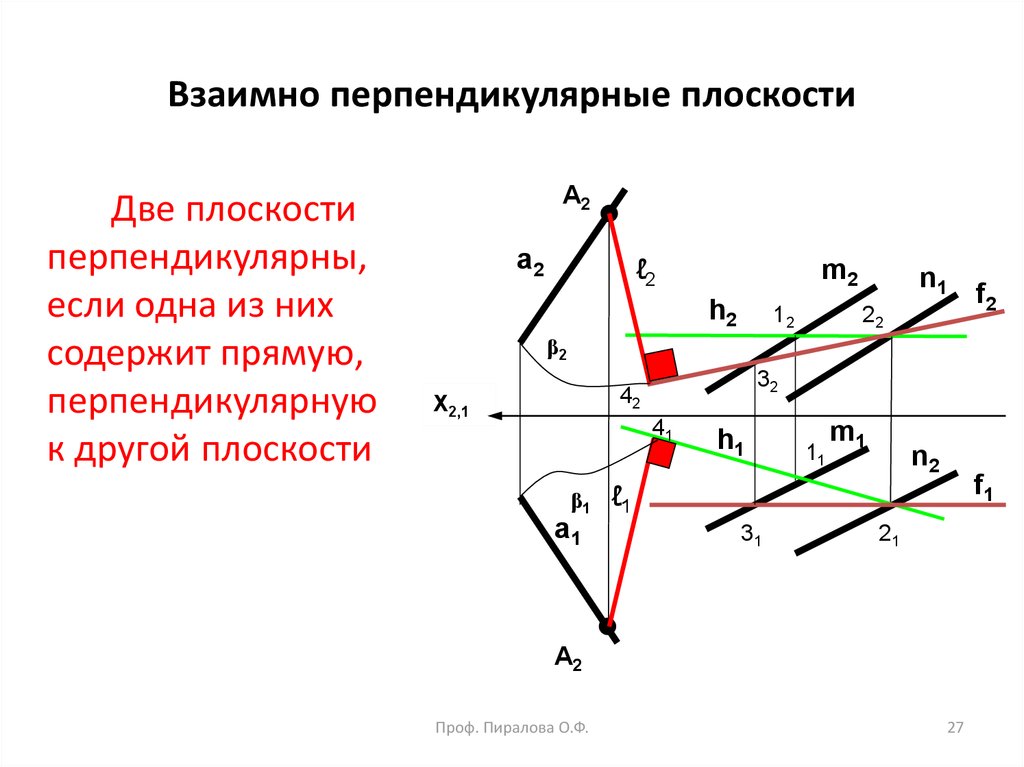
27. Взаимно перпендикулярные плоскости
Две плоскостиперпендикулярны,
если одна из них
содержит прямую,
перпендикулярную
к другой плоскости
А2
a2
ℓ2
m2
h2
12
n1
22
f2
β2
32
42
X2,1
41
β1
a1
h1
11
m1
n2
f1
ℓ1
31
21
А2
Проф. Пиралова О.Ф.
27
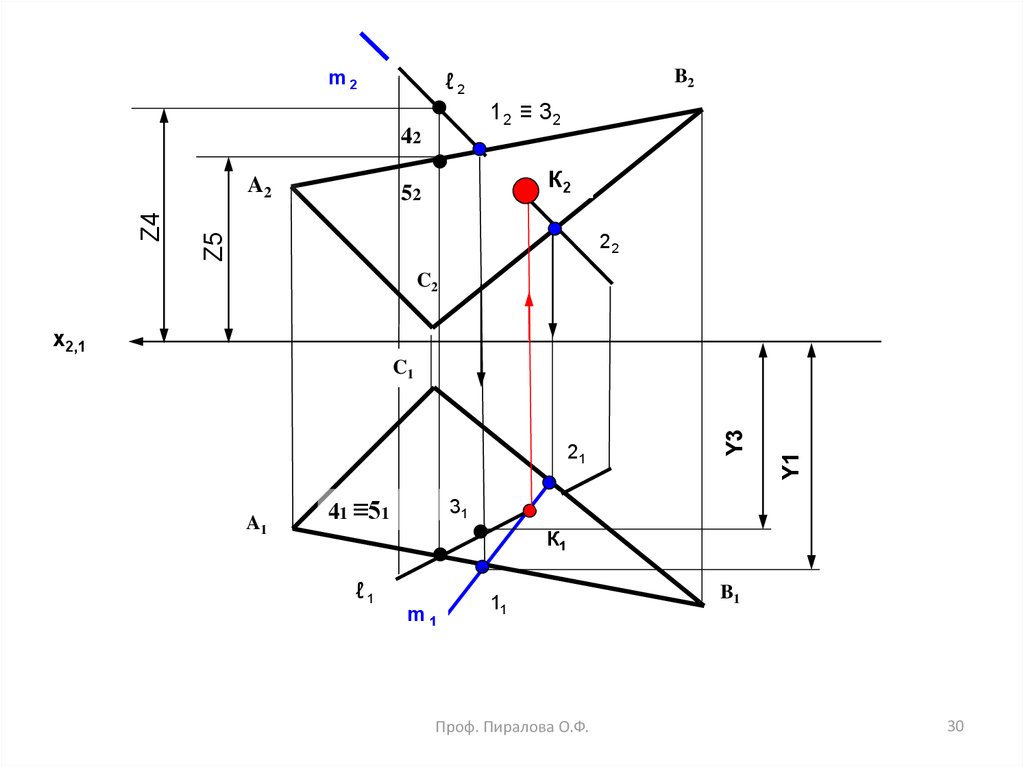
28. Пересечение линии с поверхностью
Задача сводится к решению задачи на определениеточки, принадлежащей прямой и поверхности.
Для решения необходимо:
1) через одну из проекций прямой провести
конкурирующую прямую, принадлежащую поверхности;
2) найти ее проекцию во второй плоскости проекций.
Если эта проекция пересечет проекцию заданной
прямой, значит имеется точка пересечения прямой и
поверхности.
Проф. Пиралова О.Ф.
28
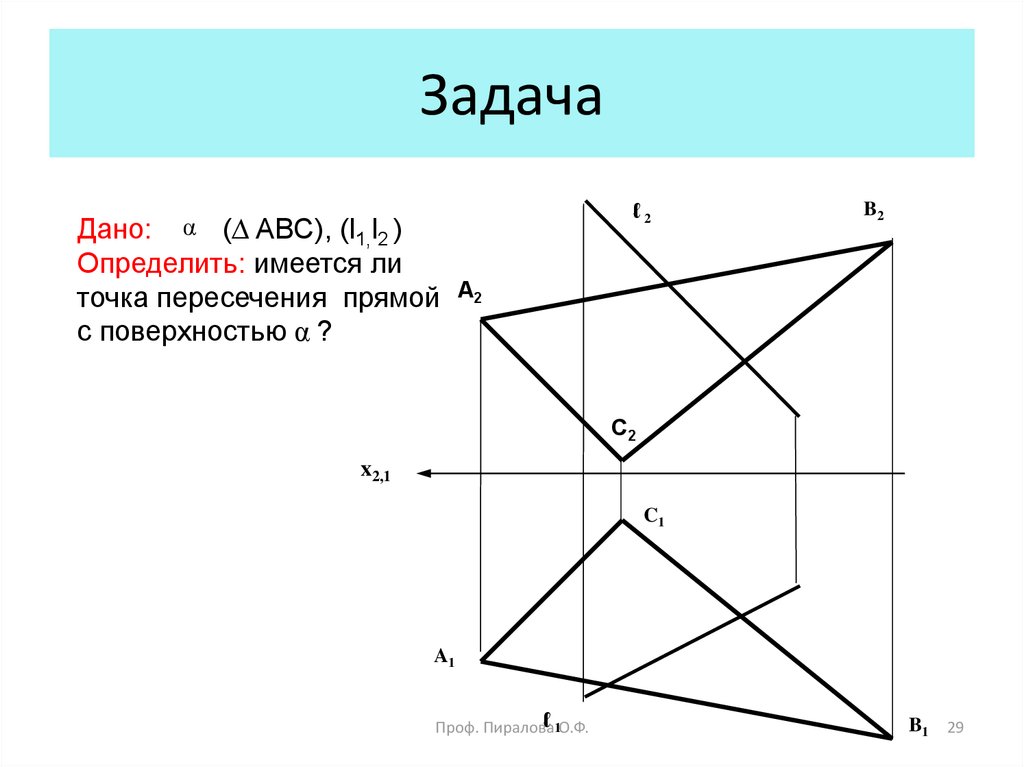
29. Задача
Дано:(∆ ABC), (l1,l2 )
Определить: имеется ли
точка пересечения прямой
с поверхностью α ?
ℓ2
α
B2
A2
C2
x2,1
C1
A1
ℓ 1О.Ф.
Проф. Пиралова
B1 29
30.
ℓ2m2
1122 ≡ 32
42
К2
52
Z5
Z4
A2
B2
22
C2
x2,1
A1
41 ≡51
Y1
21
Y3
C1
31
К1
ℓ1
m1
11
Проф. Пиралова О.Ф.
B1
30
31. Пересечение плоскостей
Две плоскостипересекаются по
прямой линии, для
определения которой
достаточно найти две
точки,
принадлежащие
одновременно
каждой из заданных
плоскостей.
Чтобы найти
такие точки
достаточно ввести
две вспомогательные
секущие плоскости.
Проф. Пиралова О.Ф.
31
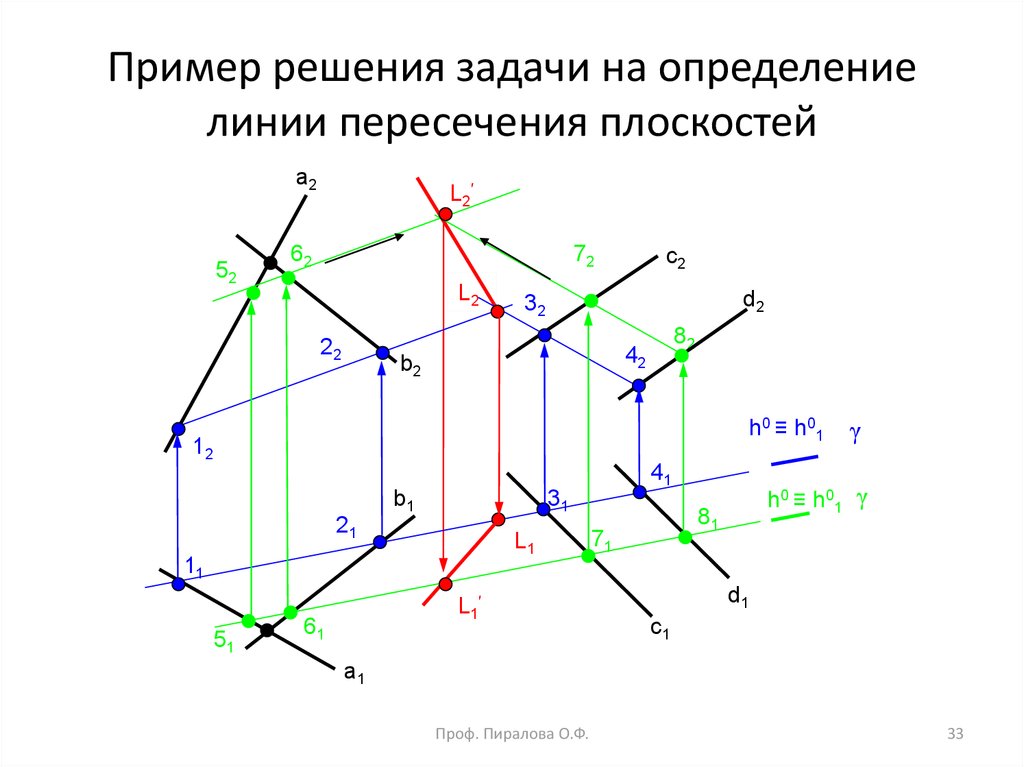
32. Пример. Определить линию пересечения плоскостей α(a b) и β(с║d).
Алгоритм решения.1. Проводим вспомогательную
горизонтально проецирующую плоскость γ
2. и 3. Определяем проекции прямых m
и n, по которым пересекаются плоскости
α(a b) и β(с║d).
4. Находим точки пересечения
одноименных фронтальных проекций
линий пересечения плоскостей α и β.
Проф. Пиралова О.Ф.
32
33. Пример решения задачи на определение линии пересечения плоскостей
a252
L2′
62
72
L2
22
c2
d2
32
82
42
b2
h0 ≡ h01
12
41
b1
31
21
L1
11
51
L1′
61
h0 ≡ h01 γ
81
71
γ
d1
c1
a1
Проф. Пиралова О.Ф.
33
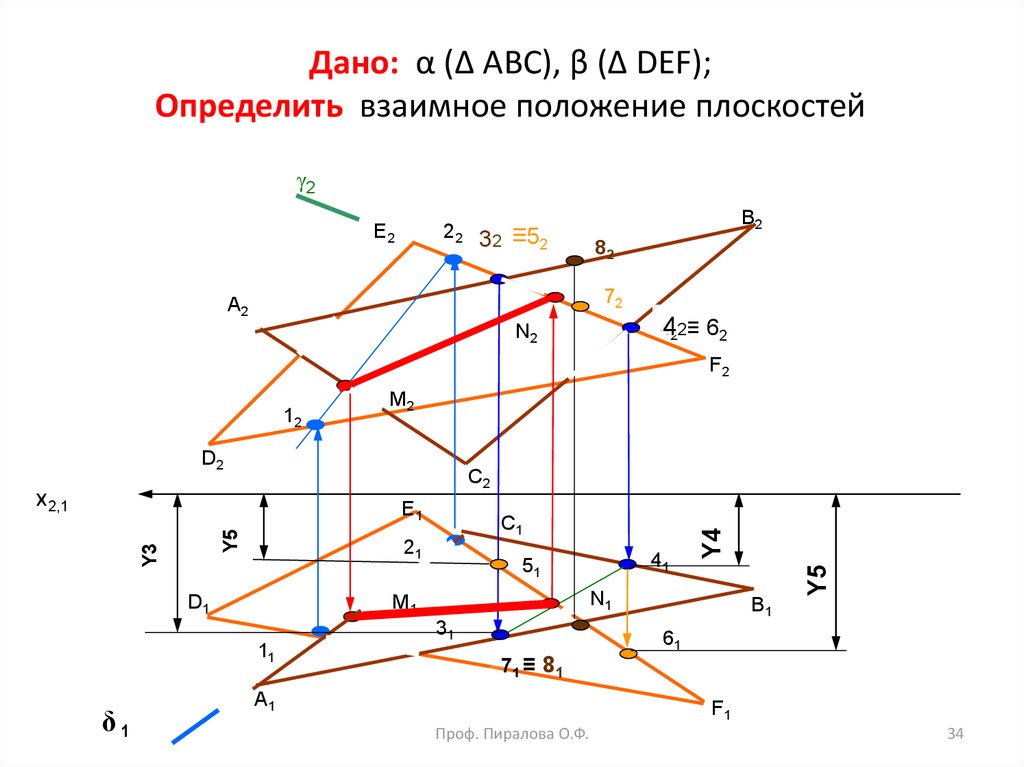
34. Дано: α (∆ ABC), β (∆ DEF); Определить взаимное положение плоскостей
γ2E2
22 32
≡ 52
В2
82
72
A2
4422≡ 62
N2
F2
12
M2
D2
Y3
Y5
E1
С1
21
D1
N1
M1
31
11
δ1
41
51
71 ≡ 81
A1
В1
Y5
x2,1
Y4
С2
61
F1
Проф. Пиралова О.Ф.
34
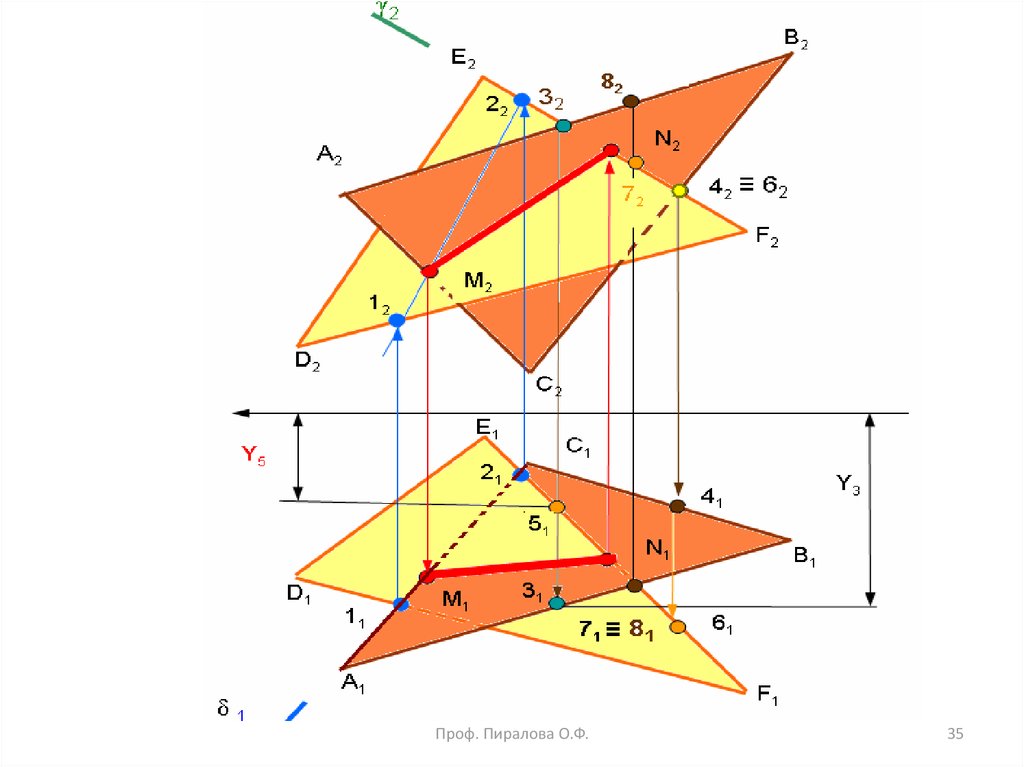
35.
Проф. Пиралова О.Ф.35













 mathematics
mathematics drafting
drafting








