Similar presentations:
Плоскость. Позиционные и метрические задачи. (Лекция 2)
1. Инженерная графика
Федеральное государственное бюджетное образовательное учреждениевысшего образования
«Уфимский государственный нефтяной технический университет»
Филиал ФГБОУ ВО УГНТУ в г. Салавате
Кафедра «Оборудование предприятий нефтехимии и нефтепереработки»
Инженерная графика
Лекция 2. Плоскость.
Позиционные и метрические задачи
Лектор доцент, к.т.н. Алушкина Татьяна Валентиновна
2. План лекции
• Способы задания плоскостей• Проецирование плоскости на плоскости
проекций
• Взаимное положение точки и плоскости,
прямой и плоскости, двух плоскостей
• Главные линии плоскости
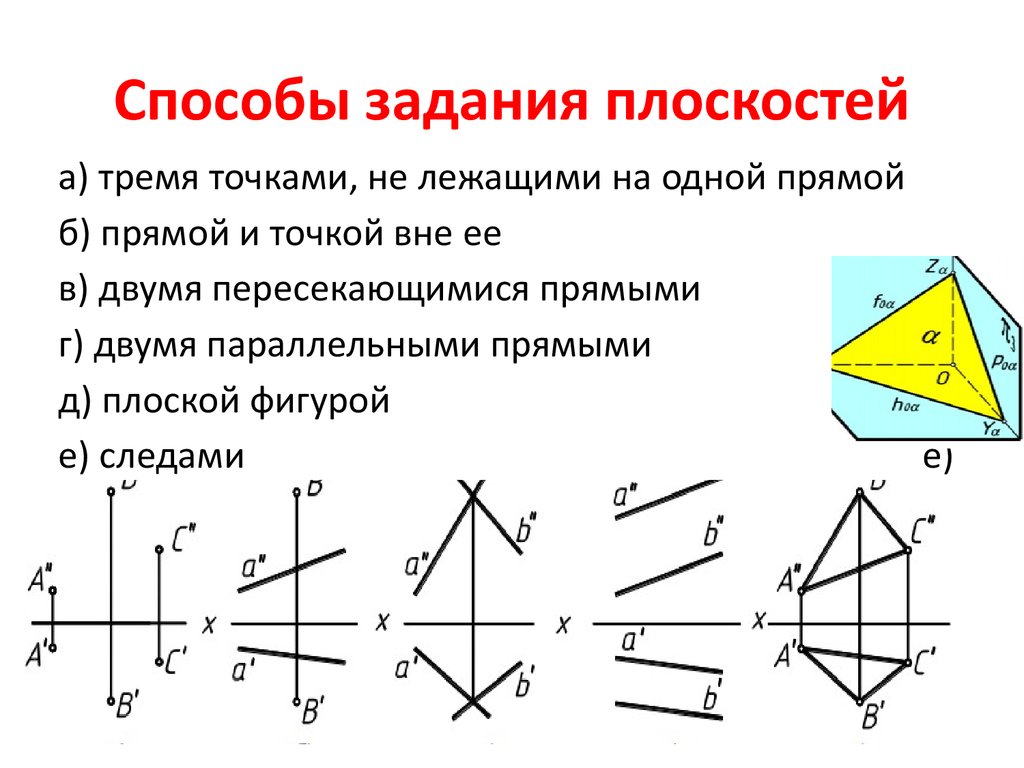
3. Способы задания плоскостей
а) тремя точками, не лежащими на одной прямойб) прямой и точкой вне ее
в) двумя пересекающимися прямыми
г) двумя параллельными прямыми
д) плоской фигурой
е) следами
е)
4. Классификация плоскостей
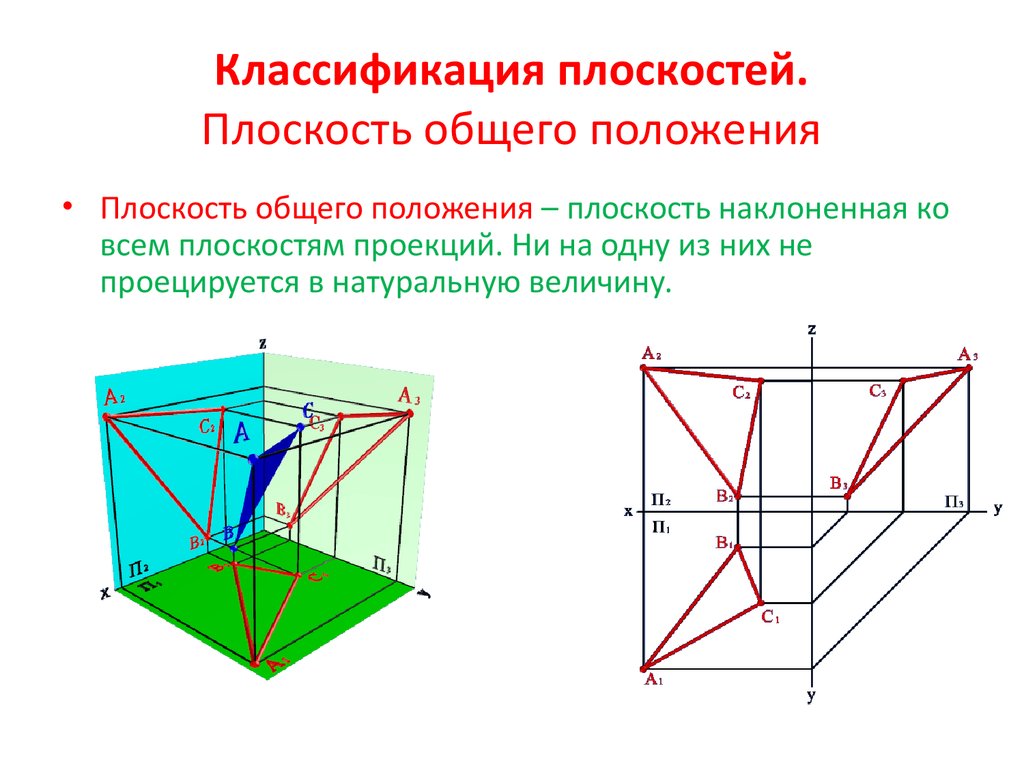
Плоскости5. Классификация плоскостей. Плоскость общего положения
• Плоскость общего положения – плоскость наклоненная ковсем плоскостям проекций. Ни на одну из них не
проецируется в натуральную величину.
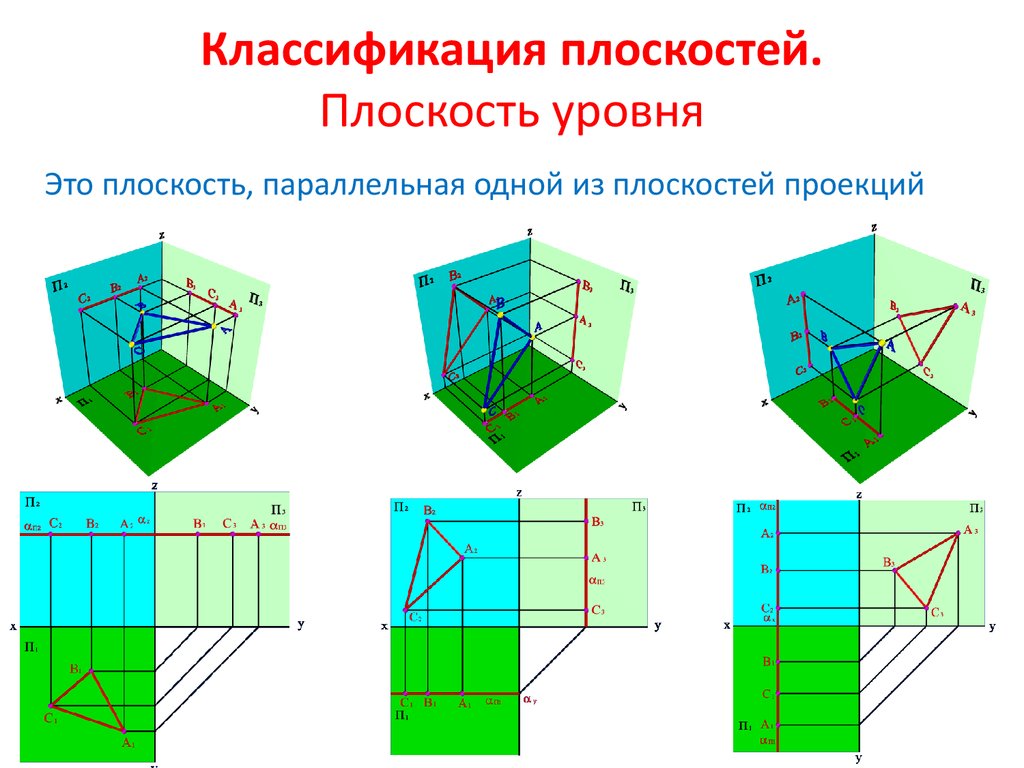
6. Классификация плоскостей. Плоскость уровня
Это плоскость, параллельная одной из плоскостей проекций7. Классификация плоскостей. Проецирующая плоскость
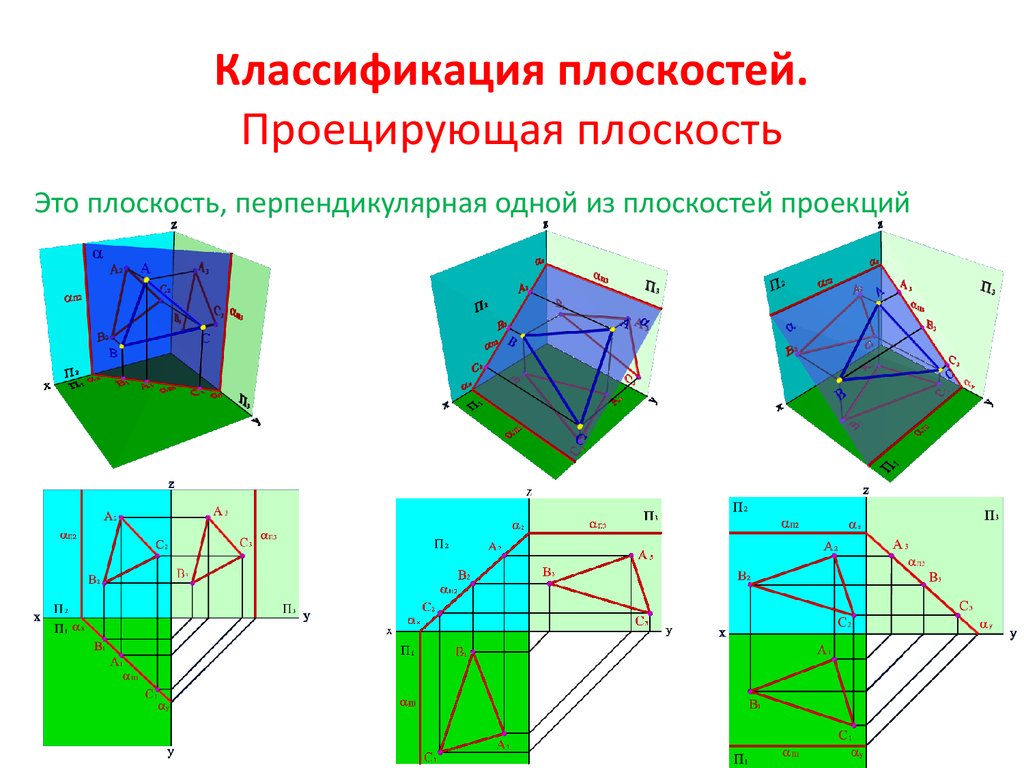
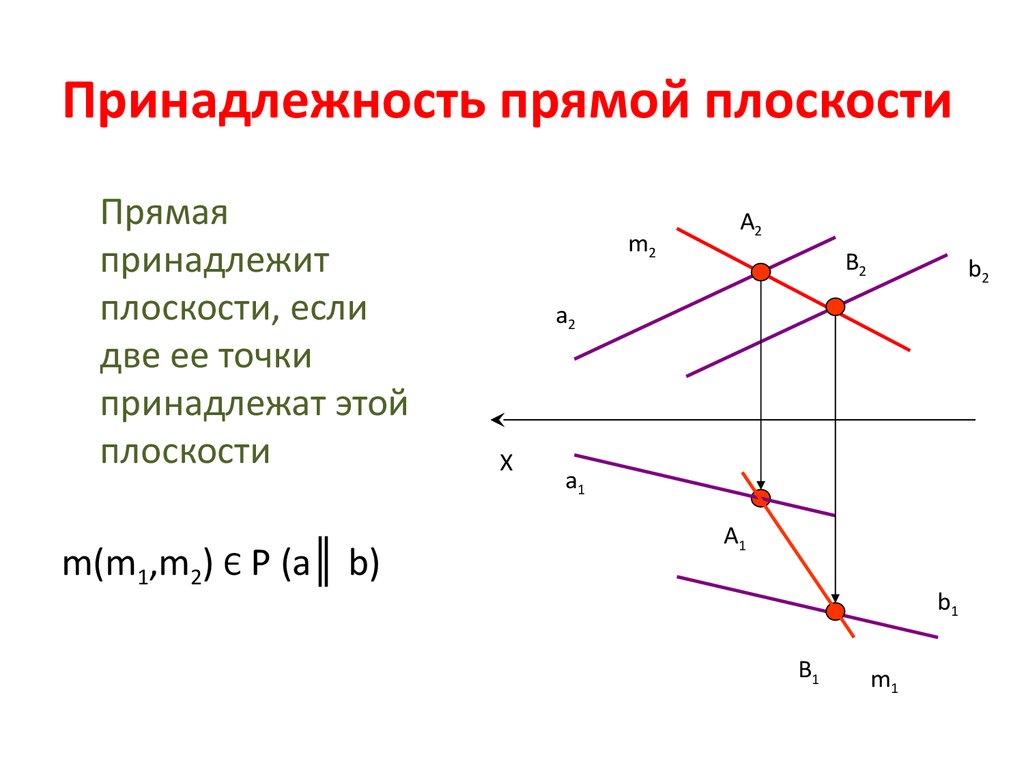
Это плоскость, перпендикулярная одной из плоскостей проекций8. Принадлежность прямой плоскости
Прямаяпринадлежит
плоскости, если
две ее точки
принадлежат этой
плоскости
m(m1,m2) Є P (a║ b)
m2
A2
B2
b2
a2
X
a1
A1
b1
B1
m1
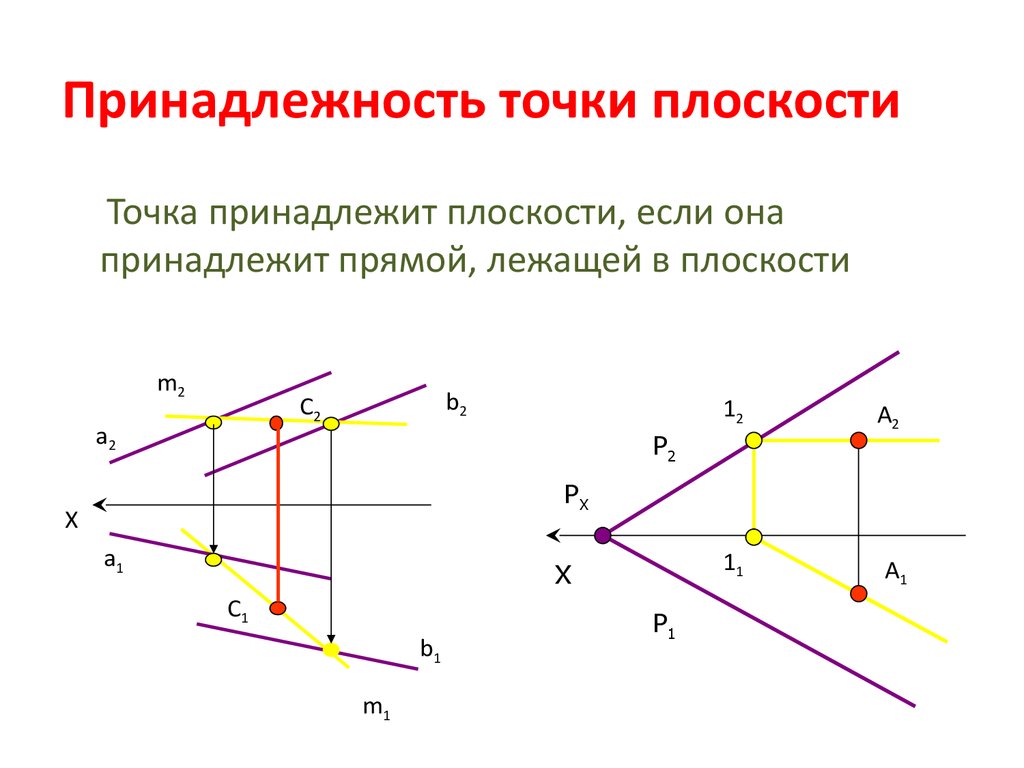
9. Принадлежность точки плоскости
Точка принадлежит плоскости, если онапринадлежит прямой, лежащей в плоскости
m2
b2
C2
a2
12
Р2
A2
PX
X
a1
11
X
C1
b1
m1
Р1
A1
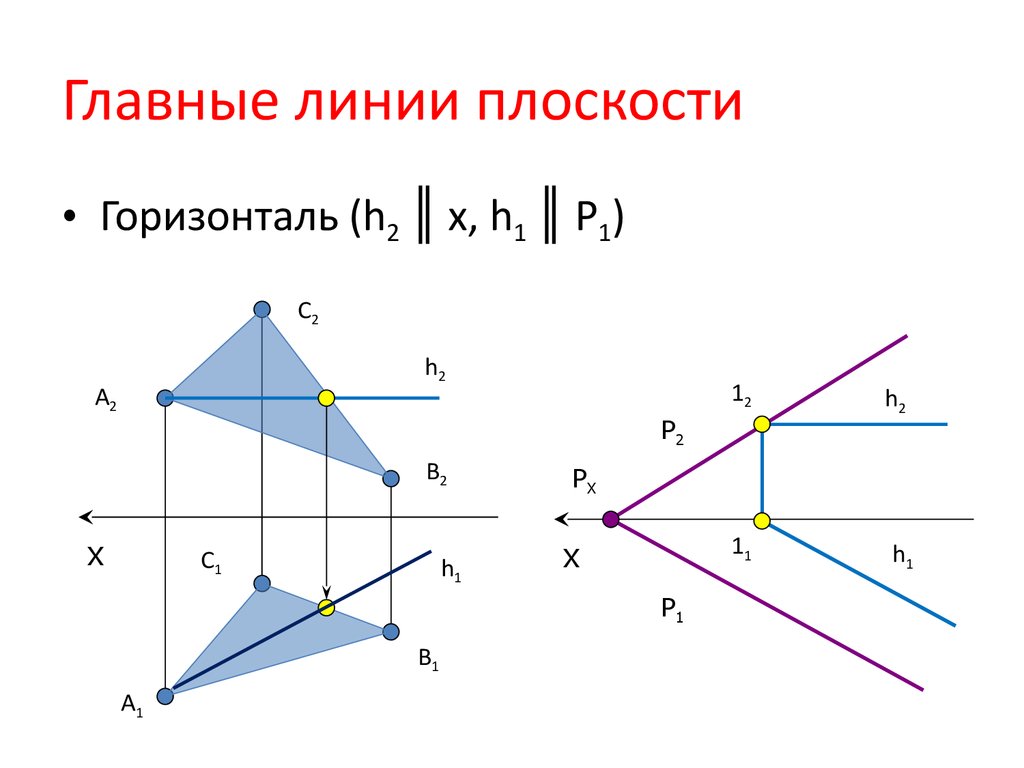
10. Главные линии плоскости
• Горизонталь (h2 ║ x, h1 ║ P1)C2
h2
A2
12
h2
11
h1
Р2
B2
X
C1
h1
PX
X
Р1
B1
A1
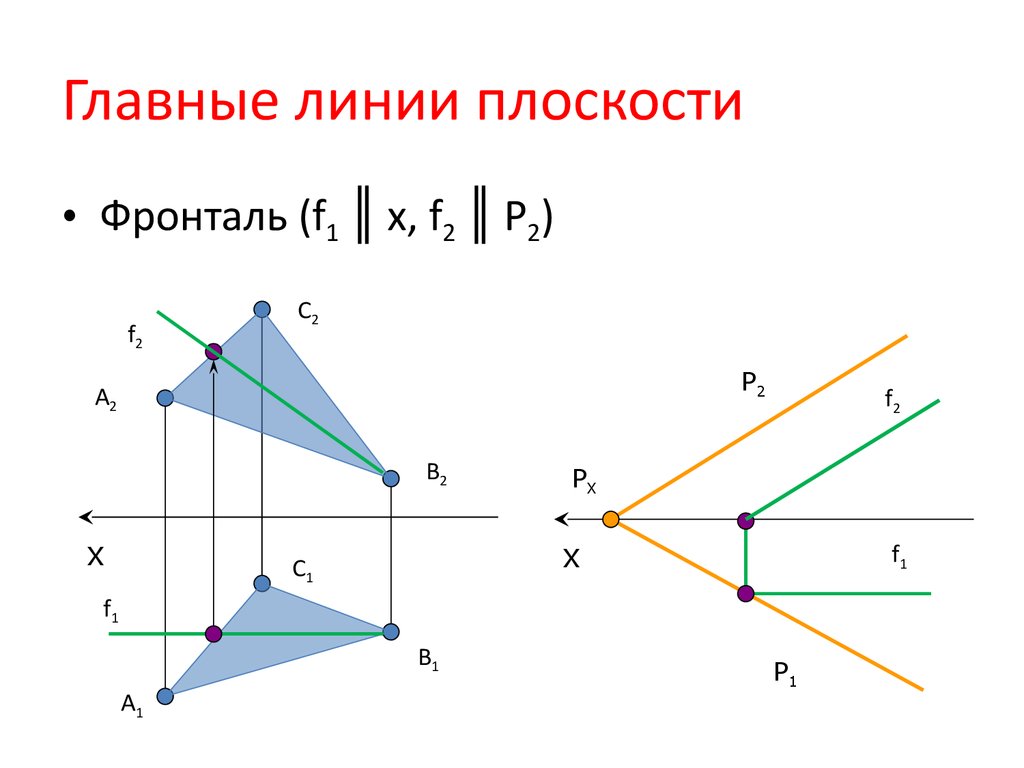
11. Главные линии плоскости
• Фронталь (f1 ║ x, f2 ║ P2)f2
C2
Р2
A2
B2
X
f2
PX
f1
X
C1
f1
B1
A1
Р1
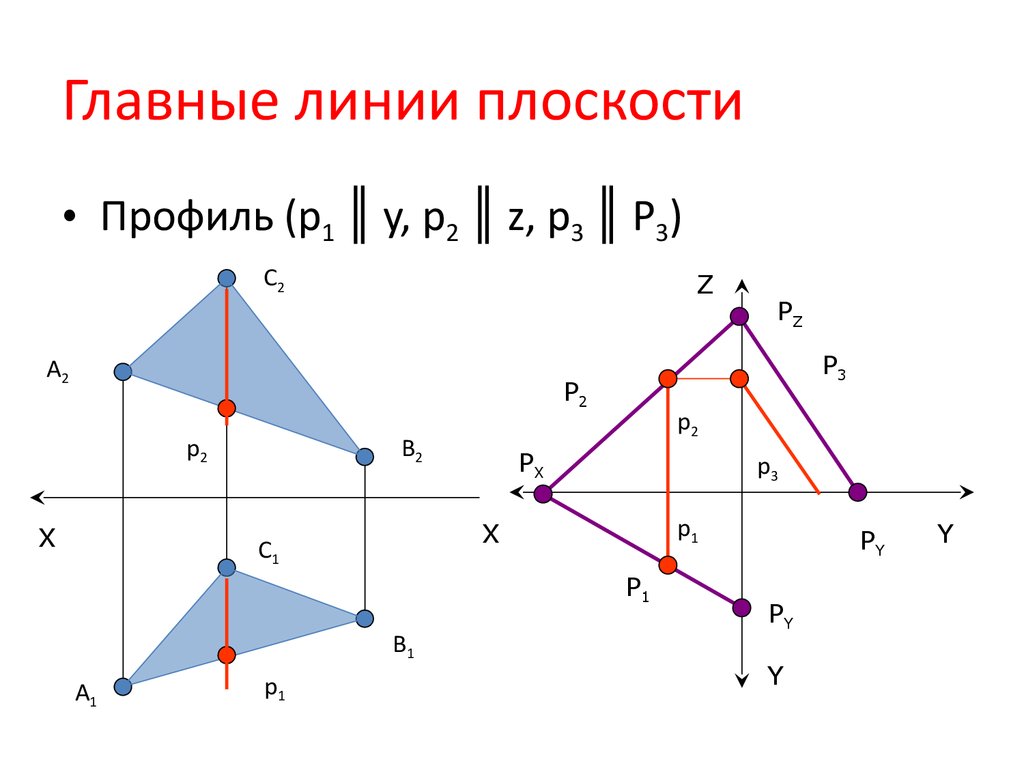
12. Главные линии плоскости
• Профиль (p1 ║ y, p2 ║ z, p3 ║ P3)C2
Z
A2
Р3
Р2
p2
X
B2
p2
PX
p3
p1
X
C1
Р1
B1
A1
p1
PZ
РY
РY
Y
Y
13. Главные линии плоскости
• Линия ската – линия, перпендикулярная главной линииплоскости (горизонтали, фронтали или профили) – n1 ┴ h1
C2
h2
A2
12
Р2
n2
X
B2
C1
A1
h1
n1
B1
h2
n2
PX
11
X
Р1
n1
h1
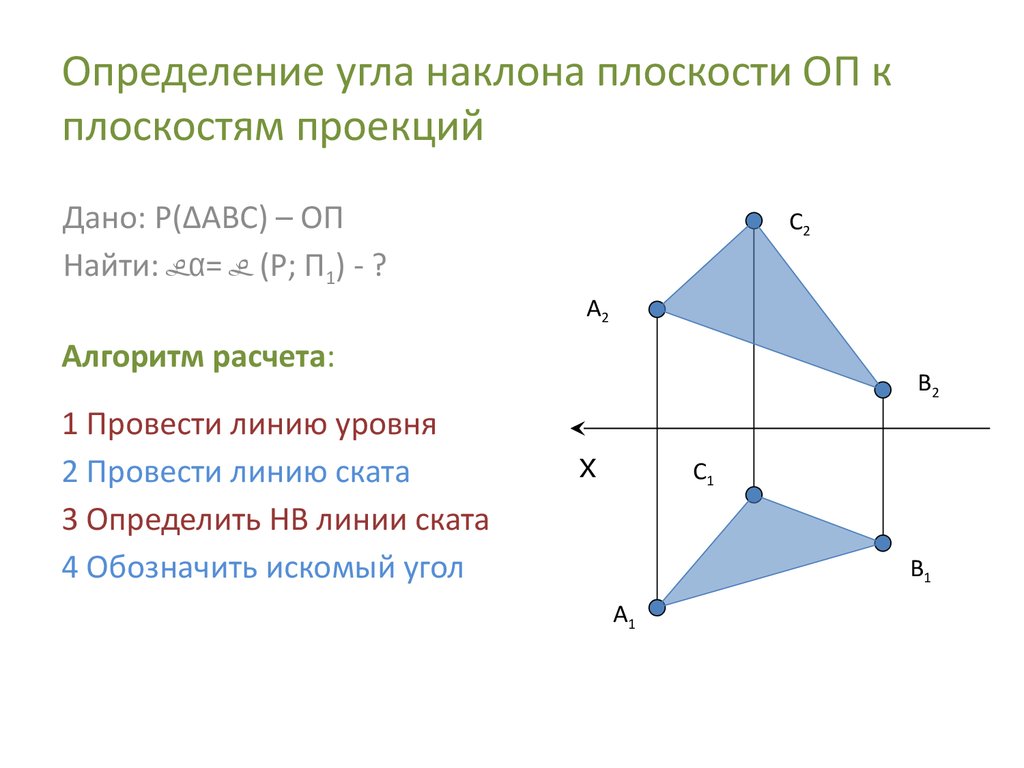
14. Определение угла наклона плоскости ОП к плоскостям проекций
Дано: Р(∆АВС) – ОПНайти: α= (Р; П1) - ?
C2
A2
Алгоритм расчета:
1 Провести линию уровня
2 Провести линию ската
3 Определить НВ линии ската
4 Обозначить искомый угол
B2
X
C1
B1
A1
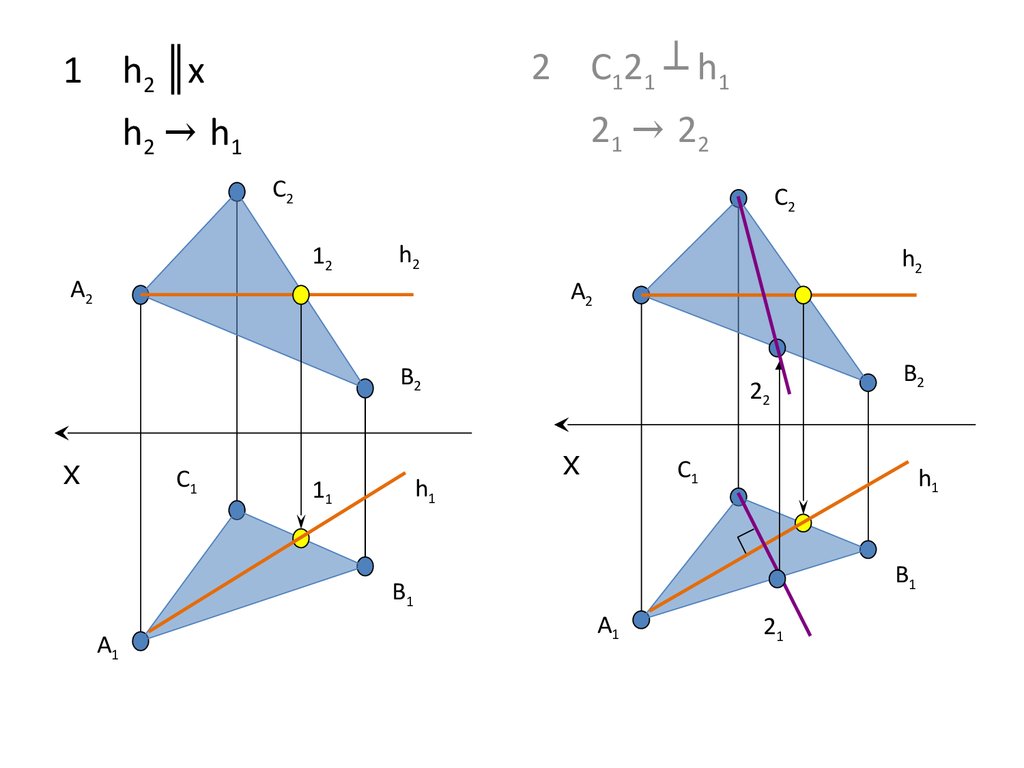
15.
2 C121 ┴ h11 h2 ║x
21 → 22
h2 → h1
C2
C2
12
A2
h2
h2
A2
B2
X
C1
h1
11
B1
A1
22
X
B2
C1
h1
B1
A1
21
16.
3 2120 ┴ С121,2021 = ∆Z
C120 – НВ линии ската
4 α = (С121; С120)
угол α – искомый
C2
C2
h2
A2
∆Z
B2
22
C1
X
h1
НВ линии
ската
A1
20
21
∆Z
h2
A2
∆Z
B1
B2
22
C1
X
A1
20
h1
21
B1
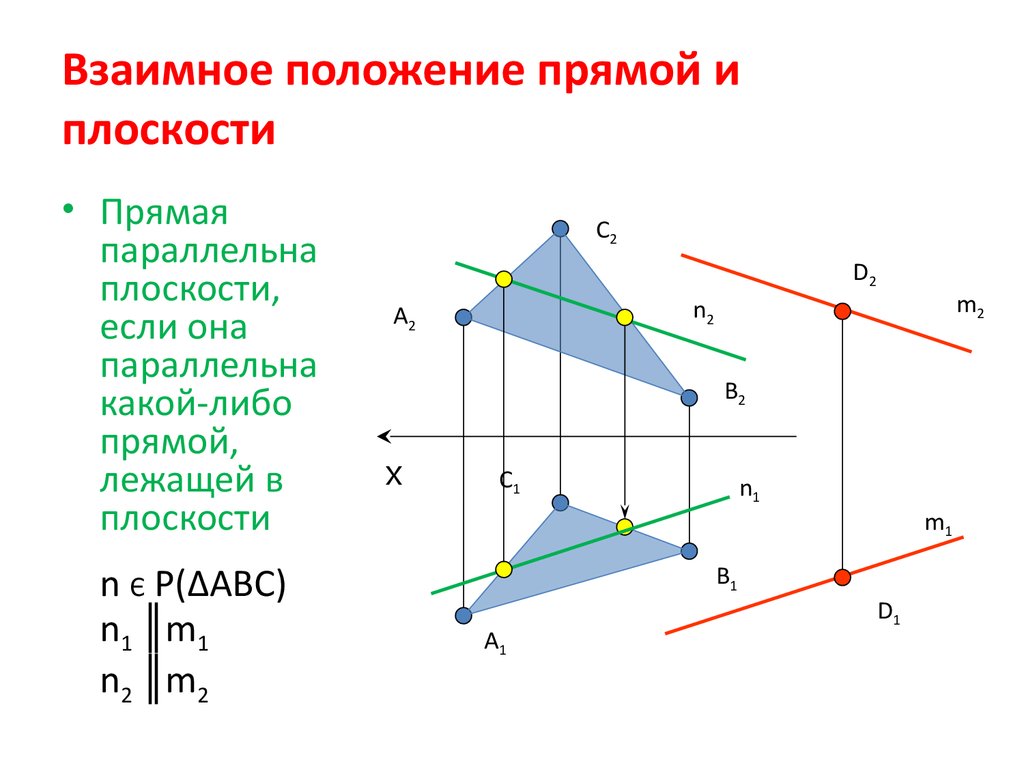
17. Взаимное положение прямой и плоскости
• Прямаяпараллельна
плоскости,
если она
параллельна
какой-либо
прямой,
лежащей в
плоскости
n Є P(∆ABC)
n1 ║m1
n2 ║m2
C2
D2
m2
n2
A2
B2
X
C1
n1
B1
A1
m1
D1
18. Взаимное положение прямой и плоскости
• Прямаяперпендикулярна
плоскости, если ее
фронтальная проекция
перпендикулярна f2, а
горизонтальная –
перпендикулярна h1
n ┴ P(∆ABC):
n1 ┴ h1
n2 ┴ f2
f2
C2
h2
A2
n2
B2
X
h1
C1
f1
B1
A1
n1
19. Пересечение прямой с плоскостью частного положения
C2Дано: Р(∆АВС) – ГПП
n(n1, n2) – ОП
Найти: (·)К=n ∩ P -?
n2
K2
A2
p2
B2
X
B1
A1
C1
K1
n1
(·)К Є n : K1Є n1; K2Є n2
(·)К Є P(ABC) :
К1 Є A1B1C1; К2 Є A2B2C2;
K1=n1 ∩ A1B1C1
K2=n2 ∩ A2B2C2
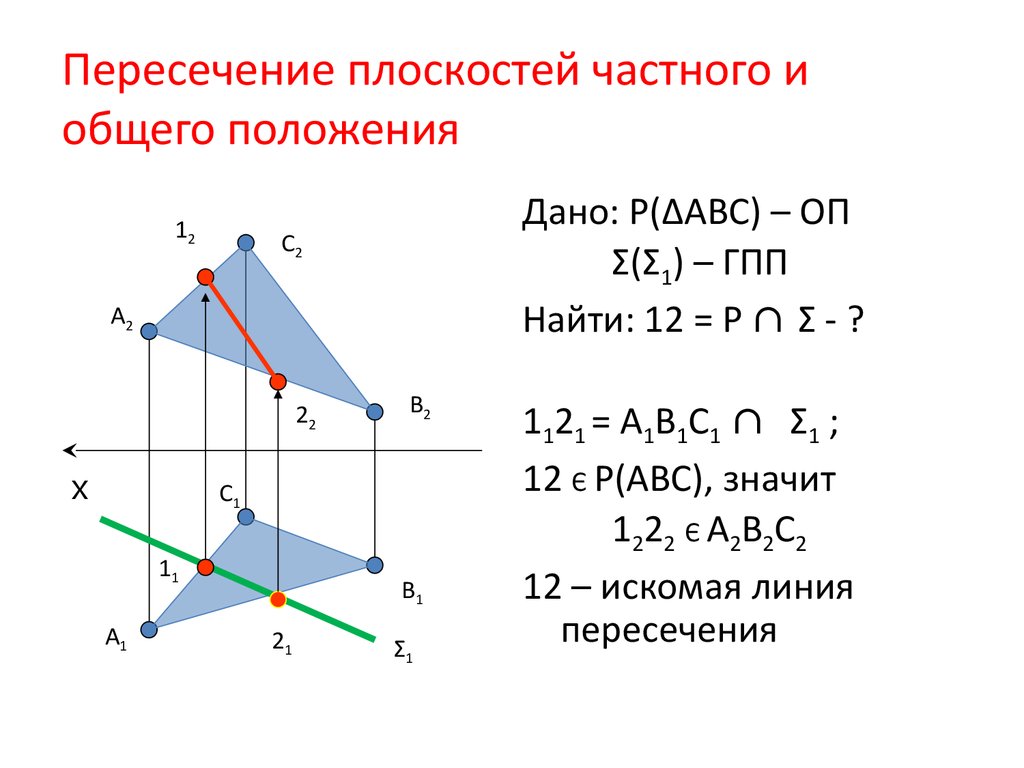
20. Пересечение плоскостей частного и общего положения
12Дано: Р(∆АВС) – ОП
Σ(Σ1) – ГПП
Найти: 12 = Р ∩ Σ - ?
C2
A2
22
X
B2
C1
11
A1
B1
21
Σ1
1121 = А1В1С1 ∩ Σ1 ;
12 Є Р(АВС), значит
1222 Є А2В2С2
12 – искомая линия
пересечения
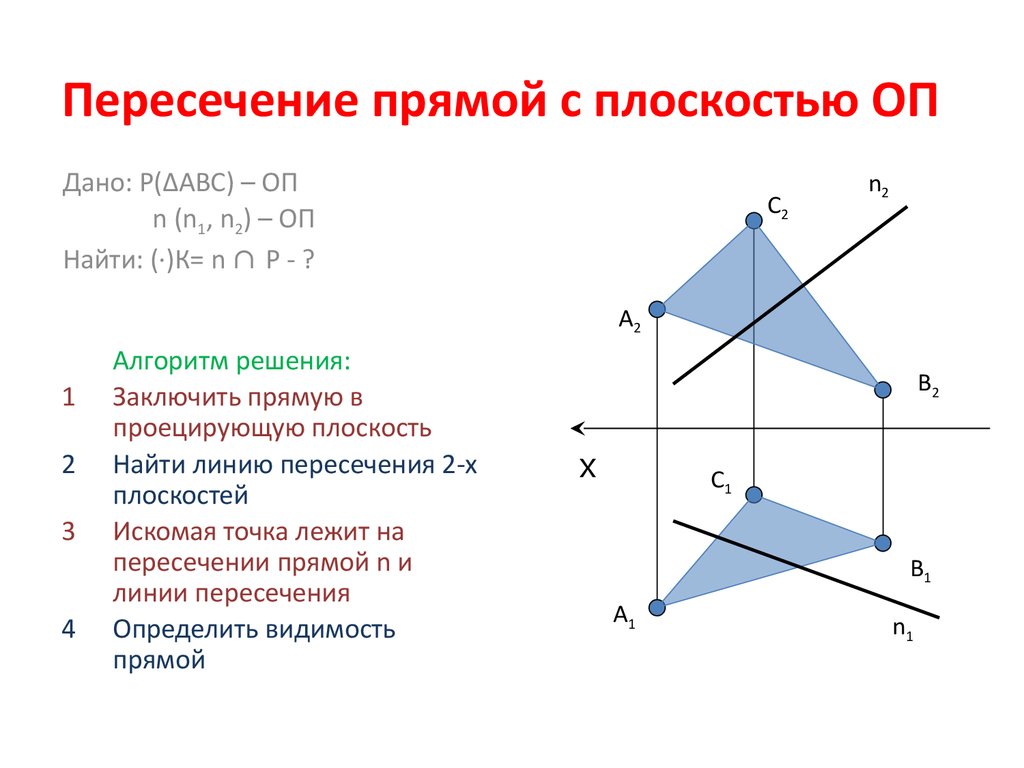
21. Пересечение прямой с плоскостью ОП
Дано: Р(∆АВС) – ОПn (n1, n2) – ОП
Найти: (·)К= n ∩ P - ?
C2
n2
A2
1
2
3
4
Алгоритм решения:
Заключить прямую в
проецирующую плоскость
Найти линию пересечения 2-х
плоскостей
Искомая точка лежит на
пересечении прямой n и
линии пересечения
Определить видимость
прямой
B2
X
C1
B1
A1
n1
22.
12
n(n1, n2) Є Σ (Σ1), ┴ П1
1121 = А1В1С1 ∩ Σ1
1121 →1222 ,
1222 – линия пересечения
плоскостей
n2
C2
12
К2
A2
A2
B2
22
X
X
C1
B1
11
21
n1
B2
22
C1
A1
К2 = 1222 ∩ n2
K2 → K 1
K – искомая точка
n2
C2
12
3
11
Σ1
A1
К1
B1
21
n1
Σ1
23.
Определяем видимостьпрямой на П1
Определяем видимость
прямой на П2
C2
12
C2
12
К2
A2
32Ξ32’
A2
12’
B2
22
X
11
К1
X
C1
B1
21
n1
B2
22
C1
A1
К2
11
Σ1
A1
К1
32’
B1
21
32
n1
Σ1
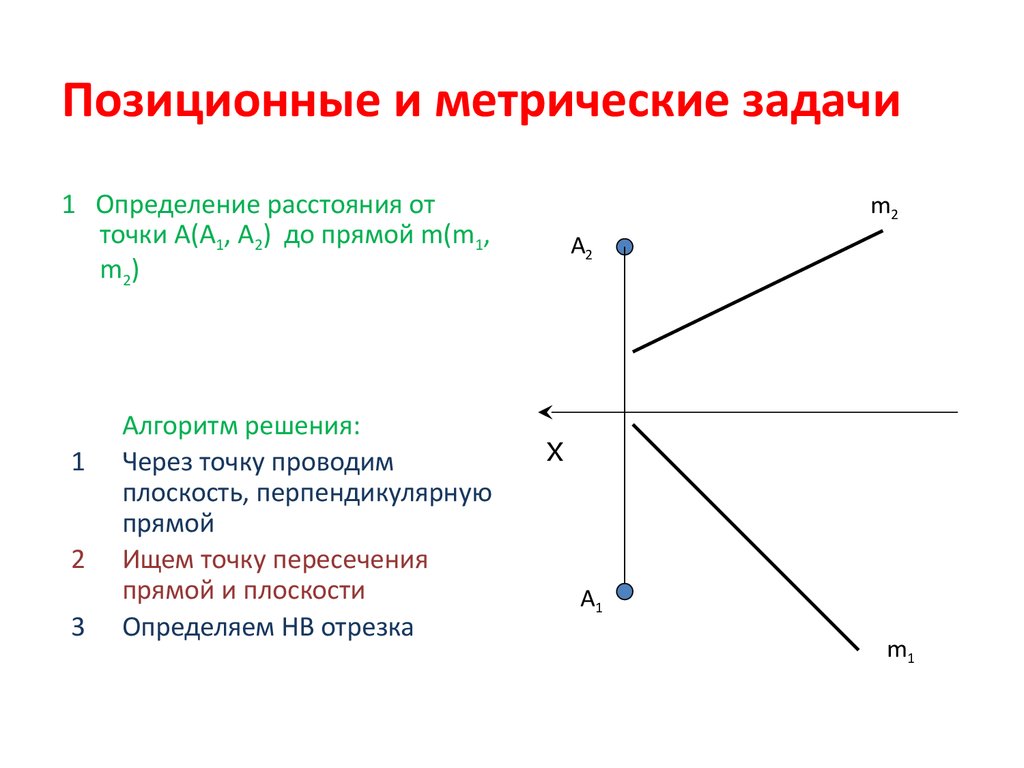
24. Позиционные и метрические задачи
1 Определение расстояния отточки А(А1, А2) до прямой m(m1,
m2)
1
2
3
Алгоритм решения:
Через точку проводим
плоскость, перпендикулярную
прямой
Ищем точку пересечения
прямой и плоскости
Определяем НВ отрезка
m2
A2
X
A1
m1
25.
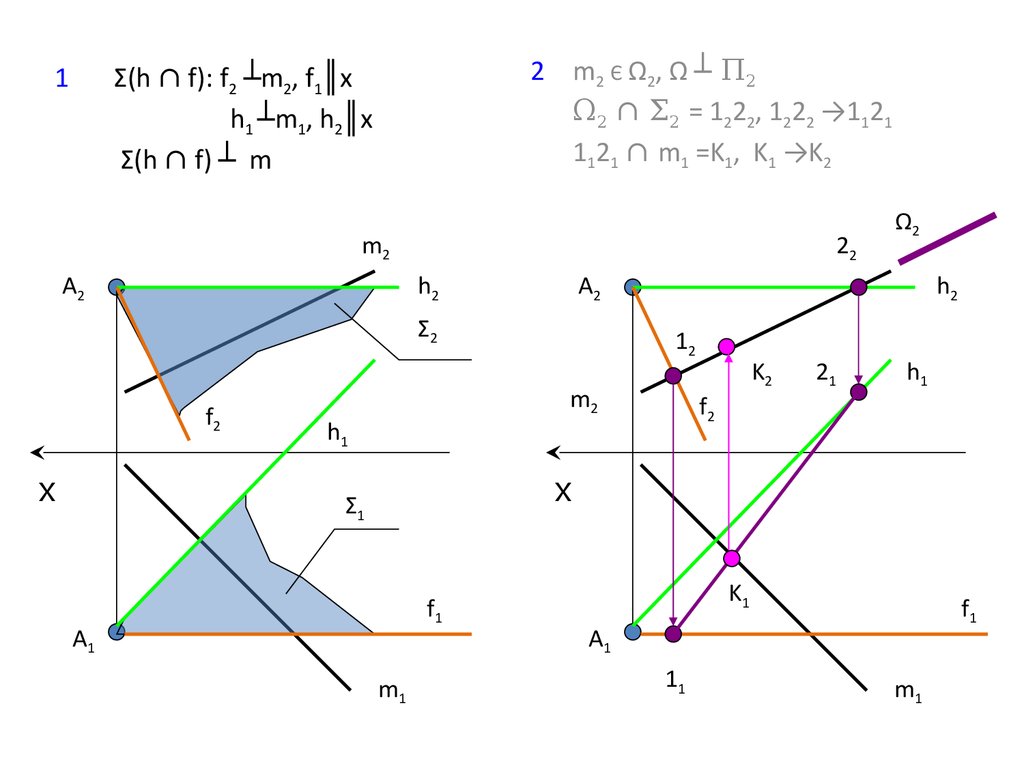
12 m2 Є Ω2, Ω ┴ П2
Ω2 ∩ Σ2 = 1222, 1222 →1121
1121 ∩ m1 =K1, K1 →K2
Σ(h ∩ f): f2 ┴m2, f1║x
h1 ┴m1, h2║x
Σ(h ∩ f) ┴ m
m2
A2
22
h2
A2
Σ2
f2
X
h2
12
m2
h1
Ω2
K2
21
h1
f2
X
Σ1
f1
A1
m1
K1
f1
A1
11
m1
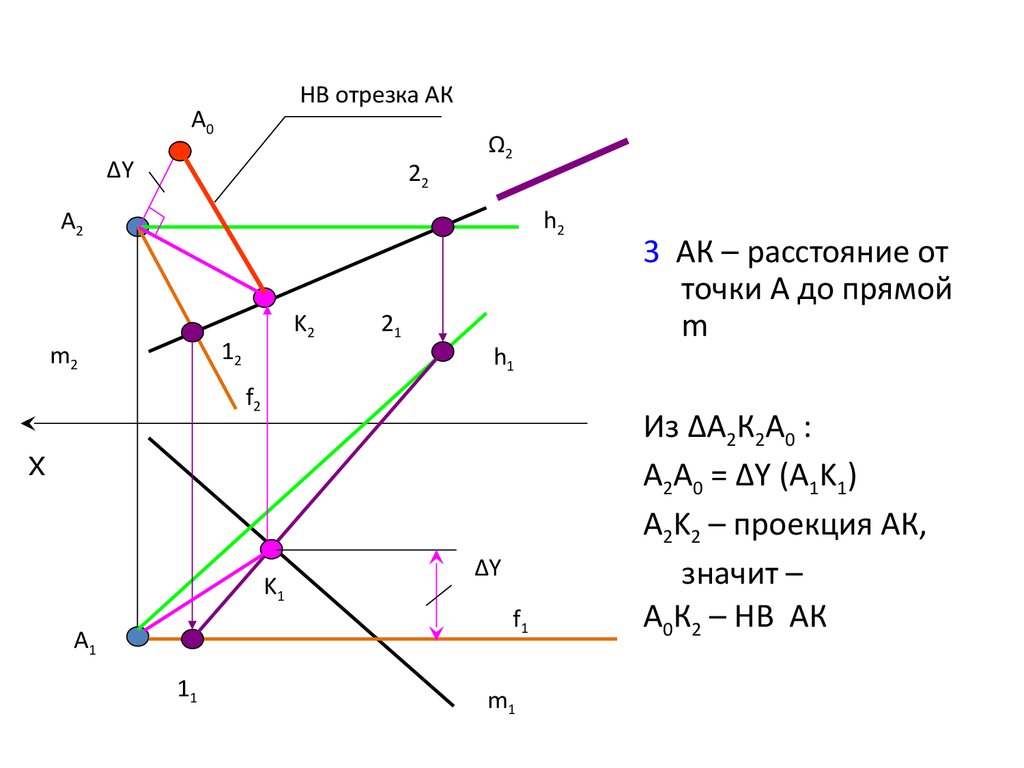
26.
НВ отрезка АКA0
∆Y
22
Ω2
h2
A2
K2
12
m2
21
h1
f2
X
K1
A1
11
∆Y
f1
m1
3 АК – расстояние от
точки А до прямой
m
Из ∆А2К2А0 :
А2А0 = ∆Y (A1K1)
A2K2 – проекция АК,
значит –
А0К2 – НВ АК
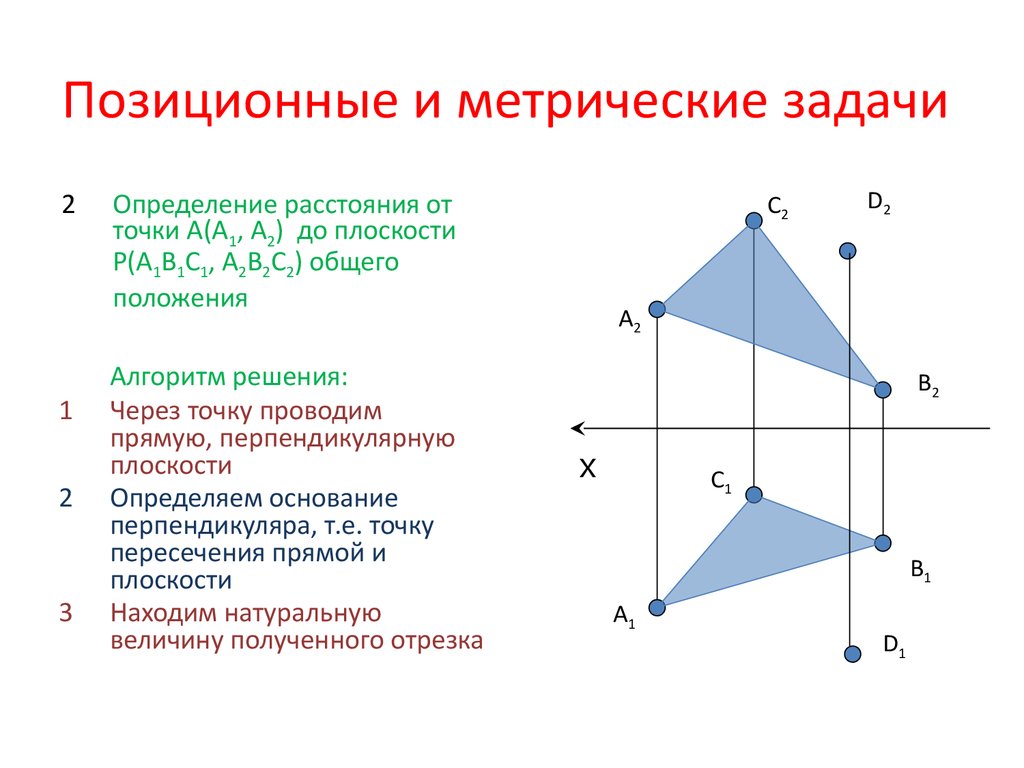
27. Позиционные и метрические задачи
21
2
3
Определение расстояния от
точки А(А1, А2) до плоскости
Р(А1В1С1, А2В2С2) общего
положения
Алгоритм решения:
Через точку проводим
прямую, перпендикулярную
плоскости
Определяем основание
перпендикуляра, т.е. точку
пересечения прямой и
плоскости
Находим натуральную
величину полученного отрезка
C2
D2
A2
B2
X
C1
B1
A1
D1
28.
D2C2
f2
n2
h2
1 n ┴ P(∆ABC) :
n1┴ h1; n2 ┴ f2
A2
B2
X
C1
h1
f1
B1
A1
n1
D1
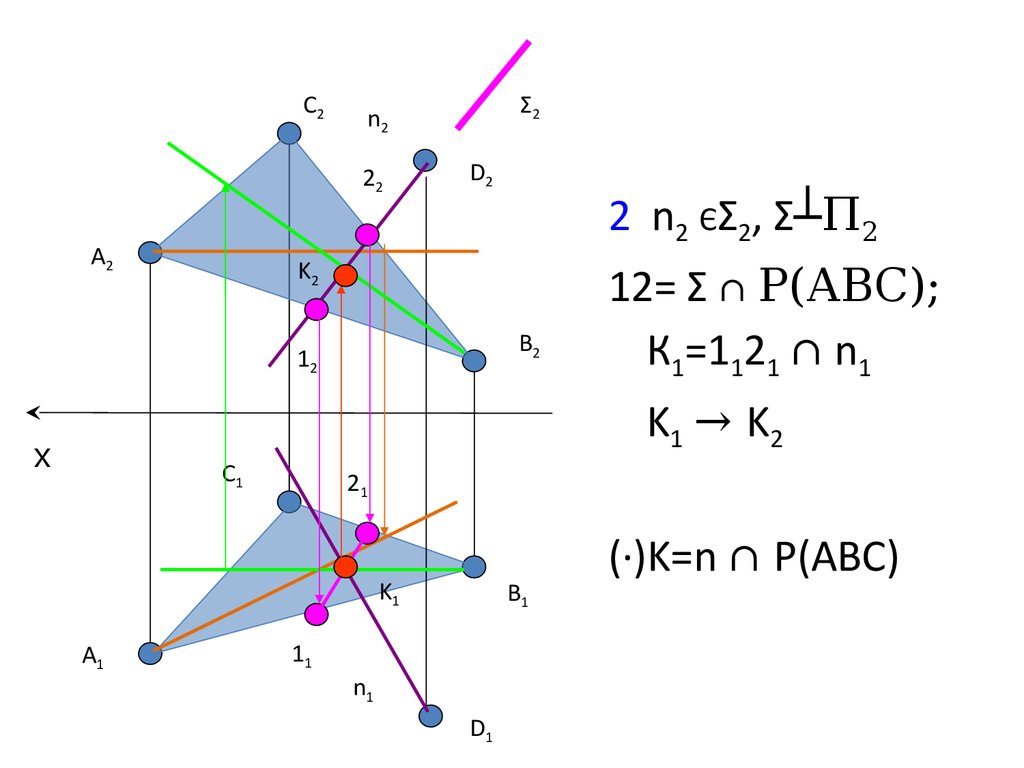
29.
C222
A2
Σ2
n2
D2
2 n2 ЄΣ2, Σ┴П2
K2
B2
12
12= Σ ∩ Р(АВС);
К1=1121 ∩ n1
K1 → K2
X
C1
21
K1
A1
11
B1
n1
D1
(·)K=n ∩ P(ABC)
30.
C2n2
22
A2
Σ2
D2
D0
K2
НВ КD
12
X
C1
B2
D2D0= ∆Y
K2D2 – проекция KD
21
B1
K1
A1
11
3 Из ∆К2D2D0 :
n1
D1
∆Y
значит –
K2D0 – НВ отрезка
KD
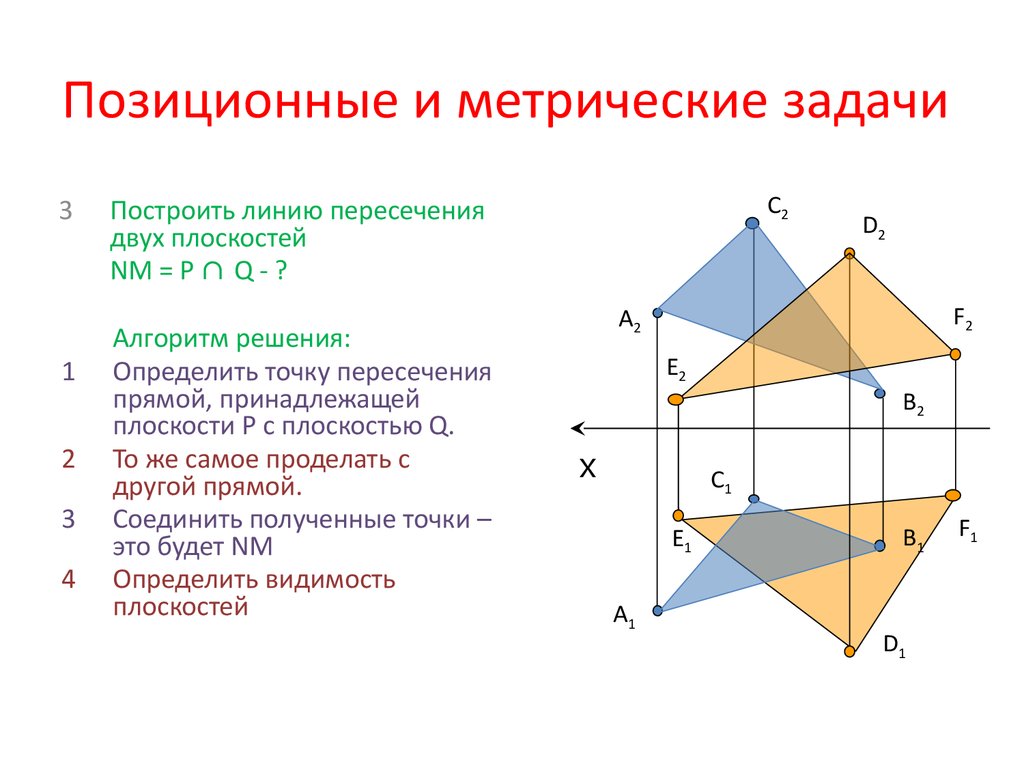
31. Позиционные и метрические задачи
31
2
3
4
C2
Построить линию пересечения
двух плоскостей
NM = P ∩ Q - ?
Алгоритм решения:
Определить точку пересечения
прямой, принадлежащей
плоскости Р с плоскостью Q.
То же самое проделать с
другой прямой.
Соединить полученные точки –
это будет NM
Определить видимость
плоскостей
D2
F2
A2
E2
B2
X
C1
E1
A1
B1
D1
F1
32.
Σ2C2
D2
12
A2
N2
E2
F2
22
1 С2В2 ЄΣ2 ;
B2
X
1222 → 1121
21
C1
E1
A1
Σ(Σ2) ┴ П2
B1
N1
11
D1
F1
N1=1121 ∩ C1B1
N1 → N2
33.
C232
12
D2
2 E1D1 Є Θ1 ;
M2
A2
42
E2
N2
F2
22
3141 → 3242
B2
X
Θ1
E1
B1
N1
31
A1
M2=3242 ∩E2D2
21
C1
M1
41
11
D1
Θ(Θ1) ┴ П1
F1
M2 → M1
34.
C2Линия
взгляда
32
A2
52
12
M2
D2
N2
F2
22
42
B2
E2
X
E1
4
21
C1
N1
51Ξ 31
A1
3
M1
41
11
D1
B1
F1
NM – искомая
линия
пересечения
плоскостей
Видимость
на П1 :
5,3 –конкурирующие точки
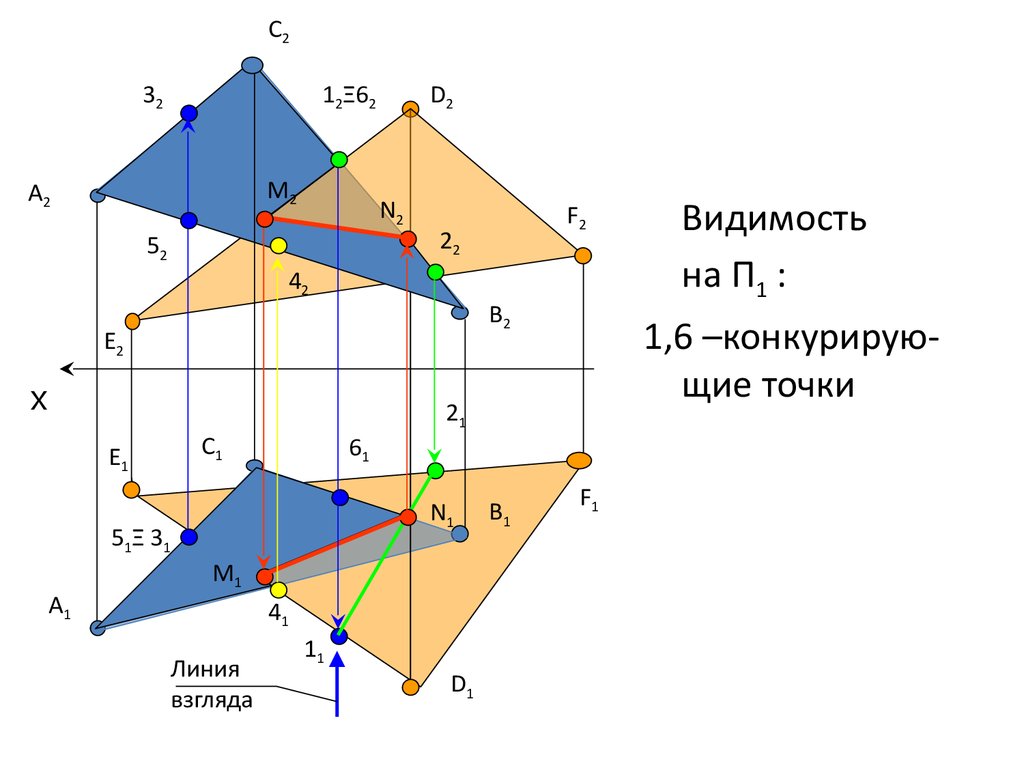
35.
C232
12Ξ62
M2
A2
D2
N2
52
22
42
B2
E2
X
E1
C1
61
A1
M1
41
Линия
взгляда
11
D1
B1
Видимость
на П1 :
1,6 –конкурирующие точки
21
N1
51Ξ 31
F2
F1














 drafting
drafting








