Similar presentations:
Взаимное положение прямой и плоскости, двух плоскостей. Позиционные задачи. Лекция 4
1.
Лекция 4Взаимное положение прямой и
плоскости, двух плоскостей.
Позиционные задачи
2. Взаимное положение прямой и плоскости, двух плоскостей
Прямая и плоскость:• Прямая принадлежит плоскости (см. тема 3): все точки
прямой являются точками плоскости
• Прямая параллельна плоскости: общих точек нет
• Прямая пересекает плоскость: одна общая точка
Две плоскости:
• Плоскости параллельны: общих прямых нет
• Плоскости пересекаются: одна общая прямая
3.
Принадлежность прямой плоскости1
m2
1
а2 2
2
2
n2
n2
m2
n1
n1
m1
22
21
2
b2
12
1
а 1 11 m
1
(n m)
(1 m) ; (2 n)
а (1 2) а
11
1
(n m) b1
(1 m) ; 1 b
b n b
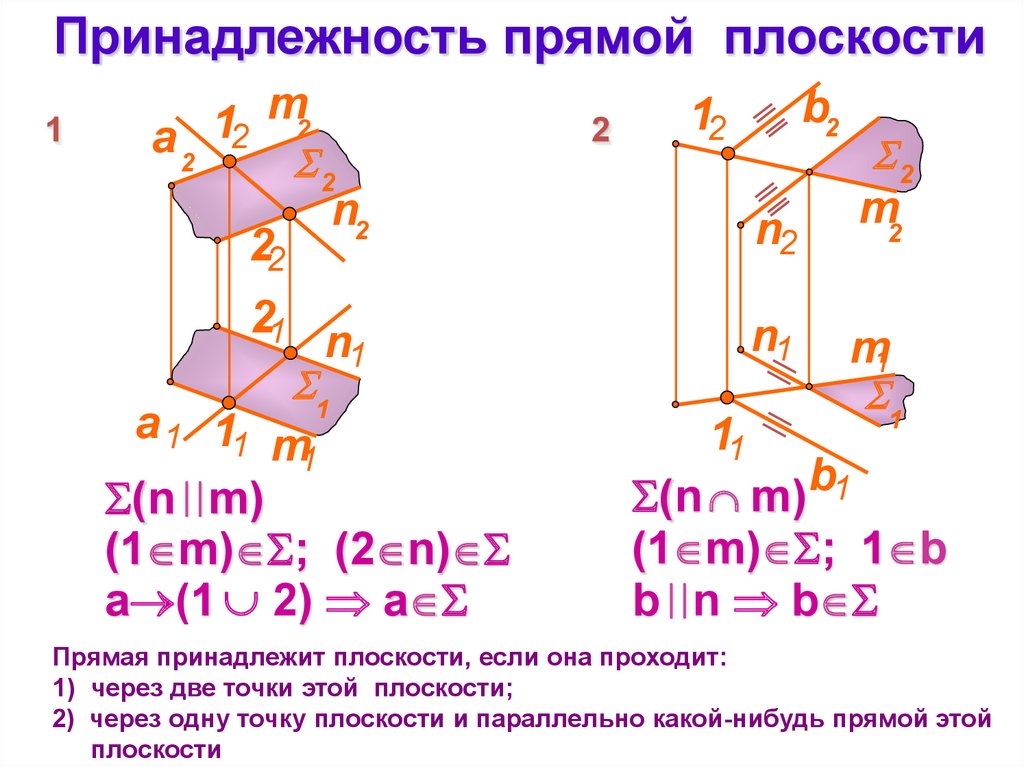
Прямая принадлежит плоскости, если она проходит:
1) через две точки этой плоскости;
2) через одну точку плоскости и параллельно какой-нибудь прямой этой
плоскости
4.
Параллельность прямой и плоскостиb
А
n
Признак параллельности:
Прямая параллельна
плоскости, если она
параллельна какой-ли
прямой, лежащей в
этой плоскости
b n b
Через точку А в пространстве можно провести бесчисленное множество
прямых линий, параллельных данной плоскости . Для однозначного
решения проведем в плоскости прямую n
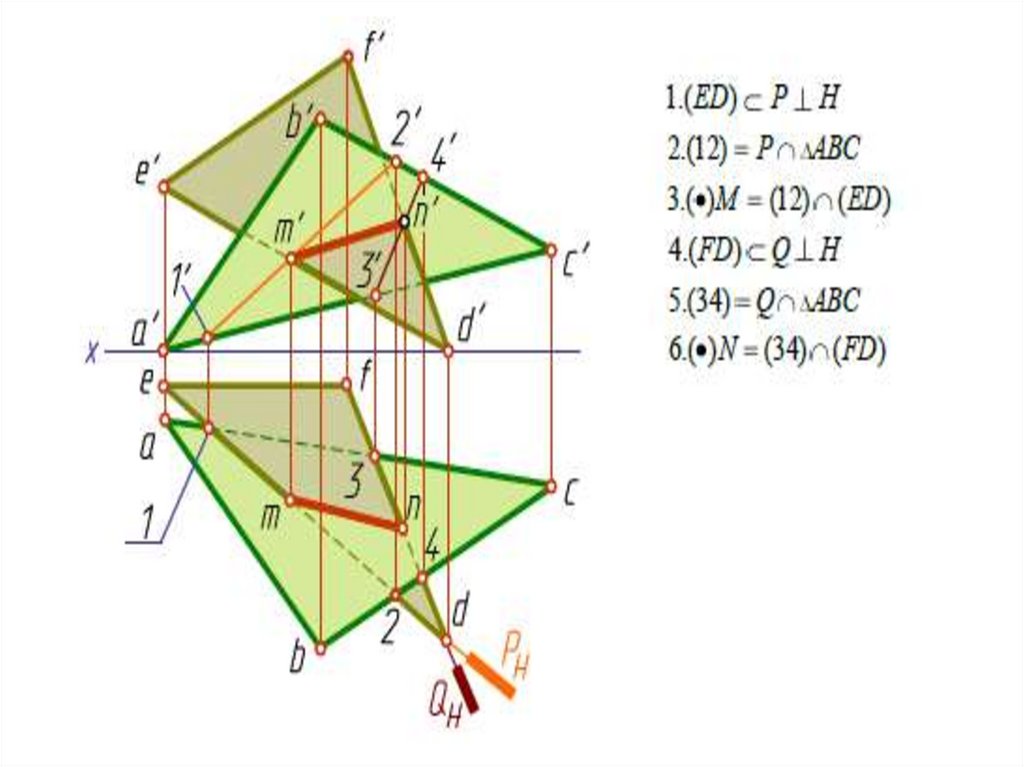
5. Параллельность прямой и плоскости
Задача:b
А
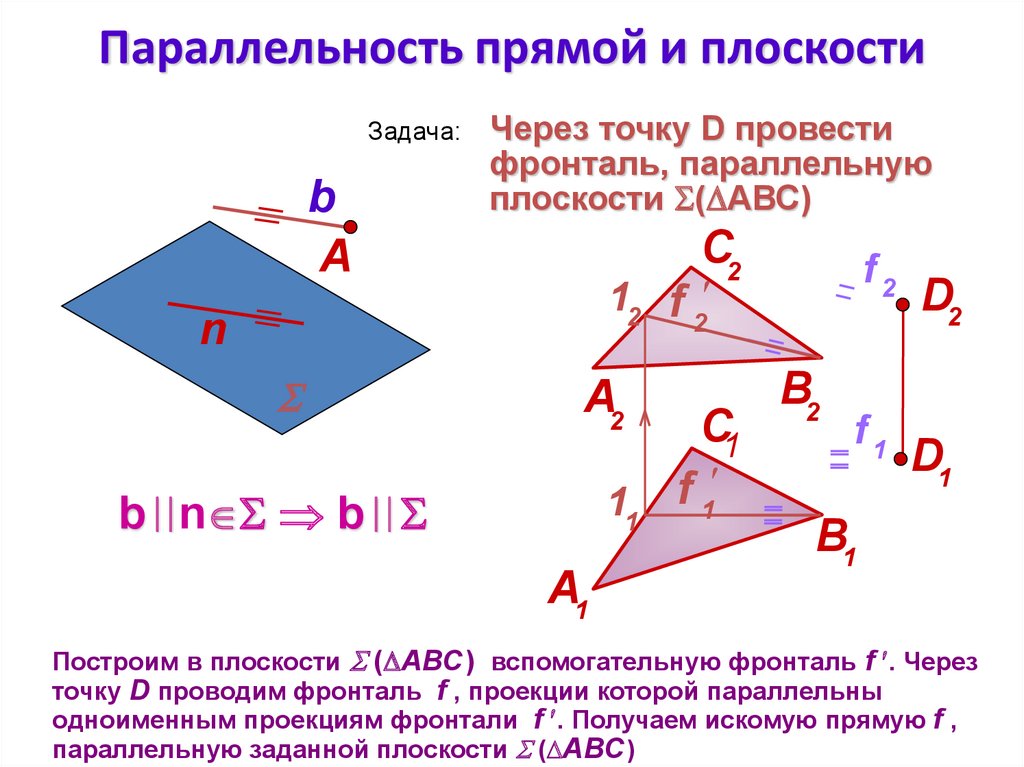
Через точку D провести
фронталь, параллельную
плоскости ( АВС)
С2
12 f
2
n
f2
А2
b n b
11
А1
С1
f 1
В2
f1
D2
D1
В1
Построим в плоскости ( АВС ) вспомогательную фронталь f . Через
точку D проводим фронталь f , проекции которой параллельны
одноименным проекциям фронтали f . Получаем искомую прямую f ,
параллельную заданной плоскости ( АВС )
6.
Параллельность прямой и плоскости2
2
x
n
х
2
n
1
1
( 1, 2)
m2
а
2
а
1
n
а
а n
x
m1
х
1
П2
m2 2 m
Если прямая а параллельна плоскости общего положения, то в плоскости
строят вспомогательную прямую n и выполняют условие параллельности одноименных проекций прямых а и n. Если плоскость проецирующая,
то одна из проекций искомой прямой m параллельна следу плоскости
7.
Параллельность двух плоскостейn
a
b
П2
m
а m
b n
2
x
х
2
х
1
1
1 1
2 2
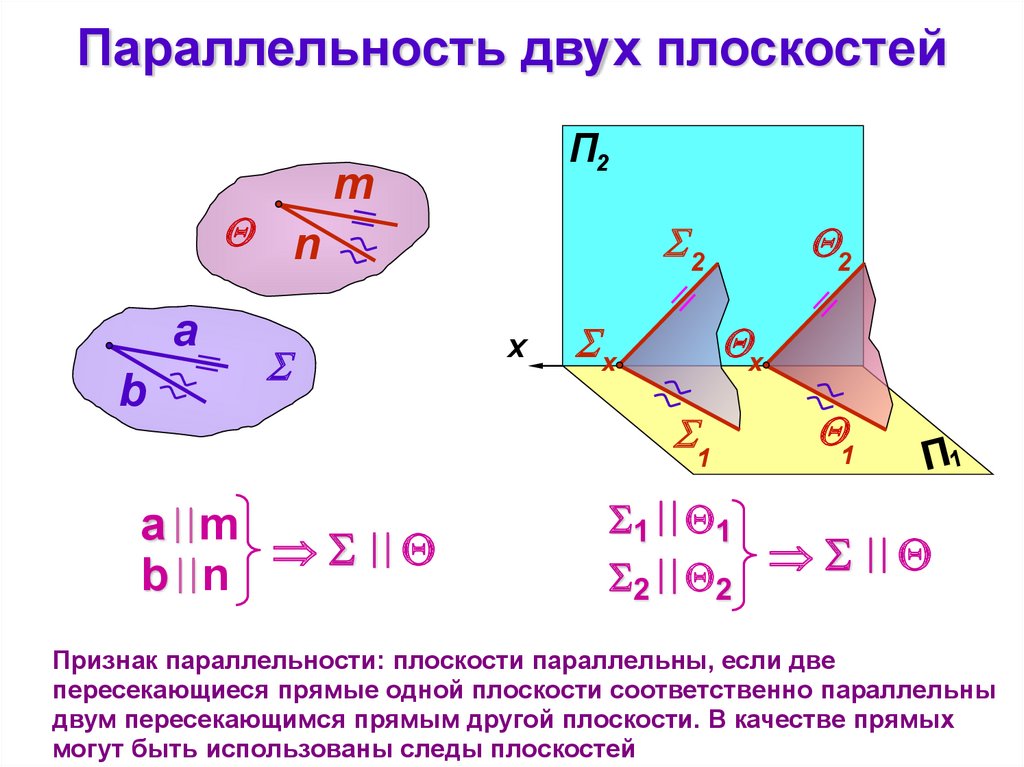
Признак параллельности: плоскости параллельны, если две
пересекающиеся прямые одной плоскости соответственно параллельны
двум пересекающимся прямым другой плоскости. В качестве прямых
могут быть использованы следы плоскостей
8.
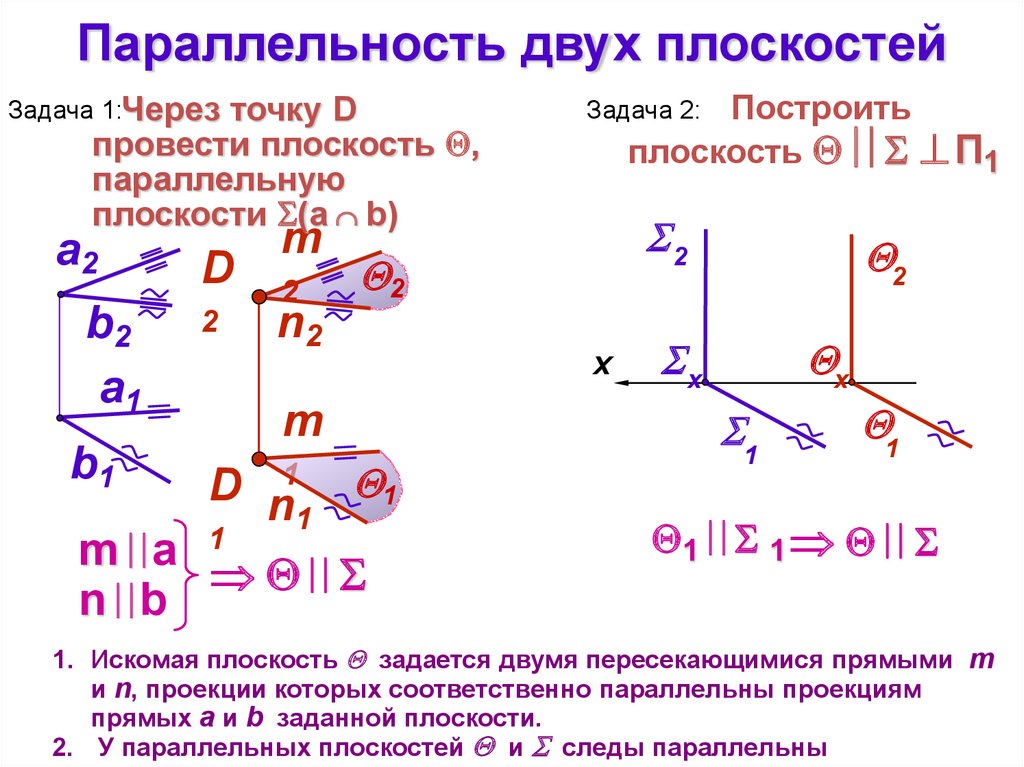
Параллельность двух плоскостейЗадача 1:Через
точку D
провести плоскость ,
параллельную
плоскости (a b)
a2
b2
a1
b1
D
2
m
2
Построить
плоскость П1
Задача 2:
2
2
n2
m
D n1 1
1
m a 1
n b
x
2
х
х
1
1
1 1
1. Искомая плоскость задается двумя пересекающимися прямыми m
и n, проекции которых соответственно параллельны проекциям
прямых а и b заданной плоскости.
2. У параллельных плоскостей и следы параллельны
9.
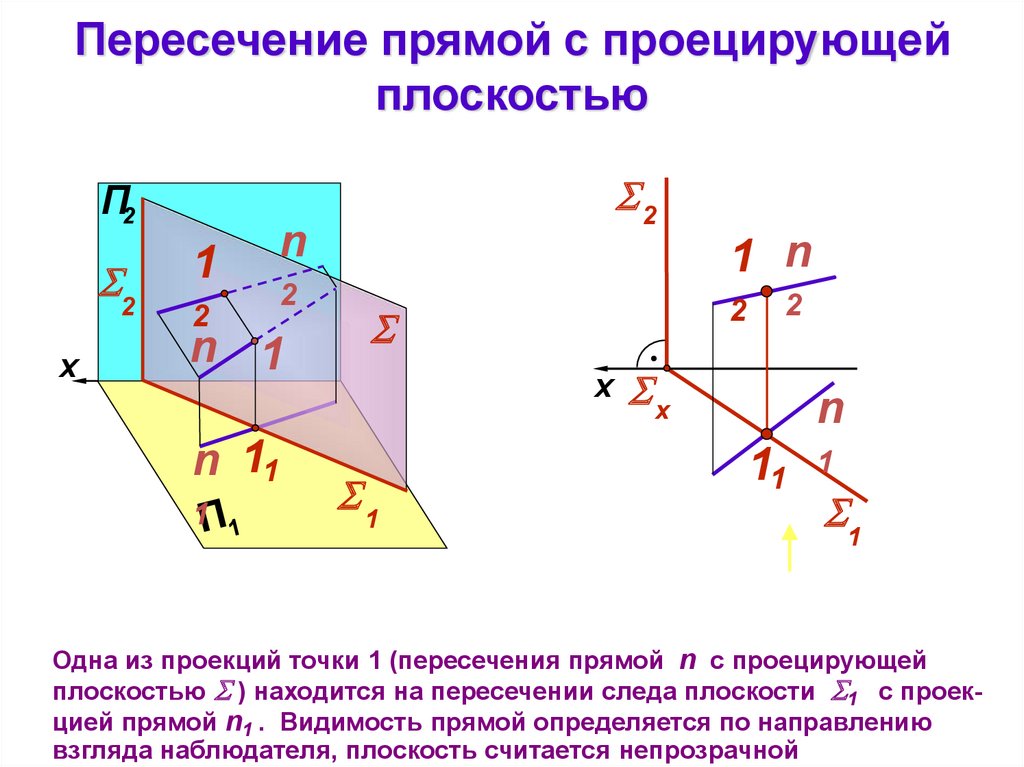
Пересечение прямой с проецирующейплоскостью
П2
2
x
х
1
2
n
2
n 1
n 11
1
2
1 n
2
x
1
2
х
n
11
1
1
Одна из проекций точки 1 (пересечения прямой n с проецирующей
плоскостью ) находится на пересечении следа плоскости 1 с проекцией прямой n1 . Видимость прямой определяется по направлению
взгляда наблюдателя, плоскость считается непрозрачной
10.
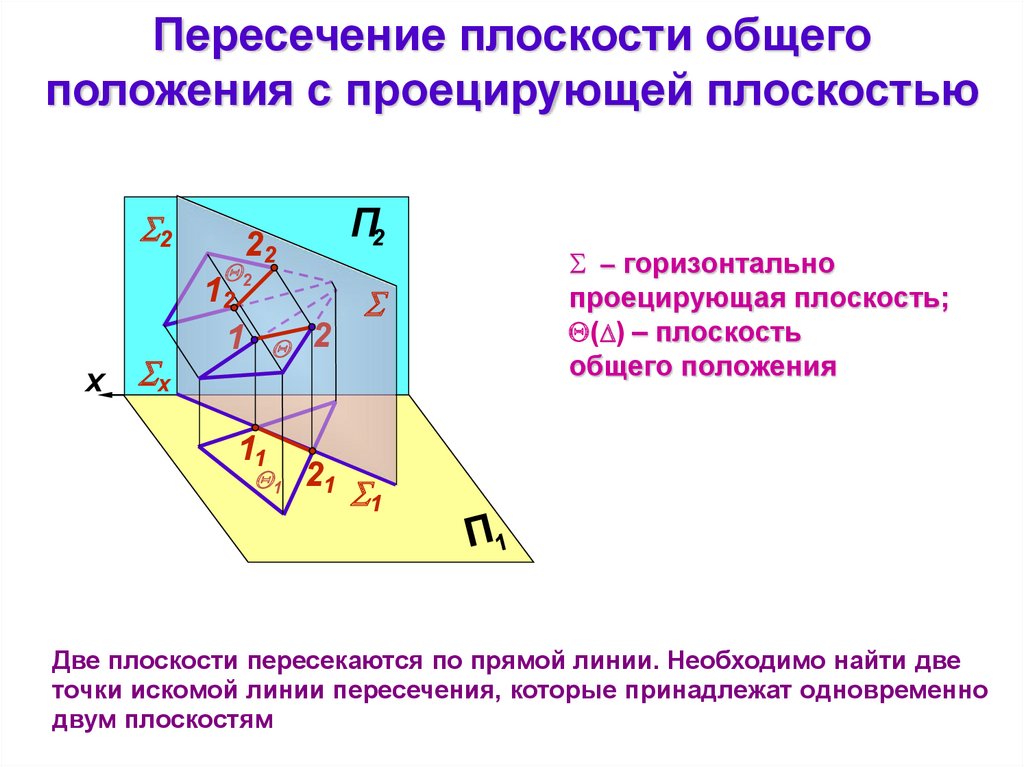
Пересечение плоскости общегоположения с проецирующей плоскостью
2
П2
22
2
x х
12
1
2
1
21
11
– горизонтально
проецирующая плоскость;
( ) – плоскость
общего положения
1
Две плоскости пересекаются по прямой линии. Необходимо найти две
точки искомой линии пересечения, которые принадлежат одновременно
двум плоскостям
11.
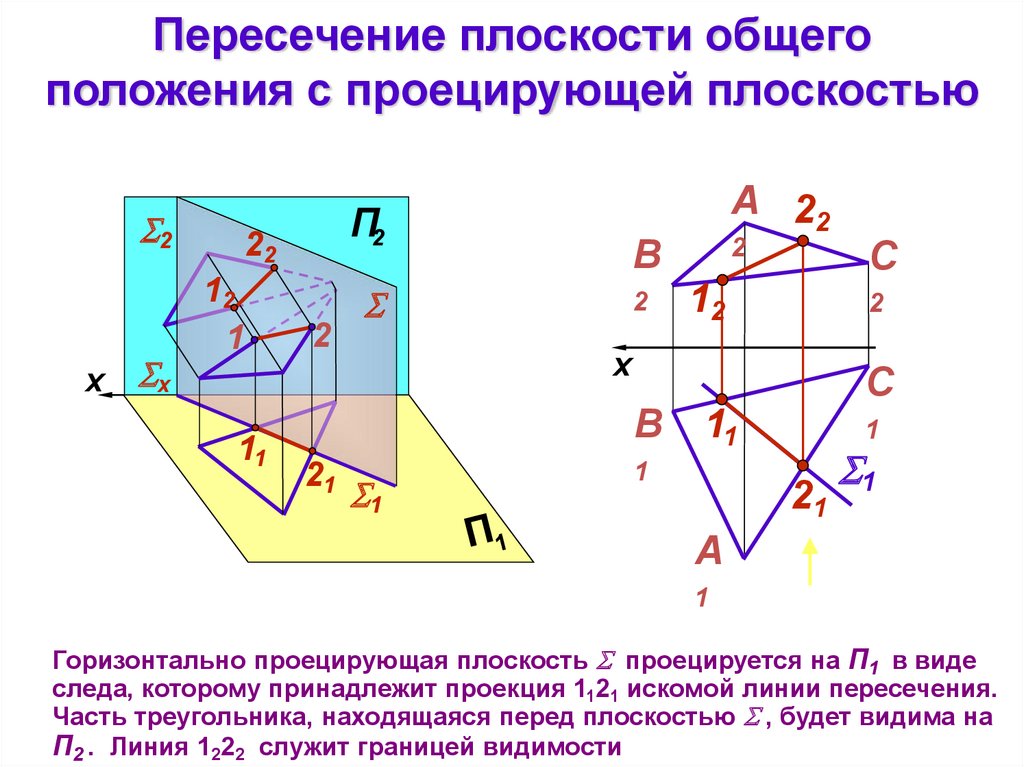
Пересечение плоскости общегоположения с проецирующей плоскостью
2
x х
П2
22
12
1
11
2
В
2
2
12
1
С
2
x
В
21
А 22
С
11
1
1
21
1
А
1
Горизонтально проецирующая плоскость проецируется на П1 в виде
следа, которому принадлежит проекция 1121 искомой линии пересечения.
Часть треугольника, находящаяся перед плоскостью , будет видима на
П2 . Линия 1222 служит границей видимости
12.
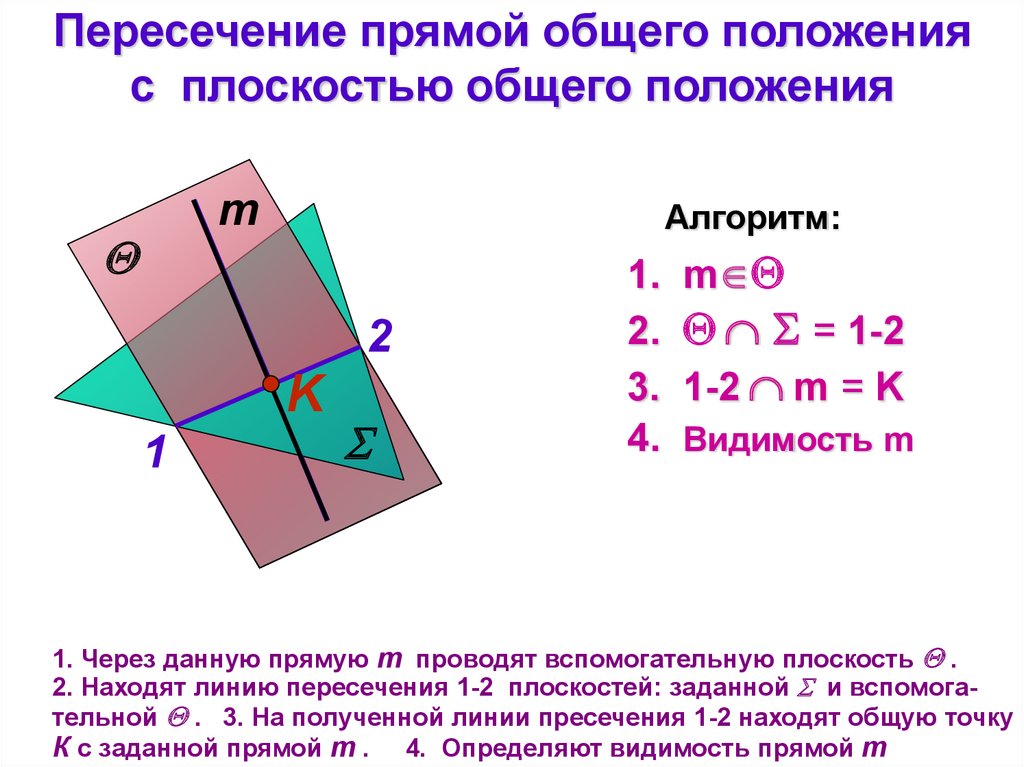
Пересечение прямой общего положенияс плоскостью общего положения
m
Алгоритм:
2
K
1
1.
2.
3.
4.
m
= 1-2
1-2 m = K
Видимость m
1. Через данную прямую m проводят вспомогательную плоскость .
2. Находят линию пересечения 1-2 плоскостей: заданной и вспомогательной . 3. На полученной линии пресечения 1-2 находят общую точку
К с заданной прямой m . 4. Определяют видимость прямой m
13.
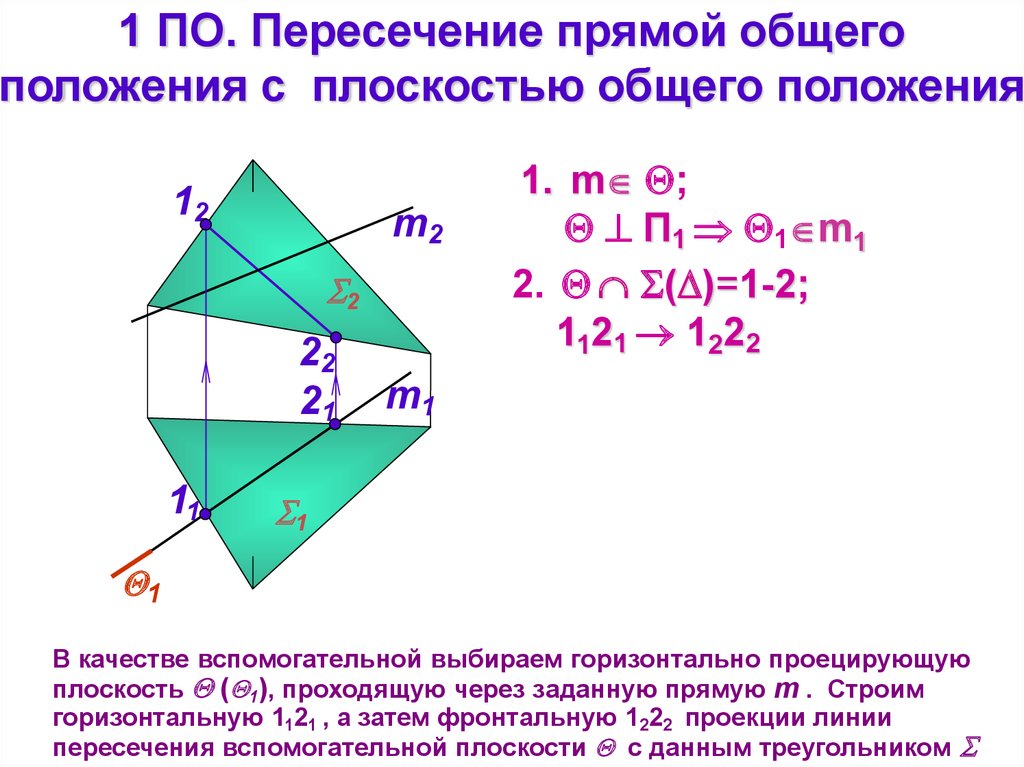
1 ПО. Пересечение прямой общегоположения с плоскостью общего положения
12
m2
2
22
21
11
1. m ;
П1 1 m1
2. ( )=1-2;
1121 1222
m1
1
1
В качестве вспомогательной выбираем горизонтально проецирующую
плоскость ( 1), проходящую через заданную прямую m . Строим
горизонтальную 1121 , а затем фронтальную 1222 проекции линии
пересечения вспомогательной плоскости с данным треугольником
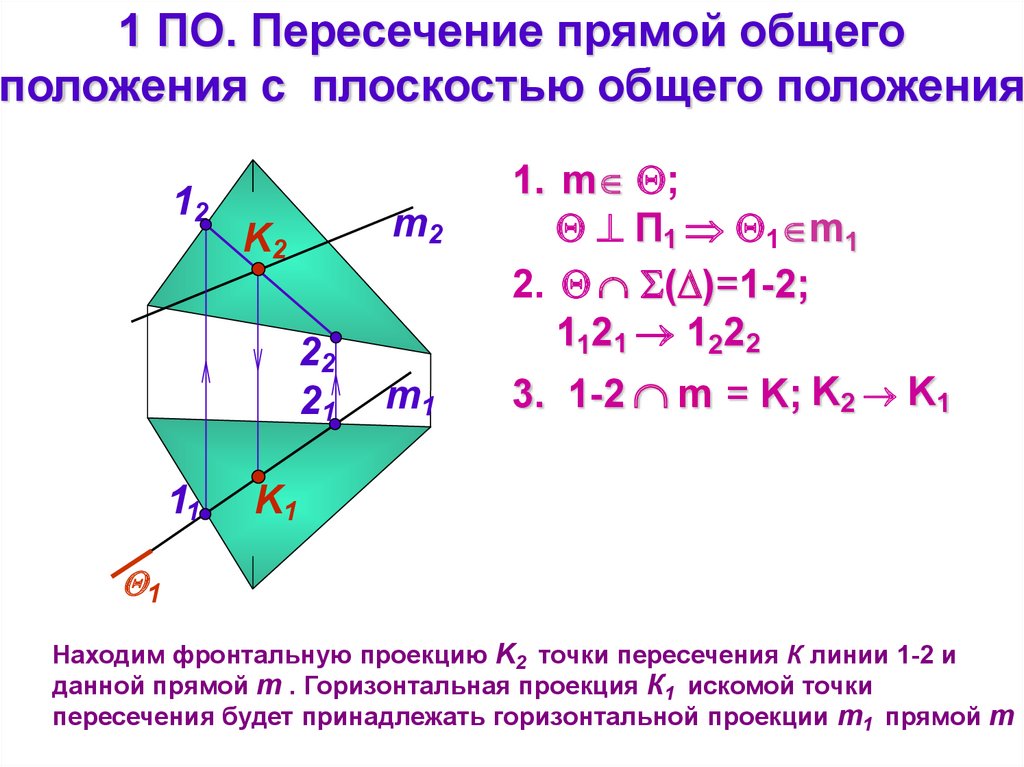
14.
1 ПО. Пересечение прямой общегоположения с плоскостью общего положения
12
m2
K2
22
21
11
m1
1. m ;
П1 1 m1
2. ( )=1-2;
1121 1222
3. 1-2 m = K; K2 K1
K1
1
Находим фронтальную проекцию K2 точки пересечения К линии 1-2 и
данной прямой m . Горизонтальная проекция К1 искомой точки
пересечения будет принадлежать горизонтальной проекции m1 прямой m
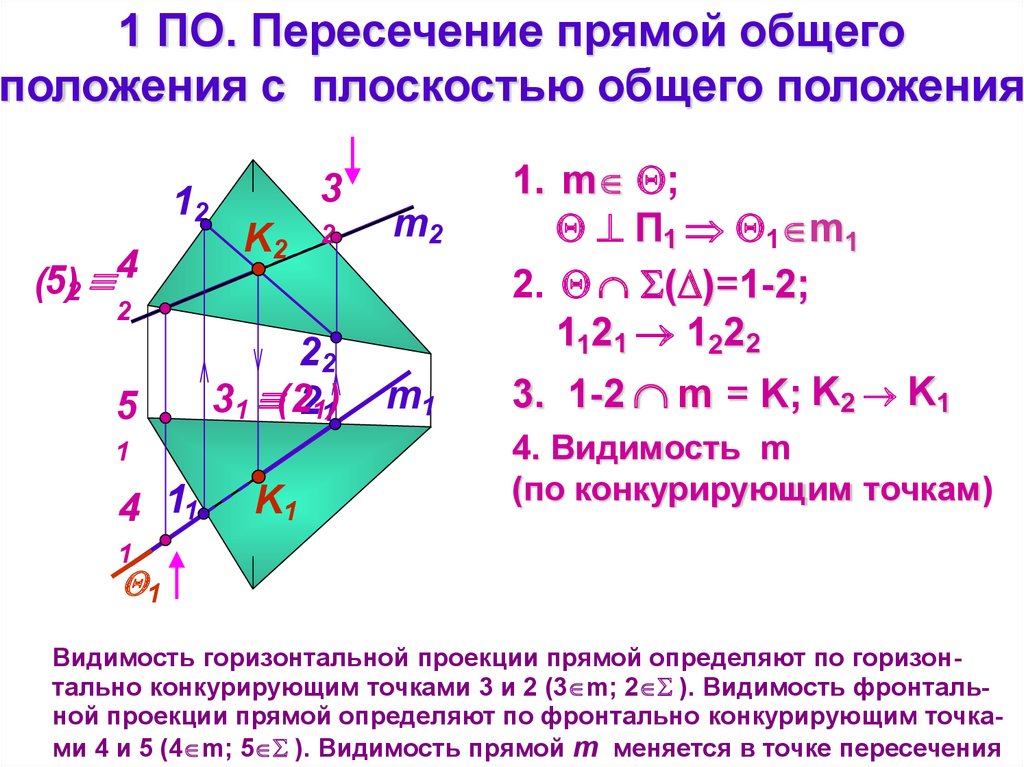
15.
1 ПО. Пересечение прямой общегоположения с плоскостью общего положения
12
4
5
( )2
3
2
m2
22
31 (2211)
m1
K2
2
5
1
4 11
K1
1. m ;
П1 1 m1
2. ( )=1-2;
1121 1222
3. 1-2 m = K; K2 K1
4. Видимость m
(по конкурирующим точкам)
1
1
Видимость горизонтальной проекции прямой определяют по горизонтально конкурирующим точками 3 и 2 (3 m; 2 ). Видимость фронтальной проекции прямой определяют по фронтально конкурирующим точками 4 и 5 (4 m; 5 ). Видимость прямой m меняется в точке пересечения




 drafting
drafting








