Similar presentations:
Основные позиционные задачи
1.
Основныепозиционные
задачи
2.
При решениипозиционных задач
выясняют
взаимное
расположение (позицию)
двух и большего числа
геометрических фигур
Понятие взаимное
расположение включает
также принадлежность
одной фигуры другой
При этом возможны случаи:
1) полной
принадлежности:
– точка принадлежит
прямой А∊ℓ;
– прямая принадлежит
плоскости ℓ∊Ф;
- точка принадлежит
плоскости А∊Ф
2) пересечения:
– двух плоскостей ∑∩θ
– прямой с плоскостью,
поверхностью ℓ∩∑
– плоскости с поверхностью;
– двух поверхностей;
3. Две геометрические фигуры, пересекаясь, дают общий элемент:
Прямая с прямой –Плоскость с поверхностью –
точку (а∩b⇒К)
Прямая с плоскостью
– точку (a∩∑⇒К)
Прямая с
поверхностью – одну
или несколько точек
(a∩∑⇒К, М…)
Плоскость с
плоскостью – прямую
линию (∑∩θ⇒m)
плоскую кривую или
плоскую ломаную (∑∩Ф⇒a)
Поверхность с
поверхностью –
пространственную
кривую или несколько
пространственных
кривых, которые в свою
очередь, могут состоять
из плоских кривых или
плоских ломаных
(∑∩θ⇒m)
4.
1.Пересечение прямой с проецирующейплоскостью
П2
2
1
2
n
2
n 1
x
2
1 n
x х
х
n1
1П11
2
1
2
n
1
1
1
1
5.
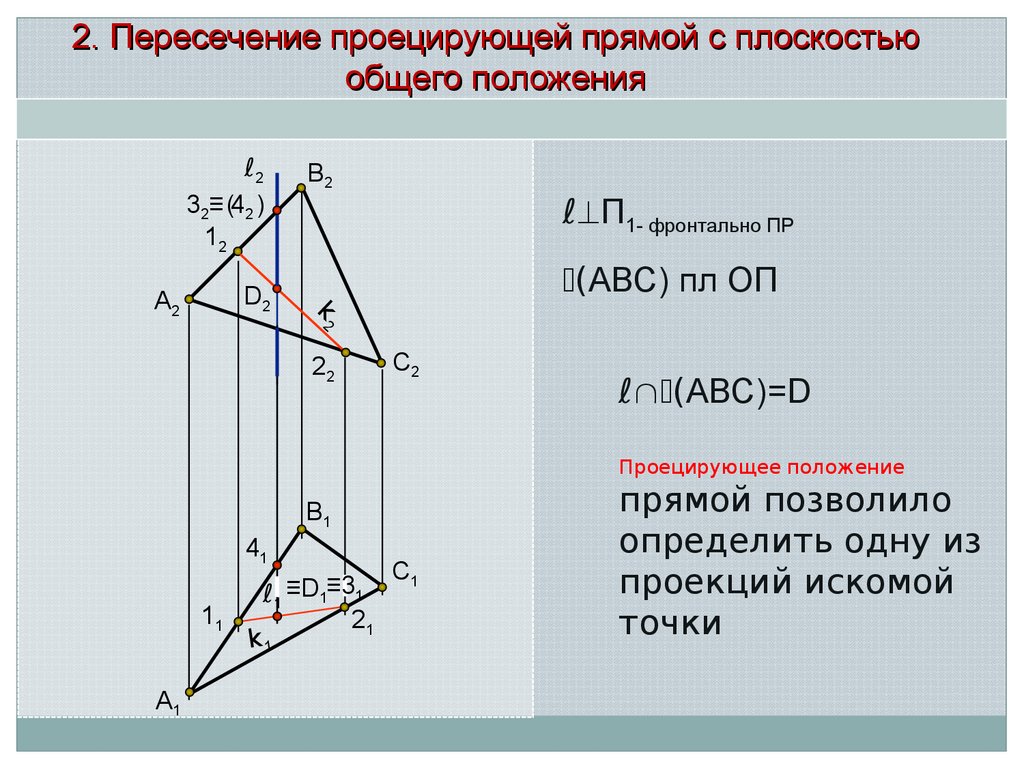
2. Пересечение проецирующей прямой с плоскостьюобщего положения
ℓ2
32≡ (42 )
12
В2
D2
k
А2
ℓ П1- фронтально ПР
(АВС) пл ОП
2
22
С2
ℓ (АВС)=D
Проецирующее положение
В1
41
11
А1
ℓ1 ≡D1≡31
21
k1
С1
прямой позволило
определить одну из
проекций искомой
точки
6.
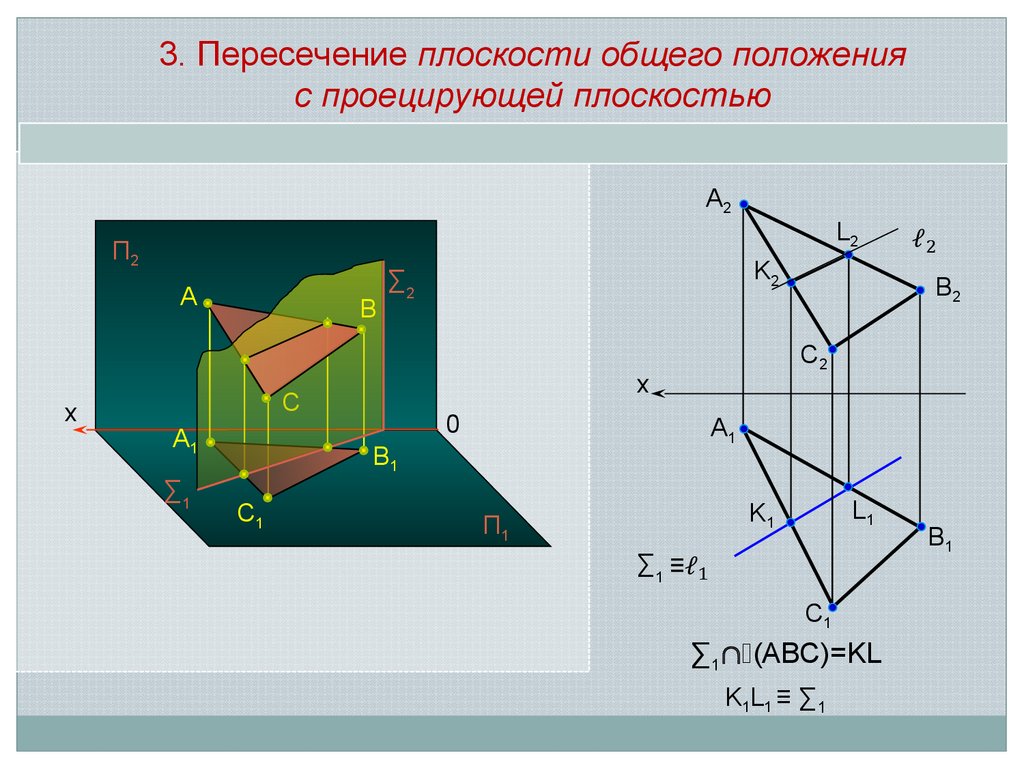
3. Пересечение плоскости общего положенияс проецирующей плоскостью
А2
L2
П2
A
x
B
∑1
0
А1
B1
C1
В2
С2
x
C
A1
K2
∑2
L1
K1
П1
∑1
С1
∑1 (АВС)=KL
K1L1 ≡ ∑1
В1
7.
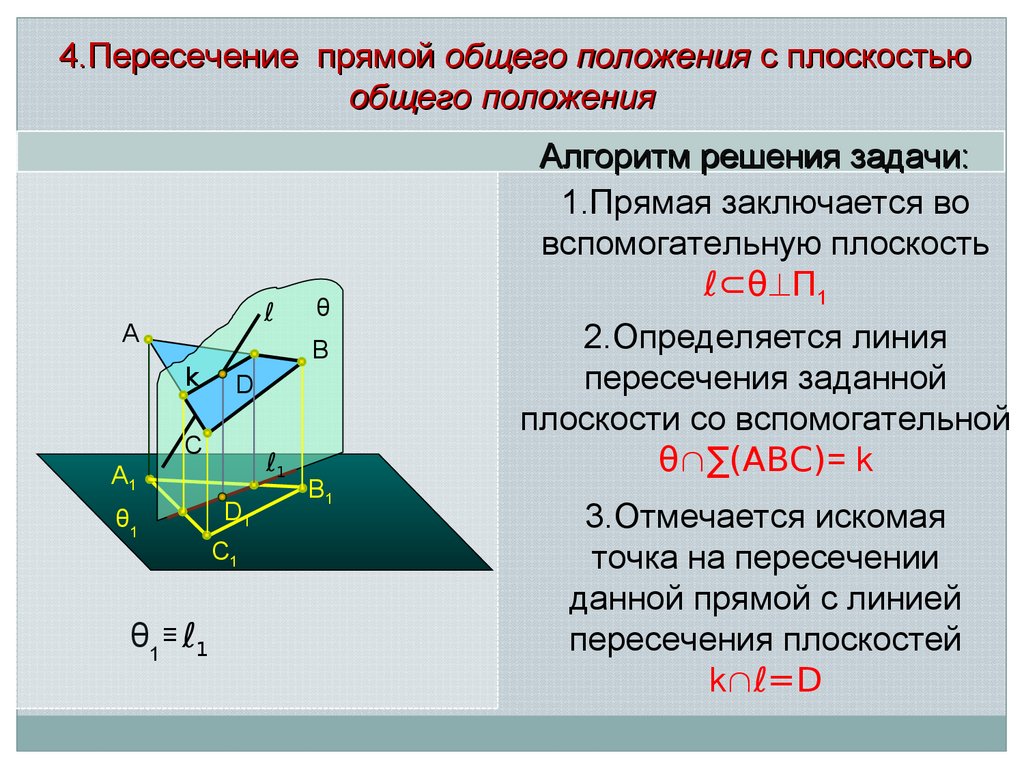
4.Пересечение прямой общего положения с плоскостьюобщего положения
ℓ
A
k
B
D
C
ℓ1
A1
θ1
θ1 ≡ ℓ1
θ
D1
C1
B1
Алгоритм решения задачи:
1.Прямая заключается во
вспомогательную плоскость
ℓ⊂θ П1
2.Определяется линия
пересечения заданной
плоскости со вспомогательной
θ ∑(АВС)= k
3.Отмечается искомая
точка на пересечении
данной прямой с линией
пересечения плоскостей
k ℓ=D
8.
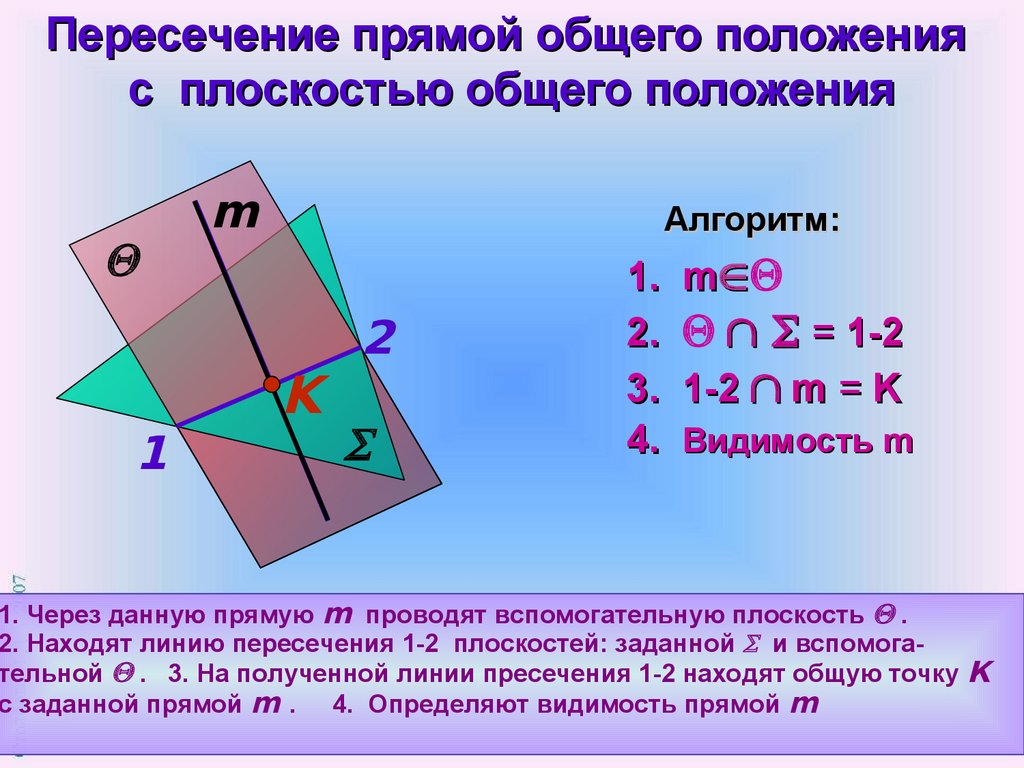
Пересечение прямой общего положенияс плоскостью общего положения
m
Алгоритм:
1
K
2
1.
2.
3.
4.
m
= 1-2
1-2 m = K
Видимость m
1. Через данную прямую m проводят вспомогательную плоскость .
2. Находят линию пересечения 1-2 плоскостей: заданной и вспомогательной . 3. На полученной линии пресечения 1-2 находят общую точку К
с заданной прямой m . 4. Определяют видимость прямой m
9.
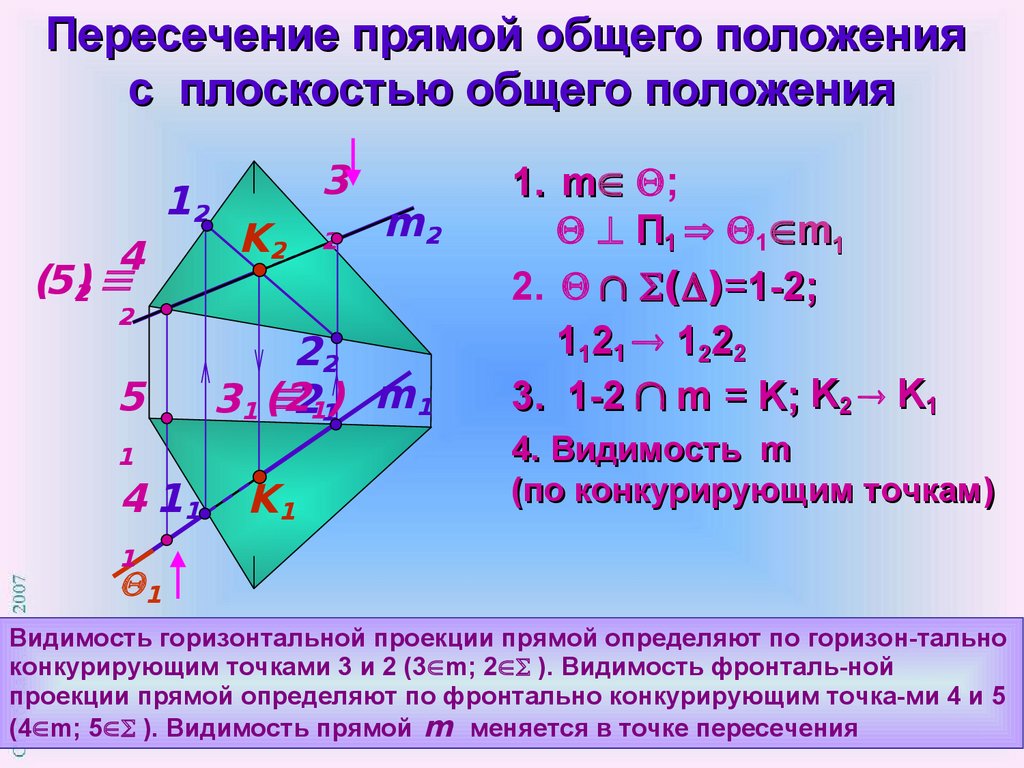
Пересечение прямой общего положенияс плоскостью общего положения
12
4
(5)2
2
5
3
K2
m2
22
31 ( 2211) m1
1
4 11
2
K1
1. m ;
П1 1 m1
2. ( )=1-2;
1121 1222
3. 1-2 m = K; K2 K1
4. Видимость m
(по конкурирующим точкам)
1
1
Видимость горизонтальной проекции прямой определяют по горизон-тально
конкурирующим точками 3 и 2 (3 m; 2 ). Видимость фронталь-ной
проекции прямой определяют по фронтально конкурирующим точка-ми 4 и 5
(4 m; 5 ). Видимость прямой m меняется в точке пересечения
10.
Способ вспомогательных секущихплоскостей
• Частный случай способа вспомогательных
секущих поверхностей
• Используется для решения позиционных
задач
• Секущие плоскости выбирают так, чтобы в
сечении получались графически простые
линии
• В качестве секущих удобно использовать
плоскости частного положения
(проецирующие или плоскости уровня)
11.
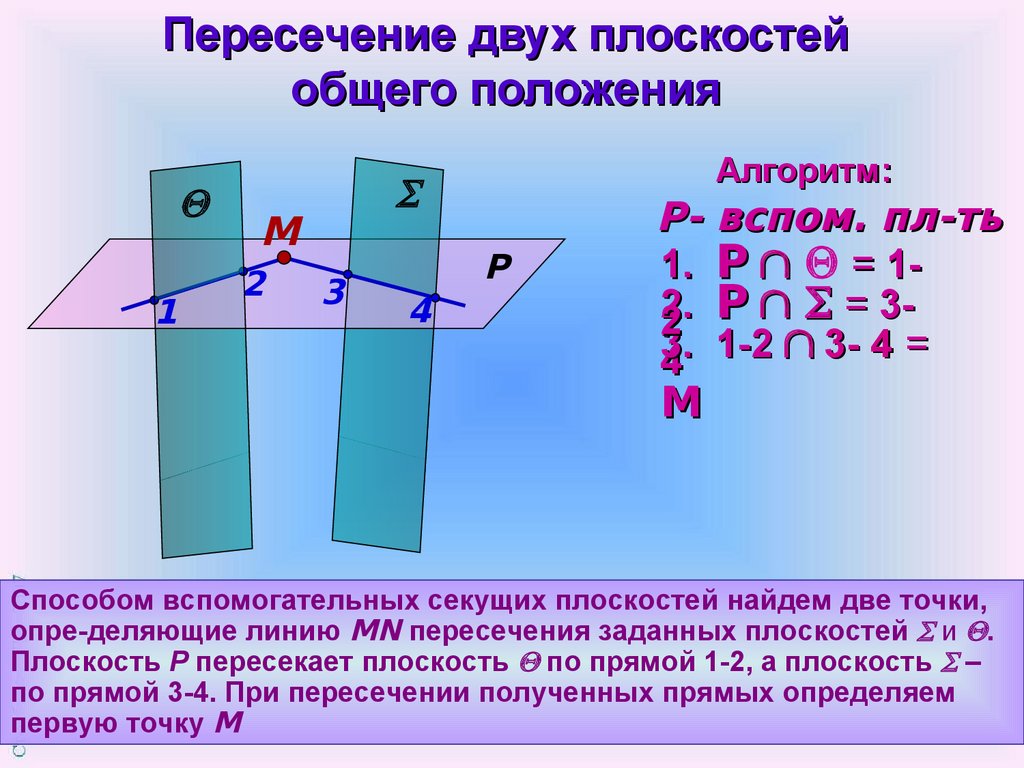
Пересечение двух плоскостейобщего положения
1
M
2
Алгоритм:
3
P
4
Р- вспом. пл-ть
1. P = 12.
2 P = 33.
4 1-2 3- 4 =
M
Способом вспомогательных секущих плоскостей найдем две точки,
опре-деляющие линию MN пересечения заданных плоскостей и .
Плоскость Р пересекает плоскость по прямой 1-2, а плоскость –
по прямой 3-4. При пересечении полученных прямых определяем
первую точку М
12.
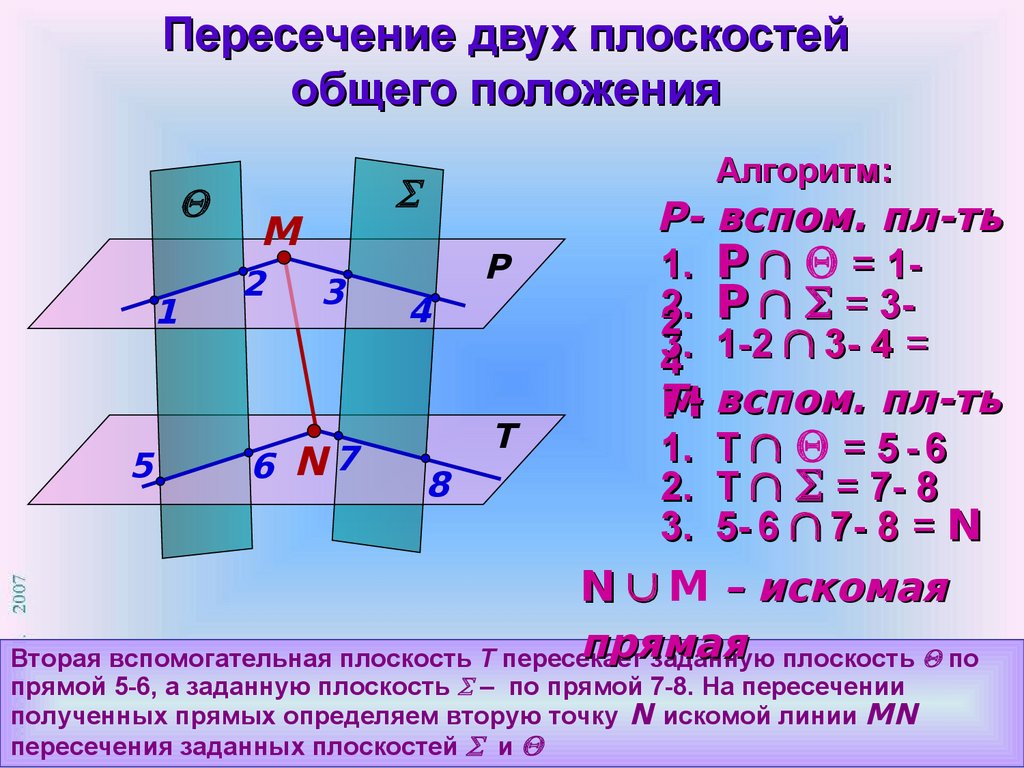
Пересечение двух плоскостейобщего положения
Алгоритм:
Р- вспом. пл-ть
1. P = 1P
2
3
2.
4
1
2 P = 33.
4 1-2 3- 4 =
ТM вспом. пл-ть
T
1. Т = 5 - 6
5
6 N7
8
2. Т = 7- 8
3. 5- 6 7- 8 = N
N M – искомая
прямая
Вторая вспомогательная плоскость Т пересекает
заданную плоскость по
M
прямой 5-6, а заданную плоскость – по прямой 7-8. На пересечении
полученных прямых определяем вторую точку N искомой линии MN
пересечения заданных плоскостей и
13.
Пересечение двух плоскостейобщего положения
Р2 12
K2
E2
M2 3 2 4 2
В2
22
1.
2.
2
3.
3.
4
F2
С2
С
А2
Алгоритм:
F1
Р- вспом.
P ( АВС)=1пл-ть
P (KF FE)=31-2 3- 4 =
M
1
А1
11
21
В
M1 3 1
K1
41
E1
1
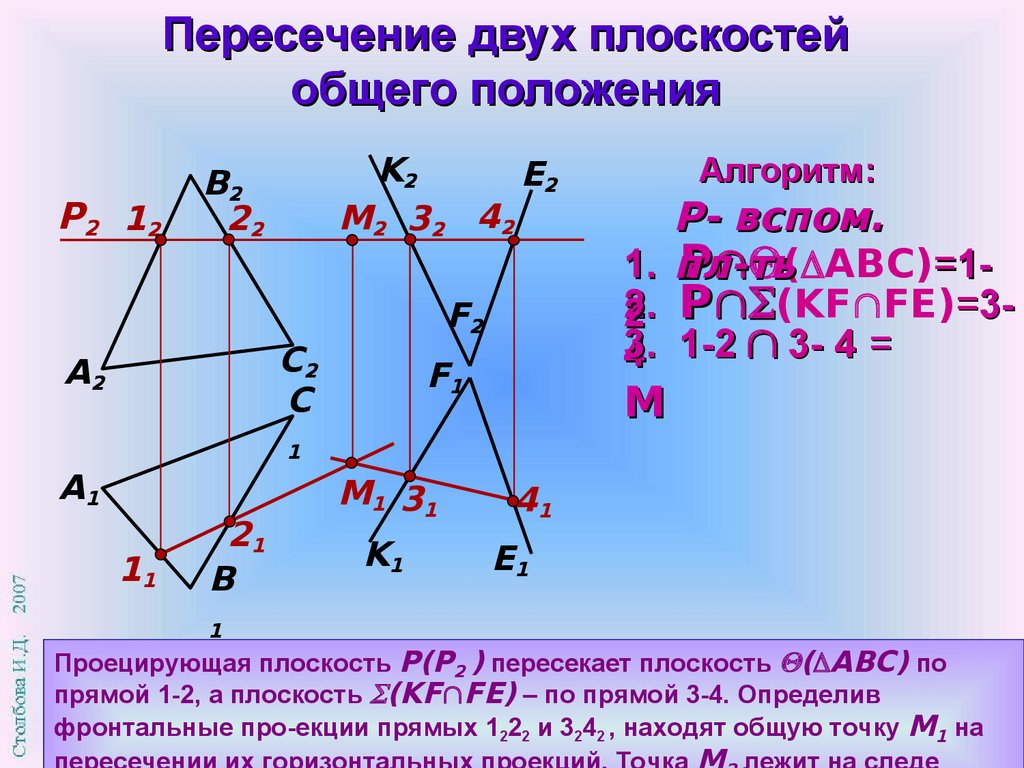
Проецирующая плоскость Р(Р2 ) пересекает плоскость ( АВС) по
прямой 1-2, а плоскость (KF FE) – по прямой 3-4. Определив
фронтальные про-екции прямых 1222 и 3242 , находят общую точку М1 на
14.
Пересечение двух плоскостейобщего положения
В2
22
62
K2
E2
M2 3 2 4 2
72 82
N2 F
Алгоритм:
Р- вспом. пл-ть
1. P ( АВС)=12.
2 P (KF FE)=32
3.
1-2 3- 4 =
4
С
2
А2
F1
С
N1
MТ- вспом. пл-ть
1. Т ( АВС)=5 61 1
71 81
А1
2.
M1 3 1
41
6 Т (KF FE)= 73.
51
3. 5- 6 7- 8 = N
21
8
K1
E1
11 В
N M – искомая
1
прямая
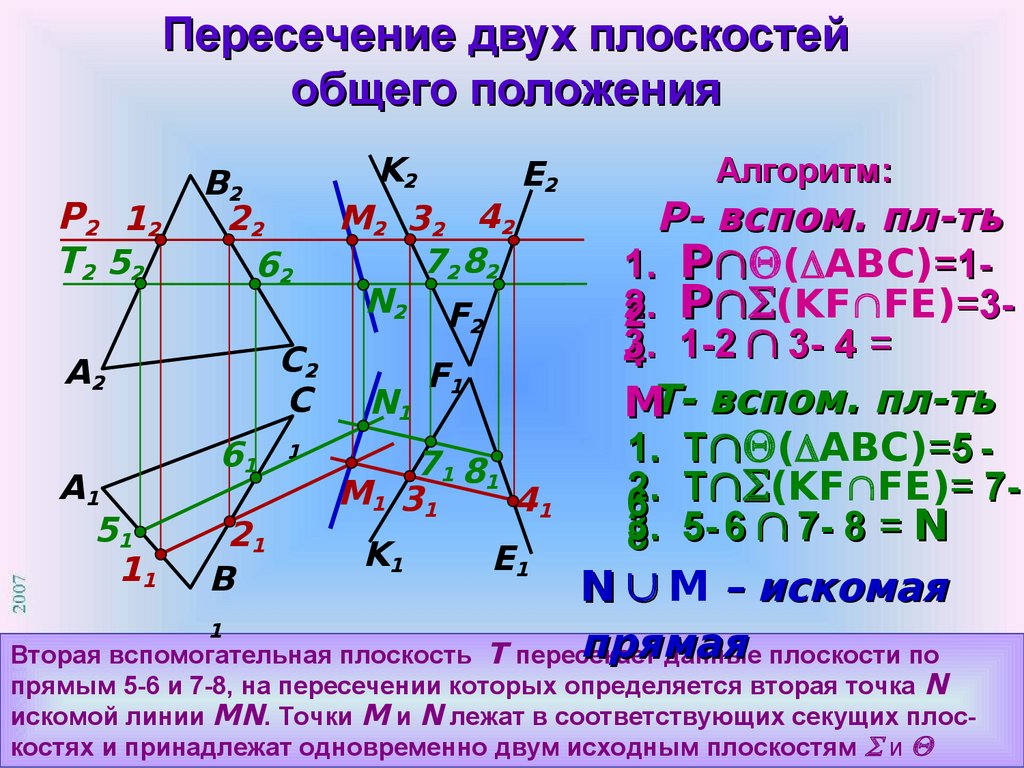
Вторая вспомогательная плоскость Т пересекает
данные плоскости по
Р2 12
T2 52
прямым 5-6 и 7-8, на пересечении которых определяется вторая точка N
искомой линии MN. Точки М и N лежат в соответствующих секущих плоскостях и принадлежат одновременно двум исходным плоскостям и
15.
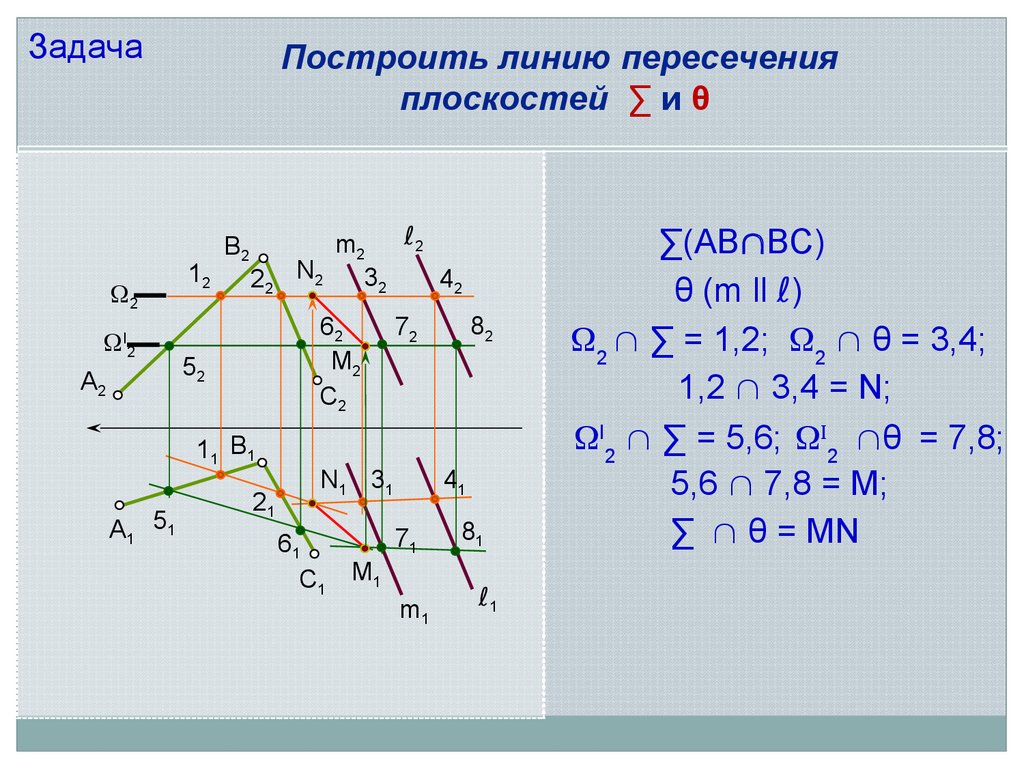
ЗадачаПостроить линию пересечения
плоскостей ∑ и θ
12
2
I2
В2
22
62
M2
С2
52
А2
11 В1
А1
51
ℓ2
m2
N2
32
42
21
N1 31
61
С1
82
72
41
71
M1
m1
81
ℓ1
∑(AB BC)
θ (m ll ℓ)
2 ∑ = 1,2; 2 θ = 3,4;
1,2 3,4 = N;
I2 ∑ = 5,6; 2 θ = 7,8;
5,6 7,8 = M;
∑ θ = MN
16.
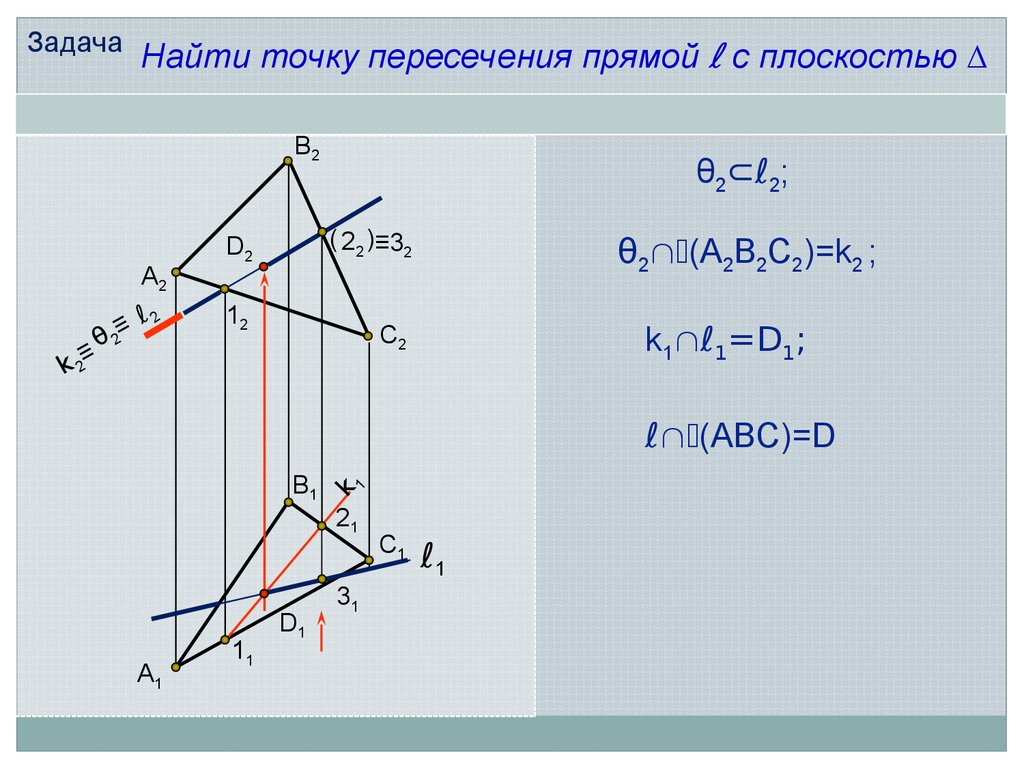
ЗадачаНайти точку пересечения прямой ℓ с плоскостью ∆
В2
А2
( 22 )≡32
D2
12
θ2 (А2В2С2)=k2 ;
k1 ℓ1=D1;
С2
В1
А1
11
D1
1
ℓ (ABC)=D
k
k 2≡
ℓ2
≡
θ2
θ2⊂ℓ2;
21
31
С1
ℓ1
17.
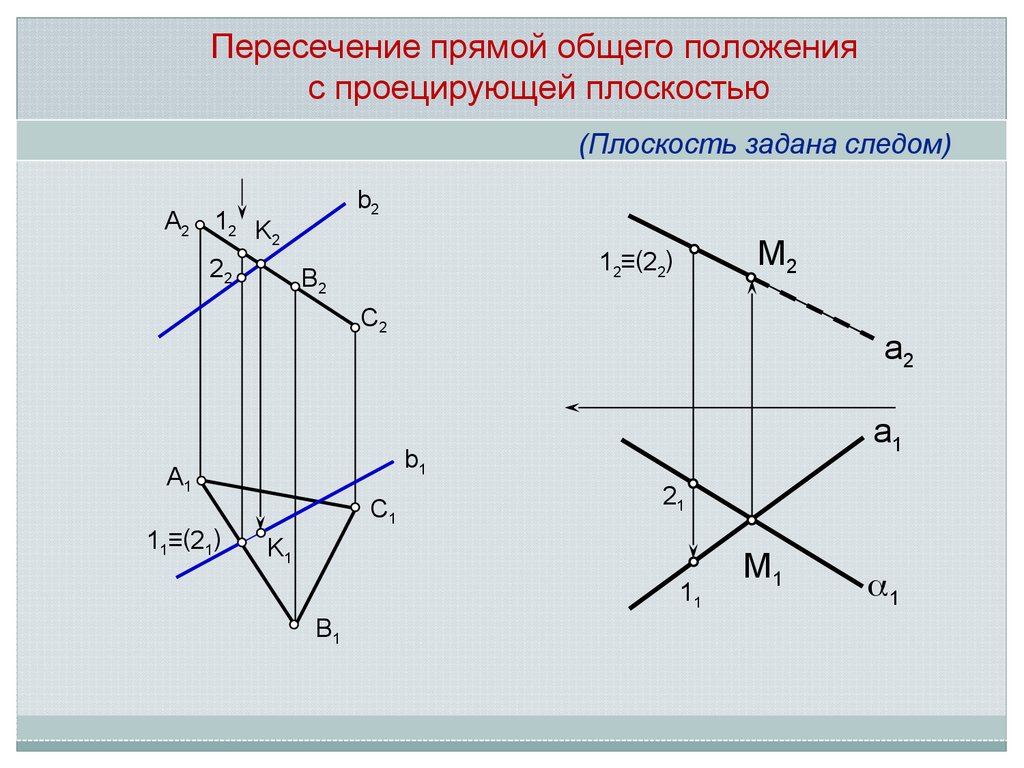
Пересечение прямой общего положенияс проецирующей плоскостью
(Плоскость задана следом)
A2 12 K
2
22
B2
b2
M2
12≡(22)
C2
a1
b1
A1
11≡(21)
a2
C1
21
K1
11
B1
M1
1



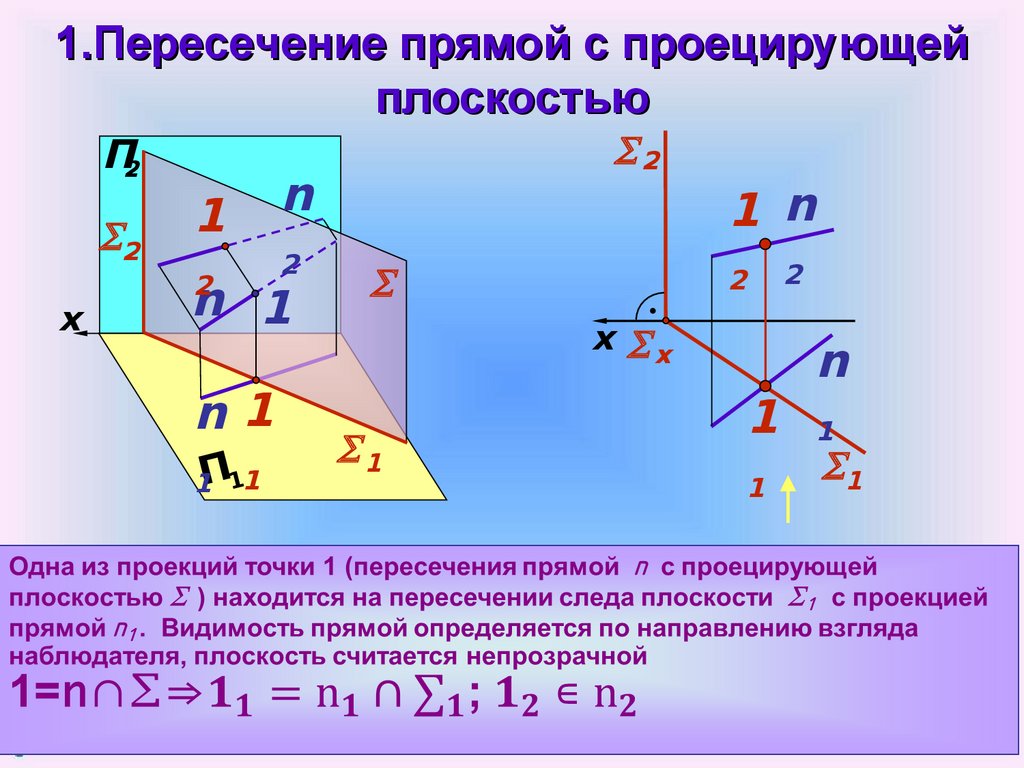


 drafting
drafting








