Инженерная и компьютерная графика

1. Инженерная и компьютерная графика

2. Позиционные задачи

Задачи, решаемые в начертательной геометрии
делятся на метрические и позиционные.
В метрических задачах определяются различные геометрические величины: длины отрезков, углы, площади, объемы и т.п.
Геометрические задачи, связанные с определением относительного расположения фигур в
пространстве, называются позиционными.

3. Пересечение поверхности плоскостью

Линия, которая получается от пересечения
поверхности с плоскостью, является плоской
кривой, лежащей в секущей плоскости.
Чтобы построить проекции этой линии на
чертеже, находят проекции её отдельных
точек и, соединяя одноимённые проекции
точек плавными кривыми (по лекалу),
получают проекции искомой линии.

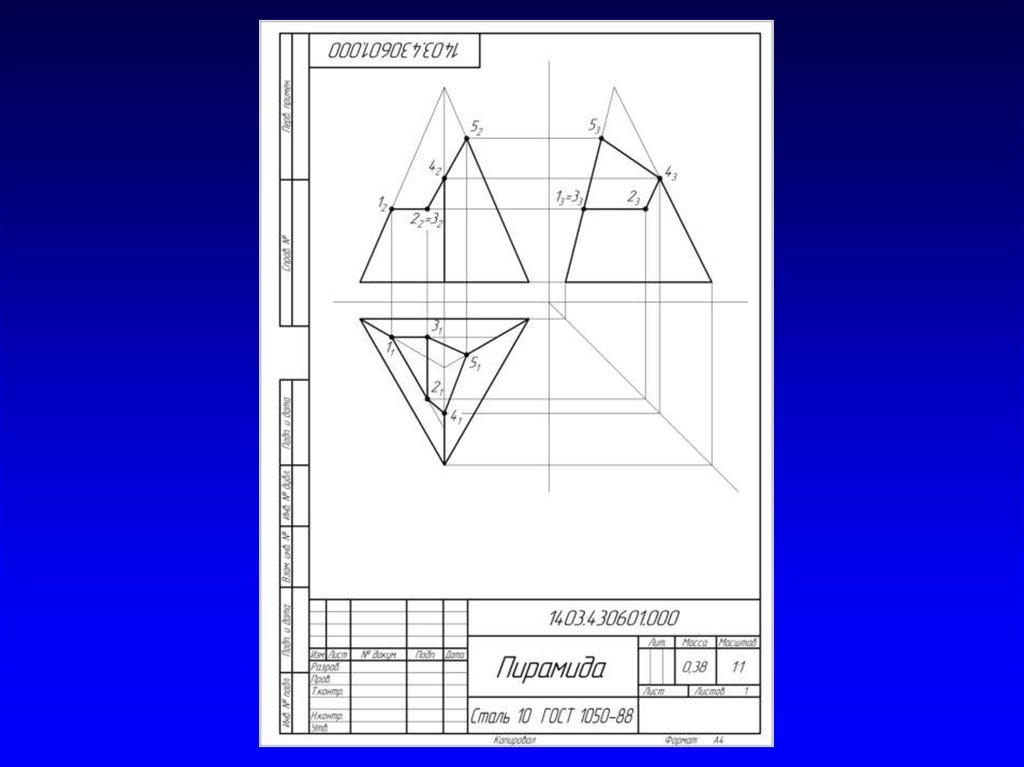
4. Пересечение гранной поверхности плоскостью

5.

6.

7.

8.

9.

10.

11.

G2=J2
Построение линии
пересечения сферы с
проецирующей плоскостью
Σ2
В2
E2=F2
С2=D2
А2
C1 E1
x12
G1
А1
В1
J1
D1 F
1

12. Сечения конуса вращения плоскостью

Пересекая прямой круговой конус секущими плоскостями
можно получить в сечении различные кривые второго
порядка.
Две совпавшие прямые
Гипербола
Парабола
Эллипс
Окружность

13.

14.

15.

16.

17.

18. Пересечение линии с поверхностью

Построение точек пересечения линии, с какой –
либо поверхностью выполняется с помощью
вспомогательной поверхности.
Алгоритм решения:
1) заданную линию заключают во вспомогательную
поверхность .
2) строим линию пересечения вспомогательной
поверхности с заданной поверхностью Ф.
3) построенная линия m и заданная линия n лежат
на поверхности , а значит, будут пересекаться.
Точка их пересечения будет являться искомой
точкой пересечения линии n с поверхностью Ф.

19. Пересечение линии с поверхностью

В качестве вспомогательной
поверхности обычно используют:
плоскость (если заданная линия
является прямой или плоской кривой);
проецирующая цилиндрическая
поверхность (если заданная линия
является пространственной кривой).

20. Общая схема решения задачи на построение точек пересечения линии с поверхностью

Θ
n
K
m
Алгоритм решения:
1. Θ ( Θ ⋐ n )
2. m = Θ ∩ Φ
3. K = m ∩ n
Φ

21.

G2=J2
Построение точек
пересечения прямой n
со сферой Φ
K2
В2
E2=F2
С2=D2
А2
L2
C1 E1
x12
Алгоритм решения:
1. Σ ( Σ ⋐ n )
2. m = Σ ∩ Φ
3. K = m ∩ n
n2 = Σ2 = m2
G1
L1
А1
В1
J1
D1 F
1
K1
n1

22. Взаимное пересечение поверхностей

В начертательной геометрии линию
пересечения двух поверхностей находят с
помощью приёма, который называется
способом вспомогательных секущих
поверхностей (способ поверхностей
посредников)

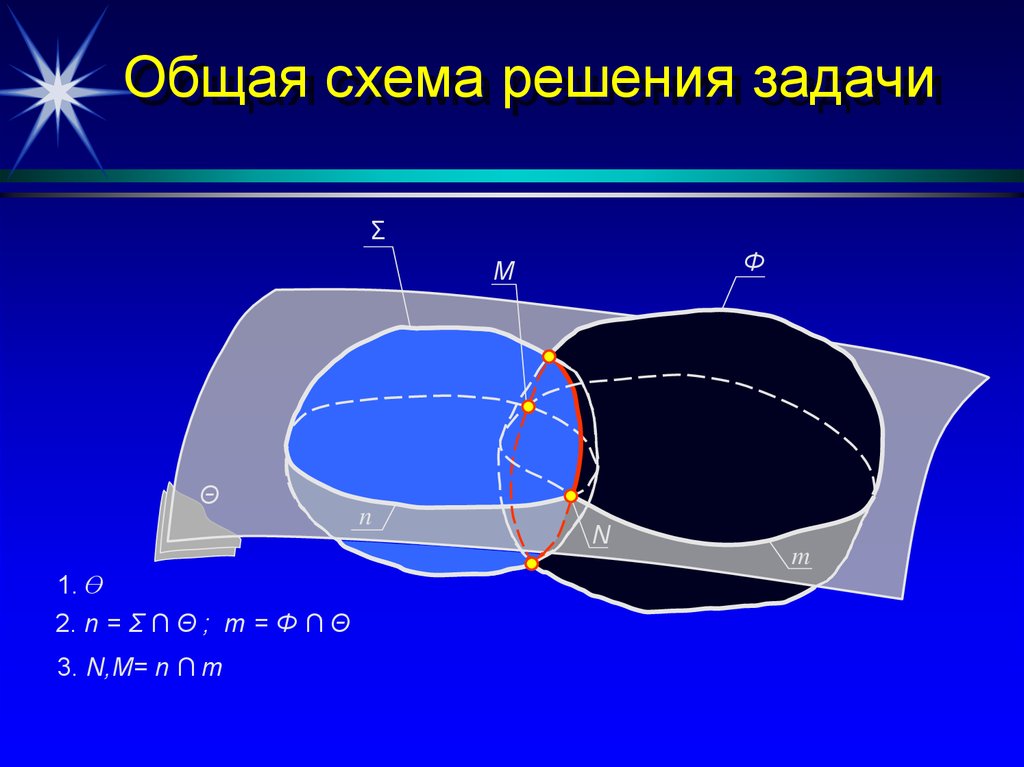
23. Общая схема решения задачи

Σ
Φ
M
Θ
1. Ө
2. n = Σ ∩ Θ ; m = Φ ∩ Θ
3. N,M= n ∩ m
n
N
m

24. Общая схема решения задачи

1. Обе заданные поверхности пересекаются
вспомогательной поверхностью Θ. В качестве
вспомогательной чаще всего используются
плоскости, сферы или проецирующие
цилиндрические поверхности.
2. Строятся линии пересечения вспомогательной
поверхности Θ с каждой из заданных поверхностей.
3. Построенные линии m и n лежат на одной и той
же поверхности Θ, а значит, пересекаются в точках
М и N. Эти точки будут общими для трёх
поверхностей: F, , Θ, а значит, будут
принадлежать искомой линии пересечения заданных
поверхностей.

25. Общая схема решения задачи

Выбор и расположение секущих вспомогательных
поверхностей определяется следующими
обстоятельствами:
1) желательно, чтобы линии пересечения
вспомогательной поверхности с заданными были
графически простыми линиями;
2) и чтобы они (эти линии) проецировались на
какую – либо плоскость проекций без искажения.

26. Метод вспомогательных секущих плоскостей

Этот способ применяют для построения точек
линии пересечения двух поверхностей тогда,
когда вспомогательные плоскости,
рассекающие данные поверхности, дают в
пересечении с каждой из них графически
простые линии, такие как прямые и
окружности.
Чаще всего в качестве вспомогательных
используются проецирующие плоскости и
плоскости уровня.

27. Метод вспомогательных секущих плоскостей

Среди точек линии пересечения есть такие, которые
выделяются своим особым положением среди
остальных точек (самая верхняя и самая нижняя,
крайняя правая и левая, точки – границы видимости
и т.д.). Такие точки называются особыми или
опорными, и строить их нужно в первую очередь.
Обычно эти точки находятся сразу без применения
дополнительных построений. Остальные точки
линии пересечения называются промежуточными,
и все они строятся с помощью одного и того же
приёма.

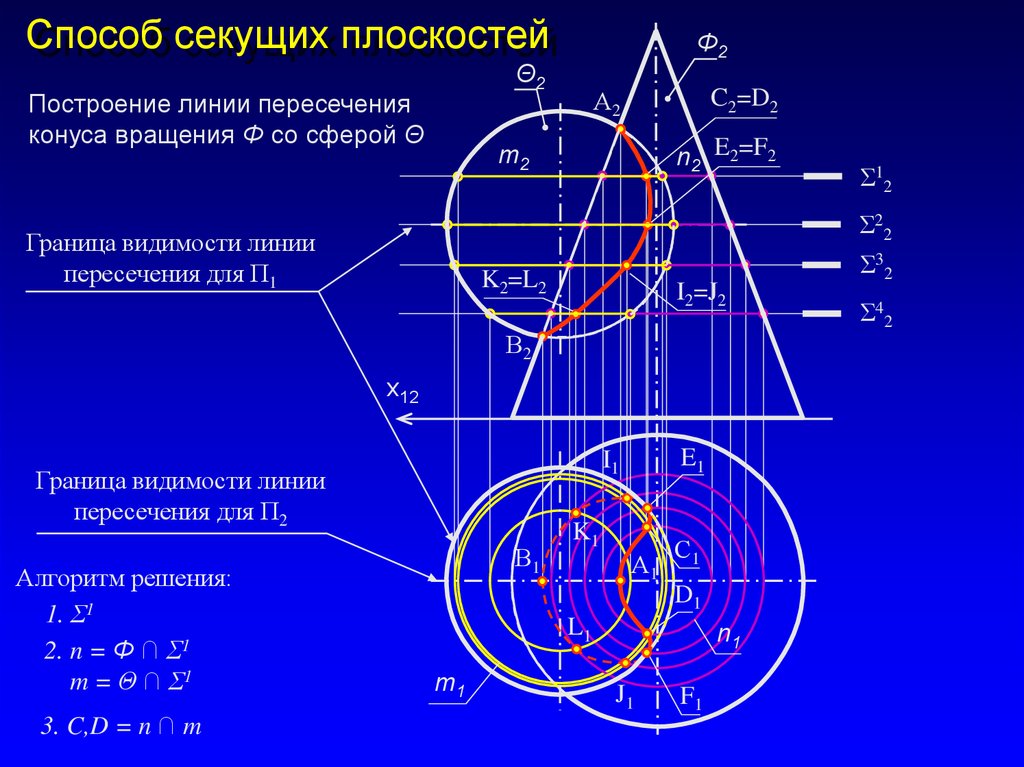
28. Способ секущих плоскостей

Φ2
Θ2
Построение линии пересечения
конуса вращения Φ со сферой Θ
А2
C2=D2
n2 E2=F2
m2
Σ22
Граница видимости линии
пересечения для П1
K2=L2
I2=J2
В2
x12
3. C,D = n ∩ m
E1
I1
Граница видимости линии
пересечения для П2
Алгоритм решения:
1. Σ1
2. n = Φ ∩ Σ1
m = Θ ∩ Σ1
Σ12
В1
K1
А1
С1
D1
L1
m1
n1
J1
F1
Σ32
Σ42

29.

Алгоритм решения:
Проводится вспомогательная горизонтальная
плоскость уровня.
Строятся окружности пересечения вспомогательной
плоскости со сферой и конусом. На фронтальную
плоскость проекций П2 эти окружности
проецируются в виде отрезков прямых, лежащих
внутри очерков сферы и конуса. На плоскость П1
окружности пересечения проецируются без
искажения.
На плоскости проекций П1 находятся
горизонтальные проекции точек пересечения
построенных окружностей. Фронтальные проекции
этих точек располагаются на фронтальной проекции
вспомогательной плоскости.
Для нахождения других точек линии пересечения
нужно ещё провести вспомогательные плоскости.