Решение позиционных задач

1. Тема 3. Решение позиционных задач

1. Пересечение геометрических
объектов, один их которых занимает
проецирующее положение.
2. Пересечение геометрических объектов
общего положения.
1

2. 2. Пересечение геометрических объектов общего положения

2.1. Общий алгоритм способа
вспомогательных секущих поверхностей.
2.2. Способ вспомогательных секущих
плоскостей.
2.3. Способ вспомогательных секущих сфер.
2.4. Теорема Монжа.
2

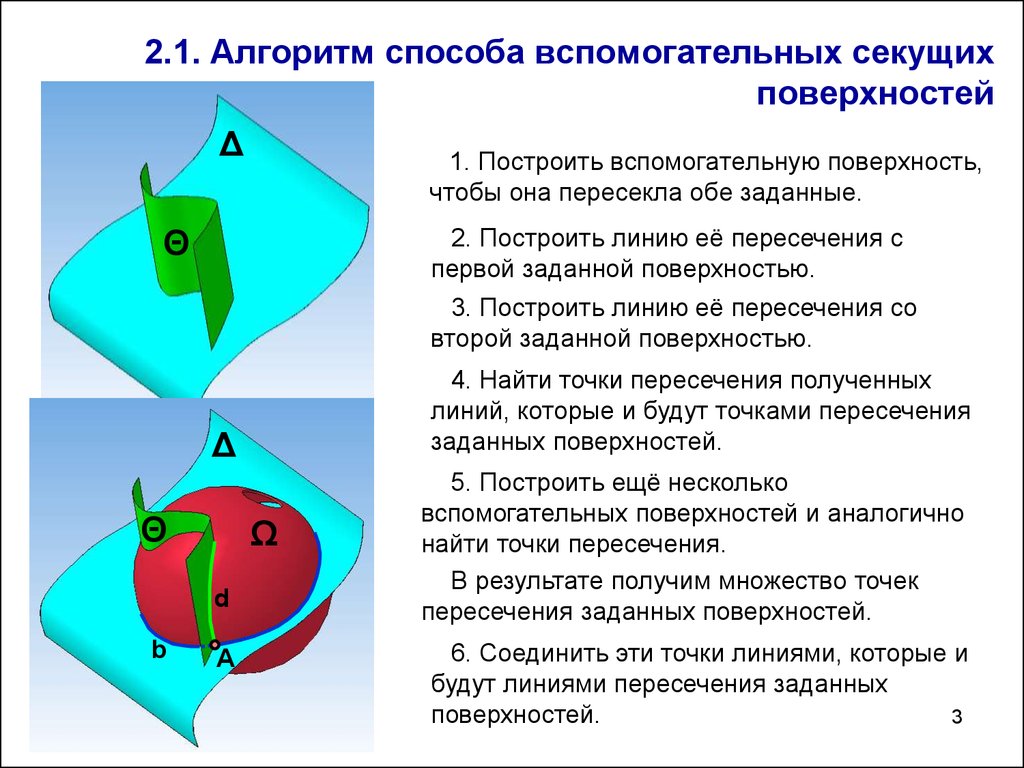
3. 2.1. Алгоритм способа вспомогательных секущих поверхностей

Δ
1. Построить вспомогательную поверхность,
чтобы она пересекла обе заданные.
2. Построить линию её пересечения с
первой заданной поверхностью.
Θ
3. Построить линию её пересечения со
второй заданной поверхностью.
4. Найти точки пересечения полученных
линий, которые и будут точками пересечения
заданных поверхностей.
Δ
Θ
Ω
d
b
A
5. Построить ещё несколько
вспомогательных поверхностей и аналогично
найти точки пересечения.
В результате получим множество точек
пересечения заданных поверхностей.
6. Соединить эти точки линиями, которые и
будут линиями пересечения заданных
поверхностей.
3

4.

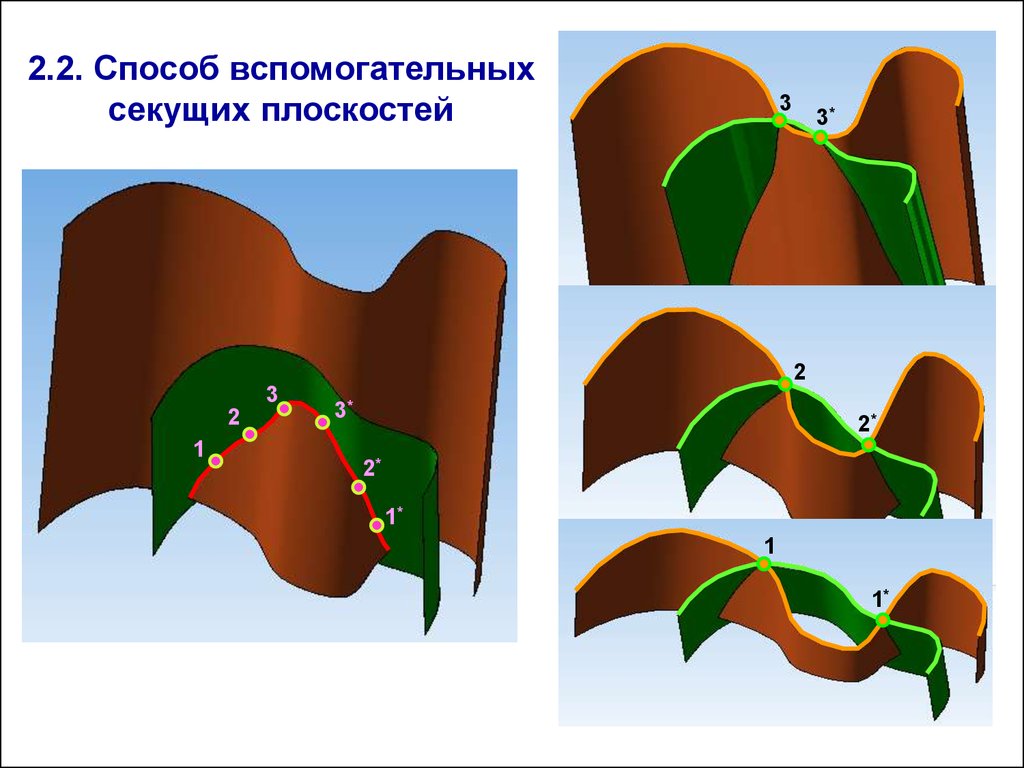
2.2. Способ вспомогательных
секущих плоскостей
3
3*
2
3
2
1
3*
2*
2*
1*
1
1*

5. Построение линии пересечения двух конусов

Θ2
12
R
r
42=(52)
22=(32)
31
51
11
41
21
5

6.

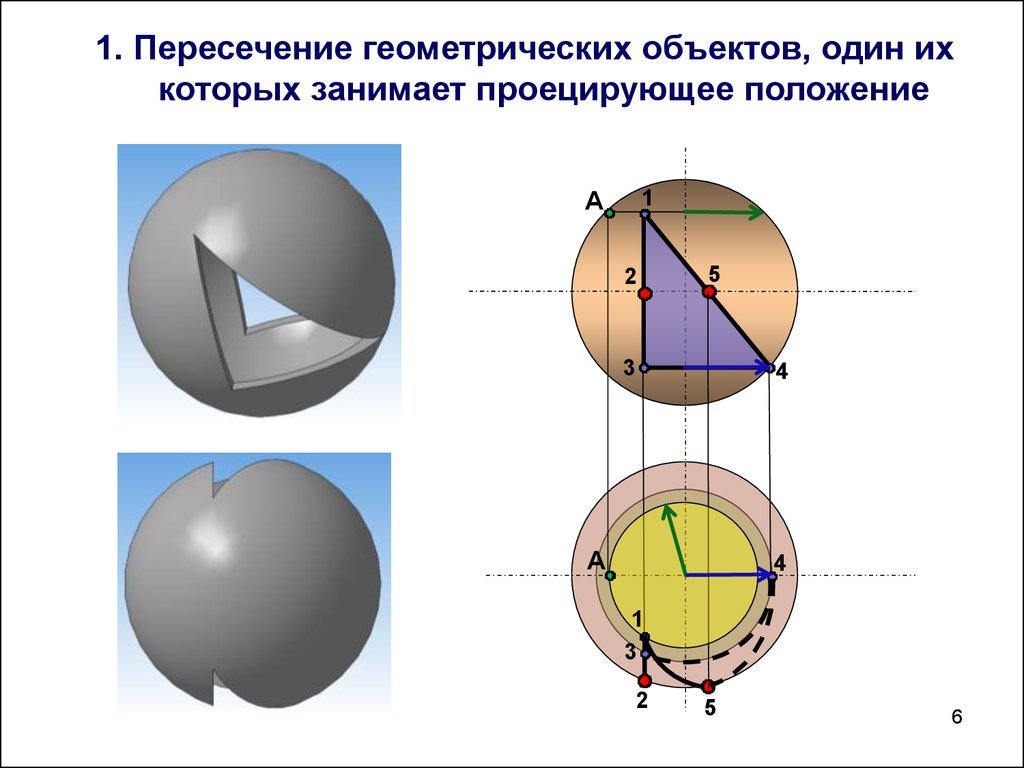
1. Пересечение геометрических объектов, один их
которых занимает проецирующее положение
1
A
2
5
3
4
A
4
1
3
2
5
6

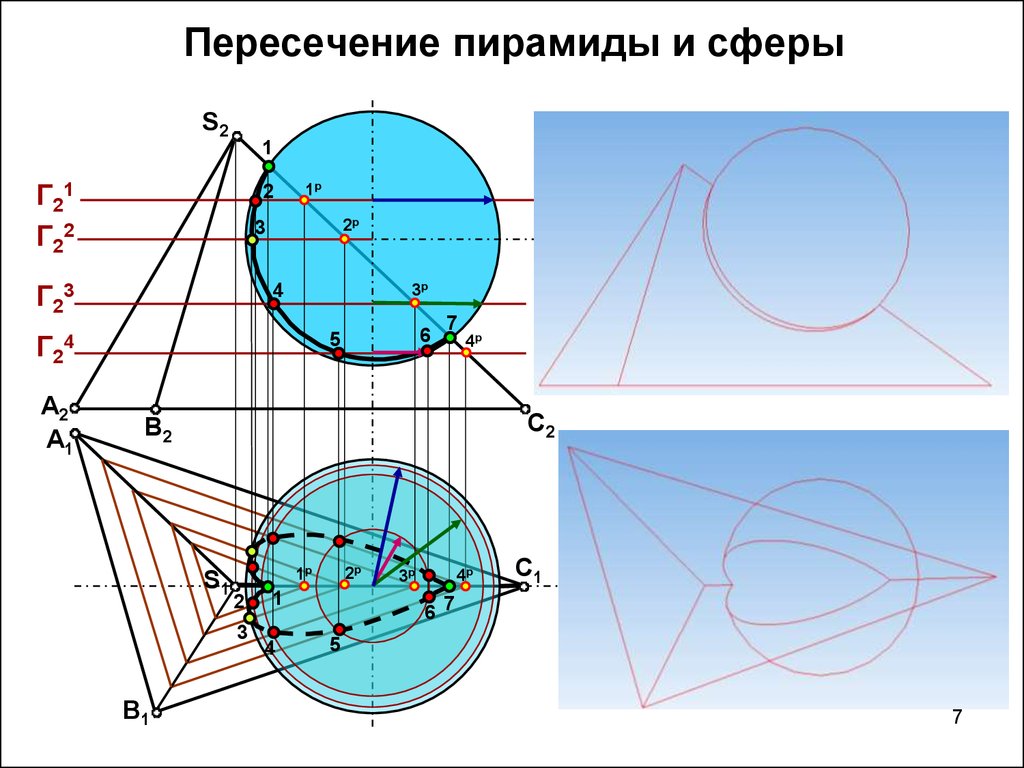
7. Пересечение пирамиды и сферы

S2
1
Г21
Г22
2
1р
2р
3
Г23
3р
4
Г24
А2
А1
6
5
7
4р
С2
В2
S1
2
3
В1
2р
1р
1
4
4р
3р
С1
67
5
7

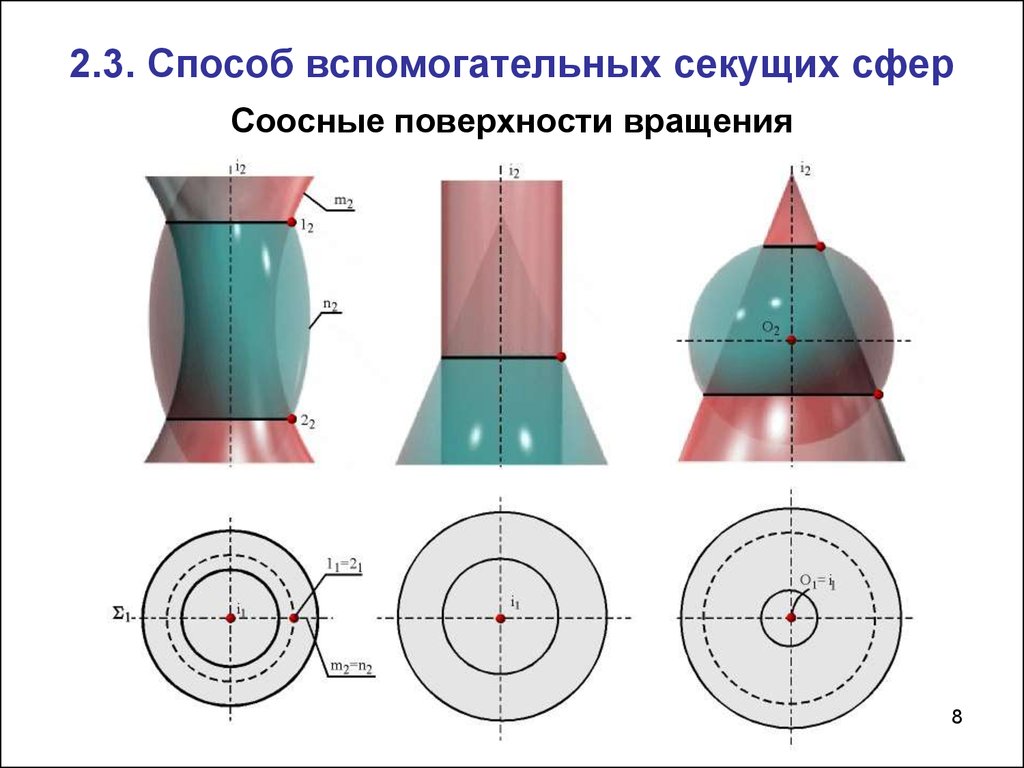
8. Соосные поверхности вращения

2.3. Способ вспомогательных секущих сфер
Соосные поверхности вращения
8

9. Пересечение сферы поверхностями вращения

Линия пересечения поверхностей вращения сферой - окружность
Условия применимости способа секущих концентрических сфер:
1. Обе пересекающиеся поверхности должны быть поверхностями
вращения.
2. Их оси должны быть параллельны одной из плоскостей проекций.
3. Оси заданных поверхностей должны пересекаться.
9

10. Применение способа концентрических сфер

S2
4
3
О2
1
S1
1=4
2

11. 2.4. Теорема Монжа

Если две поверхности второго порядка
описаны около третьей поверхности
(или вписаны в неё), то линия их
пересечения распадается на две
кривые второго порядка (эллипс,
окружность, гиперболу, параболу).
Причём плоскости этих кривых
проходят через прямую, соединяющую
точки пересечения линии касания.

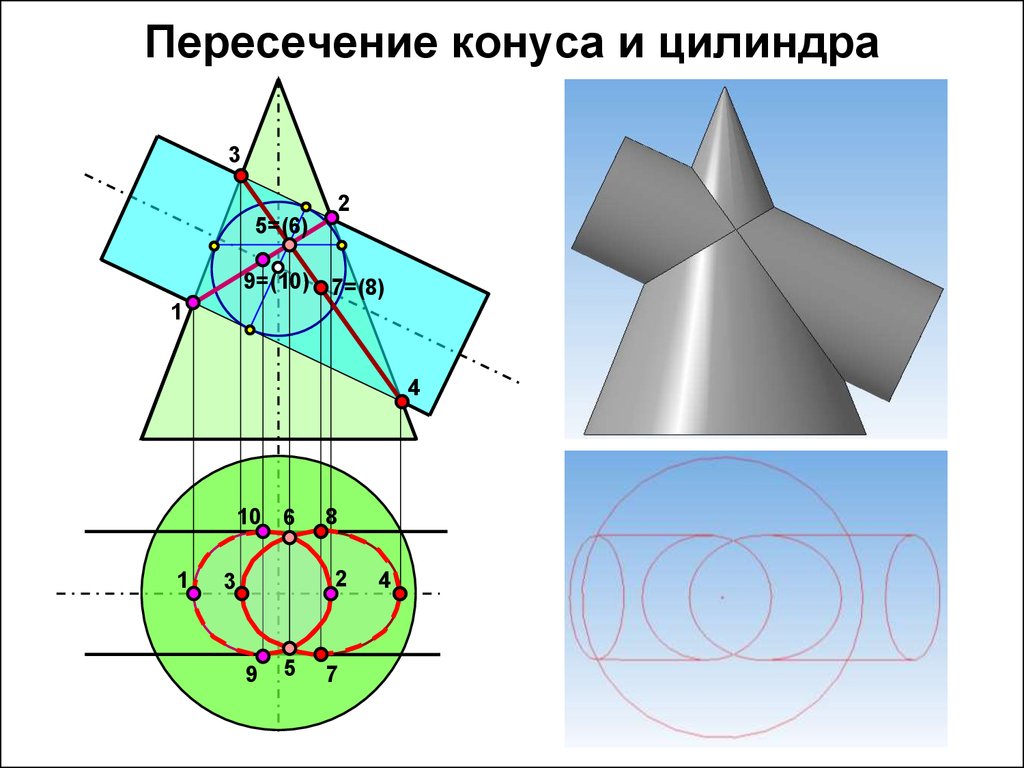
12. Пересечение конуса и цилиндра

3
2
5=(6)
9=(10) 7=(8)
1
4
10 6
1
8
2
3
9
5
7
4