Similar presentations:
Пересечение поверхности с плоскостью
1.
Лекция 5Уральский федеральный университет
имени первого Президента России Б.Н. Ельцина
Кафедра “Инженерная графика”
Дисциплина «Инженерная и компьютерная графика»
Раздел «Начертательная геометрия»
Тема 5
Пересечение
поверхности с плоскостью
Лектор: Стриганова
Лариса Юрьевна, доцент, к.п.н.
2. Цель и задачи изучения темы
• Определить способ заключения прямойлинии в плоскость
• Выявить характер возможных геометрических
фигур при пересечении поверхности и
плоскости
• Определить способ нахождения натуральной
величины фигуры сечения поверхности
плоскостью
Лекция 5. Пересечение
поверхности с плоскостью
2
3. В результате изучения темы Вы будете знать:
• Сущность способа заключения прямой линии вплоскость
• Способ вспомогательных секущих плоскостей для
построения фигур сечения поверхности
• Способ преобразования чертежа для определения
натуральной величины фигуры сечения
В результате изучения темы Вы будете уметь:
• Строить проекции сечения поверхности плоскостью
• Определять натуральную величину фигуры сечения
Лекция 5. Пересечение
поверхности с плоскостью
3
4. Пересечение прямой и поверхности
απ2N2
12 Ξ 22
В2
А2
32 Ξ 42
M2
В1
11
21
απ1
M1
N1
31
41
• При пересечении
прямой и
поверхности –
прямую заключают
в проецирующую
плоскость (απ2)
которая имеет
общие точки (MN)
с прямой линией и
поверхностью
А1
Лекция 6. Взаимное пересечение поверхностей.
Метод вспомогательных секущих плоскостей
4
5. Пересечение прямой линии с поверхностью конуса
12• Прямую
заключают во
вспомогательную
плоскостьm
• Находят общие
точки сечения,
прямой и
поверхности
αп2
βп2
R
22
R
m2
R
Лекция 6. Взаимное пересечение поверхностей. Метод
вспомогательных секущих плоскостей
21
m1
11
5
6. Пересечение прямой линии и сферы
Если прямая частногоположения
Если прямая общего
положения
Лекция 6. Взаимное пересечение поверхностей. Метод
вспомогательных секущих плоскостей
6
7. Построение фигуры сечения поверхности плоскостью
Нахождение натуральной величиныфигуры сечения
Лекция 6. Взаимное пересечение поверхностей. Метод
вспомогательных секущих плоскостей
7
8.
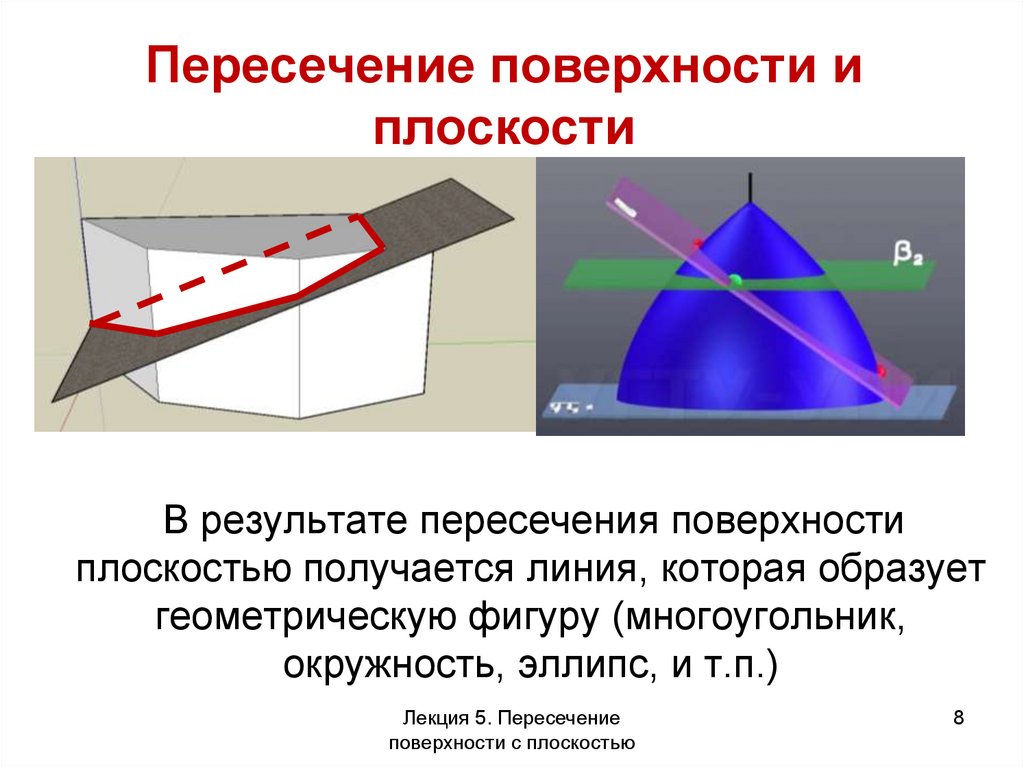
Пересечение поверхности иплоскости
В результате пересечения поверхности
плоскостью получается линия, которая образует
геометрическую фигуру (многоугольник,
окружность, эллипс, и т.п.)
Лекция 5. Пересечение
поверхности с плоскостью
8
9. СЕЧЕНИЕ ГРАННЫХ ПОВЕРХНОСТЕЙ
32 Ξ 4212 Ξ 22
11
21
31
41
• Сечение гранной
поверхности –
многоугольник,
который строится по
точкам пересечения
секущей плоскости и
ребер многогранника
Лекция 5. Пересечение поверхности с
плоскостью
9
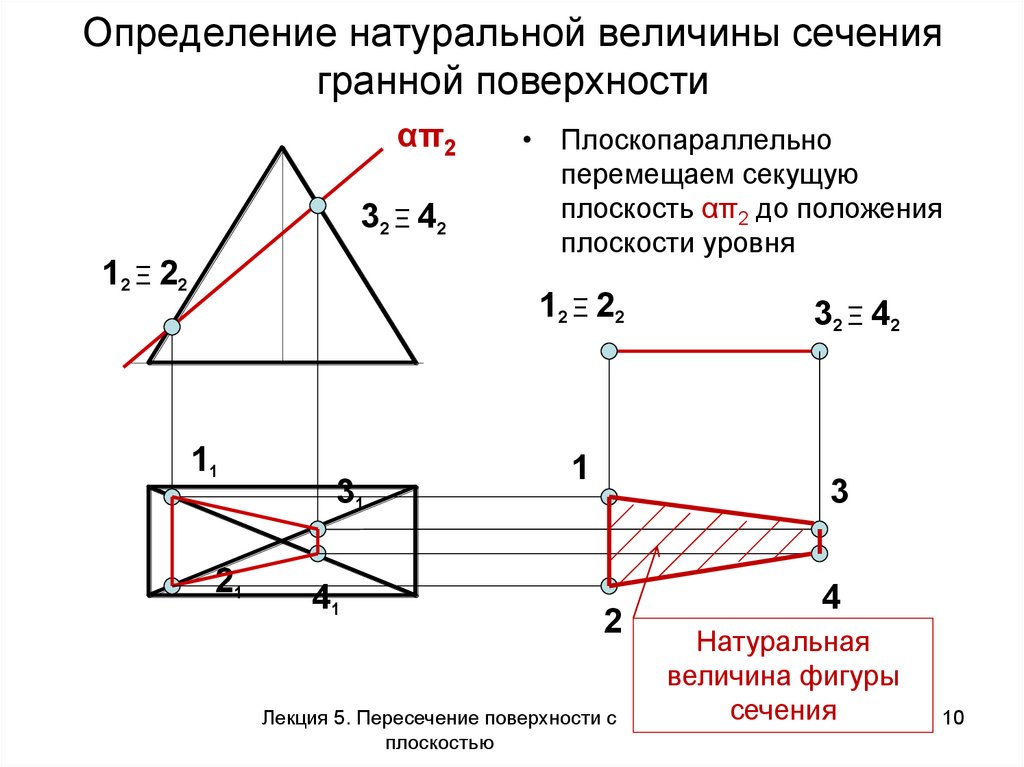
10. Определение натуральной величины сечения гранной поверхности
απ232 Ξ 42
12 Ξ 22
• Плоскопараллельно
перемещаем секущую
плоскость απ2 до положения
плоскости уровня
12 Ξ 22
11
21
31
41
1
32 Ξ 42
3
2
Лекция 5. Пересечение поверхности с
плоскостью
4
Натуральная
величина фигуры
сечения
10
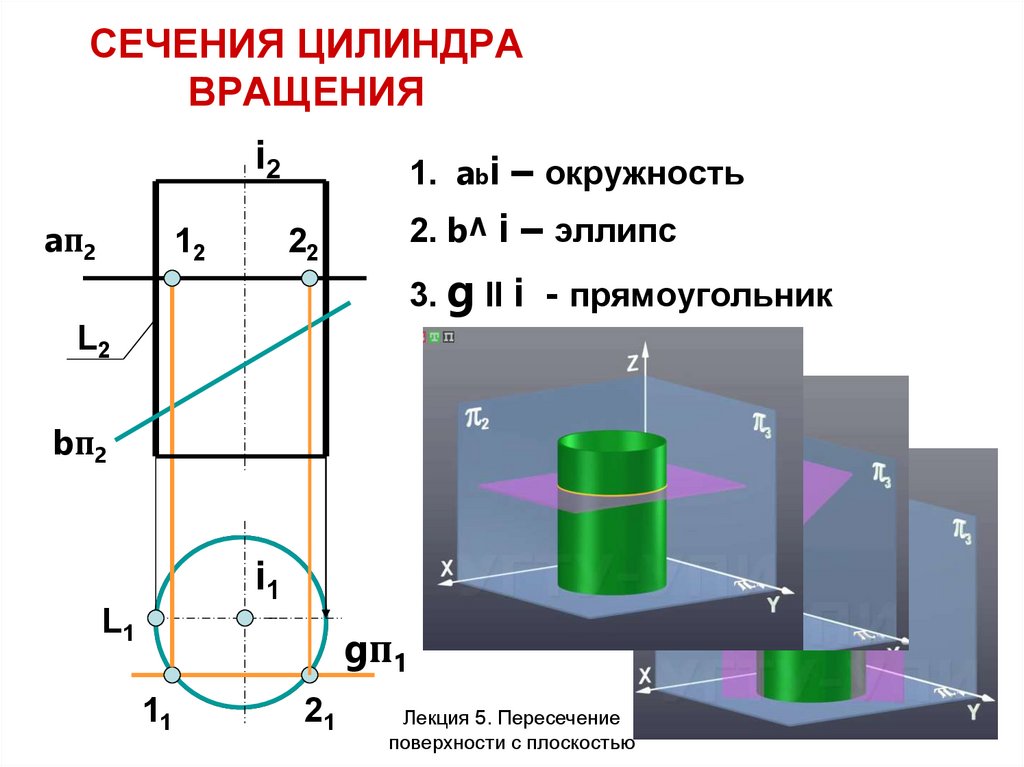
11. СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
i2aп2
12
1. abi – окружность
2. b^ i – эллипс
22
3. g ll i - прямоугольник
L2
bп2
i1
L1
gп1
11
21
Лекция 5. Пересечение
поверхности с плоскостью
11
12. СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ
22 1252
42
32
bп2
41 31 21
51
11
Сечение цилиндра
эллипс b^ i
Фигура сечения
совпадает с
очерком
поверхности на
проецирующей
плоскости
211
411
311
Лекция 5. Пересечение
поверхности с плоскостью
12
13. Определение натуральной величины фигуры сечения цилиндра вращения
Сечение цилиндра22 12
52
42
эллипс b^ i
32
521
bп2
41 31 21
51
4
11
211
411
311
1
412 312 22
3
121
bп21
2
5
1
41
31
21
Лекция 6. Взаимное пересечение поверхностей. Метод
вспомогательных секущих плоскостей
13
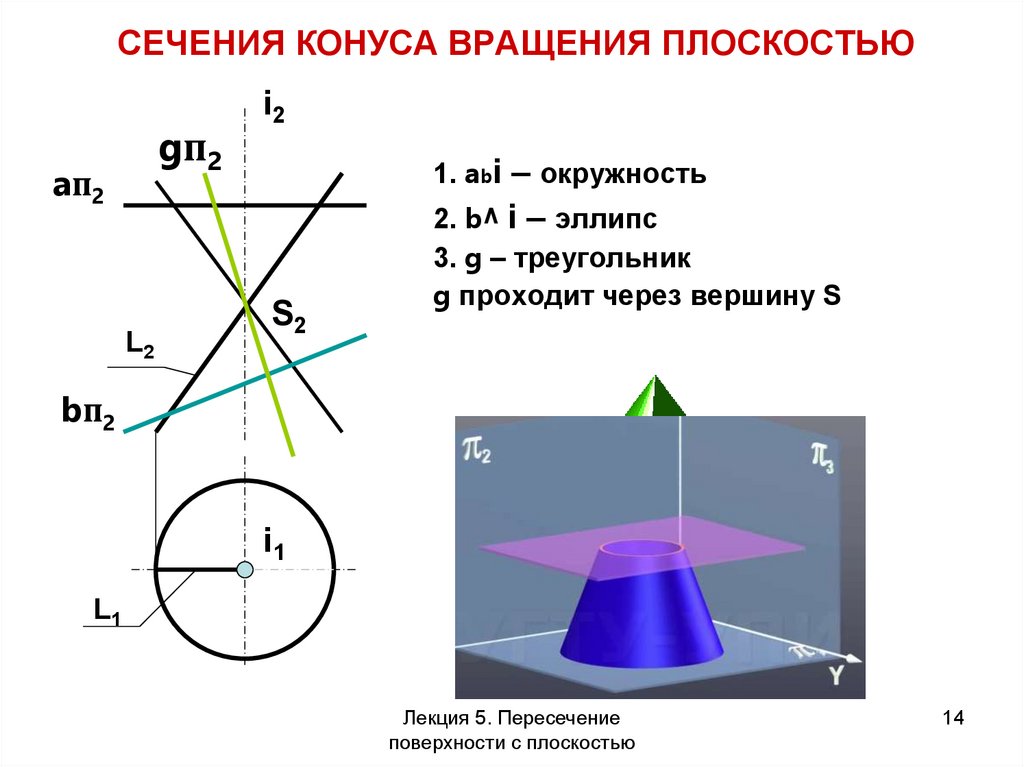
14. СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
gп2aп2
L2
i2
1. abi – окружность
S2
2. b^ i – эллипс
3. g – треугольник
g проходит через вершину S
bп2
i1
L1
Лекция 5. Пересечение
поверхности с плоскостью
14
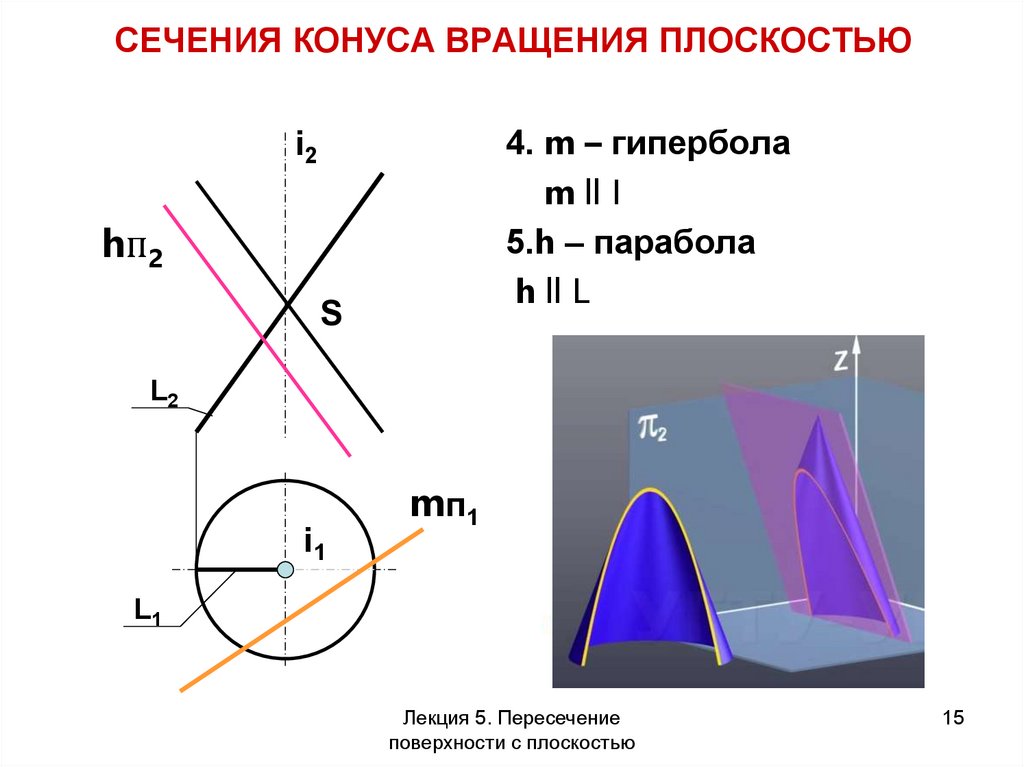
15. СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
4. m – гиперболаm ll I
5.h – парабола
h ll L
i2
hп2
S
L2
i1
mп1
L1
Лекция 5. Пересечение
поверхности с плоскостью
15
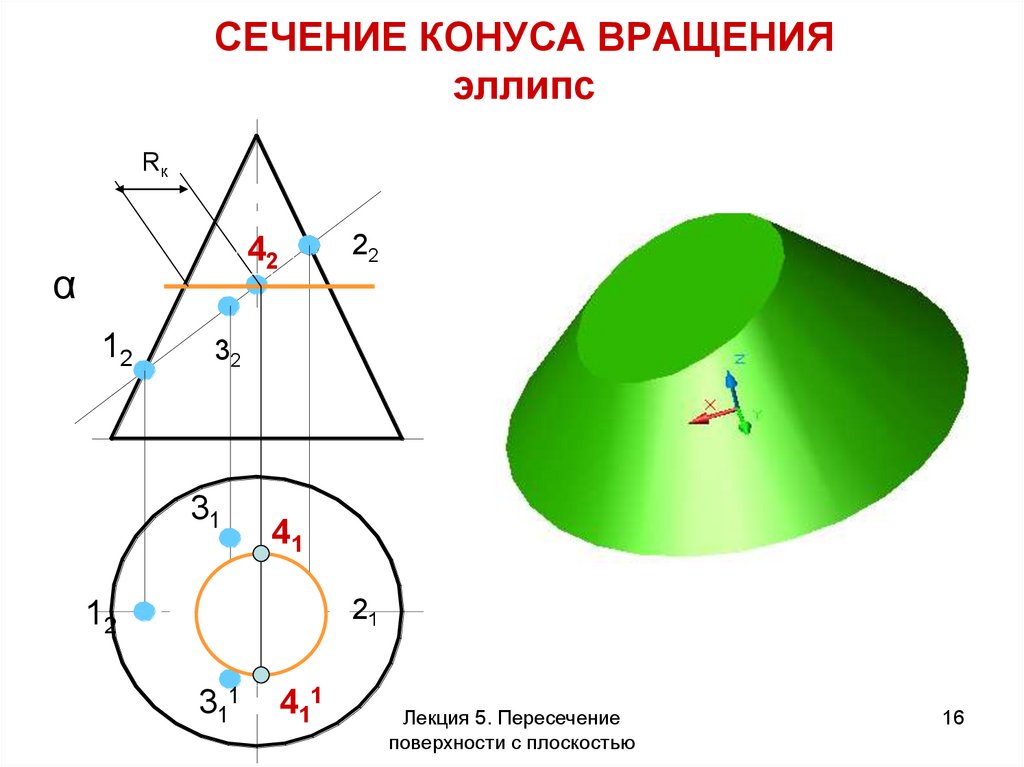
16. СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ эллипс
RкRк
22
αп2
1122
22
42
3232
3311
41
1
112
2121
31111
3
411
Лекция 5. Пересечение
поверхности с плоскостью
16
17.
2242
12
32
31
41
11
21
311
411
Лекция 5. Пересечение поверхности с плоскостью
17
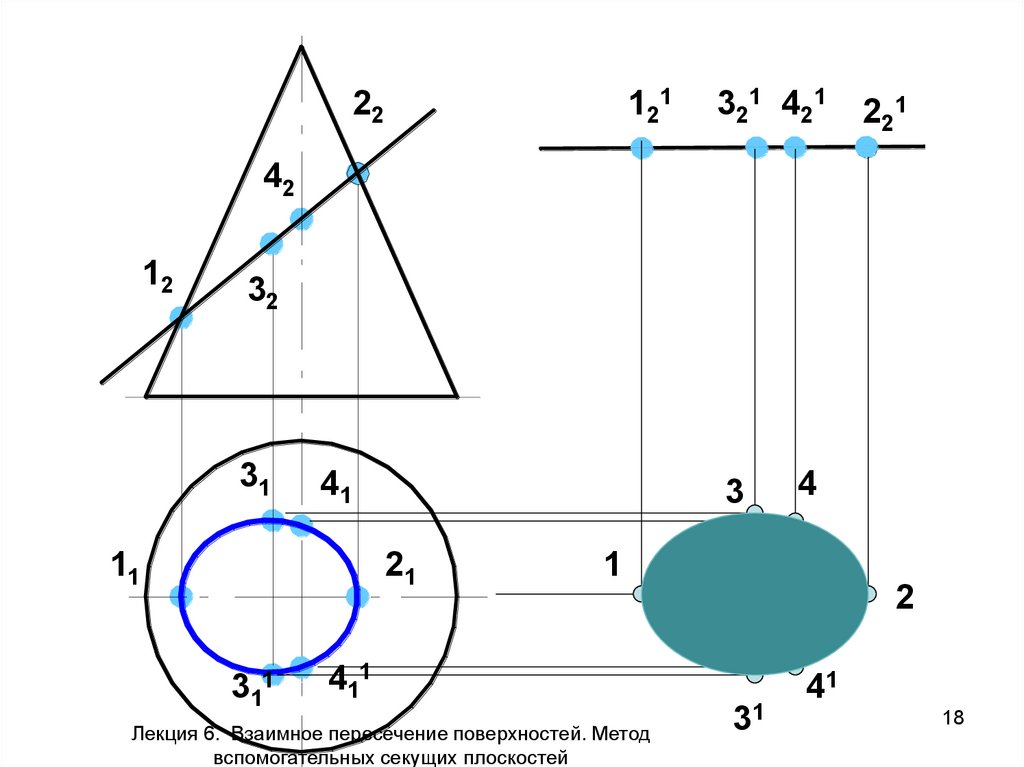
18.
12122
321 421
221
42
12
32
31
41
11
3
21
311
4
1
2
411
Лекция 6. Взаимное пересечение поверхностей. Метод
вспомогательных секущих плоскостей
31
41
18
19. СЕЧЕНИЯ СФЕРЫ
Сечение сферы плоскостью – окружность, котораяможет проецироваться как:
- прямая линия
- окружность
- эллипс
Лекция 6. Взаимное пересечение поверхностей.
Метод вспомогательных секущих плоскостей
19
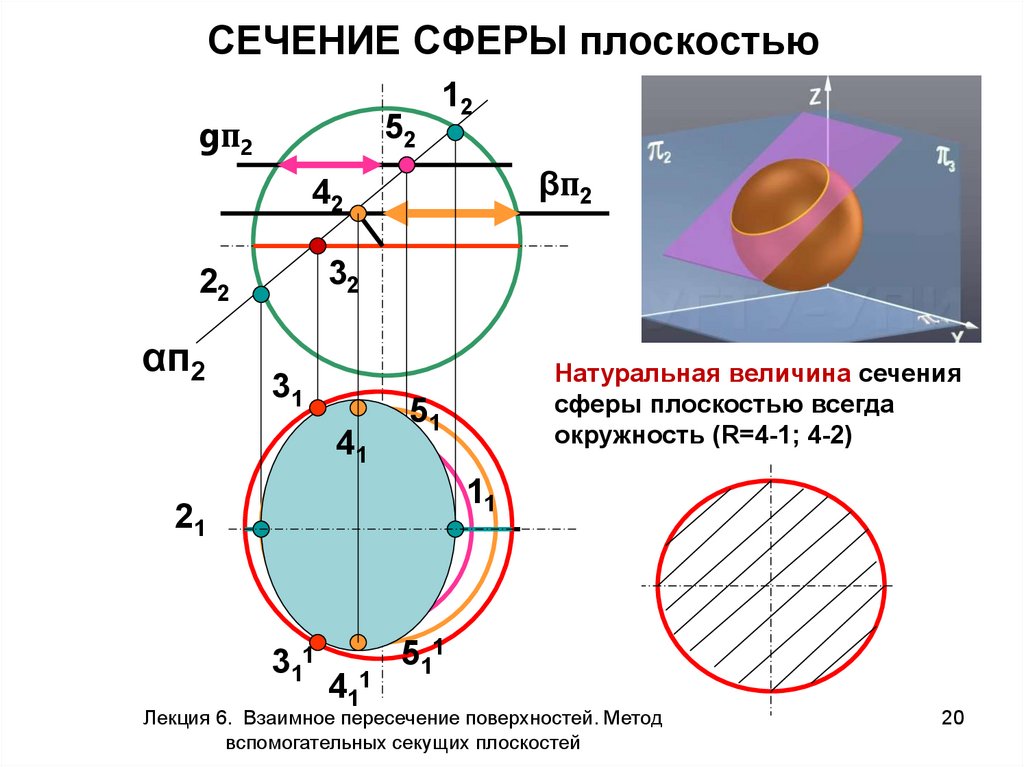
20. СЕЧЕНИЕ СФЕРЫ плоскостью
gп252
12
βп2
42
32
22
αп2
31
41
Натуральная величина сечения
сферы плоскостью всегда
окружность (R=4-1; 4-2)
51
11
21
311
411
511
Лекция 6. Взаимное пересечение поверхностей. Метод
вспомогательных секущих плоскостей
20
21. Задание на дом
• По двум проекциямгруппы поверхностей
построить третью
• Построить сечение
заданных
поверхностей
плоскостью α
• Определить
натуральную
величину фигуры
сечения
Лекция 5. Пересечение
поверхности с плоскостью
• Задание
• Образец выполнения
21
22. Выводы по теме
• Пересечение прямой и поверхности строитсяметодом заключения прямой в
дополнительную плоскость
• Сечение поверхности плоскостью
выполняется с помощью вспомогательной
плоскости – посредника
• Натуральная величина фигуры сечения
строится методом замены плоскостей
проекций или плоскопараллельного
перемещения
Лекция 5. Пересечение
поверхности с плоскостью
22
23. Рекомендованная литература
• Бударин О. С. Начертательная геометрия. Краткийкурс: учеб. пособие для студентов вузов,
обучающихся по направлениям в обл. техники и
технологий / О. С. Бударин. - 2-е изд., испр. - СанктПетербург ; Москва ; Краснодар: Лань, 2009. - 368 с.
• Королев Ю. И. Начертательная геометрия: учеб. для
вузов инженер.-техн. специальностей / Ю. И.
Королев. - 2-е изд. - Москва ; Санкт-Петербург ;
Нижний Новгород [и др.]: Питер, 2010. - 256 с.
• Чекмарев А. А. Начертательная геометрия и
черчение: учеб. для студентов вузов, обучающихся
по техн. специальностям / А. А. Чекмарев. - 3-е изд.,
перераб. и доп. - Москва: Юрайт, 2011. - 471 с.
Лекция 5. Пересечение
поверхности с плоскостью
23
24. Благодарю за внимание
Лекция 5. Пересечениеповерхности с плоскостью
24
















 drafting
drafting








