Пересечение поверхности с плоскостью. Лекция № 5

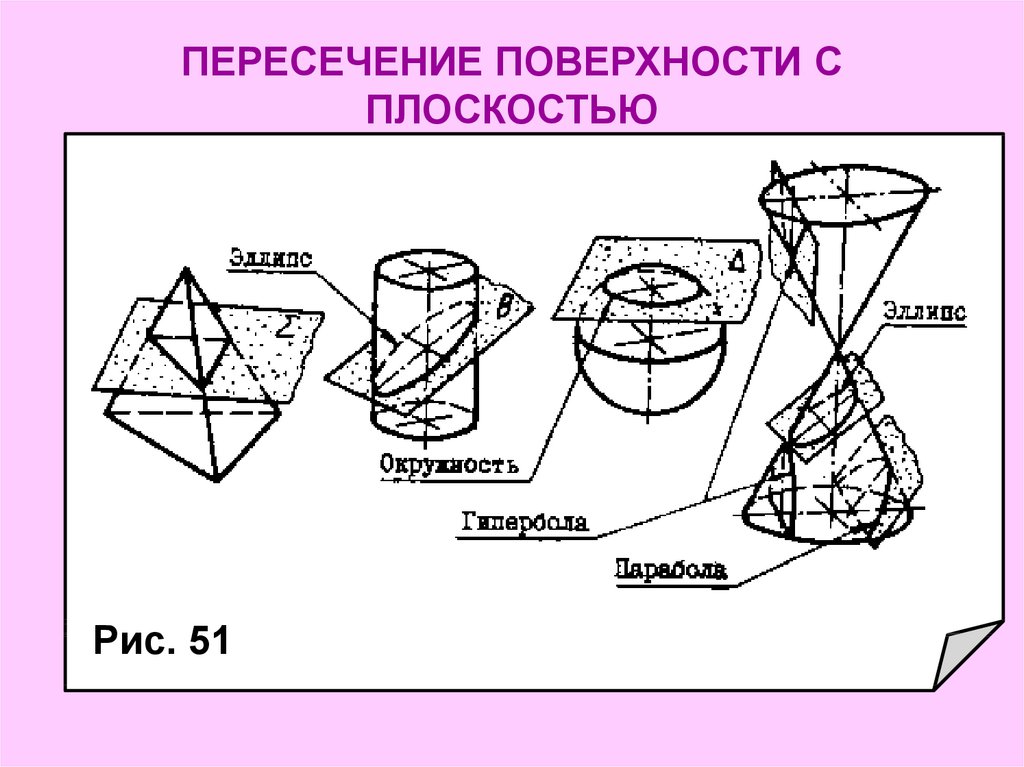
1. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ

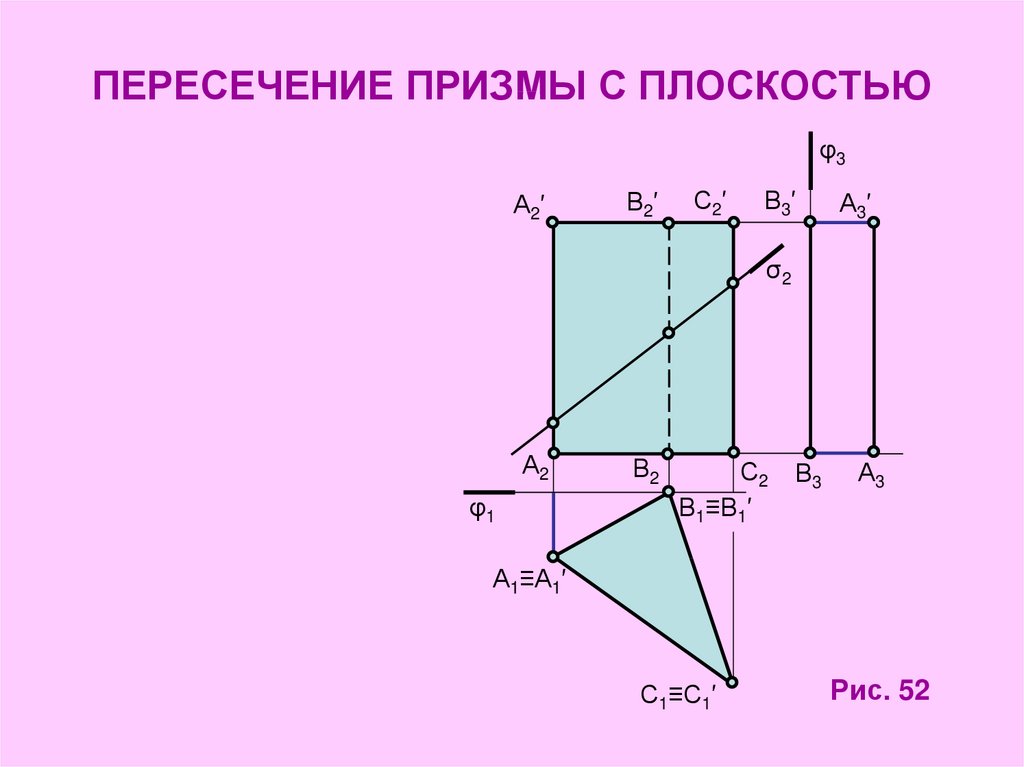
Рис. 51

2. ПЕРЕСЕЧЕНИЕ ПРИЗМЫ С ПЛОСКОСТЬЮ

φ3
А2′
В2′
С2′
В3′
А3′
σ2
А2
φ1
В2
С2
В1≡В1′
В3
А3
А1≡А1′
С1≡С1′
Рис. 52

3. ПЕРЕСЕЧЕНИЕ ПРИЗМЫ С ПЛОСКОСТЬЮ

φ3
А2′
В2′
С2′
В3′
А3′
С3′
σ2
А2
φ1
В2
С2
В1≡В1′
В3
А3
А1≡А1′
С1≡С1′
Рис. 52
С3

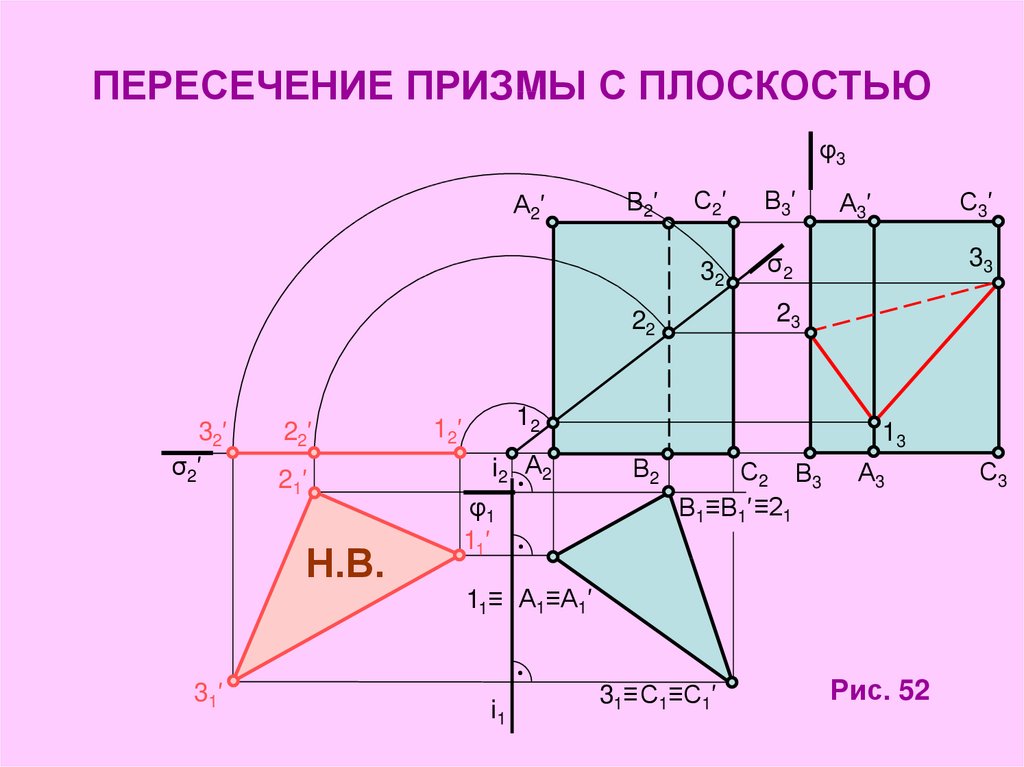
4. ПЕРЕСЕЧЕНИЕ ПРИЗМЫ С ПЛОСКОСТЬЮ

φ3
А2′
В2′
С2′
В3′
32
σ2
22′
21′
Н.В.
31′
12
12′
i2 А2
φ1
11′
33
23
22
32′
σ2′
С3′
А3′
13
В2
С2 В3
В1≡В1′ ≡21
А3
11≡ А1≡А1′
i1
31≡ С1≡С1′
Рис. 52
С3

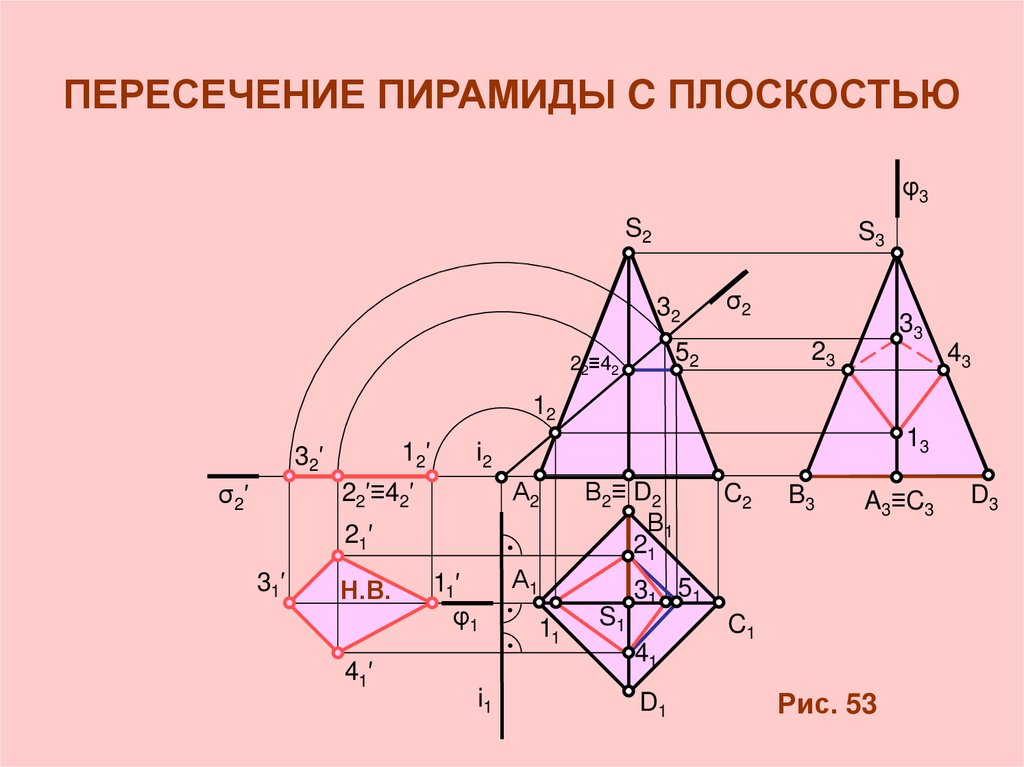
5. ПЕРЕСЕЧЕНИЕ ПИРАМИДЫ C ПЛОСКОСТЬЮ

φ3
S2
S3
32
σ2
23
52
22≡42
33
43
12
12′
32′
А2
22′≡42′
σ2′
13
i2
21′
31′
Н.В.
41′
11′
φ1
i1
В2≡ D2
В1
21
А1
11
S1
C2
B3
A3≡C3
31 51
C1
41
D1
Рис. 53
D3

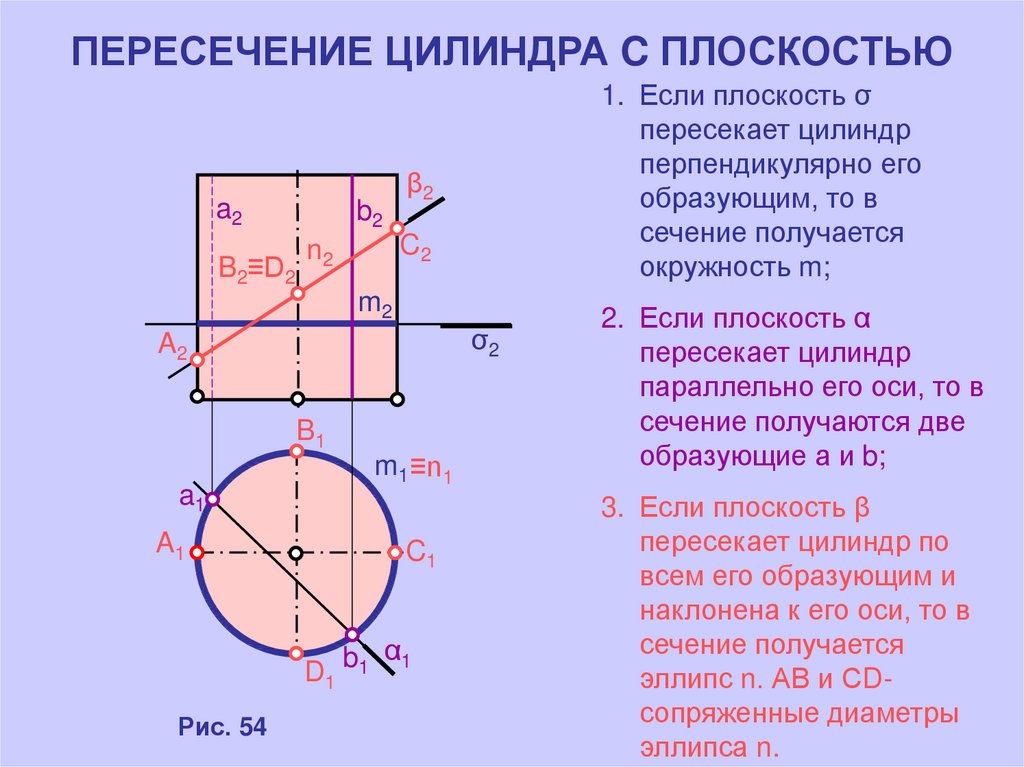
6. ПЕРЕСЕЧЕНИЕ ЦИЛИНДРА C ПЛОСКОСТЬЮ

a2
B2≡D2
b2
1. Если плоскость σ
пересекает цилиндр
перпендикулярно его
образующим, то в
сечение получается
окружность m;
β2
C2
n2
m2
σ2
A2
B1
a1
A1
C1
D1
Рис. 54
m1 ≡n1
b1 α 1
2. Если плоскость α
пересекает цилиндр
параллельно его оси, то в
сечение получаются две
образующие а и b;
3. Если плоскость β
пересекает цилиндр по
всем его образующим и
наклонена к его оси, то в
сечение получается
эллипс n. АВ и СDсопряженные диаметры
эллипса n.

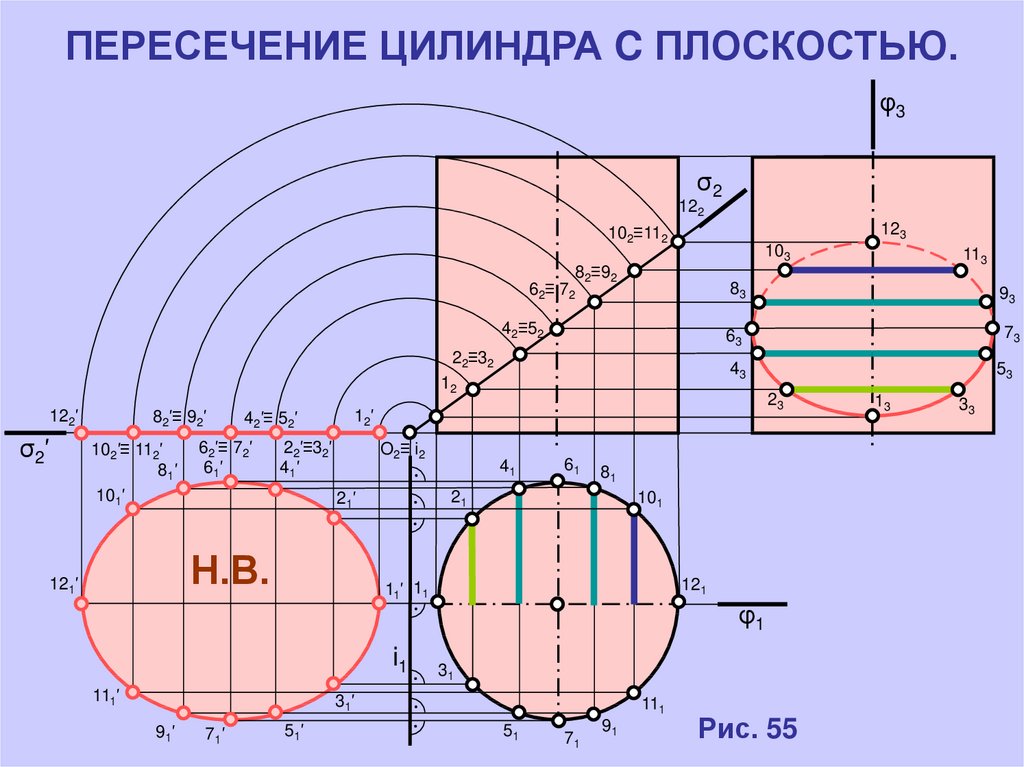
7. ПЕРЕСЕЧЕНИЕ ЦИЛИНДРА C ПЛОСКОСТЬЮ.

φ3
σ2
122
123
102≡112
103
82≡92
62≡ 72
42≡52
22≡32
σ2′
82′≡ 92′
102′≡ 112′
81′
101′
22′≡32′
41′
O2≡ i2
21′
Н.В.
121′
41
61
51′
53
101
121
φ1
31
31′
71′
73
81
21
i1
91′
63
23
11′ 11
111′
93
12′
42′≡ 52′
62′≡ 72′
61′
83
43
12
122′
113
111
51
71
91
Рис. 55
13
33

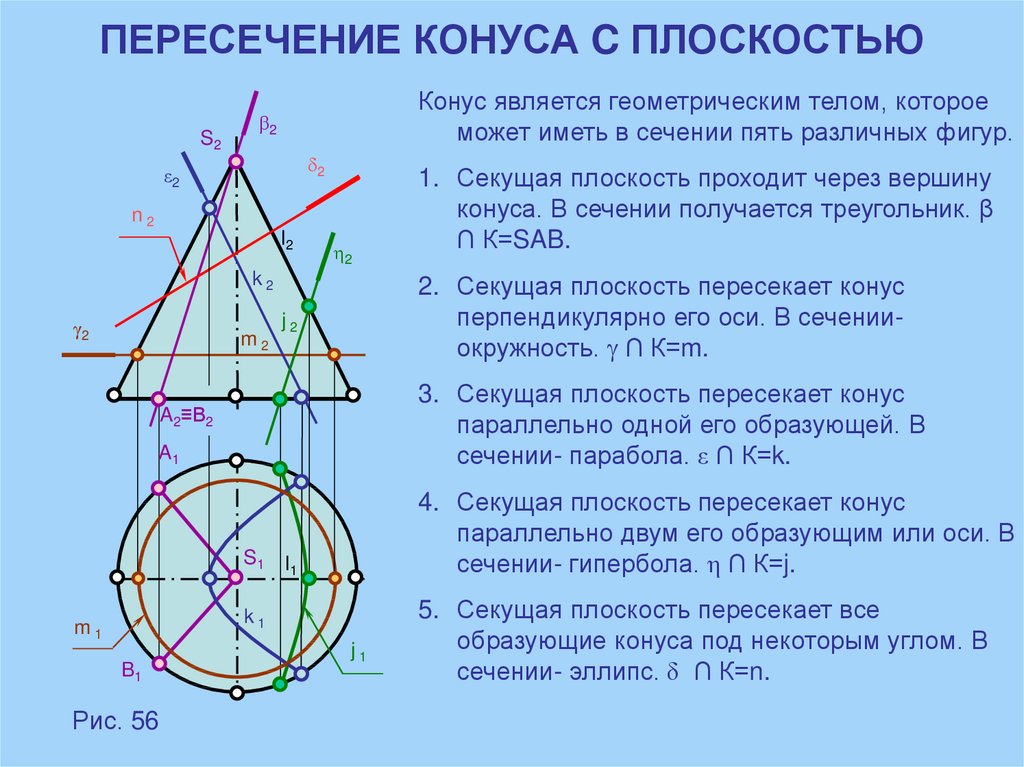
8. ПЕРЕСЕЧЕНИЕ КОНУСА C ПЛОСКОСТЬЮ

S2
Конус является геометрическим телом, которое
может иметь в сечении пять различных фигур.
β2
δ2
ε2
n2
l2
η2
k2
γ2
m2
2. Секущая плоскость пересекает конус
перпендикулярно его оси. В сеченииокружность. ∩ К=m.
j2
3. Секущая плоскость пересекает конус
параллельно одной его образующей. В
сечении- парабола. ε ∩ К=k.
A2≡B2
A1
S1
4. Секущая плоскость пересекает конус
параллельно двум его образующим или оси. В
сечении- гипербола. η ∩ К=j.
l1
k1
m1
B1
Рис. 56
1. Секущая плоскость проходит через вершину
конуса. В сечении получается треугольник. β
∩ К=SAB.
j1
5. Секущая плоскость пересекает все
образующие конуса под некоторым углом. В
сечении- эллипс. δ ∩ К=n.

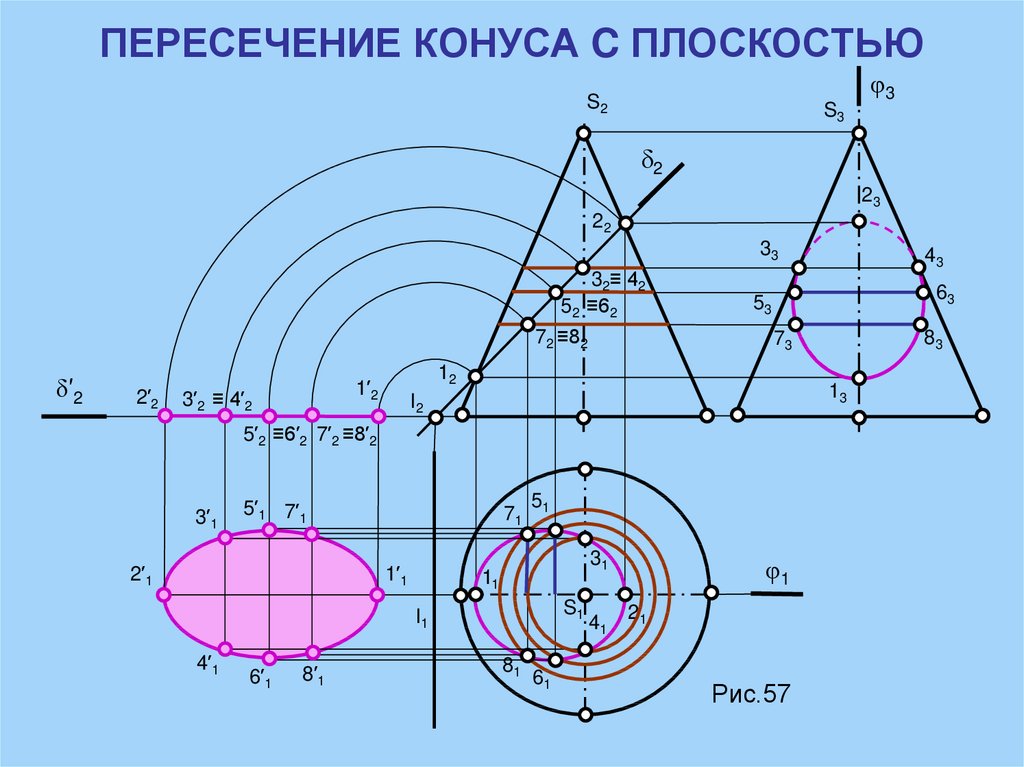
9. ПЕРЕСЕЧЕНИЕ КОНУСА C ПЛОСКОСТЬЮ

S2
S3
φ3
δ2
23
22
33
32≡ 42
52 ≡62
72 ≡82
δ′2
2′2
3′2 ≡ 4′2
63
53
13
I2
5′2 ≡6′2 7′2 ≡8′2
3′1
5′1 7′1
2′1
71
1′1
51
31
11
S1
I1
4′1
6′1
8′1
83
73
12
1′2
43
81
61
41
φ1
21
Рис.57

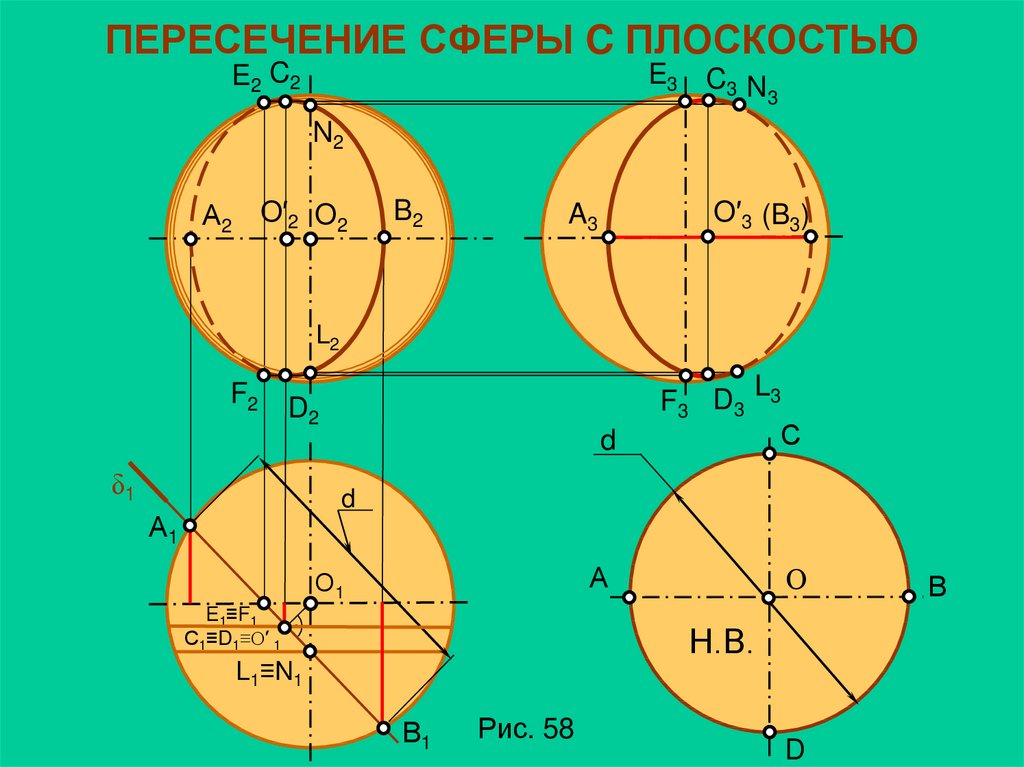
10. ПЕРЕСЕЧЕНИЕ СФЕРЫ C ПЛОСКОСТЬЮ

E2 C2
E3 C3 N
3
N2
А2 O′2 O2
B2
O′3 (B3)
A3
L2
F2
d
L
F3 D3 3
С
А
О
D2
δ1
d
А1
О1
E1≡F1
С1≡D1≡О′ 1
Н.В.
L1≡N1
В1
Рис. 58
D
В