Similar presentations:
Инженерная графика. Начертательная геометрия. Машиностроительное черчение
1. Инженерная графика
КУРГАНСКИЙ ИНСТИТУТ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА-филиал федерального государственного бюджетного
образовательного учреждения высшего профессионального образования
«Уральский государственный университет путей сообщения»
в г. Кургане
Факультет среднего профессионального образования
Инженерная графика
Начертательная геометрия
Машиностроительное черчение
Данилин
Александр Петрович
Курган 2015
2. Список использованных источников
Куликов В.П., Кузин А.В. Инженерная графика / Учебник. – 4-еизд. – М.: Форум., 2009. – 368 с. – (Профессиональное
образование).
Боголюбов С.К. Инженерная графика : Учебник для средних
специальных учебных заведений. – 3-е изд., испр. и дополн.
М.:Машиностроение, 2004. – 352 с.: ил.
Чекмарёв А. А. Инженерная графика. Машиностроительное
черчение: учебник. – М.: ИНФРА-М, 2014. – 397с.
Березина Н.А. Инженерная графика: учебное пособие. – М.:
Альфа-М, - 2014. - 356 с.
Сорокин Н.П. Инженерная графика: Учебник. – СПб.: Лань,
2011. – 400 с.
3. Содержание
Начертательная геометрияОсновные обозначения
1.Методы проецирования
2. Точка, прямая, плоскость
3. Позиционные задачи
4.Перпендикулярность прямых и плоскостей
5.Преобразования комплексного чертежа
6.Метрические задачи
7.Поверхности
8.Позиционные задачи на поверхности
9.Построение разверток
10.Плоскости, касательные к поверхности
11.Аксонометрические проекции
4. Начертательная геометрия
В презентации использованы материалы авторов Пираловой О.Ф., Ведякина Ф.Ф.«Краткий конспект лекций по начертательной геометрии»
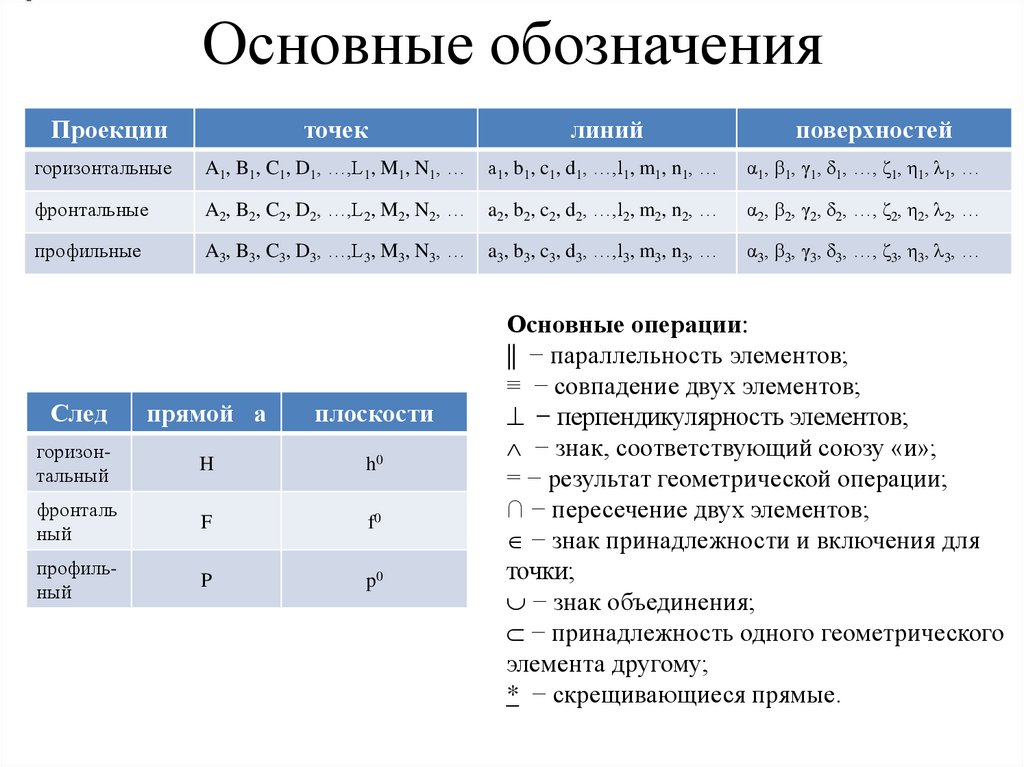
5. Основные обозначения
Геометрическая фигура − Ф.Точки: A, B, C, D, …,L, M, N, … или 1, 2, 3, 4, …, 12, 13, 14, …
Линии, произвольно расположенные по отношению к плоскостям проекций:
a, b, c, d, …,l, m, n, …
Линии уровня: h − горизонталь; f − фронталь; p − профильная прямая.
Для прямых используются следующие обозначения:
(AB) − прямая, проходящая через точки A и B;
[AB) − луч с началом в точке А;
[AB] − отрезок прямой, ограниченный точками A и B.
Поверхности : α, β, γ, δ, …, ζ, η, λ, …
Углы:
АВС − угол с вершиной в точке В, а также αº,βº, …, φº, ...
Угловая величина: φº − величина угла φ.
Прямой угол отмечается квадратом с точкой внутри.
Плоскости проекций: π1 − горизонтальная; π2 − фронтальная; π3 − профильная.
При замене плоскостей проекций или введении новых плоскостей проекций
последние обозначаются π4, π5 и т.д.
Оси проекций: x − ось абсцисс; y− ось ординат; z − ось аппликат.
Постоянная прямая эпюра Монжа – k.
6. Основные обозначения
Проекцииточек
линий
горизонтальные
A1, B1, C1, D1, …,L1, M1, N1, …
а1, b1, c1, d1, …,l1, m1, n1, …
α1, β1, γ1, δ1, …, ζ1, η1, λ1, …
фронтальные
A2, B2, C2, D2, …,L2, M2, N2, …
a2, b2, c2, d2, …,l2, m2, n2, …
α2, β2, γ2, δ2, …, ζ2, η2, λ2, …
профильные
A3, B3, C3, D3, …,L3, M3, N3, …
a3, b3, c3, d3, …,l3, m3, n3, …
α3, β3, γ3, δ3, …, ζ3, η3, λ3, …
След
прямой а
плоскости
горизонтальный
H
h0
фронталь
ный
F
f0
профильный
P
p0
поверхностей
Основные операции:
|| − параллельность элементов;
≡ − совпадение двух элементов;
− перпендикулярность элементов;
− знак, соответствующий союзу «и»;
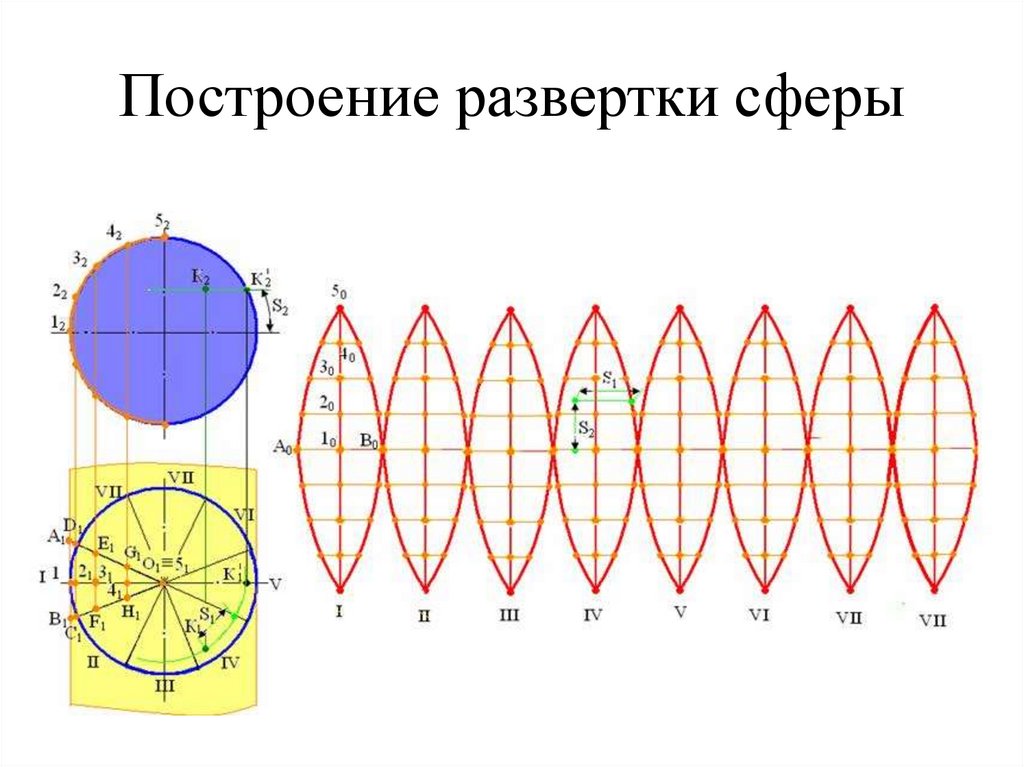
= − результат геометрической операции;
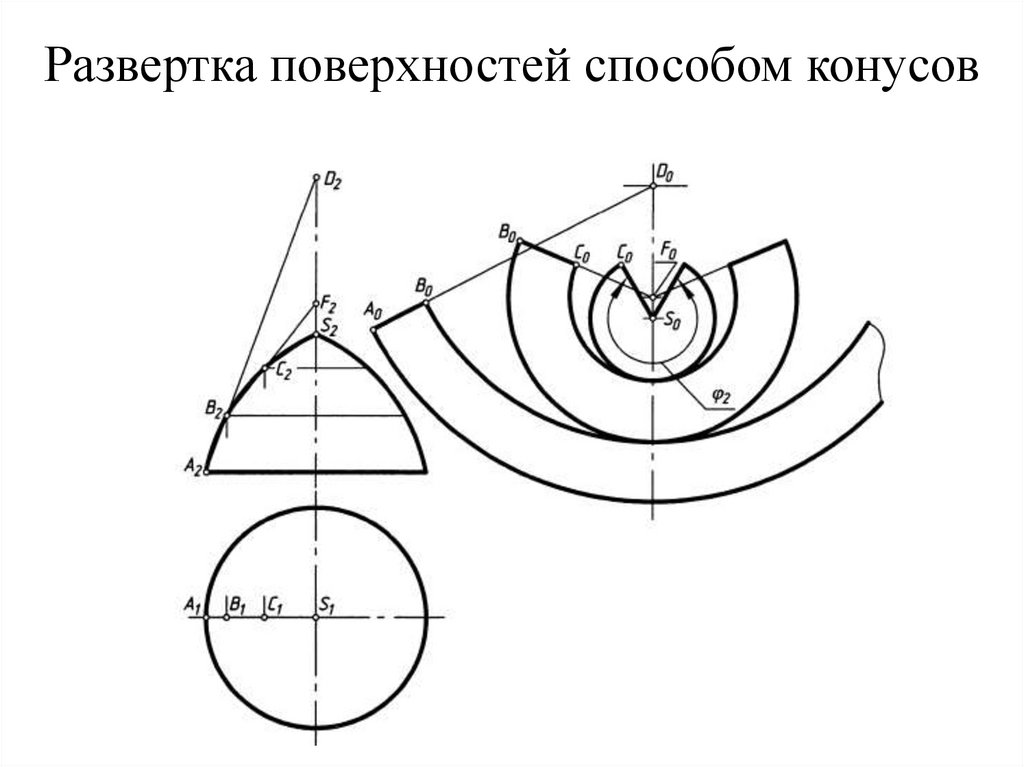
∩ − пересечение двух элементов;
− знак принадлежности и включения для
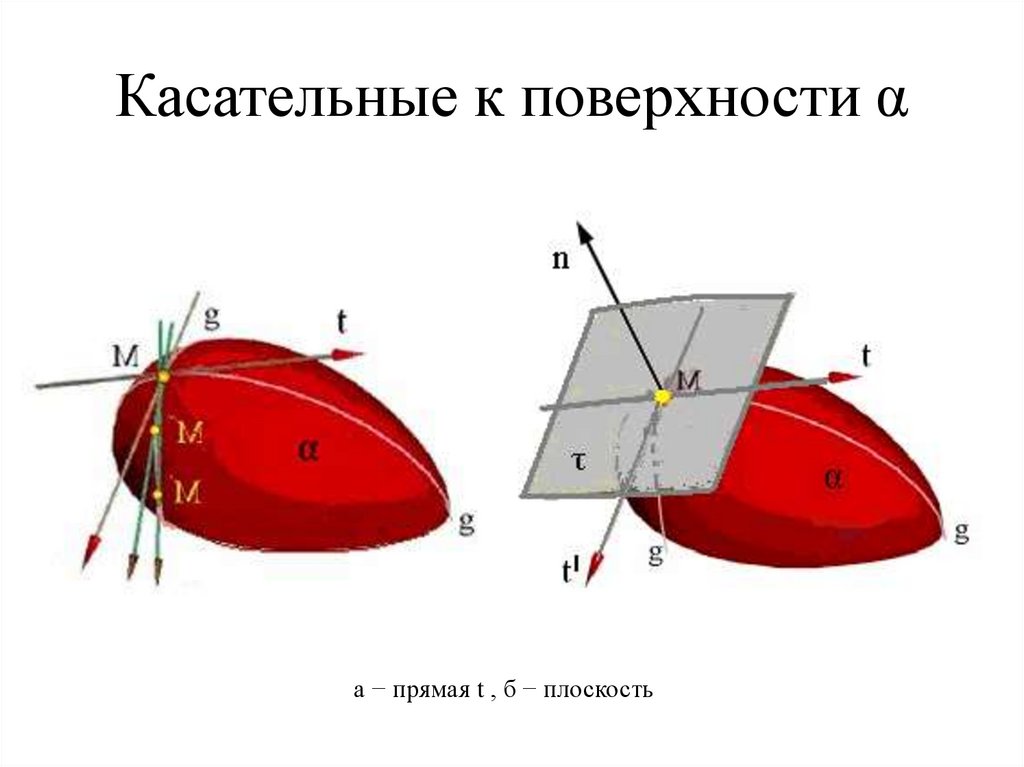
точки;
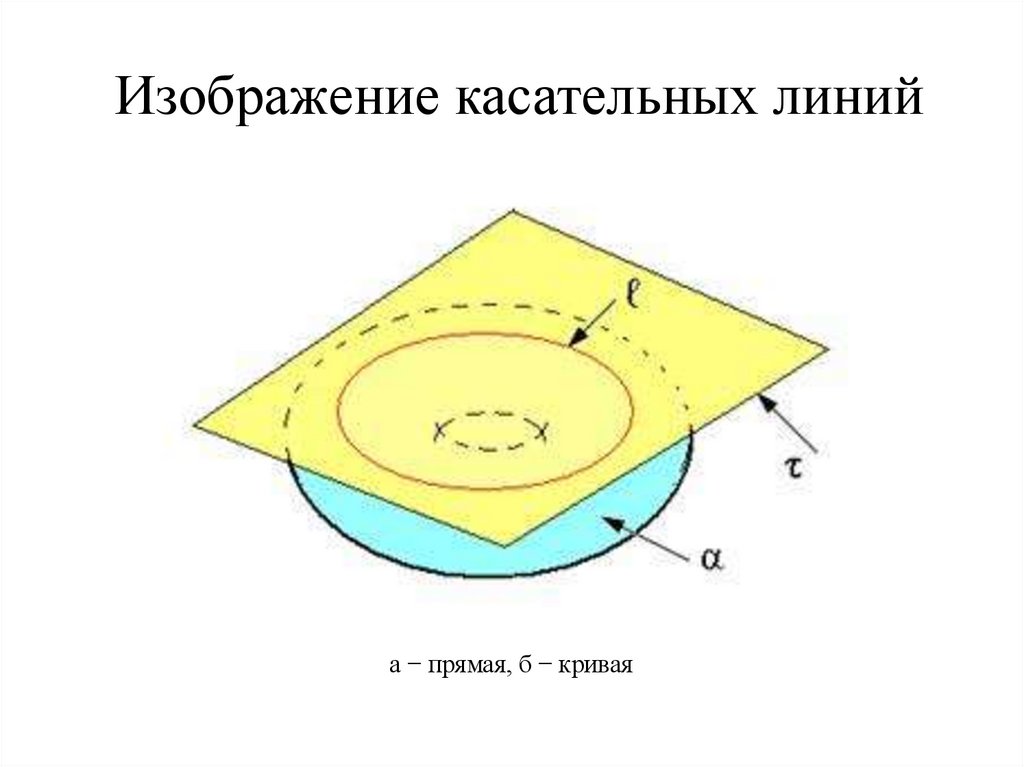
− знак объединения;
− принадлежность одного геометрического
элемента другому;
* − скрещивающиеся прямые.
7. Методы проецирования
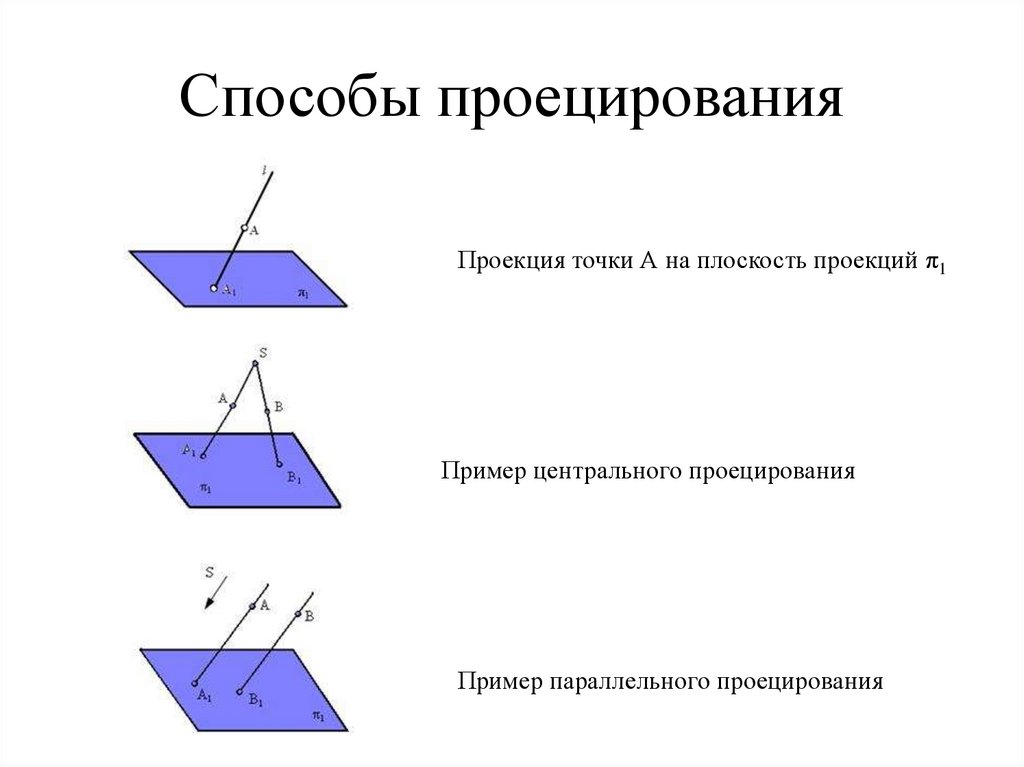
8. Способы проецирования
Проекция точки А на плоскость проекций π1Пример центрального проецирования
Пример параллельного проецирования
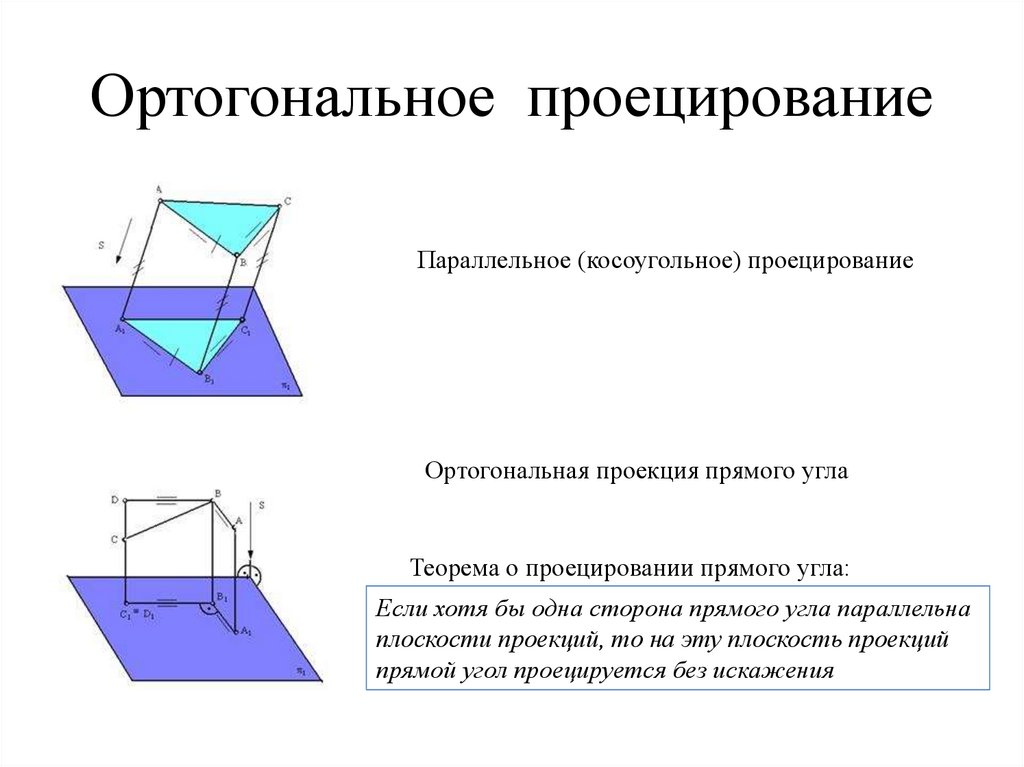
9. Ортогональное проецирование
Параллельное (косоугольное) проецированиеОртогональная проекция прямого угла
Теорема о проецировании прямого угла:
Если хотя бы одна сторона прямого угла параллельна
плоскости проекций, то на эту плоскость проекций
прямой угол проецируется без искажения
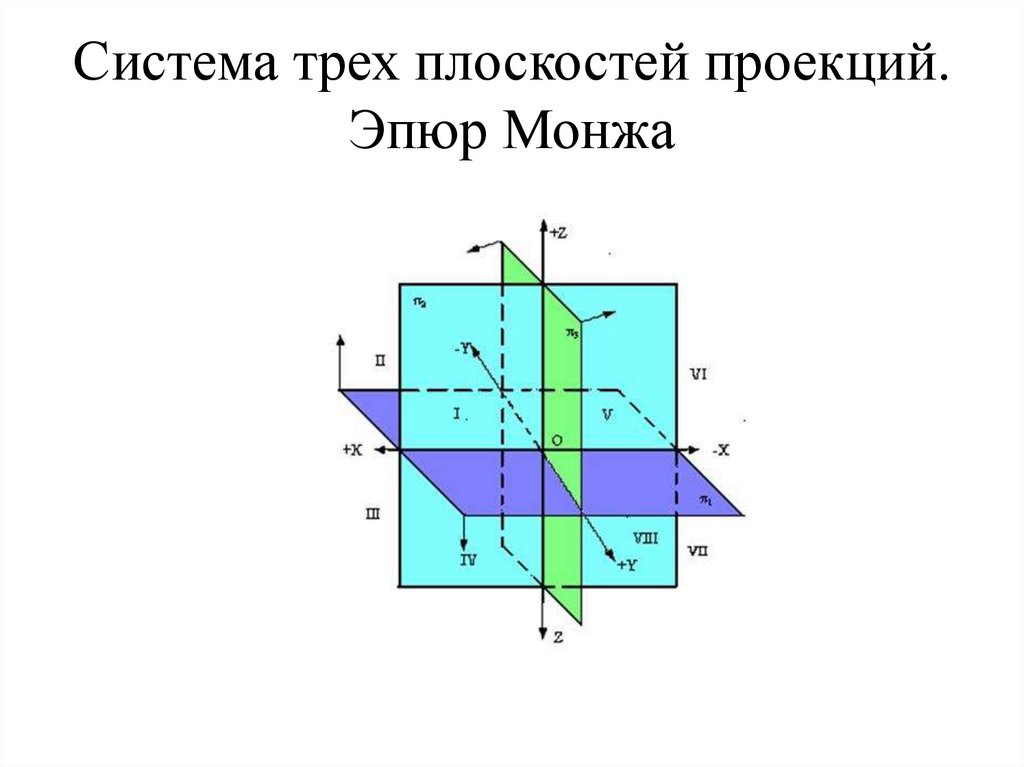
10. Система трех плоскостей проекций. Эпюр Монжа
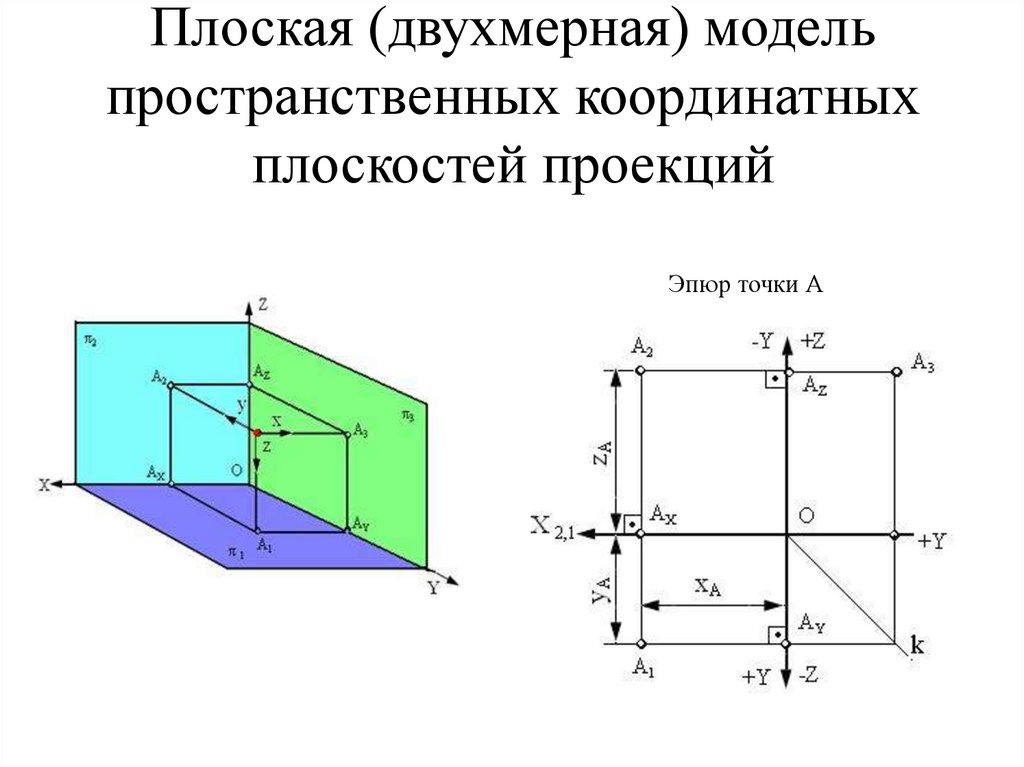
11. Плоская (двухмерная) модель пространственных координатных плоскостей проекций
Эпюр точки А12. Точка, прямая, плоскость
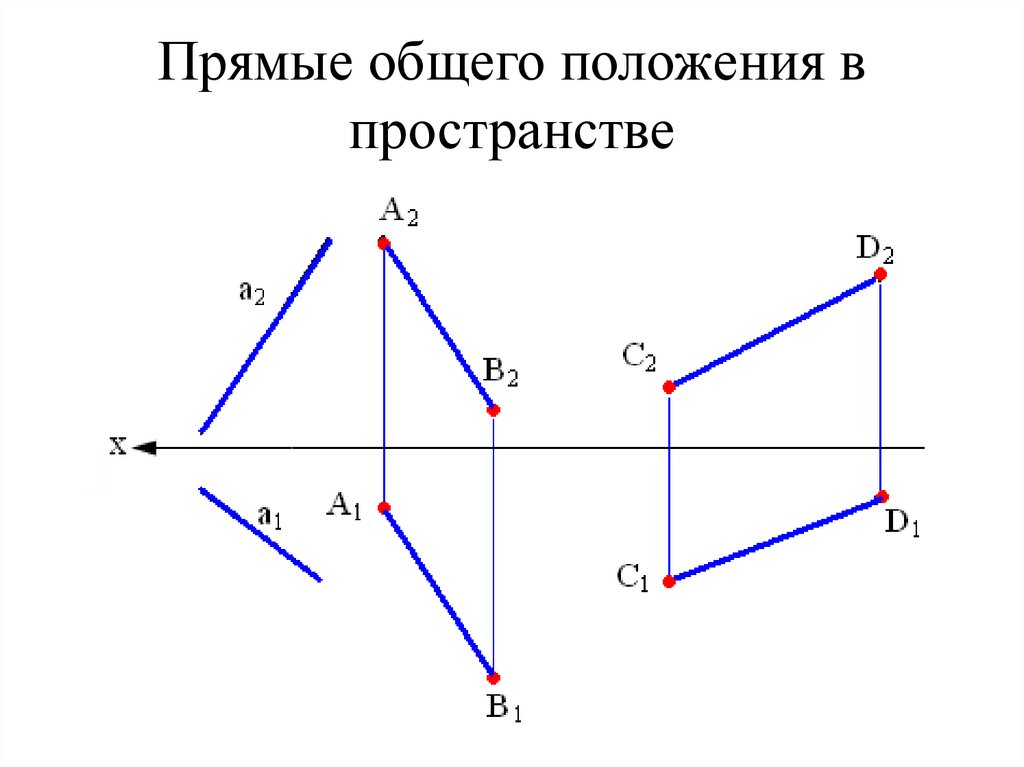
13. Прямые общего положения в пространстве
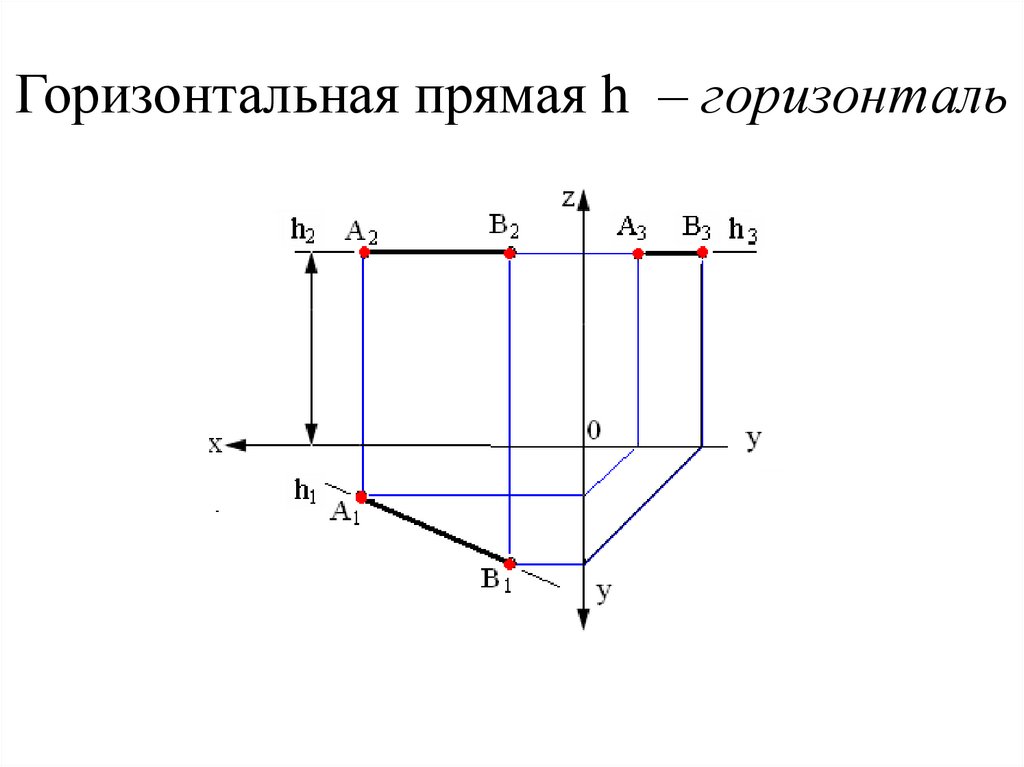
14. Горизонтальная прямая h – горизонталь
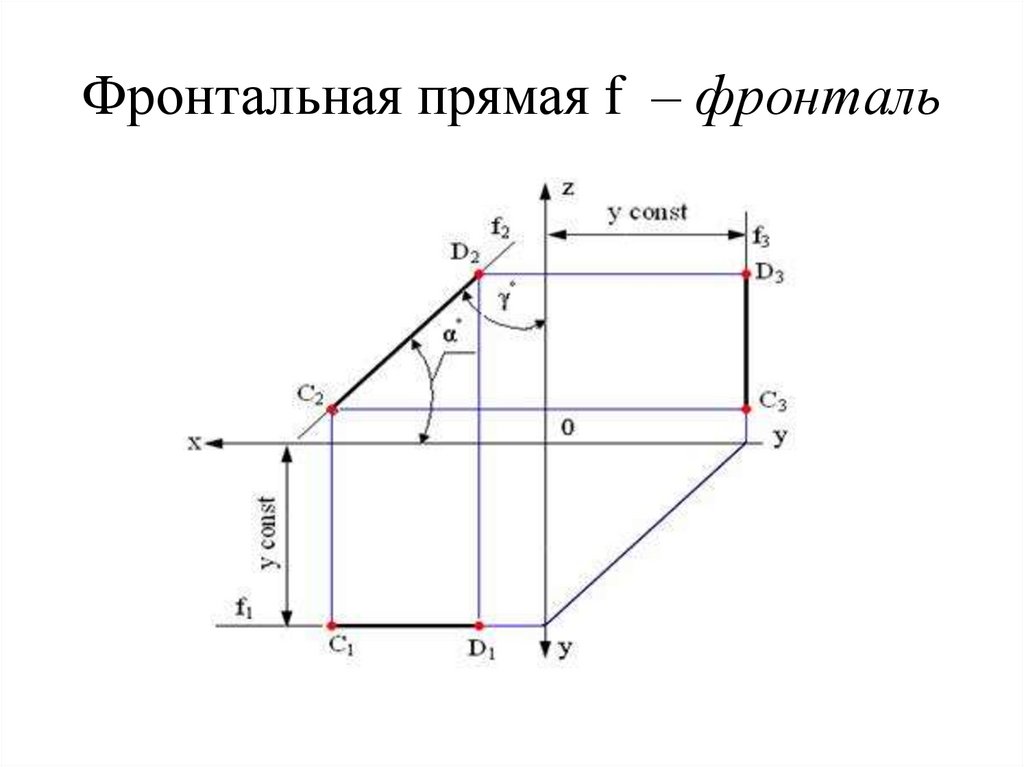
Горизонтальная прямая h – горизонталь15. Фронтальная прямая f – фронталь
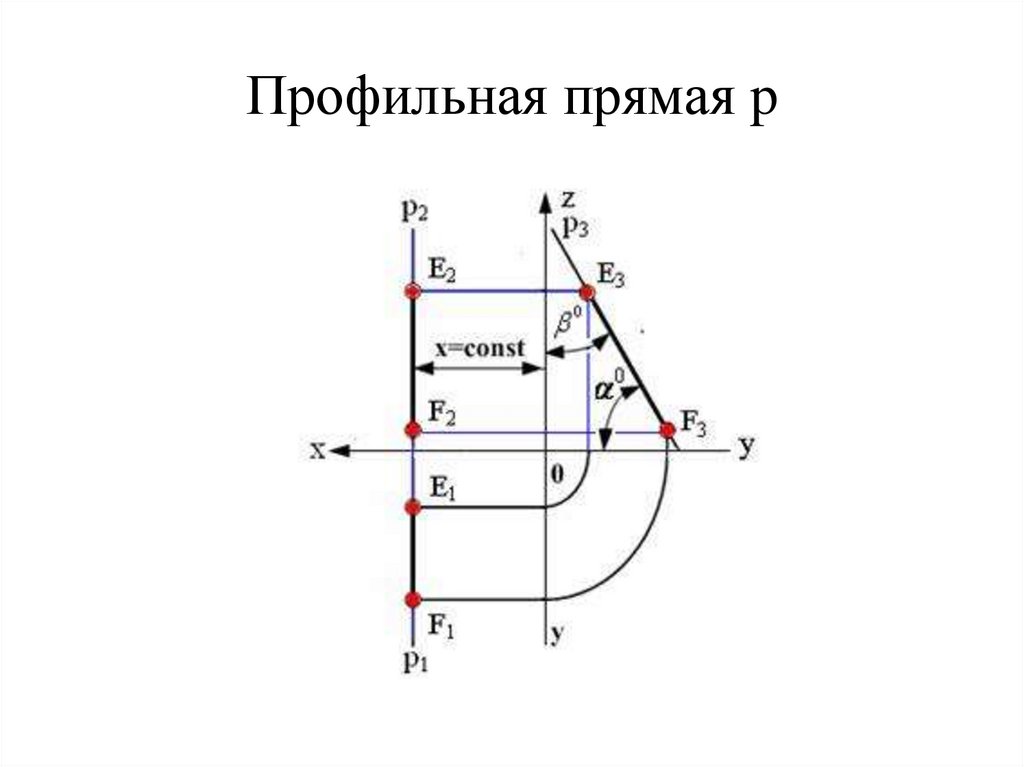
Фронтальная прямая f – фронталь16. Профильная прямая p
Профильная прямая p17. Частные случаи горизонтали, фронтали и профильной прямой
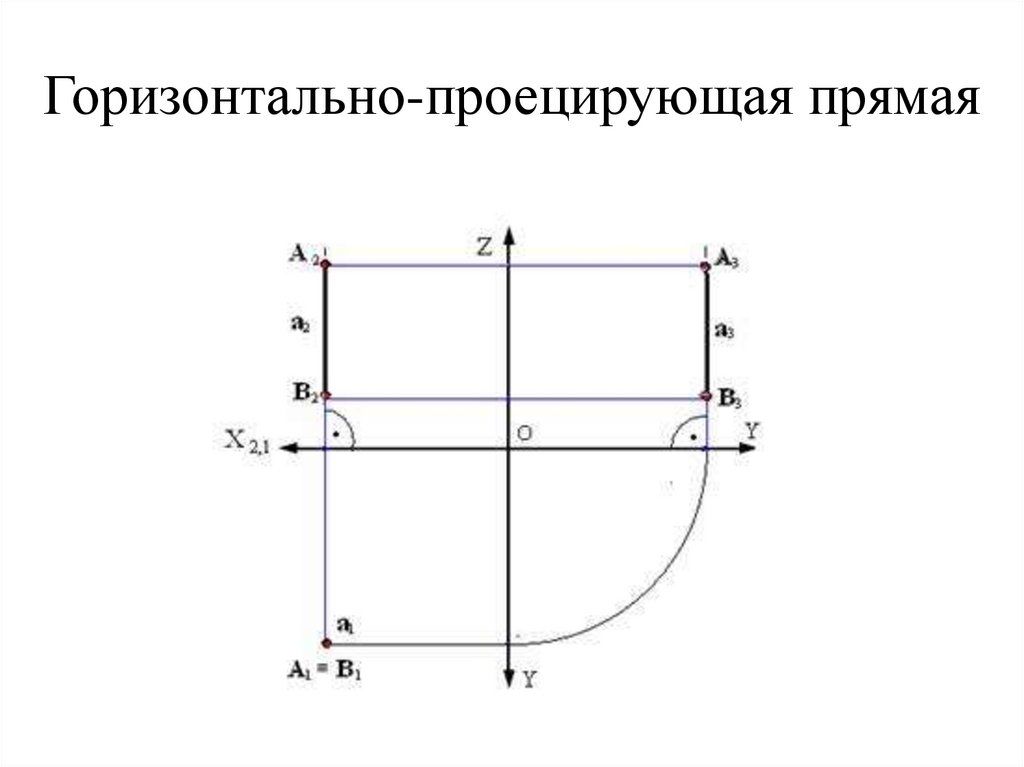
18. Горизонтально-проецирующая прямая
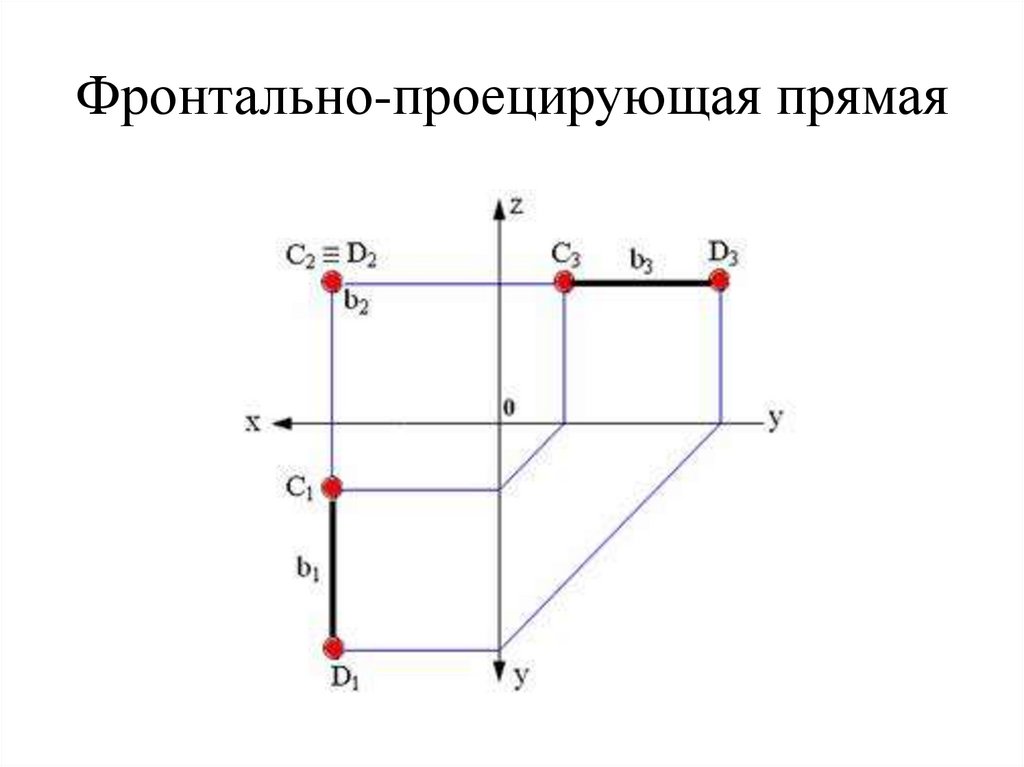
19. Фронтально-проецирующая прямая
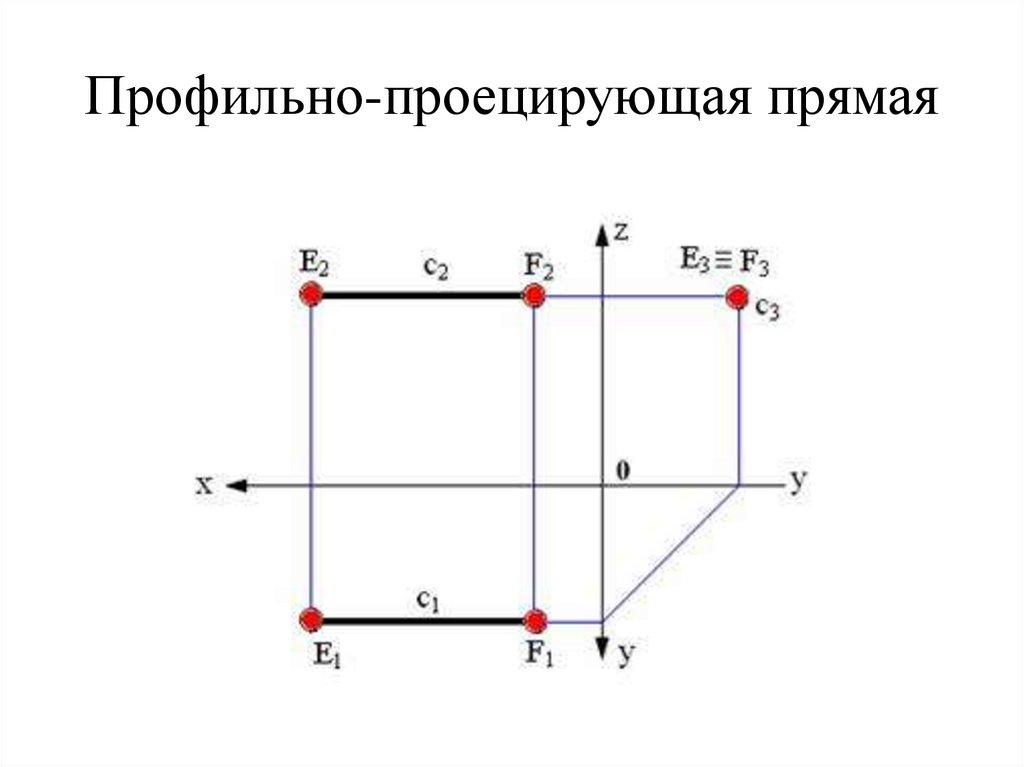
20. Профильно-проецирующая прямая
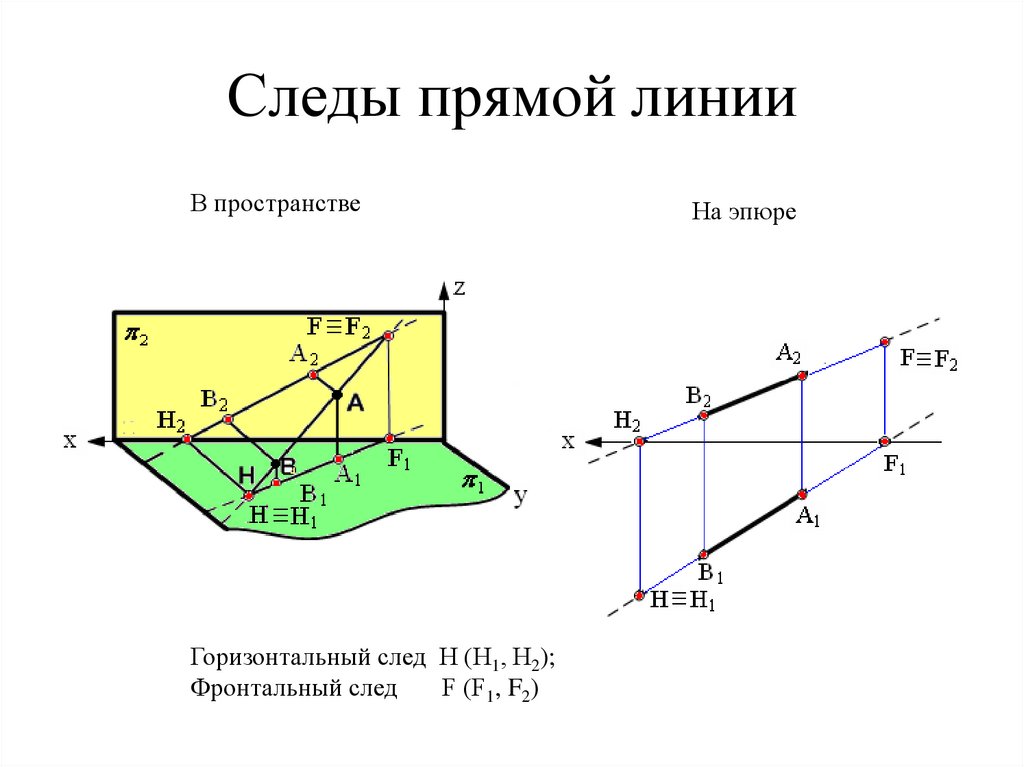
21. Следы прямой линии
В пространствеГоризонтальный след Н (Н1, Н2);
Фронтальный след
F (F1, F2)
На эпюре
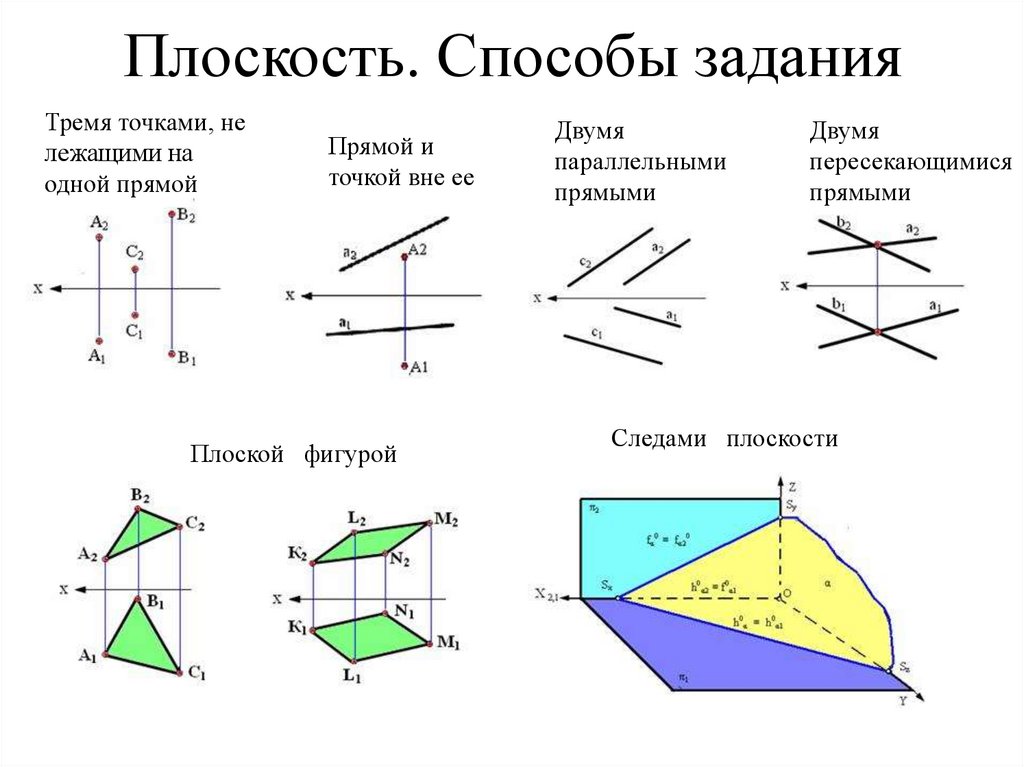
22. Плоскость. Способы задания
Тремя точками, нележащими на
одной прямой
Прямой и
точкой вне ее
Плоской фигурой
Двумя
параллельными
прямыми
Двумя
пересекающимися
прямыми
Следами плоскости
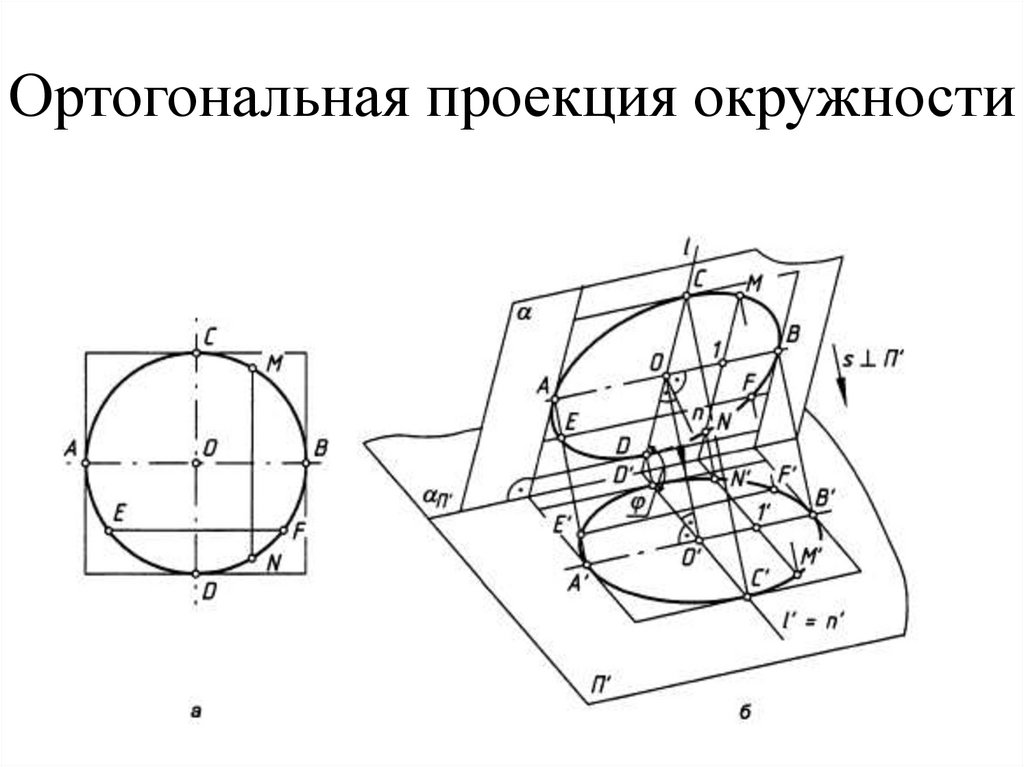
23. Ортогональная проекция окружности
24. Построение ортогональной поверхности окружности
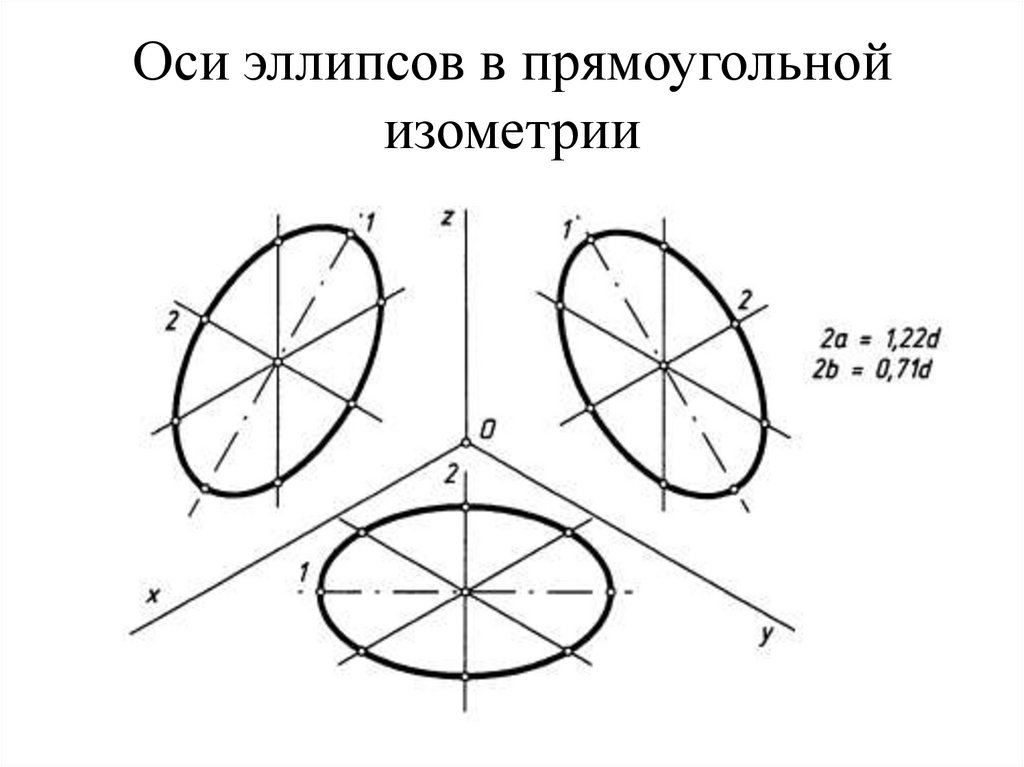
25. Оси эллипсов в прямоугольной изометрии
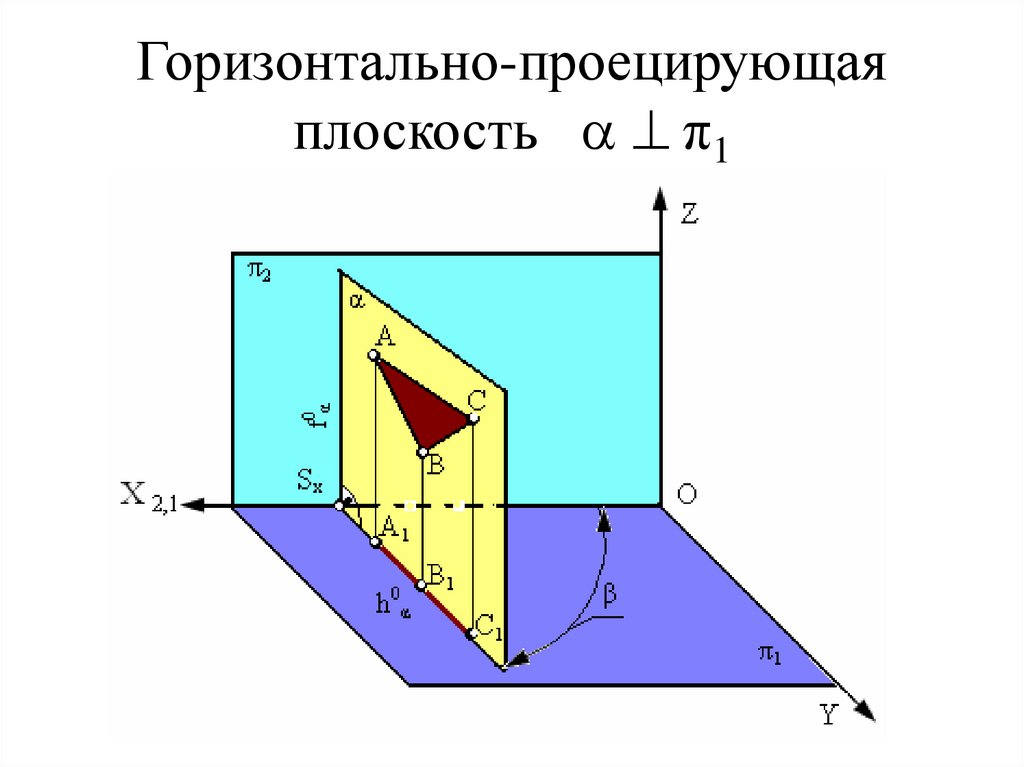
26. Горизонтально-проецирующая плоскость π1
Горизонтально-проецирующаяплоскость π1
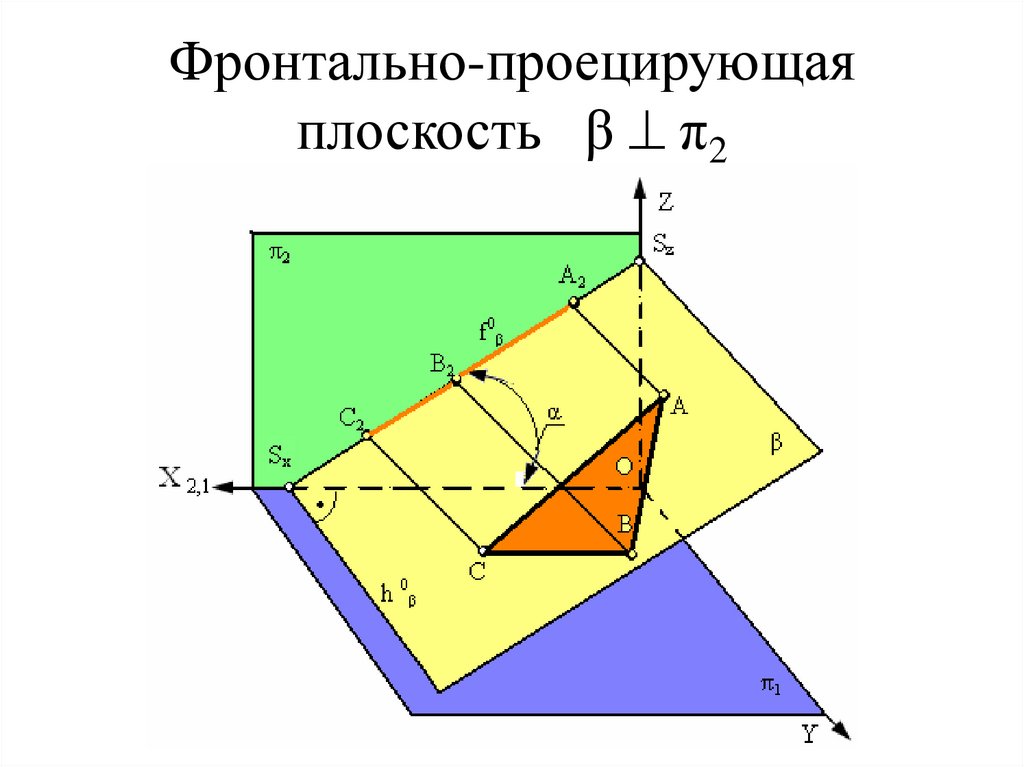
27. Фронтально-проецирующая плоскость β π2
Фронтально-проецирующаяплоскость β π2
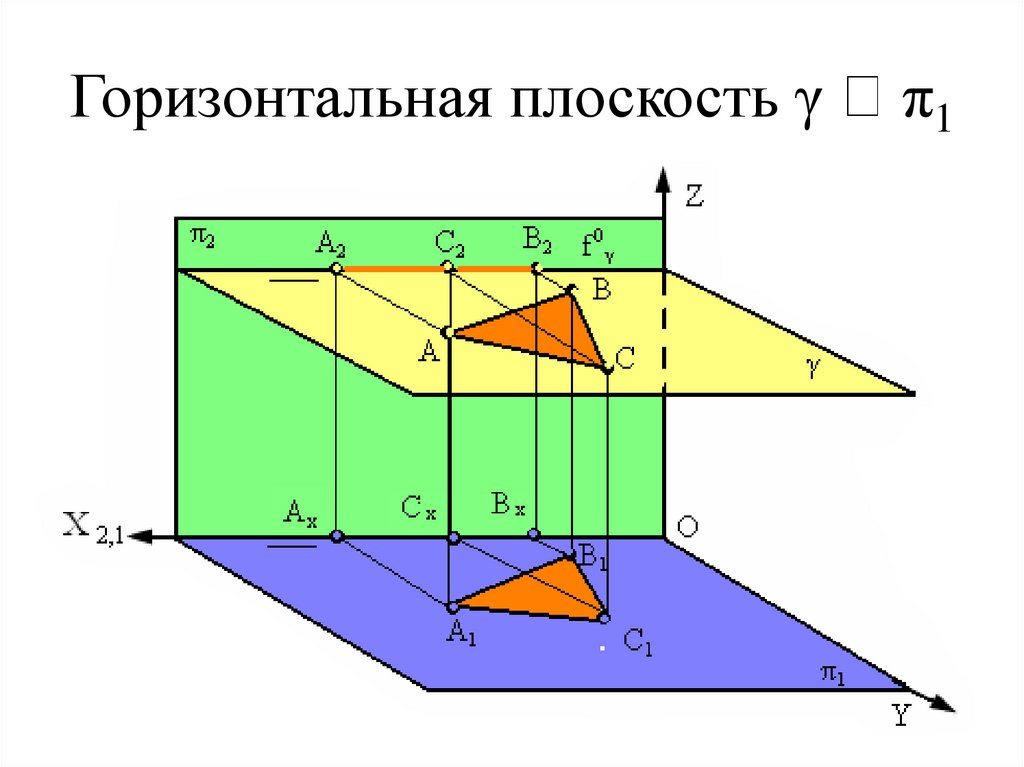
28. Горизонтальная плоскость γ π1
Горизонтальная плоскость γπ1
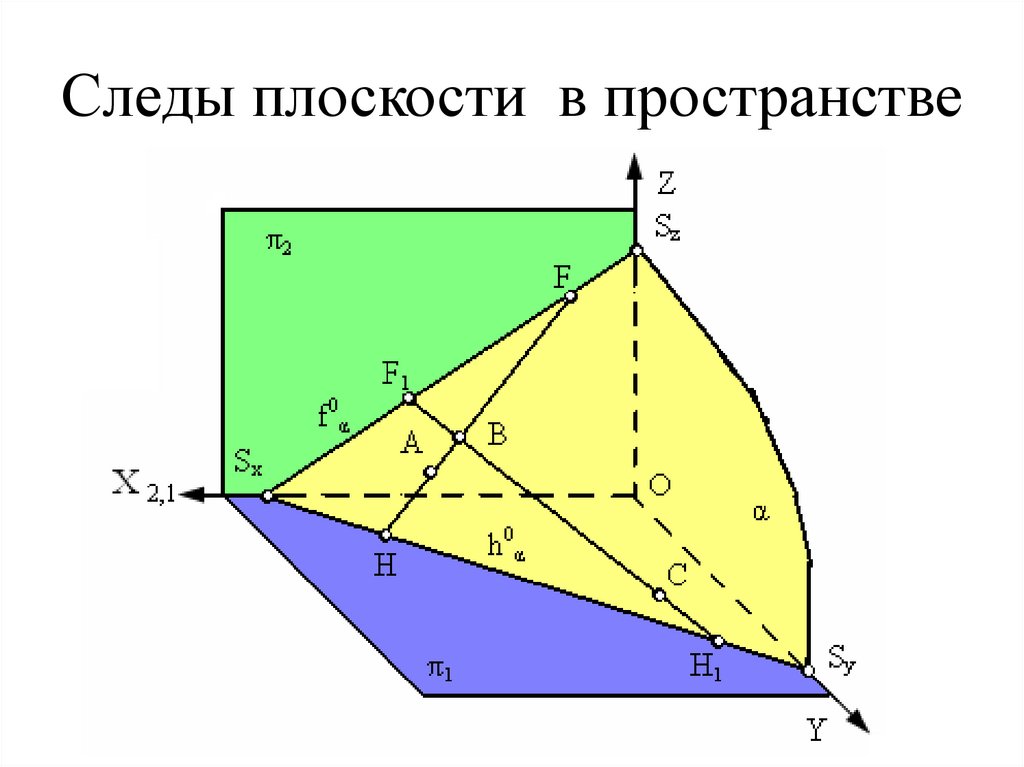
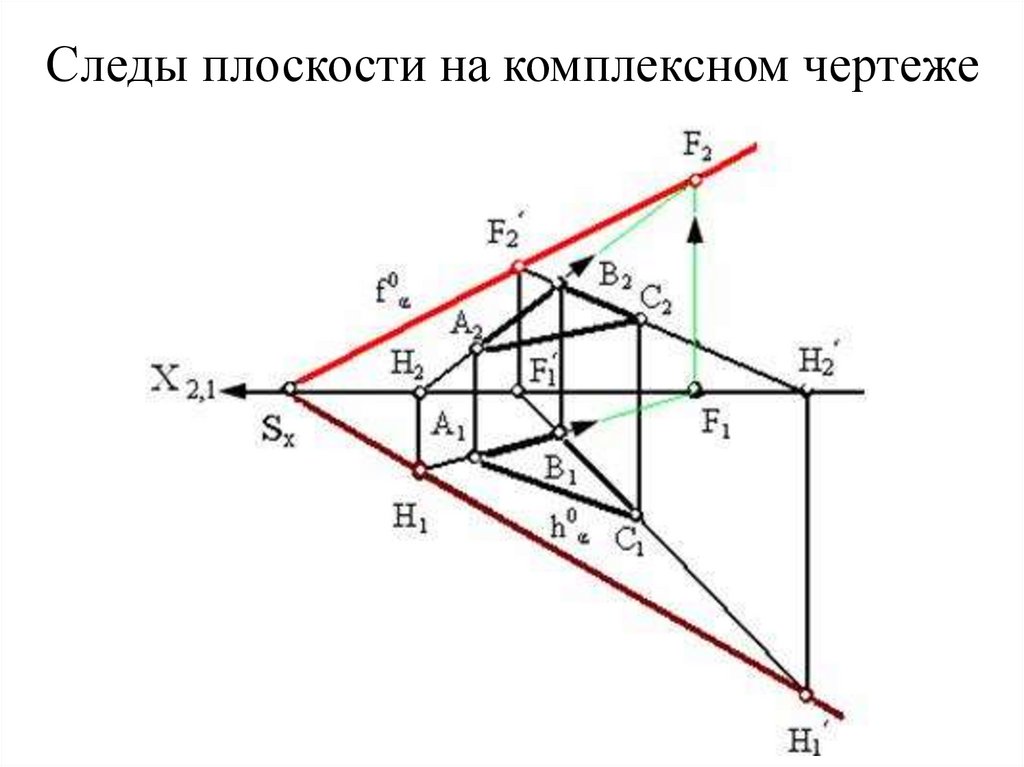
29. Следы плоскости в пространстве
Следы плоскости в пространстве30. Следы плоскости на комплексном чертеже
31. Позиционные задачи
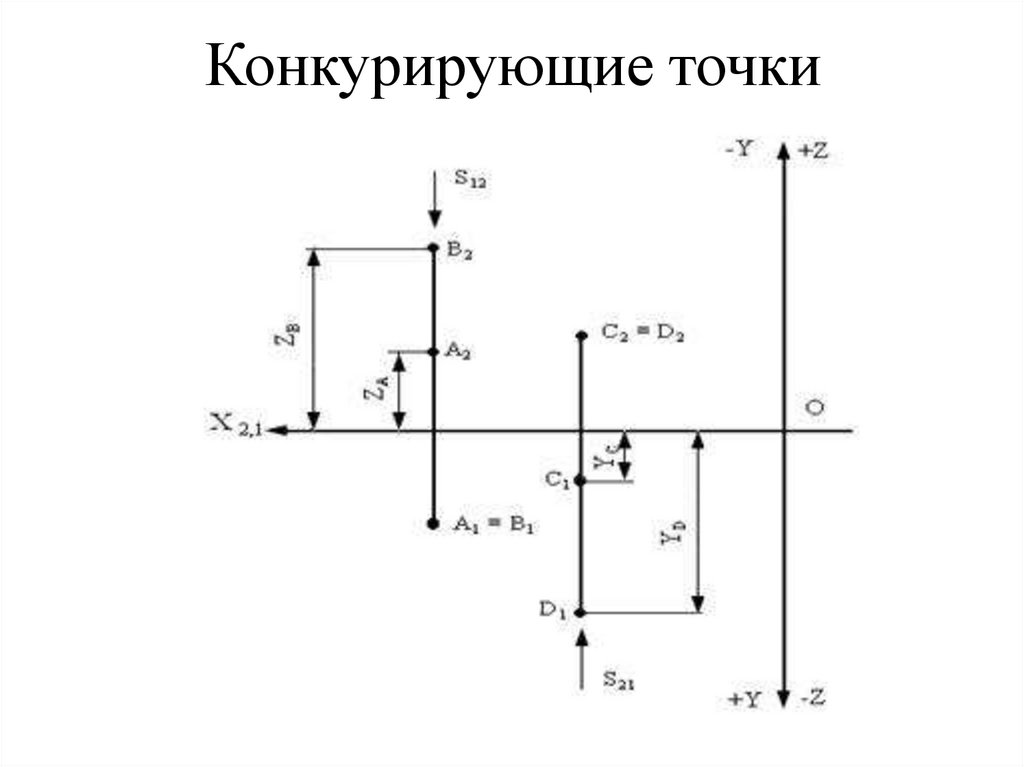
32. Конкурирующие точки
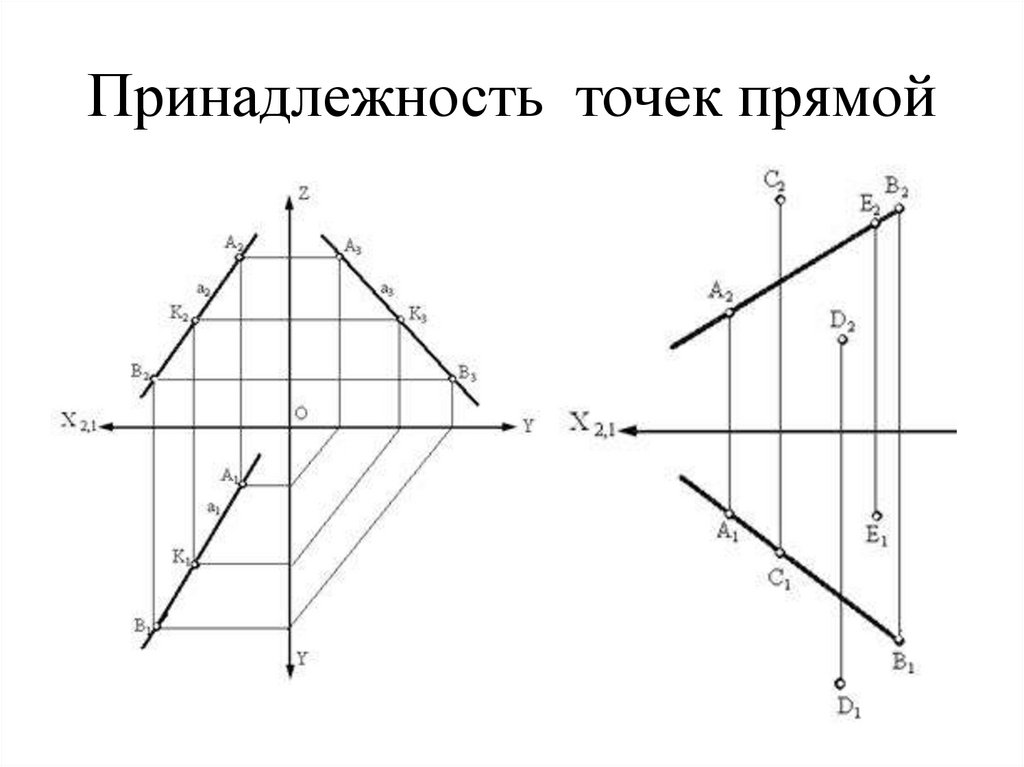
33. Принадлежность точек прямой
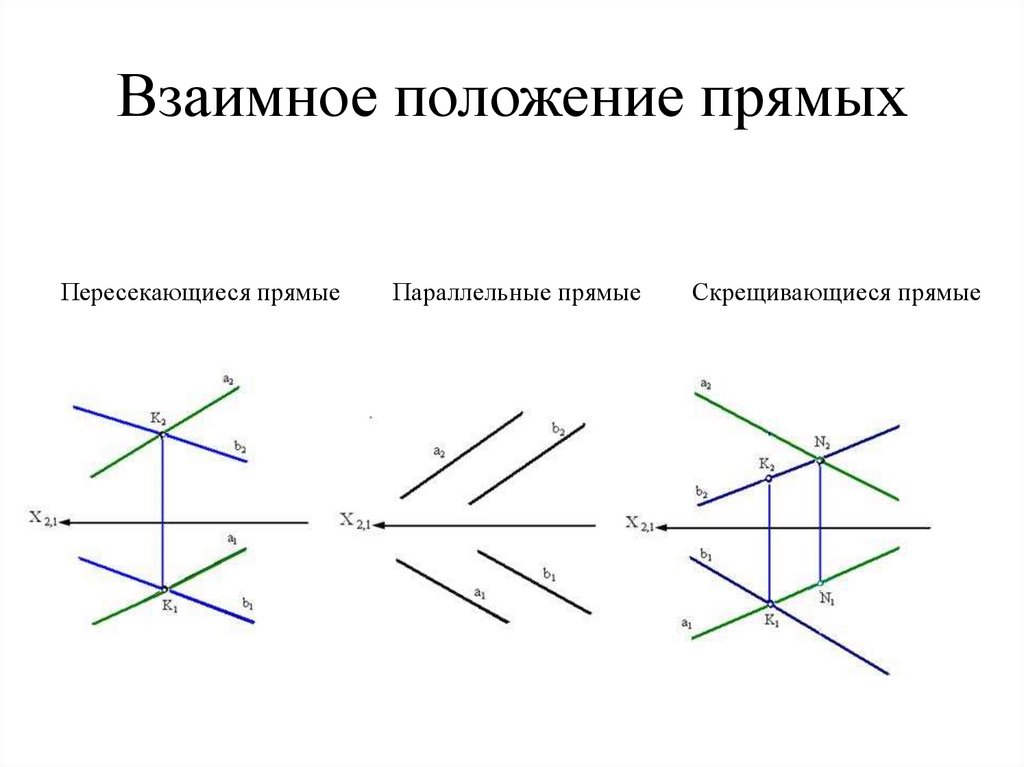
34. Взаимное положение прямых
Пересекающиеся прямыеПараллельные прямые
Скрещивающиеся прямые
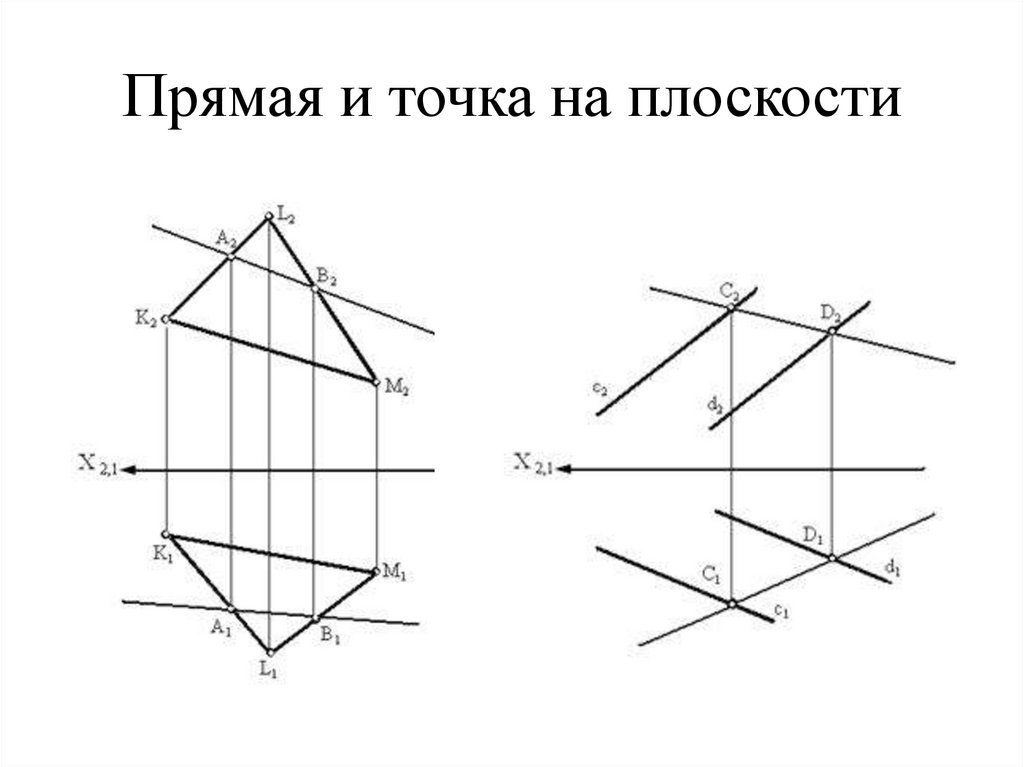
35. Прямая и точка на плоскости
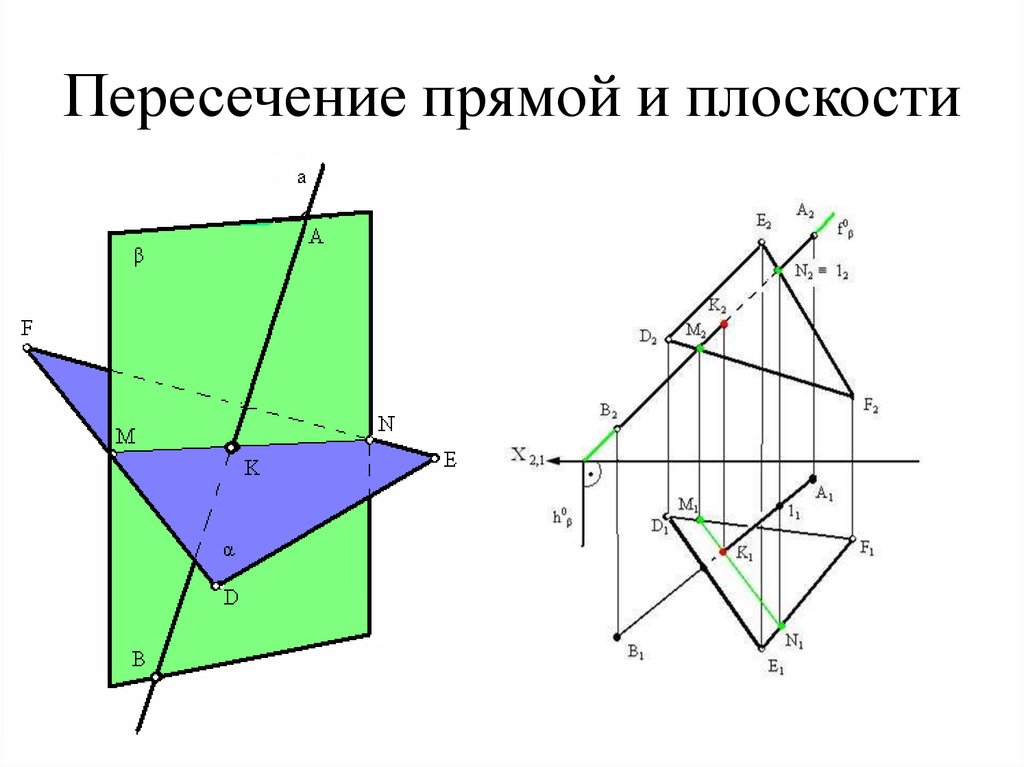
36. Пересечение прямой и плоскости
37. Перпендикулярность прямых и плоскостей
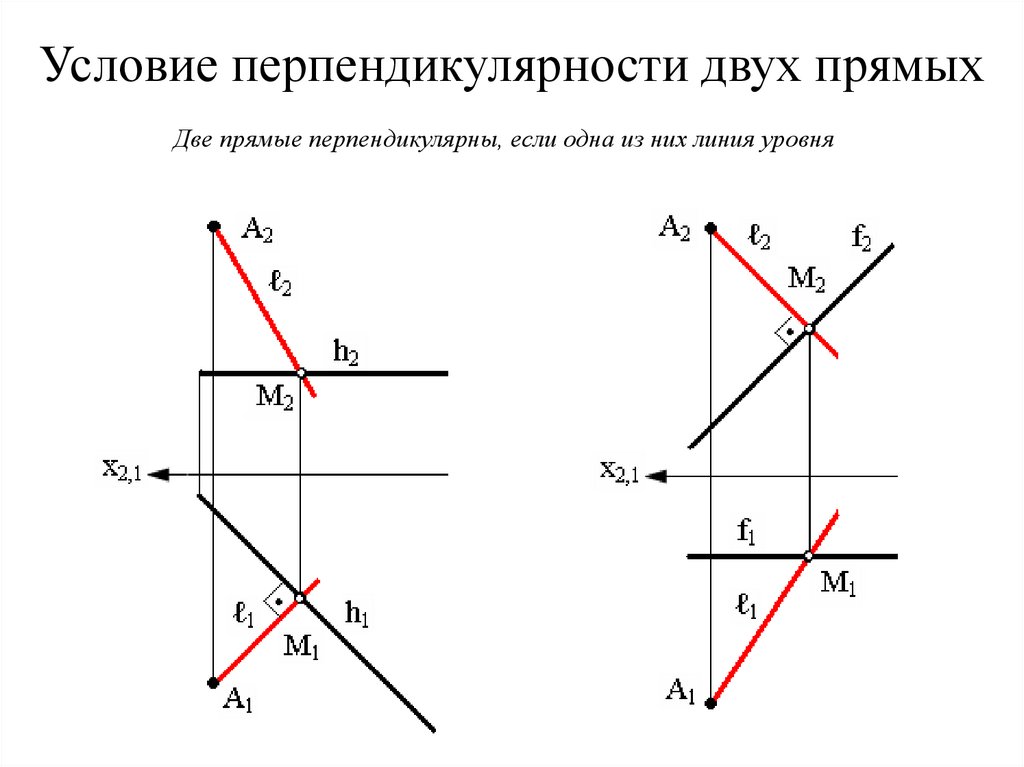
38. Условие перпендикулярности двух прямых
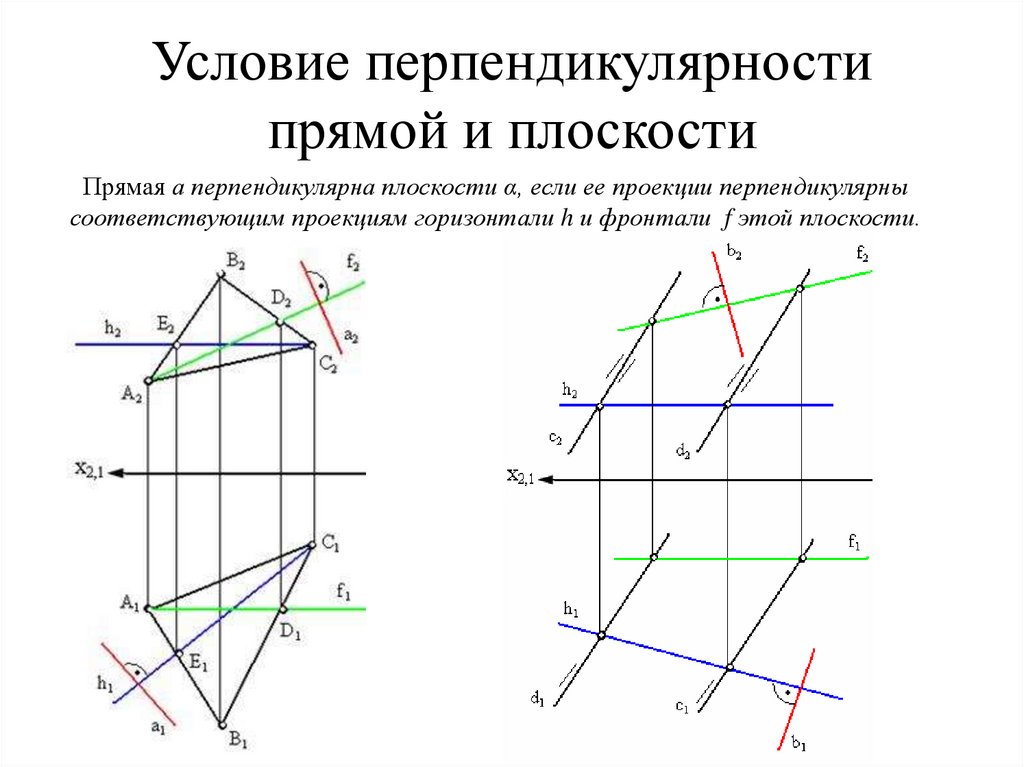
Две прямые перпендикулярны, если одна из них линия уровня39. Условие перпендикулярности прямой и плоскости
Прямая а перпендикулярна плоскости α, если ее проекции перпендикулярнысоответствующим проекциям горизонтали h и фронтали f этой плоскости.
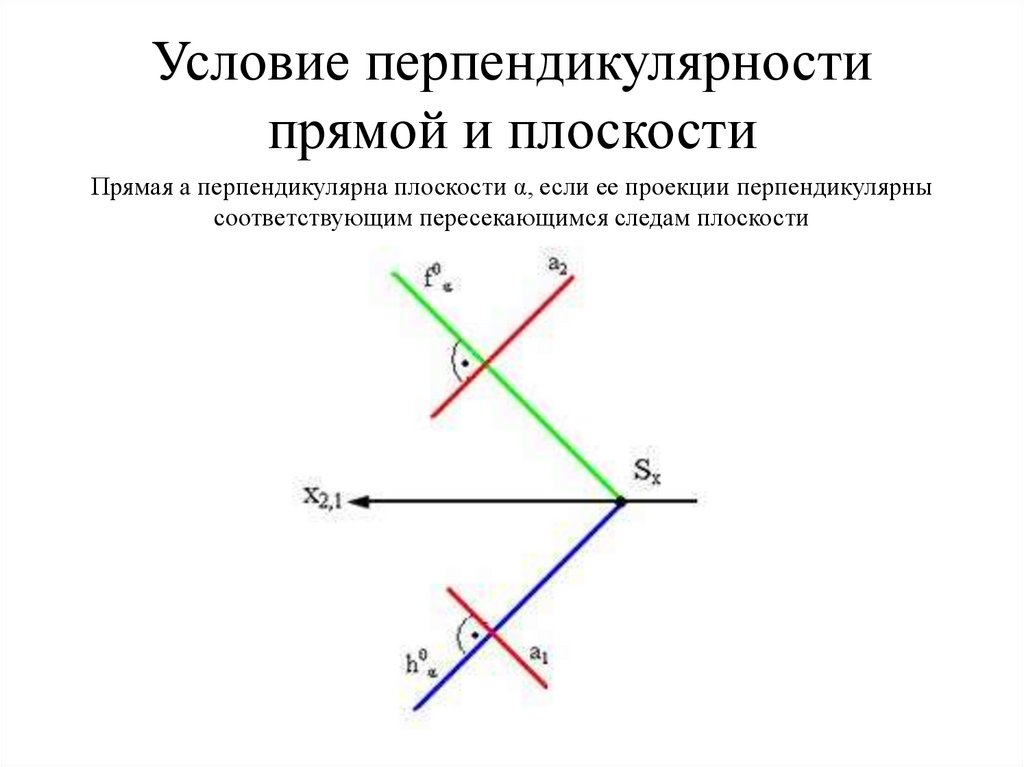
40. Условие перпендикулярности прямой и плоскости
Прямая а перпендикулярна плоскости α, если ее проекции перпендикулярнысоответствующим пересекающимся следам плоскости
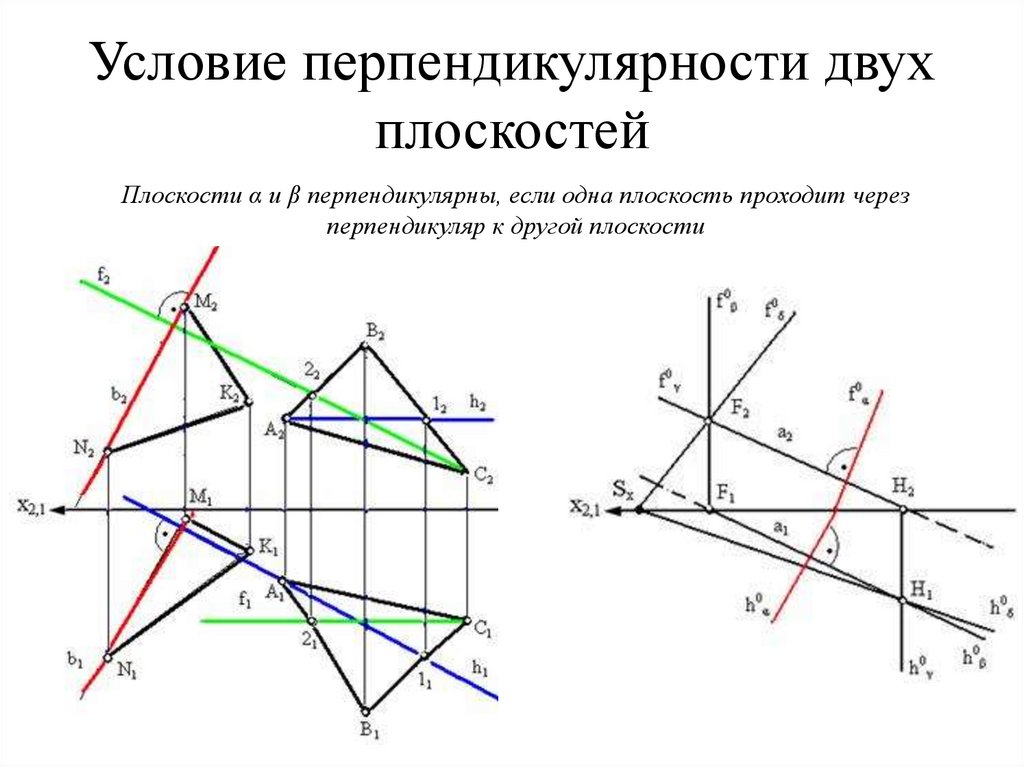
41. Условие перпендикулярности двух плоскостей
Плоскости α и β перпендикулярны, если одна плоскость проходит черезперпендикуляр к другой плоскости
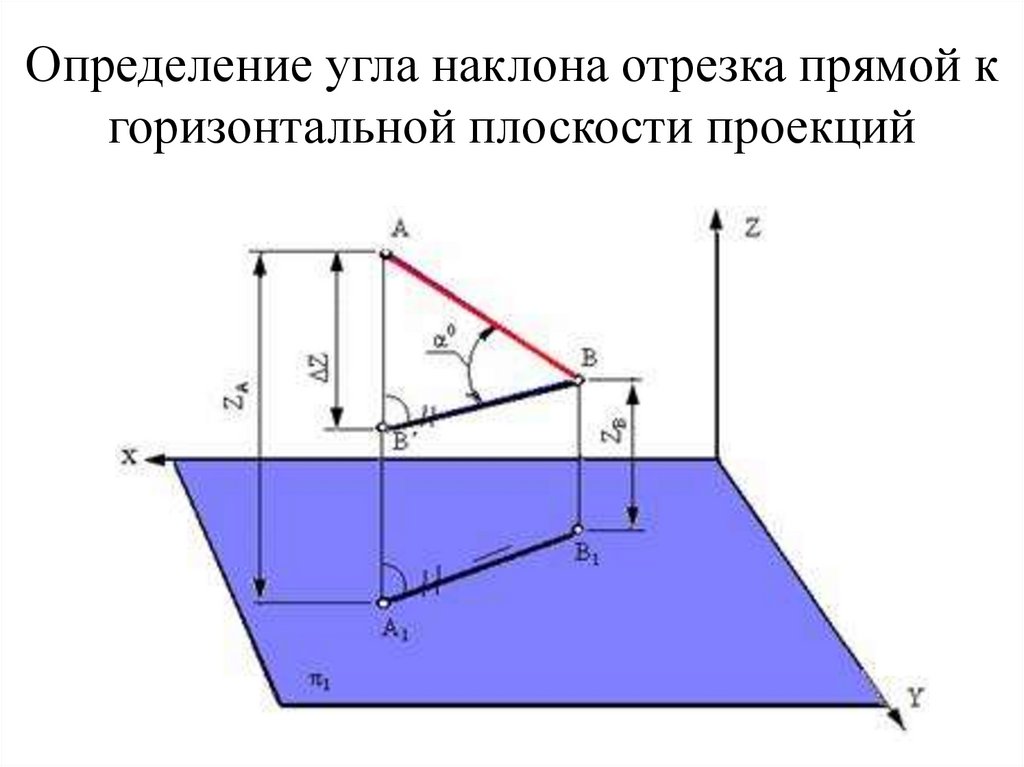
42. Определение угла наклона отрезка прямой к горизонтальной плоскости проекций
43. Определение угла наклона отрезка прямой к фронтальной плоскости проекций
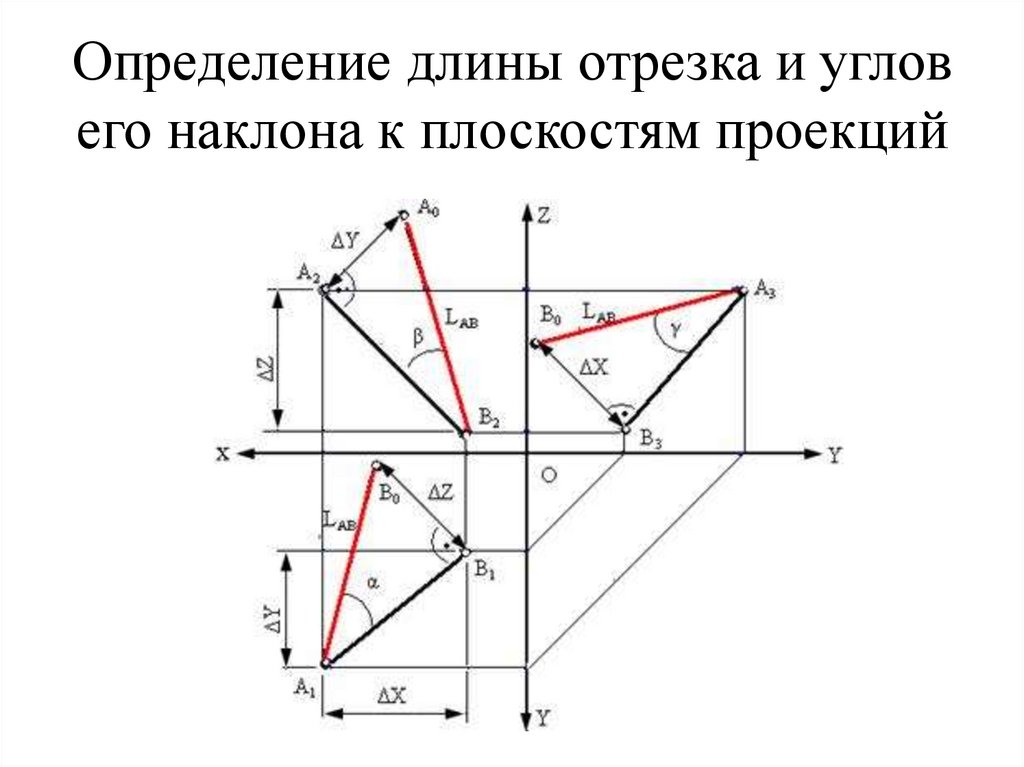
44. Определение длины отрезка и углов его наклона к плоскостям проекций
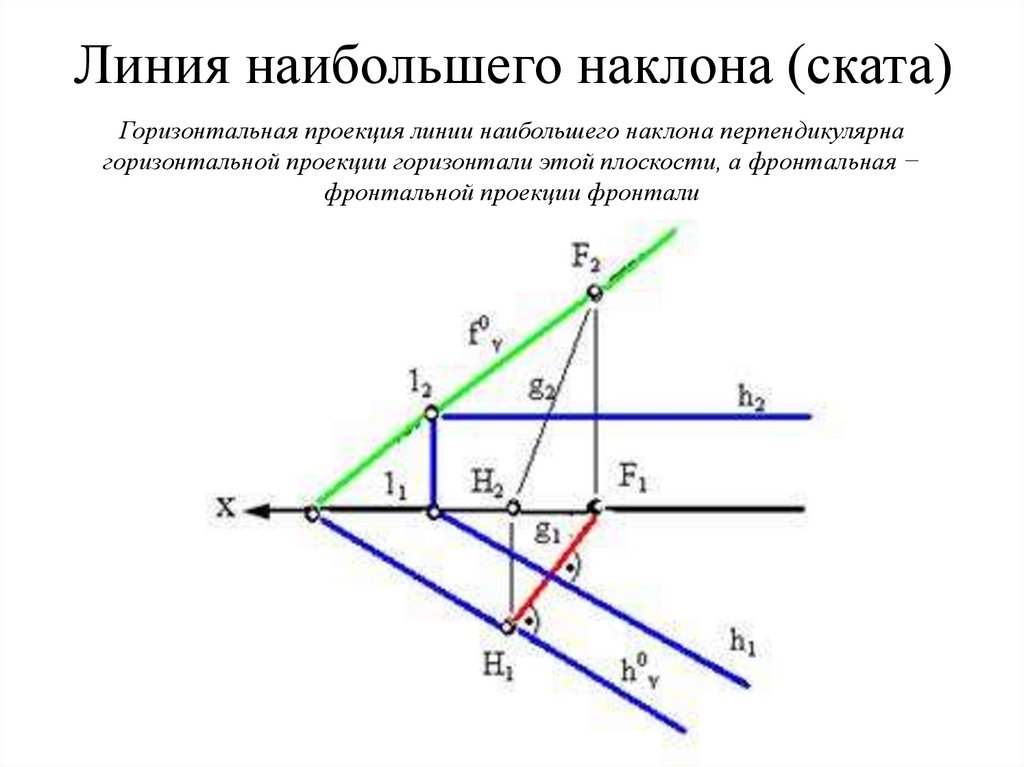
45. Линия наибольшего наклона (ската)
Горизонтальная проекция линии наибольшего наклона перпендикулярнагоризонтальной проекции горизонтали этой плоскости, а фронтальная −
фронтальной проекции фронтали
46. Преобразования комплексного чертежа
47.
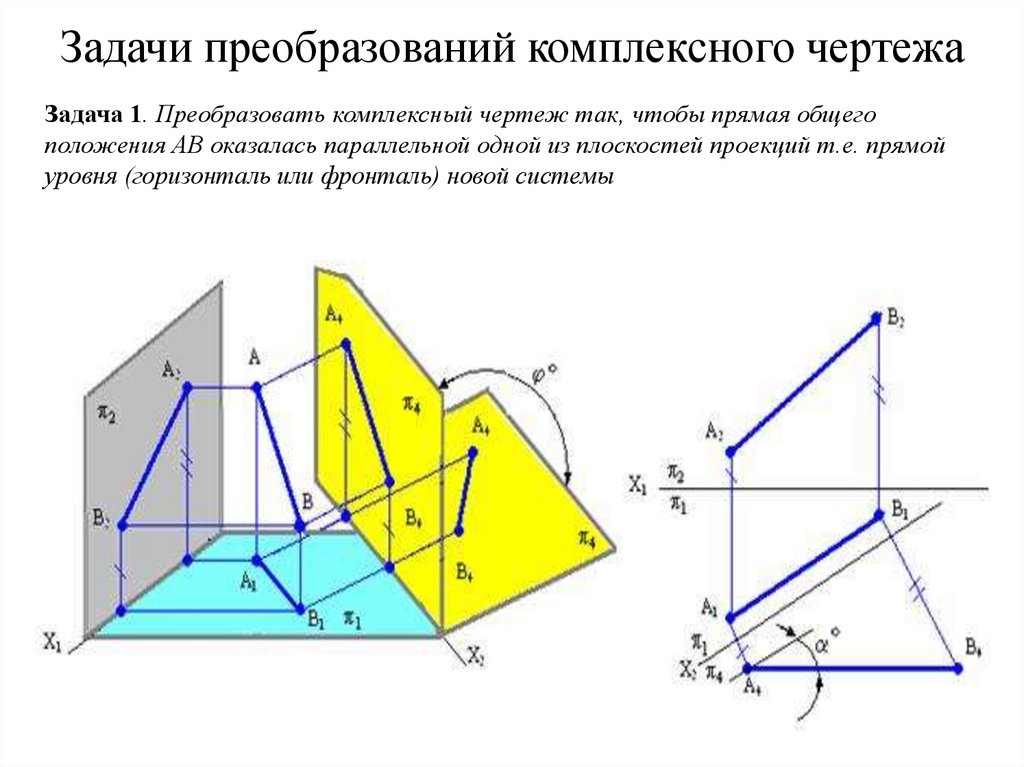
Задачи преобразований комплексного чертежаЗадача 1. Преобразовать комплексный чертеж так, чтобы прямая общего
положения АВ оказалась параллельной одной из плоскостей проекций т.е. прямой
уровня (горизонталь или фронталь) новой системы
48.
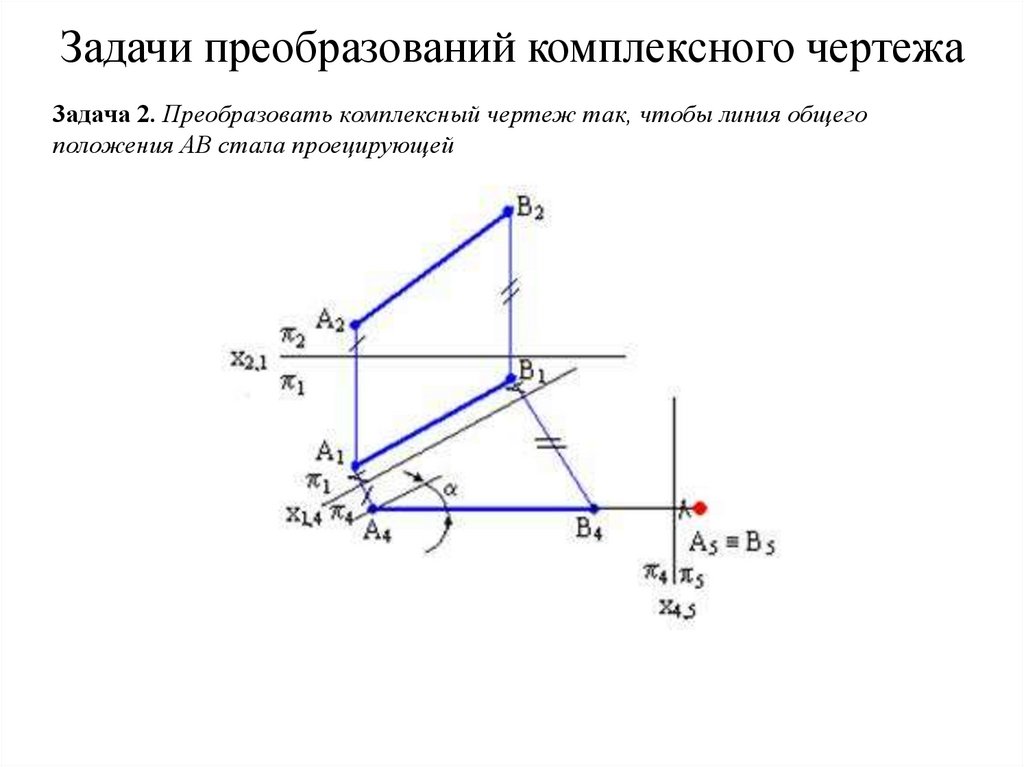
Задачи преобразований комплексного чертежа3адача 2. Преобразовать комплексный чертеж так, чтобы линия общего
положения АВ стала проецирующей
49. Задачи преобразований комплексного чертежа
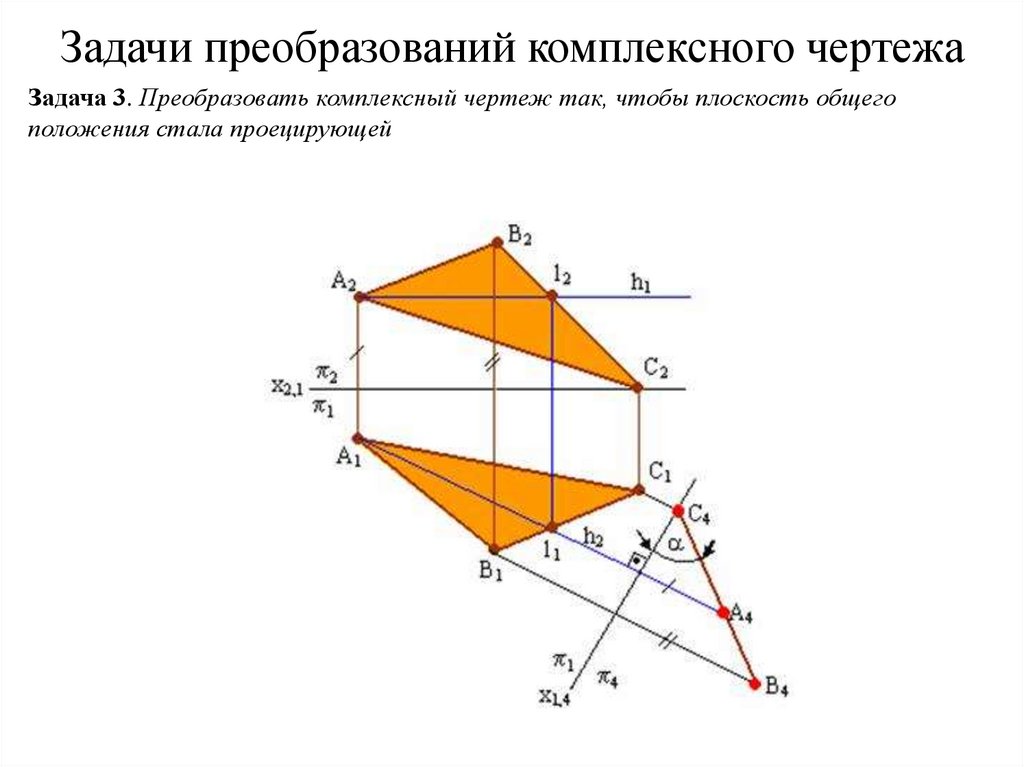
Задача 3. Преобразовать комплексный чертеж так, чтобы плоскость общегоположения стала проецирующей
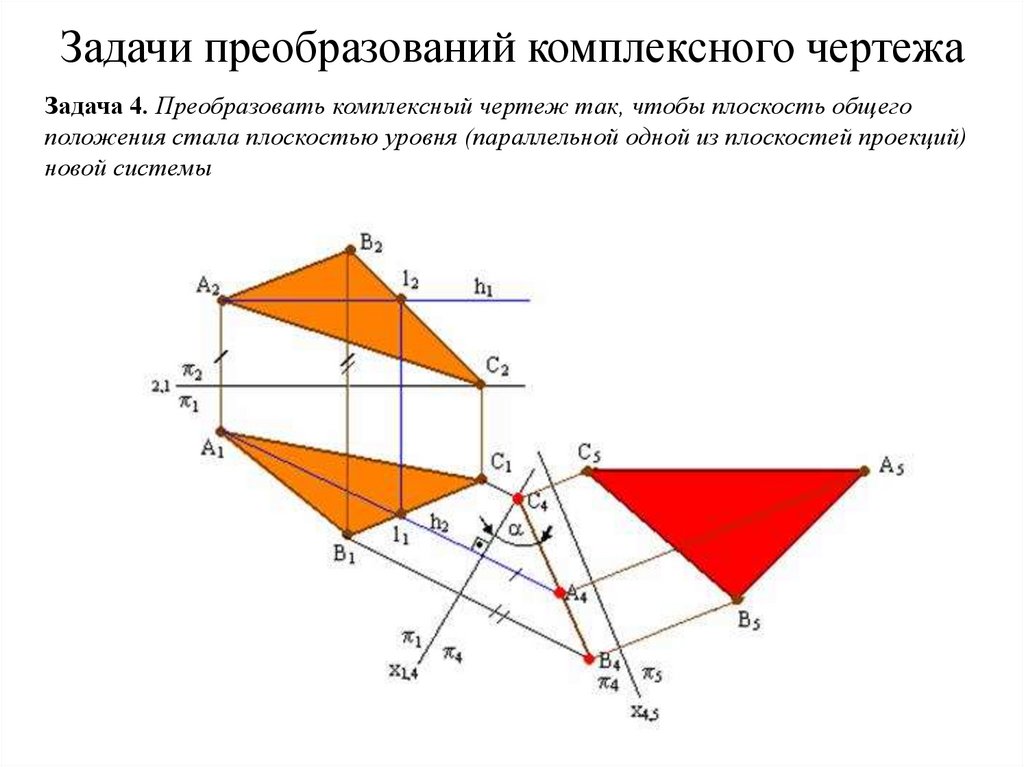
50. Задачи преобразований комплексного чертежа
Задача 4. Преобразовать комплексный чертеж так, чтобы плоскость общегоположения стала плоскостью уровня (параллельной одной из плоскостей проекций)
новой системы
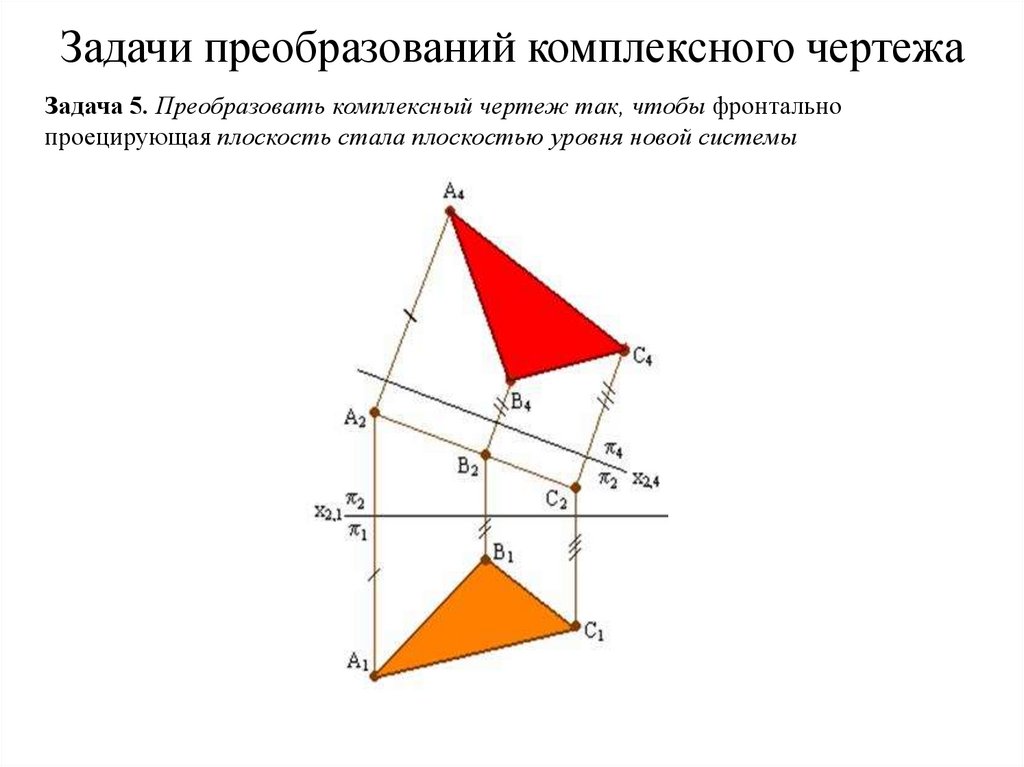
51. Задачи преобразований комплексного чертежа
Задача 5. Преобразовать комплексный чертеж так, чтобы фронтальнопроецирующая плоскость стала плоскостью уровня новой системы
52. Метрические задачи
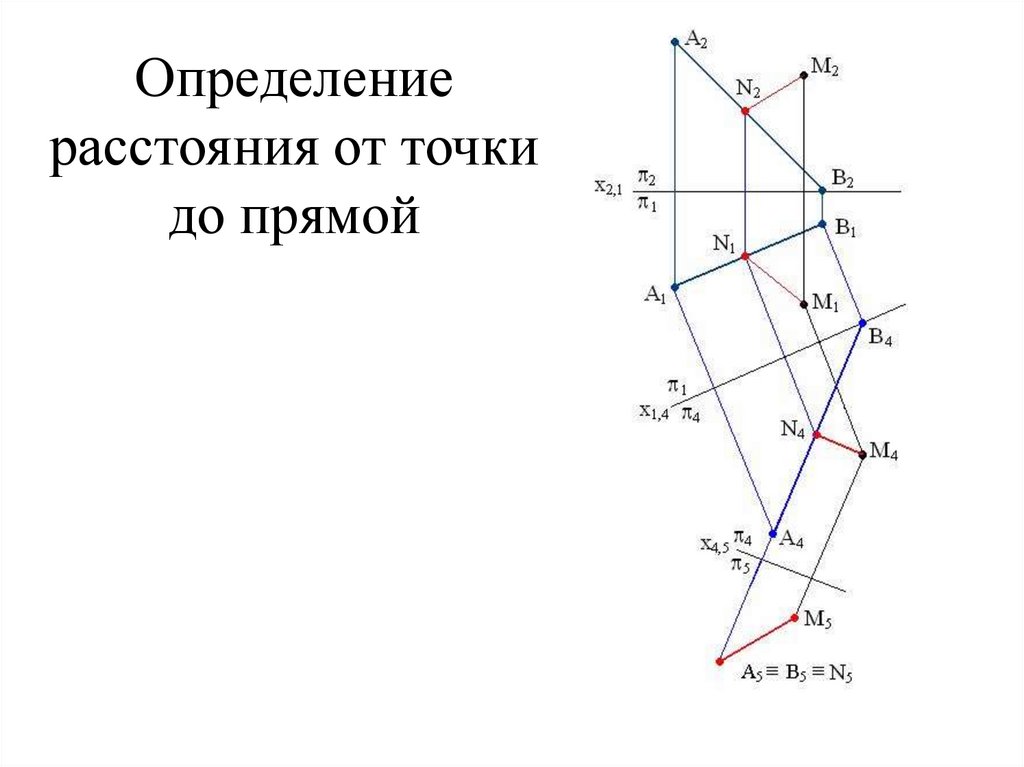
53. Определение расстояния от точки до прямой
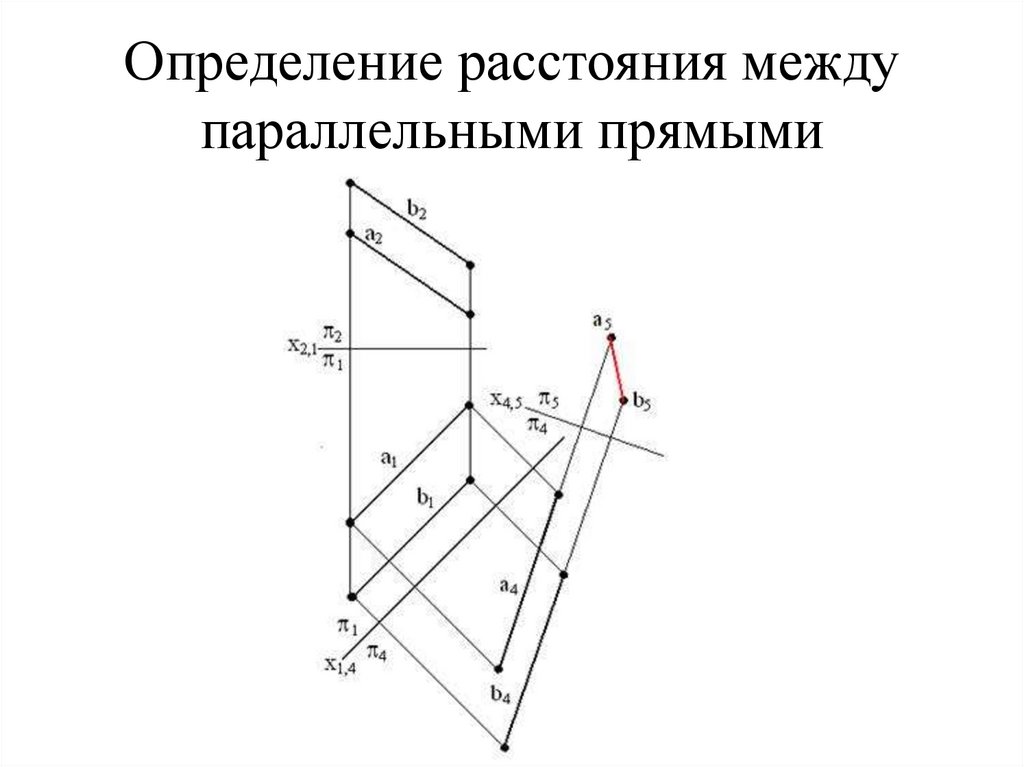
54. Определение расстояния между параллельными прямыми
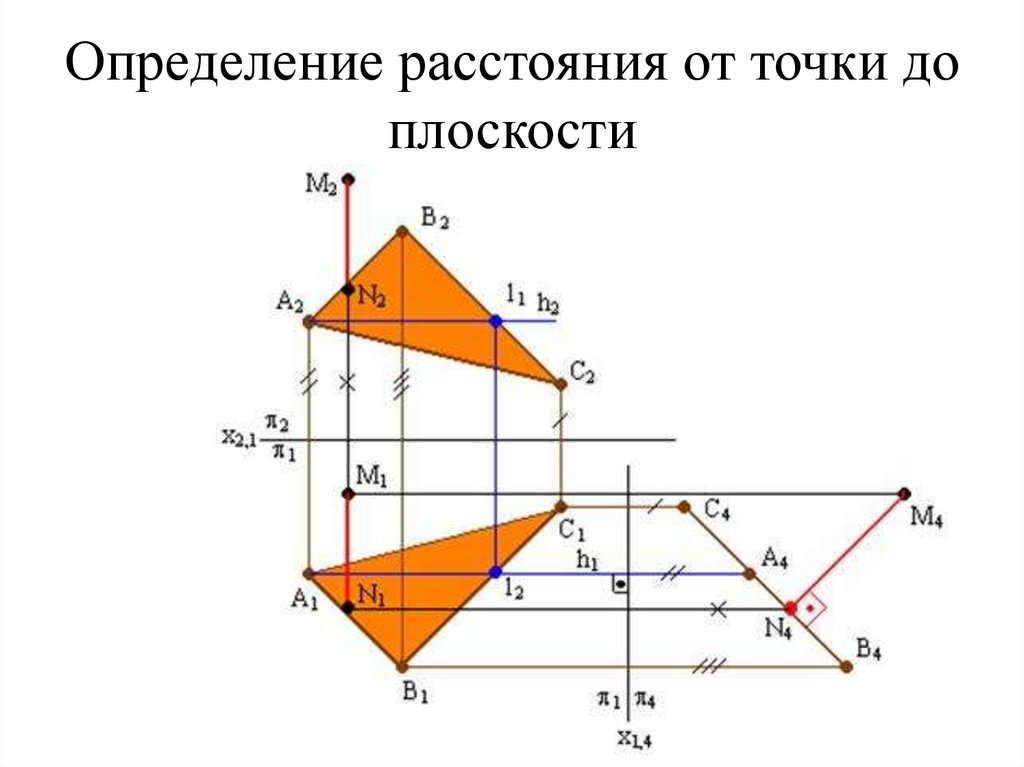
55. Определение расстояния от точки до плоскости
56. Определение угла, образованного двумя пересекающимися прямыми
Определение угла, образованногодвумя пересекающимися прямыми
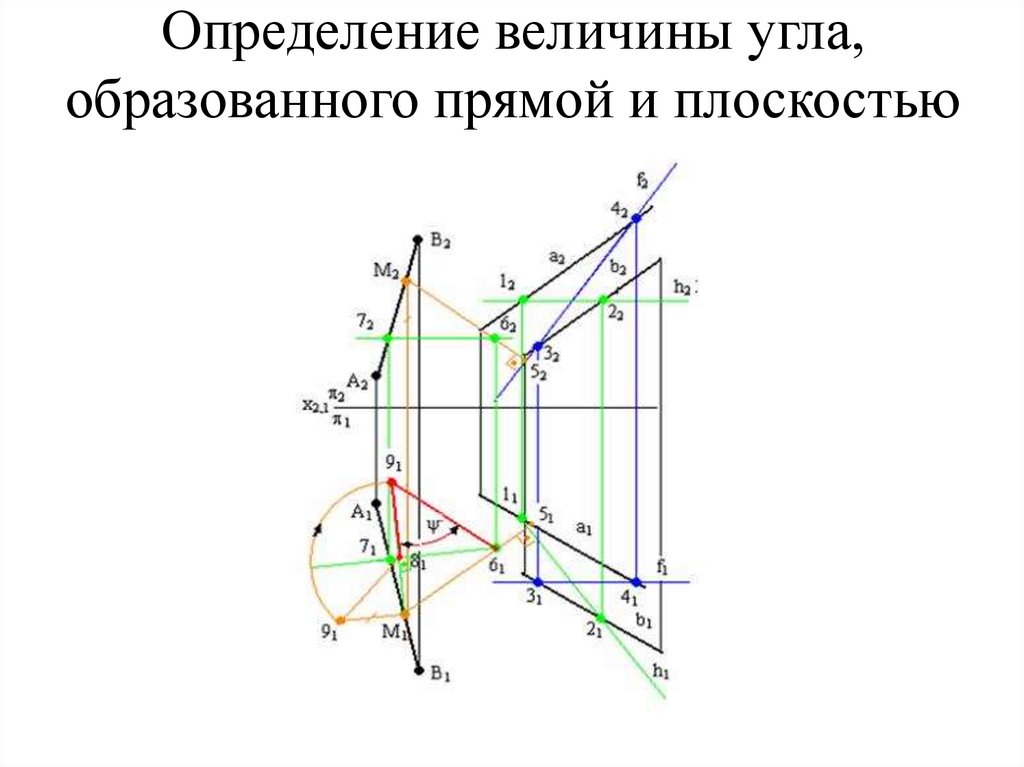
57. Определение величины угла, образованного прямой и плоскостью
58. Определение величины угла между двумя пересекающимися плоскостями
Мерой угла между двумя плоскостями служит линейный угол, образованный двумяпрямыми – сечениями граней этого угла плоскостью, перпендикулярной к их ребру.
В задаче необходимо линию пересечения АВ плоскостей ∑ и Γ преобразовать в
прямую уровня, а затем в линию проецирующую.
Общей схемой решения задач на построение в плоскости общего положения
геометрических фигур по заданным размерам является:
1) преобразование заданной плоскости общего положения в плоскость уровня;
2) решение в плоскости уровня заданной метрической задачи.
59. Поверхности
60. Поверхности. Понятия и определения
Поверхность - совокупность всех последовательных положений некоторойперемещающейся в пространстве линии.
Линия - непрерывное однопараметрическое множество точек.
Поверхность - непрерывное двупараметрическое множество точек.
Закон перемещения линии целесообразно задавать графически в виде
совокупности линий и указаний о характере перемещения линии. Эти указания
могут быть заданы графически, в частности с помощью направляющей
поверхности. В процессе образования поверхностей линия может оставаться
неизменной или менять свою форму. Такой способ образования поверхности
называется кинематическим, а сама поверхность − кинематической.
Закон перемещения образующей линии, как правило, задается при помощи
направляющих линий и алгоритма перемещения образующей по направляющим.
Подвижная линия называется образующей, неподвижные линии и поверхность –
направляющими.
Примером такого способа образования могут служить все технологические
процессы обработки металлов режущей кромкой, когда поверхность изделия несет
на себе «отпечаток» профиля резца.
61. Способы задания кривых поверхностей
1. Аналитический - при помощи уравненийПример поверхности, заданной аналитически
62. Способы задания кривых поверхностей
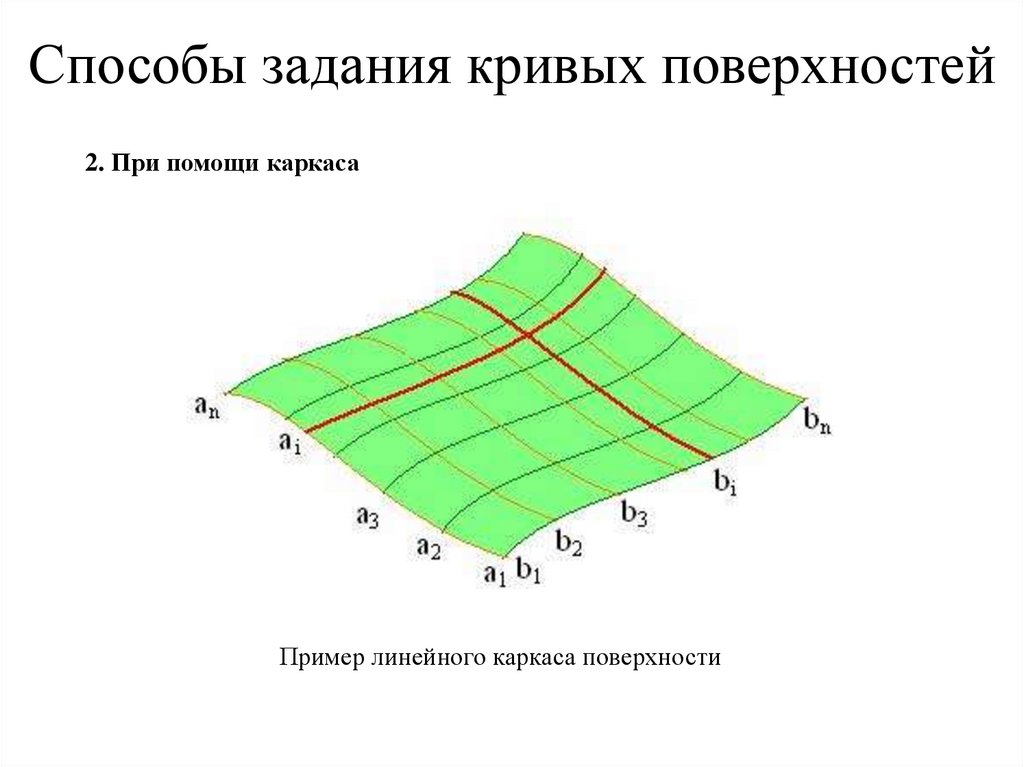
2. При помощи каркасаПример линейного каркаса поверхности
63. Способы задания кривых поверхностей
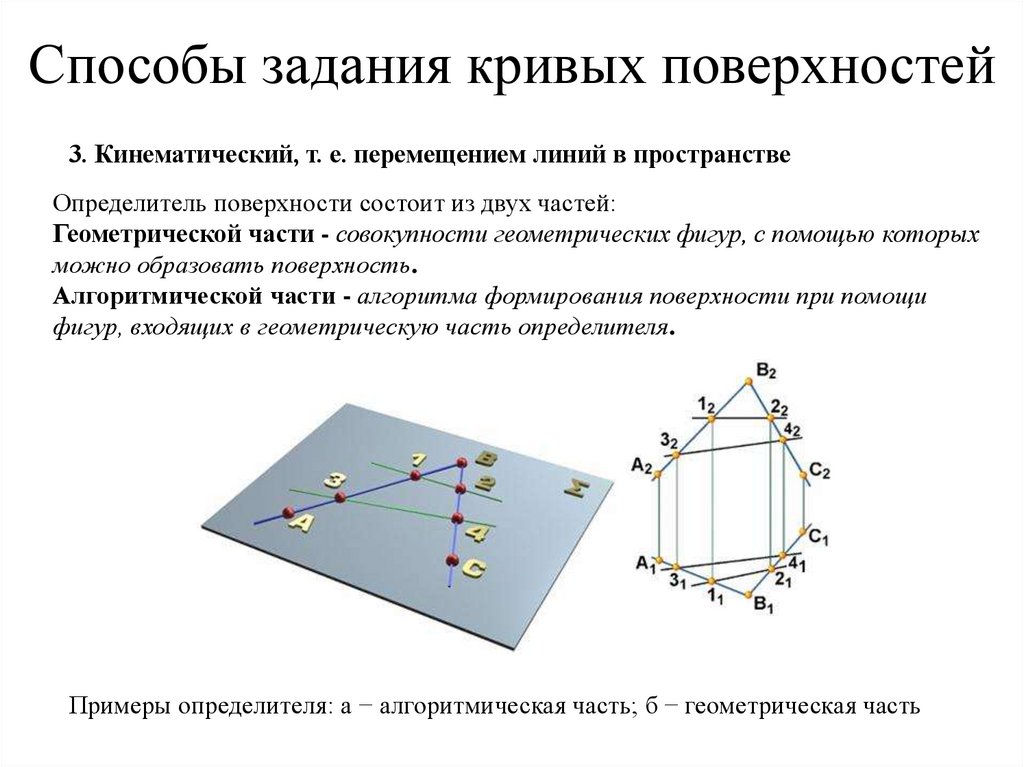
3. Кинематический, т. е. перемещением линий в пространствеОпределитель поверхности состоит из двух частей:
Геометрической части - совокупности геометрических фигур, с помощью которых
можно образовать поверхность.
Алгоритмической части - алгоритма формирования поверхности при помощи
фигур, входящих в геометрическую часть определителя.
Примеры определителя: а − алгоритмическая часть; б − геометрическая часть
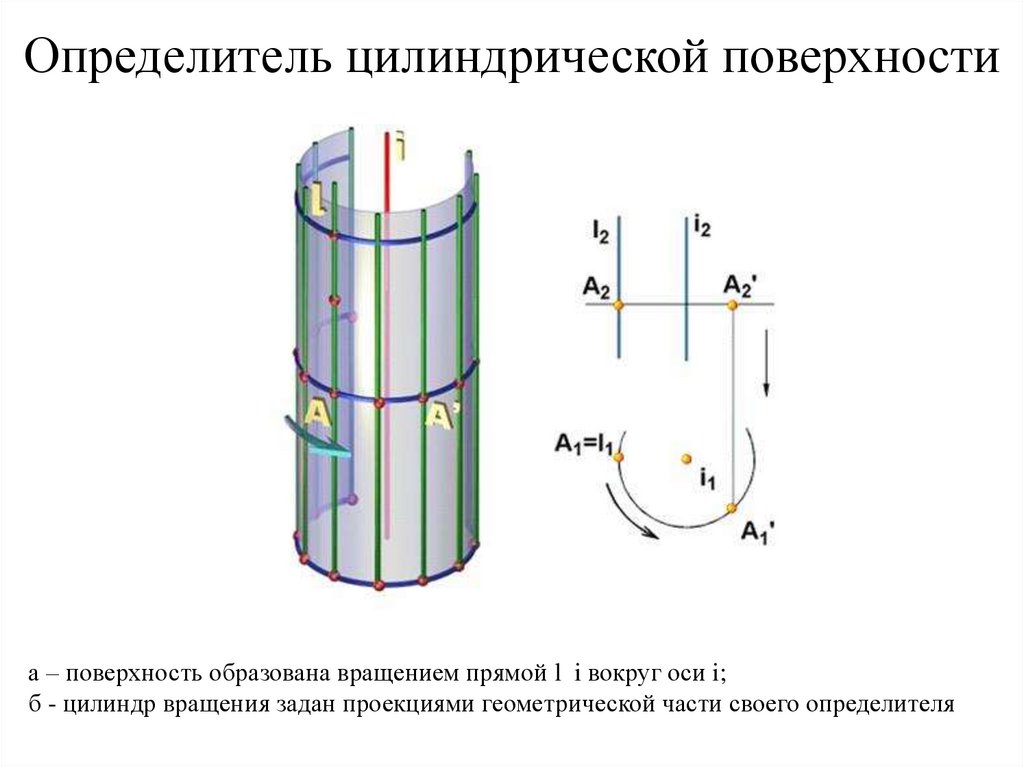
64. Определитель цилиндрической поверхности
а – поверхность образована вращением прямой l i вокруг оси i;б - цилиндр вращения задан проекциями геометрической части своего определителя
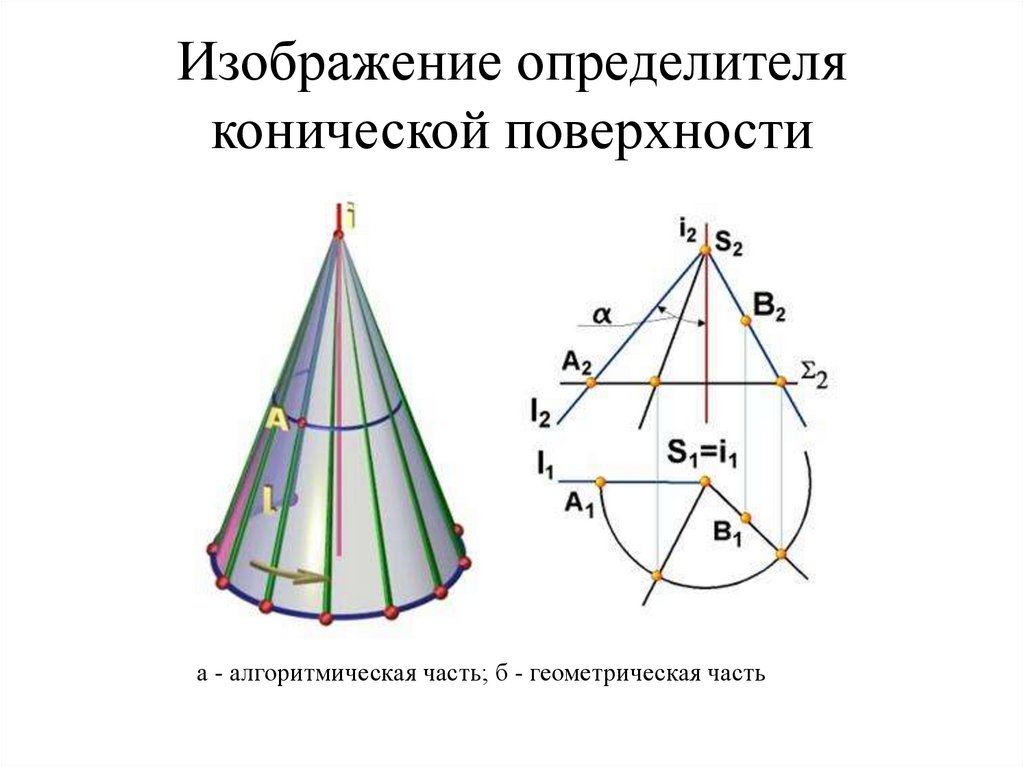
65. Изображение определителя конической поверхности
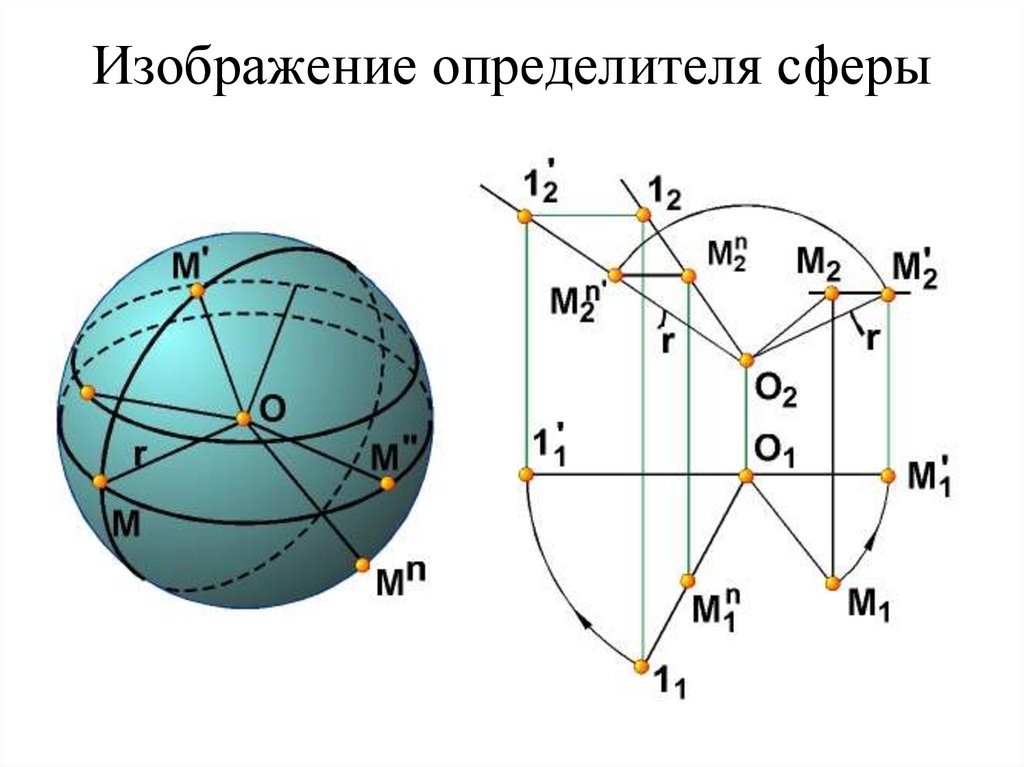
а - алгоритмическая часть; б - геометрическая часть66. Изображение определителя сферы
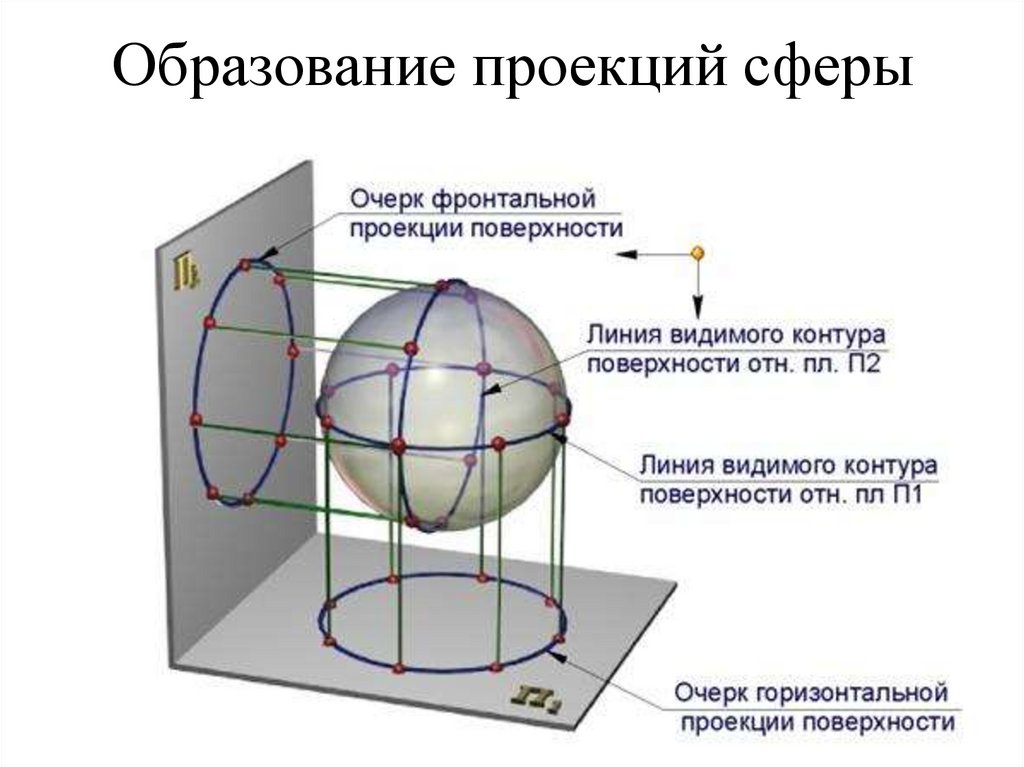
Изображение определителя сферы67. Образование проекций сферы
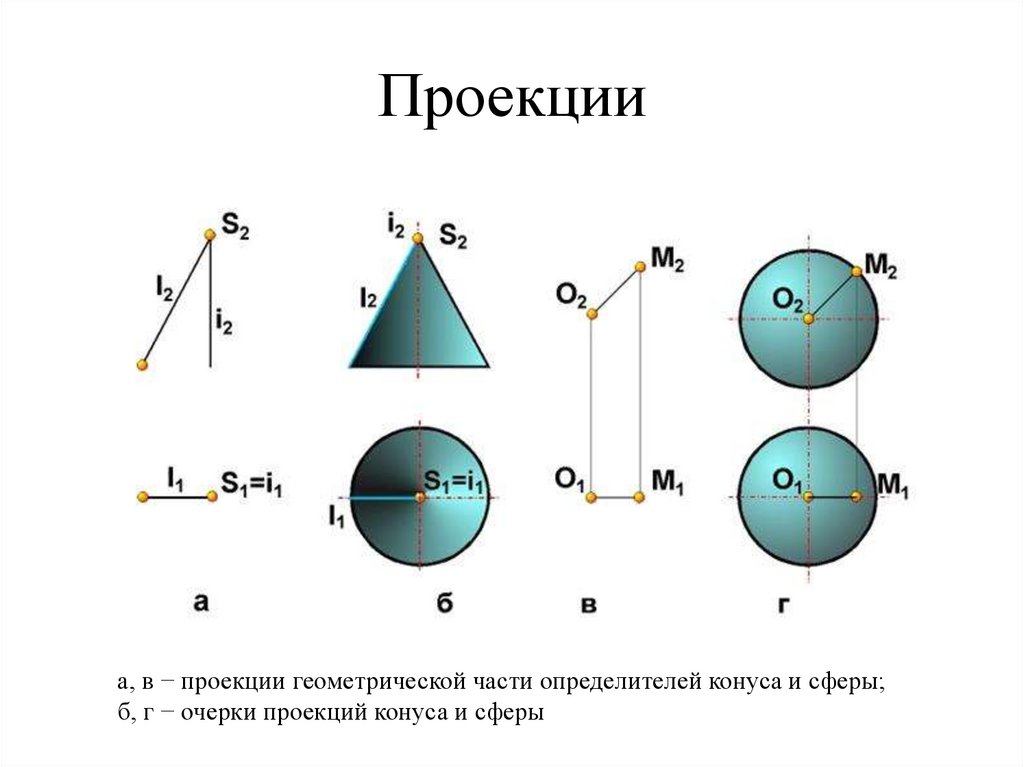
68. Проекции
а, в − проекции геометрической части определителей конуса и сферы;б, г − очерки проекций конуса и сферы
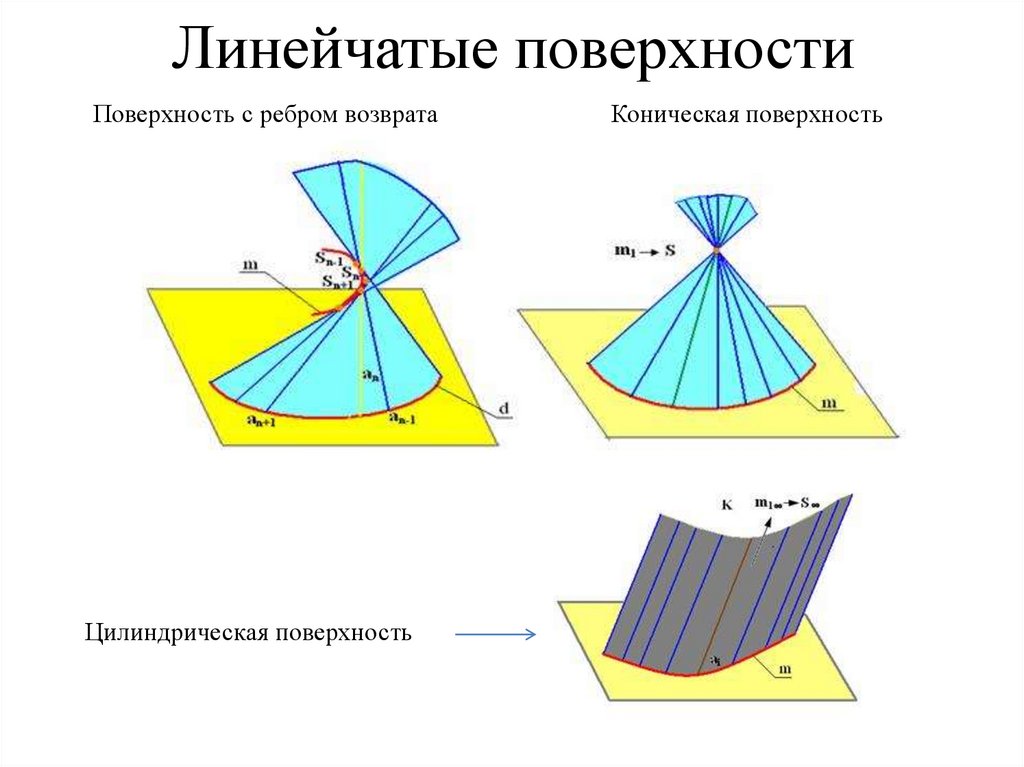
69. Линейчатые поверхности
Поверхность с ребром возвратаЦилиндрическая поверхность
Коническая поверхность
70. Неразвертывающиеся (косые) линейчатые поверхности
71. Дважды косой цилиндроид
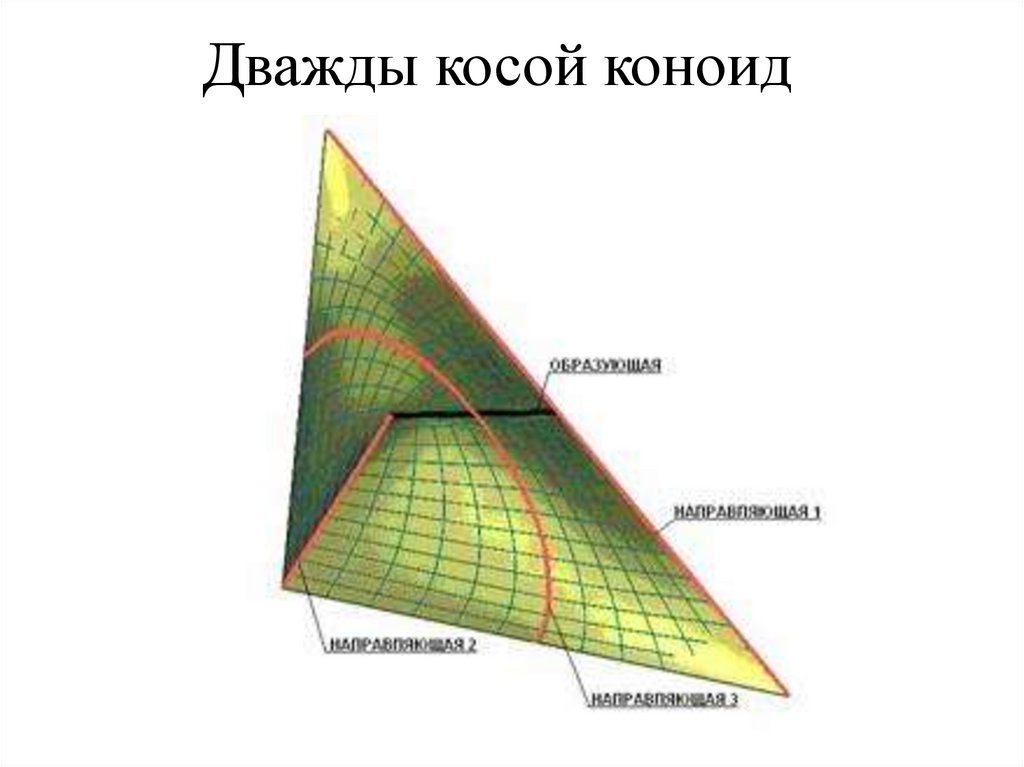
72. Дважды косой коноид
73. Позиционные задачи на поверхности
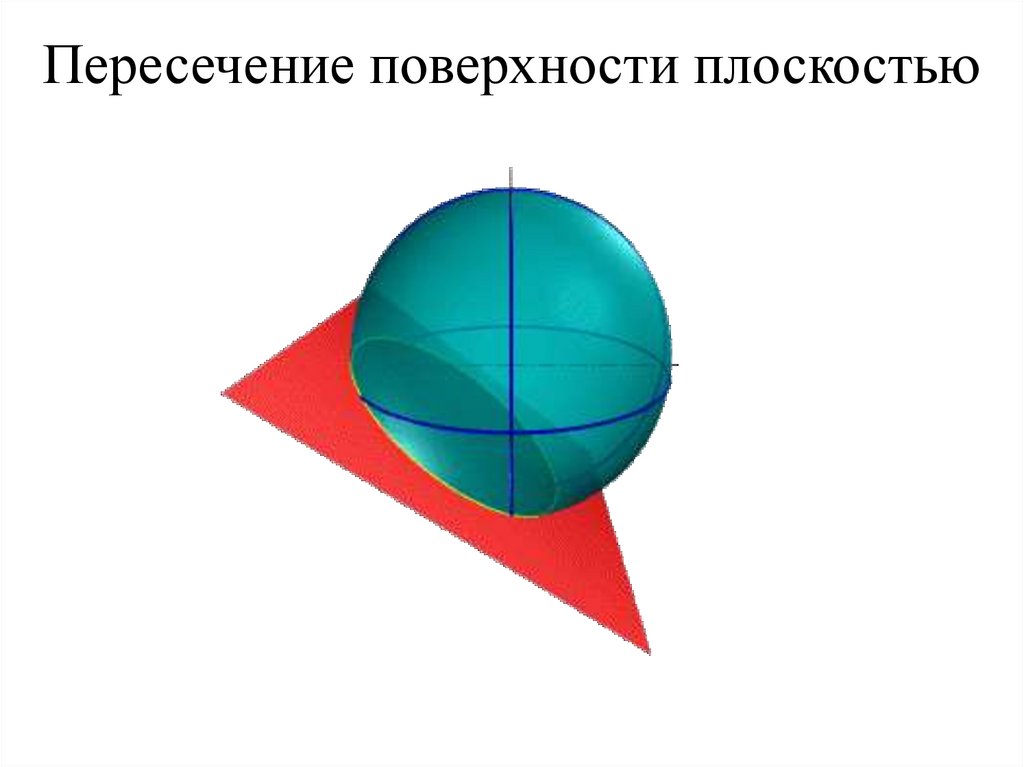
74. Пересечение поверхности плоскостью
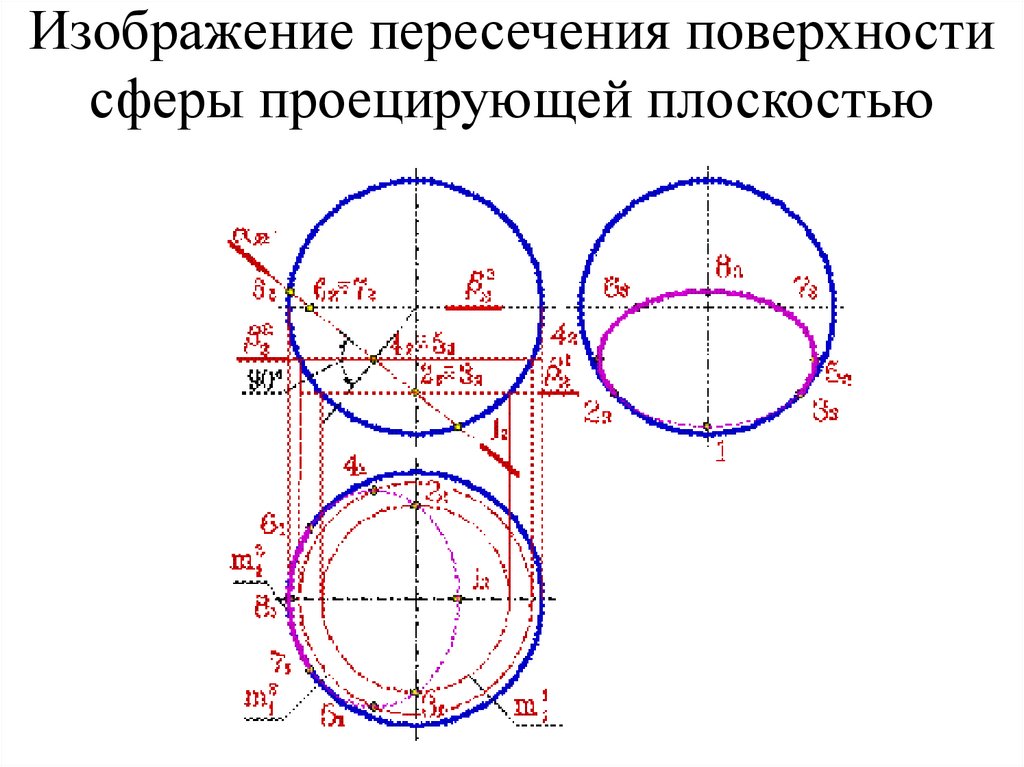
75. Изображение пересечения поверхности сферы проецирующей плоскостью
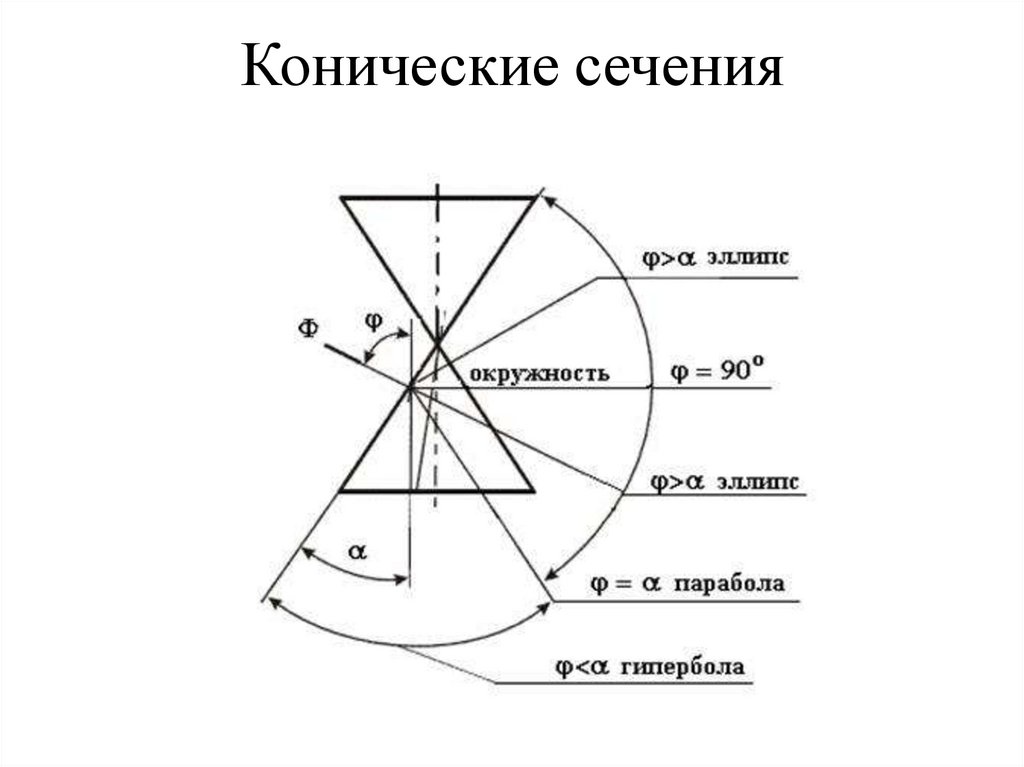
76. Конические сечения
77. Изображение линии сечения поверхности конуса плоскостью (эллипс)
78. Изображение линии сечения поверхности конуса плоскостью (окружность)
79. Изображение линии сечения поверхности конуса плоскостью (парабола)
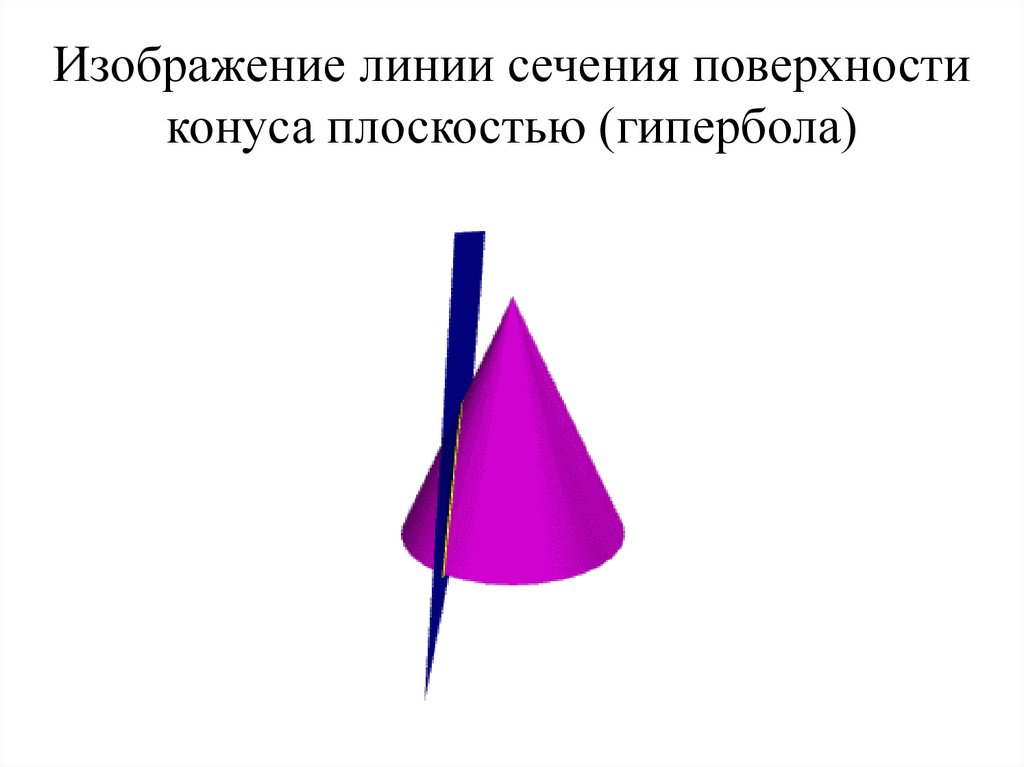
80. Изображение линии сечения поверхности конуса плоскостью (гипербола)
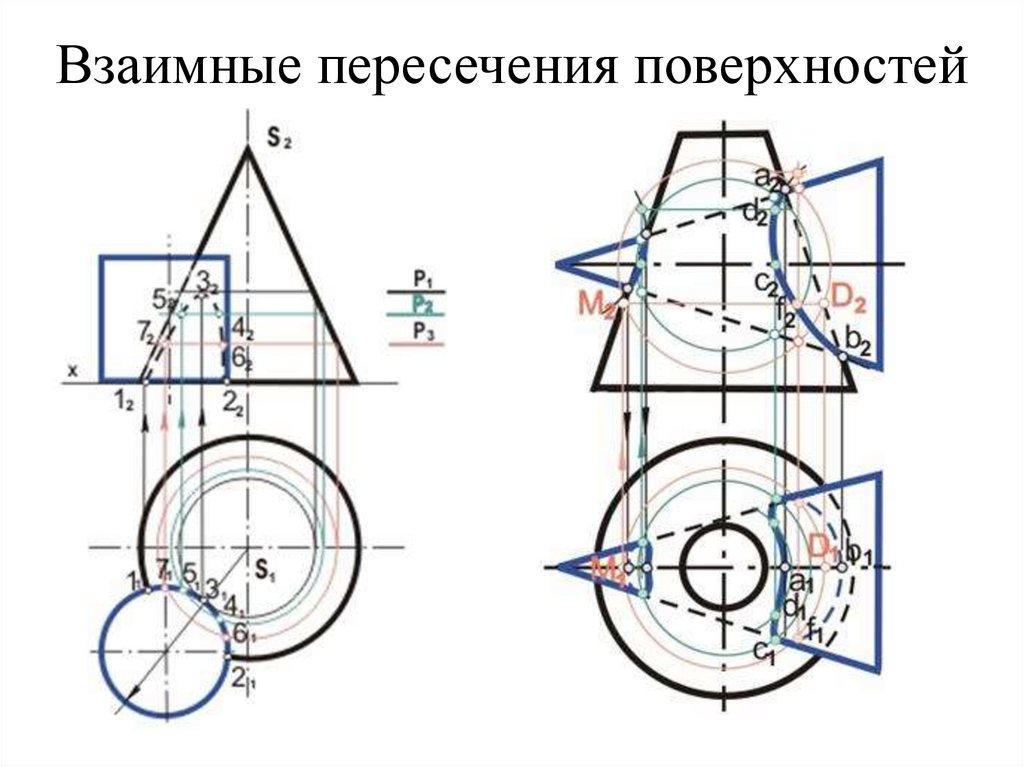
81. Взаимные пересечения поверхностей
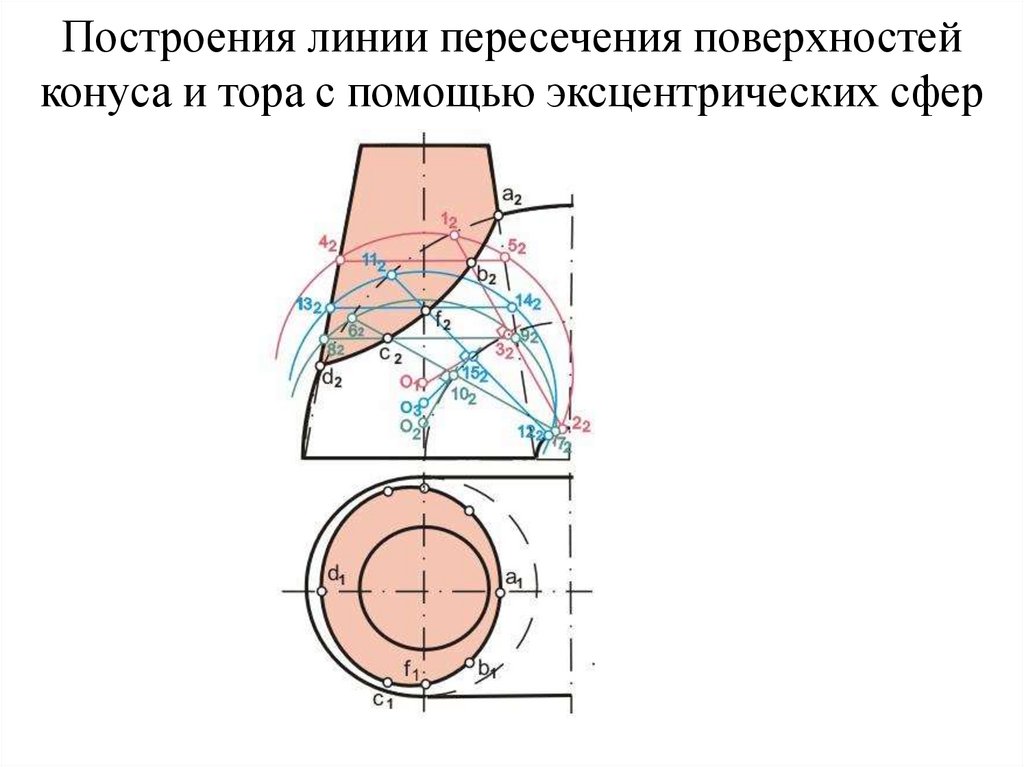
82. Построения линии пересечения поверхностей конуса и тора с помощью эксцентрических сфер
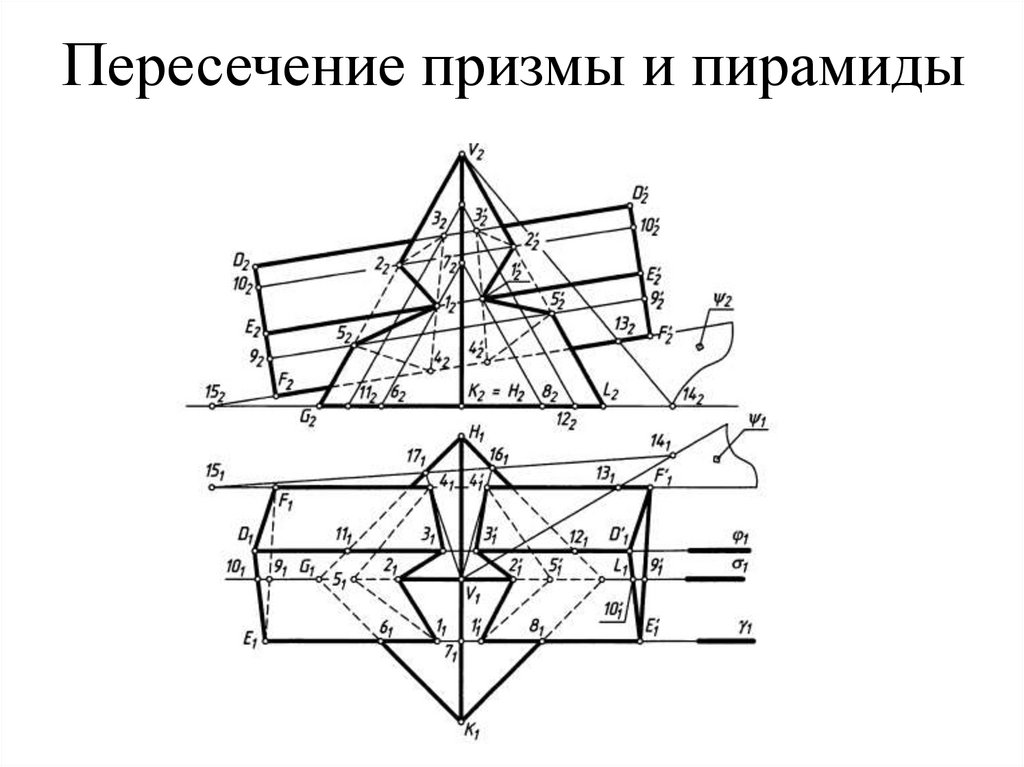
83. Пересечение призмы и пирамиды
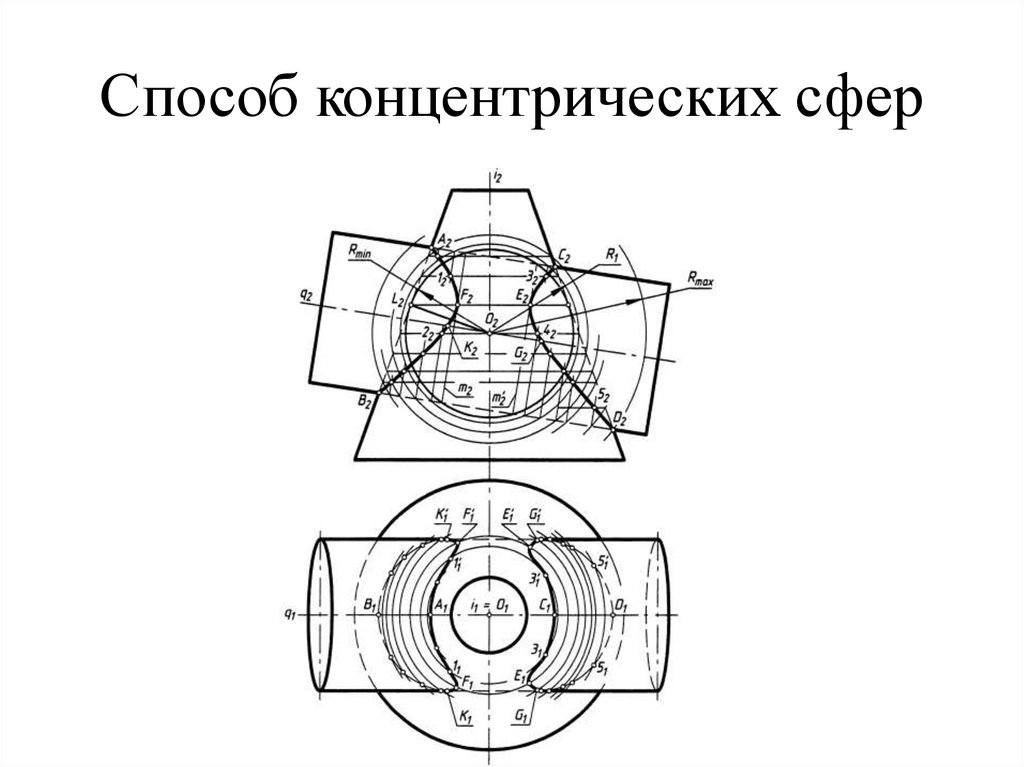
84. Способ концентрических сфер
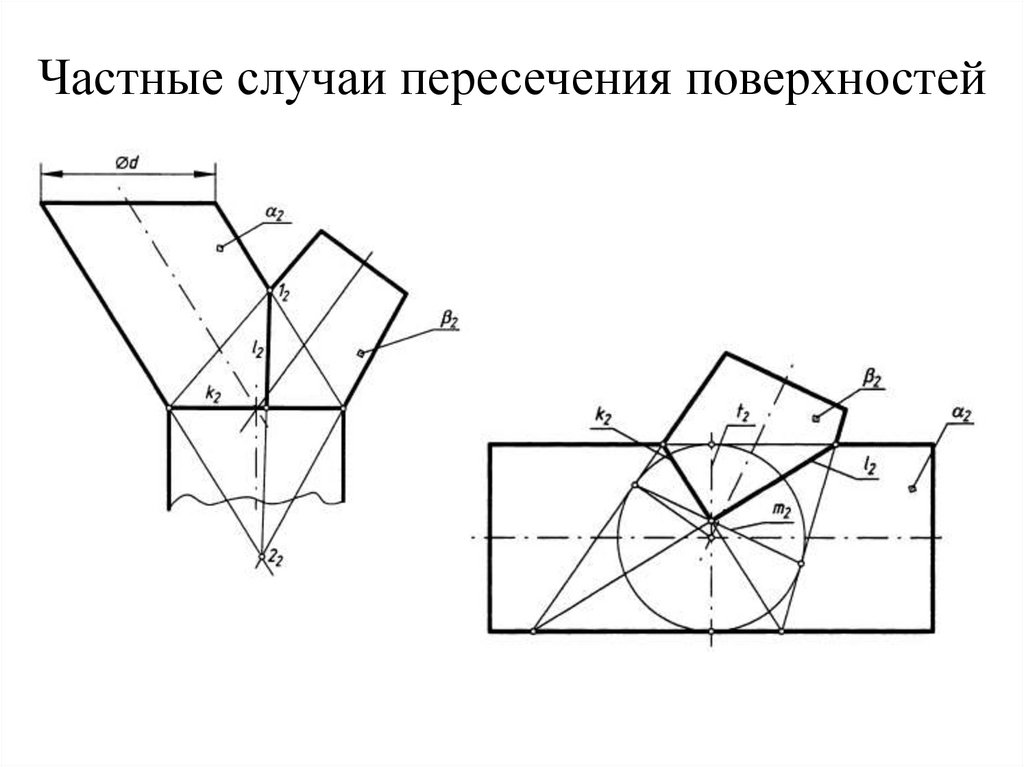
85. Частные случаи пересечения поверхностей
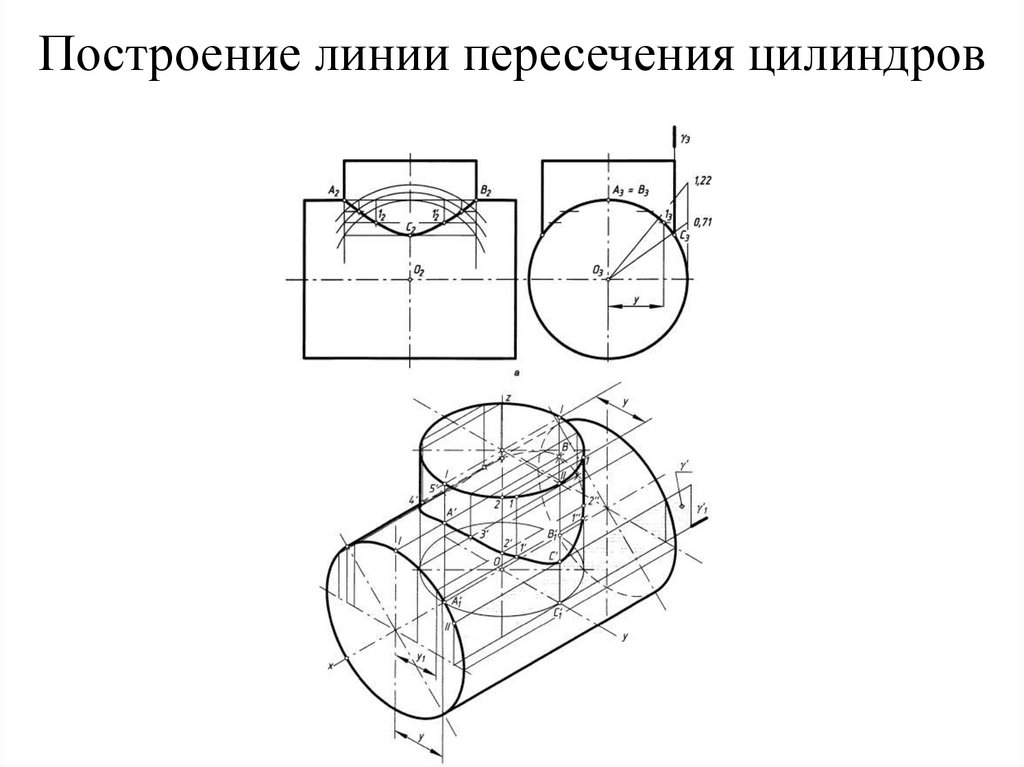
86. Построение линии пересечения цилиндров
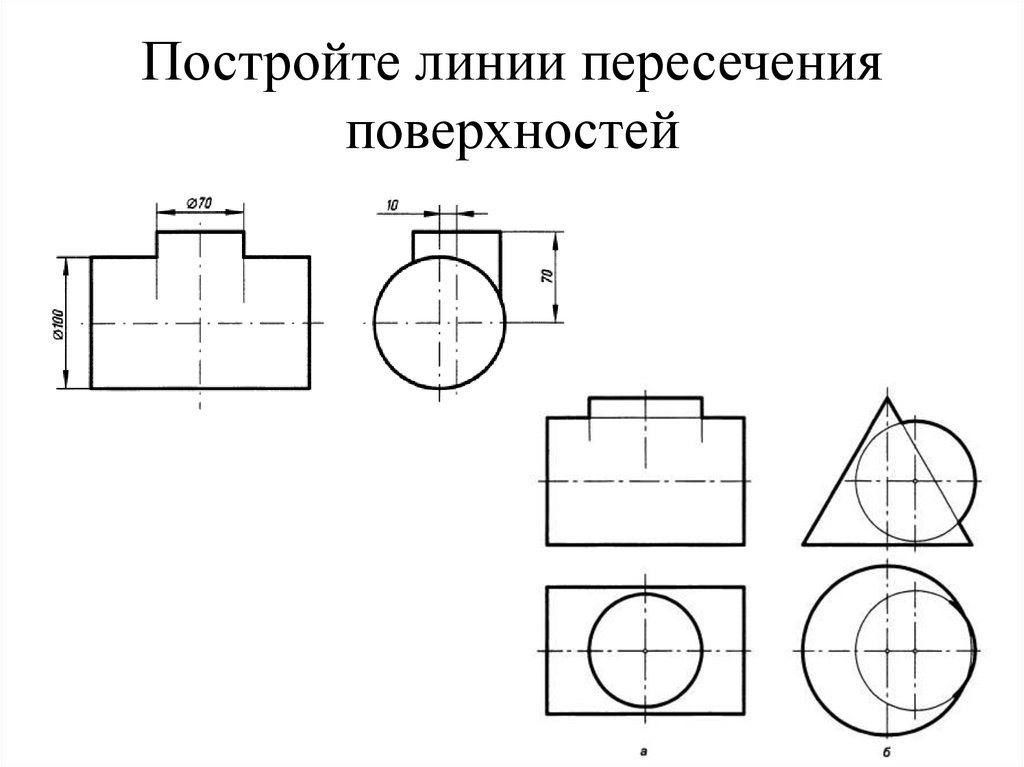
87. Постройте линии пересечения поверхностей
88. Построение разверток
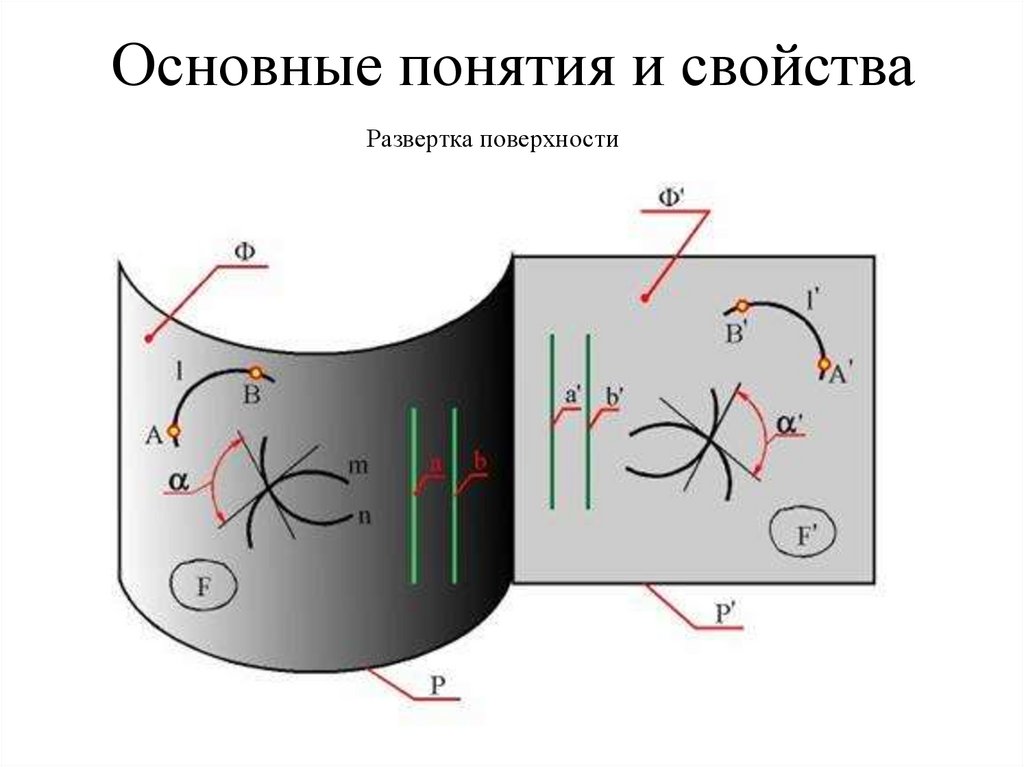
89. Основные понятия и свойства
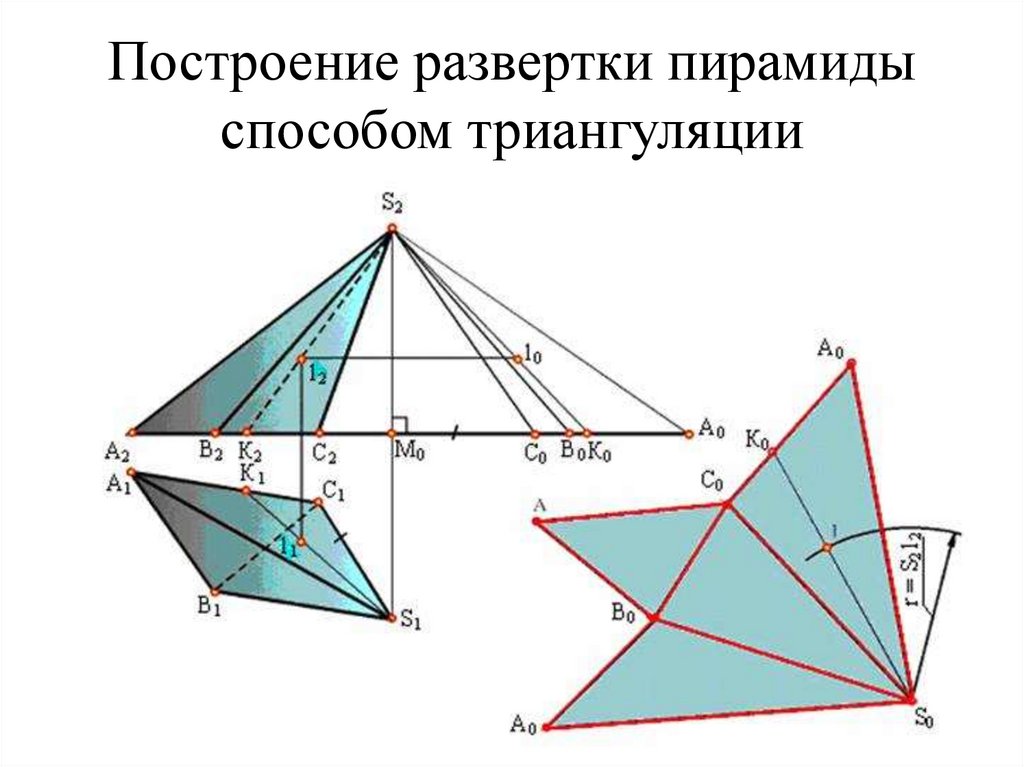
Развертка поверхности90. Построение развертки пирамиды способом триангуляции
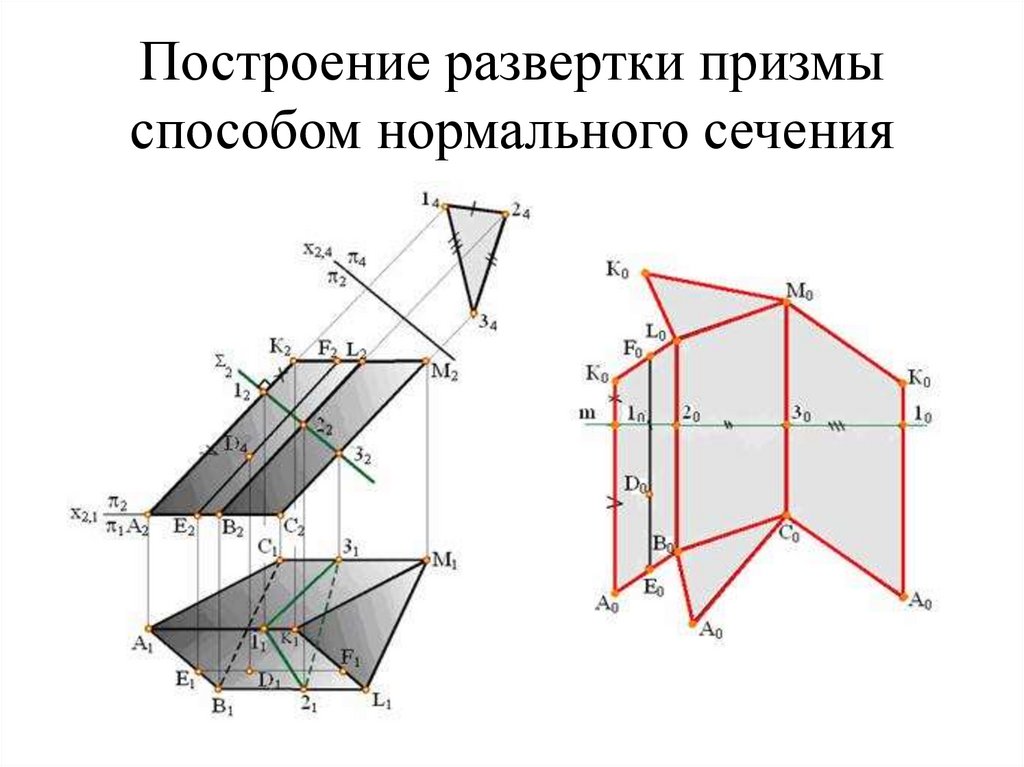
91. Построение развертки призмы способом нормального сечения
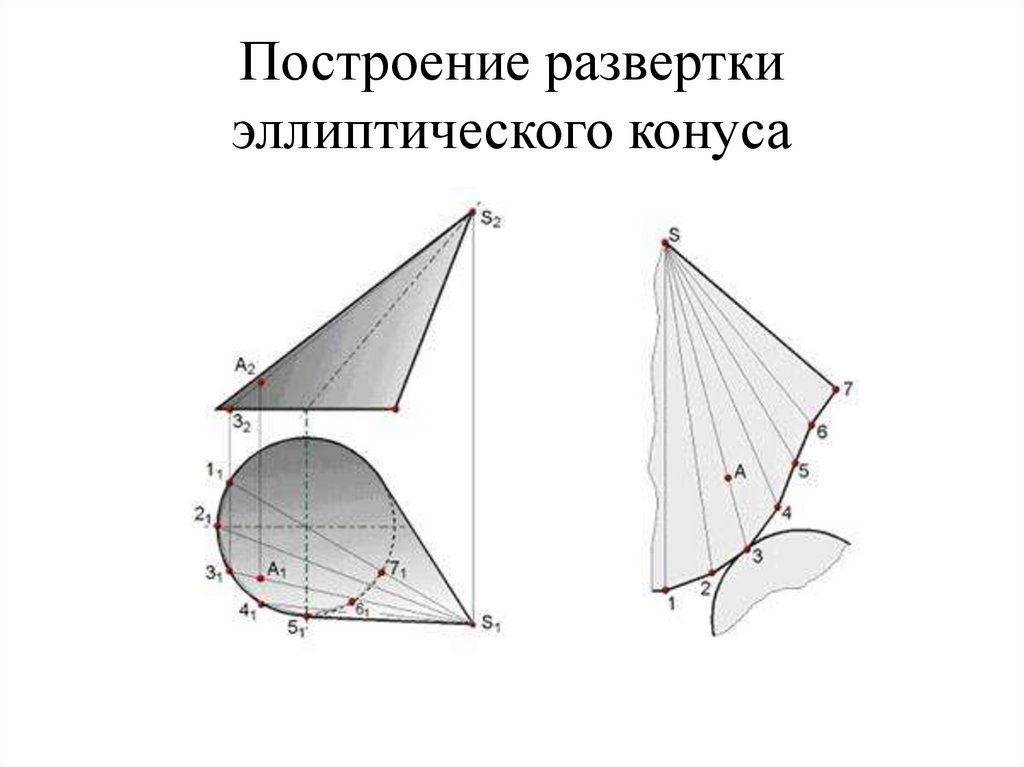
92. Построение развертки эллиптического конуса
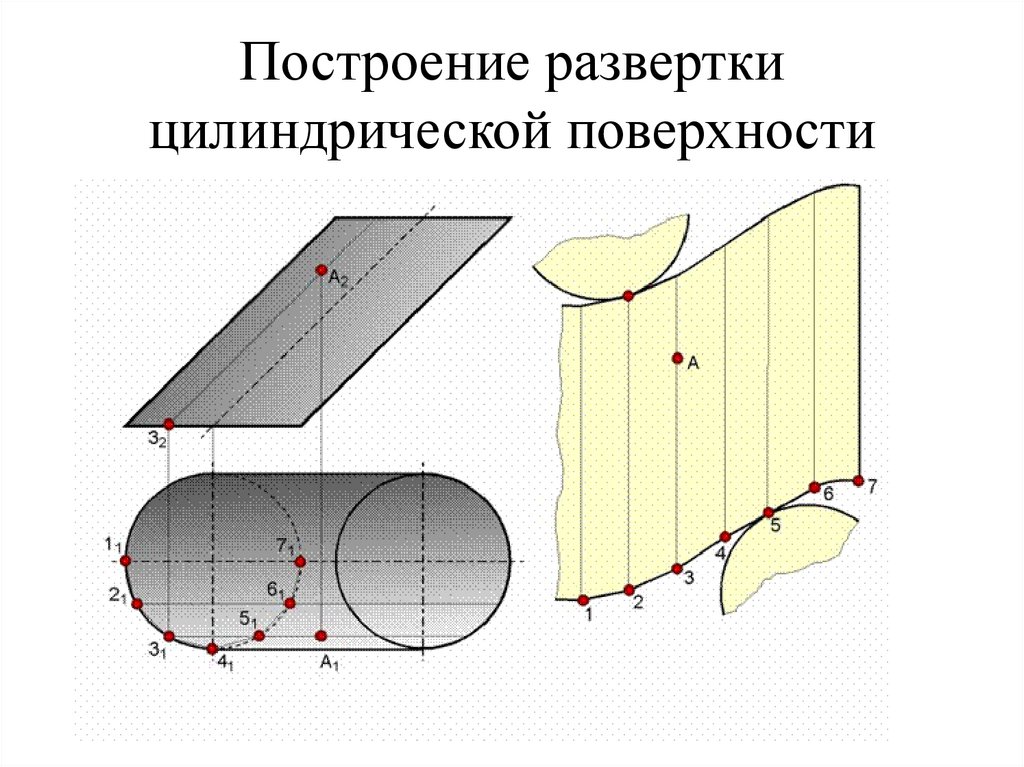
93. Построение развертки цилиндрической поверхности
94. Построение развертки сферы
95. Развертка поверхностей способом конусов
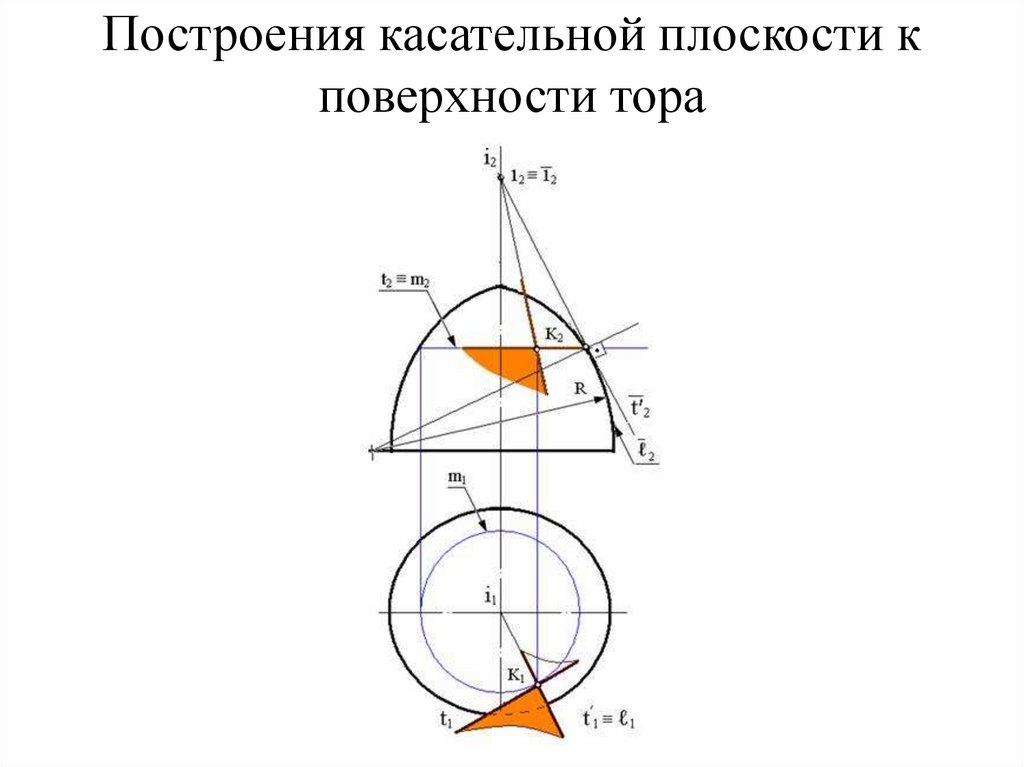
96. Плоскости, касательные к поверхности
97. Касательные к поверхности α
а − прямая t , б − плоскость98. Изображение касательных линий
Изображение касательных линийа − прямая, б − кривая
99. Построения касательной плоскости к поверхности тора
100. Аксонометрические проекции
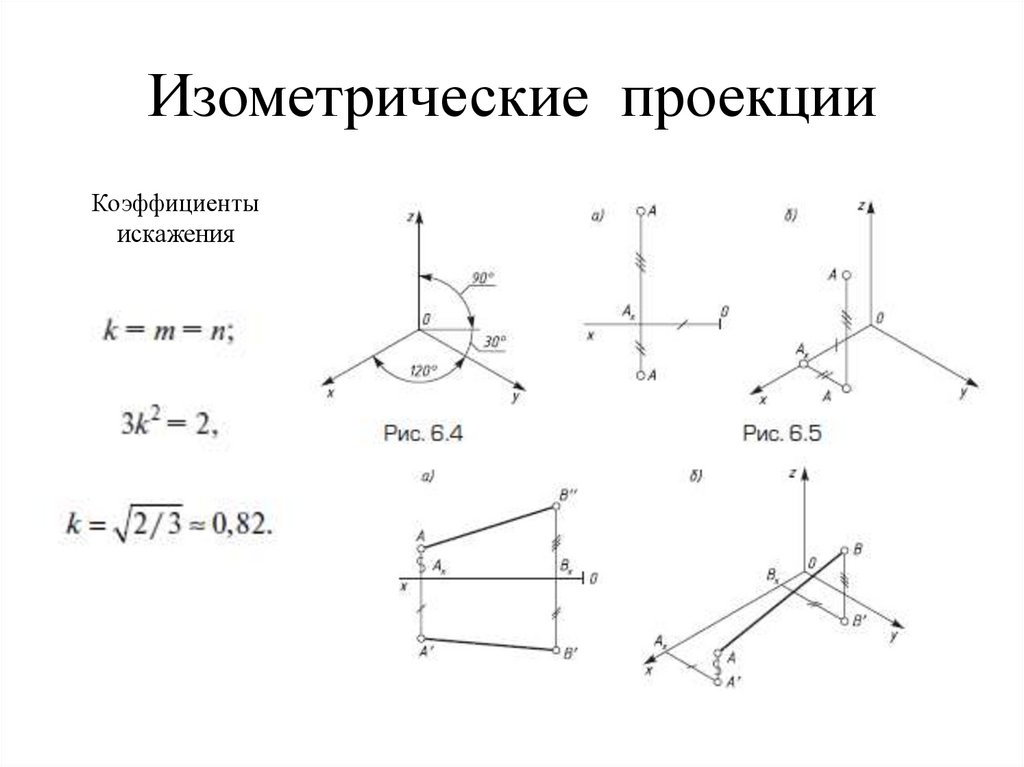
101. Изометрические проекции
Коэффициентыискажения
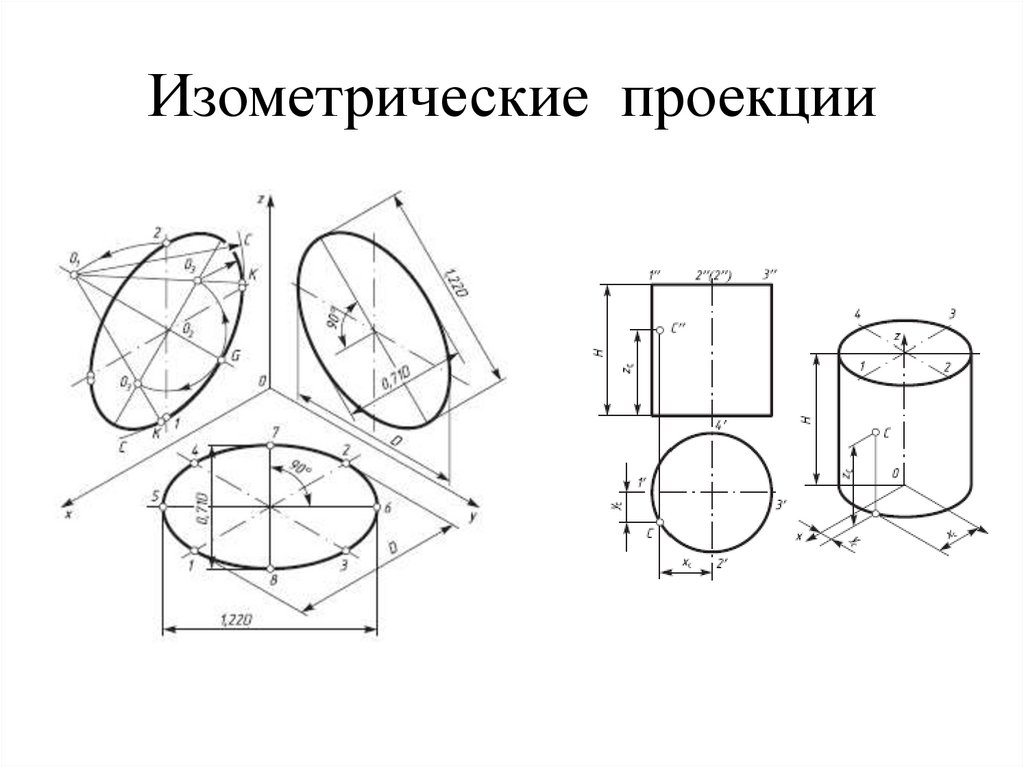
102. Изометрические проекции
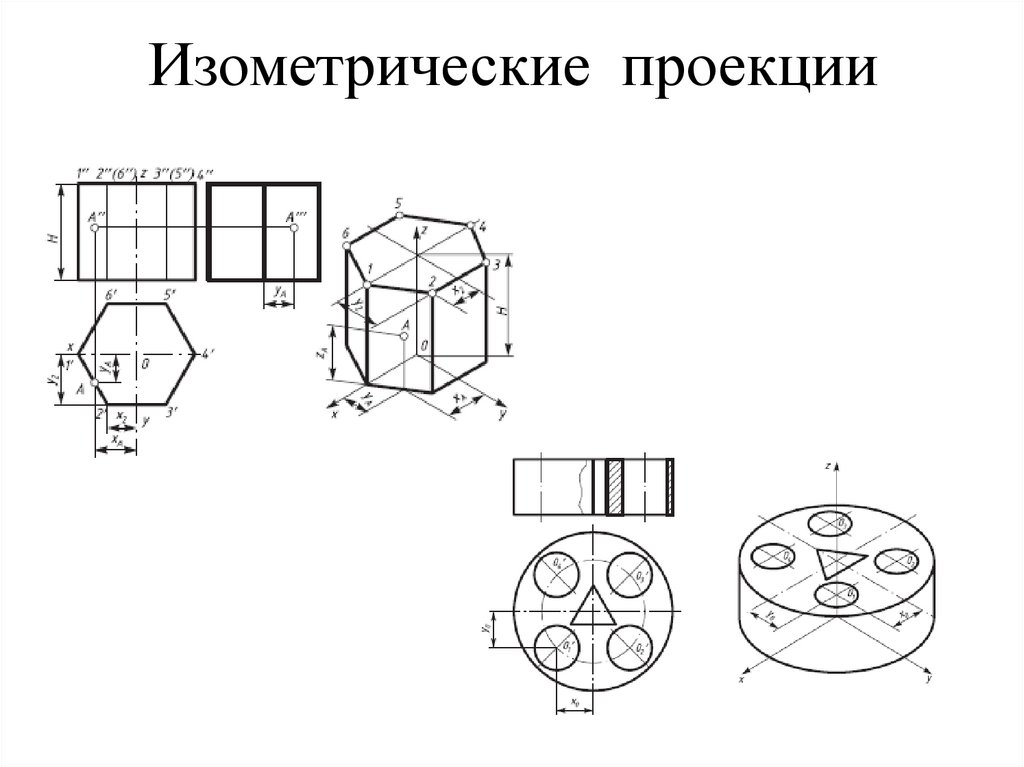
103. Изометрические проекции
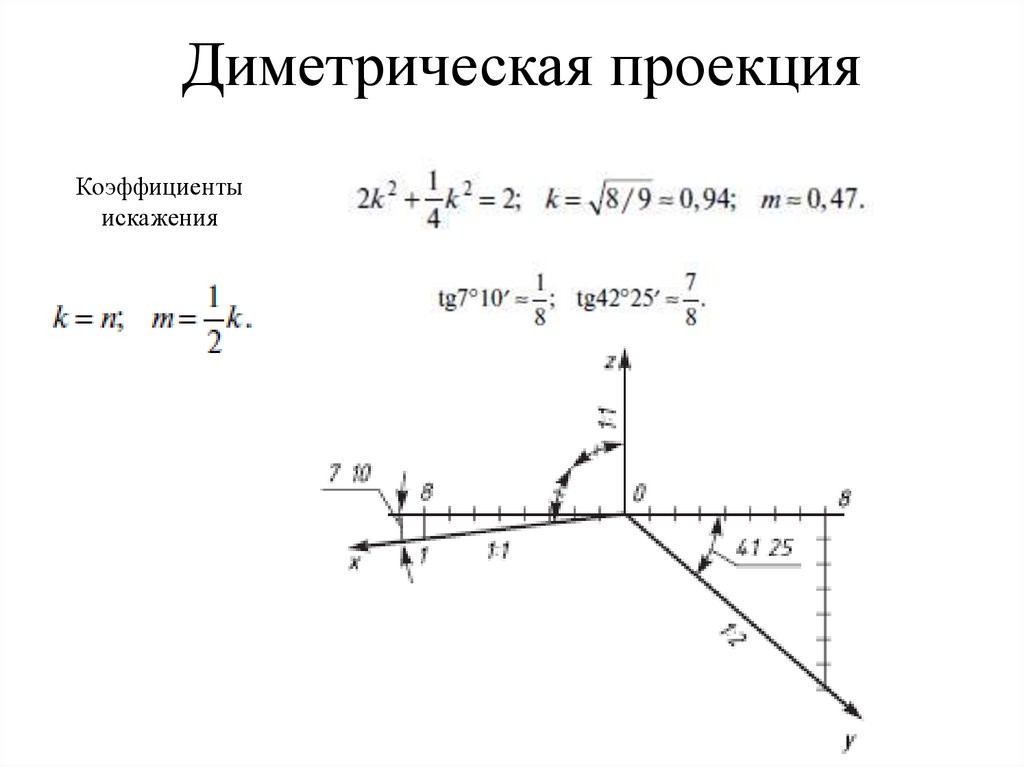
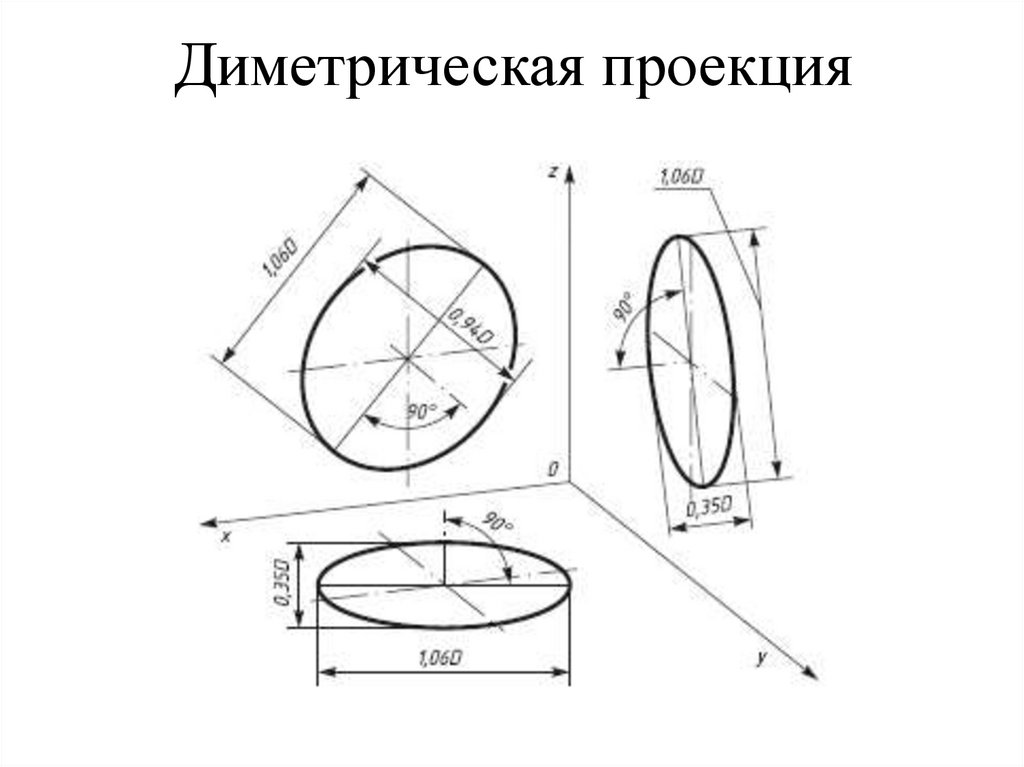
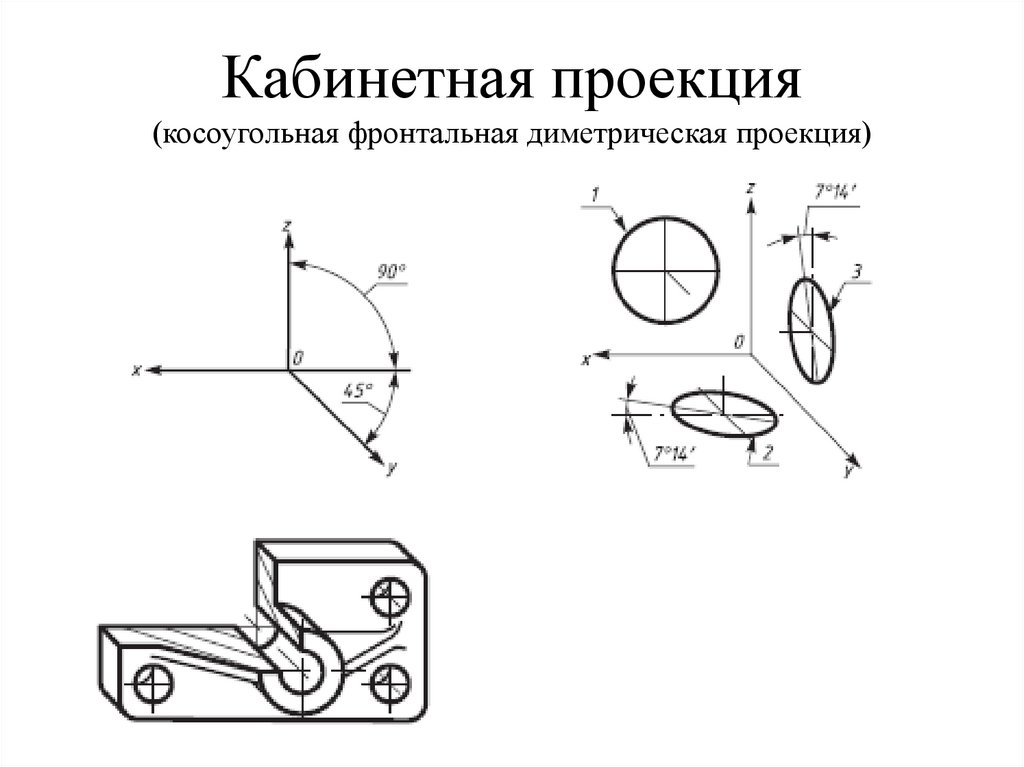
104. Диметрическая проекция
Коэффициентыискажения



























 drafting
drafting








