Расчёт частотных и импульсных характеристик БИХ-цепей 2-го порядка

1. Лекция по учебной дисциплине «Цифровая схемотехника и обработка сигналов» (Д-0205-1) Тема № 9: «Описание ЛДС в частотной

ВОЕННАЯ АКАДЕМИЯ СВЯЗИ
Лекция
по учебной дисциплине «Цифровая схемотехника и обработка
сигналов»
(Д-0205-1)
Тема № 9: «Описание ЛДС в частотной области»
Занятие № 32: «Расчёт частотных и импульсных
характеристик БИХ-цепей 2-го порядка»
Руководитель занятия – доцент кафедры, к.т.н., доцент,
полковник Филимонов Василий Александрович
г. Санкт-Петербург
2018

2. Учебные цели:

2
Учебные цели:
Сформировать у курсантов навыки
самостоятельного расчёта и анализа
передаточных функций, частотных и
импульсных характеристик БИХ- цепей.
2.
Подготовить
курсантов
к
лабораторной работе
1.
Кафедра №2, ВАС

3. Учебные вопросы:

3
Учебные вопросы:
1. Расчёт ИХ БИХ-цепей 2-го
порядка.
2. Расчёт
частотных
характеристик БИХ-цепей 2-го
порядка.
Кафедра №2, ВАС

4. Литература:

4
Литература:
1. Цифровая обработка сигналов. Краткий курс / Д.А.
Улахович. – СПб.: ВАС, 2017 – 408 с. (стр. 44 – 49,
74 – 76, 88 – 105).
2. Цифровая обработка сигналов./ Авторы: Д. А.
Улахович, А. А. Давыдов, О. И. Кривошей/
Электронное учеб. пособие /– СПб.: ВАС, 2015.
3. Лабораторный практикум по курсу «Цифровая
обработка сигналов»/ Авторы: Д. А. Улахович, В. А.
Филимонов/ – СПб, ВАС, 2015 (стр. 13-20).
Кафедра №2, ВАС

5. Первый учебный вопрос

5
Первый учебный вопрос
Расчёт ИХ БИХ-цепей 2-го
порядка
Кафедра №2, ВАС

6. Первый учебный вопрос

6
Задача 1. Вычислить 10 отчетов импульсной характеристики по
заданному разностному уравнению:
y (n) b0 x(n) b1 x(n 1) b2 x(n 2) a1 y (n 1) a2 y (n 2) ,
которому соответствует передаточная функция:
b0 b1 z 1 b2 z 2
H ( z)
1 a1 z 1 a2 z 2
Результаты занести в таблицу:
n
0
1
2
3
4
5
6
7
8
9
h(n)
y(n)
Построить график импульсной характеристики.
Кафедра №2, ВАС

7. Второй учебный вопрос

7
Второй учебный вопрос
Расчёт частотных
характеристик БИХ-цепей
2-го порядка
Кафедра №2, ВАС

8.

8
Второй учебный вопрос
Задача 2. Получить выражения для расчета нулей и полюсов ПФ, АЧХ,
ФЧХ и формулы экспресс-анализа для вычисления АЧХ БИХ-цепи по
заданному разностному уравнению:
y (n) b0 x(n) b1 x(n 1) b2 x(n 2) a1 y (n 1) a2 y (n 2) .
Решение.
Передаточная функция:
Y ( z ) b0 b1 z 1 b2 z 2
;
H ( z)
X ( z ) 1 a1z 1 a2 z 2
Нули 1, 2 и полюсы 1, 2 ПФ определяются из решения уравнений:
b0 z 2 b1 z1 b2 0 и z 2 a1 z1 a2 0 ,
получаемых приравниванием к нулю числителя и знаменателя
передаточной функции после их умножения на z2. Результатом решения
уравнений являются:
а) нули:
1,2 z01,2
b1 b12 4b0 b2
2b0
b12 4b0b2
b1
.
2b0
2b0
Кафедра №2, ВАС

9.

9
Второй учебный вопрос
Если дискриминант неотрицательный, то ПФ содержит только
вещественные нули; в противном случае ПФ обладает двумя комплексносопряжёнными нулями:
1 z01 r0 e j и 2 z02 r0 e j ; 2 1 ,
0
0
где r0 – радиус нуля; ω0 – частота (угол).
Тогда
1,2 z01,2
r0 0 0 ;
2
2
b12 4b0 b2
b1
0 j 0 r0 e j 0
2b0
2b0
;
4b0 b2 b12
0
ˆ 0 arctg
arctg
0
b1
[рад];
Кафедра №2, ВАС

10.

10
Второй учебный вопрос
б) полюсы:
a1 a12 4a2
a1
a12
12 z 12
a2 .
2
2
4
Если дискриминант неотрицательный, то имеем вещественные
полюсы; в противном случае ПФ обладает двумя комплексно-сопряжёнными
полюсами:
1 z 1 r e jω̂ и
*
2 z 2 r e jω̂* ,
где r – радиус полюса; ̂* – частота полюса.
Отсюда получаем:
a
r a2 ; ˆ arccos 1 .
2r
*
Эти соотношения позволяют записать формулы для коэффициентов
знаменателя ПФ:
ˆ ),
a2 r 2 ; a1 2r cos(
откуда следует, что при комплексных полюсах коэффициент а2 > 0.
Кафедра №2, ВАС

11.

Второй учебный вопрос
11
j
j
-1
̂0
r0
r0
r*
̂*
ˆ*
ˆ0
r*
1
j
Рисунок. 1. Пример расположения комплексно-сопряжённых
полюсов и нулей
ˆ
Из передаточной функции при z e j нетрудно получить выражения
для АЧХ и ФЧХ:
ˆ)
A(
ˆ ) arctg
(
ˆ b2 cos 2
ˆ ) 2 (b1 sin
ˆ b2 sin 2
ˆ )2
(b0 b1 cos
ˆ a2 cos 2
ˆ )2 (a1 sin a2 sin 2
ˆ )2 ;
(1 a1 cos
ˆ a2 sin 2
ˆ
ˆ b2 sin 2
ˆ
a1 sin
b1 sin
arctg
ˆ a2 cos 2
ˆ
ˆ b2 cos 2
ˆ .
1 a1 cos
b0 b1 cos
Кафедра №2, ВАС

12.

12
Второй учебный вопрос
Из этих формул легко получаются удобные выражения (формулы
экспресс-анализа) для вычисления АЧХ и ФЧХ на трёх частотах:
ˆ 0 , z 1,
1.
A(0) H (1)
b0 b1 b2
; (0) 0 .
1 a1 a2
ˆ /2, z j,
2.
(b0 b2 ) 2 b12
A( / 2) H ( j )
(1 a2 ) 2 a12 ;
( / 2) arctg
a1
b
arctg 1 .
1 a1
b0 b2
3. ̂ , z 1 ,
A( ) H ( 1)
b0 b1 b2
( ) 0 .
1 a1 a2 ;
Кафедра №2, ВАС

13.

13
Второй учебный вопрос
Важно: для оценки вида АЧХ цепи 2-го порядка необходимо
произвести также вычисления A( ˆ ) на частотах нуля ˆ ˆ 0 и полюса ˆ ˆ *
передаточной функции:
4. ˆ ˆ * ,
(b0 b1 cos ˆ * b2 cos 2 ˆ * ) 2 (b1 sin ˆ * b2 sin 2 ˆ * ) 2
A( ˆ * )
(1 a1 cos ˆ * a2 cos 2 ˆ * ) 2 (a1 sin ˆ * a2 sin 2 ˆ * ) 2 .
5. ˆ ˆ 0 ,
(b0 b1 cos ˆ 0 b2 cos 2 ˆ 0 )2 (b1 sin ˆ 0 b2 sin 2 ˆ 0 ) 2
A( ˆ 0 )
(1 a1 cos ˆ 0 a2 cos 2 ˆ 0 ) 2 (a1 sin ˆ 0 a2 sin 2 ˆ 0 ) 2 .
Кафедра №2, ВАС

14.

14
Второй учебный вопрос
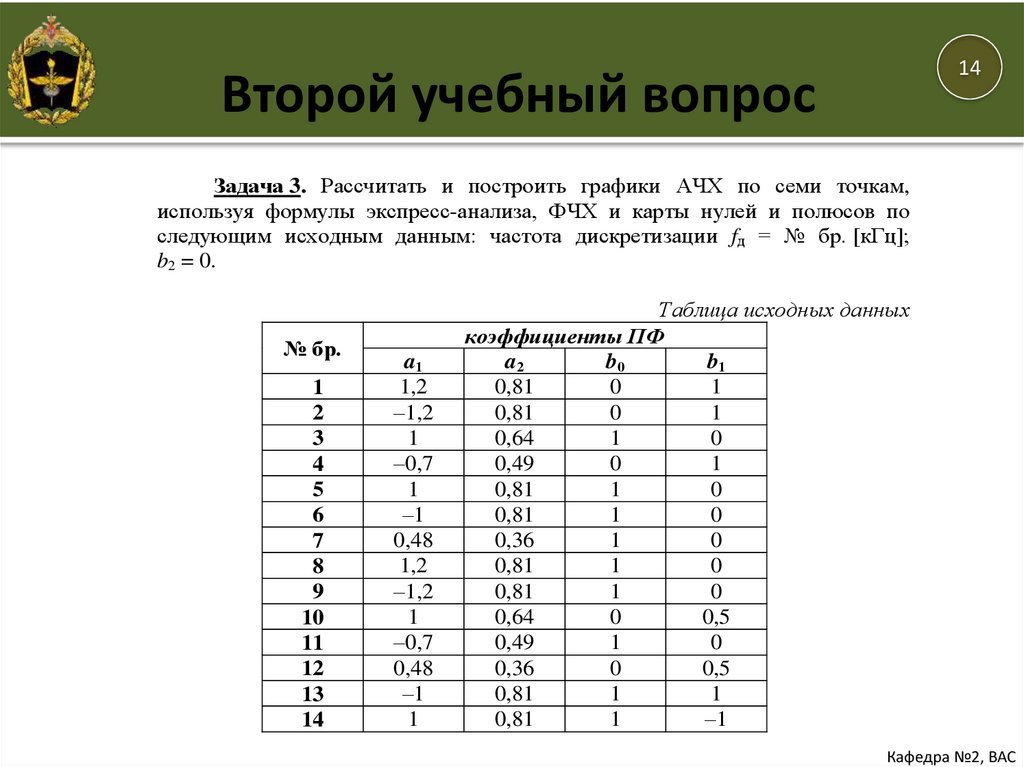
Задача 3. Рассчитать и построить графики АЧХ по семи точкам,
используя формулы экспресс-анализа, ФЧХ и карты нулей и полюсов по
следующим исходным данным: частота дискретизации fд = № бр. [кГц];
b2 = 0.
№ бр.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
a1
1,2
–1,2
1
–0,7
1
–1
0,48
1,2
–1,2
1
–0,7
0,48
–1
1
Таблица исходных данных
коэффициенты ПФ
a2
b0
b1
0,81
0
1
0,81
0
1
0,64
1
0
0,49
0
1
0,81
1
0
0,81
1
0
0,36
1
0
0,81
1
0
0,81
1
0
0,64
0
0,5
0,49
1
0
0,36
0
0,5
0,81
1
1
0,81
1
–1
Кафедра №2, ВАС

15.

Второй учебный вопрос
15
Анализ полученных решений:
частотные характеристики являются периодическими функциями
частоты;
нули и полюсы цепей второго порядка могут быть как вещественными
так и комплексно-сопряженными;
изменение знака коэффициента a1 приводит к АЧХ симметричной
относительно ω̂ π ;
коэффициент a1 отвечает за центральную частоту полосы пропускания;
увеличение коэффициента a2 по модулю приводит к более высокой
избирательности АЧХ;
АЧХ цифровой цепи может превышать 1, т. е. цифровые цепи обладают
свойством усиления;
Кафедра №2, ВАС